Základné pojmy
V tejto kapitole sa budeme venovať jednému z najdôležitejších prepojení medzi matematickou logikou a programovaním – Curry–Howardovej korešpondencii. Ide o prekvapivo jednoduchú, no mimoriadne hlbokú myšlienku:
Logické výroky sú typy a dôkazy sú programy.
V prvej časti budú predstavené základné pojmy intuicionistickej logiky, prirodzenej dedukcie a spôsob, akým sa dôkazy konštruujú v dedukčných systémoch. Následne uvidíme, že rovnaké štruktúry, ktoré sa používajú na tvorbu logických dôkazov, môžu byť interpretované ako typy a programy v jednoducho typovanom λ-kalkule.
Táto kapitola bude rozdelená do troch hlavných blokov:
-
Intuicionistická logika a prirodzená dedukcia
– predstavíme syntax, sémantiku a dedukčný kalkul, čo bude tvoriť “logickú” stranu korešpondencie. -
Curry–Howardova korešpondencia
– ukážeme, ako logické spojky zodpovedajú typovým konštruktorom, ako dôkazy zodpovedajú termom, a ako odvodzovacie pravidlá dedukčného kalkulu zodpovedajú typovacím pravidlám. -
Hľadanie termu typu (type inhabitation)
– predstavíme spôsob generovania dôkazov/programov z logických špecifikácií a príklady, ktoré ilustrujú, ako sa konštruktívne dôkazy premietajú do programov.
Cieľom tejto prednášky je nielen vysvetliť formálnu korešpondenciu medzi dvoma odlišnými svetmi — logikou a programovaním — ale ukázať aj to, prečo ide o základný koncept v návrhu typových systémov, verifikácii programov a automatických či interaktívnych dokazovacích systémoch.
Curry–Howardova korešpondencia
Curry–Howardova korešpondencia (niekedy nazývaná aj Curry–Howardov izomorfizmus) je základný koncept v informatike a matematickej logike, ktorý opisuje hlbokú súvislosť medzi logickými systémami a teóriami typov. Definuje, že výroky v logike zodpovedajú typom v teórii typov, a dôkazy týchto výrokov zodpovedajú programom, ktoré majú daný typ.
Inými slovami:
| Logika | Teória typov / Programovanie |
|---|---|
| výrok (formula) | typ |
| dôkaz | term (program) |
| normalizácia dôkazu | redukcia termu (beh programu) |
Takýto pohľad umožňuje interpretovať programy ako konštruktívne dôkazy a typy ako výroky, ktoré tieto programy dokazujú. Správne typovaný program vo funkcionálnom jazyku je teda konštruktívnym dôkazom výroku korešpondujúceho s jeho typom.
Vo všeobecnosti ide o korešpondenciu medzi konkrétnou intuicionistickou logikou a vhodne zvolenou teóriou typov. V našom prístupe sa budeme zaoberať korešpondenciou medzi intuicionistickou výrokovou logikou a jednoducho typovaným λ-kalkulom.
Typová kontrola, Odvodenie typu, Nájdenie termu typu
Pri práci s teóriou typov (a teda aj v rámci Curry–Howardovej korešpondencie) rozlišujeme tri kľúčové problémy:
-
Type checking (kontrola typov)
Má daný term t typ T?
Formálne: overujeme, či platíΓ ⊢ t : T. -
Type inference (odvodenie typov)
Aký typ má term t?
Formálne: hľadáme typ T taký, žeΓ ⊢ t : ?. -
Type inhabitation (hľadanie termu)
Existuje term t taký, že má typ T?
Inými slovami: má typ T (logický výrok) term (dôkaz)?
Formálne: hľadáme term t taký, žeΓ ⊢ ? : T.
Doteraz sme sa venovali predovšetkým prvým dvom problémom:
- kontrole typov (type checking),
- a odvodeniu typov (type inference).
V tejto kapitole sa však sústredíme na tretí problém — nájdenie termu typu (type inhabitation).
Ten je v kontexte Curry–Howardovej korešpondencie kľúčový, pretože:
- term typu $T$ zodpovedá dôkazu korešpondujúceho výroku $\varphi$,
- teda hľadať program typu T znamená hľadať konštruktívny dôkaz korešpondujúceho výroku $\varphi$.
Poznámka
Hľadanie termu daného typu je základom mnohých:
- interaktívnych dokazovacích systémov (ako je Rocq, Agda, Isabelle/HOL, ...),
- automatických dokazovacích systémov (Vampire, E Theorem Prover, ...),
- generátorov programov zo špecifikácií a mnoho ďalších.
Intuicionistická logika
Intuicionistická logika (nazývaná aj konštruktívna logika), môže byť stručne opísaná ako klasická logika bez:
- Aristotelovho pravidla vylúčenia tretieho: $$φ \lor \neg φ,$$
- zákonu dvojitej negácie $$¬¬φ ≡ φ.$$
Intuicionizmus je filozofický a matematický prístup, ktorý sa zameriava na konštruktívny postup v matematike a tvrdí, že matematické objekty musia byť skutočne skonštruované, nie iba abstraktne definované. Intuicionisti odmietajú princípy klasického deduktívneho dôkazu, ktorý sa vychádza zo zákona vylúčenia tretieho, ktorý hovorí, že ak existuje nejaký výrok, tak je buď pravdivý alebo nepravdivý.
Konštruktívny dôkaz je druh matematického dôkazu, ktorý dokazuje existenciu matematického objektu tým, že ukáže spôsob, ako tento objekt skutočne skonštruovať. Tento prístup k matematickému dôkazu sa líši od tradičného dôkazu, ktorý iba dokazuje existenciu objektu bez skutočnej konštrukcie.
Formálny dôkaz je konečná postupnosť viet (v prípade logiky sú to formuly), z ktorých každá je axiómou, predpokladom alebo je odvodená z predchádzajúcich viet pomocou dedukčného pravidla. Od idiomatického dôkazu pomocou prirodzeného jazyka sa formálny dôkaz líši tým, že je rigorózny, jednoznačný a mechanicky overiteľný.
Jazyk intuicionistickej logiky
Jazyk intuicionistickej logiky je rovnaký ako jazyk klasickej logiky, avšak logické spojky intuicionistickej logiky nie sú definované rovnakým spôsobom ako v klasickej logike.
Syntax výrokovej intuicionistickej logiky v BNF
Je definovaná produkčným pravidlom v Backus-Naurovej forme, prostredníctvom ktorého je možné konštruovať všetky prípustné tvary formúl: $$ \varphi ::= p \mid \top \mid \bot \mid \neg\varphi \mid \varphi \land \psi \mid \varphi \lor \psi \mid \varphi \Rightarrow \psi, $$ kde p je množina atomických výrokov. Platí rovnaká priorita a asociativita operátorov ako v klasickej výrokovej logike.
Priorita a asociativita
| Operátor | Názov | Priorita | Asociativita |
|---|---|---|---|
| ¬ | Negácia | 1 | – (unárny prefix) |
| ∧ | Konjunkcia | 2 | neasociatívna |
| ∨ | Disjunkcia | 3 | neasociatívna |
| ⇒ | Implikácia | 4 | pravostranná |
Poznámka
Pravá asociativita implikácie znamená: $$ \varphi \Rightarrow \psi \Rightarrow \theta \equiv \varphi \Rightarrow ( \psi \Rightarrow \theta) $$ Neasociatívnosť konjunkcie a disjunkcie znamená:
$$ \begin{array} ~ \varphi \wedge \psi \wedge \theta \equiv \varphi \wedge ( \psi \wedge \theta) \equiv (\varphi \wedge \psi) \wedge \theta \\ ~ \varphi \vee \psi \vee \theta \equiv \varphi \vee ( \psi \vee \theta) \equiv (\varphi \vee \psi) \vee \theta \end{array} $$
Vlastnosti syntaxe intuicionistickej logiky
Žiadnu zo základných logických spojok nemožno vyjadriť pomocou ostatných a preto je nutná prítomnosť všetkých štyroch.
- Negácia ($\neg$) je definovaná ako implikácia do absurda $\neg φ ≡ φ ⇒ ⊥$.
- Vérum ($\top$) je definované ako $\bot \Rightarrow \bot$.
- Ekvivalencia ($\Leftrightarrow$) nie je považovaná za základnú spojku, ale rovnako ako v klasickej výrokovej logike za konjunkciu dvoch implikácií.
Mnoho tautológii klasickej logiky neplatí v intuicionistickej logike. To zahŕňa nielen zákon vylúčenia tretieho či eliminácie dvojitej negácie, ale tiež Peirceové pravidlo $(((φ \Rightarrow ψ) \Rightarrow φ) \Rightarrow φ)$. Pretože nie všetky tautológie klasickej logiky sú teorémy intuicionistickej logiky, ale všetky teorémy intuicionistickej logiky platia v klasickej logike, je možné sa na intuicionistickú logiku pozerať ako na oslabenie klasickej logiky, avšak s mnohými užitočnými vlastnosťami.
Poznámka
Fakt, že princíp vylúčenia tretieho nie je intuicionisticky korektný, by ale nemal byť chápaný tak, že v intuicionistickej logike sú možné viac ako dve logické hodnoty. Každý predpoklad tvaru $\neg (φ \vee \neg φ)$ vedie v intuicionistickej logike k sporu. Z toho, že nejaké tvrdenie, v našom prípade $φ \vee \neg φ$, nie je intuicionisticky logicky platné, nemožno usudzovať, že za nejakých okolností by mohol platiť jeho opak.
Sémantika intuicionistickej logiky
Keďže intuicionistická logika neakceptuje niektoré klasické zákony (napríklad zákon vylúčenia tretieho, či princíp dôkazu sporom), jej sémantika nie je viazaná výhradne na klasické pravdivostné hodnoty. Umožňuje rôzne interpretácie, ktoré zachytávajú jej konštruktívny charakter.
Definícia: Tautologický dôsledok
Nech $\Gamma$ je množina formúl (predpokladov) a $\varphi$ je formula.
Potom zápis:
$$ \Gamma \models \varphi $$
znamená, že φ je tautologickým dôsledkom množiny predpokladov Γ, t.j. že $\varphi$ platí vo všetkých modeloch, v ktorých platia všetky formuly z $\Gamma$.
Poznámka
Pre účely demonštrácie Curry–Howardovej korešpondencie nie je nutné podrobne rozpracovať celú sémantiku intuicionistickej logiky. Preto predstavíme len jednu neformálnu, no postačujúcu interpretáciu — Brouwer–Heyting–Kolmogorovu (BHK) interpretáciu, ktorá priamo vystihuje konštruktívny význam logických spojok.
Brouwer–Heyting–Kolmogorova (BHK) interpretácia
BHK interpretácia poskytuje neformálnu konštruktívnu sémantiku. Namiesto klasických pravdivostných hodnôt opisuje význam logických spojok pomocou konštruktívnych dôkazov.
Intuitívne:
Význam formuly je daný tým, čo znamená mať jej konštruktívny dôkaz.
BHK podmienky:
-
Konjunkcia (
φ ∧ ψ)
Konštruktívny dôkaz pozostáva z dôkazuφa dôkazuψ. -
Disjunkcia (
φ ∨ ψ)
Konštruktívny dôkaz pozostáva buď z dôkazuφ, alebo dôkazuψ, spolu s informáciou, ktorá vetva bola zvolená. -
Implikácia (
φ ⇒ ψ)
Dôkaz je funkcia, ktorá každý dôkazφprevedie na dôkazψ. -
Negácia (
¬φ)
Definovaná akoφ ⇒ ⊥. Dôkaz je konštrukcia, ktorá každý dôkazφprevedie na absurdum⊥. -
Absurdum (
⊥)
Nemá žiadny konštruktívny dôkaz. -
Vérum (
⊤)
Má triviálny konštruktívny dôkaz.
Intuitívna interpretácia v štýle „programovanie ako dôkaz“
Formuly môžeme predstaviť ako úlohy/problémy, a dôkazy ako metódy/programy, ktoré ich riešia:
φ, ψ, θ, …→ úlohy/problémya, b, c, …→ dôkazy/metódy/programy
Interpretácia základných logických spojok:
-
Konjunkcia
Dôkazφ ∧ ψje dvojica⟨a, b⟩, kdeariešiφabriešiψ. -
Disjunkcia
Dôkazφ ∨ ψje označený variant:⟨a, b⟩.1– dôkazφ(ľavá vetva)⟨a, b⟩.2– dôkazψ(pravá vetva)
-
Implikácia
Dôkazφ ⇒ ψje funkciaf, ktorá z každého dôkazuaformulyφvytvorí dôkazf(a)formulyψ.
BHK interpretácia tvorí konceptuálny most medzi intuicionistickou logikou a konštruktívnym programovaním. Je priamym predchodcom Curry–Howardovej korešpondencie, kde sa konštruktívne dôkazy korešpondujú s programami a logické formuly s typmi.
Prirodzená dedukcia
Je to dedukčný kalkul (niekedy nazývaný aj dôkazový systém) prostredníctvom ktorého je možné dokazovať pravdivosť formúl. Prirodzenú dedukciu predstavil Gerhard Gentzen. Pre intuicionistickú logiku sa používa systém NJ, pre klasickú logiku existuje systém NK.
Prirodzená dedukcia umožňuje zapisovať dôkazy tak, aby každý krok odvodzoval ďalšie formuly logicky priamo z predpokladov, teda spôsobom „prirodzeným“ pre ľudské uvažovanie.
Prirodzená dedukcia pre intuicionistickú logiku (NJ) sa dá definovať ako dedukčný kalkul klasickej logiky (NK) bez pravidla sporu.
Definícia: Sekvent
V dedukčných kalkuloch logických systémov sa formuly najčastejšie zapisujú v tvare sekventu: $$ \Gamma \vdash \varphi $$ kde:
- $\Gamma$ je kontext - množina predpokladov (premís) v tvare: $\varphi_1, ..., \varphi_n$,
- $\varphi$ je formula (cieľ), ktorú chceme dokázať.
Sekvent teda vyjadruje, že z množiny predpokladov $\Gamma$ možno dokázať formulu $\varphi$ pomocou príslušného dedukčného systému.
Poznámka
Prí zápise sekventu nebudeme používať klasické množinové notácie pre zápis kontextu (množiny predpokladov), ale budeme využívať následujúce praktické konvencie:
- $\varphi, \psi \vdash \theta$ namiesto $\{\varphi, \psi \} \vdash \theta$,
- $\Gamma, \Delta$ namiesto $\Gamma \cup \Delta$,
- $\Gamma, \varphi$ namiesto $\Gamma \cup \{ \varphi \}$,
- $ \vdash \varphi $ namiesto $ \emptyset \vdash \varphi$.
Vlastnosti prirodzenej dedukcie:
Konzistentnosť a úplnosť dedukčného kalkulu (Soundness and Completeness)
- Konzistentnosť voči sémantike logického systému. Ak v dedukčnom kalkule je formula $\varphi$ dokázateľná z množiny predpokladov $Γ$, potom formula $φ$ vyplýva z množiny predpokladov $Γ$ vzhľadom na definovanú sémantiku daného logického systému: $$\text{ak} \quad Γ \vdash φ, \quad \text{potom}~ \quad Γ \models φ.$$
- Úplnosť voči dedukčnému kalkulu logického systému. Ak formula $φ$ vyplýva z množiny predpokladov $Γ$ vzhľadom na definovanú sémantiku daného logického systému, potom v dedukčnom kalkule je formula $\varphi$ dokázateľná z množiny predpokladov $Γ$. $$\text{ak} \quad Γ \models φ, \quad \text{potom}~ \quad Γ \vdash φ.$$
- Dedukčný kalkul je konzistentný a úplný (silná forma vety) ak platí: $$Γ \models φ \quad \text{vtt.}~ \quad Γ \vdash φ.$$
Inými slovami a zjednodušene, ak je formula tautológia vzhľadom na definíciu sémantiky v danom logickom systéme, potom musí byť aj dokázateľná v jeho dedukčnom kalkule a vice versa. To hovorí slabá veta forma vety konzistentnosti a úplnosti dedukčného kalkulu: $$\models φ \quad \text{vtt.}~ \quad \vdash φ.$$
Poznámka
$~$
- Konzistentnosť - každá dokázateľná formula musí byť tautológia.
- Úplnosť - každá tautológia musí byť dokázateľná.
Poznámka
Intuicionistická a klasická logika: každá formula dokázateľná v intuicionistickej logike je dokázateľná aj v klasickej logike, ale naopak to neplatí.
Poznámka
Dedukčné kalkuly sú vytvorené na dokazovanie formúl. Možno ich považovať za "dokazovací stroj", ktorého výsledkom sú dokázateľné formuly. Takýto stroj je definovaný konečnou množinou dedukčných pravidiel. Dedukčné pravidlá opisujú spôsob ako je možné transformovať formuly v rámci systému, pričom axiómy slúžia ako počiatočné body. Proces takejto transformácie je formálny dôkaz, ktorý je možné načrtnúť nasledovne:
Axiómy
↓↓↓
Dedukčné pravidlá aplikované na axiómy
↓↓↓
Dokázateľné formuly
↓↓↓
Dedukčné pravidlá aplikované na dokázateľné formuly
↓↓↓
Nové dokázateľné formuly
↓↓↓
... a pod. ...
Dedukčný kalkul prirodzenej dedukcie
Dedukčný kalkul pozostáva zo sady odvodzovacích (dedukčných) pravidiel, ktoré určujú, ako možno odvodiť nové formuly zo zadaných predpokladov.
Každé odvodzovacie pravidlo má tvar:
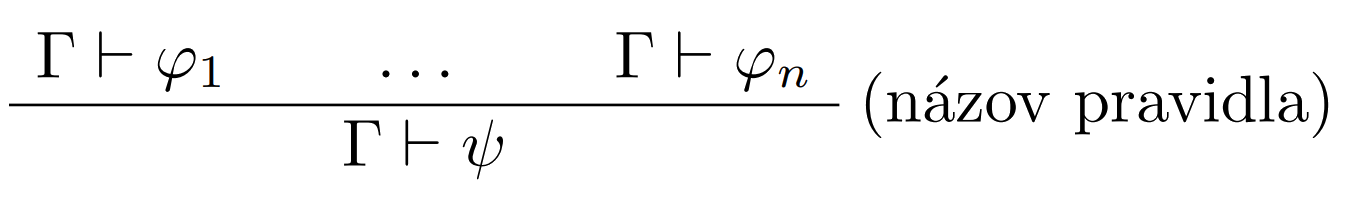
kde horná časť pravidla obsahuje nula až $n$ predpokladov a dolná časť je formula (záver) odvodená týmto pravidlom.
Typy odvodzovacích pravidiel v prirodzenej dedukcii
Odvodzovacie pravidlá v prirodzenej dedukcii môžeme kategorizovať nasledovne:
-
Pravidlá zavádzajúce (Introduction, I): Opisujú, ako získať novú formulu s danou logickou spojkou.
-
Pravidlá eliminujúce (Elimination, E): Umožňujú využiť existujúcu formulu na odvodenie ďalších logických záverov.
-
Axiómy: pravidlá bez predpokladov, ktoré ukončujú vetvy dôkazu.
Táto štruktúra je základom prirodzenej dedukcie a slúži ako rámec pre formálne odvodzovanie v intuicionistickej aj klasickej logike.
Dôkaz formuly prirodzenou dedukciou
Dôkazom sekventu $\Gamma \vdash \varphi$ je dôkazový strom, ktorý je zostrojený následovným spôsobom:
- V koreni stromu sa nachádza dokazovaný sekvent $\Gamma \vdash \varphi$.
- Každý uzol stromu vznikol aplikáciou jedného odvodzovacieho pravidla.
- Všetky listy stromu sú axiómy.
Zjednodušene:
Dôkaz konštruujeme od konca, t.j. od dokazovaného výroku, aplikáciou príslušných odvodzovacích pravidiel, pokiaľ všetky listy stromu niesu axiómy.
Poznámka
V literatúre sa často používajú aj iné spôsoby notácie pre prirodzenú dedukciu. Okrem tejto formy v tvare sekventu s explicitným kontextom, existujú napríklad aj zápisy s implicitným kontextom, kde sa hypotézy neuvádzajú explicitne pri každom kroku.
Notácia s implicitným kontextom je používaná napr. v rámci predmetu Logika pre informatikov.
Odvodzovacie pravidlá
Axióma:

Poznámka
V niektorej literatúre sa pravidlo axiómy zapisuje nasledovne:
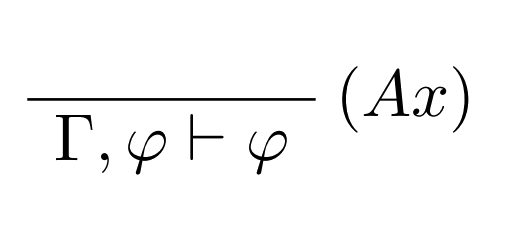
Dedukčné pravidlá systému NJ:

Pravidlo sporu (platí v klasickej logike, neplatí v intuicionistickej logike)
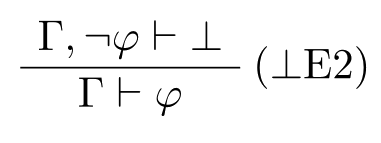
Príklad
Dôkaz formuly $$(a \Rightarrow b) \wedge (b \Rightarrow c) \Rightarrow a \Rightarrow c$$ prirodzenou dedukciou:

Curry–Howardová korešpondencia medzi jednoducho typovaným $λ$-kalkulom a výrokovou intuicionistickou logikou
V 1943 Haskell Curry spozoroval korešpondenciu medzi intuicionistickym logickým systémom a teóriou typov, ktorú neskôr znovuobjavil William Howard v 1969 a publikoval v 1980.
Korešpondencia definuje presný vzťah medzi jednoducho typovaným $λ$-kalkulom a intuicionistickou logikou:
- Výrok $φ$ považujeme za typ.
- Dôkaz výroku $φ$ je term typu $T$.
- Dokazovanie formuly prirodzenou dedukciou korešponduje s typovou kontrolou.
- Zjednodušenie dôkazov korešponduje s vyhodnocovaním termu.
| Intuicionistická logika | Jednoducho typovaný λ-kalkul |
|---|---|
| výrok $p$ | typ $T$ |
| $φ⇒ψ$ | $T_1 → T_2$ |
| $φ∧ψ$ | $T_1 × T_2$ |
| $φ∨ψ$ | $T_1 + T_2$ |
| $⊤$ | $Unit$ |
| $⊥$ | prázdny typ |
Korešpondencia typovacích pravidiel $\lambda_\rightarrow$ a odvodzovacích pravidiel Systému NJ
Typovacie pravidlá korešpondujú s dedukčnými pravidlami systému NJ.
| Jednoducho typovaný λ-kalkul | Intuicionistická logika |
|---|---|
| \begin{prooftree} \AxiomC{Γ, x:T1 ⊢ t:T2} \RightLabel{ (abs)} \UnaryInfC{Γ ⊢ λx:T1.t:T1→T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ, T1 ⊢ T2} \RightLabel{ (⇒I)} \UnaryInfC{Γ ⊢ T1⇒T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t1:T1 → T2} \AxiomC{Γ ⊢ t2:T1} \RightLabel{ (app)} \BinaryInfC{Γ ⊢ t1 t2:T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1 ⇒ T2} \AxiomC{Γ ⊢ T1} \RightLabel{ (⇒E)} \BinaryInfC{Γ ⊢ T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ⊢ t1:T1} \AxiomC{Γ⊢ t2:T2} \RightLabel{ (times)} \BinaryInfC{Γ ⊢ ⟨t1,t2⟩:T1×T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ⊢ T1} \AxiomC{Γ⊢ T2} \RightLabel{ (∧I)} \BinaryInfC{Γ ⊢ T1∧T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t:T1×T2} \RightLabel{ (proj1)} \UnaryInfC{Γ ⊢ t.1:T1} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1∧T2} \RightLabel{ (∧E1)} \UnaryInfC{Γ ⊢ T1} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t:T1×T2} \RightLabel{ (proj2)} \UnaryInfC{Γ ⊢ t.2:T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1∧T2} \RightLabel{ (∧E2)} \UnaryInfC{Γ ⊢ T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t1:T1} \RightLabel{(inl)} \UnaryInfC{Γ ⊢ inl t1 : T1 + T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1} \RightLabel{(∨I1)} \UnaryInfC{Γ ⊢ T1 ∨ T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t2:T2} \RightLabel{(inr)} \UnaryInfC{Γ ⊢ inr t2 : T1 + T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T2} \RightLabel{(∨I2)} \UnaryInfC{Γ ⊢ T1 ∨ T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t:T1 + T2} \AxiomC{Γ, x1:T1 ⊢ t1:T} \AxiomC{Γ, x2:T2 ⊢ t2:T} \RightLabel{(case)} \TrinaryInfC{Γ ⊢ case t of inl x1 ⇒ t1 || inr x2 ⇒ t2 : T} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1 ∨ T2} \AxiomC{Γ, T1 ⊢ T} \AxiomC{Γ, T2 ⊢ T} \RightLabel{(∨E)} \TrinaryInfC{Γ ⊢ T} \end{prooftree} |
Motivačný príklad: Extrakcia programu z dôkazu
Ako prvý motivačný príklad uvedieme jednoduchý program Swap. Na vstupe dostane dvojicu a na výstupe vráti tú istú dvojicu, avšak v obrátenom poradí.
Intuitívne typ takéhoto programu bude: $$A \times B \to B \times A,$$ čo korešponduje s intuicionistickou formulou: $$B∧A ⇒ A∧B.$$
Dôkaz formuly $B∧A ⇒ A∧B$ prirodzenou dedukciou je možné skonštruovať nasledovne:
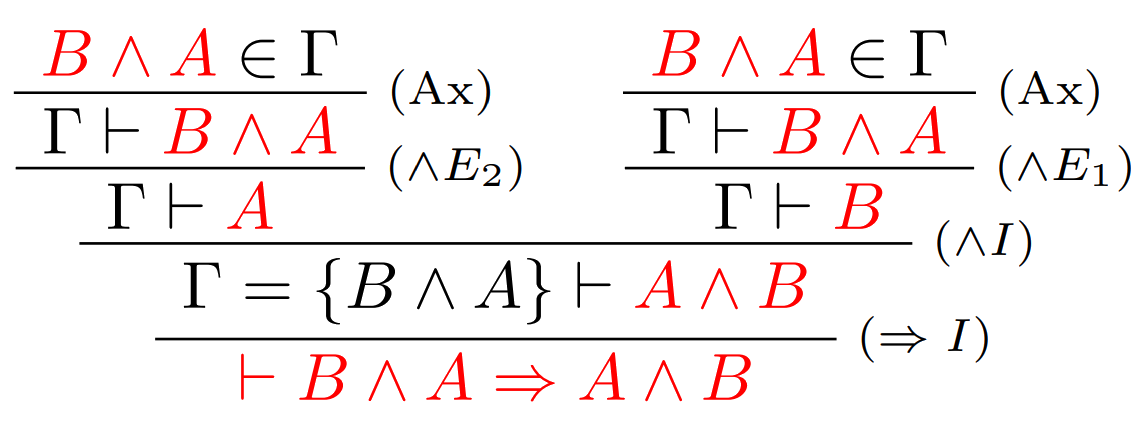
Poznámka
Proces dokazovania formúl (matematických viet) je nerozhodnutelný problém. To znamená, že neexistuje algoritmus, ktorý by pre každé matematické tvrdenie rozhodol, či je pravdivé alebo nie.
Z vyššie uvedeného dôkazu môžeme priamo prečítať aj príslušný program. Každý krok dôkazu zodpovedá určitej konštrukcii v λ-kalkule:
- Záverečný krok → zavedenie λ-abstrakcie
- Eliminácie konjunkcie → projekcie
z.1,z.2 - Zavedenie konjunkcie → konštrukcia dvojice
<_, _>
V dôkaze sa nachádza hypotéza v kontexte, ktorú označíme premennou $$z : B ∧ A,$$ čo v λ-kalkule zodpovedá výrazu typu $$z : B × A.$$
Následne v dôkazovom strome používame pravidlá ∧E₁ a ∧E₂, ktoré nám umožnia získať jednotlivé zložky dvojice.
V λ-kalkule sa tieto kroky prejavia ako projekcie:
- z pravidla
∧E₁získame prvú zložku:z.1 : B - z pravidla
∧E₂získame druhú zložku:z.2 : A
Potom aplikujeme pravidlo ∧I, ktoré v konštrukcii programu znamená, že z oboch výsledkov vytvoríme novú dvojicu:
$$⟨ z.2 , z.1 ⟩ : A × B$$
Nakoniec posledný krok dôkazu využíva pravidlo implikácie ⇒I, ktoré sa v λ-kalkule prejaví ako zavedenie λ-abstrakcie:
$$λz : B × A. ⟨ z.2 , z.1 ⟩: A \times B \to A × B $$
Typová kontrola termu:
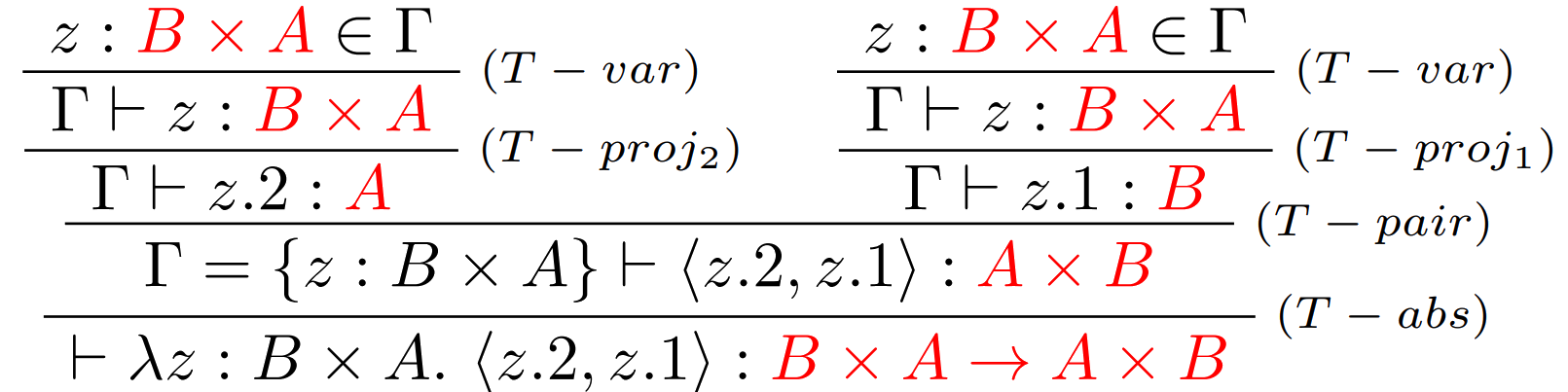
Poznámka
Korešpondenciu medzi redukciou a zjednodušením dôkazu nebudeme detailne rozoberať.
Zjednodušene, redukcia dôkazu na logickej strane presne zodpovedá β-redukcii v λ-kalkule:
zjednodušenie dôkazu = zjednodušenie programu.
Tieto súvislosti vychádzajú z ekvivalencie medzi elimináciou a zavedením spojok v prirodzenej dedukcii a aplikáciou λ-termov.
Motivačný príklad: Extrakcia dôkazu z programu
V predchádzajúcom príklade bolo demonštrované, ako je možné z dôkazu v prirodzenej dedukcii extrahovať príslušný program v λ-kalkule.
Tento príklad je zameraný na opačný smer: z typu programu odvodíme jeho korešpondujúcu logickú formulu a následne sformulujeme aj jej dôkaz na základe príslušného termu daného typu.
Uvažujme nasledujúci funkčný typ:
$$ A + B \;\to\; (A \to C) \;\to\; (B \to C) \;\to\; C $$
Tento typ korešponduje s nasledujúcou intuicionistickou formulou:
$$ A \lor B \;\Rightarrow\; (A \Rightarrow C) \;\Rightarrow\; (B \Rightarrow C) \;\Rightarrow\; C. $$
Intuitívne ide o klasickú konštrukciu case-analysis:
ak máme dôkaz disjunkcie $A \lor B$, tak:
- ak platí $A$, môžeme použiť dôkaz $A \Rightarrow C$,
- ak platí $B$, môžeme použiť dôkaz $B \Rightarrow C$.
V oboch prípadoch získame dôkaz $C$.
Z programu vidíme dôkaz.
Pri pohľade na typové a dedukčné pravidlá, je možné pozorovať nasledujúcu korešpondenciu:
- zavedenie implikácie →
λ-abstrakcia, - eliminácia disjunkcie →
case … of, - eliminácia implikácie → aplikácia funkcie.
Korešpondujúci program je:
$$ \begin{array}{l} λx : A + B.\; λf : A \to C.\; λg : B \to C.\; \\ \qquad \text{case } x \text{ of } \\ \qquad \qquad \ \ \ \text{inl } a \Rightarrow f\; a \\ \qquad \qquad \mid\mid \text{inr } b \Rightarrow g\; b \\ : A + B \;\to\; (A \to C) \;\to\; (B \to C) \;\to\; C \end{array} $$
Typová kontrola daného termu:
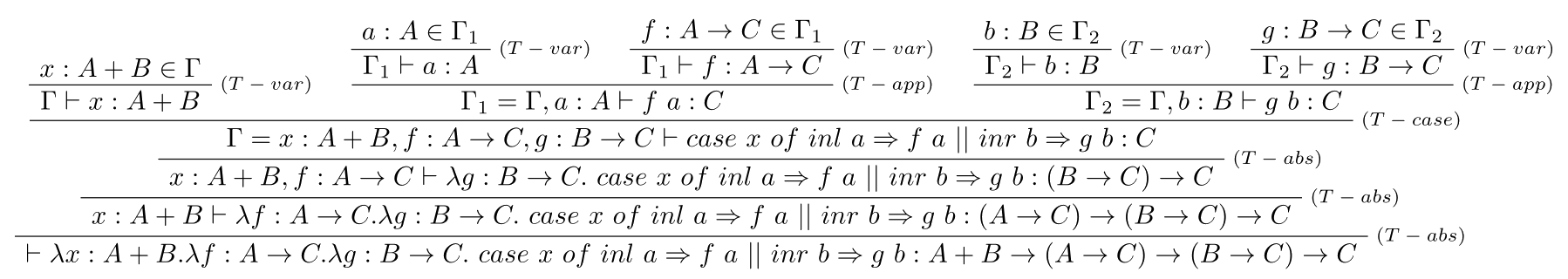
Dôkaz formuly
$$
A \lor B \;\Rightarrow\; (A \Rightarrow C) \;\Rightarrow\; (B \Rightarrow C) \;\Rightarrow\; C
$$
prirodzenou dedukciou na základe stromu typovej kontroly je možné zostaviť nasledovne:
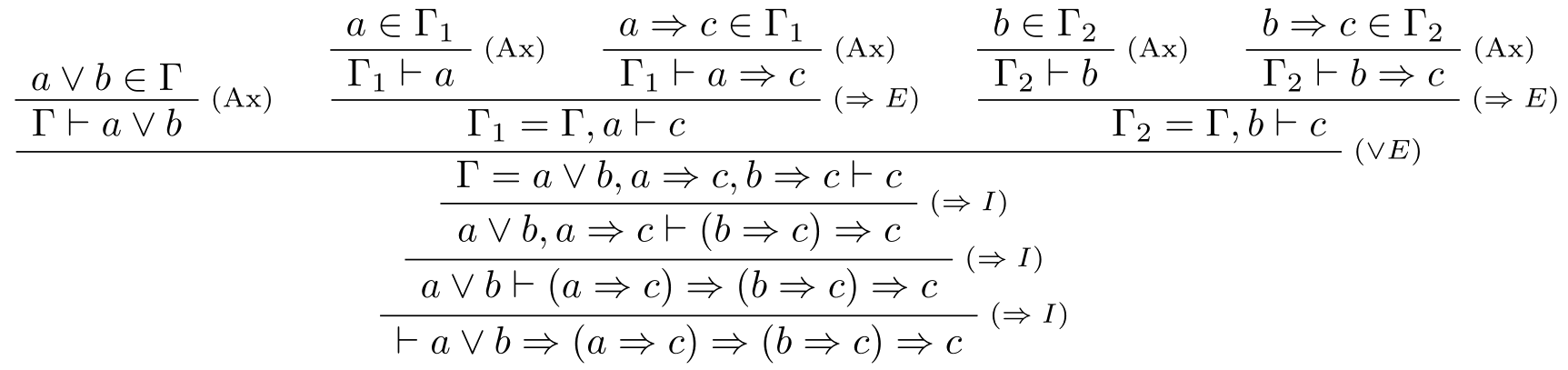
Poznámka
Tento príklad ilustruje opačný smer Curry–Howardovej korešpondencie:
typ funkcie zodpovedá formule, a správne typovaný program zodpovedá jej dôkazu.
V praxi to znamená, že dôkazy je možné programovať a programy je možné dokazovať.
Poznámka
Pri dokazovaní logických formúl môže existovať nekonečne veľa rôznych dôkazov tej istej vety.
Prirodzená dedukcia umožňuje rôzne stratégie, rôzne poradia aplikácie pravidiel či rôzne medzikroky.
Naopak, typová kontrola programu je jednoznačný proces:
pre daný λ-term existuje presne jeden spôsob, ako mu priradiť typ (ak vôbec existuje).
Inými slovami:
- pri dôkazoch skúmame veľký priestor možných dôkazových stromov,
- pri typovaní iba mechanicky overujeme, či je konkrétny program správne typovaný podľa presných pravidiel.
Tento kontrast ilustruje, prečo je hľadanie dôkazov zložité (a vo všeobecnosti nerozhodnuteľné), zatiaľ čo typová kontrola je efektívny a deterministický proces.
Záver
Jedným z najvýznamnejších objavov informatiky minulého storočia je Curry–Howardova korešpondencia, ktorá odhaľuje hlboké prepojenie medzi logikou a programovaním. Tento koncept ukazuje, že každý konštruktívny dôkaz logického výroku môže byť interpretovaný ako program, a naopak, každý správne typovaný program predstavuje dôkaz výroku. Táto idea je základom moderných typových systémov a interaktívnych dokazovacích systémov (kde patrí aj systém Rocq).
- Dôkaz formuly konštruuje funkciu daného typu – každý konštruktívny dôkaz korešponduje s konkrétnym termom v jednoducho typovanom λ-kalkule.
- Rozhodnuteľnosť typovej kontroly – overenie, či je daný λ-term správne typovaný, je algoritmicky rozhodnuteľné a deterministické.
- Hľadanie dôkazu (type inhabitation) – existencia termu daného typu, resp. dôkazu pre daný výrok, je vo všeobecnosti nerozhodnuteľný problém.
- Funkcia dôkazu tvrdenia – typová kontrola funguje ako algoritmus, ktorý overuje, či je tvrdenie dokázateľné, a ukazuje spôsob, ako môže byť dôkaz (program) konštruovaný.
- Význam intuicionistickej logiky – konštruktívny prístup k dôkazom, odmietanie zákona vylúčenia tretieho a dvojitej negácie, dôraz na explicitnú konštrukciu matematických objektov (programov).
- Korešpondencia typovacích a dedukčných pravidiel – každý λ-term a jeho typ zodpovedá konkrétnemu dôkazu a odvodzovaciemu pravidlu v prirodzenej dedukcii.
- Redukcia dôkazu = β-redukcia programu – zjednodušenie dôkazu zodpovedá zjednodušeniu programu, čo ukazuje presnú korešpondenciu medzi logikou a λ-kalkulom.
- Kontrast dôkazov a typovania – dôkazy môžu mať nekonečne veľa variantov, zatiaľ čo typová kontrola je jednoznačná a deterministická.
- Praktický význam – základy pre typové systémy, verifikáciu programov, interaktívne a automatické dokazovanie, generovanie programov zo špecifikácií.
Kľúčová myšlienka:
Každý správne typovaný program je konštruktívnym dôkazom výroku, čo umožňuje premostiť svet matematickej logiky a funkcionálneho programovania.
Korešpondencie medzi typovými systémami a logikami
| Teória typov / Typový systém | Zodpovedajúca logika | Poznámka |
|---|---|---|
| Jednoducho typovaný λ-kalkul (λ→) | Intuicionistická výroková logika | Každý term typu je dôkazom logického výroku |
| System F (polymorfné typy) | Druh intuicionistickej logiky 2. rádu (predikátová logika 2. rádu) | Typy ako univerzálne kvantifikované výroky |
| System P (závisle typy) | Intuicionistická predikátová logika | Typy zodpovedajú formulám s kvantifikátormi |
| System $\underline{\omega}$ (Typové konštruktory) | Rozšírená intuicionistická výroková logika | Typy môžu byť funkcie nad typmi |
| Calculus of Constructions (CoC) | Intuicionistická logika vyššieho rádu | Kombinuje polymorfizmus, typové konštruktory a závisle typy, základ pre Rocq |
Poznámka
Tieto korešpondencie sú prirodzeným rozšírením Curry–Howardovej myšlienky:
logický výrok ↔ typ, dôkaz ↔ program, redukcia dôkazu ↔ beh programu.
Poznámka
Pre demonštráciu Curry–Howardovej korešpondencie odporúčam využiť vizualizačný nástroj ProjectProof, ktorý je dostupný na adrese https://projectproof.kpi.fei.tuke.sk/.
Zdroje
- Pierce, Benjamin C. Types and programming languages. MIT press, Cambridge, 2001 (Перевод на русский язык: Бенджамин Пирс. Типы в языках программирования. — Добросвет, 2012. — ISBN 978-5-7913-0082-9)
- Sørensen, M. H., Urzyczyn, P., Lectures on the Curry-Howard isomorphism (Vol. 149). Elsevier. 2006
- Wadler, P., Propositions as types. Communications of the ACM, 58 (12), 75-84. 2015
- Open Logic Project, 2025
- OCaml Programming: Correct + Efficient + Beautiful: Lecture notes, Cornell University, 2025
- Брагилевский, В. Н. Соответствие Карри–Ховарда: от математической логики к программированию, Летняя школа «Современная математика», посвященная памяти Виталия Арнольда, 2017
- Брагилевский, В. Н. Соответствие Карри—Ховарда: от математической логики к программированию и обратно, Записи лекций на XVII Летней школе «Современная математика», 2017
- Крупский, В.Н., Кузнецов, С.Л., Практикум по математической логике. COQ. МГУ имени М.В. Ломоносова, 2013