Úvod
Táto prednáška je venovaná typovým systémom - statickej analýze programu, ktorá klasifikuje výrazy podľa ich "tvaru".
V prvej kapitole využijeme jednoduchý funkcionálny jazyk NBL (ktorý bol definovaný ako netypovaný jazyk v prvej prednáške), na ktorom budú predstavené základné myšlienky zavedenia:
- typov
- typovacích pravidiel,
do programovacieho jazyka, ako aj základné teorémy, ktoré vyjadrujú dôležité vlastnosti každého typového systému:
- jednoznačnosť typov,
- typová bezpečnosť, ktorá pozostáva z dvoch viet:
- typovej progresie,
- typovej stability.
Nasledujúca podkapitola bude venovaná zavedeniu typov do $\lambda$-kalkulu a najjednoduchšej teórii typov: jednoducho typovanému $\lambda$-kalkul.
Na záver, budú definované a dokázané dôležité vlastnosti typovaných jazykov na príklade jednoducho typovaného $\lambda$-kalkulu a predstavená $\lambda$-kocka, ktorá opisuje vzťahy medzi jednotlivými teóriami typov.
Typovaný jazyk čísel a Boolean hodnôt
Zavedenie typov do jazyka bude demonštrované na jednoduchom programovacom jazyku NBL, v ktorom existuje možnosť formulovať syntakticky legálne termy jazyka, ako napríklad: $$succ\ true$$ ktoré vedú k nezmyselným, chybným programom (vyhodnotením nie je možné získať výsledok).
Pri písaní programov v takýchto jazykoch sa typy termov predpokladajú implicitne a prípadná nezmyselnosť termov sa zistí až pri vyhodnotení (v runtime), keď nie je možné nájsť vhodné vyhodnocovacie pravidlo.
Zavedením typového systému do jazyka je možné určiť už pred vyhodnotením, či sú termy jazyka zmysluplné.
Jazyk NBL bude rozšírený tak, aby bolo možné explicitne rozlíšiť:
- ktoré termy budú mať numerickú hodnotu,
- ktoré termy budú mať pravdivostnú hodnotu.
Zavedieme dva typy:
- $Nat$,
- $Bool$.
Tieto typy sa nazývajú základné typy, väčšinou sú to preddefinované typy jazyka.
Každému termu bude priradený jednoznačný typ prostredníctvom typovacej relácie: $$\boxed{\ t: T\ }$$ kde
- $t$ je term,
- $T$ je typ.
Poznámka
Zápis $t: T\ $ sa nazýva aj typová anotácia.
Príklad
Príklady typových anotácií: $$ \begin{array}{l} 0: Nat \\ succ~( succ~ 0) :~ Nat\\ iszero(succ~0): Bool \\ if~true~then~succ~0~else~0: Nat \end{array} $$
Pred vyhodnotením termu je potrebné overiť, či je typová anotácia správna. Takéto overovanie sa nazýva typová kontrola (z ang. type checking), ktorá sa vykonáva v prekladači, vo fáze sémantickej analýzy.
Formálna definícia typovaného jazyka NBL pozostáva z:
- formálnej definície syntaxe,
- definície typovacej relácie a typovacích pravidiel
- definície sémantiky - vyhodnocovacej relácie a vyhodnocovacích pravidiel.
Postup zavedenia typového systému do jazyka NBL:
- V prvom kroku bude rozšírená syntax jazyka NBL o typy,
- následne bude definovaná typovacia relácia a typovacie pravidlá pre novú syntax,
- na záver bude uvedená definícia sémantiky, ktorá oproti netypovanému jazyku ostáva nezmenená.
Poznámka
Ako bolo spomenuté, typová kontrola prebieha pri preklade vo fáze sémantickej analýzy. Týmto bude zabezpečené, že žiadny term, ktorý nemá význam sa nezačne vyhodnocovať (vykonávať). Typová kontrola vylúči všetky termy pri ktorých by došlo k situácii, že pri pokuse o vyhodnotenie nie je možné aplikovať žiadne vyhodnocovacie pravidlo.
Syntax typovaného NBL
Syntax typovaného jazyka NBL rozšírime o produkčné pravidlo pre typy $T$, pričom typ v jazyku NBL môže byť $Bool$ alebo $Nat$.
Takéto rozšírenie opisuje nasledujúca gramatika v Backus-Naurovej forme: $$ \begin{array}{ll} t::= & true\ |\ false \ |\ if\ t\ then\ t\ else\ t \ |\ 0 \ |\ succ\ t\ |\ pred\ t\ |\ iszero\ t \\ v::= & true\ |\ false \ |\ nv \\ nv::=& 0\ |\ succ\ nv \\ T::= & Bool\ |\ Nat \end{array} $$ Typy všeobecne budeme označovať počiatočným veľkým písmenom, napríklad $T_{1}, T_{2, \ldots}$, $Nat, Bool.$
Typová relácia a typovacie pravidlá
Typovacia relácia v NBL je typová anotácia v tvare: $$\boxed{\ t: T\ }$$
Je definovaná pomocou typovacích pravidiel pre všetky tvary termov tak, aby bolo zaručené, že každému termu jazyka je možné jednoznačne priradiť typ.
Hovoríme, že term $t$ jazyka je správne typovaný (well-typed), ak existuje typ $T$ taký, že $t: T$.
Typovacie pravidlá

Kontrola typov je formálne vykonávaná konštrukciou dokazovacieho stromu, v ktorom:
- Koreň stromu obsahuje kontrolovaný term.
- V každom kroku je aplikované vhodné typovacie pravidlo, pričom voľba konkrétneho pravidla je vždy jedinečná.
- Ak sú všetky listy stromu axiómy, skonštruovali sme formálny dôkaz tvrdenia v koreni stromu: term je správne typovaný.
Typový systém v tomto jazyku môže byť využitý na:
- kontrolu typov: je term $t$ typu $T$ správne typovaný
- odvodzovanie typov: existuje typ $T$ pre term $t$ taký, že platí $t:T$?
Príklad
Majme daný nasledujúci term typovaného jazyka NBL: $$succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0)))) : Nat$$ Overte či je správne typovaný.
Riešenie
Strom typovej kontroly:
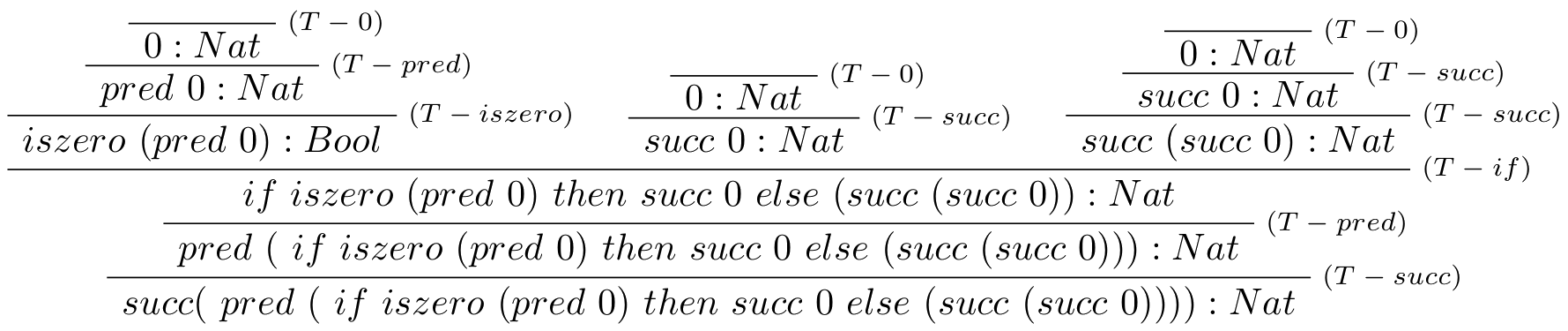
Príklad
Majme daný nasledujúci term typovaného jazyka NBL: $$succ(\ if\ iszero\ (pred\ 0)\ then\ true\ else\ false) : Nat$$ Overte či je správne typovaný.
Riešenie
Strom typovej kontroly:
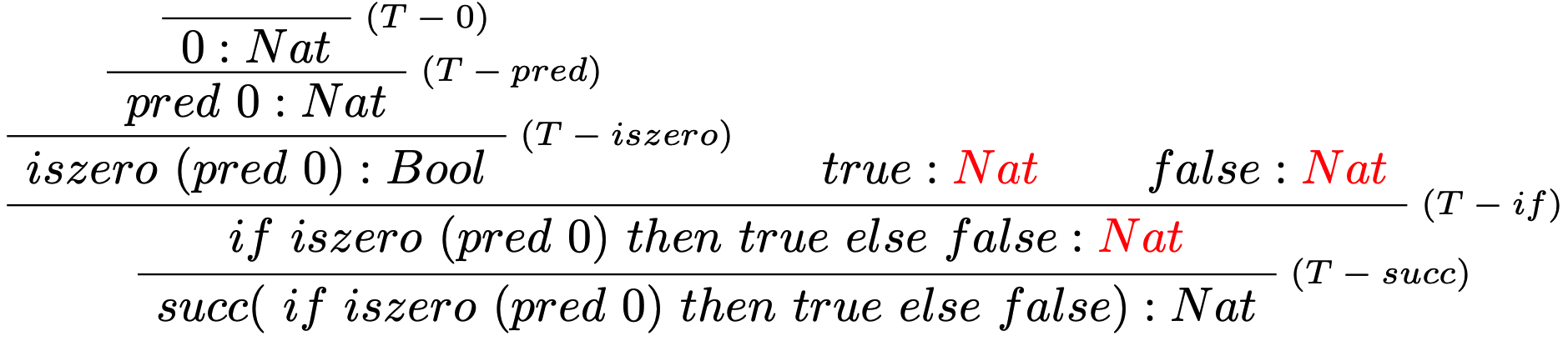
Term nie je správne typovaný.
- Pravidlo $T-if$ vyžaduje aby druhý a tretí predpoklad bol typu $Nat$,
- avšak termy v daných predpokladoch sú typu $Bool$,
- to znamená, že nie je možné ďalej aplikovať akékoľvek typovacie pravidlo a typová kontrola je neúspešná.
Veta o inverzii typovej relácie
Pri formálnom uvažovaní o typovej relácii je často potrebné vytvárať tvrdenia typu: "ak je term $t$ správne typovaný, potom jeho typ je $T$" Veta o inverzii typovej relácie poskytuje sadu takýchto tvrdení.
Veta Inverzia typovej relácie $$ \begin{align*} 1.\;& \text{ak } \text{true} : R, &&\text{potom } R = \text{Bool},\\ 2.\;& \text{ak } \text{false} : R, &&\text{potom } R = \text{Bool},\\ 3.\;& \text{ak } \text{if } t_1 \text{ then } t_2 \text{ else } t_3 : R, &&\text{potom } t_1 : \text{Bool},\; t_2 : R,\; t_3 : R,\\ 4.\;& \text{ak } 0 : R, &&\text{potom } R = \text{Nat},\\ 5.\;& \text{ak } \text{succ } t_1 : R, &&\text{potom } R = \text{Nat},\; t_1 : \text{Nat},\\ 6.\;& \text{ak } \text{pred } t_1 : R, &&\text{potom } R = \text{Nat},\; t_1 : \text{Nat},\\ 7.\;& \text{ak } \text{iszero } t_1 : R, &&\text{potom } R = \text{Bool},\; t_1 : \text{Nat}. \end{align*} $$
Dôkaz: Plynie priamo z definície typovej vzťahu.
Táto veta sa niekedy nazýva aj „generačná veta pre typovú reláciu, pretože pre každý sprváne typovaný výraz zobrazuje, ako mohol byť dôkaz tohto tvrdenia skonštruovaný (vygenerovaný)..
Poznámka
Veta o inverzii vedie priamo k rekurzívnemu algoritmu na odvodenie typov termov, pretože hovorí, ako pre syntaktický tvar termu vypočítať jeho typ (ak existuje) z typov jeho podtermov.
Sémantika typovaného NBL
Sémantika typovaného NBL je definovaná vyhodnocovacou reláciou $$\boxed{\ t \to t'\ }$$ a vyhodnocovacími pravidlami:

Vlastnosti typového systému jazyka NBL
V každom typovanom jazyku sú skúmané nasledujúce vlastnosti:
- Jednoznačnosť: každý správne typovaný term jazyka NBL má práve jeden typ (buď $Nat$ alebo $Bool$).
Nech $t$ je term jazyka $NBL$ a $T_1, T_2$ sú typu, potom: $$ (\forall t, T_1, T_2) ( \ t : T_1 \;\wedge\; t : T_2 \;\Rightarrow\; T_1 = T_2) $$ Inými slovami: pre každý správne typovaný term jazyka existuje jediný strom kontroly typov konštruovaný jednoznačným aplikovaním typovacích pravidiel jazyka.
- Bezpečnosť: jazyk je bezpečný (safe), ak spĺňa nasledujúce dve vlastnosti:
- platí progresia: správne typovaný term je buď hodnota, alebo sa na neho dá aplikovať niektoré vyhodnocovacie pravidlo jazyka, t.j. je redex;
Nech $t$ je term jazyka $NBL$, $T$ je typ a $isvalue$ je predikát, ktorý vráti hodnotu pravda ak term $t$ je hodnota, potom: $$ (\forall t, T)( \ t : T \;\Rightarrow\; isvalue(t) \;\vee\; (\exists t')( \ t \to t')) $$
- platí stabilita: vyhodnotenie zachováva typy, teda typ termu sa počas vyhodnotenia nemení.
Nech $t, t'$ sú termy jazyka $NBL$, $T$ je typ a $isvalue$ je predikát, ktorý vráti hodnotu pravda ak term $t$ je hodnota, potom: $$ (\forall t, t', T)\; \big( t : T \;\wedge\; t \to t' \;\Rightarrow\; t' : T \big) $$
Jazyk $NBL$ je bezpečný, ak spĺňa vlastnosti progresie a stability.
Poznámka
Je jednoduché dokázať (štrukturálnou indukciou na syntaxi NBL), že jazyk NBL je jednoznačný a bezpečný.
V rámci cvičení venovaných interaktívnemu systému Rocq, budú formálne dokázané tieto vlastnosti.
Jednoducho typovaný $\lambda$-kalkul
Jednoducho typovaný $\lambda$-kalkul (označovaný ako $\lambda_{\to}$) je teória typov postavená:
- na základných typoch (napríklad $Bool, Nat, String, Unit, ...$)
- na jedinom typovom konštruktore funkčného typu ($\to$).
Konkrétna voľba základných typov nie je dôležitá, keďže formálna definícia jazyka a jeho vlastností je postavená na rovnakom princípe bez ohľadu aká je zvolená množina základných typov.
Množina základných typov sa nazýva $A$.
Typ bude vo všeobecnosti označovaný metapremennou $T$, prípadne s indexom.
Najskôr bude predstavená definícia čistého jednoducho typovaného $\lambda$-kalkulu, v ktorom $A = \emptyset$. Následne bude táto definícia rozšírená pridaním základných typov $A = \{ Bool, Nat \}$ a príslušných operácii nad nimi.
Jednoduché typy
je generovaná nasledujúcou gramatikou: $$T::=\ A\ |\ T \to T$$ Typový konštruktor funkčného typu $\to$ je pravo asociatívny: $$T_1 \to T_2 \to T_3 = T_1 \to (T_2 \to T_3)$$ Jednoduché typy sú základné typy, alebo sú vytvorené prostredníctvom typových konštruktorov.
Typová relácia
Aby bolo možné priradiť typ $\lambda$-abstrakcii $\lambda x.t$ je potrebné vypočítať čo sa stane, ak je abstrakcia aplikovaná na nejaký argument. Taktiež vzniká otázka: ako zistiť, aký typ argumentov daná funkcia očakáva. Existujú dve možnosti riešenie tohto problému:
- Explicitne uviesť typovú anotáciu každému parametru a taktiež celej $\lambda$-abstrakcii.
- Analyzovať telo abstrakcie, ako sa argument používa a z toho odvodiť typ.
Druhá možnosť by vyžadovala zaviesť do jazyka netriviálne vlastnosti a konštrukcie ako je spôsob odvodenia typu pre implicitne typovaný jazyk a s tým aj istý druh polymorfizmu. Tomu sa budeme venovať v závere semestra.
Z tohto dôvodu bude aktuálne zvolená prvá možnosť, a to namiesto zápisu: $$\lambda x.t$$ bude v $\lambda$-abstrakcii explicitne uvedená typová anotácia každého parametra: $$\lambda x:T.t$$
Ak je známy typ argumentu $\lambda$-abstrakcie je zrejme, že kodoména funkcie bude typ tela $t$, kde všetky voľné výskyty premennej $x$ v $t$ budú označovať termy typu $T_1$. Takéto uvažovanie opisuje nasledujúce pravidlo:
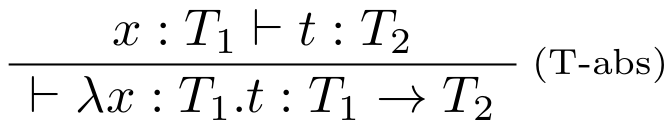
Keďže termy môžu obsahovať vnorené abstrakcie, aj premenných môže byť viac. To znamená, že je potrebné do jazyka zaviesť možnosť usudzovania aj nad takouto množinou predpokladov. Preto rozšírime typovú reláciu z dvojice: $$t:T$$ na trojicu $$\Gamma \vdash t:T,$$ kde $\Gamma$ je množina predpokladov o typoch voľných premenných v terme $t$. Tento zápis je možné prečítať "term $t$ je typu $T$ v typovom kontexte $\Gamma$"
Formálne, sa $\Gamma$ nazýva typový kontext (niekedy aj prostredie premenných). Je to postupnosť premenných s ich typovými anotáciami, ktoré sú oddelené čiarkou.
Prázdny kontext $$\vdash t:T$$ označuje, že uzavretý term $t$ je typu $T$.
Poznámka
Symbol $\vdash$ nie je symbolom jazyka jednoducho typovaného $\lambda$-kalkulu, ale slúži ako "oddeľovač" predpokladov (pravá strana) a záveru (ľavá strana).
Poznámka
Typová relácia $$\Gamma \vdash t:T,$$ je niekedy nazývaná aj sekvent
Poznámka
Jediná podmienka, ktorú je potrebné dodržať je, že všetky premenné vnorených abstrakcií musia mať rozdielny názov. V prípade že term obsahuje viacero premenných s rovnakým názvom je možné ich premenovať, keďže platí $\alpha$-konverzia.
Formálna definícia čistého jednoducho typovaného $\lambda$-kalkulu
Formálna definícia pozostáva zo:
- syntaxe,
- typovacej relácie a typovacích pravidiel,
- vyhodnocovacej relácie a vyhodnocovacích pravidiel.
Syntax čistého jednoducho typovaného $\lambda$-kalkulu
opisuje nasledujúca gramatika: $$ \begin{array}{lll} t&::=& x~|~\lambda x:T.~t~|~t~t \\ v&::=& \lambda x:T.t \\ T&::=& A\ |\ T \rightarrow T \\ \Gamma&::= & ~\varepsilon~|~\Gamma, x:T \end{array} $$ kde $A$ je množina základných typov a symbol $\varepsilon$ označuje prázdny kontext.
Typovacia relácia a typovacie pravidlá jednoducho typovaného $\lambda$-kalkulu
Typovacia relácia je usporiadaná trojica: $$\boxed{\ \Gamma \vdash t:T\ }$$
Typovacie pravidlá sú definované nasledovne:
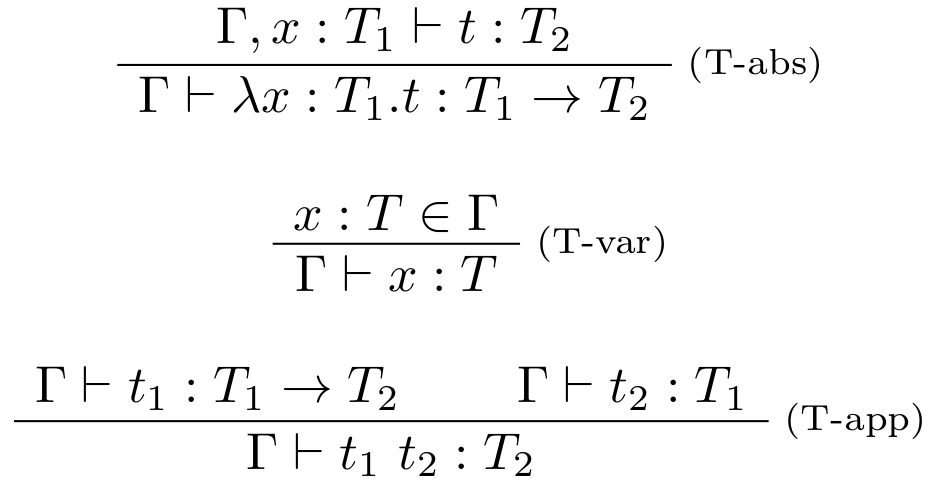
- Pravidlo pre abstrakciu hovorí, že celý výraz musí byť funkčného typu. Pridá do kontextu premennú s jej typom z čoho je možné odvodiť, že telo abstrakcie musí byť typu kodomény celej abstrakcie.
- Pravidlo pre premennú definuje, že premenná je akéhokoľvek typu ak sa daná premenná s takýmto typom nachádza v typovom kontexte.
- Pravidlo pre aplikáciu opisuje, že aplikácia termu $t_1$ na argument $t_2$ je typu $T_2$ vtedy, ak term $t_1$ je funkcia nejakého typu $T_1 \to T_2$ a argument $t_2$ musí byť typu $T_1$ ako je doména funkčného typu termu $t_1$.
Príklad
Majme daný nasledujúci sekvent: $$\vdash \lambda x: A \to B \to C.\lambda y: A. \lambda z: B.\ x\ y\ z:(A \to B \to C) \to A \to B \to C$$ Overte či je term je správne typovaný v prázdnom typovom kontexte. Pričom $A,B,C$ sú metapremenné označujúce ľubovoľný (neinterpretovaný) typ.
Riešenie
Konštruujeme dôkaz - strom typovej kontroly tak, že dokazované tvrdenie sa nachádza v koreni stromu a v každom kroku odvodenia je jednoznačne aplikované typovacie pravidlo, až pokiaľ všetky listy stromu nie sú axiómy.
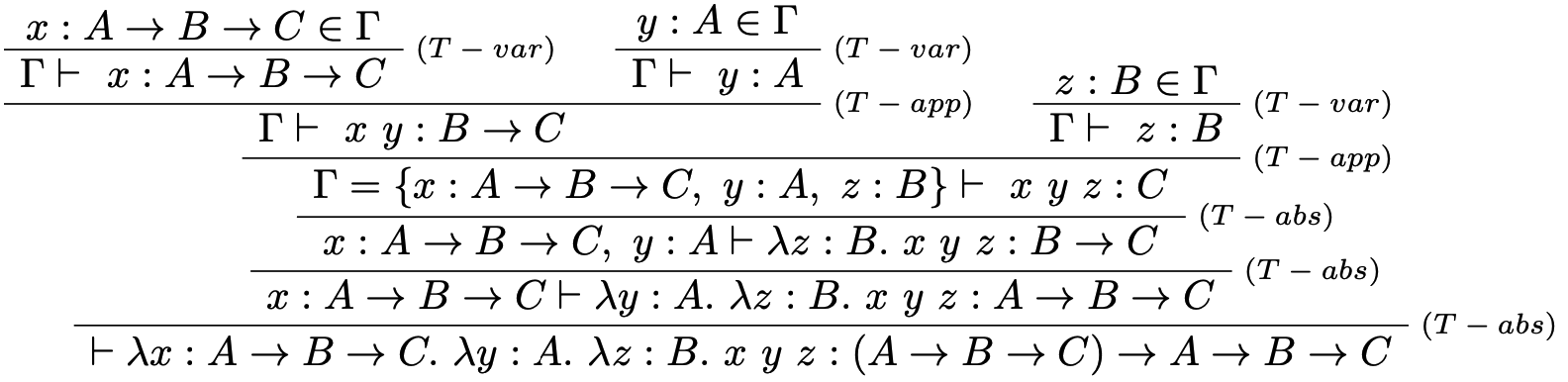
Sémantika jednoducho typovaného $\lambda$-kalkulu
Definujeme na základe redukčnej stratégie volania hodnotou pre nasledujúcu vyhodnocovaciu reláciu: $$\boxed{\ t \to t'\ }$$ vo forme vyhodnocovacích pravidiel:
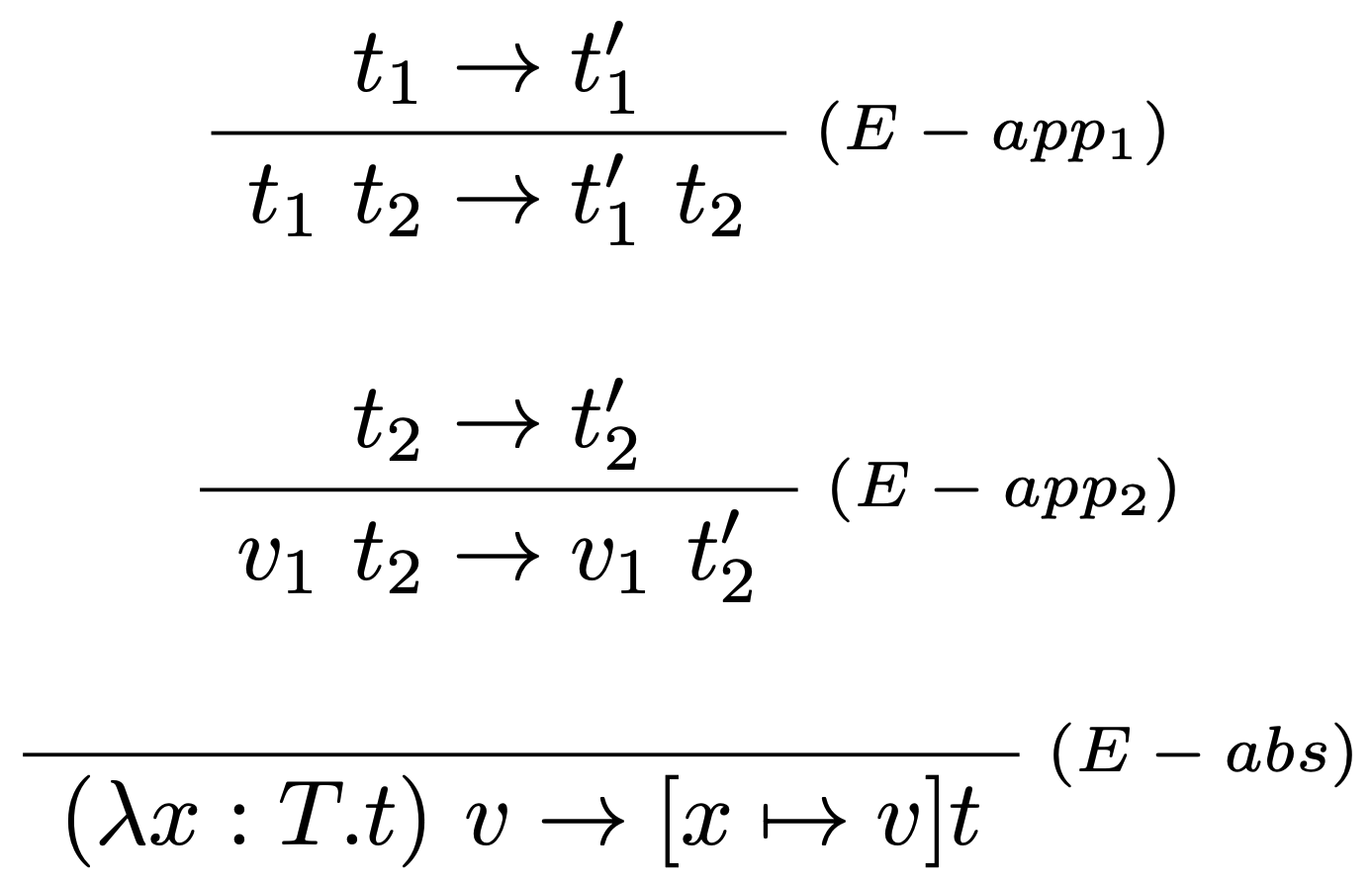
Typová kontrola, Odvodenie typu, Obývanie typu
Majme danú typovaciu reláciu: $$\Gamma \vdash t:T$$ Vzhľadom na túto reláciu je možné položiť tri dôležité otázky:
- Typová kontrola: Je term $t$ typu $T$ správne typovaný v kontexte $\Gamma$? $$\Gamma \vdash t:T$$
- Odvodenie typu: Existuje typ $T$ pre term $t$ a typový kontext $\Gamma$ taký, že: $$\Gamma \vdash t:?$$
- Obývanie typu: Existuje term $t$ pre typ $T$ v kontexte $\Gamma$ taký, že: $$\Gamma \vdash ?:T$$ Pričom:
- Typová kontrola je využívaná pri explicitne typovaných jazykoch.
- Odvodenie typu je využívané pri implicitne typovaných jazykoch.
- Obývanie typu je využívaná najmä v rámci Curry-Howardovej korešpondencie, kde každý typ je interpretovaný ako logický výrok a každý term ako dôkaz tohto výroku. Obývanie typu znamená, že existuje dôkaz pre daný výrok, čo má významné dôsledky v oblasti formálnych dôkazov a teórie dokazovania.
Poznámka
Curry-Howardovej korešpondencii sa budeme venovať v jednej z nasledujúcich prednášok.
Poznámka
V anglickom jazyku sa tieto tri problémy nazývajú:
- type checking
- type inference
- type inhabitation
Rozšírenie $\lambda_{\rightarrow}$-kalkulu o základné typy $Bool$ a $Nat$
V predchádzajúcej kapitole bol definovaný čistý $\lambda_{\rightarrow}$-kalkul, ktorý obsahuje prázdnu množinu základných typov. S takýmto jazykom je možné pracovať len na abstraktnej úrovni konštruovať termy ktorých typ bude obsahovať len metapremenné. Aby bolo možné $\lambda_{\rightarrow}$-kalkule vytvárať reálne programy, ktoré dokážu narábať so skutočnými hodnotami, je potrebné do jazyka $\lambda_{\rightarrow}$-kalkulu zaviesť nejaké základné typy.
Rozšírime množinu základných typov o typ boolean hodnôt a prirodzených čísel: $$A = \{Bool, Nat\}$$ a syntax jazyka o ich hodnoty a operácie $Succ, Pred, Iszero, If~Then~Else$ nad hodnotami takýchto typov, ako v jazyku NBL.
Formálna definícia $\lambda_{\rightarrow}$ s NBL Formálna definícia pozostáva zo:
- syntaxe,
- typovacej relácie a typovacích pravidiel,
- vyhodnocovacej relácie a vyhodnocovacích pravidiel.
Syntax $\lambda_{\rightarrow}$ s NBL
opisuje nasledujúca gramatika: $$ \begin{array}{lll} t&::=& x~|~\lambda x:T.~t~|~t~t\ |\ true\ |\ false |\ if\ t\ then\ t\ else\ t \\ & & |\ 0\ |\ succ\ t\ |\ pred\ t\ |\ iszero\ t\ \\ v&::=& \lambda x:T.t \ |\ true\ |\ false\ |\ nv \\ nv&::=& 0\ |\ succ\ nv \\ T&::=& A\ |\ T \rightarrow T \\ A&::=& Bool\ |\ Nat \\ \Gamma&::= & ~\varepsilon~|~\Gamma, x:T \end{array} $$ kde $A$ je množina základných typov a symbol $\varepsilon$ označuje prázdny kontext.
Typovacia relácia a typovacie pravidlá $\lambda_{\rightarrow}$ s NBL
Typovacia relácia je usporiadaná trojica: $$\boxed{\ \Gamma \vdash t:T\ }$$
Typovacie pravidlá sú definované nasledovne:
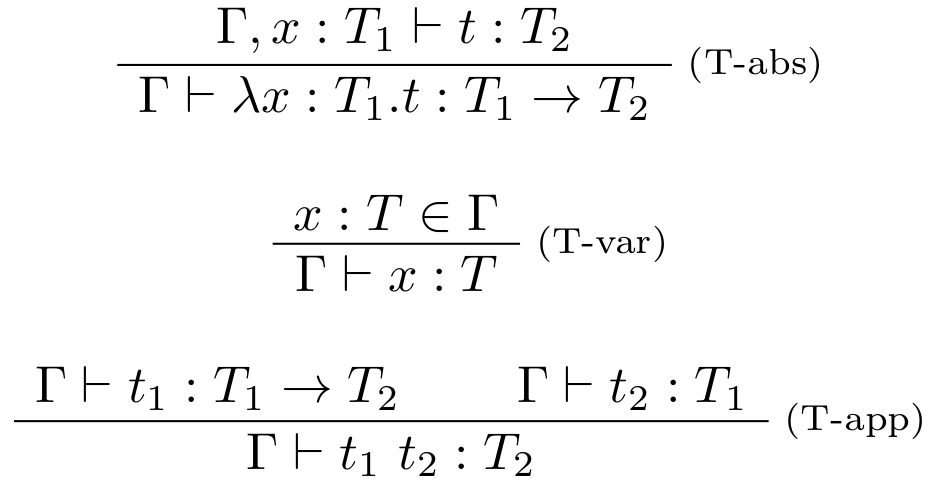

Sémantika $\lambda_{\rightarrow}$ s NBL
Definujeme na základe redukčnej stratégie volania hodnotou pre nasledujúcu vyhodnocovaciu reláciu: $$\boxed{\ t \to t'\ }$$ vo forme vyhodnocovacích pravidiel pre čistý $\lambda_{\rightarrow}$:
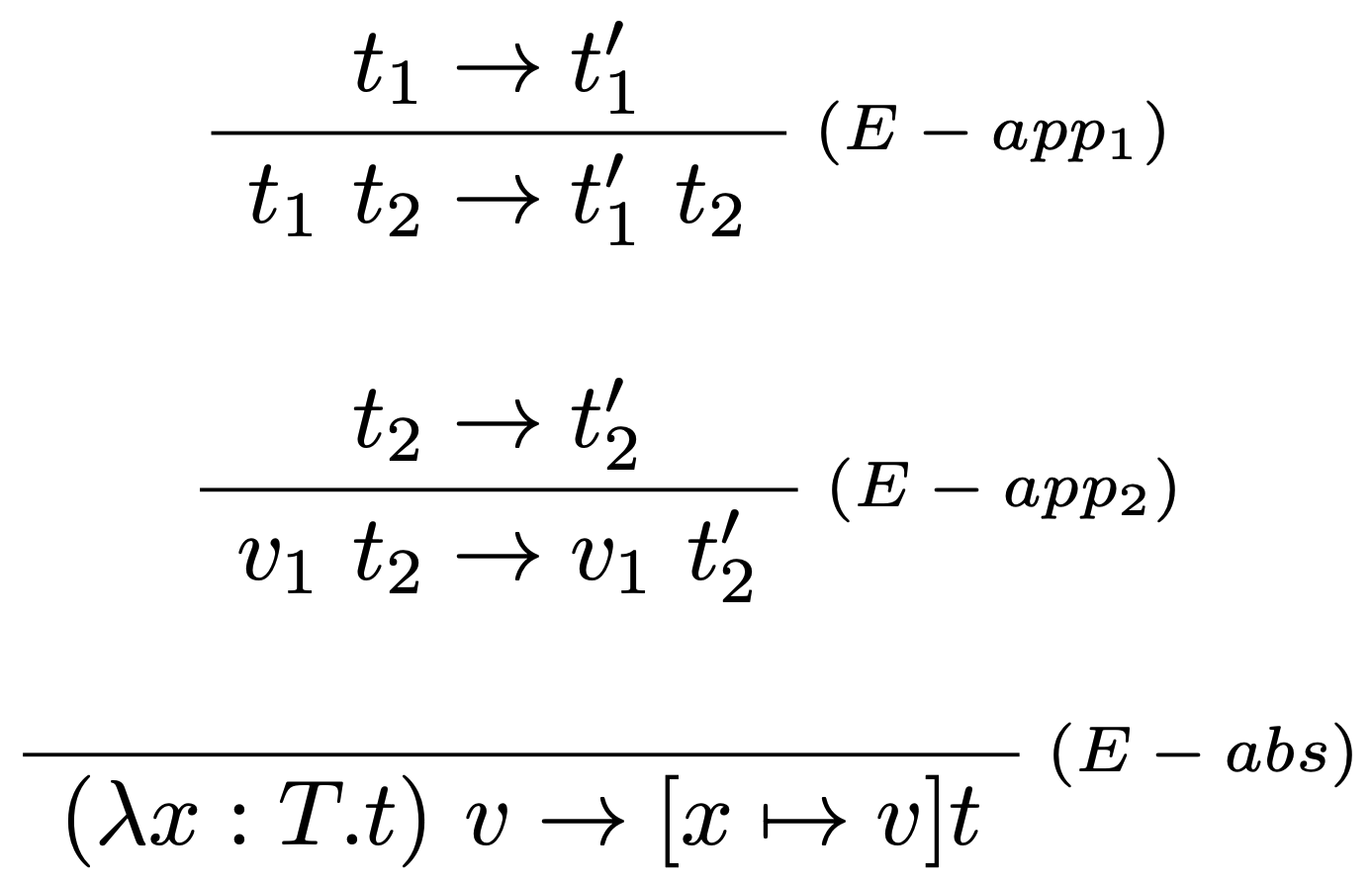
ktoré rozšírime o definíciu vyhodnocovacích pravidiel pre rozšírenia jazyka:

Poznámka
Množinu základných typov, ich hodnôt a operácii definuje návrhár jazyka. V prípade typu $Nat$ je možné definovať ako základné termy jazyka aj iné aritmetické operácie ako je napríklad operácia sčítania $t+t$ a jej príslušné typovacie a vyhodnocovacie pravidlá:
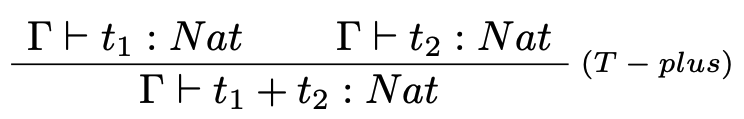
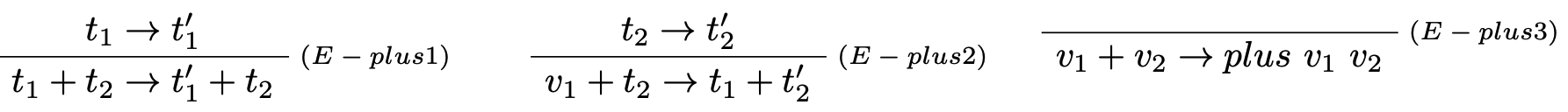
Avšak symbol $+$ bude neskôr použitý na definíciu súčtových typov, preto budeme pristupovať pri práci s operátorom $+$ ako k funkcii $$plus: Nat \to Nat \to Nat$$ a v niektorých prípadoch využívať aj infixný zápis syntaktického cukru $$t_1+t_2,$$ ktorý v skutočnosti znamená $$plus\ t_1\ t_2.$$
Príklad
Majme daný následujúci sekvent: $$\Gamma \vdash \lambda x: Nat. \lambda y: Nat.\ plus\ x\ y: Nat \to Nat \to Nat$$ Overte či je daný term správne typovaný v nasledujúcom typovom kontexte: $$\Gamma = \{plus: Nat \to Nat \to Nat \}$$
Riešenie
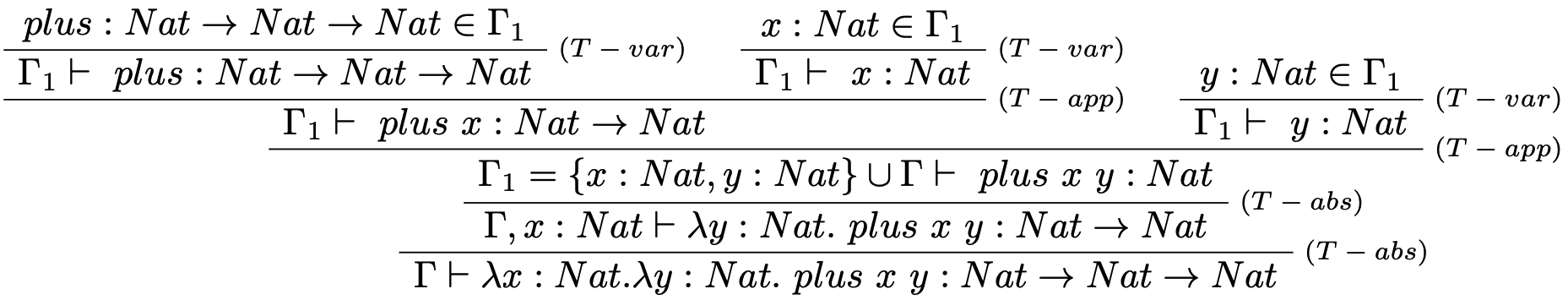
Základné vlastnosti $\lambda_{\rightarrow}$-kalkulu
Aby sme mohli tvrdiť, že jazyk $\lambda_{\rightarrow}$ s implementovaným typovým systémom je korektne navrhnutý, musíme sformulovať a dokázať jeho základné vlastnosti, ktoré zaručujú konzistentnosť a bezpečnosť typového systému.
Veta o inverzii typovej relácie
Veta o inverzii opisuje, ako vznikajú typovacie derivácie.
Pre každý syntaktický tvar termu určuje, aké typy musia mať jeho podtermy, ak má byť celý term správne typovaný.
Veta: Inverzia typovej relácie
- Ak $\Gamma \vdash x : R$, potom $x : R \in \Gamma$.
- Ak $\Gamma \vdash \lambda x:T_1.\ t_2 : R$, potom $R = T_1 \to R_2$ pre nejaké $R_2$ také, že $\Gamma, x:T_1 \vdash t_2 : R_2$.
- Ak $\Gamma \vdash t_1\ t_2 : R$, potom existuje typ $T_{11}$ taký, že $\Gamma \vdash t_1 : T_{11} \to R$ a $\Gamma \vdash t_2 : T_{11}$.
- Ak $\Gamma \vdash \text{true} : R$, potom $R = \text{Bool}$.
- Ak $\Gamma \vdash \text{false} : R$, potom $R = \text{Bool}$.
- Ak $\Gamma \vdash \text{if } t_1 \text{ then } t_2 \text{ else } t_3 : R$, potom $\Gamma \vdash t_1 : \text{Bool}$ a $\Gamma \vdash t_2, t_3 : R$.
- Ak $\Gamma \vdash 0 : R$, potom $R = \text{Nat}$.
- Ak $\Gamma \vdash \text{succ } t_1 : R$, potom $R = \text{Nat}$ a $\Gamma \vdash t_1 : \text{Nat}$.
- Ak $\Gamma \vdash \text{pred } t_1 : R$, potom $R = \text{Nat}$ a $\Gamma \vdash t_1 : \text{Nat}$.
- Ak $\Gamma \vdash \text{iszero } t_1 : R$, potom $R = \text{Bool}$ a $\Gamma \vdash t_1 : \text{Nat}$.
Dôkaz: Plynie priamo z definície typovacej relácie.
Poznámka
V rámci prednášok sa nebudeme venovať neformálnym matematickým dôkazom. Všetky tieto vlastnosti budú formálne dokázané v systéme Rocq v rámci cvičení.
I. Jednoznačnosť typov;
II. Bezpečnosť jazyka, ktorá pozostáva z vlastností:
- II.1. Progresia
- II.2. Stabilita
Progresia
Pre jednoducho typovaný $\lambda$-kalkul formulujeme vlastnosť progresie nasledujúcimi krokmi:
- II.1.A. Vetou o kanonických tvaroch hodnôt,
- II.1.B. Vetou o progresii.
Stabilita
Vlastnosť stability formulujeme pomocou nasledujúcich viet:
- II.2.C. Veta o komutatívnosti typového kontextu,
- II.2.D. Veta o zoslabení,
- II.2.E. Veta o zachovávaní typov substitúciou,
- II.2.F. Veta o stabilite.
Všetky tieto vlastnosti sú formulované (a boli dokázané) ako teorémy.
I. Jednoznačnosť typov jednoducho typovaného $\lambda$-kalkulu
Veta o jednoznačnosti typov:
Jednoducho typovaný term $t$ má v typovom kontexte $\Gamma$, $\Gamma~ \vdash~t:T$, najviac jeden typ $T$.
Formálne, nech $t$ je term, $T_1, T_2$ sú typy a $\Gamma$ je typový kontext. Potom platí: $$ (\forall t, T_1, T_2, \Gamma)(\ \Gamma \vdash t:T_1 \ \wedge\ \Gamma \vdash t:T_2 \ \Rightarrow\ T_1 = T_2\ ) $$
Dôsledky:
- Ak je term typovateľný, potom má jediný typ;
- Existuje práve jeden strom kontroly typov (alebo strom odvodenia) termu.
Uvedomme si, že táto veta platí len pre jednoduché typy. Pre ostatné typy musíme niekedy modifikovať túto vlastnosť.
II.1 Progresia
II.1.A. Veta o kanonických tvaroch hodnôt:
- Ak $v$ je hodnota typu $\mathtt{Bool}$, potom $v$ je buď $\mathtt{true}$ alebo $\mathtt{false}$;
- Ak $nv$ je hodnota typu $\mathtt{Nat}$, potom $nv$ je buď $\mathtt{0}$ alebo $\mathtt{succ}(nv)$;
- Ak $v$ je hodnota typu $T_1\rightarrow T_2$, potom $v = \lambda x:T_1.t_2$.
Poznámka
- Táto veta hovorí o tom, aké sú možné tvary hodnôt typov v jednoducho typovanom $\lambda$-kalkule.
- Kanonický tvar hodnôt je jednoznačný tvar, v ktorom môžu byť hodnoty prezentované.
Pomocou tejto vety môžeme formulovať nasledujúcu vetu o progresii pre jednoduché typy.
II.1.B. Veta o progresii:
Nech $t$ je uzavretý správne typovaný term $\vdash t:T$ pre určitý typ $T$.
Potom buď:
- $t$ je hodnota, alebo
- existuje term $t'$, taký, že $t \rightarrow t'$.
Formálne, nech $t$ je term, $T$ je typ a predikát $isvalue$ vráti hodnotu pravda ak $t$ je hodnota, potom: $$ (\forall t, T)(\ \vdash t:T \ \Rightarrow\ isvalue(t)\ \vee\ (\exists t')(\ t \rightarrow t'\ )\ ) $$
Všimnime si, že term $\vdash t:T$ má prázdny typový kontext $\Gamma$, pretože je to uzavretý term.
II.2 Stabilita
Ďalej dokážeme, že vyhodnocovací proces zachováva typy, t.j., že jednoducho typovaný $\lambda$-kalkul má vlastnosť stability.
Najprv uvedieme dve pomocné vety, ktoré vyjadrujú vlastnosti typového kontextu, a potom vlastnosť substitúcie.
II.2.C. Veta o komutatívnosti typového kontextu:
Táto veta hovorí, že na poradí deklarácií v typovom kontexte nezáleží.
Nech $\Gamma \vdash t:T$ je term a $\Delta$ je permutáciou $\Gamma$. Potom $\Delta \vdash t:T$ je rovnaký term.
Formálne, nech $\Gamma$ a $\Delta$ sú typové kontexty, $t$ je term a $T$ je typ, potom: $$ (\forall \Gamma, \Delta, t, T)(\ \text{perm}(\Gamma, \Delta)\ \wedge\ \Gamma \vdash t:T \ \Rightarrow\ \Delta \vdash t:T\ ) $$
Nemení sa ani hĺbka stromu kontroly typov.
Poznámka
Permutácia $\text{perm}(\Gamma, \Delta)$ znamená, že $\Delta$ obsahuje presne tie isté deklarácie ako $\Gamma$, len možno v inom poradí. Poradie deklarácií teda neovplyvňuje typovanie termu.
II.2.D. Veta o zoslabení:
Táto veta hovorí, že do typového kontextu môžeme pridať deklaráciu ľubovoľnej premennej, ktorá sa nevyskytuje v terme na pravej strane sekventu.
Nech $\Gamma \vdash t:T$ je term a $x:S$ je premenná, ktorá nie je deklarovaná v typovom kontexte $\Gamma$.
Potom $\Gamma, x:S \vdash t:T$ je term.
Jeho strom kontroly typov má rovnakú hĺbku ako pôvodný strom.
Formálne, nech $\Gamma$ je typový kontext, $t$ je term, $T$ a $S$ sú typy, a $x$ je premenná, potom: $$ (\forall \Gamma, t, T, x, S)(\ \Gamma \vdash t:T\ \wedge\ x \notin \text{dom}(\Gamma)\ \Rightarrow\ \Gamma, x:S \vdash t:T\ ) $$
Poznámka
$\text{dom}(\Gamma)$ označuje množinu premenných, ktoré sú deklarované v typovom kontexte $\Gamma$.
II.2.E. Veta o zachovávaní typov substitúciou:
Táto veta hovorí, že substitúcia zachováva typy, t.j. po vykonaní substitúcie na terme sa jeho typ nemení.
Nasledujúca veta vyjadruje dôležitú vlastnosť typovacej relácie pri substitúcii.
Ak máme termy $\Gamma,x:S\vdash t:T$ a $\Gamma\vdash s:S$,
potom substitúciou termu $s$ za premennú $x$ sa typ termu $t$ nezmení:
$$ \Gamma\vdash~[x\mapsto s]~t:T $$
Formálne, nech $\Gamma$ je typový kontext, $t$ a $s$ sú termy, $x$ je premenná a $S, T$ sú typy, potom: $$ (\forall \Gamma, t, s, x, S, T)(\ \Gamma, x:S \vdash t:T\ \wedge\ \Gamma \vdash s:S\ \Rightarrow\ \Gamma \vdash [x \mapsto s]t:T\ ) $$
II.2.F. Veta o stabilite:
Táto veta hovorí, že počas vyhodnotenia (redukcie) sa typ termu nemení, zachováva sa.
Až teraz môžeme formulovať vetu o stabilite, t.j. zachovaní typov vyhodnotením.
Ak máme term $\Gamma\vdash t:T$ a term $t$ sa redukuje v jednom kroku na $t'$, t.j.
$$ t \rightarrow t', $$
potom
$$ \Gamma\vdash~t':T $$
je term toho istého typu.
Formálne, nech $\Gamma$ je typový kontext, $t$ a $t'$ sú termy a $T$ je typ, potom: $$ (\forall \Gamma, t, t', T)(\ \Gamma \vdash t:T\ \wedge\ t \rightarrow t'\ \Rightarrow\ \Gamma \vdash t':T\ ) $$
Po dokázaní týchto vlastností môžeme konštatovať, že
Jednoducho typovaný $\lambda_{\rightarrow}$-kalkul je jednoznačne typovaný a bezpečný.
$\lambda$-kocka
$\lambda$-kocka opisuje vzťahy medzi dôležitými teóriami typov. Vychádzajúc z $\lambda{\rightarrow}$ kalkulu v ľavo dole až po kalkul induktívnych konštrukcií (na ktorom je postavený systém Rocq) v pravo hode, zobrazuje v rôznych osiach ako môžu byť definované jednotlivé teórie typov kombináciou rôznych vlastností.
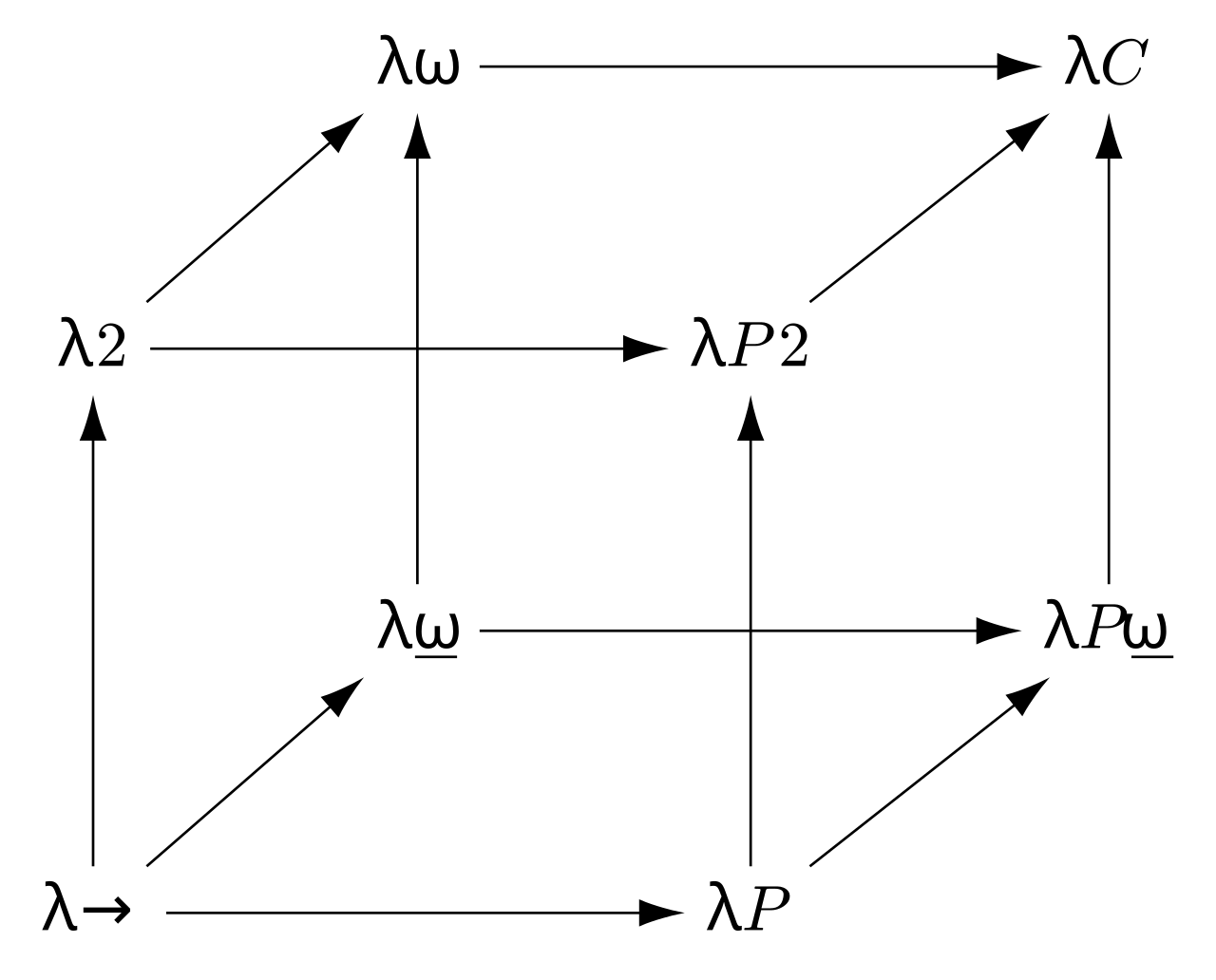
- Každý rozmer kocky zodpovedá novému typu vzťahov medzi termami a typmi.
- Vzťah znamená schopnosť termu alebo typu byť aplikovaný na iný term alebo typ.
Príslušné rozmery λ-kocky zodpovedajú:
- x-os (→): typy môžu byť aplikované na termy, čo zodpovedá závislým typom.
- y-os (↑): termy môžu byť aplikované na typy, čo zodpovedá polymorfizmu.
- z-os (↗): typy môžu byť aplikované na typy, čo zodpovedá (viazaným) typovým operátorom.
Rôzne spôsoby, ako kombinovať tieto tri rozmery, vytvárajú 8 vrcholov kocky, pričom každý zodpovedá inému typu typovaného systému.
V následujúcej tabuľke sú zhrnuté vrcholy $\lambda$-kocky a vlastnosti, ktoré jednotlivé teórie typov podporujú.
| $t$ $t$ | $t$ $T$ | $T$ $t$ | $T$ $T$ | |
|---|---|---|---|---|
| λ→ | áno | nie | nie | nie |
| λP | áno | áno | nie | nie |
| λ2 | áno | nie | áno | nie |
| λ$\underline{ω}$ | áno | nie | nie | áno |
| λP2 | áno | áno | áno | nie |
| λP$\underline{ω}$ | áno | áno | nie | áno |
| λω | áno | nie | áno | áno |
| λC | áno | áno | áno | áno |
V rámci nasledujúcich prednášok budeme jazyk $\lambda\to$ rozširovať do troch rozmerov a konštruovať nasledujúce teorie typov:
- Lambda $λP$ (niekedy označovaný aj $λ\Pi$) pridaním závislých typov.
- Systém $\lambda \underline{\omega}$ pre zavedenie typových konštruktorov.
- Systém F (niekedy označovaný aj $λ2$) pridaním polymorfizmu.
Zdroje
- Pierce, Benjamin C. Types and programming languages. MIT press, Cambridge, 2001 (Перевод на русский язык: Бенджамин Пирс. Типы в языках программирования. — Добросвет, 2012. — ISBN 978-5-7913-0082-9)
- Pierce, Benjamin C et al.: Software Foundations, Electronic textbook, 2024
- Lecture notes, CS 152: Programming Languages, Harvard University, 2024
- Lecture notes, CS242: Programming Languages, Stanford University, 2024
- Valerie Novitzká, Daniel Mihályi: Teória typov, TU Košice, 2015