Základne pojmy
Teória typov
- Zaoberá sa štúdiom princípov a vlastností typových systémov.
- Je formálna reprezentácia určitého typového systému.
Typový systém
v informatike je semiformálna metóda pre
- zavedenie základných, preddefinovaných typov jazyka a ich operácií,
- popis konštrukcie jednoduchých a zložených typov a ich vlastností,
- priradenie typu každej vypočítanej hodnote (typová anotácia),
- dôkaz neprítomnosti chybného správania programov (type checking).
Typ
- súbor hodnôt, ktoré môžu byť reprezentované v počítači spolu s
- množinou operácií, ktoré sa na nich môžu vykonávať.
Statické vs dynamické typované jazyky
-
Statické typované jazyky: kontrola sa vykonáva počas kompilácie, čo znamená, že typy premenných a funkcií sú overené pred spustením programu. Týmto spôsobom programátor získava cennú spätnú väzbu už v čase kompilácie, čím sa znižuje pravdepodobnosť chýb pri behu.
-
Dynamické typované jazyky: umožňujú priraďovať typy k premenným až počas behu programu, čo poskytuje flexibilitu a rýchlejšie prototypovanie. Avšak dynamické typovanie môže viesť k runtime chybám, ktoré nie sú zachytené pred spustením programu.
Silné vs slabé typované jazyky
-
Silné typované jazyky: vyžadujú prísne dodržiavanie typov, to znamená, že pri pokuse vykonať operáciu s hodnotami rôznych typov, prekladač vráti chybu.
-
Slabé typované jazyky: umožňujú implicitné konverzie medzi rôznymi typmi, čo uľahčuje písanie kódu, avšak môže viesť k neočakávaným výsledkom alebo chybám.
Implicitné vs explicitné typované jazyky
-
Implicitné typované jazyky: umožňuje prekladaču odvodzovať typy bez nutnosti, aby ich programátor vyjadroval explicitne.
-
Explicitné typované jazyky: naopak vyžadujú, aby programátor určil typy premenných jasne, čím sa zvyšuje čitateľnosť kódu, ale aj jeho zložitosť jeho písania.
Úvod do teórie typov a výpočtových modelov
V roku 1901 Bertrand Russell publikoval kontradikciu, ktorú objavil v teórii množín analýzou Cantorovej vety, že neexistuje zobrazenie
$$ F: X \to \mathcal{P}(X) $$
ktoré by bolo surjektívne.
To znamená, že $F$ nemôže byť také, že každý prvok $b$ množiny $\mathcal{P}(X)$ je rovný $F(a)$ pre nejaký prvok $a$ množiny $X$. To sa dá „intuitívne“ vyjadriť tým, že existuje viac podmnožín $X$ ako prvkov $X$. Dôkaz tejto skutočnosti je prostý. Majme nasledujúcu podmnožinu $X$:
$$ A = \{ x \in X \mid x \notin F(x) \}. $$
Táto podmnožina nemôže byť v v obore hodnôt $F$. Ak by totiž platilo $A = F(a)$ pre nejaké $a$, potom $$ \begin{array}{lcl} a \in F(a) & \text{ vtt. } & a \in A \\ & \text{ vtt. } & a \notin F(a) \end{array} $$ čo je kontradikcia.
Russell analyzoval, čo sa stane, ak túto vetu aplikujeme na prípad, keď $A$ je množina všetkých množín, pričom pripustíme, že takáto množina existuje. Z toho odvodil existenciu špeciálnej množiny množín, ktoré nepatria do seba samých: $$ R = \{ x \mid x \notin x \}. $$
Potom platí:
$$ R \in R \quad \text{ vtt. } \quad R \notin R. $$
Teória typov bola predstavená Bertrandom Russellom vo svojom diele The Principles of Mathematics v prílohe B: The Doctrine of Types z roku 1903, s cieľom riešiť niektoré kontradikcie, ktoré objavil v teórii množín.
Pokračovaním v tejto práci Whitehead a Russel v knihe Principia Mathematica z roku 1913 demonštrovali, že formálna logika dokáže vyjadriť veľkú časť matematiky.

Entscheidungsproblem
Entscheidungsproblem (problém rozhodnuteľnosti) kladie otázku, či je možné vytvoriť algoritmus, ktorý pre ľubovoľné matematické tvrdenie rozhodne, či je všeobecne pravdivé alebo nie. Tento problém bol formulovaný v roku 1928 Davidom Hilbertom a Wilhelmom Ackermannom, vychádzajúc z práce Bertranda Russella.

Výpočtové modely
Pred tým ako bolo možné odpovedať na otázku ktorú formuloval Entscheidungsproblem, bolo potrebné formálne definovať čo je vypočitateľná funkcia, algoritmus a výpočtový model, ktorý by vedel daný algoritmus aplikovať na matematické tvrdenia.
Výpočtový model je formálny model, ktorý slúži na opis toho, ako je možné vykonať výpočet, to znamená ako je vypočítaný výstup danej danej matematickej funkcie vzhľadom na daný vstup. Ide o matematickú abstrakciu, ktorá nám umožňuje skúmať rôzne aspekty výpočtov, ako sú rýchlosť, efektivita, zložitosť a limity toho, čo je možné vypočítať.
Čo znamená, že funkcia $$f: \mathbb{N} \to \mathbb{N}$$ je vypočítateľná?
Neformálne, funkcia je vypočitateľná, ak je možné za pomoci pera a papiera vypočítať $f(n)$, pre akékoľvek $n\in \mathbb{N}$.
V 30-tych rokov 20-teho storočia prišli traja výskumníci s tromi rozdielnymi výpočtovými modelmi.
Turingov stroj
V roku 1935 Alan Turing definoval počítač ako Turingov stroj.

- Funkcia je vypočítateľná ak môže byť vypočítaná Turingovým strojom.
- Je to matematický model výpočtu, ktorý pozostáva z:
- nekonečne dlhej pásky rozdelenej na bunky, ktoré môžu obsahovať symboly z určitej abecedy,
- hlavy, ktorá môže čítať alebo zapisovať symboly na páske a pohybovať sa po nej doľava alebo doprava,
- riadiacej jednotky so súborom stavov, ktoré určujú správanie stroja.
Výpočet prebieha podľa prechodovej funkcie, ktorá na základe aktuálneho stavu a prečítaného symbolu určuje nový stav, zápis na pásku a pohyb hlavy.
V roku 1936 Alan Turing vyvrátil Entscheidungsproblem prostredníctvom dôkazu problému zastavenia (halting problem).
Čiastočne rekurzívne funkcie
Kurt Gödel v roku 1929 definoval triedu čiastočne rekurzívne funkcie vo svojej práci v oblasti teórie formálnych systémov.

Čiastočne rekurzívne funkcie sú trieda funkcií, ktoré sú definované na prirodzených číslach. Tieto funkcie zahŕňajú tri základné typy operácií:
-
Primárna rekurzia - funkcie sú definované rekurzívnym spôsobom, pričom sú založené na jednoducho definovaných funkciách ako napríklad funkcia nuly (vždy vráti nulu) a funkcia nasledovníka (inkrementácia o 1).
-
Kompozícia - nové funkcie sú vytvárané zložením iných funkcií.
-
Minimizácia (hľadanie minima) - umožňuje definovať funkcie vyhľadávaním najmenšej hodnoty, pre ktorú platí určitá podmienka.
Kurt Gödel vyvrátil Entscheidungsproblem prostredníctvom svojich slávnych teorém neúplnosti (incompleteness theorems), ktoré publikoval v rokoch 1931 a 1935.
Gödelove výsledky ukázali, že:
-
Prvá teoréma o neúplnosti: Pre každý konzistentný formálny systém, ktorý je dostatočne silný na to, aby zahŕňal základnú aritmetiku, existujú výroky, ktoré nie je možné dokázať ani vyvrátiť v rámci tohto systému. To znamená, že niektoré pravdy sú "neprístupné" v rámci daného systému.
-
Druhá veta o neúplnosti: Žiadny dostatočne silný a konzistentný formálny systém nemôže dokázať svoju vlastnú konzistenciu. To implikuje, že ak je systém konzistentný, jeho konzistenciu nemožno dokázať pomocou jeho vlastných pravidiel.
Tieto výsledky znamenajú, že neexistuje univerzálny algoritmus, ktorý by mohol rozhodnúť pravdivosť všetkých výrokov v matematike, a teda Gödel dokázal, že Entscheidungsproblem nemá riešenie. Týmto spôsobom prispel k hlbokému prehodnoteniu základov matematiky a formálnych systémov, a jeho práca mala obrovský dopad na filozofiu matematiky, logiku a teoretickú informatiku.
$\lambda$-kalkul
V rokoch 1929 až 1932 Alfonzo Church definoval $\lambda$-kalkul ako formálny systém pre matematickú logiky. Následne dokázal, že funkcia je vypočítateľná len vtedy, ak ju je možné formulovať ako $\lambda$-term.
Church ukázal, že ak existuje algoritmus rozhodnuteľnosti pre všetky výrokové formuly v predikátovej logike, existuje aj algoritmus pre $\lambda$-kalkul. Avšak, pretože $\lambda$-kalkul umožňuje vytváranie nekonečných cyklov, vyplýva z toho, že neexistuje univerzálny algoritmus rozhodnuteľnosti.
Poznámka
Alfonzo Church bol školiteľom Alana Turinga počas doktorandského štúdia.
Poznámka
$\lambda$-kalkul sa neskôr stal základom pre programovacie jazyky funkcionálnej paradigmy.
Netypovaný jazyk čísel a boolovských hodnôt (NBL)
Pre demonštratívne účely začneme s definíciou jednoduchého funkcionálneho jazyka čísel boolovských hodnôt (NBL). Tento jazyk obsahuje iba niekoľko syntaktických prvkov, avšak poslúži ako vhodný úvod do netriviálnych konceptov definície programovacích jazykov, ako je abstraktná syntax, induktívne definície, dôkazy, sémantika (vyhodnotenie) a pod.
Základné syntaktické konštrukcie tohto jazyka sú termy.
Term je syntaktická fráza, ktorá reprezentuje výpočet.
Formálna definícia jazyka pozostáva z definície:
- formálnej syntaxe,
- formálnej sémantiky.
Formálna (abstraktná) syntax môže byť definovaná rôznymi spôsobmi, napríklad:
- gramatikou v Backus-Nuarovej forme,
- induktívne,
- odvodzovacími pravidlami.
Poznámka
Pri formálnej definícii jazyka je využívaná abstraktná syntax. Konkrétna syntax opisuje konkrétne programy.
- Konkrétna syntax sa týka špecifickej formy kódu, vrátane všetkých detailov, ako sú interpunkcia a kľúčové slová.
- Abstraktná syntax sa týka logického obsahu a štruktúry kódu, pracuje s ňou prekladač alebo interpreter.
Rozdiel medzi abstraktnou a konkrétnou syntaxou je zhrnutý v následujúcej tabuľke:
| Aspekt | Konkrétna syntax | Abstraktná syntax |
|---|---|---|
| Definícia | Ako je kód napísaný a viditeľný | Ako je štruktúra kódu logicky reprezentovaná |
| Účel | Definuje presnú formu a pravidlá jazyka | Reprezentuje logickú štruktúru a vzťahy |
| Obsahuje | Interpunkcia, kľúčové slová, formátovanie | Základné komponenty (výrazy, príkazy, atď.) |
| Príklad | if x > 0: print("Positive") |
Abstraktná reprezentácia s uzlami pre podmienku a akciu |
| Fáza preklad | Spracováva syntaktický analyzátor (parser) | Spracováva prekladač alebo interpreter na analýzu a transformácie |
Syntax NBL
Množinu legálnych termov $t$ jazyka nazveme $t \in Term$.
Induktívna definícia syntaxe NBL
Syntax NBL je možné definovať ako najmenšiu množinu $Term$ následovne:
- $\{true, false, 0 \} \subset Term$,
- ak $t_1 \in Term$ potom $\{succ\ t_1, pred\ t_1, iszero\ t_1 \} \subset Term$,
- ak $t_1, t_2, t_3 \in Term$ potom $if\ t_1\ then\ t_2\ else\ t_3 \in Term$.
Slovo najmenšia znamená, že term jazyka NBL nie je možné skonštruovať inak ako pomocou pravidiel 1-3.
Backus–Naurova forma (BNF)
BNF používa na opis syntaxe produkčné pravidlá:
$$t::=\ true\ |\ false\ |\ if\ t\ then\ t\ else\ t\ |\ 0\ |\ succ\ t\ |\ pred\ t\ |\ iszero\ t$$
- $t$ na ľavej strane znamená, že definujeme syntax termov, ktoré všeobecne označujeme $t$,
- $::=$ oddeľuje ľavú a pravú stranu produkčného pravidla
- $|$ oddeľuje možné tvary, štruktúru termov (syntaktické frázy)
- $t$ na pravej strane je metapremenná, t.j.
– premenná, pretože za ňu možno dosadiť ľubovoľný term a
– meta, pretože nie je premennou jazyka NBL, ale metajazyka, ktorý popisuje NBL.
Gramatika v tvare odvodzovacích pravidiel
Odvodzovacie pravidlo má všeobecný tvar:
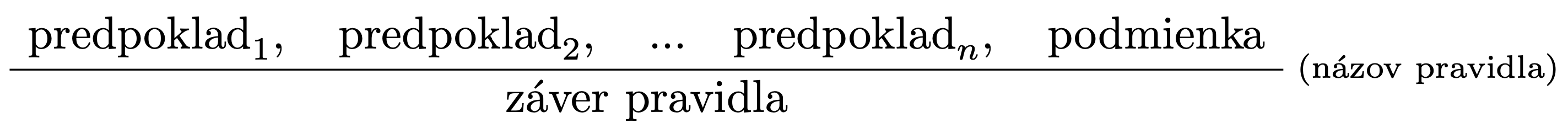
- Predpoklady aj záver sú tvrdenia; ak sú všetky predpoklady pravdivé, potom je pravdivý aj záver.
- Záver je len jeden.
- Názov pravidla je zvyčajne skratka, ktorá identifikuje pravidlo.
- Ak odvodzovacie pravidlo nemá predpoklady, nazýva sa axióma.
- Odvodzovacie pravidlo môže obsahovať aj podmienku, ktorá definuje kedy je možné dané pravidlo aplikovať.
Syntax jazyka NBL je možné zadefinovať prostredníctvom následujúcich odvodzovacích pravidiel:

Príklad
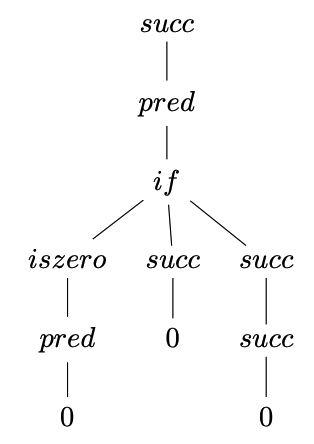
Majme daný nasledujúci term jazyka NBL: $$t=succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))$$ Načrtnite abstraktný syntaktický strom termu $t$.
Riešenie
Abstraktný syntaktický strom termu $t$
Príklad
Dokážte prostredníctvom vyššie definovaných odvodzovacích pravidiel, že term $t$ patrí do množiny $Term$ (je syntakticky korektne skonštruovaný). $$t=succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))$$
Riešenie
- Odvodzovací strom (dôkaz) je konštruovaný od koreňa k listom.
- V koreni sa nachádza dokazované tvrdenie (v našom prípade $t\in Term$).
- Následne je konštruovaný strom tak, že v každom kroku odvodenia je aplikované príslušné odvodzovacie pravidlo.
- Strom je korektne skonštruovaný, ak všetky listy stromu sú axiómy a teda je možné tvrdiť, že výraz v koreni stromu je dokázaný.

Funkcie na termoch NBL
Je možné definovať viacero funkcií, ktoré umožňujú skúmať rôzne vlastnosti termov v jazyku NBL.
Funkciu poskytujúcu veľkosť termu (počet uzlov v syntaktickom strome) je možné špecifikovať ako: $$size : Term \to Nat$$ a definovať induktívne: $$ \begin{aligned} size(true) &= 1 \\ size(false) &= 1 \\ size(0) &= 1 \\ size(succ \, t_1) &= size(t_1) + 1 \\ size(pred \, t_1) &= size(t_1) + 1 \\ size(iszero \, t_1) &= size(t_1) + 1 \\ size(if \, t_1 \, \text{then} \, t_2 \, \text{else} \, t_3) &= size(t_1) + size(t_2) + size(t_3) + 1 \end{aligned} $$
Funkciu poskytujúcu hĺbku termu (počet uzlov v najdlhšej vetve syntaktického stromu) je možné špecifikovať ako:
$$depth : Term \to Nat$$
a definovať induktívne:
$$ \begin{aligned} depth(true) &= 1 \\ depth(false) &= 1 \\ depth(0) &= 1 \\ depth(succ \, t_1) &= depth(t_1) + 1 \\ depth(pred \, t_1) &= depth(t_1) + 1 \\ depth(iszero \, t_1) &= depth(t_1) + 1 \\ depth(if \, t_1 \, \text{then} \, t_2 \, \text{else} \, t_3) &= max(depth(t_1),\ depth(t_2),\ depth(t_3)) + 1 \end{aligned} $$
Funkciu poskytujúcu množinu konštánt $Con(t)$ v terme $t$ je možné špecifikovať ako:
$$Con : Term \to P(\{0, true, false\})$$ a definovať induktívne:
$$ \begin{aligned} Con(true) &= \{true\} \\ Con(false) &= \{false\} \\ Con(0) &= \{0\} \\ Con(succ \, t_1) &= Con(t_1) \\ Con(pred \, t_1) &= Con(t_1) \\ Con(iszero \, t_1) &= Con(t_1) \\ Con(if \, t_1 \, \text{then} \, t_2 \, \text{else} \, t_3) &= Con(t_1) \cup Con(t_2) \cup Con(t_3) \end{aligned} $$
Poznámka
Funkcie $size, depth, con$ sú štrukturálne rekurzívne.
Príklad
Majme daný následujúci term $t$: $$t=succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))$$ Vypočítajte jeho veľkosť.
Riešenie
Aplikujeme funkciu $size$ na term $t$:
$$ \begin{array}{ll} size(\ succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))\ ) & = \\ size(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0)))\ ) + 1 & = \\ size(\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))\ ) + 1 + 1 & = \\ size(\ iszero\ (pred\ 0)\ ) + size(\ succ\ 0\ ) + size(\ succ\ (succ\ 0)\ ) + 1 + 1 + 1 & = \\ size(\ pred\ 0\ ) + 1 + size(\ 0\ ) + 1 + size(\ succ\ 0\ ) + 1 + 1 + 1 + 1 & = \\ size(\ 0\ ) + 1 + 1 + 1 + 1 + size(\ 0\ ) + 1 + 1 + 1 + 1 + 1 & = \\ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 & = \\ 11 \end{array} $$
Príklad
Majme daný následujúci term $t$: $$t=succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))$$ Vypočítajte jeho hĺbku.
Riešenie
Aplikujeme funkciu $depth$ na term $t$: $$ \begin{array}{ll} depth(\ succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))\ ) & = \\ depth(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0)))\ ) + 1 & = \\ depth(\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))\ ) + 1 + 1 & = \\ max(\ depth(\ iszero\ (pred\ 0)\ ),\ depth(\ succ\ 0\ ),\ depth(\ succ\ (succ\ 0)\ )\ ) + 1 + 1 + 1 & = \\ max(\ depth(\ pred\ 0\ ) + 1,\ depth(\ 0\ ) + 1,\ depth(\ succ\ 0\ ) + 1\ ) + 3 & = \\ max(\ depth(\ 0\ ) + 1 + 1,\ 1 + 1,\ depth(\ 0\ ) + 1 + 1\ ) + 3 & = \\ max(\ 1 + 1 + 1,\ 1 + 1,\ 1 + 1 + 1\ ) + 3 & = \\ max(\ 3,\ 2,\ 3\ ) + 3 & = \\ 3 + 3 = 6 \end{array} $$
Príklad
Majme daný následujúci term $t$: $$t=succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))$$ Vypočítajte množinu konštánt, ktoré obsahuje term $t$.
Riešenie
Aplikujeme funkciu $con$ na term $t$: $$ \begin{array}{ll} con(\ succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))\ ) & = \\ con(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0)))\ ) & = \\ con(\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))\ ) & = \\ con(\ iszero\ (pred\ 0)\ ) \cup con(\ succ\ 0\ ) \cup con(\ succ\ (succ\ 0)\ ) & = \\ con(\ pred\ 0\ ) \cup con(\ 0\ ) \cup con(\ succ\ 0\ ) & = \\ con(\ 0\ ) \cup \{ 0 \} \cup con(\ 0\ ) & = \\ \{ 0 \} \cup \{ 0 \} \cup \{ 0 \} = \{ 0 \} \end{array} $$
Využitím vyššie definovaných funkcií je možné formulovať množstvo zaujímavých vlastností prostredníctvom ktorých, je možné matematicky dokázať korektnosť našej formálnej definície.
Veta: Počet rozličných konštánt v terme $t$ nie je väčší ako veľkosť termu $t$. $$ \forall t.(\ |con(t)| \leq size(t)\ )$$
Poznámka
Dané vlastnosti je možné dokázať neformálnymi matematickými dôkazmi, zväčša za využitia metódy nazývanej štrukturálna indukcia. Avšak v rámci prednášok resp. práce na doma, budeme dané vlastnosti dokazovať prostredníctvom formálnych dôkazov v rámci interaktívneho dokazovacieho systému Coq.
Sémantika NBL
Pre definíciu sémantiky termov jazyka NBL bude využitá sémantická metóda: štrukturálna operačná sémantika, niekedy nazývaná aj sémantika malých krokov (z ang. small step semantics).
Sémantika jazyka termov NBL je definovaná ako relácia vyhodnotenia (prechod) a uskutočňuje sa redukciou termov: $$\boxed{ t \to t'} $$ Čítame: term $t$ sa vyhodnotí na term $t'$ v jednom kroku.
Je potrebné ešte zadefinovať produkčné pravidlá pre hodnoty $v$: $$ \begin{align*} & v ::= true \,|\, false \,|\, nv \\ & nv ::= 0 \,|\, succ \,~ nv \end{align*} $$
pričom množinu, ktorú opisuje daná gramatika nazveme $$\mathbb{Z} \cup \mathbb{N}_0$$
Sémantickú funkciu je následne možné špecifikovať ako $$S_{NBL}:Term \rightharpoonup \mathbb{Z} \cup \mathbb{N}_0$$ a je definovaná následovne: $$ S_{NBL}[|\ t\ |] = \begin{cases} v \quad \quad \text{ak } t \to^* v, \\ \\ \bot \quad \quad \text{inak}. \end{cases} $$
pričom správanie vyhodnocovacej relácie opisujú následujúce vyhodnocovacie pravidlá:

Príklad
Majme daný nasledujúci term $t$: $$t=succ(\ pred\ (\ if\ iszero\ (pred\ 0)\ then\ succ\ 0\ else\ (succ\ (succ\ 0))))$$ Vyhodnoťte ho.
Riešenie
Pre vyhodnotenie termu $t$ je potrebné opakovane aplikovať príslušné vyhodnocovacie pravidlá až do stavu, pokiaľ redukovaný term nie je v tvare hodnoty, alebo nie je možné použiť žiadne pravidlo.
$$ \begin{array}{l} succ(\ pred\ (\ if\ \underline{iszero\ (pred\ 0)}\ then\ succ\ 0\ else\ (succ\ (succ\ 0)))) \to \\ succ(\ pred\ (\ if\ \underline{iszero\ 0}\ then\ succ\ 0\ else\ (succ\ (succ\ 0)))) \to \\ succ(\ pred\ (\ \underline{if\ true\ then\ succ\ 0\ else\ (succ\ (succ\ 0))})) \to \\ succ(\ \underline{ pred\ (\ succ\ 0\ )} ) \to \\ succ(\ 0\ ) \end{array} $$
Nezmyselné termy
Takto definovaný netypovaný jazyk NBL umožňuje konštruovanie syntaktický správnych avšak nezmyselných termov, ako napríklad:
$$succ(true).$$
Je možné jednoducho dokázať, že $succ(true) \in Term$, avšak pri pokuse o jeho vyhodnotenie, nie je možné aplikovať žiadne pravidlo a vyhodnotenie sa zasekne (z ang. stucked). V takomto prípade daný term nemá význam.
Poznámka
Pridaním typového systému do jazyka je možné už pri syntaktickej kontrole odhaliť nezmyselné termy.
$\lambda$-kalkul
Je univerzálny formálny výpočtový model, ktorý je dokáže simulovať akýkoľvek Turingov stroj (a vice versa). $\lambda$-kalkul má široké využitie v informatike, medzi ktoré patri špecifikácia čŕt programovacích jazykov, návrh jazykov, implementácia jazykov a pri štúdiu typových systémov, pričom jeho definícia je základom programovacích jazykov funkcionálnej paradigmy.
Dôležitosť $\lambda$-kalkulu spočíva v tom, že ho možno súčasne chápať ako:
- najjednoduchší univerzálny Turingovsky úplný programovací jazyk,
- matematický objekt, o ktorom možno dokázať dôležité vlastnosti.
$\lambda$-kalkul pozostáva z jedného pravidla redukcie (nahradenie premenných) a jedného tvaru definície funkcie. λ-kalkulus je univerzálny v tom zmysle, že akúkoľvek vypočítateľnú funkciu možno vyjadriť a vyhodnotiť pomocou tohto modelu. Je teda ekvivalentný s Turingovými strojmi. Avšak $\lambda$-kalkul kladie dôraz na použitie redukčných pravidiel a nezaujíma sa o samotný stroj, ktorý ich implementuje. Je to prístup viac súvisiaci so softvérom než s hardvérom.
Základným konceptom v $\lambda$-kalkule je "Všetko je funkcia!". V $\lambda$-kalkule je funkcia definovaná ako $\lambda$-abstrakcia: $$\lambda x.t,$$ kde:
- $\lambda$ je metapremenná označujúca začiatok funkcie,
- $x$ je parameter funkcie,
- $t$ je telo funkcie.
Príklad
V klasickej matematickej notácii je možné funkciu nasledovníka celého čísla definovať nasledovne: $$f(x)=x+1,$$ kde: $f$ je meno funkcie, $x$ je parameter funkcie, $x+1$ je telo funkcie.
Tú istú funkciu $f$ je možné prepísať do notácie $\lambda$-kalkulu nasledovne: $$f=\lambda x.x+1.$$ Funkciu $f$ je nasledne možné aplikovať na ľubovoľný argument napr. číslo $3$ a jeho dosadením - substitúciou za parameter $x$ v tele termu: $$f ~3= 3+1=4.$$
Poznámka
$f ~3$ znamená aplikáciu funkcie $f$ na argument $3$.
Syntax $\lambda$-kalkulu
Syntax netypovaného čistého (pure) $\lambda$-kalkulu definujeme nasledujúcim produkčným pravidlom v Backus-Naurovej forme: $$t::= x\ |\ \lambda x.t\ |\ t\ t$$ kde:
- $t$ označuje $\lambda$-term,
- $x$ označuje ľubovoľnú premennú
- $\lambda x.t$ je $\lambda$-abstrakcia, definícia funkcie s parametrom $x$ a telom funkcie $t$.
- $\ t\ t$ je aplikácia funkcie $t$ na argument $t$ (prvé $t$ je aplikované na druhé $t$).
Množinu ktorú opisuje táto gramatika nazývame jazyk $\Lambda$, pričom množinu všetkých premenných nazveme $Var$. Term $t$ je správne skonštruovaný ak $t \in \Lambda$.
Konvencie syntaxe $\lambda$-kalkulu
Pre doplnenie definície abstraktnej syntaxe $\lambda$-kalkulu, budeme využívať nasledujúce konvencie:
-
Vynechávame vonkajšie zátvorky: $$(t\ u) = t\ u $$
-
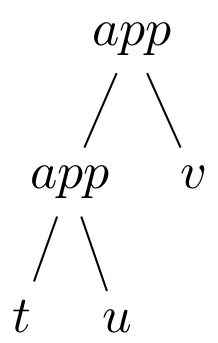
Aplikácia je ľavo asociatívna: $$t\ u\ v = (t\ u)\ v$$ Pričom abstraktný syntaktický strom termu $t\ u\ v$ je zobrazený na následujúcom obrázku:
-
$\lambda$-abstrakcia je pravo asociatívna (t.j. telo abstrakcie sa tiahne do prava, pokiaľ je to možné): \begin{align*} \lambda x. t\ u & = \lambda x. (t\ u) \newline \lambda x.\lambda y. x\ y\ z & = \lambda x.(\lambda y.(\ (x\ y)\ z)\ ) \end{align*} Pričom abstraktný syntaktický strom termu $\lambda x.\lambda y. x\ y\ z$ je zobrazený na následujúcom obrázku:
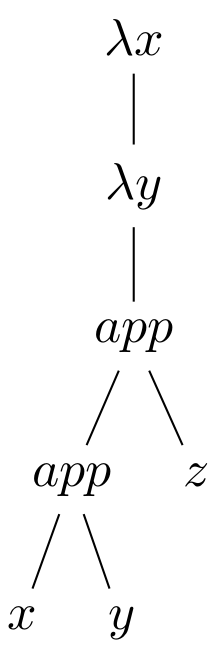
-
Zápis viacnásobnej abstrakcie je možné skrátiť: $$\lambda x.\lambda y.\lambda z.t = \lambda x\ y\ z.t$$
Syntax v tvare odvodzovacích pravidiel
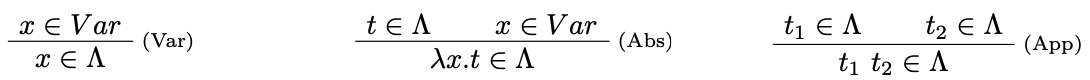
Funkcia viacerých premenných
Z predchádzajúcich sekcií je zrejme, že syntax $\lambda$-kalkulu umožňuje definíciu funkcií s viacerými parametrami. Napríklad funkciu: $$f(x,y)=x-y,$$ je možné definovať v $\lambda$-kalkule ako: $$\lambda x. \lambda y. x - y$$
Poznámka
Pre demonštračné účely aktuálne miešame infixnú s postfixnou notáciou, avšak je potrebné si uvedomiť, že všetko v $\lambda$-kalkule je funkcia. Operátor minus $-$ je taktiež definovaný ako samostatná funkcia a preto v čistom $\lambda$-kalkule je funkcia $f(x,y)=x-y$ definovaná ako $\lambda x. \lambda y. minus\ x\ y$, kde je term $minus$ je funkcia dvoch premenných.
Príklad
Ďalšie funkcie a ich definícia v $\lambda$-kalkule:
| Matematická notácia | $\lambda$-kalkul |
|---|---|
| $ f(x) = x $ | $ \lambda x. x $ |
| $ f(x, y) = x $ | $ \lambda x. \lambda y. x $ |
| $ f(f(x)) $ | $ \lambda f. \lambda x. f\ (f\ x) $ |
Poznámka
Syntaktický správny term nemusí byť vypočítateľný.
Voľné a viazané premenné
Pred definíciou sémantiky λ-kalkulu musíme definovať pojmy výskytu voľnej a viazanej premennej.
- Výskyt premennej $x$ je viazaný, ak sa $x$ nachádza v abstrakcii $\lambda x.t$ v tele termu $t$. Inými slovami: abstrakcia $\lambda x.t$ viaže premennú $x$ v terme $t$.
- Výskyt premennej $x$ je voľný, ak sa nachádza v pozícii, kde nie je viazaná abstrakciou.
Napríklad, v $\lambda$-termoch:
- $x\ y$
- $\lambda y.x\ y$
sú výskyty premennej $x$ voľné, ale v termoch:
- $\lambda x.x$
- $\lambda z.\lambda x.\lambda y.x(y\ z)$
sú výskyty $x$ viazané.
Poznámka
Pojem výskyt voľnej premennej sa často skracuje na pojem voľná premenná.
Formálne je možné zadefinovať pojem voľnej premennej ako funkciu $FV$, ktorá vráti množinu všetkých voľných premenných nasledovne: $$FV (x) = \{x\}$$ $$FV (\lambda x.t) = FV(t)\ \backslash\ \{x\}$$ $$FV(t_1\ t_2) = FV(t_1) \cup FV(t_2) $$
Kombinátor
Term bez voľných premenných sa nazýva uzavretý. Uzavreté termy sa nazývajú kombinátory.
Štandardné (často používané) kombinátory sa zvyknú označovať: \begin{align*} I & = \lambda x.x \newline K & = \lambda x.\lambda y.x \newline S & = \lambda f.\lambda g.\lambda x.f \ x \ (g \ x) \newline D & = \lambda x.x \ x \newline Y & = \lambda f.(\lambda x.(f \ (x \ x))\ \lambda x.(f \ (x \ x))) \end{align*}
Každý kombinátor sa dá vyjadriť použitím kombinátorov S, K a I.
$\alpha$-ekvivalencia
$\lambda$-kalkul používa statický rozsah viditeľnosti (static scoping). To znamená, že $$(\lambda \textcolor{blue}{x}. \textcolor{blue}{x}) (\lambda \textcolor{red}{x}. \textcolor{red}{x})$$ je ekvivalentné $$(\lambda \textcolor{blue}{x}. \textcolor{blue}{x}) (\lambda \textcolor{red}{y}. \textcolor{red}{y})$$
Premenovanie viazaných premenných zachováva význam. Nazýva sa $\alpha$-konverzia.
Substitúcia
Pre definovanie sémantiky netypovaného $\lambda$-kalkulu ešte potrebujeme definovať substitúciu.
Zavedieme označenie: $$ [x \mapsto t_2 ]t_1, $$ ktoré znamená, že v $\lambda$-terme $t_1$ nahradíme všetky voľné výskyty premennej $ x$ termom $ t_2 $.
Substitúciu definujeme (induktívne) pre všetky $\lambda$-termy nasledovne: \begin{array}{lcl} [x \mapsto s]x &=& s \newline [x \mapsto s]y &=& y \quad \quad \quad \quad \quad \quad \text{ ak } x \neq y \newline [x \mapsto s](\lambda y.t_1) &=& \lambda y.[x \mapsto s]t_1 \quad \text{ ak } y \neq x \text{ a } y \notin FV(s) \newline [x \mapsto s](t_1 \ t_2) &=& [x \mapsto s]t_1 \ [x \mapsto s]t_2 \end{array}
Substitúcia je asociatívna zľava: $$ [x \mapsto t_2]t_1 \ [y \mapsto t_4]t_3 = ([x \mapsto t_2]t_1) \ [y \mapsto t_4]t_3 $$
Príklad
Príklady substitúcie termov (modrou farbou sú označené argumenty, teda hodnoty, ktoré sa substituujú za parametre):
- Substitúcia sa neuskutoční, pretože premenná $x$ je síce viazaná, ale nevyskytuje sa v tele $y$: $$[x \mapsto \textcolor{blue}{\lambda x.y}](\lambda x.y) = \lambda x.y$$
- premenná $y$ je v tele abstrakcie voľná, nahradíme ju termom $\lambda x.y$: $$[y \mapsto \textcolor{blue}{\lambda x.y}](\lambda x.y) = \lambda x.\textcolor{blue}{\lambda x.y} = \lambda x x.y$$
- $y$ je v tele abstrakcie $y$ voľná, nahradíme ju termom $\lambda x.x$; $$[y \mapsto \textcolor{blue}{\lambda x.x}](\lambda x.y) = \lambda x.\textcolor{blue}{\lambda x.x} = \lambda x x.x$$
- $y$ je v tele abstrakcie $y$ voľná, nahradíme ju termom $\lambda y.y$ $$[y \mapsto \textcolor{blue}{\lambda y.y}](\lambda x.y) = \lambda x.\textcolor{blue}{\lambda y.y} = \lambda x y.y$$
Sémantika $\lambda$-kalkulu
Sémantiku $\lambda$-kalkulu definujeme prostredníctvom sémantickej metódy nazývanej štrukturálna operačná sémantika (sémantika malých krokov).
$\beta$-redukcia je proces vyhodnotenia $\lambda$-termov postupným "vkladaním argumentov do funkcií".
Majme term: $$(\lambda x. t_1)\ t_2$$ kde:
- $x$ je parameter funkcie,
- $t_1$ je telo funkcie,
- $t_2$ je argument funkcie.
Vyhodnotenie
Sémantika termu $\lambda$-kalkulu je postupne aplikovanie funkcii na argumenty.
- Každý krok pozostáva z prepísania termu aplikácie (kde prvý člen aplikácie musí byť abstrakcia) tak, že substituujeme druhý člen aplikácie $t_2$ (argument) za parameter $x$ v tele $t_1$.
- Podmienkou je aby parameter $x$ bol v tele $t_1$ voľný.
- Tento proces sa nazýva $\beta$-redukcia, pretože sa redukuje - skracuje pôvodný term.
Formálne definujeme $\beta$-redukciu ako vyhodnocovaciu reláciu: $$\boxed{t \to t'}$$ ktorú je možné prečítať ako "term $t$ sa redukuje na term $t'$".
- Term, ktorý nie je možné ďalej redukovať je v normálnej forme.
- Každý term, ktorý sa dá redukovať sa nazýva redex.
$\beta$ - redukcia je proces nahradenia každého voľného výskytu parametra $x$ v tele funkcie $t_1$ argumentom $t_2$. (Z pôvodného termu sa odstráni $\lambda x$.) $$(\lambda x. t_1)\ t_2 \to [x \mapsto t_2]t_1.$$ Napríklad: \begin{align*} & (\lambda x. x)\ y \rightarrow [x \mapsto y] x = y \newline & (\lambda x. (f\ x))\ y \rightarrow [x \mapsto y] f\ x = f\ y \newline & (\lambda x. \lambda y. f \ x \ y)\ u\ v \rightarrow ([x \mapsto u] \lambda y. f \ x \ y)\ v = (\lambda y. f \ u \ y)\ v \rightarrow [y \mapsto v] f \ u \ y = f \ u \ v \end{align*}
Poznámka
Medzikroky so zápisom substitúcie budeme vynechávať. Napríklad namiesto zápisu redukcie posledného termu budeme používať len: $$(\lambda x. \lambda y. f \ x \ y)\ u\ v \rightarrow (\lambda y. f\ u \ y)\ v \rightarrow f \ u \ v$$
Normálne formy v $\lambda$-kalkule
V $\lambda$-kalkule je koncept normálnych foriem kľúčový pre pochopenie toho, ako sa termy (výrazy) môžu redukovať alebo zjednodušovať. Existuje niekoľko druhov normálnych foriem, ktoré určujú, kedy sa $\lambda$-term už nemôže ďalej redukovať. Tieto normálne formy vznikajú aplikáciou $\beta$-redukcie $\eta$-redukcie, ktoré sú základnými operáciami používanými na zjednodušenie $\lambda$-výrazov. My sa budeme venovať dvom, ktoré sú potrebné pre demonštráciu rôznych redukčných stratégií.
1. Normálna forma (NF)
$\lambda$-term je v normálnej forme, ak sa už nemôže ďalej redukovať pomocou akéhokoľvek operácie, či už $\beta$-redukciou alebo $\eta$-redukciou. Toto je najúplnejší redukovaný stav, kde sa žiadne podvýrazy nemôžu ďalej zjednodušovať.
Príklad
Term nie je v normálnej forme:
$$(\lambda x. x\ y)\ z$$
Tento term sa môže redukovať na $z\ y$.
Na term v normálnej forme $z\ y$ nie možné aplikovať $\beta$-redukcie alebo $\eta$-redukcie, čo znamená, že term je úplne vyhodnotený.
2. Slabá normálna forma
$\lambda$-term je v slabej normálnej forme, ak vonkajšia časť výrazu už nemôže byť ďalej redukovaná, hoci podvýrazy môžu byť stále redukovateľné. Inými slovami, vrchol výrazu musí byť buď premenná, alebo lambda abstrakcia a na najvyššej úrovni sa nemôžu vykonávať žiadne $\beta$-redukcie.
Príklad
Term nie je v slabej normálnej forme:
$$(\lambda x. (\lambda y. (\lambda z.z)\ x))\ u$$
Na najvyššej úrovni je možná $\beta$-redukcia, term je redukovateľný.
Term je v slabej normálnej forme po jednom kroku redukcie:
$$(\lambda y. (\lambda z.z)\ u)$$
Vonkajšia časť (funkcia) nie je redukovateľná, hoci vnútorná časť $(\lambda z.z)\ u$ môže byť stále zjednodušená.
Táto normálna forma je dôležitá pri redukčných stratégiách, ktoré využívajú nestriktnú stratégiu vyhodnotenia. Výpočty môžu byť odložené a iba vonkajšia štruktúra je spočiatku vyhodnotená.
Striktné vs nestriktné stratégia vyhodnotenia
Striktná stratégia
(ang. Eager Evaluation) argumenty funkcií sa vyhodnotia vždy, bez ohľadu na to, čí sa nachádzajú v tele funkcie alebo nie.
Nestriktná stratégia
(ang. Lazy Evaluation) vyhodnotia sa len tie argumenty, ktoré sa používajú.
| Vyhodnotenie | Výhody | Nevýhody |
|---|---|---|
| Striktnáe vyhodnotenie | - Jednoduchosť ladenia | - Vyššia spotreba pamäte |
| - Predvídateľnosť správania programu | - Nemožnosť práce s nekonečnými štruktúrami | |
| Nestriktné vyhodnotenie | - Efektívnosť pamäte | - Zložitosti pri ladení |
| - Možnosť práce s nekonečnými štruktúrami | - Môže mať vyššie latencie | |
Redukčné stratégie
Vo všeobecnosti môže byť na konkrétnom $\lambda$-terme vykonaných mnoho možných $\beta$-redukcií. Ako je zvolená konkrétna $\beta$-redukcia, to opisuje špecifikácia, na základe ktorej je určené, ktorú z možných $\beta$-redukcií vykonať ako ďalšiu. Takáto špecifikácia sa nazýva redukčná stratégia. $\lambda$-kalkul nešpecifikuje redukčnú stratégiu, to znamená je nedeterministický. Avšak redukčná stratégia je potrebná v reálnych programovacích jazykoch na vyriešenie nedeterminismu.
Majme term: $$(\lambda x.x)\ ((\lambda x.x)\ (\lambda z.(\lambda x.x)\ z))$$ Nech $id=(\lambda x.x)$, potom predchádzajúci term je možné prepísať ako: $$id\ (id\ (\lambda z.id\ z))$$ V danom terme sa vyskytujú tri redexy:
- $\underline{id\ (id\ (\lambda z.id\ z))}$
- $id\ (\underline{id\ (\lambda z.id\ z)})$
- $id\ (id\ (\lambda z.\underline{id\ z}))$
Existuje niekoľko rôznych stratégií vyhodnotenia, ktoré sa skúmajú pri návrhu programovacích jazykov. Každá stratégia jednoznačne definuje, ktorý redex má byť použitý v ďalšom kroku vyhodnotenia. Uvedieme 4 populárne stratégie.
Úplná $\beta$-redukcia
Striktná stratégia, pričom v každom kroku redukcie je zvolený ľubovoľný redex: $$id\ (id\ (\lambda z.\underline{id\ z})) \to id\ (\underline{id\ (\lambda z. z)}) \to \underline{id\ (\lambda z. z)} \to (\lambda z. z) $$
Normálna $\beta$-redukcia
Striktná stratégia, pričom v každom kroku redukcie je zvolený ľavý vonkajší redex: $$\underline{id\ (id\ (\lambda z.id\ z))} \to \underline{id\ (\lambda z.id\ z)}\to \lambda z.\underline{id\ z} \to \lambda z.z$$
Stratégia volania menom (z ang. call by name)
Nestriktná stratégia. Nedovoľuje redukciu vo vnútri abstrakcie, pričom v každom kroku redukcie je zvolený ľavý vonkajší redex: $$\underline{id\ (id\ (\lambda z.id\ z))} \to \underline{id\ (\lambda z.id\ z)}\to \lambda z.id\ z$$
Poznámka
Táto stratégia po miernej úprave, nazývaná stratégia volania podľa potreby (z ang. call by need) sa používa v programovacom jazyku Haskell.
Stratégia volania hodnotou (z ang. call by value)
Striktná stratégia. Nedovoľuje redukciu vo vnútri vonkajšej abstrakcie. Najskôr sú úplne vyhodnotené argumenty pred tým ako je volaná funkcia:
$$id\ \underline{(id\ (\lambda z.id\ z))} \to id\ \underline{(\lambda z.id\ z)}\to \lambda z.id\ z$$
Výsledok môže byt v normalnej forme aj v slabej normálnej forme.
Poznámka
Táto stratégia je používaná v programovacom jazyku OCaml.
Poznámka
V rámci tohto predmetu budeme používať stratégiu volania hodnotou.
Formálna definícia vyhodnocovacej relácie $t \to t'$ na základe redukčnej stratégie volania hodnotou.
Pred samotnou definíciou pravidiel vyhodnocovacej relácie $$\boxed{t \to t'}$$ je potrebné zaviesť nový pojem hodnota $v$.
Hodnota $v$ v $\lambda$-kalkule je term v normálnej forme.
Vyhodnocovacie pravidlá sú definované následovne:
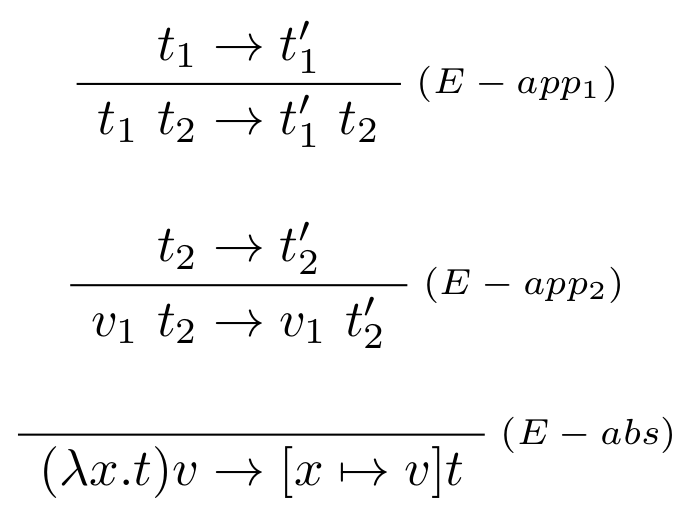
Teoréma Churcha-Rossera
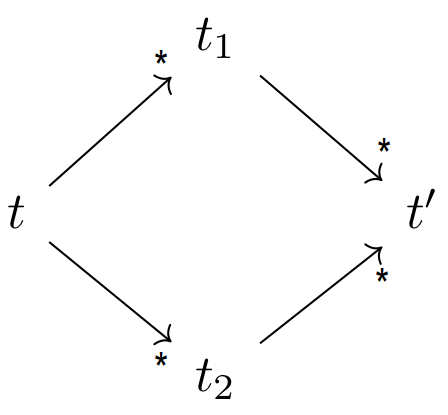
Teoréma Churcha-Rossera je dôležitá vlastnosť $\lambda$-kalkulu, ktorá vyjadruje následovné:
Ak existujú rôzne spôsoby ako aplikovať redukciu na term t, tak všetky možné cesty začínajúce týmto termom, vedú k rovnakému výsledku, ak sú redukovateľné do normálnej formy. Formálne: $$\forall t, t_1, t_2 \in \Lambda . (t \to^* t_1 \wedge t \to^* t_2 \Rightarrow \exists t' \in \Lambda. (t_1 \to^* t' \wedge t_2 \to^* t'\ )\ )$$
Poznámka
Hviezdička $\to^*$ znamená konečný počet krokov $0$ až $n$.
Zjednodušene je možné si túto vlastnosť predstaviť ako nasledujúci diagram:
Príklad
Majme nasledujúci term: $$(\lambda x.\ x\ x)\ (\ (\lambda x.y)\ z )$$ Tento term obsahuje dva redexy. Podľa teórie Church-Rossera môžeme zvoliť akýkoľvek redex v ktoromkoľvek kroku a vždy dospejeme k rovnakej normálnej forme.
Riešenie
Neterminácia a možná neterminácia
Niektoré termy nemajú normálnu formu.
Majme nasledujúci term: $$\omega = \lambda x.x\ x.$$ Majme term $\Omega$, ktorý je aplikáciou termu $\omega$ na $\omega$, potom ak sa pokúsime vyhodnotiť tento term, tak sa dostaneme do nasledujúcej situácie: $$\Omega = \omega\ \omega = (\lambda x.x\ x)\ (\lambda x.x\ x) \to [x \mapsto \lambda x.x\ x]x\ x = (\lambda x.x\ x)\ (\lambda x.x\ x) \to (\lambda x.x\ x)\ (\lambda x.x\ x) \to ... $$ Hovoríme, že takýto term diverguje.
Zatiaľ čo iné termy môžu alebo nemusia mať normálnu formu, v závislosti od použitej redukčnej stratégie.
Majme term: $$(\lambda x. y)\ \Omega.$$ Pri využití normálnej $\beta$-redukcie term je možné vyhodnotiť na jeho normálnu formu: $$(\lambda x. y)\ \Omega \to y$$ Avšak pri použití napríklad redukčnej stratégie volania hodnotou sa v prvom kroku pokúsime redukovať term $(\lambda x. y)$, ktorý je už hodnota. Pokračujeme termom $\Omega$ ako je vidieť na predchádzajúcom príklade, vyhodnotenie takéhoto termu diverguje: $$(\lambda x. y)\ \Omega \to (\lambda x. y)\ ((\lambda x.x\ x)\ (\lambda x.x\ x)) \to (\lambda x. y)\ ((\lambda x.x\ x)\ (\lambda x.x\ x)) \to ...$$
Normalizácia
Majme ľubovoľný term a ľubovoľnú redukčnú stratégiu. Hovoríme, že term normalizuje pod danou stratégiou ak jeho redukcia vedie k normálnej forme. Existuju dva typy normalizácie:
- Slabá normalizácia: Term slabo normalizuje ak existuje aspoň jedna redukčná sekvencia, ktorá vedie k normálnej forme.
- Silná normalizácia Term silno normalizuje ak každá redukčná sekvencia, vedie k normálnej forme bez ohľadu na použitú redukčnú stratégiu.
$\alpha$-redukcia
V prípade, že pri aplikovaní $\beta$-redukcie by sa z voľnej premennej stala viazaná, je potrebné využiť vlastnosť $\alpha$-ekvivalencie a najskor premenovať parameter daného termu, ktorý by viazal voľnú premennú. Tento proces sa nazýva $\alpha$-redukcia.
Majme term: $$(\lambda x. \lambda \textcolor{red}{y}.\ x\ \textcolor{red}{y})\ \textcolor{blue}{y}$$ Po vykonaní $\beta-redukcie$ by sa z voľnej premennej $\textcolor{blue}{y}$ stala viazaná premenná vnútorným parametrom termu $ \lambda \textcolor{red}{y}.\ x\ \textcolor{red}{y}$: $$(\lambda x. \lambda \textcolor{red}{y}.\ x\ \textcolor{red}{y})\ \textcolor{blue}{y} \to \lambda \textcolor{red}{y}.\ \textcolor{blue}{y}\ \textcolor{red}{y} $$ Čo je nesprávny postup!
V takomto prípade je potrebné pristúpiť k $\alpha$-redukcii: $$(\lambda x. \lambda \textcolor{red}{y}.\ x\ \textcolor{red}{y})\ \textcolor{blue}{y} \to_\alpha (\lambda x. \lambda \textcolor{red}{z}.\ x\ \textcolor{red}{z})\ \textcolor{blue}{y} $$
Daný term je následne možné redukovať prostredníctvom $\beta$-redukcie: $$(\lambda x. \lambda \textcolor{red}{y}.\ x\ \textcolor{red}{y})\ \textcolor{blue}{y} \to_\alpha (\lambda x. \lambda \textcolor{red}{z}.\ x\ \textcolor{red}{z})\ \textcolor{blue}{y} \to \lambda \textcolor{red}{z}.\ \textcolor{blue}{y}\ \textcolor{red}{z} $$
Poznámka
Všimnime si rozdiel vo výsledku v prípade nesprávneho postupu a pri využití $\alpha$-redukcie:
- Nesprávny postup: $$\lambda \textcolor{red}{y}.\ \textcolor{blue}{y}\ \textcolor{red}{y}$$
- Správny postup: $$\lambda \textcolor{red}{z}.\ \textcolor{blue}{y}\ \textcolor{red}{z}$$
$\eta$-redukcia
Posledné pravidlo redukcie sa nazýva $\eta$-redukcia. Ak máme term v tvare $$\lambda \textcolor{red}{x}.\ t\ \textcolor{red}{x}$$ je možné ho ďalej redukovať prostredníctvom $\eta$-redukcie: $$\lambda \textcolor{red}{x}.\ t\ \textcolor{red}{x} \to_\eta t \quad \quad \text{ak }\ x \notin FV(t)$$ za podmienky, že term $t$ neobsahuje žiadnu voľnu premennú $x$.
Príklad z predchádzajúcej sekcie je možné redukovať na jeho normálnu formu nasledovne: $$(\lambda x. \lambda \textcolor{red}{y}.\ x\ \textcolor{red}{y})\ \textcolor{blue}{y} \to_\alpha (\lambda x. \lambda \textcolor{red}{z}.\ x\ \textcolor{red}{z})\ \textcolor{blue}{y} \to \lambda \textcolor{red}{z}.\ y\ \textcolor{red}{z} \to_\eta y $$
Zdroje
- Pierce, Benjamin C.: Types and programming languages. MIT press, Cambridge, 2001 (Перевод на русский язык: Бенджамин Пирс. Типы в языках программирования. — Добросвет, 2012. — 680 с. — ISBN 978-5-7913-0082-9)
- Pierce, Benjamin C et al.: Software Foundations, Electronic textbook, 2024
- Sestoft, Peter.: "Demonstrating lambda calculus reduction." The essence of computation: complexity, analysis, transformation (2002): 420-435.
- Selinger, Peter.: "Lecture notes on the lambda calculus." arXiv preprint arXiv:0804.3434 (2008).
- Valerie Novitzká, Daniel Mihályi: Teória typov, TU Košice, 2015