Polymorfizmus
V teórii programovacích jazykov a teórii typov, polymorfizmus znamená použitie jedného symbolu na reprezentáciu viacerých rôznych typov.
Poznámka
Slovo "polymorfizmus" pochádza z gréckeho jazyka, kde "poly" znamená "veľa" a "morphe" znamená "tvar" alebo "forma".
Druhy polymorfizmu
Existuje niekoľko druhov polymorfizmu, ktoré nie sú disjunktné, teda v jednom jazyku sa môže vyskytnúť viac druhov naraz.
Parametrický polymorfizmus
Niekedy nazývaný aj generický polymorfizmus. Je to najčastejší druh polymorfizmu (téma dnešnej aj predchádzajúcej prednášky). Používa typové premenné ako parametre, ktoré nahradzuje konkrétnymi typmi podľa potreby. Nahradenie parametra konkrétnym typom vytvorí inštanciu typu.
Medzi parametricky polymorfizmus používaný vo funkcionálnych jazykoch patria:
-
Predikatívny polymorfizmus (niekedy nazývaný aj prenexný polymrofizmus) v ktorom nie je možné inštancovať typové premenné polymorfnými typmi. Predikatívne teórie typov zahŕňajú napríklad Let-polymorfizmus, ktorý má niekoľko iných syntaktických obmedzení. Tieto obmedzenia robia rozdiel medzi polymorfnými a nepolymorfnými typmi veľmi dôležitým. Z tohto dôvodu preto sa v predikatívnych systémoch polymorfné typy niekedy označujú ako typové schémy, aby sa odlíšili od bežných (monomorfných) typov, ktoré sa niekedy nazývajú monotypy. Dôsledkom toho je, že všetky typy možno napísať formou, ktorá umiestňuje všetky kvantifikátory na najvonkajšiu (prenexnú) pozíciu.
-
Impredikatívny polymorfizmus (nazývaný tiež polymorfizmus prvého rádu) je najsilenejší druh parametrického polymorfizmu. Vo formálnej logike je definícia považovaná za impredikatívnu, ak je samoreferenčná. V teórii typov sa to týka schopnosti, aby typ mohol byť v doméne kvantifikátora, ktorý obsahuje. To umožňuje inštancovanie akéhokoľvek typovej premennej s akýmkoľvek typom, vrátane polymorfných typov. Príkladom takéhoto systému je Systém F, ktorý umožňuje inštancovanie $\forall \alpha .\alpha \rightarrow \alpha$ s akýmkoľvek typom, vrátane seba samého.
Ad-hoc polymorfizmus
umožňuje rôzne správanie podľa substituovania rôznymi konkrétnymi typmi. Tu patria:
- Preťaženie (overloading) - môžeme použiť to isté meno funkcie pre rôzne implementácie. Prekladač vyberie vhodnú implementáciu pre každú aplikáciu funkcie na základe typov argumentov,
- Viacnásobne preťaženie (multi-method dispatch) zovšeobecnený overloading používaný v takých objektovo-orientovaných jazykoch, ktoré nemajú v čase prekladu explicitne definovane typy. Typy sa priraďujú až v čase vykonávania. Medzi takéto jazyky patria CLOS, Cecil, atď.
Intenzionálny polymorfizmus
dovoľuje obmedzene výpočty nad typmi v runtime. Používa sa pri implementačných technikách pre polymorfné jazyky (garbage collector, polymorfné usporiadanie).
Podtypový polymorfizmus
poskytuje termu viac inštancií typov podľa pravidiel podtypovania. Používa sa v objektovo-orientovaných programovacích jazykoch.
Motivácia
V rámci predchádzajúcej prednášky bol predstavený algoritmus Hindley–Milnera ako spôsob nájdenia najvšeobecnejšieho typu pre daný term, vďaka čomu sme do jazyka zaviedli typové odvodenie (z ang. type inference), čo umožnilo zápis termov nášho jazyka bez nutnosti uvádzania typových anotácií a zároveň sme týmto získali aj určitú formu parametrického polymorfizmu (z ang. parametric polymorphism).
Avšak je nutné poznamenať, že tento typový systém, hoci poskytuje vysokú mieru polymorfizmu a umožňuje elegantné a beztypové vyjadrovanie termov, naráža na nasledujúci problém.
Majme term: $$ (\lambda f. if~f~true~then~f~5~else~f~8)~(\lambda x.x). $$ Je zrejme, že v netypovanom $\lambda$-kalkule má daný term význam, avšak náš typový systém mu nedokáže odvodiť typ.
- Zostríme štruktúru typového stromu:

- Doplníme typy a obmedzenia:
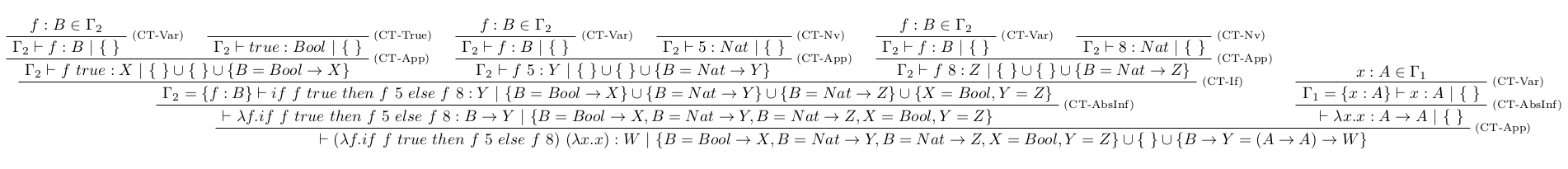
Pri pokuse o odvedenie typu sme získali nasledujúcu množinu obmedzení $C$: $$ \begin{array}{lcl} C&=& \{A=Bool \rightarrow X, A=Nat \rightarrow Y,\\ & & A=Nat \rightarrow Z, X = Bool, Y=Z, \\ & & A \rightarrow Y = (B\rightarrow B) \rightarrow W\}, \end{array} $$ avšak unifikačný algoritmus zlyhá pri pokuse o nájdenie najvšeobecnejšieho unifikátora.
Keď sa pozrieme na množinu obmedzení je zrejme, že je sporná.
Máme obmedzenie: $$A \rightarrow Y = (B\rightarrow B) \rightarrow W.$$ Vidíme, že typ $A$ bude nahradený typom $B\rightarrow B$ (v tomto prípade typom identickej funkcie). Následne, keď v prvých dvoch obmedzeniach vykonáme substitúciu $[A \mapsto B\rightarrow B]$ získame: $$ \begin{array}{l} B\rightarrow B = Bool \rightarrow X,\\ B\rightarrow B = Nat \rightarrow Y, \end{array} $$ z čoho odvodíme, že typ $B$ musí byť zároveň $Bool$ aj $Nat$, čo je sporné.
Jazyk OCaml poskytne nasledujúcu chybovú hlášku:
utop # (fun f -> if f true then f 5 else f 8) (fun x -> x);;
Error: This expression has type int
but an expression was expected of type bool
Tento problém je možné vyriešiť zavedením nového typového konštruktora, ktorý kvantifikuje nad typmi: $$\forall X. T.$$
Poznámka
Univerzálny kvantifikátor $\forall$ má v tomto prípade rovnaký význam ako v predikátovej logike.
Definícia: Typová schéma:
Typ $\forall X. T$ sa nazýva typová schéma (niekedy aj polymorfný typ), kde:
- Typ $T$ je "vzor" typu, z ktorého je možné vytvoriť inštanciu konkrétneho typu.
- Kvantifikátor $\forall X$ kvantifikuje všetky voľné výskyty premennej $X$ v type $T$, ktoré môžu byť nahradené ľubovoľným typom a tým je získaná jeho inštancia - konkrétny typ (analógia so všeobecným kvantifikátorom v predikátovej logike).
Takýmto rozšírením jazyka vzniká systém, ktorý sa nazýva Systém F.
Systém F
Systém F bol nezávisle objavený dva krát pri skúmaní rôznych teórií. Najskôr ho objavil francúzsky logik Jean-Yves Girard v roku 1972, ktorý skúmal teóriu dôkazov v logike. O dva roky neskôr v roku 1974 ho znovu objavil americký informatik John C. Reynolds, ktorý skúmal parametrický polymorfizmus. Z tohto dôvodu je Systém F niekedy nazývaný ako polymorfný $\lambda$-kalkul alebo aj $\lambda$-kalkul druhého rádu $(\Lambda 2)$, keďže korešponduje podľa Curry-Howardovej korešpondencie s intuicionistickou logikou druhého rádu, ktorá povoľuje kvantifikáciu nie len nad termami ale aj nad predikátmi (typmi).
Systém F je možné považovať za priame rozšírenie jednoducho typovaného $\lambda$-kalkulu.
- Termy môžu mať argument typ, preto zavedieme do jazyka nový tvar typovej abstrakcie, ktorej parameter je typ: $$\Lambda X.t.$$
- Potrebujeme spôsob ako z typovej schémy vytvoriť konkrétny typ - inštanciu, preto zavedieme do jazyka nový tvar typovej aplikácie - inštanciácia: $$t ~[T].$$
- Ako už bolo spomenuté v predchádzajúcej kapitole, zavedieme nový typový konštruktor pre typovú schému: $$\forall X. T.$$
Syntax Systému F
Výsledná syntax Systému F je definovaná nasledovne:
$$ \begin{array}{lcl} t & ::= & x ~|~ \lambda x :T.t ~|~ t~t ~|~ \Lambda X.t ~|~ t [T] \\ v & ::= & \lambda x:T.t ~|~ \Lambda X.t \\ T & ::= & A ~|~ T \rightarrow T ~|~ X ~|~ \forall X.T\\ A & ::= & Nat ~|~ Bool \end{array} $$
Vyhodnocovacie pravidlá
Pri vyhodnocovaní je postup nasledovný:
- V procese vyhodnotenia termu $t ~[T]$, najskôr redukujeme $t$ na hodnotu $(E-Tapp)$,
- a následne pristúpime k typovej inštanciácii $(E-TappTabs)$:
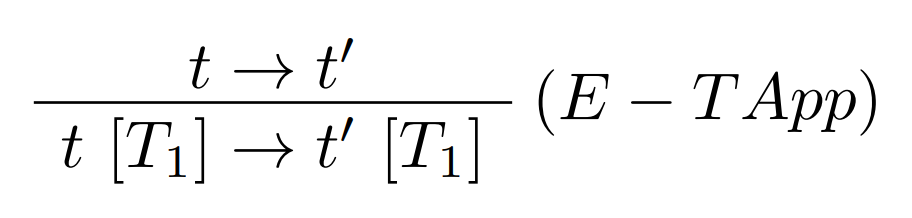
$$(\Lambda X.t)~[T] \rightarrow [X \mapsto T]t \quad (E-TappTabs)$$
Poznámka
Vyhodnocovacie pravidlá pre ostatne tvary termov sú rovnaké ako v jednoducho typovanom $\lambda$-kalkule.
Príklad
Majme danú polymorfnú identickú funkciu $$id=\Lambda X. \lambda x: X. x: \forall X. X \rightarrow X.$$ V prípade jej aplikácie na konkrétny typ prostredníctvom typovej abstrakcie získame nasledujúci term: $$id ~[Nat] \rightarrow \lambda x: Nat. x,$$ ktorá je typu $Nat \rightarrow Nat$.
V prípade, že polymorfnú identickú funkciu aplikujeme na typ a na ďalší konkrétny argument, získame nasledujúci term: $$id ~[Nat]~3 \rightarrow (\lambda x: Nat. x) ~3 \rightarrow ~3.$$
Typové pravidlá
Typové pravidlá pre typovú abstrakciu a typovú aplikáciu sú analogické s pravidlami pre abstrakciu a aplikáciu na úrovni termov.
Typová abstrakcia
Pri typovej abstrakcii je typová premenná $X$ pridaná do kontextu a je potrebné skontrolovať, či sa premenná s rovnakým názvom nenachádza v kontexte. V prípade konfliktu názvov premenných, je možné tento konflikt vyriešiť prostredníctvom $\alpha$-konverzie.
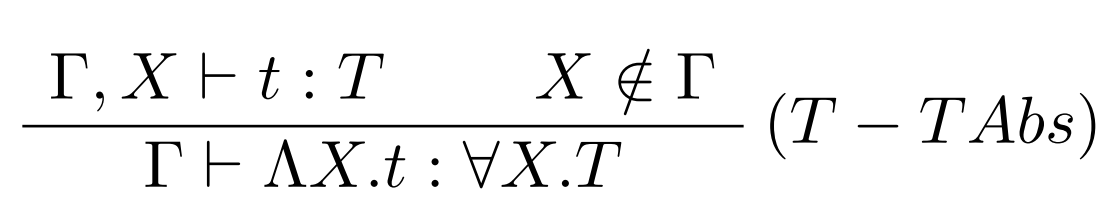
Typová aplikácia
V predpoklade pravidla odvodíme typovú schému $\forall X.T$ pre term $t$. V závere pravidla získame typ termu substitúciou argumentu $[T_1]$ za premennú $X$ v type $T$.
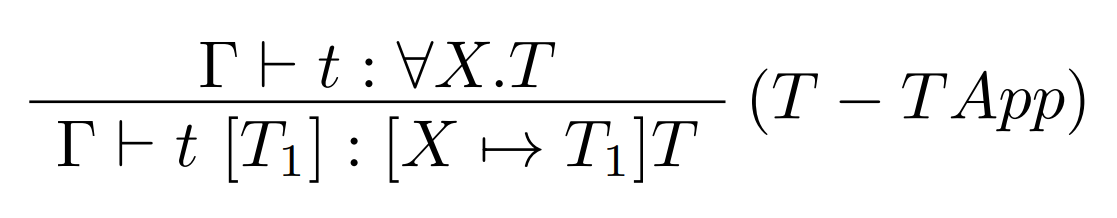
Poznámka
Typové pravidlá pre ostatné tvary termov sú rovnaké ako v jednoducho typovanom $\lambda$-kalkule.
Príklad
Odvoďte typ následujúcej polymorfnej identickej funkcie prostredníctvom Systému F: $$\vdash \Lambda A. \lambda x:A .x$$
Riešenie
Polymorfný typ takejto funkcie je možné odvodiť prostredníctvom Systému F následovne:
- Zostrojíme odvodzovací strom bez typov:
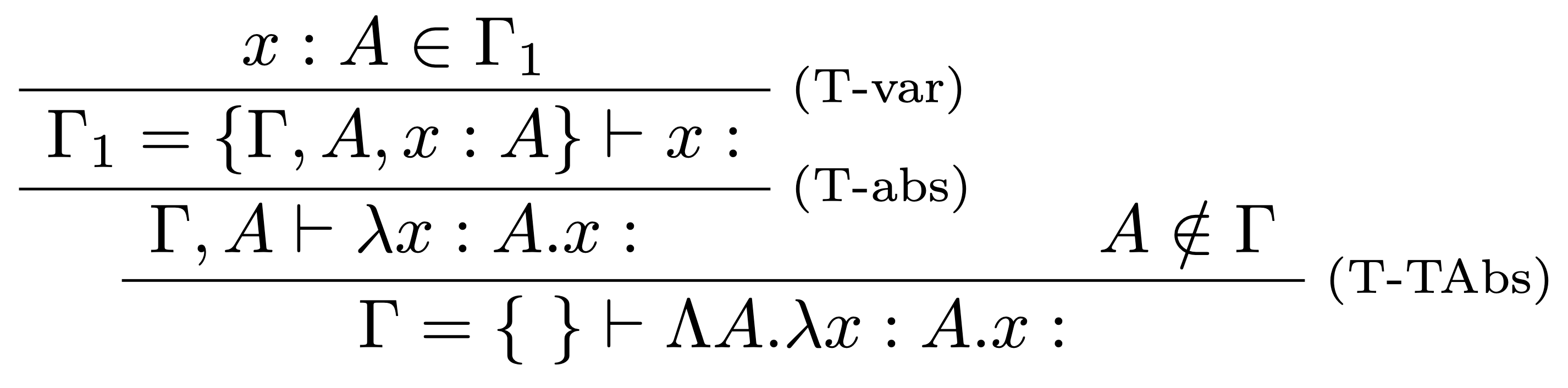
- Doplníme typy podľa typových pravidiel:
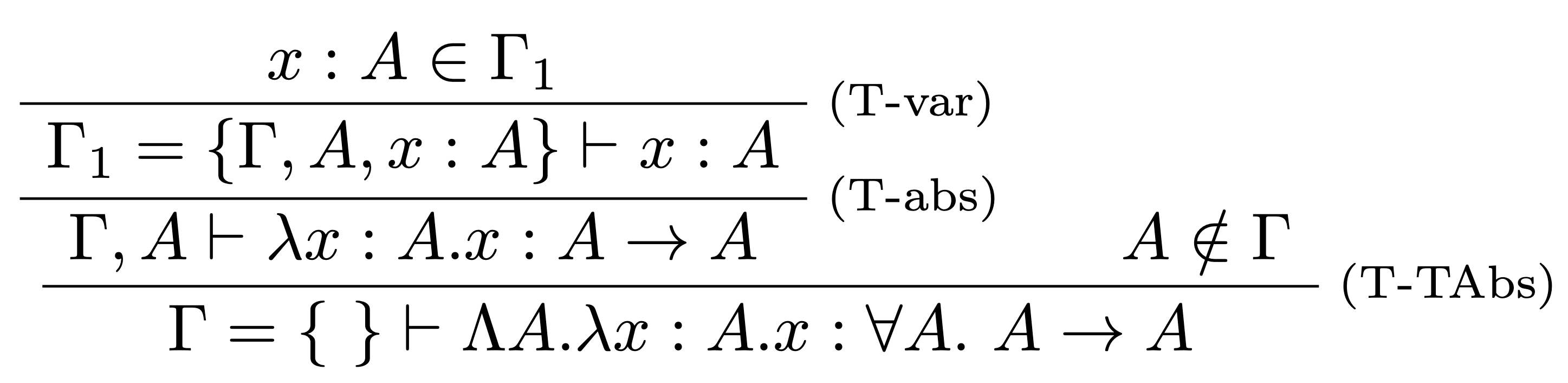
Príklad
Odvoďte typ následujúcej polymorfnej funkcie prostredníctvom Systému F: $$\vdash (\Lambda A. \lambda x:A.~x) ~[Bool]~true$$
Riešenie
Polymorfný typ takejto funkcie je možné odvodiť prostredníctvom Systému F následovne:
- Zostrojíme odvodzovací strom bez typov:

- Doplníme typy podľa typových pravidiel:


Term seba-aplikácie $\lambda x.x~x$ a Systém F
V jednoducho typovanom $\lambda$-kalkule pri pokuse odviesť typ termu $$\lambda x.x~x$$ narazíme na nasledujúci problém:
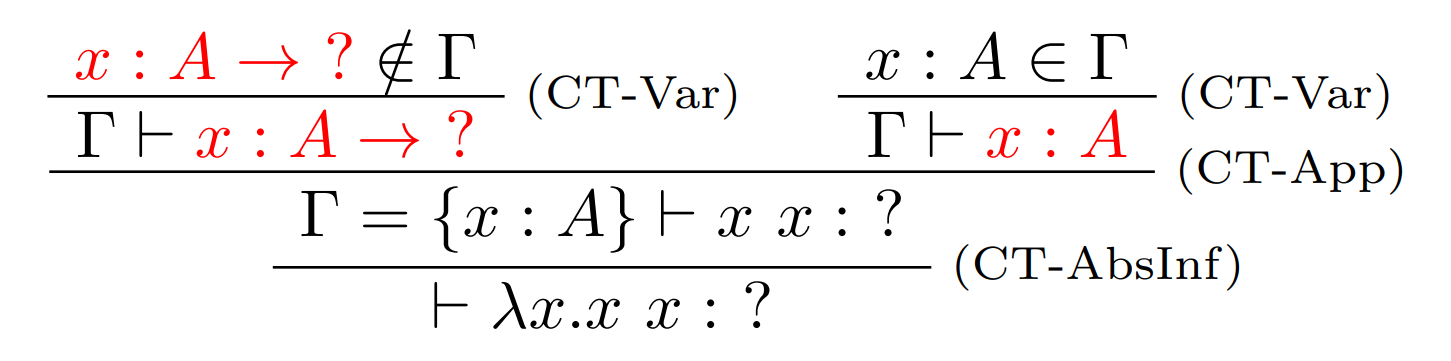
Pri odvodení typu je postup nasledovný:
- Do typového kontextu $\Gamma$ je pridaná premenná $x$, ktorej je priradená nová typová premenná $A$.
- Na sekvent $\Gamma \vdash x~x$ je aplikované pravidlo pre aplikáciu, čo spôsobí rozvetvenie stromu:
- Pravú vetvu je možné uzavrieť aplikovaním pravidla pre premennú $x:A \in \Gamma$.
- V ľavej vetve podľa pravidla aplikácie musí byť $x$ funkčného typu $A \rightarrow ~ ?$, pričom v kontexte $\Gamma$ sa nachádza premenná $x:A$, z čoho je zrejme, že danú vetvu nie je možné uzavrieť a tento term nemá typ v jednoducho typovanom $\lambda$-kalkule.
Keďže vyjadrovacia sila Systému F je vyššia ako v prípade jednoducho typovaného $\lambda$-kalkulu, term $\lambda x.x~x$ je správne typovaný v Systéme F. Typ tohto termu je možné odviesť nasledovane:
-
Zostrojíme odvodzovací strom bez typov:
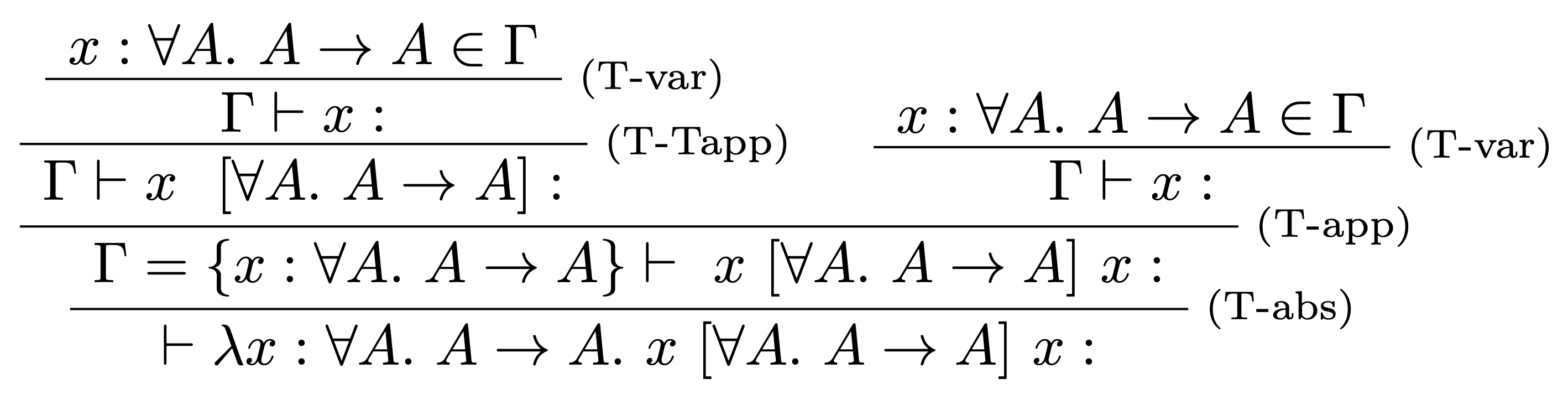
-
Doplníme typy podľa typových pravidiel:
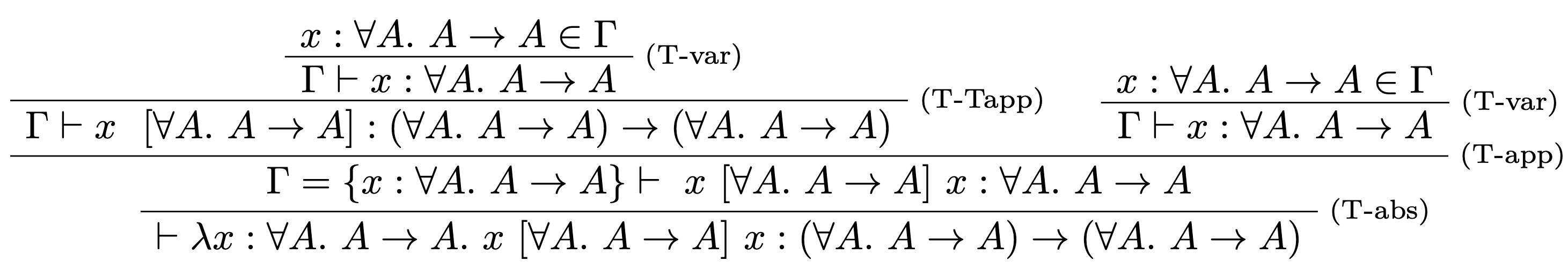
Pozrime sa bližšie na vetvu: $$\Gamma \vdash x~~[\forall A.~ A \rightarrow A]:$$ Podľa pravidla (T-Tapp) je pre odvodenie typu termu ($x~~[\forall A.~ A \rightarrow A]$) potrebné vykonať substitúciu: $$[\forall A.~ A \rightarrow A](A \rightarrow A) = (\forall A.~ A \rightarrow A) \rightarrow (\forall A.~ A \rightarrow A).$$
Poznámka
Všimnite si, že pre odvodenie typu termu $\lambda x.x~x$ bolo potrebné uviesť explicitne jeho typovú anotáciu aj typ ako argument.
Fragmenty Systému F a problém rozhodnuteľnosti odvodenia typu
Kvôli svojej silnej vyjadrovacej schopnosti sa Systém F stal významným nástrojom pri teoretickom skúmaní polymorfizmu. Avšak jeho nevýhodou je strata rozhodnuteľnosti pri probléme odvodenia typu. To znamená, že v určitých prípadoch musí programátor explicitne uviesť typové anotácie, bez ktorých by Systém F nedokázal typ odvodiť.
Strata rozhodnuteľnosti pri probléme odvodenia typu je pre väčšinu návrhárov jazykov priveľká cena za určité vlastnosti, ktoré majú v praxi len zriedkavé využitie. To viedlo k definícii viacerých obmedzených fragmentov Systému F, v ktorých je odvodenie typu rozhodnuteľným problémom.
Najznámejším fragmentom Systému F s rozhodnuteľným odvodením typu je Let polymorfizmus, ktorý je využívaný v mnohých populárnych jazykoch ako OCaml či Haskell.
Poznámka
V následujúcej kapitole sa vrátime späť k algoritmu typovej rekonštrukcie, ktorý bol témou predchádzajúcej prednášky. Jazyk jednoducho-typovaného $\lambda$-kalkulu s NBL rozšírime o nový tvar termov - konštrukciu Let, kde budú využité určite vlastnosti Systém F. Takýmto rozšírením vzniká nový typový systém nazývaný Let polymorfizmus. Z tohto dôvodu o Let polymorfizme hovoríme ako o fragmente Systému F.
Let polymorfizmus - Algoritmus Hindley–Milnera
V Let polymorfizme je rozhodnuteľnosť odvodenia typov získaná prostredníctvom určitého obmedzenia tvaru typovej schémy a zároveň je možné ju využiť len v konštrukcii Let.
Obmedzený tvar typovej schémy: $$\forall X_1, ..., \forall X_n.T,$$ kde v type $T$ sa nenachádzajú kvantifikátory. Z tohto dôvodu sa Let polymorfizmus niekedy nazýva aj prenexný polymorfizmus.
Odvodenie typov prebieha prostredníctvom typovej rekonštrukcie (Algoritmus Hindley-Milnera).
Náš jazyk z predchádzajúcej prednášky rozšírime o nový tvar termov - konštrukciu Let: $$t::= ...~|~ let~x=t~in~t,$$ pričom typová schéma sa bude môcť nachádzať len v konštrukcii Let. Na základe toho definujeme nové pravidlo:
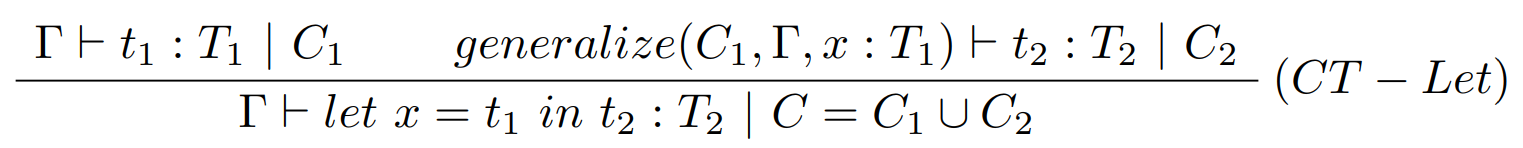
Pričom funkcia zovšeobecnenia kontextu $generalize$ je definovaná nasledovne: $$ generalize(C_1, \Gamma, x:T_1 )=\begin{cases} \Gamma_1,x: \forall X_1,...,\forall X_n. U_1,\\ \qquad \text{ ak }FTV(U_1)- FTV(\Gamma_1)=\{X_1,...,X_n\}\\ ~\\ \Gamma_1,x: U_1,\\ \qquad \text{ ak }FTV(U_1) - FTV(\Gamma_1)=\{ ~\}, \end{cases} $$ kde:
- $U_1$ je najvšeobecnejší typ, ktorý je získaný vyriešením sekventu $\Gamma \vdash t_1 : T_1 ~|~ C_1$.
- Prostredníctvom unifikačného algoritmu získame najvšeobecnejší unifikátor $\sigma_{mgu}$ pre množinu obmedzení $C_1$.
- Typ $U_1 = \sigma_{mgu} ~ T_1$.
- $\Gamma_1$ je nový typový kontext, ktorý vznikne aplikáciou najvšeobecnejšieho unifikátora $\sigma_{mgu}$ na kontext $\Gamma$ získaného z riešenia množiny obmedzení $C_1$.
- $FTV$ je funkcia, ktorá vráti množinu s názvami voľných typových premenných z typového kontextu alebo typového výrazu.
Výsledkom funkcie $generalize$ - zovšeobecnenia kontextu je nový typový kontext $\Gamma_1$, rozšírený o premennú $x$ s typovou anotáciou v tvare:
- $x:\forall X_1,...,\forall X_n. U_1$, kde sú všeobecne kvantifikované všetky voľné typové premenné, ktoré sa nachádzajú v type $U_1$ a zároveň nenachádzajú v $\Gamma_1$. Voľbu typových premenných formálne definujeme nasledovne: $$FTV(U_1)- FTV(\Gamma_1)=\{X_1,...,X_n\}.$$
- $x: U_1$, ak: $$FTV(U_1)- FTV(\Gamma_1)=\{~\}.$$
Taktiež je potrebné pridať nové pravidlo pre inštanciáciu typu upravením typového pravidla pre premennú nasledovne: $$\Gamma \vdash x: instantiate(x: T \in \Gamma) ~|~ \{~\} \quad (CT-VarLet)$$
Funkcia $instantiate$ inštanciácie väzme typovú schému z kontextu $\Gamma$ a vytvorí konkrétny typ - typovú inštanciu s novými typovými premennými. Napríklad:
- nech $x:\forall X. X \rightarrow X \in \Gamma$,
- potom výsledok $instantiate(x:\forall X. X \rightarrow X \in \Gamma)$ môže byť napríklad $x:A \rightarrow A$.
Príklad
V úvode prednášky bol rozobratý príklad termu, ktorý v našom jazyku nie je správne typovaný: $$ (\lambda f. if~~f~true~~then~~f~5~~else~~f~8)~(\lambda x.x). $$ Po jeho prepise na ekvivalentnú formu využitím konštrukcie let: $$ let~~id=\lambda x.x~~in~~if~~id~true~~then~~id~5~~else~~id~8, $$ je tento term v typovom systéme Let polymorfizmu správne typovaný.
Riešenie
- Najskôr je potrebné odvodiť ľavú vetvu s termom $t_1$, v ktorej sa nachádza sekvent: $$\vdash \lambda x.x :$$

- Doplníme typy a obmedzenia:
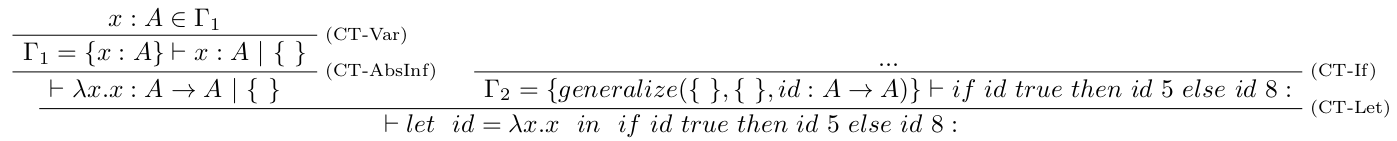
- Funkcia zovšeobecnia poskytne výsledok: $$ generalize(\{~\}, \{~\}, id: A \rightarrow A) = id: \forall A . A \rightarrow A $$ To vytvára nasledujúci strom:
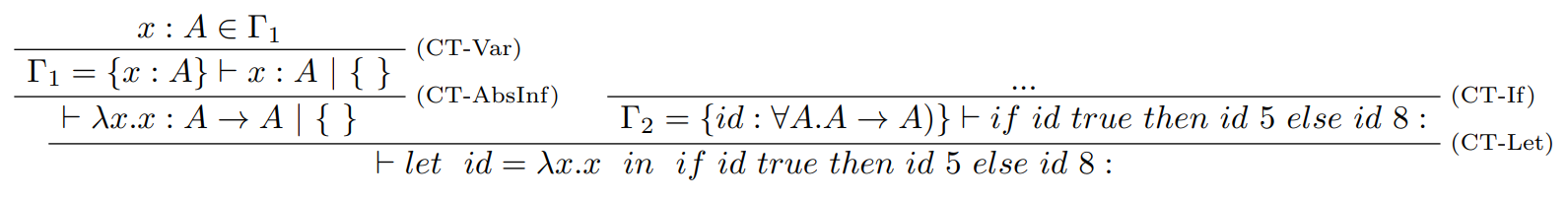
- Pokračujeme odvodením štruktúry stromu aplikáciou príslušných pravidiel:
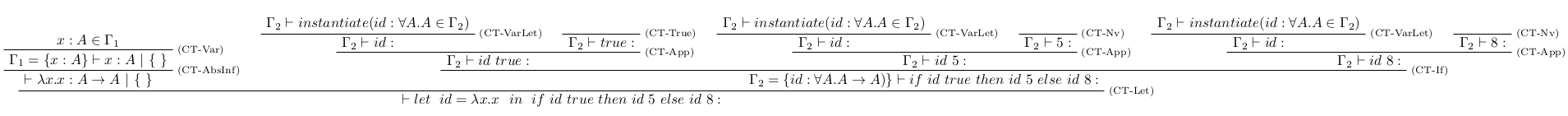
- Postupujeme nasledovne:
- V každej z týchto vetiev, premennej $id$ funkcia $instantiate$ vytvorí novú inštanciu typovej schémy: $ \forall A . A \in \Gamma_2$ tak, že vždy je zvolená nová typová premenná.
- Následne doplníme vo zvyšku stromu typy a obmedzenia.
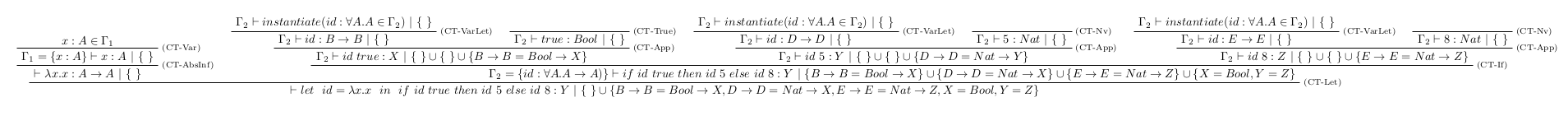
Skonštruovaním stromu odvodenia typu, bolo odvodené nasledujúce:
- Typ termu: $$let~~id=\lambda x.x~~in~~if~~id~true~~then~~id~5~~else~~id~8:~Y,$$
- Množina obmedzení $C$: $$ \begin{array}{lll} C=\{ & B \rightarrow B = Bool \rightarrow X, & \\ & D \rightarrow D = Nat \rightarrow Y, & \\ & E \rightarrow E = Nat \rightarrow Z, & \\ & X = Bool, Y=Z & \}\\ \end{array} $$
Prostredníctvom unifikačného algoritmu bol nájdený nasledujúci najvšeobecnejší unifikátor $\sigma_{mgu}$: $$ \begin{array}{l} Unify(C)= \\ [~] \circ [Z \mapsto Nat] \circ [E \mapsto Nat] \circ [Y \mapsto Nat] \circ [D \mapsto Nat] \circ [X \mapsto Bool] \circ [B \mapsto Bool] = \\ = \sigma_{mgu} \end{array} $$ Množina obmedzení bola vyriešená nasledovné:
| $Unify$ Iterácia |
Množina obmedzení $C$ |
|---|---|
| 1. | $\{ B \rightarrow B = Bool \rightarrow X,~ D \rightarrow D = Nat \rightarrow Y,~ E \rightarrow E = Nat \rightarrow Z,~ X = Bool,~ Y=Z \}$ |
| 2. | $\{ B = Bool,~ B = X,~ D \rightarrow D = Nat \rightarrow Y,~ E \rightarrow E = Nat \rightarrow Z,~ X = Bool,~ Y=Z \}$ |
| 3. | $\{ Bool = X,~ D \rightarrow D = Nat \rightarrow Y,~ E \rightarrow E = Nat \rightarrow Z,~ X = Bool,~ Y=Z \}$ |
| 4. | $\{D \rightarrow D = Nat \rightarrow Y,~ E \rightarrow E = Nat \rightarrow Z,~ Bool = Bool,~ Y=Z \}$ |
| 5. | $\{D = Nat,~ D = Y,~ E \rightarrow E = Nat \rightarrow Z,~ Bool = Bool,~ Y=Z \}$ |
| 6. | $\{Nat = Y,~ E \rightarrow E = Nat \rightarrow Z,~ Bool = Bool,~ Y=Z \}$ |
| 7. | $\{E \rightarrow E = Nat \rightarrow Z,~ Bool = Bool,~ Nat=Z \}$ |
| 8. | $\{E = Nat,~ E = Z,~ Bool = Bool,~ Nat=Z \}$ |
| 9. | $\{Nat = Z,~ Bool = Bool,~ Nat=Z \}$ |
| 10. | $\{Bool = Bool,~ Nat=Nat \}$ |
| 11. | $\{Nat=Nat \}$ |
| 12. | $\{~\}$ |
Po aplikovaní najvšeobecnejšieho unifikátora $\sigma_{mgu}$ na odvodený typ $Y$ bol získaný najvšeobecnejší typ termu: $$\sigma_{mgu}~Y = Nat.$$ Riešenie v jazyku OCaml
utop # let id=fun x -> x in if id true then id 5 else id 8;;
- : int = 5
Zdroje
- Benjamin C.Pierce, Types and programming languages. MIT press, 2002.
- Michael R. Clarkson et al., OCaml Programming: Correct + Efficient + Beautiful, Cornell University, 2023
- Lecture notes, CS 6110 - Advanced Programming Languages, Cornell University, 2019
- Lecture notes, CS 4110 - Programming Languages and Logics, Cornell University, 2021
- Stephen A. Edwards - Lecture notes, COMS 6998 007 - Types, Languages and Compilers, Columbia University, 2023
- Stephen Chong, Nada Amin, Radu Rugina, Andrew Myers, Nate Foster, Jeff Vaughan, and Christos Dimoulas - Lecture notes, CS 152: Programming Languages, Harvard University, 2023
- Степан Львович Кузнецов, Лямбда-исчисление, Математический институт им. В. А. Стеклова Российской академии наук, 2021
- Valerie Novitzká, Daniel Mihályi: Teória typov, TU Košice, 2015