Úvod
$\lambda$-kocka (v krátkosti predstavená v tretej prednáške) je formálny model, ktorý systematicky klasifikuje rôzne teórie typov na základe troch dimenzií závislostí medzi typmi a termami. Jej osi reprezentujú možné rozšírenia jednoducho typovaného $\lambda$-kalkulu.
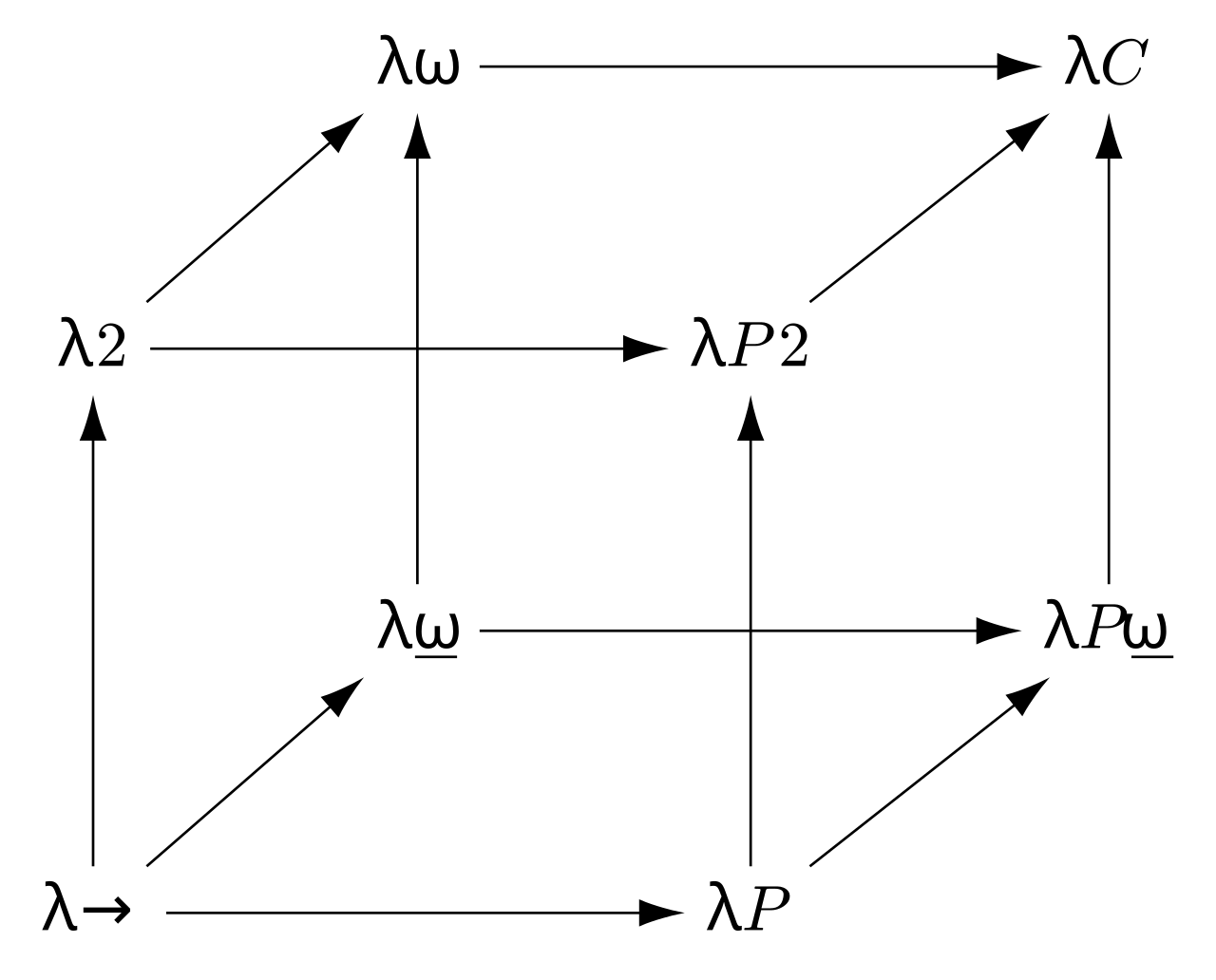
Kde:
- x-os (→): Typy môžu byť aplikované na termy (závislé typy).
- y-os (↑): Termy môžu byť aplikované na typy (polymorfizmus).
- z-os (↗): Typy môžu byť aplikované na typy (typové konštruktory).
Tieto osi nám umožňujú preskúmať jednotlivé teórie typov od základných až po najvyspelejšie systémy, pričom každá z nich pridáva novú dimenziu vyjadrovacej sily a možnosti definície typov.
V predchádzajúcej kapitole sme sa venovali skúmaniu teórií typov, ktoré tvoria štruktúru znázornenú v $\lambda$-kocke. Tieto teórie predstavujú systematické rozšírenia jednoducho typovaného $\lambda$-kalkulu. Zavedením polymorfizmu v Systéme F sme vytvorili možnosť aplikácie termov na typy, čo predstavuje pohyb po $y$-osi $\lambda$-kocky.
V tejto kapitole rozšírime naše skúmanie a zameriame sa na závislosti medzi typmi a typmi, pričom sa budeme venovať osi $z$ na $\lambda$-kocke.
Hlavným cieľom tejto kapitoly je predstaviť systém $\lambda \underline{\omega}$, ktorý rozširuje možnosti typového systému umožnením závislostí medzi typmi. Systém $\lambda \underline{\omega}$ predstavuje kľúčový krok na ceste k závislým typom, ktoré budú predmetom ďalšej prednášky.
Závislosti medzi termami a typmi
Termy závisia na termoch ($\lambda_\to$)
V jednoducho typovanom $\lambda$-kalkule termy závisia od termov. Výsledok aplikovania termu $$\lambda x: A. x: A \to A$$ závisí od jeho argumentu: $$(\lambda x: A. x)\ y \to y,$$ pričom argument $y \in t$ musí byť term a $y:A$.
Termy závisia na typoch (Systém F)
V predchádzajúcej kapitole bol rozšírený $\lambda_\to$ o polymorfné typy, čím vznikla nová teória typov s názvom Systém F ($\lambda 2$). Obdobne ako v $\lambda_\to$, aj v Systéme F termy závisia na termoch a avšak aj na typoch. Výsledok aplikovania termu: $$\Lambda A. \lambda x:A. x: \forall A. A \to A$$ na argument $$(\Lambda A. \lambda x:A. x) [Nat] \to \lambda x:Nat. x,$$ pričom $Nat$ je typ.
Prirodzene je možné uvažovať o zvyšných dvoch kombináciách vzájomných závislostí medzi typmi a termami, kde:
- Typy závisia na typoch: Systém $\lambda \underline{\omega}$ (obsah dnešnej prednášky)
- Typy závisia na termoch: Závisle typy $\lambda P$ (budúci týždeň).
Jednotlivé závislosti sú zhrnuté v nasledujúcej tabuľke:
| Teória typov | $t\ t$ | $t\ T$ | $T\ T$ | $T\ t$ |
|---|---|---|---|---|
| $\lambda_\to$ | ✓ | ✗ | ✗ | ✗ |
| $\lambda 2$ | ✓ | ✓ | ✗ | ✓ |
| $\lambda \underline{\omega}$ | ✓ | ✗ | ✓ | ✗ |
| $\lambda P$ | ✓ | ✗ | ✗ | ✓ |
Typy závisia na typoch (Systém $\lambda \underline{\omega}$)
Jednoduchým príkladom typu ktorý závisí na inom type môže byť typ $A\to A$, ktorý závisí na type $A$. Formálne, ak $A$ je typ, potom je možné uvažovať o funkcii: $$f(A)= A \to A.$$
Systém $\lambda \underline{\omega}$ umožňuje definovať takéto termy zavedením abstrakcie a aplikácie na úrovní typov.
Typy typov (Kinds)
Pokúsme sa definovať typovú abstrakciu v $\lambda \underline{\omega}$ obdobne ako termovú abstrakciu v $\lambda_\to$. Pre zopakovanie termová abstrakcia je definovaná nasledovne: $$\lambda x:T.t,$$ kde $x$ je termová premenná, $T$ je typ a term $t$ je telo abstrakcie.
Definícia typovej abstrakcie by mohla vyzerať nasledovne: $$\lambda A:?.T,$$ kde $A$ je typová premenná a typ $T$ je telo abstrakcie. Typová abstrakcia ako aj v prípade termovej abstrakcie potrebuje anotáciu. To indikuje, že je potrebné zaviesť "typ typov" alebo inými slovami "supertyp" pre parameter typovej abstrakcie.
"Supertyp" resp. typ typov budeme označovať ako typovú triedu.
Poznámka
Typy typov sa v anglickom jazyku označujú ako Kinds, avšak neskôr bude potrebné zaviesť do jazyka "typ typov typov" (supertyp typovej triedy), ktorý sa spoločne s typovými triedami nazývajú v anglickom jazyku Sorts, kde zavedieme názov druh.
Do jazyka zavedieme konštantu $*$ (hviezdička) pre konštantnú typovú triedu, pričom zápis:
$$A:*,$$
je možné prečítať ako "typ $A$ je typovej triedy *". Intuitívne je tento zápis možné chápať ako prosté tvrdenie: $A$ je typ.
Typovú abstrakciu je možné zadefinovať využitím konštanty * nasledovne: $$\lambda A:*. T$$
Funkcia $f$ z úvodu môže byt definovaná ako term $$f = \lambda A:*.A\to A$$ Typová trieda takéhoto výrazu je: $$* \to *$$ a term je typu $$\lambda A:*.A\to A:* \to *$$
Poznámka
Výraz $\lambda A:*.A\to A$ nie je typ, ale je to typový konštruktor (supertypu $* \to *$), ktorý očakáva ako argument $*$ - typ a vráti typ.
To znamená, že neexistuje term $t$, pre ktorý by platilo: $$t:\lambda A:*.A\to A $$ Avšak ak aplikujeme na typový konštruktor nejaký typ, výsledok redukcie bude konkrétny typ: $$(\lambda A:*.A\to A)\ B \quad \to_\beta \quad B \to B$$ Ak existuje term $t$, taký že: $$t:B \to B$$ potom platí: $$t:(\lambda A:*.A\to A)\ B,$$
a môžeme tvrdiť že typy $((\lambda A:*.A\to A)\ B)$ a $(B \to B)$ sú $\beta$-ekvivalentné: $$(\lambda A:*.A\to A)\ B \quad \equiv_\beta \quad B \to B$$
Na základe predchádzajúceho príkladu v poznámke je zrejme, že neexistuje iba jediná0 typová trieda a to samotná $*$ ale existuje ďalšia typová trieda $* \to *$. Z toho vyplýva, že pri zavedení funkcií do jazyka na typoch vzniká nekonečné množstvo typových tried (označíme $K$): $$K=\{*, * \to *, * \to * \to *, (* \to *) \to *, (* \to *) \to * \to *, ...\}$$
Typové triedy ($Kinds$) definuje nasledujúca gramatika: $$K::= * \ |\ K \to K.$$
Supertyp typových tried
Pre potrebné formálne odvodzovanie nad typovými triedami je potrebné zaviesť nový "supertyp supertypov" $\square$ (alebo "supertyp typových tried"), taký že pre každú typovu triedu $k$ platí: $$k:\square \qquad \text{ak} \qquad k \in K.$$
Typové konštruktory
Nech $$\vdash k:\square$$ a zároveň $$\vdash T:k,$$ potom $T$ sa nazýva konštruktor typovej triedy $k$.
Ak $T:*$, potom každý prvok typu $T$ je konštruktor typovej triedy $*$.
Napríklad $\lambda A:*.A\to A$ je konštruktor typovej triedy $* \to *$.
Poznámka
Typové konštruktory sa niekedy nazývajú aj typové operátory.
Typová relácia
Typovú relácia sa rozšírila z termov a typov o typové triedy a $\square$. Týmto sa vytvára postupnosť, ktorú je možné rozdeliť do nasledujúcich úrovní:
$$ \begin{array}{ccccccc} \textbf{Úroveň 1} & & \textbf{Úroveň 2} & & \textbf{Úroveň 3} & & \textbf{Úroveň 4} \\ \hline \\ \underbrace{\lambda x: A. x}_{term} & : & \underbrace{A \to A}_{typ/konštruktor} & : & \underbrace{*}_{typová\ trieda} & : & \square \\ \\ & & \underbrace{\lambda B:*. B \to B}_{konštruktor} & : & \underbrace{* \to *}_{typová\ trieda} & : & \square \\ \end{array} $$
- V prvom riadku je možné vidieť, že na prvej úrovni sa nachádzajú termy, ktoré sú typu, ktoré sú (konštantnej) typovej triedy $*$ a tá je typu $\square$.
- V druhom riadku sa na druhej úrovni nachádza typový konštruktor, ktorý sa samostatne nespráva ako typ. Z tohto dôvodu sa na prvej úrovni sa nenachádza žiaden term.
Druhy (sorts)
Množinu druhov $s$ je definovaná nasledovne: $$s=\{*, \square\}$$
Syntax Systému $\lambda \underline{\omega}$
Syntax termov a typov Systému $\lambda \underline{\omega}$ opisuje nasledujúca gramatika:
$$\mathcal{T} ::= X\ |\ *\ |\ \square\ |\ \lambda X:\mathcal{T} . \mathcal{T}\ |\ \mathcal{T}\ \mathcal{T}\ |\ \mathcal{T} \to \mathcal{T},$$ kde $X$ je množina (termových aj typových) premenných.
Keďže termy aj typy sú definované tou istou množinou $\mathcal{T}$, je potrebné pozmeniť definíciu kontextu $\Gamma$ na lineárne usporiadanú množinu, ktorú opisuje následujúca gramatika: $$\Gamma ::= \epsilon\ |\ \Gamma, X:\mathcal{T}$$
Poznámka
V kontexte sa musia najskôr nachádzať typové premenné a až po nich môžu nasledovať termové premenné.
Lineárne usporiadanie kontextu $\Gamma$ je nutné z nasledujúceho dôvodu. Nech je daný predpoklad: $$x:A, A:* \vdash x:A.$$ Predpokladajme pravidlo pre abstrakciu, potom by bolo možné odvodiť nasledujúci nezmyselný záver: $$x:A \vdash \lambda A:*.x: * \to A,$$ kde $A$ sa nachádza voľne a zároveň aj viazane.
Pri aplikácii podmienky lineárneho usporiadania kontextu: $$A:*, x:A \vdash x:A $$ je možné odvodiť korektný záver: $$A:* \vdash \lambda x:A.x: A \to A.$$
Poznámka
Aj keď je možné v Systéme $\lambda \underline{\omega}$ definovať termy a typy osobitne, budeme definovať syntax $\lambda \underline{\omega}$ ako jednu spoločnú množinu $\mathcal{T}$ z dôvodu prípravy na definíciu závislých typov v nasledujúcej prednáške.
Typovacie pravidlá Systému $\lambda \underline{\omega}$
Zoznam všetkých siedmych typovacích pravidiel Systému $\lambda \underline{\omega}$:

Poznámka
Všetky pravidlá sú slovne opísané vo štvrtej kapitole knihy "Type theory and formal proof: an introduction" od Nederpelta a Geuversa.
Príklad OCaml:
utop # type 'a list = Nil | Cons of 'a * 'a list;;
type 'a list = Nil | Cons of 'a * 'a list
utop # type intlist = int list;;
type intlist = int list
utop # #show list;;
type 'a list = Nil | Cons of 'a * 'a list
utop # #show intlist;;
type intlist = int list
Príklad Haskell:
Prelude> :kind Int
Int :: *
Prelude> :kind []
[] :: * -> *
Prelude> data List a = Nil | Cons a (List a)
Prelude> :kind List
List :: * -> *
Zdroje
- Nederpelt, Rob, and Herman Geuvers. Type theory and formal proof: an introduction. Cambridge University Press, 2014.
- Barendregt, Henk P. "Lambda calculi with types." (1992).
- Lecture notes, CS 152: Programming Languages, Harvard University, 2024
- Lecture notes, CS 4110 - Programming Languages and Logics, Cornell University, 2021
- Lecture notes, CS 6110 - Advanced Programming Languages, Cornell University, 2019