Závislé typy - Typy závisia na termoch
V predchádzajúcich prednáškach sme rozšírili jednoducho typovaný $\lambda$-kalkul v dvoch dimenziách $\lambda$-kocky:
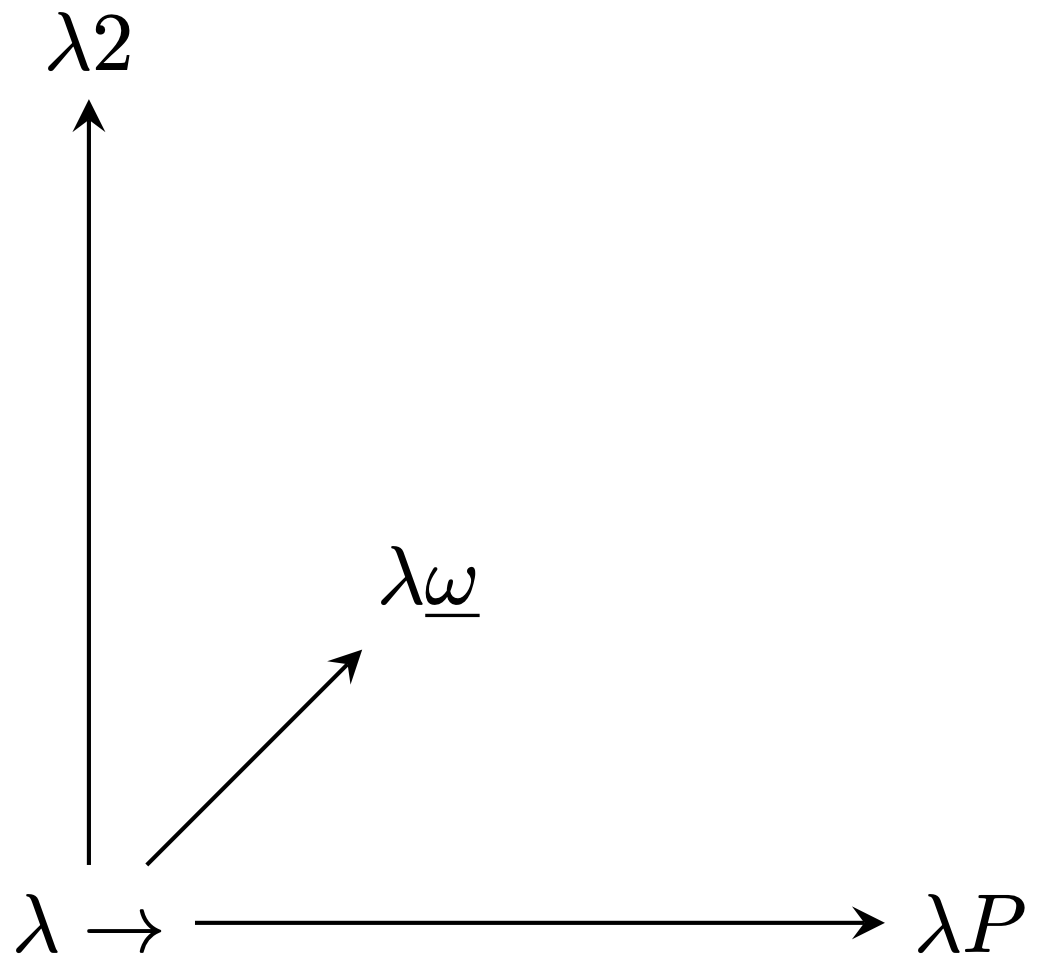
- Systém $F$ ($y$-os), kde termy môžu závisieť na typoch,
- Systém $\lambda\underline{\omega}$ ($z$-os), kde typy môžu závisieť na typoch.
V tejto kapitole bude zavedený Systém $\lambda P$, ktorý rozširuje $\lambda_\to$ o možnosť závislosti typov na termoch - závisle typy.
Jednotlivé závislosti medzi termami a typmi sú zhrnuté v nasledujúcej tabuľke:
| Teória typov | $t\ t$ | $t\ T$ | $T\ T$ | $T\ t$ |
|---|---|---|---|---|
| $\lambda_\to$ | ✓ | ✗ | ✗ | ✗ |
| $\lambda 2$ | ✓ | ✓ | ✗ | ✓ |
| $\lambda \underline{\omega}$ | ✓ | ✗ | ✓ | ✗ |
| $\lambda P$ | ✓ | ✗ | ✗ | ✓ |
$\lambda$-kocka je rozšírená o $x$-os nasledovne:
Poznámka
Systém $\lambda P$ nemá väčšiu vyjadrovaciu silu ako $\lambda_\to$ avšak umožňuje definovať špecifickejšie resp. konkrétnejšie typy.
Typ závisiaci na terme má vo všeobecnosti nasledujúci tvar: $$\lambda x:A.M$$ kde:
- $x$ - termová premenná.
- $A$ - typ.
- $M$ - typ. Potom $\lambda x:A.M$ závisí na terme $x$ a je to typový konštruktor.
Príklad
Majme daný typ $$S_n,$$ pričom $$n:Nat.$$ Potom $$\lambda n:Nat. S_n$$ je typ (presnejšie typový konštruktor).
Príklad
Majme danú množinu násobkov $n$: $$S_n = \{0, n, 2n, 3n, ... \}$$ kde $n:Nat$.
Potom $$ \lambda n:Nat. S_n $$ je typový konštruktor, ktorý ak je aplikovaný na term typu $Nat$ konštruuje nasledujúce typy:
$$ \begin{array}{l} (\lambda n:Nat. S_n)\ 0 \to \{0 \} \\ (\lambda n:Nat. S_n)\ 1 \to \{0, 1, 2, 3, ... \} \qquad = Nat - \text{Prirodzené čísla}\\ (\lambda n:Nat. S_n)\ 2 \to \{0, 2, 4, 6, ... \} \qquad = Even - \text{Párne čísla}\\ ... \end{array} $$
Systém $\lambda P$
Uvažujme typový konštruktor z predchádzajúceho príkladu: $$ \lambda n:Nat. S_n.$$ Akého je "typu"?
Keďže $n:Nat$ a $S_n:*$, potom $$ \lambda n:Nat. S_n:Nat \to *,$$ pričom $Nat \to *$ je typová trieda (Kind).
Z tohto dôvodu je potrebné upraviť gramatiku typových tried (oproti systému $\lambda\underline{\omega}$) nasledovne:
$$K::= * \ |\ T \to K.$$
$\Pi$-typ
$\Pi$-typ zovšeobecňuje spôsob zápisu funkčných typov tak, že umožňuje vyjadriť závislé typy.
Pre reprezentáciu závislých typov bude využitý $\Pi$-typ v tvare: $$\Pi x: A. M,$$ kde:
- $A:*$ - $A$ je typ.
- $x$ - termová premenná.
- $M$ - typ, ktorý môže obsahovať premennú $x$.
Príklad
Nasledujúci typový konštruktor: $$\lambda a:A.\lambda x:B_a.x$$ je typovej triedy: $$\Pi a:A.(B_a\to B_a)$$
Táto notácia umožňuje definovať aj "klasické" funkčné typy na úrovni termov.
Majme daný nasledujúci term, pričom $b:B$:
$$\lambda x:A.b : A \to B.$$
Potom typ $A\to B$ je možné vyjadriť prostredníctvom $\Pi$-notácie nasledovne: $$A\to B \equiv \Pi x:A.\ B$$ pričom $x$ sa nenachádza voľne v $B$.
Poznámka
$\Pi$-notácia a klasická notácia vo forme funkčných typov sa často používajú spoločne, pretože každá má svoje špecifické výhody a využitie. $\Pi$-notácia, používaná na reprezentáciu závislých typov, umožňuje presne vyjadriť vzťahy, kde výstupný typ závisí od konkrétneho vstupného. Klasická notácia funkčných typov, ako $A\to B$, predstavuje špeciálny prípad $\Pi$-notácie, kde výstupný typ nie je závislý od vstupného, a je preferovaná v situáciách, kde je potrebné jednoduchosť a čitateľnosť.
Typová relácia
Typovú relácia v systéme $\lambda P$ obdobne ako v systéme $\lambda \underline{\omega}$ pozostáva zo štyroch úrovní:
$$ \begin{array}{ccccccc} \textbf{Úroveň 1} & & \textbf{Úroveň 2} & & \textbf{Úroveň 3} & & \textbf{Úroveň 4} \\ \hline \\ \underbrace{\lambda x: A. b}_{term} & : & \underbrace{\Pi x:A. B}_{typ} & : & \underbrace{*}_{typová\ trieda} & : & \square \\ \\ & & \underbrace{\lambda x:A. P_x}_{konštruktor} & : & \underbrace{\Pi x:A.*}_{typová\ trieda} & : & \square \\ \end{array} $$
Poznámka
Typ $\Pi x:A. B$ je v tomto prípade ekvivalentný typu $A\to B$.
Syntax systému $\lambda P$
Syntax termov a typov Systému $\lambda P$ opisuje nasledujúca gramatika:
$$\mathcal{T} ::= X\ |\ *\ |\ \square\ |\ \lambda X:\mathcal{T} . \mathcal{T}\ |\ \mathcal{T}\ \mathcal{T}\ |\ \Pi x:\mathcal{T}. \mathcal{T},$$ kde $X$ je množina (termových aj typových) premenných.
Typový kontext $\Gamma$ je lineárne usporiadaná množina, ktorú opisuje následujúca gramatika: $$\Gamma ::= \epsilon\ |\ \Gamma, X:\mathcal{T}$$
Poznámka
V kontexte sa musia najskôr nachádzať typové premenné a až po nich môžu nasledovať termové premenné.
Typovacie pravidlá systému $\lambda P$
Typovacie pravidlá systému $\lambda P$ sú nasledovne:
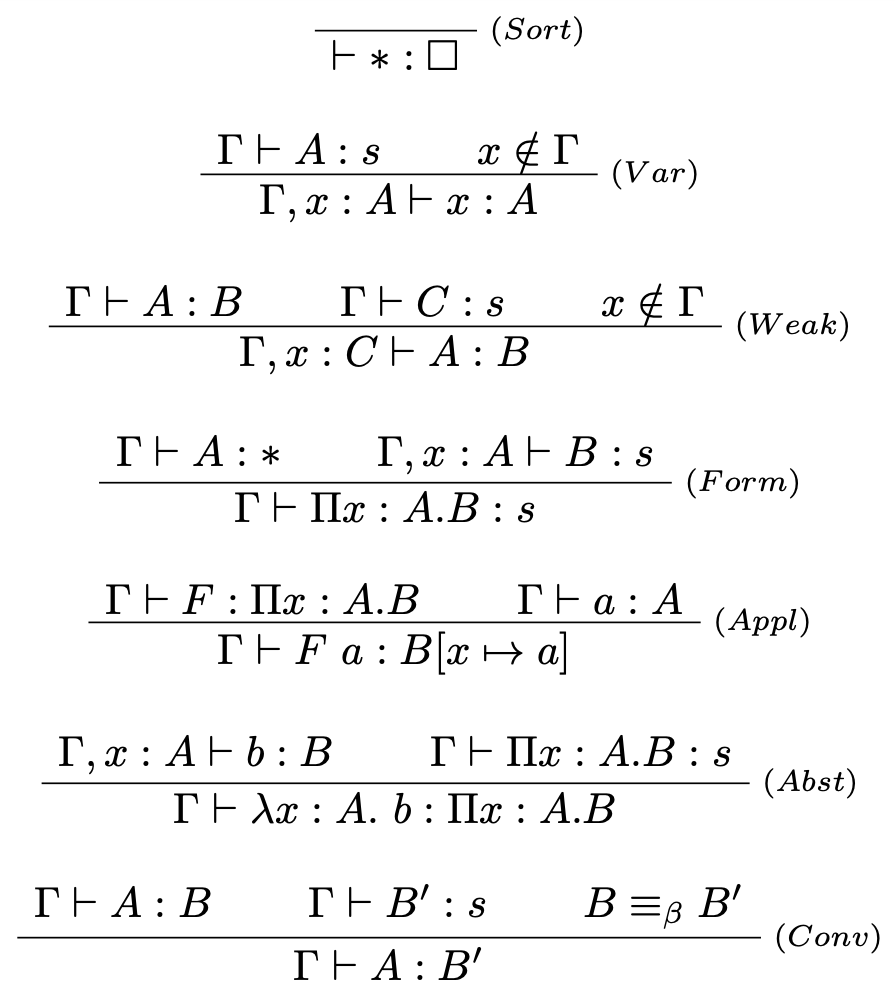
Pričom pravidlá pre aplikáciu a formuláciu majú dvojité využitie. V prípade, že typ $B$ nezávisí od premennej $x$, tak ich správanie je ekvivalentné s pravidlami:
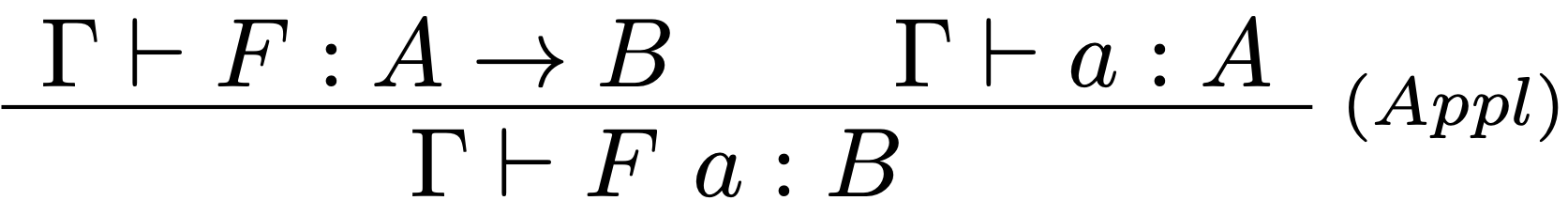
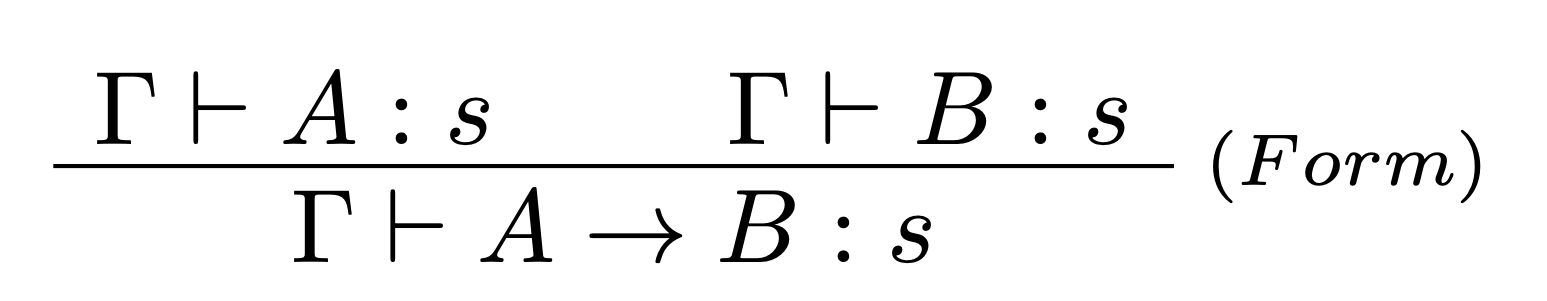
Poznámka
Všetky pravidlá sú slovne opísané v piatej kapitole knihy "Type theory and formal proof: an introduction" od Nederpelta a Geuversa.
Príklad
Častým príkladom závislých typov je typ vektor. Je to typ zoznam s fixnou dĺžkou. V systéme Coq je implementovaný v knižnici Vectors.Vector.
Require Import Coq.Vectors.Vector.
Import VectorNotations.
Check t nat.
(* Output:
t nat
: nat -> Set
*)
Print t.
(* Output:
Inductive t (A : Type) : nat -> Type :=
| nil : t A 0
| cons : A -> forall n : nat, t A n -> t A (S n)
*)
Compute nil nat.
(* Output:
= []
: t nat 0
*)
Check [1;2;3].
(* Output:
[1; 2; 3]
: t nat 3
*)
(* Function to create a vector of length n filled with zeroes *)
Fixpoint vec_zeroes (n : nat) : t nat n :=
match n with
| 0 => [] (* Base case: a vector of length 0 is empty *)
| S n' => 0 :: vec_zeroes n' (* Recursive case: prepend 0 to a vector of length n' *)
end.
(* Example usage *)
Definition example_vector := vec_zeroes 6.
(* Verify the result *)
Compute example_vector.
(* Output:
[0; 0; 0; 0; 0]
*)
Check ([0;0] : t nat 2 ).
(* Output:
[1; 2; 3]
: t nat 3
*)
(* Append two vectors: Concatenate a vector of size n with a vector of size m *)
Fixpoint vec_append {A : Type} {n m : nat} (v1 : t A n) (v2 : t A m) : t A (n + m) :=
match v1 with
| [] => v2 (* If the first vector is empty, return the second vector *)
| x :: xs => x :: vec_append xs v2 (* Prepend the head of v1 to the appended result *)
end.
(* Example usage *)
Definition vec1 : t nat 3 := [1; 2; 3].
Definition vec2 : t nat 2 := [4; 5].
Definition appended_vec : t nat 5 := vec_append vec1 vec2.
(* Verify the result *)
Compute appended_vec.
(* Output:
[1; 2; 3; 4; 5]
*)
Zdroje
- Nederpelt, Rob, and Herman Geuvers. Type theory and formal proof: an introduction. Cambridge University Press, 2014.
- Barendregt, Henk P. "Lambda calculi with types." (1992).
- Lecture notes, CS 152: Programming Languages, Harvard University, 2024
- Lecture notes, CS 4110 - Programming Languages and Logics, Cornell University, 2021
- Lecture notes, CS 6110 - Advanced Programming Languages, Cornell University, 2019