Úvod do funkcionálneho programovania v Coq

Coq - Interaktívny dokazovací systém

Coq je interaktívny dokazovací systém, ktorý umožňuje vytváranie formálnych matematických dôkazov a overovanie korektnosti algoritmov. Je založený na komplexnej teórii typov, známej ako calculus of inductive constructions (CIC). CIC poskytuje vysokú vyjadrovaciu silu na reprezentáciu rôznych matematických tvrdení a umožňuje formálne dokázať ich správnosť. Táto teória typov kombinuje:

• Induktívne definície, ktoré umožňujú konštrukciu dátových typov (napr. prirodzených čísel),
• Konštruktívnu logiku, ktorá vyžaduje, aby každé dokázané tvrdenie bolo konštruktívne.

Coq sa stáva silným nástrojom nielen v akademickom prostredí, ale aj v oblasti softvérového inžinierstva, kde sa používa na formálnu verifikáciu softvéru, čo prispieva k tvorbe bezpečnejšieho a spoľahlivejšieho softvéru.

Poznámka: Coq má uplatnenie v matematických teóriách a formálnych dôkazoch, ale zároveň je používaný v priemysle na overovanie správnosti kritických softvérových komponentov. Napríklad, CompCert C verified compiler je prekladač jazyka C, ktorý bol formálne verifikovaný pomocou Coq-u. Vďaka tomu sa eliminuje celý rad chýb, ktoré by mohli nastať v neoverených prekladačoch.

Coq ako viacúrovňový systém

Coq je modulárny systém, ktorý pozostáva z troch hlavných jazykov, ktoré spolu interagujú:

1. Gallina:
   • Gallina je základný funkcionálny programovací jazyk v Coq-u, v ktorom sa píšu definície a matematické tvrdenia. Je to čistý jazyk vyššej úrovne, ktorý podporuje rekurziu, prehľadávanie podľa vzorov a ďalšie konštrukcie potrebné na tvorbu matematických štruktúr.

• Príklad:

  Definition faktorial (n : nat) : nat :=
    match n with
    | 0 => 1
    | S n' => n * faktorial n'
    end.
  

2. Vernacular príkazy:
   • Vernacular je jazyk príkazov používaný na manipuláciu s objektmi v Coq-u. Umožňuje písať definície, lemy, definovať induktívne typy, teórie a podobne.
   • Kľúčové príkazy zahŕňajú:
     • Definition, Fixpoint (definície funkcií),
     • Lemma, Theorem (deklarácia dôkazov),
     • Print, Check (výpis a kontrola typov objektov).

• Príklad:

  Print nat.
  Definition názov_funkcie....
  

3. Ltac:
   • Ltac je taktický jazyk pre automatizáciu dôkazov. Poskytuje silné nástroje na manipuláciu s cieľmi v dôkazovom stave, čo uľahčuje opakovateľné a zložité dôkazové kroky.
   • Používanie taktík umožňuje interaktívne vedenie dôkazov a ich čiastočnú automatizáciu.
   • Príklad: intro, simpl, reflexivity

• Príklad:

  Lemma plus_0_r : forall n : nat, n + 0 = n.
  Proof.
    intros n.
    induction n.
    - reflexivity.
    - simpl. rewrite IHn. reflexivity.
  Qed.
  

Inštalácia Coq

Pre inštaláciu interaktívneho dokazovacieho systému Coq postupujte podľa návodu na domovskej stránke projektu:

https://coq.inria.fr/download.

Coq môžete používať rôznymi spôsobmi:

• Oficiálne IDE - CoqIDE:

  • Poskytuje grafické rozhranie na interaktívnu prácu s Coq-om. Vhodné pre používateľov, ktorí preferujú jednoduché IDE pre prácu s dôkazmi.

• Visual Studio Code:

  • Plugin pre Coq, ktorý umožňuje používať Visual Studio Code ako editor s podporou Coq-u, poskytujúci všetky funkcie moderného IDE, vrátane zvýrazňovania syntaxe, automatického dokončovania a interaktívneho dokazovania.

• Emacs:

  • Pokročilí používatelia často preferujú Emacs s rozšírením ProofGeneral pre plnohodnotnú interakciu s Coq-om priamo v Emacs-e.

Ovládanie CoqIDE – Stručný prehľad

CoqIDE sa skladá z troch hlavných častí, spolu s ovládacím panelom pre prácu s dôkazmi:

Hlavné okná:

1. Textové okno (vľavo):
   • Píšete kód: Definície, tvrdenia a dôkazy.
   • Ovládanie:
     • Windows: Ctrl+↓ (krok dopredu), Ctrl+↑ (krok dozadu).
     • Mac: Cmd+↓ (krok dopredu), Cmd+↑ (krok dozadu).

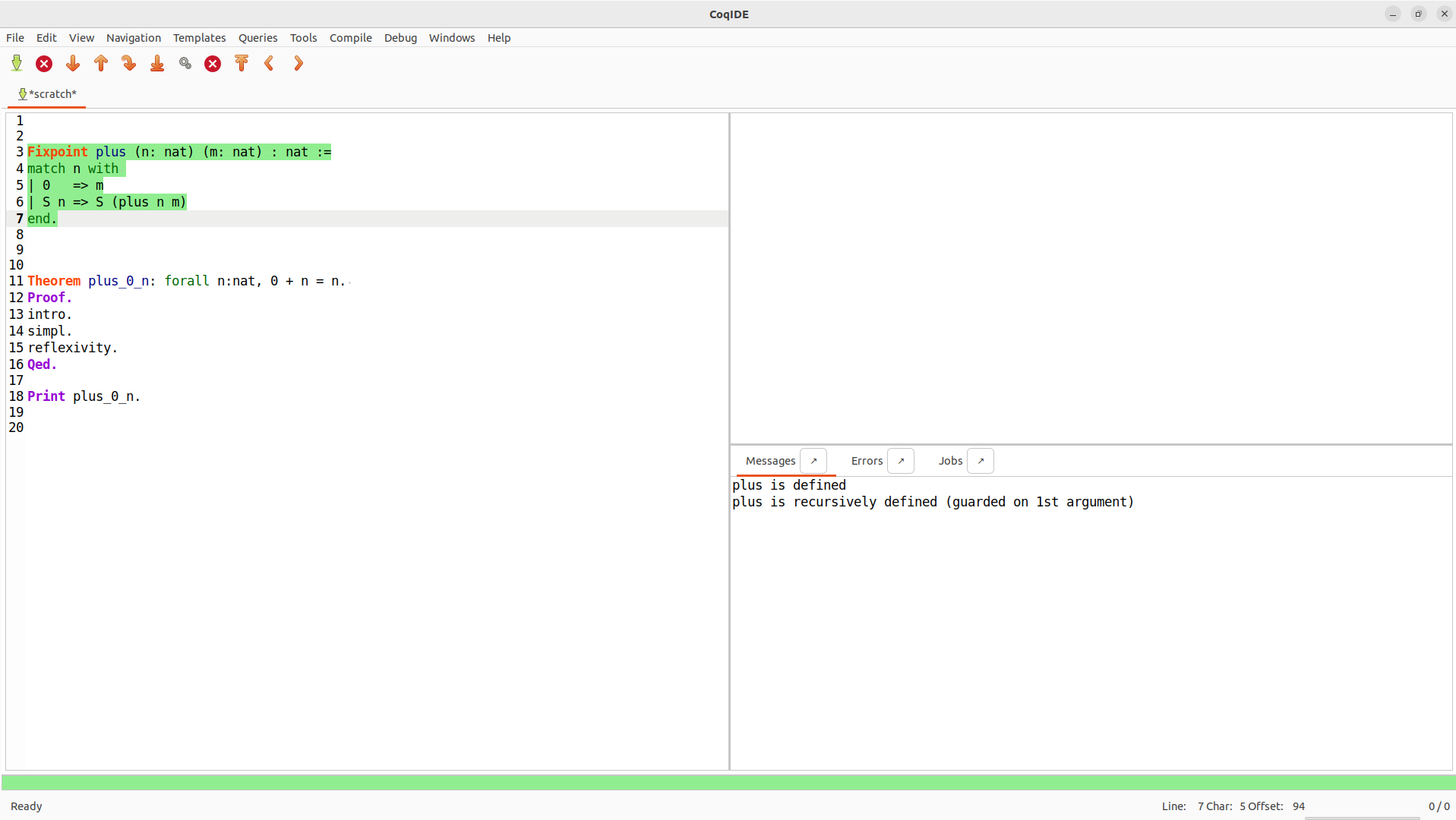
2. Interaktívne okno aktuálnych cieľov ("Goals") (vpravo hore):
   • Ukazuje aktuálne ciele: Zobrazuje stavy dôkazov, subciele (goals), ktoré treba dokázať.
   • Dôležité pre sledovanie priebehu dôkazu.

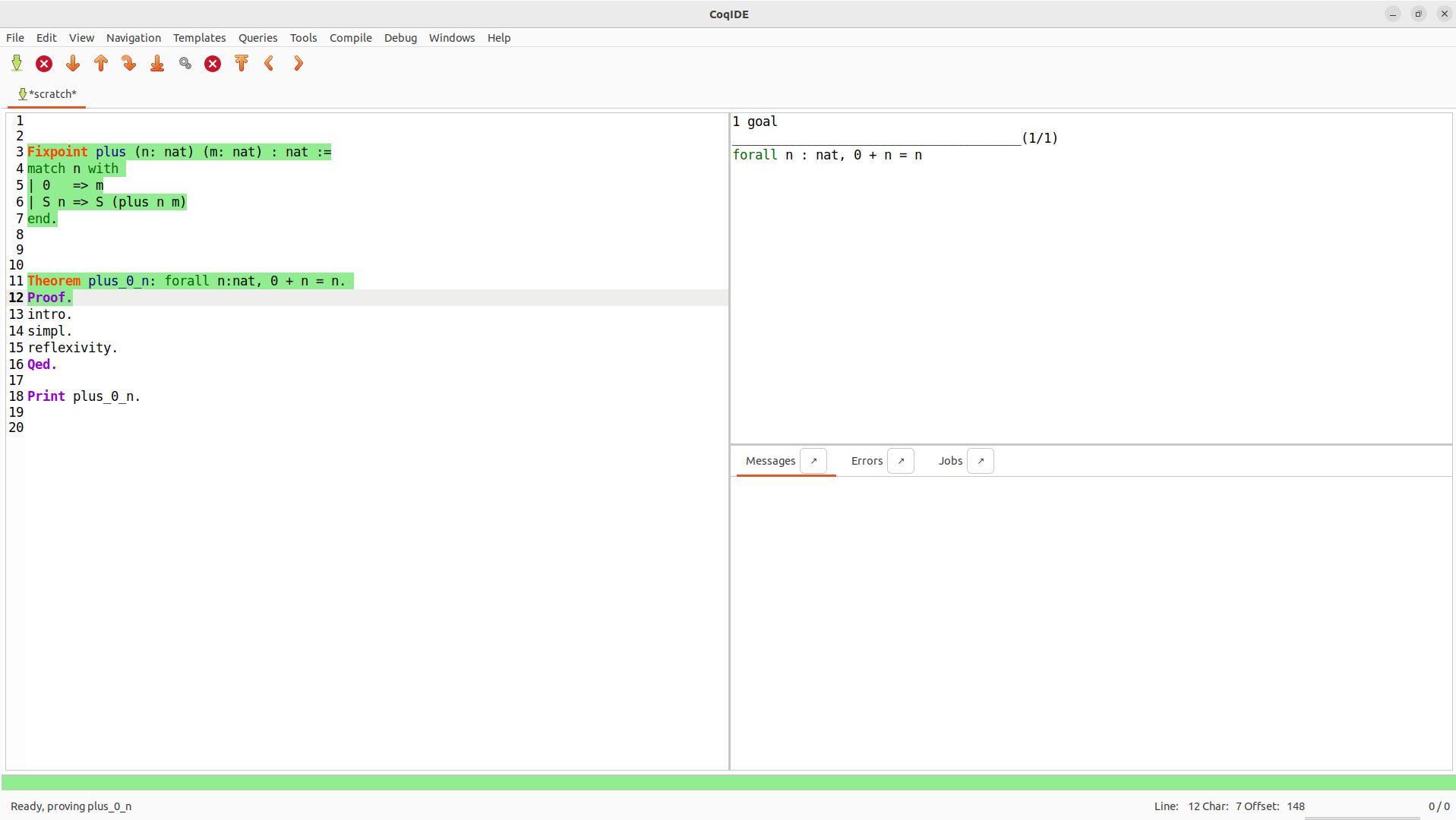
3. Okno správ ("Messages") (vpravo dole):
   • Chybové hlásenia a výsledky: Zobrazuje chyby, informácie o príkazoch a výsledky ako napr. Check, Print.

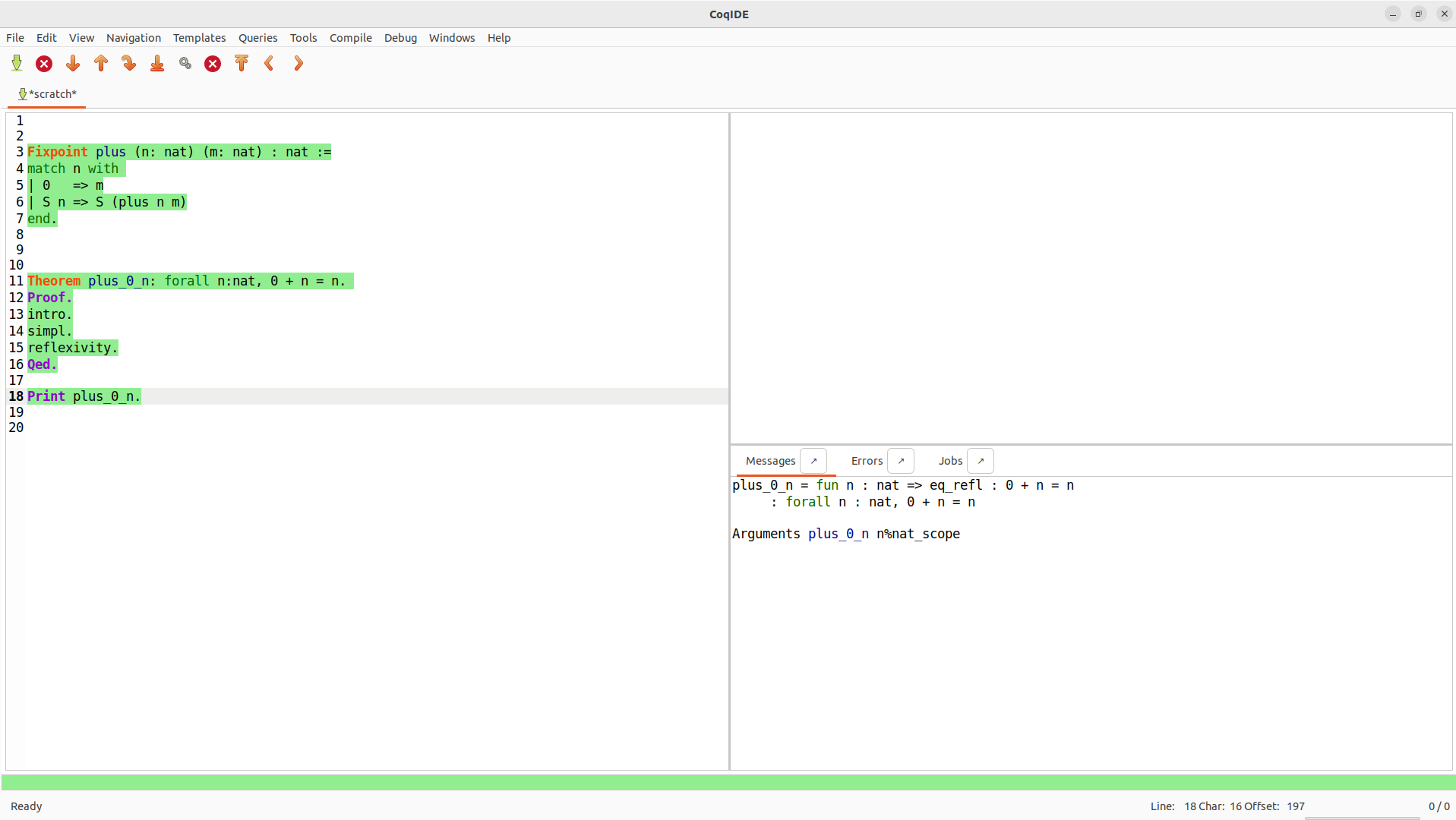
Ovládací panel:

• Next/Previous:

  • Krokovanie dopredu/dozadu v dôkaze.
  • Windows skratky: Ctrl+↓ (Next), Ctrl+↑ (Previous).
  • Mac skratky: Cmd+↓ (Next), Cmd+↑ (Previous).

• Reset: Reštartuje celý dôkaz od začiatku.

• Run to end: Skontroluje celý súbor.

• a ďalšie...

Úvod funkcionálneho programovania v Coq

Funkcionálne programovanie je jednou z hlavných programovacích paradigiem, ktorá je založená na používaní funkcií ako základných stavebných prvkov. Tento prístup zdôrazňuje používanie čistých funkcií (bez vedľajších efektov) a využíva imutabilné (nemenné) dátové štruktúry. Coq ako interaktívny dokazovací systém je zároveň aj funkcionálnym programovacím jazykom, čo znamená, že v Coq je možné písať programy podobne ako vo funkcionálnych jazykoch OCaml alebo Haskell.

Funkcie v Coq sú prvotriedne objekty, čo znamená, že môžu byť odovzdávané ako argumenty iným funkciám alebo vrátené ako výsledky. Tento prístup k programovaniu sa nazýva funkcionálne programovanie a má veľké výhody pri formálnom dokazovaní vlastností programov.

Základné koncepty funkcionálneho programovania v Coq

1. Imutabilita: V Coq, podobne ako vo väčšine funkcionálnych jazykov, sú premenné imutabilné. Ak je raz hodnota priradená premennej, táto hodnota sa už nedá zmeniť.

2. Funkcie ako hodnoty: Funkcie sú v Coq prvotriednymi objekty jazyka. To znamená, že ich môžeme priraďovať premenným, odovzdávať ako argumenty iným funkciám a vrátiť ich ako výsledky.

3. Čisté funkcie: V Coq, všetky funkcie sú čisté, čo znamená, že ich výsledok závisí iba od ich vstupov a nemajú žiadne vedľajšie efekty (napr. modifikovanie globálnych premenných).

Komentáre

• Komentáre sú uzatvorené v (* a *).
• Jednoriadkové komentáre nie su podporované.

Premenné, funkcie a základné príkazy Vernacular

Coq je možné ovládať a dopytovať prostredníctvom príkazového jazyka nazývaného Vernacular. Kľúčové slová jazyka Vernacular sú písané s veľkým začiatočným písmenom a príkazy končia bodkou. Deklarácie premenných a funkcií sa tvoria pomocou príkazu "Definition" jazyka Vernacular.

Definition x := 10.

Coq vo väčšine prípadov dokáže odvodiť typ argumentov, avšak je konvenciou ich explicitne uvádzať.

Definition succ (x : nat) : nat := x + 1.

Definíciu (akejkoľvek) funkcie je možné vypísať na obrazovku prostredníctvom príkazu Print.

Vykonanie príkazu

Print succ.

poskytne výstup:

succ = fun x : nat => x + 1
     : nat -> nat

Arguments succ _%nat_scope

Príkazy na dopytovanie informácií

Existuje veľké množstvo užitočných Vernacular príkazov na dopytovanie informácií.

• Vypočítať výsledok:

Compute (1 + 1). (* 2 : nat *)

• Typ vyrazu:

Check 1.

• Informácie o objekte:

About plus. 

• Informácie vrátane definície:

Print Nat.add.

• Vyhľadávanie:

Search nat. (* Vráti zoznam hodnôt súvisiacich s nat *)
Search "_ + _". (* Vyhľadávanie podľa vzorov *)

• Locate vypíše, odkiaľ pochádza notácia. Veľmi užitočné, v prípade na novej notácie.

Locate "+".

Vypíše následovné:

Notation "{ A } + { B }" := (sumbool A B) : type_scope
  (default interpretation)
Notation "A + { B }" := (sumor A B) : type_scope
  (default interpretation)
Notation "x + y" := (Nat.add x y) : nat_scope (default interpretation)
Notation "x + y" := (sum x y) : type_scope

Funkcie vyššieho rádu

Vo funkcionálnej paradigme je všetko funkcia. Aj keď hovoríme, že funkcia má viacero parametrov, v skutočnosti je každá funkcia implementovaná ako funkcia, ktorá očakáva jeden argument a vráti funkciu, ktorá spracuje ďalší argument. Preto zavolanie funkcie s nedostatočným počtom argumentov nespôsobí chybu, ale vytvorí novú funkciu.

Definition plus x y := x + y. (* plus je typu nat -> nat -> nat *)
Definition plus2 := plus 2.   (* plus2 je nat -> nat *)
Compute plus2 3. (* Vráti 5 *)

Konštrukcia let ... in

Definície môžu byť reťazené pomocou konštrukcie "let x:=t1 in t2".

Definition add_xy : nat := let x := 10 in
                           let y := 20 in
                           x + y.

Pattern matching

Pattern matching je konštrukt, ktorý umožňuje rozložiť hodnoty dátových typov a rozhodnúť sa na základe ich tvaru alebo štruktúry.

Definition is_zero (x : nat) :=
    match x with
    | 0 => true
    | _ => false  (* vzor "_" znamená "hocičo iné". *)
    end.

Úplne definované funkcie

Coq je totálny programovací jazyk. To znamená, že akceptuje programy len vtedy, keď dokáže pochopiť, že terminujú. Preto nie je povolené písať čiastočne definované funkcie. To spôsobuje, že jazyk Coq nie je Turingovsky úplný, čo však neznižuje jeho reálnu vyjadrovaciu silu.

Z tohto dôvodu v Coq nie je akceptovaná takáto definícia funkcie:

Definition negb (b : bool) :=
    match b with
    | true => false
    end.

Avšak obdobná definícia v jazykoch ako OCaml alebo Haskell je v poriadku.

Rekurzívne funkcie

Pre definíciu rekurzívnych funkcií slúži kľúčové slovo Fixpoint.

Priama rekurzia

Majme následujúcu rekurzívnu definíciu funkcie faktoriál: $$ faktorial(n)= \begin{cases} 1 \quad \text{ak}~n=0,\\ ~ \\ n*faktorial(n-1) \end{cases} $$ kde $n \in \mathbf{N}$.

Túto funkciu je možné vyjadriť definovať následovne:

Fixpoint factorial n := match n with
                        | 0 => 1
                        | (S n') => n * factorial n'
                        end.

Nepriama rekurzia

Funkcie ktoré su nepriamo rekurzívne (mutually recursive) je možné definovať prostredníctvom kľúčového slova with

Fixpoint is_even (n : nat) : bool := match n with
  | 0 => true
  | (S n) => is_odd n
end with
  is_odd n := match n with
  | 0 => false
  | (S n) => is_even n
end.

Anonymné $\lambda$ funkcie

Anonymné funkcie je možné definovať prostredníctvom konštrukcie:

fun x => x

Napríklad identická funkcia na prirodzených číslach môže byt definovaná následovne:

Definition id_nat : nat -> nat := fun x => x.

Takáto definícia obmedzuje použitie tejto funkcie len na typ nat. Využitím polymorfných typov je možné identickú funkciu definovať pre ľubovoľný typ:

Definition id_poly (A : Type) (x : A) : A := x.
Definition id_poly2 : forall A : Type, A -> A := fun A x => x.
Compute id_poly nat 3. (* 3 : nat *)

Coq, dokáže odvodiť výrazy využitím podčiarkovníka:

Compute id_poly _ 3.

Implicitný argument funkcie je argument, ktorý môže byť odvoditeľný z kontextu. Predvolené, parametre uzavreté v { } sú implicitné.

Definition id_poly3 {A : Type} (x : A) : A := x.
Compute id_poly3 3. (* 3 : nat *)

Niekedy je potrebné implicitnosť parametrov vypnúť pomocou @.

Compute @d_poly3 nat 3.

Alebo je možné uviesť všetky argumenty spolu s ich menom:

Compute d_poly3 (A:=nat) 3.

Vlastné údajové typy

Pre definíciu údajových typov slúži Vernacular príkaz Inductive.

Všeobecná syntax pre induktívne typy

Inductive TypeName : Type :=
  | Constructor1 : Type1 -> TypeName
  | Constructor2 : Type2 -> TypeName
  | Constructor3 : Type3 -> TypeName
  | ... (* Viac konštruktorov podľa potreby *)
  | ConstructorN : TypeN -> TypeName.

Základná štruktúra:

• Inductive: Kľúčové slovo označuje začiatok definície induktívneho typu.
• TypeName: Názov typu, ktorý definujete.
• Type Tento parameter zvyčajne špecifikuje typ induktívneho typu. Ak to nešpecifikujete, Coq predpokladá, že ide o Type. Ďalšou možnosťou je Set alebo Prop (viď dokumentáciuu)

Každý konštruktor definuje spôsob, ako vytvoriť hodnotu induktívneho typu:

• Názov konštruktora musí byť jedinečný.
• Argumenty: Konštruktory môžu brať argumenty rôznych typov, vrátane iných induktívnych typov.

Induktívne typy môžu mať aj viaceré parametre. Napríklad:

Inductive TypeName (param1 : Type1) (param2 : Type2) : Type :=
  | Constructor1 : TypeName param1 param2
  | Constructor2 : ... -> TypeName param1 param2.

Inductive day : Type :=
  | Monday
  | Tuesday
  | Wednesday
  | Thursday
  | Friday
  | Saturday
  | Sunday.

Definition next_weekday (d : day) : day :=
  match d with
  | Monday    => Tuesday
  | Tuesday   => Wednesday
  | Wednesday => Thursday
  | Thursday  => Friday
  | Friday    => Saturday
  | Saturday  => Sunday
  | Sunday    => Monday
  end.

Coq podporuje aj rekurzívne typy, napríklad prirodzené čísla je možné definovať ako induktívny typ nat:

Inductive nat : Type :=
  | O
  | S (n : nat).

Moduly

Niekedy je potrebné fragment kódu uzavrieť do oddelenej časti - modulu.

Module NazovModulu.
Definition foo.
End NazovModulu.

Mimo daného modulu je možný prístup k jeho objektom prostredníctvom operátora bodky:

NazovModulu.foo 

Napríklad, je možné zadefinovať vlastný typ nat, ktorý obsahuje štandardná knižnica systému Coq. V prípade, že takýto typ je zadefinovaný priamo v zdrojovom kóde (nie je uzavretý v module), preťaží definíciu zo štandardnej knižnice.

Module NatPlayground.

Inductive nat : Type :=
  | O
  | S (n : nat).

Fixpoint plus (n: nat) (m: nat) : nat :=
match n with 
| O   => m
| S n => S (plus n m)
end.

Fixpoint mult (n: nat) (m: nat) : nat :=
match n with 
| O   => O
| S n => plus m (mult n m)
end.

Compute (plus (S O) (S O)).
Compute (mult (S(S O)) (S(S O))).

End NatPlayground.

Notácie

Coq má veľmi silný systém Notácie, ktorý sa dá využiť na písanie výrazov v prirodzenejších formách.

Compute Nat.add 3 4. (* 7 : nat *)
Compute 3 + 4. (* 7 : nat *)

Notácia je syntaktická transformácia aplikovaná na text programu pred jeho vyhodnotením. Notácia je organizovaná do rozsahov (scope) notácie. Použitie rôznych rozsahov notácie umožňuje preťažovanie.

Coq ma preddefinované nasledujúce rozsahy:

• core_scope,
• type_scope,
• function_scope,
• nat_scope,
• bool_scope,
• list_scope,
• int_scope a
• uint_scope.
• Numerické rozsahy Z_scope (celé čísla) a Q_scope (zlomky) sú taktiež zahrnuté v moduloch ZArith a QArith.

Prostredníctvom príkazu Print je možné vypísať obsah rozsahu:

Print Scope nat_scope.

Notation "x --" := (pred x)(at level 30).
Notation "x * y" := (plus x y)(at level 40, left associativity).
Notation "x + y" := (plus x y)(at level 50, left associativity).

Extrakcia kódu

Coq dokáže extrahovať kód do rôznych programovacích jazykov ako je OCaml, Haskell a Scheme.

Napríklad:

Require Extraction.
Extraction Language OCaml.
Extraction "factorial.ml" factorial.