Úvod
V tejto prednáške sa budeme venovať rozšíreniam jazyka $\lambda_\to$ kalkulu a ich formálnej definícii.
- V úvode upresníme definície typov a zavedieme nový základný typ Unit (jednotkový typ).
- V nasledujúcej kapitole sa budeme venovať odvodeným tvarom termov.
- V záverečnej časti pridáme do jazyka nový typový konštruktor pre súčinové typy, čo nám umožní definovať v jazyku $\lambda_\to$ kalkulu viaceré údajové štruktúry.
Základné typy, neinterpretované typy a jednoduché typy
Typované programovacie jazyky zvyčajne poskytujú viacero základných typov - množiny jednoduchých neštruktúrovaných hodnôt ako celé čísla, znaky, reťazce alebo boolean hodnoty nad ktorými sú definované príslušné základné operácie pre manipuláciu s hodnotami daných typov.
V predchádzajúcej definícii $\lambda_\to$ kalkulu rozšíreného o NBL boli definované dva základne typy: $Bool$ a $Nat$ a niekoľko operácii nad nimi.
V nasledujúcich kapitolách budú používané aj iné typy, napríklad:
- celé čísla ($Int$) s operáciami $+, -, *, /, ...$
- reálne čísla ($Float$) s operáciami $+, -, *, /, ...$
- symboly ($Char$) s operáciami $ord, char, ...$
- reťazce ($String$) s operáciami $concat, ... $
- a pod.
Základný typ je skupina (množina) jednoduchých neštruktúrovaných hodnôt spolu s primitívnymi operáciami na nich.
Pre teoretické potreby logického uvažovania a formálnych definícií je vhodné abstrahovať z konkrétnych základných typov a ich operácií a zaviesť do jazyka množinu neinterpretovaných (abstraktných) typov $\mathcal{A}$, ktoré budú označené veľkými písmenami latinskej abecedy: $$A,B,C,... \in \mathcal{A}$$ prípadne s indexmi.
Gramatika, ktorá opisuje množinu jednoduchých typov v $\lambda_\to$ s NBL je upravená nasledovne: $$T::= A\ |\ T \to T\ |\ Bool\ |\ Nat$$ kde $A$ bude reprezentovať množinu neinterpretovaných typov.
Poznámka
Symbol $A$ bude použitý pre neinterpretovaný typ ako aj množinu neinterpretovaných typov: $$A \in A$$
Poznámka
Neinterpretované typy majú okrem teoretických definícii využitie v reálnych vlastnostiach ako je polymorfizmus, ktorému sa budeme venovať v závere semestra. Napríklad, polymorfná identická funkcia môže byť definovaná nasledovne: $$id = \lambda x :A . x : A \to A,$$ kde za $A$ môže byť substituovaný ľubovoľný typ.
Jednotkový typ
Jazyk $\lambda_\to$ rozšírime o základný typ: $$Unit$$ nazývaný jednotkový typ alebo singleton.
Jednotkový typ na rozdiel od neinterpretovaných typov je interpretovaný najjednoduchším možným spôsobom:
- Má jediný prvok, konštantu $\mathbf{unit}$, ktorá je zároveň aj jediná hodnota, akú term typu $Unit$ môže nadobudnúť.
- Výsledkom vyhodnotenia termu typu $Unit$ je vždy hodnota $\mathbf{unit}$.
Rozšírime syntax $\lambda_\to$ nasledovné: $$ \begin{array}{ll} t::= & \ldots~|~ unit \\ v::= & \ldots~|~ unit\\ T::= & \ldots~|~ Unit \end{array} $$
Pridáme nové typovacie pravidlo: $$ \Gamma \vdash \mathtt{unit: Unit} ~~~~~~~~~~\mathrm{(T-unit)} $$
Poznámka
Typ $Unit$ sa často používa v jazykoch, ktoré povoľujú vznik vedľajších účinkov (side effects).
Poznámka
Jednotkový typ bude neskôr využitý pri konštrukcii:
- odvodených tvarov termov,
- enumeračných typov,
- referenčných typov.
Odvodené tvary termov
Odvodené tvary umožňujú:
- zavedenie skratiek do λ-termov;
- indikujú postup pri vyhodnocovaní λ-termov;
- uľahčujú písanie a zvyšujú čitateľnosť programov.
Všetky odvodené tvary sa dajú vyjadriť pomocou základných tvarov λ-kalkulu!
Zavedieme nasledujúce odvodené tvary λ-termov:
- zoradenie (sequencing);
- zastúpenie (wildcards);
- pripísanie (ascription);
- väzba let (let binding).
Poznámka
Vo funkcionálnych jazykoch je možné definovať aj ďalšie odvodené tvary, podľa potreby navrhovaného jazyka.
Zoradenie (sequencing)
V jazykoch, ktoré podporujú vedľajšie účinky (side effects) je užitočné vyhodnotiť dva alebo viac výrazov zoradených za sebou.
Notácia: $$t_1;t_2$$ znamená:
- najprv sa vyhodnotí výraz $t_1$,
- triviálny výsledok (hodnota $unit$) sa odstráni (zabudne, odhodí) a
- pokračuje sa vyhodnotením výrazu $t_2$.
Tento odvodený tvar neznamená postupné vyhodnotenie termov, len v tom prípade, ak na výsledku (hodnote) prvého termu nezáleží!
Existujú dva rozdielne spôsoby formalizácie zoradenia:
1.spôsob:
Postup je rovnaký ako pri iných syntaktických tvaroch:
- rozšírime syntax o novú alternatívu $t_1;t_2$ v produkčnom pravidle pre termy:
$$t::= ... |\ t_1;t_2$$
- pridáme nové vyhodnocovacie pravidlá:
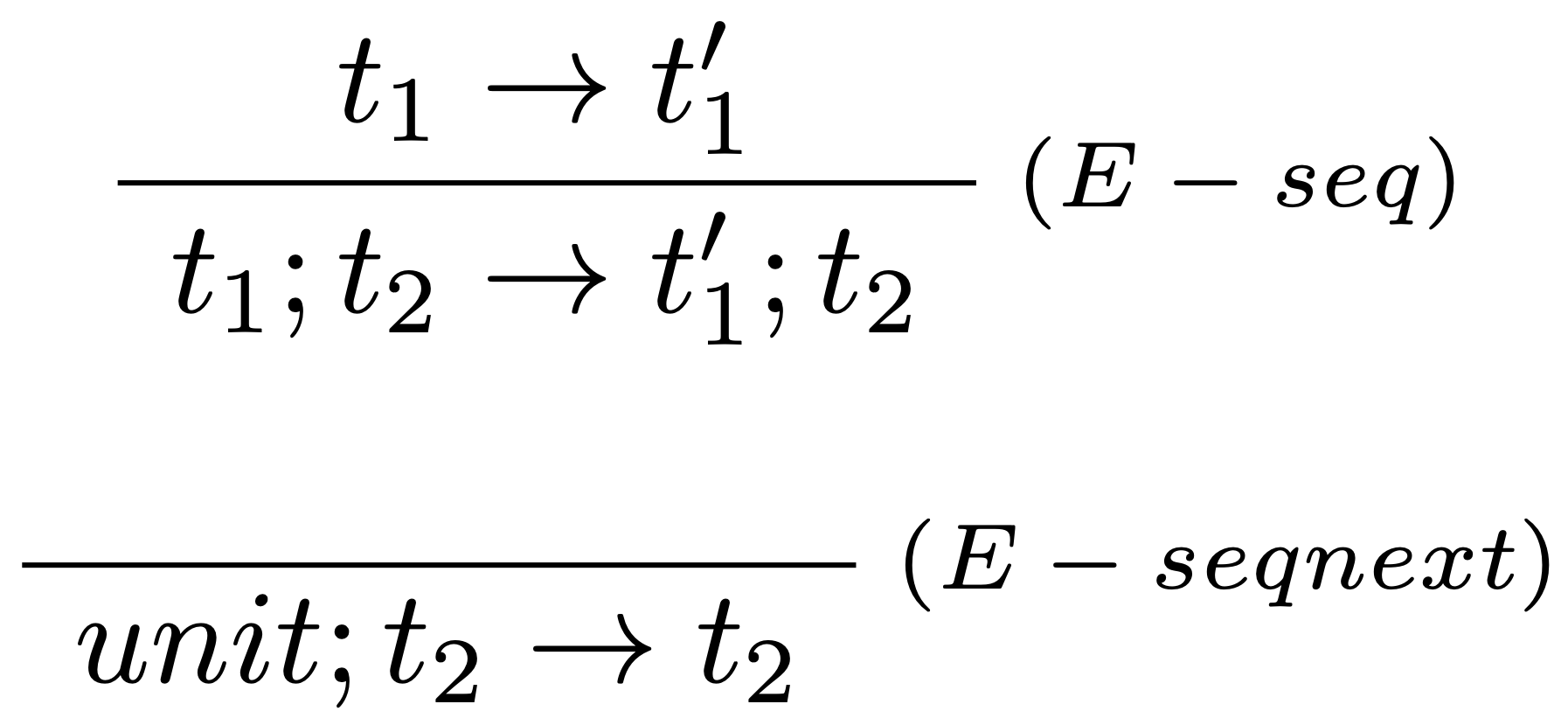
- a nakoniec definujeme typovacie pravidlo:
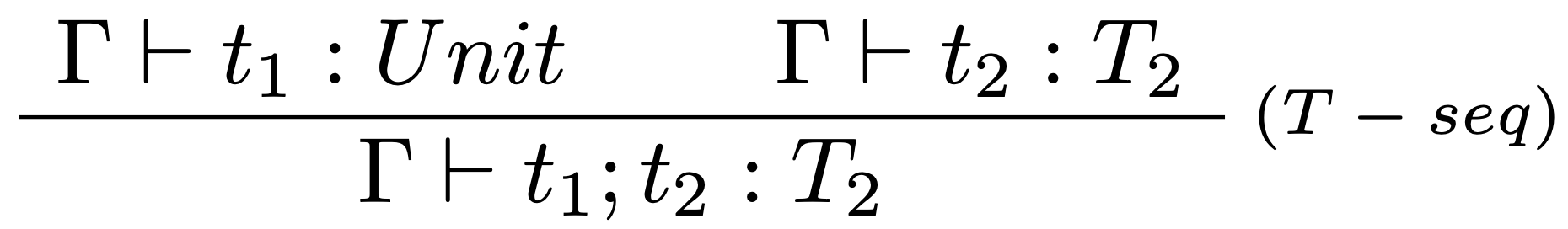
2.spôsob:
Zápis $t_1;t_2$ je považovaný za skratku termu:
$$(\lambda x:Unit.t_2)\ t_1$$
Všimnime si, že parameter tejto funkcie je typu $Unit$!
Príklad
Aj keď jazyk OCaml je funkcionálny jazyk, nie je považovaný za čistý funkcionálny jazyk z dôvodu, že podporuje vedľajšie účinky.
Vedľajšie účinky sú implementované ako funkcie, ktoré vykonajú daný účinok (napríklad výpis na obrazovku) a vrátia hodnotu $unit$.
Napríklad funkcie print_string a print_newline:
utop # print_string;;
- : string -> unit = <fun>
utop # print_string "Hello, OCaml!";;
Hello, OCaml!- : unit = ()
utop # print_newline;;
- : unit -> unit = <fun>
Zoradenie v jazyku OCaml je možné využiť nasledovne:
utop #
print_string "Hello, ";
print_string "world!";
print_newline (); (* hodnota unit je v OCaml reprezentovaná ako () *)
succ 4;; (* po výpise na obrazovku reťazca
"Hello, world!" pokračuje výpočet*)
Hello, world!
- : int = 5
Poznámka
Jazyk Haskell je považovaný za čistý funkcionálny jazyk, ktorý priamo nepodporuje vedľajšie účinky. Avšak efekt vedľajších účinkov je možné získať prostredníctvom monád.
Interný a externý jazyk
Majme jednoducho typovaný $\lambda$-kalkul, ktorý je rozšírený o jednotkový typ.
Zavedieme pojmy:
- Externý jazyk $\lambda^{E}$: je jednoducho typovaný $\lambda$-kalkul s typom $\mathtt{Unit}$ a konštruktorom zoradenia ''$;$''.
- Interný jazyk $\lambda^{I}$: je jednoducho typovaný $\lambda$-kalkul len s typom $\mathtt{Unit}$.
Veta o zoradení
Pri preklade textu programu je potrebné preložiť odvodený tvar v externom jazyku do tvaru v internom jazyku. Formulujeme nasledujúce tvrdenie:
Veta:
Nech $e$ je spracujúca funkcia elaborating function
$$ e : \lambda^{E} \rightarrow \lambda^{I} $$
ktorá spracuje (preloží) externý jazyk $\lambda^{E}$ do interného jazyka $\lambda^{I}$ tak, že nahradí každý výskyt zoradenia $t_1;t_2$ termom
$$ (\lambda x:Unit.t_2) t_1 $$
Potom pre každý term $t$ z externého jazyka $\lambda^{E}$ platí: $$ \begin{array}{lcl} t \rightarrow_{E} t' & \mathrm{vtt.} & e(t) \rightarrow_{I} e(t') \\ \Gamma \vdash_{E} t:T & \mathrm{vtt.} & \Gamma \vdash_{I} e(t):T \end{array} $$
$\Box$
Táto veta hovorí, že zoradenie je odvodený tvar, pretože dokázateľne tvrdí, že typovanie a správanie konštrukcie zoradenia možno odvodiť zo základných operácií abstrakcie a aplikácie.
Syntactic sugar
Použitie odvodených tvarov ako je napríklad zoradenia sa niekedy nazýva syntaktický cukor (z ang. syntactic sugar), pretože uľahčuje písanie aj čítanie $\lambda$-termov:
- zavedie nové tvary termov bez zmeny interného jazyka,
- uľahčuje písanie a čitateľnosť programov,
- typová bezpečnosť jazyka zostane zachovaná.
Spätné nahradenie (rozvinutie) odvodenej formy (skratky) do svojho pôvodného tvaru v internom jazyku sa nazýva desugaring a vykonáva sa počas syntaktickej analýzy v parseri.
Zastúpenie
Niekedy potrebujeme zapísať prázdnu dummy abstrakciu, v ktorej sa parameter nepoužíva v tele abstrakcie.
Takáto funkcia je konštantná.
V takomto prípade je zbytočné explicitne zvoliť a písať premennú (parameter) viazaný abstrakciou.
Namiesto toho je možné použiť zastúpenie v tvare:
$$ \lambda\_: S. t $$
čo znamená skratku pre term $\lambda x: S. t$, pričom v terme $t$ sa premenná $x:S$ nevyskytuje.
Poznámka
Aj v prázdnej abstrakcii je potrebné uviesť typ parametra kvôli typovej kontrole.
Rozšírime formálnu definíciu jazyka pridaním nasledujúceho typovacieho a vyhodnocovacieho pravidla:
Typovacie pravidlo:
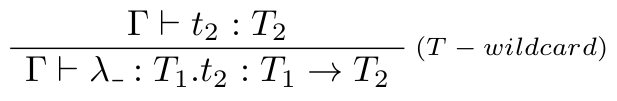
Vyhodnocovacie pravidlo:
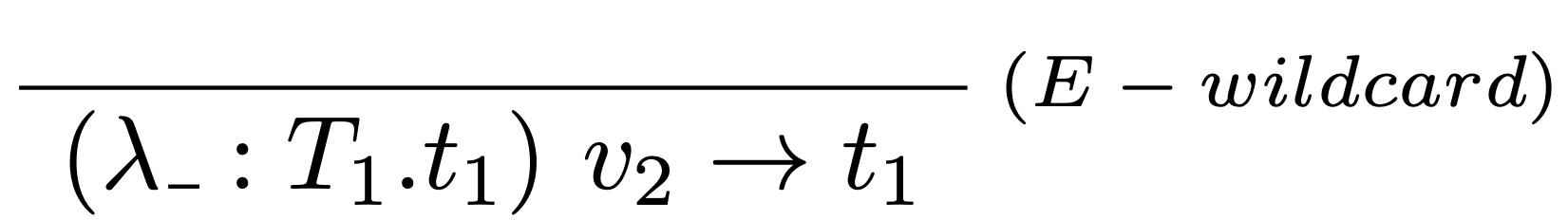
Príklad
Programovací jazyk OCaml podporuje zastúpenie (wildcard) na úrovni premennej aj typu využitím symbolu " _ ". Napríklad konštantná funkcia, ktorá vráti určitú hodnotu typu $int$.
utop # let kons1 _:int = 4;;
val kons1 : 'a -> int = <fun>
utop # let kons2 x:_ = 4;;
val kons2 : 'a -> int = <fun>
Pripísanie
Pripísanie (z ang. ascription) umožňuje explicitne pripísať danému termu určitý typ.
Rozšírime syntax pridaním nového tvaru $\lambda$-termov: $$ t::=~\ldots~|~t~\mathtt{as}~T $$ ktorý je možné prečítať "term $t$ má pripísaný typ $T$".
Vyhodnocovacie pravidlá:
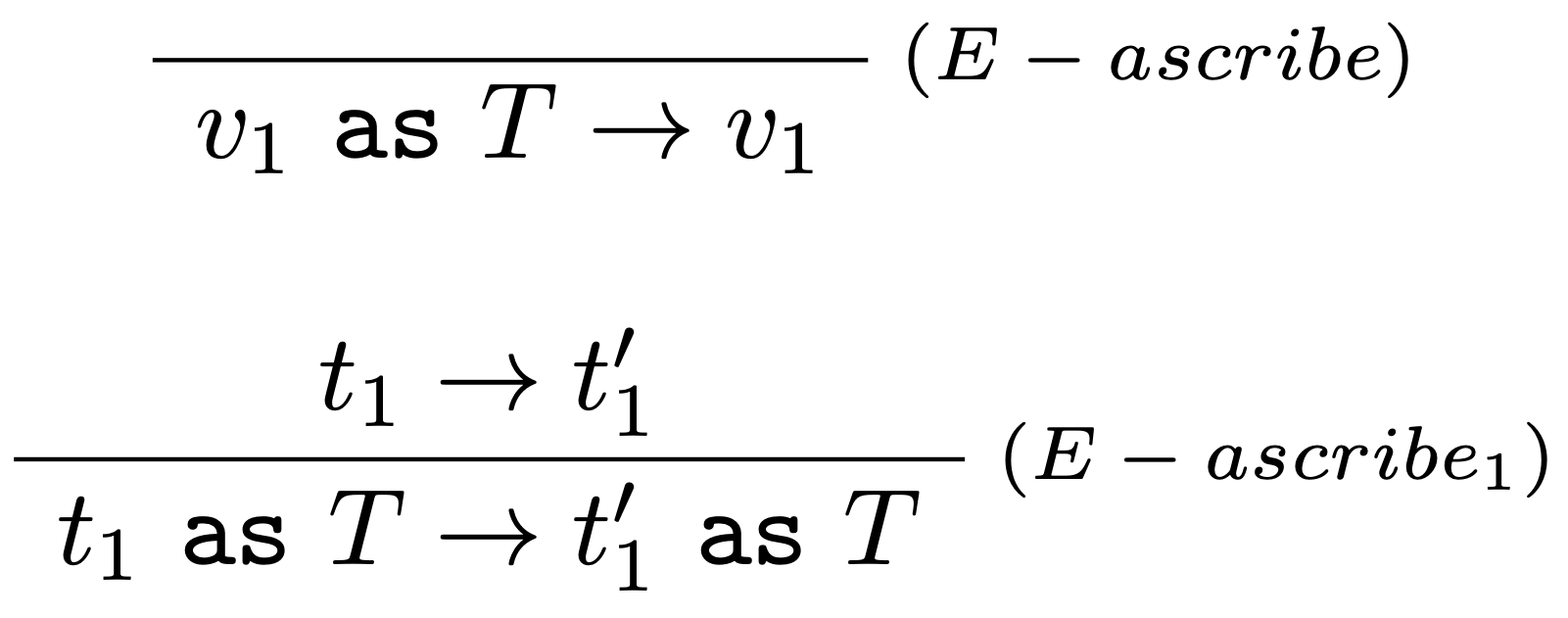
Typovacie pravidlo:
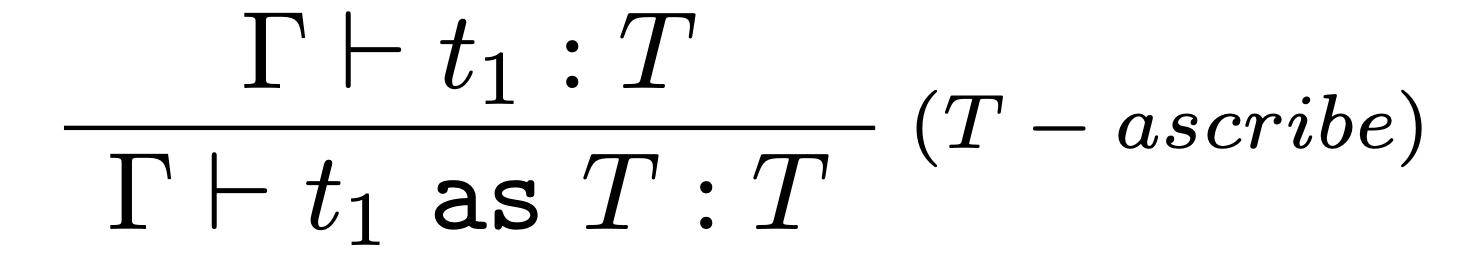
Poznámka
Pripísanie je vlastnosť, ktorá bude neskôr užitočná pri zavádzaní komplexnejších konštrukcií do jazyka napríklad pri súčtových typoch, kde vďaka pripísaniu bude možné jednoducho dodržať vetu o jednoznačnosti typov.
Existuje mnoho iných situácií, kedy je pripísanie v programovaní užitočné:
- v dokumentácii: uľahčuje písanie a zvyšuje čitateľnosť programov:
- explicitná informácia o type podtermov zvyšuje pochopiteľnosť,
- pre programátora nie vždy je na prvý pohľad jasný typ podtermov, pripísanie mu uľahčuje prácu.
Väzba Let
Väzba Let (z ang. let bindings) je užitočná pre odstránenie opakovaného písania termov a taktiež zvyšuje čitateľnosť kódu.
Zápis $$ \mathtt{let}~x= t_1~\mathtt{in}~t_2 $$ je možné prečítať: term $t_1$ je vyhodnotený a pomenovaný $x$, v nasledujúcom výpočte termu $t_2$.
Konštrukcia $\mathtt{let}$ viaže meno premennej $x$ k hodnote termu $t_1$ v rámci termu $t_2$.
Konštrukciu $\mathtt{let}$ používa stratégia vyhodnotenia hodnotou, t.j. term viazaný touto konštrukciou (term $t_{1}$) musí byť vyhodnotený predtým, než sa začne vyhodnocovať telo (term $t_{2}$) konštrukcie $\mathtt{let}$.
Postup:
- najprv je vyhodnotený term $t_1$;
- výsledná hodnota je pomenovaná $x$;
- následne sa vyhodnotí telo konštrukcie $\mathtt{let}$, t.j. term $t_2$ tak, že za každý výskyt termu $t_1$ sa dosadí hodnota $x$.
Formálne zavedieme let väzbu do jednoducho typovaného $\lambda$-kalkulu nasledujúcim spôsobom:
Rozšírime syntax o nový tvar termov:
$$ t ::=~\ldots~|~let~x = t~in~t $$
Pridáme dve nové vyhodnocovacie pravidlá:
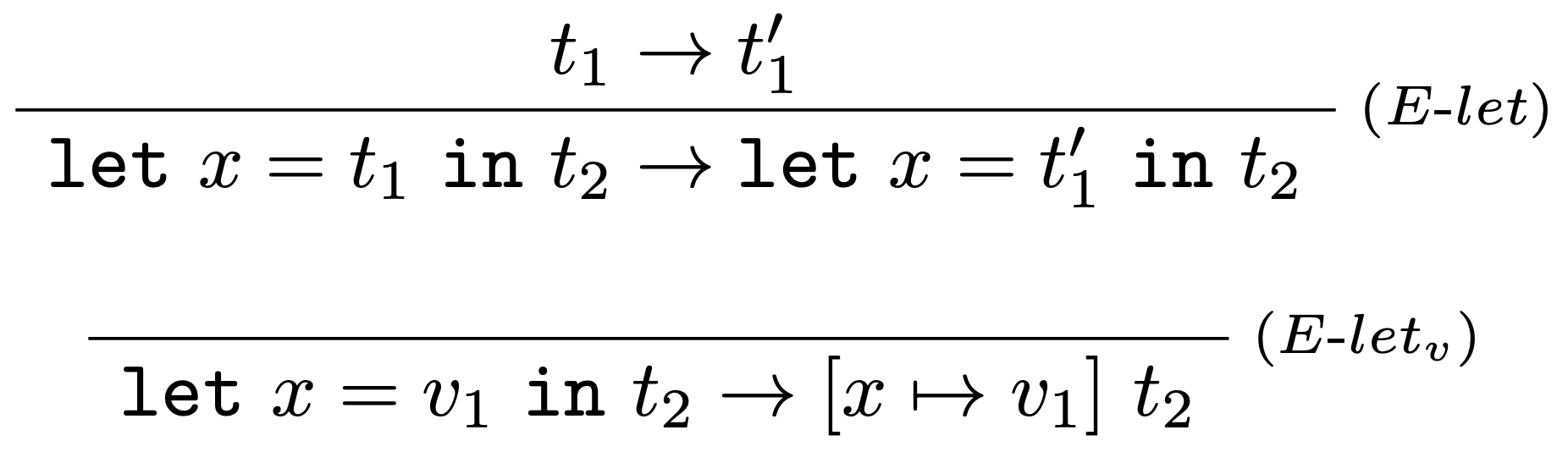
a nové typovacie pravidlo:
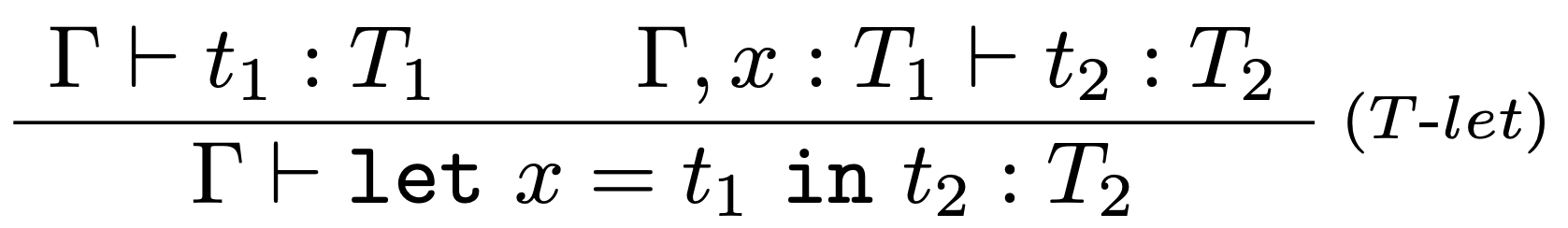
Ak má byť let odvodený tvar, musí sa dať preložiť do termu interného jazyka $\lambda^{I}$.
$$ \mathtt{let}~x= t_1~\mathtt{in}~t_2~=_{def}~(\lambda x:T_1 .t_2)~t_1 $$
Typ termu $t_1$ nie je v tejto notácií explicitne uvedený. Preto vzniká otázka, odkiaľ syntaktický analyzátor (ktorý robí desugaring) zistí aký typ $T_1$ má generovať ako typovú anotáciu $x$?
Táto informácia sa získa až pri kontrole typov a získame ju odvodením typu termu $t_1$.
Konštrukcia let je iný druh odvodeného tvaru:
- pri syntaktickej analýze sa nevykoná desugaring (transformácia termov do interného jazyka), ale
- pri kontrole typov typechecker doplní žiadanú informáciu na základe svojej analýzy (ide teda o transformáciu typového odvodenia).
Kontrola typov konštruuje odvodzovací strom pre $let$ term
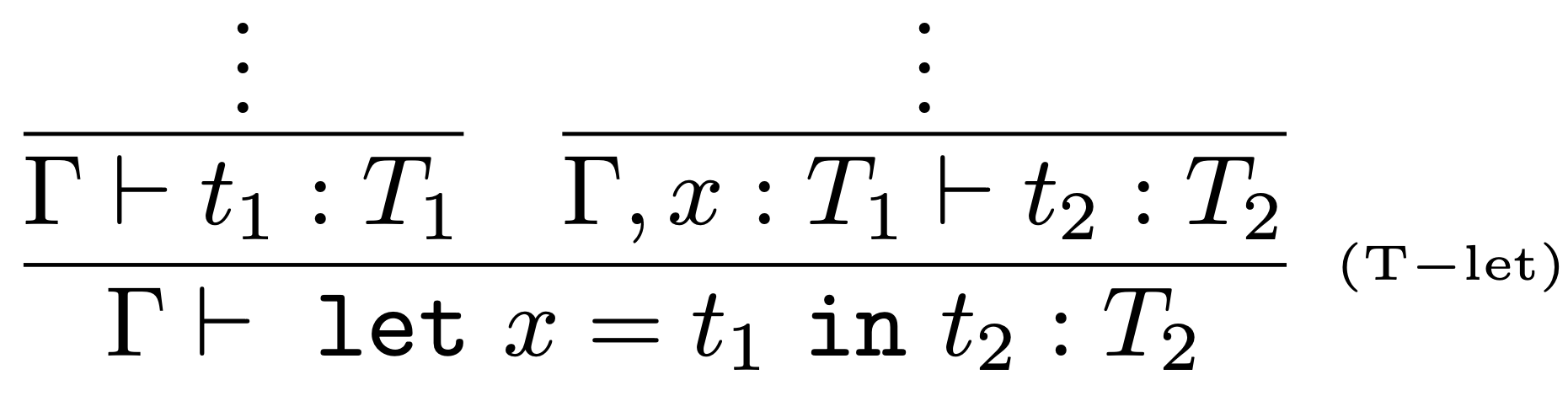
a transformuje ho do odvodzovacieho stromu v internom jazyku:
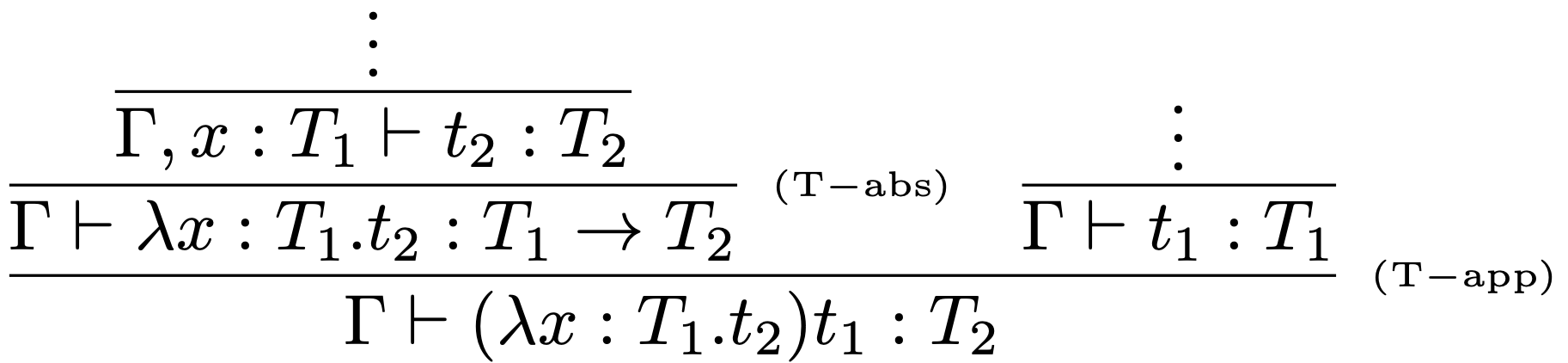
Poznámka
Let väzba zohráva dôležitú úlohu v návrhu jazyka OCaml a polymorfného typového systému Let polymorfizmus, ktorému sa budeme venovať v závere semestra.
Súčinové typy
Väčšina programovacích jazykov poskytuje podporu pre konštruovanie zložených údajových štruktúr. V tejto kapitole rozšírime náš jazyk $\lambda_\to$ o ďalšie jednoduché typy využitím súčinového typového konštruktora prostredníctvom ktorého, budeme formálne definovať nasledujúce údajové štruktúry:
- Dvojica: (z ang. Pair) najjednoduchšia údajová štruktúra pozostávajúca zo súčinu dvoch hodnôt.
- N-tica: (z ang. Tuple) zovšeobecnenie dvojice na súčin $n$ hodnôt.
- Záznam (z ang. Record) zovšeobecnenie n-tice na n-ticu s pomenovanými položkami.
Typový konštruktor súčinového typu označíme symbolom $\times$.
Dvojica
Binárny súčin typov $T_1, T_2$ je nový jednoduchý typ, ktorý opisuje zápis: $$T_1 \times T_2,$$ pričom termy takéhoto typu sú usporiadané dvojice v tvare: $$ \langle t_1 \times t_2 \rangle: T_1 \times T_2,$$ kde $t_1:T_1$ a $t_2:T_2$.
Príklad
Prvky binárneho súčinu typov sú napríklad: $$ \begin{array}{l} \langle 1, 4 \rangle : Nat \times Nat \\ \langle true, 0 \rangle : Bool \times Nat\\ \langle iszero\ 0, 4 \rangle : Nat \times Nat\\ \langle false, if\ iszero\ 0\ then\ true\ else\ false\rangle : Bool \times Bool\\ \langle \langle 1,2\rangle , true \rangle : (Nat \times Nat) \times Bool \end{array} $$
Syntax $\lambda_\to$ kalkulu rozšírime o podporu nového termu v tvare: $$\langle t_1 \times t_2 \rangle : T_1 \times T_2,$$ spolu s operáciami nad termami tohto typu a to prvou a druhou projekciou, ktoré poskytnú prvý resp. druhý prvok dvojice:
- Prvá projekcia: $$t.1$$
- Druhá projekcia: $$t.2$$
Prvá a druhá projekcia sú jediné operácie, ktoré je možné vykonať na binárnom súčinovom type:
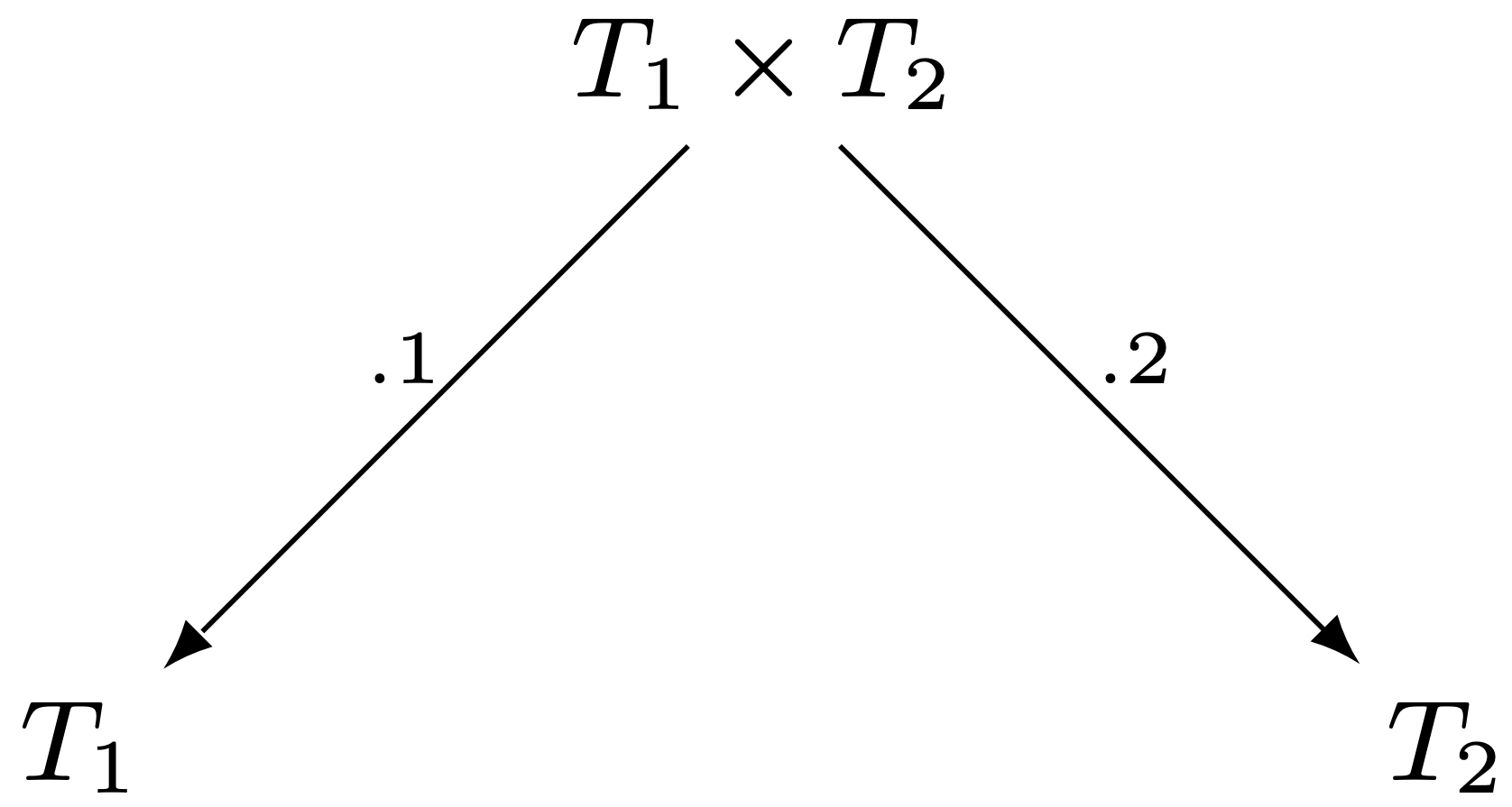
Formálne syntax $\lambda_\to$ kalkulu je potrebné rozšíriť o:
- nové tvary termov,
- nové tvary hodnôt,
- nový jednoduchý typ - binárny súčin typov.
$$ \begin{array}{ll} t::= & \ldots~|~\langle t, t\rangle~|~t.1~|~t.2 \\ \\ v::= & \ldots~|~\langle v,v\rangle \\ \\ T::= & \ldots~|~T\times T \end{array} $$
Typovacie pravidlá:
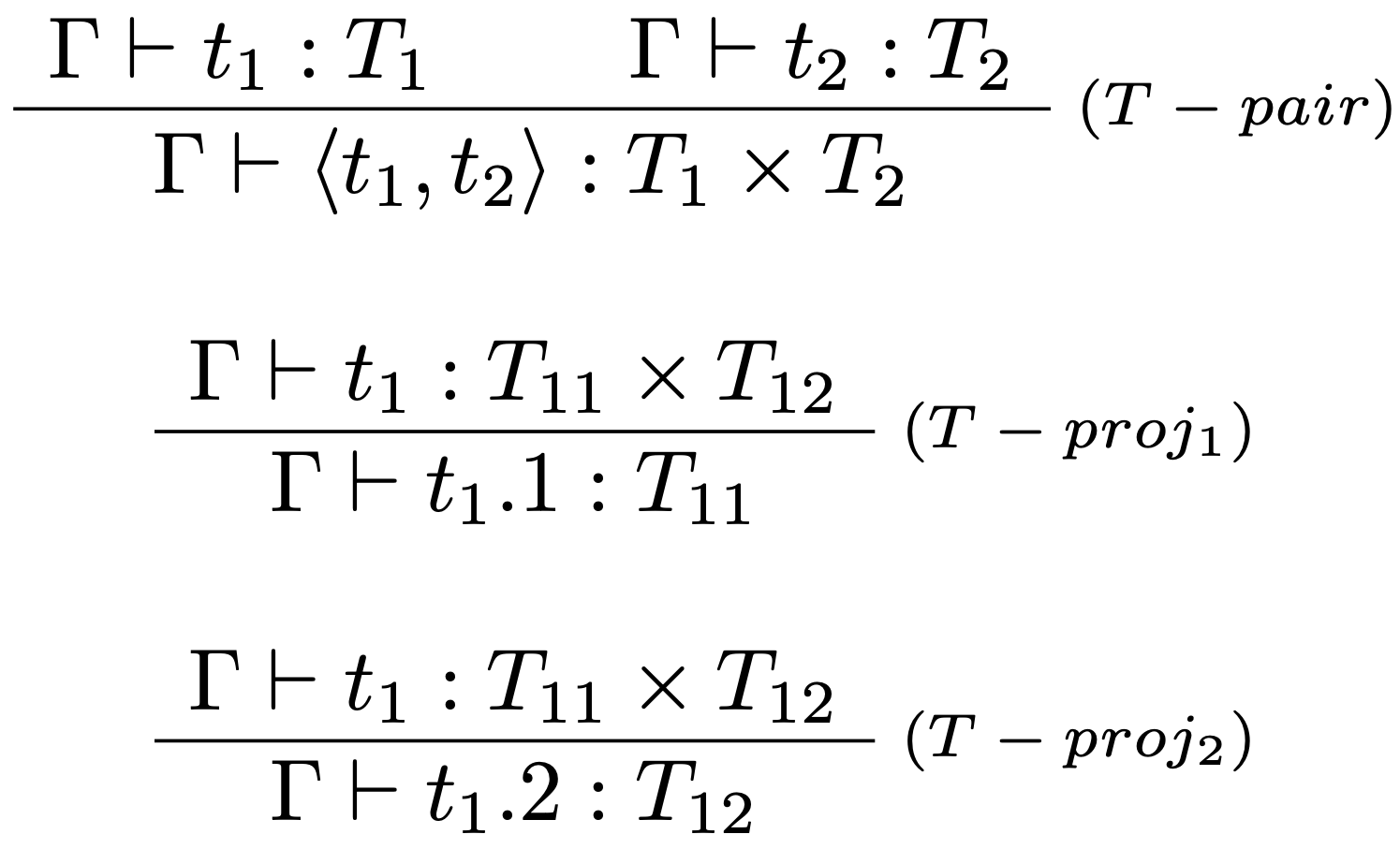
Vyhodnocovacie pravidlá
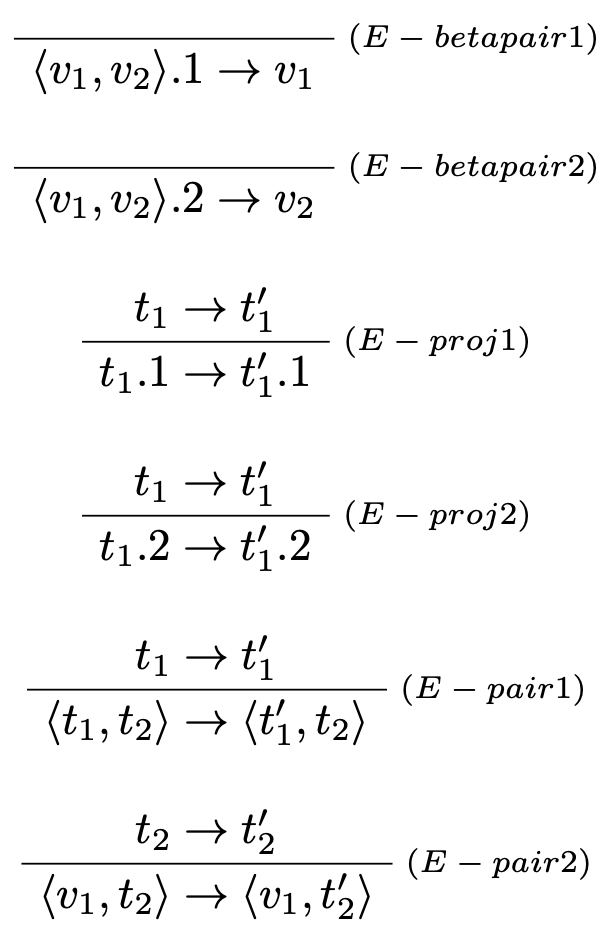
Poznámka
Všimnime si spôsob ako sú definované vyhodnocovacie pravidlá. Používame redukčnú stratégiu volania hodnotou to znamená, že najskôr je potrebné oba jej prvky vyhodnotiť na hodnotu a až následne je možné vykonať príslušnú projekciu nad daným termom.
Príklad
Majme daný nasledujúci term: $$\langle \mathtt{pred}~4, \mathtt{if~true~then~false~else~false}\rangle.1$$ Vyhodnoťte ho.
Riešenie
VVyhodnotíme daný term nasledujúcim (jediným možným) spôsobom: $$ \begin{array}{ll} & \langle \mathtt{pred}~4, \mathtt{if~true~then~false~else~false}\rangle.1 \\ \rightarrow^{\scriptscriptstyle{(E-pair1)}} & \langle 3, \mathtt{if~true~then~false~else~false}\rangle.1 \\ \rightarrow^{\scriptscriptstyle{(E-pair2)}} & \langle 3, \mathtt{false}\rangle.1 \\ \rightarrow^{\scriptscriptstyle{(E-betapair1)}} & 3 \end{array} $$
Príklad
Majme daný nasledujúci term: $$(\lambda x: \mathtt{Nat}\times \mathtt{Nat}. x.2) \langle \mathtt{pred}~4, \mathtt{pred}~5\rangle $$ Vyhodnoťte ho.
Riešenie
V prípade dvojíc je potrebné funkciu aplikovať na dvojicu hodnôt, t.j. dvojica termov musí byť najprv vyhodnotená a až potom je možné aplikovať funkciu na danú dvojicu (pravidlá redukčnej stratégie volania hodnotou):
$$ \begin{array}{ll} & (\lambda x: \mathtt{Nat}\times \mathtt{Nat}. x.2) \langle \mathtt{pred}~4, \mathtt{pred}~5\rangle \\ \rightarrow^{\scriptscriptstyle{(E-pair1)}} & (\lambda x: \mathtt{Nat}\times \mathtt{Nat}. x.2) \langle 3, \mathtt{pred}~5\rangle \\ \rightarrow^{\scriptscriptstyle{(E-pair2)}} & (\lambda x: \mathtt{Nat}\times \mathtt{Nat}. x.2) \langle 3, 4\rangle \\ \rightarrow^{\scriptscriptstyle{(E-appabs)}} & \langle 3, 4\rangle.2 \\ \rightarrow^{\scriptscriptstyle{(E-betapair2)}} & 4 \end{array} $$
Príklad
V programovacom jazyku OCaml je term typu dvojica uzavretý v zátvorkách (t1,t2), kde jeho prvky sú oddelené čiarkou, kde symbol hviezdička " * " označujú typový konštruktor súčinového typu.
Napríklad:
utop # (1,true);;
- : int * bool = (1, true)
Projekcie sú definované ako funkcie fst a snd, ktoré vrátia prvý resp. druhý prvok dvojice:
utop # fst;;
- : 'a * 'b -> 'a = <fun>
utop # snd;;
- : 'a * 'b -> 'b = <fun>
Napríklad:
utop # fst (1,true);;
- : int = 1
utop # snd (1,true);;
- : bool = true
Súčin $n$ typov: N-tica
Binárny súčin možno zovšeobecniť na konečný súčin $n$ typov, pričom $n$ môže byť ľubovoľné konečné prirodzené číslo.
Používame tiež konštruktor ''$\times$'' a takýto súčinový typ označíme
$$ T_1 \times T_2 \times \ldots \times T_n $$
Termy tohto typu sú usporiadané $n$-tice tvaru:
$$ \langle t_1, t_2, \dots, t_n\rangle : T_1 \times T_2 \times \ldots \times T_n $$
Príklad
Termy typu $n$-tica: $$ \begin{array}{l} \langle 1, 2, \mathtt{true}\rangle: \mathtt{Nat}\times \mathtt{Nat}\times \mathtt{Bool} \\ \\ \langle \mathtt{false}, 365, \mathtt{true}, \mathtt{unit}\rangle: \mathtt{Bool} \times \mathtt{Nat}\times \mathtt{Bool} \times \mathtt{Unit} \end{array} $$
Pre skrátenie a prehľadnosť zápisu syntaxe a sémantiky súčinového typu zavedieme nové označenie:
Pre súčinové typy zavedieme označenie:
$$ \langle T_i~^{i\in 1..n}\rangle~~~~~~~~~~\mathrm{\check{c}o~odpoved\acute{a}~ typu}~~~~~~~~~~T_1\times\ldots\times T_n $$ Pre termy súčinových typov zavedieme označenie $$ t = \langle t_i~^{i\in 1..n}\rangle~~~~~~~~~~\mathrm{\check{c}o~odpoved\acute{a}~ termu}~~~~~~~~~~t = \langle t_1,\ldots, t_n\rangle $$
Nad termami súčinového typu definujeme operáciu $i$-tej projekcie: $$ t.i $$ kde $t.i$ vráti $i$-ty prvok $n$-tice $t$.
Hodnota $n$ však môže byť aj $0$. Potom interval $1..n$ je prázdny term:
$$ t = \langle t_i~^{i\in 1..n} \rangle~~~~~\mathrm{je}~~~~\langle~ \rangle,~~~~~\mathrm{pr\acute{a}zdna}~n\mathrm{-tica} $$
- Hovoríme, že term má prázdny, nulárny súčinový typ.
- Je zrejmé, že prázdny súčinový typ nemá žiadnu projekciu.
- Prázdny súčinový typ je teoretickou nutnosťou, v praktickom programovaní sa nezvykne používať.
Ak má n-tica 1 prvok je unárneho súčinového typu.
Je potrebné si uvedomiť rozdiel medzi:
- číselnou hodnotou $5: \mathtt{Nat}$ a
- jednoprvkovou $n$-ticou $ \langle 5\rangle: \langle\mathtt{Nat}\rangle$.
V prvom prípade typ $\mathtt{Nat}$ je základný typ, v druhom prípade je $\langle\mathtt{Nat}\rangle$ unárny súčinový typ, kde:
- na hodnotu $5$ je možné použiť operácie pre typ $\mathtt{Nat}$, napríklad $succ, pred$, ale
- na jednoprvkovú $n$-ticu $\langle 5\rangle$ je možné použiť jedinú operáciu a to (prvú) projekciu.
Formálne rozšírime syntax $\lambda_\to$ kalkulu pridaním:
- zápis $n$-tíc termov,
- zápis hodnôt,
- zápis typov, nasledovne: $$ \begin{array}{ll} t::= & \ldots~|~\langle t_i~^{i\in 1..n}\rangle~|~t.i \\ v::= & \ldots~|~\langle v_i~^{i\in 1..n}\rangle \\ T::= & \ldots~|~\langle T_i~^{i\in 1..n}\rangle \end{array} $$
Vyhodnocovacie pravidlá:
Každé pravidlo pre dvojice sa zovšeobecní na $n$-árny prípad a každý pár pravidiel pre obe projekcie sa stáva jediným pravidlom pre ľubovoľnú projekciu z $n$-tice.
Pravidlo (E-tuple) kombinuje a zovšeobecňuje pravidlá (E-pair1) a (E-pair2) pre dvojice.
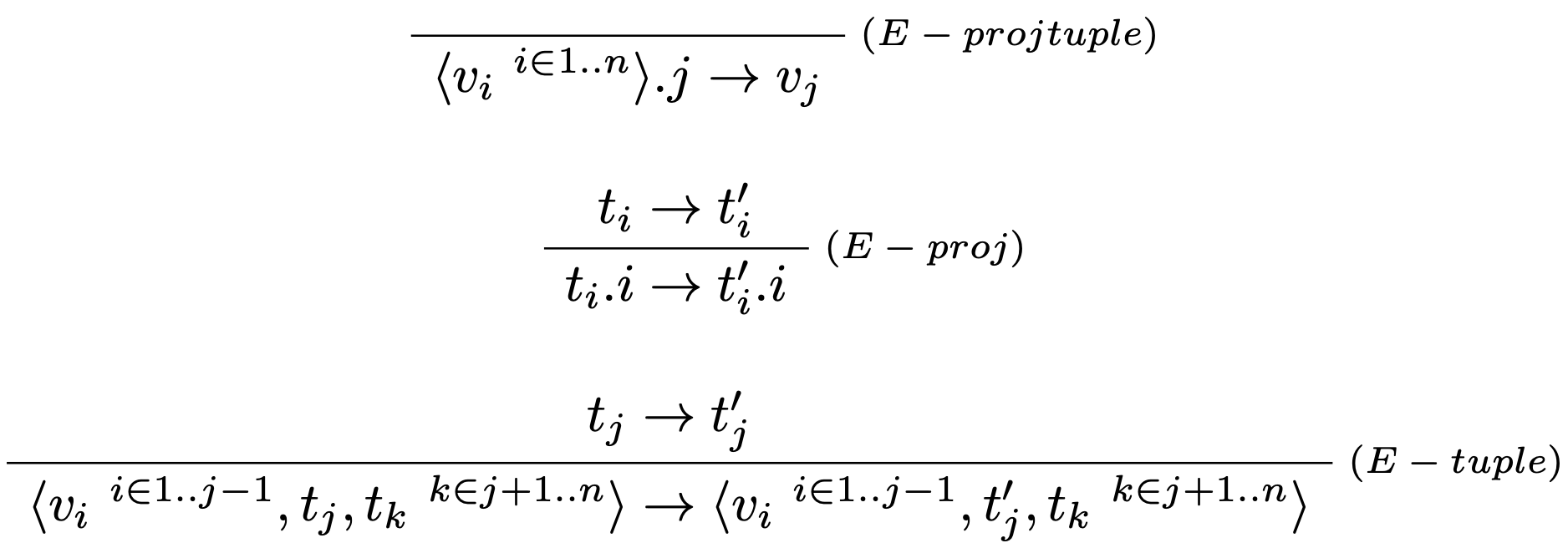
Všimnime si, že pre vyhodnotenie $j$-teho člena $n$-tice musia byť už predošlé členy redukované na hodnotu.
Typovacie pravidlá:
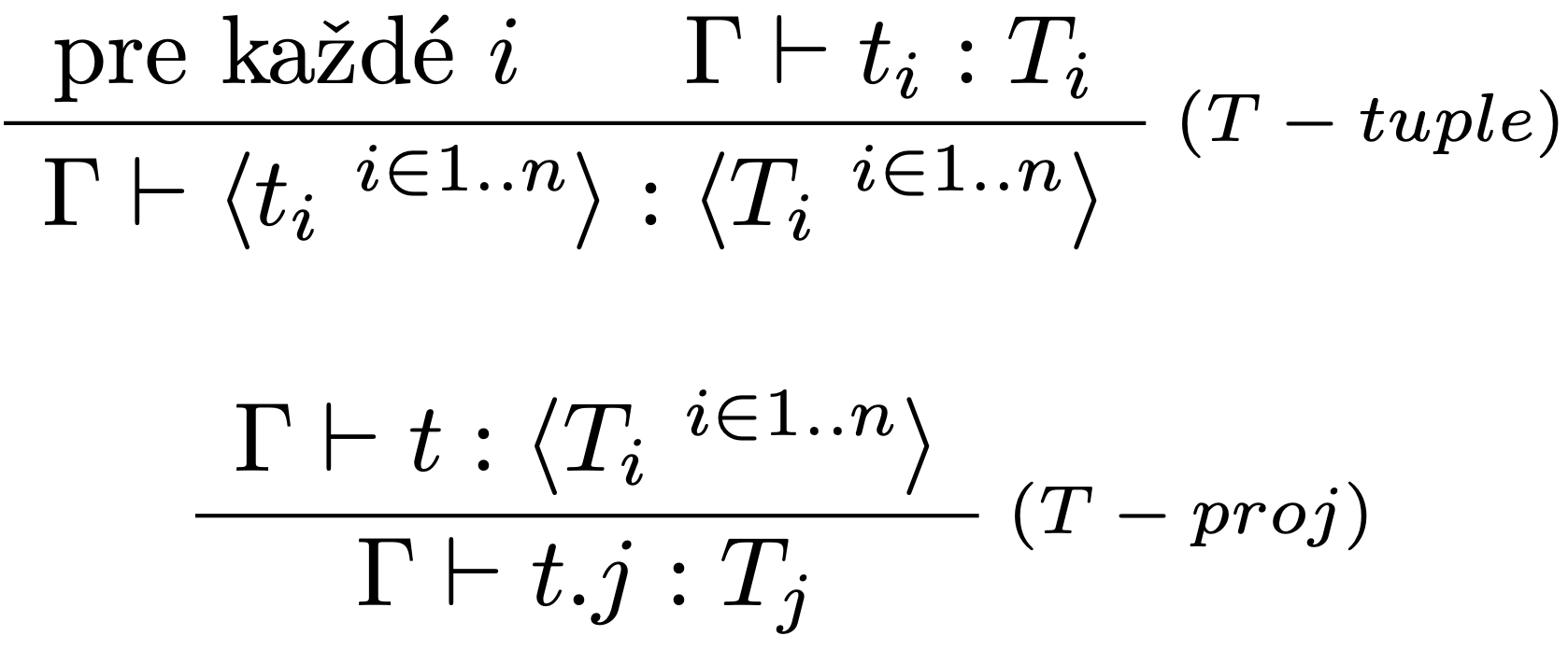
Údajové štruktúry tvaru $n$-tíc, teda súčinového typu sa používajú v mnohých programovacích jazykoch.
Poznámka
V reálnych programovacích jazykoch sa zovšeobecnený súčinový typ najčastejšie používa pre:
- Polia (Arrays)
- Záznamy (Records)
Príklad
V jazyku OCaml je $n$-tica zovšeobecnením dvojice (t1, t2, ..., tn).
utop # (1,true,4.2);;
- : int * bool * float = (1, true, 4.2)
avšak $i$-te projekcie nie su definované ako funkcie podobne ako v prípade dvojice, ale je možné využiť prehľadávanie podľa vzorov (pattern matching)
utop # let third x = match x with
| (_,_,x) -> x;;
val third : 'a * 'b * 'c -> 'c = <fun>
utop # third (1,true,4.2);;
- : float = 4.2
Záznam
Záznam (z ang. Record) je údajová štruktúra, ktorá je implementovaná v mnohých programovacích jazykoch (napríklad: C, Java, Python, OCaml, Haskell, Rust a mnoho ďalších).
V našej definícii $\lambda_\to$ kalkulu ju získame zovšeobecnením $n$-tice jednoduchým pridaním anotácii $l_i$ vo forme návestí k jej prvkom $t_i$.
Každá položka záznamu má tvar: $$ label = t $$ pričom $t$ je term a $label$ je návestie, ktoré pomenúva danú položku.
Projekcia nad záznamom je možná prostredníctvom návestí, kde zápisom: $$t.label$$ je získaný prístup k položke záznamu s návestím $label$.
Typová anotácia položiek má tvar: $$ label: T $$
Záznam je zovšeobecnenie $n$-tíc hodnôt, kde:
- každý člen $n$-tice je položka,
- každá položka je pomenovaná návestím.
Príklad
Nasledujúce termy sú termy typu záznam: $$ \begin{array}{l} \langle x=5 \rangle \\ \langle meno=\text{" Tichomír "}, vek=25 \rangle \end{array} $$ Pričom ich typy sú: $$ \begin{array}{l} \langle x:Nat \rangle \\ \langle meno:String, vek:Nat \rangle \end{array} $$ Prístup k jednotlivým prvkom typu záznam je možný prostredníctvom projekcie využitím návestia: $$ \begin{array}{l} \langle x=5 \rangle.x \to 5 \\ \langle meno=\text{" Tichomír "}, vek=25 \rangle.vek \to 25 \\ \langle meno=\text{" Tichomír "}, vek=25 \rangle.meno \to \text{" Tichomír "} \\ \end{array} $$
Poznámka
V našej definícii implicitne predpokladáme spočítateľnú množinu návestí, $\mathcal{L}$.
Pre formálnu definíciu typu záznam postupujeme analogicky ako v predchádzajúcich prípadoch:
- Rozšírime syntax $\lambda_\to$ kalkulu o nove tvary termov, hodnôt a typov.
- Definujeme príslušné typovacie pravidlá.
- Definujeme príslušné vyhodnocovacie pravidlá.
Syntax rozšírime nasledovne: $$ \begin{array}{ll} t::= & \ldots~|~\langle lab_i= t_i~^{i\in 1..n}\rangle~|~t.lab \\ \\ v::= & \ldots~|~\langle lab_i= v_i~^{i\in 1..n}\rangle \\ \\ T::= & \ldots~|~\langle lab_i:T_i~^{i\in 1..n}\rangle \end{array} $$
Typovacie pravidlá:
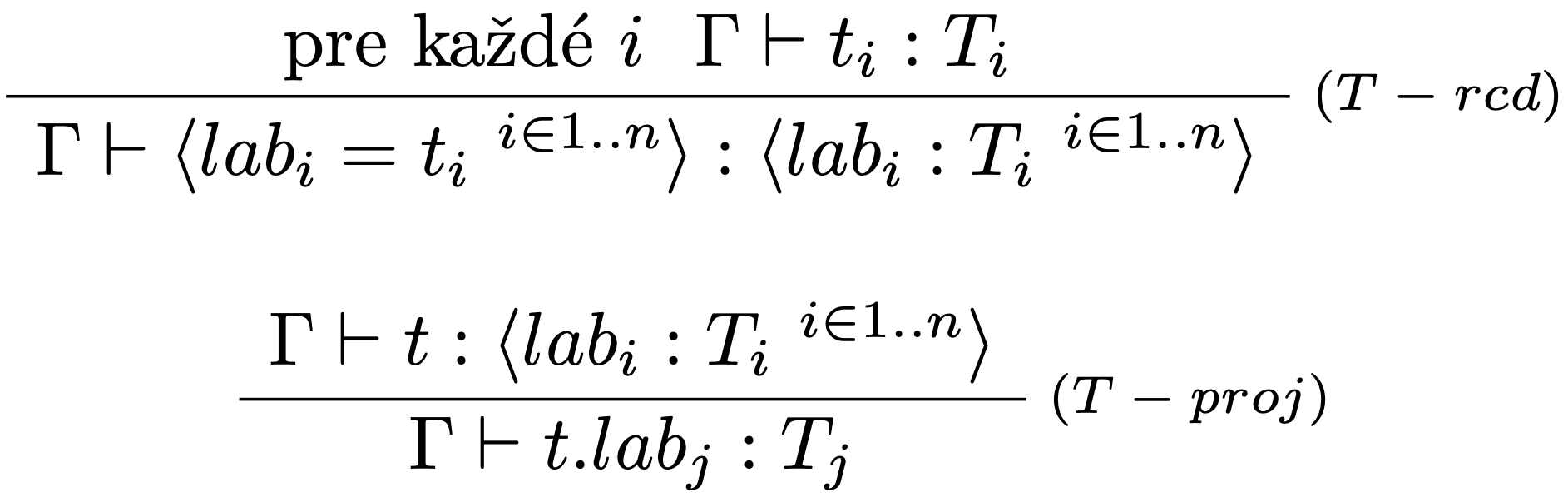
Vyhodnocovacie pravidlá:
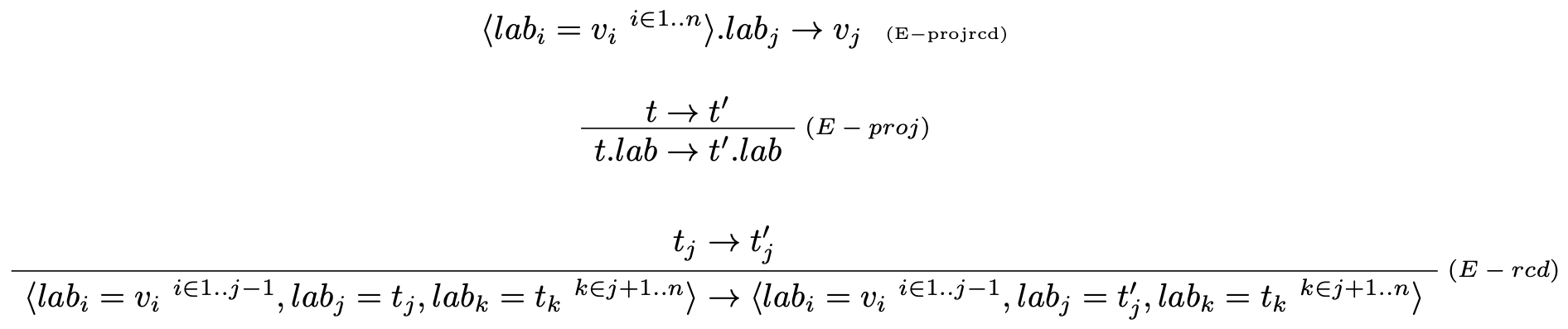
Poznámka
V rôznych programovacích jazykoch je typ záznam implementovaný rozdielne vzhľadom na to ako pristupujú k poradiu položiek.
- Poradie položiek nemá vplyv na typ záznam, napríklad: $$ \langle meno=\text{" Boleslav "}, vek=28 \rangle \quad \text{a} \quad \langle vek=28, meno=\text{" Boleslav "} \rangle $$ sú rovnaké termy a ich typy: $$ \langle meno:String, vek:Nat \rangle \quad \text{a} \quad \langle vek:Nat, meno:String \rangle $$ sú taktiež rovnaké.
- Poradie položiek v zázname je dôležité, napríklad: $$ \langle meno=\text{" Boleslav "}, vek=28 \rangle \quad \text{a} \quad \langle vek=28, meno=\text{" Boleslav "} \rangle $$ sú rozdielne termy a ich typy: $$ \langle meno:String, vek:Nat \rangle \quad \text{a} \quad \langle vek:Nat, meno:String \rangle $$ sú taktiež rozdielne.
V našej definícií budeme využívať druhý spôsob.
Príklad
V programovacom jazyku OCaml je typ záznam implementovaný nasledovne:
- V prvom kroku je potrebné definovať konkrétny typ nového záznamu, ktorý bude opisovať štruktúru jeho prvkov:
utop # type student = {meno:string; vek:int};;
type student = { meno : string; vek : int; }
Následne je možné vytvoriť konkrétne termy typu student
utop # let ab123bc = {meno="Budislav"; vek=19};;
val ab123bc : student = {meno = "Budislav"; vek = 19}
Prístup k prvkom konkrétneho termu je možný prostredníctvom projekcií využitím návestí (rovnako ako v našej definícii $\lambda_\to$ kalkulu):
utop # ab123bc.meno;;
- : string = "Budislav"
utop # ab123bc.vek;;
- : int = 19
Zdroje
- Pierce, Benjamin C. Types and programming languages. MIT press, Cambridge, 2001 (Перевод на русский язык: Бенджамин Пирс. Типы в языках программирования. — Добросвет, 2012. — ISBN 978-5-7913-0082-9)
- Pierce, Benjamin C et al.: Software Foundations, Electronic textbook, 2024
- Lecture notes, CS 152: Programming Languages, Harvard University, 2024
- Lecture notes, CS242: Programming Languages, Stanford University, 2024
- Valerie Novitzká, Daniel Mihályi: Teória typov, TU Košice, 2015