Typová rekonštrukcia
V rámci predchádzajúcich prednášok sme venovali algoritmu typovej kontroly, ktorá vyžadovala explicitné typové anotácie. Pri $\lambda$-abstrakcii je nutné explicitne uviesť typ jej argumentu, ako aj typ celého termu. V dnešnej prednáške sa budeme venovať algoritmu typovej rekonštrukcie (odvodenie typu), vďaka ktorému je možné vynechať niektoré resp. aj všetky typové anotácie.
Poznámka
Zavedenie typovej rekonštrukcie do rozšírení jazyka ako sú súčtové typy alebo podtypy je náročný a obšírny proces. Pre jednoduchosť a demonštratívne účely sa budeme venovať len jednoducho typovanému $\lambda$-kalkulu so základnými typmi.
Poznámka
Odvodenie typu
Odvodenie typu je proces určenia vhodných typov výrazu na základe toho ako sú použité. Napríklad môžeme jednoducho odvodiť, že vo výraze $$\lambda f. f~3,$$ $3$ - argument funkcie je konštanta typu $Nat$ a $f$ je funkcia (nie kvôli svojmu názvu $f$, ale kvôli tomu, že je aplikovaná na nejaký argument). Na základe uvedených podmienok (obmedzení) je možné odvodiť: $$f:Nat \rightarrow X$$ a celý výraz je typu: $$\lambda f. f~3:(Nat \rightarrow X) \rightarrow X.$$
$X$ reprezentuje typovú premennú. Keďže funkcia očakáva na vstupe funkciu, ktorá má parameter typu $Nat$, avšak nevieme aký bude výstup. Pojem typová premenná je vysvetlený nižšie.
Pre overenie korektnosti nášho uvažovania prepíšeme daný term do jazyka OCaml, prostredníctvom ktorého sa následne pokúsime odvodiť typ.
utop # fun f -> f 3;;
- : (int -> 'a) -> 'a = <fun>
Poznámka
V jazyku OCaml sú typové premenné označované: 'a, 'b, 'c,....
Upravíme náš program a znova sa pokúsime odvodiť typ:
utop # fun f -> f (f 3);;
- : (int -> int) -> int = <fun>
utop # fun f -> f (f "ahoj");;
- : (string -> string) -> string = <fun>
utop # fun f -> f (f 3, f 4);;
Error: This expression has type int but an expression was expected of type
'a * 'b
Pozrime sa bližšie na výstup z interpretera jazyka OCaml. Pouvažujte, ako v prvom prípade OCaml vedel, že výstup funkcie $f$ je typu $Int$. Pretože vo výraze $f~(f~3)$ je vnútorné $f$ aplikované na argument typu $Int$ a tento výstup je vstupom pre vonkajšie $f$.
Definícia:
Ak je term správne typovaný potom jeho typ môže byť odvodený.
Príklad
Majme nasledujúci term: $$ \begin{array}{l} let~sq=\lambda z . z*z~in \\ \quad \lambda f. \lambda x. \lambda y.\\ \qquad if ~ (f~x~y) \\ \qquad then ~ (f~(sq ~ x)~y) \\ \qquad else ~ (f~x~(f ~ x~y)) \end{array} $$ Z uvedeného termu je možné vydedukovať jeho typ naivným spôsobom nasledovne:
- Na premennú $z$ je aplikovaný operátor násobenia, to znamená $z:Nat$ a preto:
- $\lambda z . z*z: Nat \rightarrow Nat,$
- $sq: Nat \rightarrow Nat.$
- Vidíme, že $f$ musí byť nejakého typu v tvare: $f: T_1 \rightarrow T_2 \rightarrow Bool$, keďže je aplikované na dva argumenty $x~y$ a táto aplikácia sa nachádza na mieste podmienky v príkaze $if$, preto výsledok musí byť typu $Bool$.
- Vo vetve then je $f$ aplikované na $sq~x$ ako prvý argument, to znamená $T_1=Nat$.
- Vo vetve else je $f$ aplikované na $f ~ x~y$ ako druhý argument, to znamená $T_2=Bool$.
- Odvodili sme, že:
- $f:Nat\rightarrow Bool \rightarrow Bool$,
- $x:Nat$,
- $y:Bool$.
- Náš term očakáva argumenty $f,x,y$ a vráti hodnotu typu $Bool$.
- Typ termu je: $(Nat\rightarrow Bool \rightarrow Bool)\rightarrow Nat \rightarrow Bool \rightarrow Bool.$ Pre overenie korektnosti nášho uvažovania prepíšme program do jazyka OCaml:
utop #
let sq=fun z -> z*z in
fun f -> fun x -> fun y ->
if f x y
then (f (sq x) y)
else (f x (f x y));;
- : (int -> bool -> bool) -> int -> bool -> bool = <fun>
Obsah
- Typová premenná.
- Typová substitúcia.
- Odvodenie typu na základe obmedzení (z ang. constraint-based typing).
- Obmedzenie.
- Typová relácia s obmedzeniami a príslušné typové pravidlá.
- Množina obmedzení $C$.
- Unifikačný algoritmus - riešenie množiny obmedzení.
- Najvšeobecnejší unifikátor (z ang. most general unifier).
- Najvšeobecnejší typ (z ang. principle type).
Postup
Majme dané ľubovoľný term $t$ a kontext $\Gamma$.
- Prostredníctvom typových pravidiel pre novú typovú reláciu, odvodíme typ $S$ a množinu obmedzení $C$ pre term $t$ a kontext $\Gamma$.
- Nájdeme riešenie množiny obmedzení $C$, prostredníctvom algoritmu unifikácie.
- Vstup: množina obmedzení.
- Výstup: najvšeobecnejší unifikátor - substitúcia $\sigma$.
- Aplikujeme substitúciu $\sigma$ na odvodený typ $S$ a získame najvšeobecnejší typ $T$.
Typové premenné
V jednoducho typovanom $\lambda$-kalkule je definovaná množina základných typov ako napr. Bool, Nat, Unit, ktorá zároveň obsahuje aj neinterpretované typy $T_1,T_2...$. Neinterpretované typy je možné definovať ako typové premenné.
Množina $\chi$ obsahujúca typové premenné $X,Y,Z$ je definovaná nasledovne: $$\chi=\{X,Y,Z,...\}.$$
- Z typových premenných a typových konštruktorov je možné vytvárať typové výrazy.
- Substitúcia typovej premennej konkrétnym typom vytvára typovú inštanciu.
- Množinu všetkých typov označíme ako $Types$.
Príklad: Typové výrazy:
$X \rightarrow Y,\quad $ $X + Y \rightarrow Z,\quad $ $X \rightarrow Nat,\quad $ $Bool$ a podobne.
- Množina $Types=\{T_1,T_2,...,Bool, Nat, Unit, ...\}$ obsahuje konkrétne typy jazyka.
- Množina $\chi=\{X,Y,Z,...\}$ obsahuje typové premenné.
Typová substitúcia
Neformálne, operáciu typovej substitúcie (ďalej len substitúcie, kde je z kontextu jasné, že sa jedná o typovú substitúciu) je možné chápať ako dosadenie konkrétneho typu za typovú premennú.
Špecifikácia zobrazenia substitúcie
Formálne substitúcia $\sigma$ je konečné zobrazenie špecifikované nasledovne: $$\sigma: \chi \rightarrow Types,$$ z typových premenných do typov. To znamená, aplikáciou zobrazenia $\sigma$ na určitý typový výraz získame konkrétny typ - inštanciu typového výrazu.
Príklad
Nech $X$ je typová premenná a substitúcia $\sigma$ definovaná nasledovne: $$\sigma=[X \mapsto Bool].$$ Potom aplikácia substitúcie $\sigma$ na typový výraz $X \rightarrow X$ vytvorí nasledujúcu inštanciu typového výrazu: $$\sigma(X \rightarrow X)=Bool \rightarrow Bool.$$
Poznámka
Definujeme nasledujúce funkcie:
- Definičný obor substitúcie $$dom(\sigma) = \chi,$$ je množina typových premenných.
- Obor hodnôt substitúcie $$range(\sigma)=Types,$$ je množina typov, ktoré je možné dosadiť za typovú premennú.
Príklad
Nech je daná substitúcia $\sigma=[X \mapsto Nat \rightarrow Bool]$. Potom $$dom(\sigma)=X, \quad range(\sigma)= Nat \rightarrow Bool.$$
Definícia zobrazenia substitúcie
Nech $\sigma$ je substitúcia, $X$ je typová premenná, $T$ je typ. Potom konečné zobrazenie typovej substitúcie je možné definovať nasledovne: $$ \begin{array}{lcl} \sigma(X) & = & \begin{cases} T \quad ak \quad (X \mapsto T) \in \sigma \\ X \quad ak \quad X \notin dom(\sigma) \\ \end{cases} \\ \sigma(Nat) & = & Nat \\ \sigma(Bool) & = & Bool \\ \sigma(T_1 \rightarrow T_2) & = & \sigma T_1 \rightarrow \sigma T_2 \end{array} $$
Substitúcia aplikovaná na kontext: $$ \begin{array}{lcl} \sigma(x_1:T_1,... ,x_n:T_n) & = & x_1:\sigma T_1,... , \sigma x_n: \sigma T_n. \end{array} $$
Analogicky v prípade aplikácie substitúcie na term $t$, je substitúcia aplikovaná na všetky typy, ktoré sa nachádzajú v typových anotáciách $t$.
Nech $\sigma, \gamma$ sú substitúcie, potom kompozícia typových substitúcií $\sigma \circ \gamma$ je definovaná nasledovne:
$$ \sigma \circ \gamma = \left[ \begin{array}{ll} X \mapsto \sigma(T)\quad & \text{pre každé } (X \mapsto T) \in \gamma\\ X \mapsto T \quad & \text{pre každé } (X \mapsto T) \in \sigma \text{ také, že } X \notin dom(\gamma)\\ \end{array} \right] $$
Poznámka
Je potrebné si uvedomiť, že: $$(\sigma \circ \gamma)S = \sigma (\gamma S) $$
Príklad
Nech je daná substitúcia: $$\sigma=[A \mapsto Nat] \circ [B \mapsto A \rightarrow Bool],$$ typový výraz: $$T=A \rightarrow B \rightarrow C.$$ Aplikujte $\sigma$ na $T$.
Riešenie
$$ \begin{array}{lcl} \sigma T & = & \sigma (A \rightarrow B \rightarrow C)\\ & = & \sigma A \rightarrow \sigma (B \rightarrow C)\\ & = & \sigma A \rightarrow \sigma B \rightarrow \sigma C \\ & = & [A \mapsto Nat] A \rightarrow [A \mapsto Nat] (A \rightarrow Bool) \rightarrow [A \mapsto Nat] C \\ & = & Nat \rightarrow ([A \mapsto Nat] A \rightarrow [A \mapsto Nat] Bool) \rightarrow C \\ & = & Nat \rightarrow ( Nat \rightarrow Bool) \rightarrow C \\ \end{array} $$
Poznámka
Pouvažujte aký výsledok by by vznikol ak by bolo zmenené poradie kompozície substitúcie následovne: $$\sigma'=[B \mapsto A \rightarrow Bool] \circ [A \mapsto Nat].$$
Odvodenie typu na základe obmedzení
V tejto kapitole si predstavíme algoritmus, ktorý pre ľubovoľný term $t$ a kontext $\Gamma$ vypočíta množinu obmedzení - rovností medzi typovými výrazmi (prípadne aj typovými premennými), ktorá musí byť splnená v akékoľvek riešení pre ($\Gamma, t$).
Definícia: Množina obmedzení $C$ je množina rovností v tvare: $$C=\{S_i=T_i^{i\in 1...n}\},$$ kde $S_i, T_i$ sú ľubovoľné typy.
Obmedzenie má tvar $T_1 = T_2$, pre akékoľvek $T_1, T_2$.
Definícia: Unifikácia rovnosti $S$ a $T$ je taká substitúcia $\sigma$, že $$\sigma S = \sigma T.$$ Hovoríme, že substitúcia $\sigma$ unifikuje (spĺňa) množinu obmedzení $C$, ak unifikuje každú rovnosť v $C$.
Definícia: Typová relácia s obmedzeniami: $$\Gamma \vdash t:T~|~C,$$ ktorú je možné prečítať ako "term $t$ odvodzuje typ $T$ v prostredí $\Gamma$ a generuje množinu obmedzení $C$".
Ak uvažujeme o tejto relácii ako o funkcii, potom:
- dvojbodka $:$ v strede oddeľuje vstup od výstupu,
- vstup: $\Gamma, t$, chceme zistiť či term $t$ v prostredí $\Gamma$ má typ,
- výstup: typ $T$ a množina obmedzení $C$, ktorú musí typ $T$ spĺňať aby term $t$ v prostredí $\Gamma$ bol správne typovaný.
Jednoducho typovaný $\lambda$-kalkul
Pripomeňme si fragment nášho jazyka jednoducho typovaného $\lambda$-kalkulu s NBL, pre ktorý následne zadefinujeme typové pravidlá pre typovú reláciu s obmedzeniami: $$ \begin{array}{lcl} t & ::= & x ~|~ \lambda x :T.t ~|~ \lambda x.t ~|~t~t ~|~ 0 ~|~ true ~|~ false ~|~ succ~t ~|~\\ & & ~|~ pred~t ~|~ iszero~t ~|~~if~t~then~t~else~t~ \\ v & ::= & \lambda x:T.t ~|~ \lambda x.t ~|~ true ~|~ false ~|~ nv\\ nv & ::= & 0 ~|~ succ~nv\\ T & ::= & A ~|~ T \rightarrow T ~|~ X\\ A & ::= & Nat ~|~ Bool \end{array} $$
Poznámka
Jazyk $\lambda_\to$ bol rozšírený o $\lambda$-abstrakciu $\lambda x.t$ bez explicitnej typovej anotácie, čím bola odstránená nutnosť explicitne uvádzať akékoľvek typy. Zároveň bola v jazyku ponechaná aj pôvodná abstrakcia, kde je táto možnosť stále ponechaná.
Typové pravidlá pre typovú reláciu s obmedzeniami
Pravidlá pre konštanty sú axiómy a pravidlo pre premennú kontroluje jej výskyt v typovom kontexte. Tieto pravidla negenerujú obmedzenia.

Pravidlá pre abstrakciu sú dve a to pre prípad kde je uvedená typová anotácia parametra abstrakcie (CT-Abs) alebo nie je (CT-AbsInf). V druhom prípade (CT-AbsInf) je potrebné zaviesť novú typovú premennú $X$ (niekedy v ang. nazývaná fresh variable).
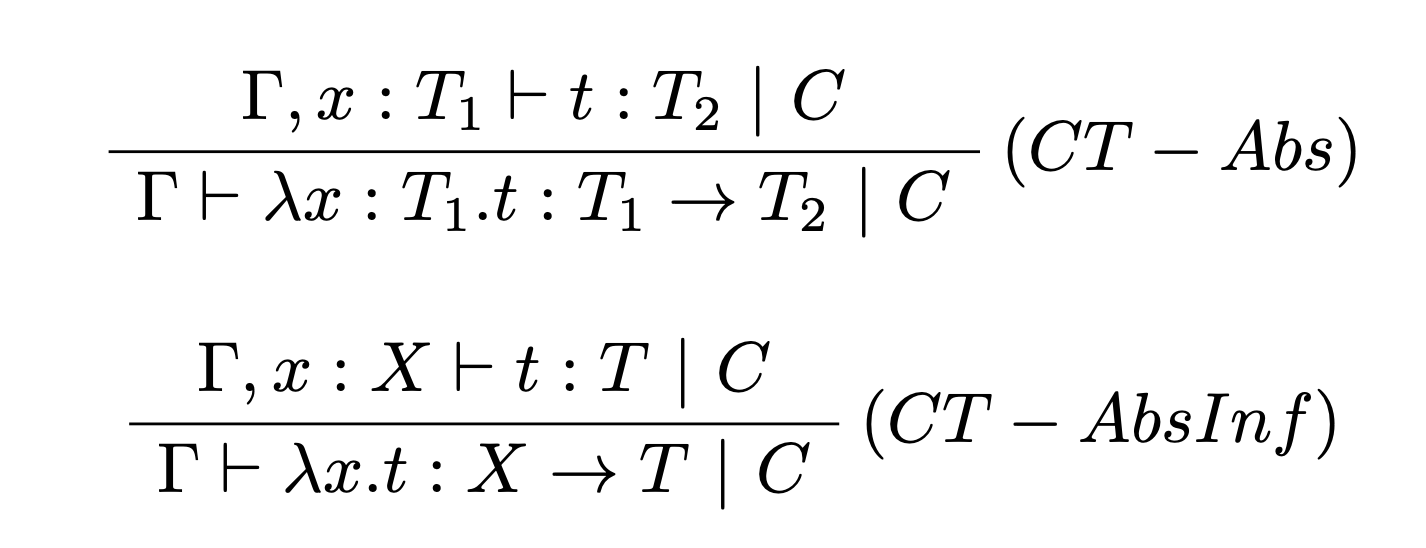
Pravidlo pre aplikáciu vyžaduje zavedenie novej typovej premennej $X$ a vytvára obmedzenie $C$, ktoré je zjednotením obmedzení oboch predpokladov a rozširuje množinu o rovnosť $T_1=T_2\rightarrow X$, pričom $X$ musí byť nová typová premenná.
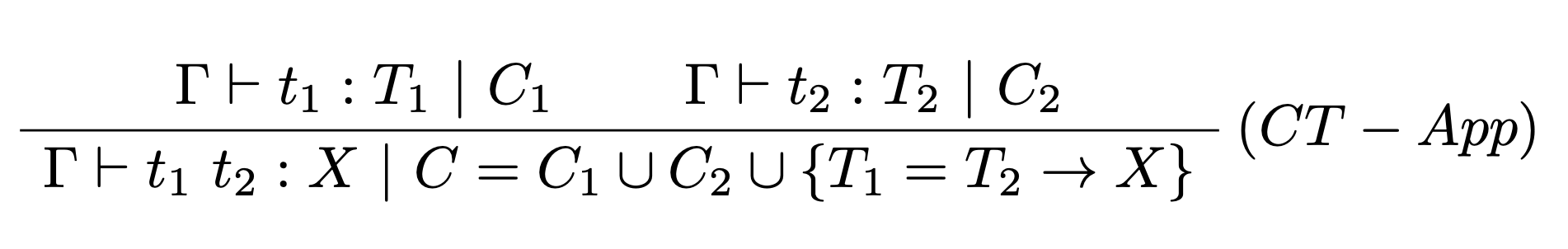
Pravidlá pre termy If, Succ, Pred, Iszero vytvárajú nové obmedzenie $C$ nasledovne:
- V prípade pravidla pre $CT-If$ nové obmedzenie $C$ pozostáva zo zjednotení obmedzení zo všetkých predpokladov pravidla a rozširuje ho o rovnosti $T_1=Bool, T_2=T_3$.
- V prípade pravidiel $CT-Succ, CT-Pred, CT-Iszero$ nové obmedzenie pozostáva zo zjednotenia obmedzenia z predpokladu pravidla o rovnosť $T=Nat$.
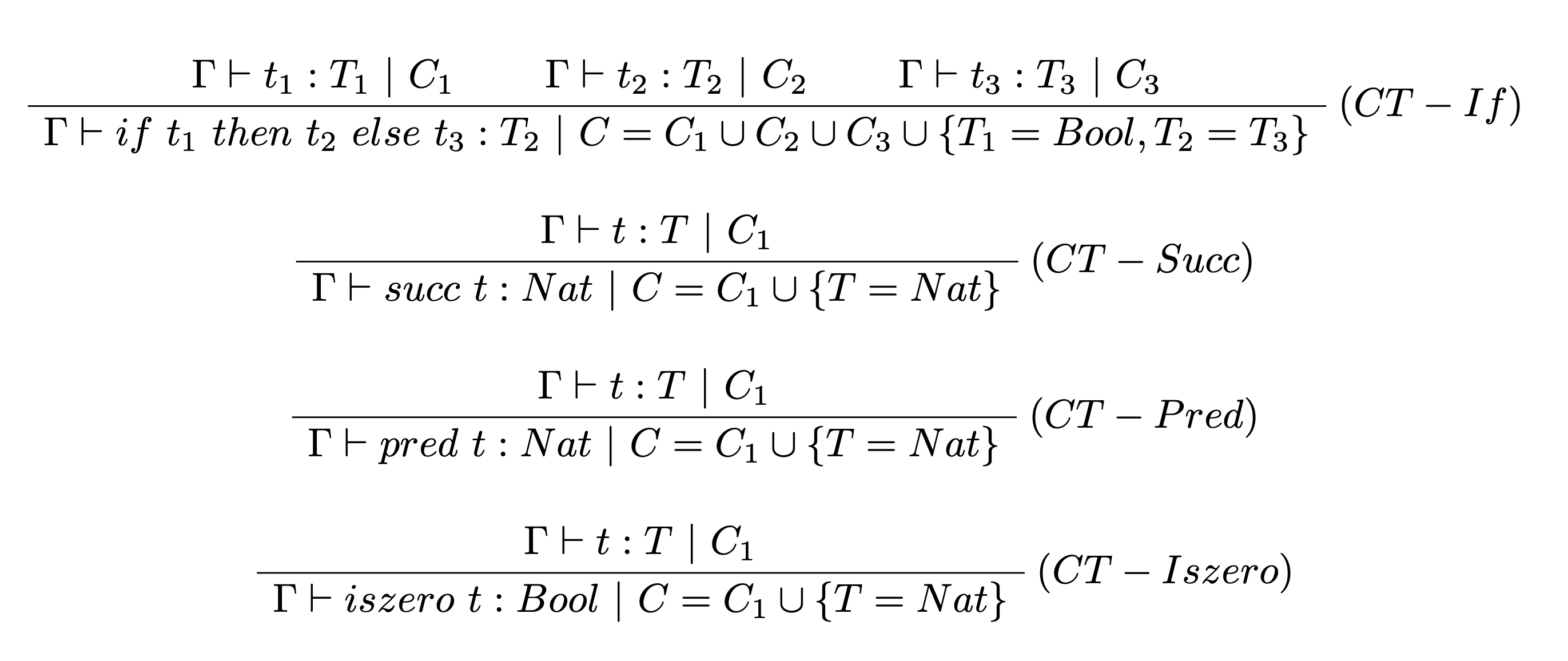
Definícia:
Nech je daný nasledujúci sekvent:
$$\Gamma \vdash t:S ~|~ C.$$
Potom riešenie štvorice
$$(\Gamma,t,S,C)$$
je taká dvojica $$(\sigma, T),$$
že $\sigma$ spĺňa $C$ a zároveň:
$$\sigma S = T.$$
Poznámka
Je potrebné si uvedomiť, že pri typovej rekonštrukcii máme na vstupe typový kontext $\Gamma$ a term $t$. Princíp ostáva rovnaký ako pri typovej kontrole. Aplikujeme typové pravidlá, pomocou ktorých zostrojíme typový strom a následne spätným prechádzaním stromu získame typ $S$ a príslušnú množinu obmedzení $C$.
Hlavným rozdielom je, že pri typovej rekonštrukcii je strom vždy možné zostrojiť, avšak pri nesprávne typovaných termoch, resp. termoch ktoré nemajú typ je v strome vytvorená nekonzistentná množina obmedzení.
Príklad
Majme dané $\Gamma= \{\}$ a $t = \lambda x. if~x~then~1~else~0$. Prostredníctvom typovej rekonštrukcie pokúste nájsť typ termu $t$.
Riešenie
Máme daný sekvet: $$\vdash \lambda x. if~x~then~1~else~0: S~|~C.$$ V prvom kroku aplikáciou typových pravidiel zostrojíme typový strom pre $\Gamma, t$ bez typových anotácií a množiny obmedzení:
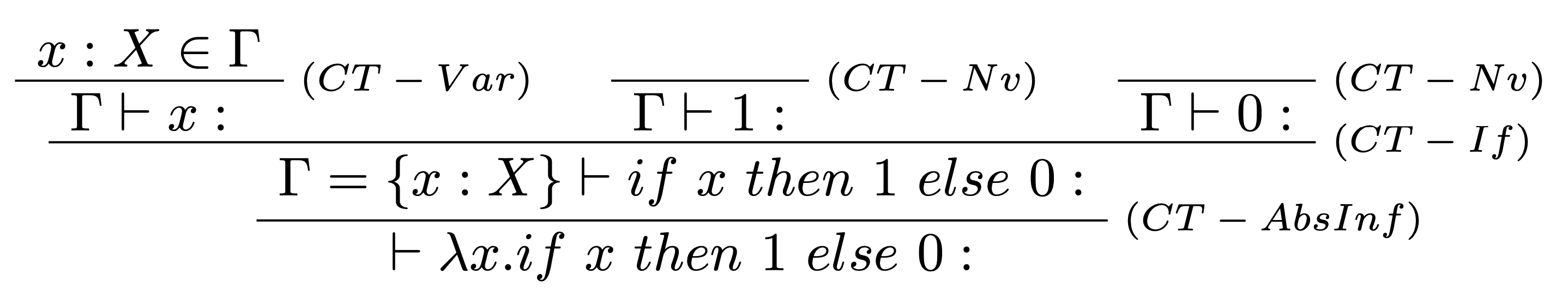
V druhom kroku podľa typových pravidiel odvodíme príslušný typ $S$ a množinu obmedzení $C$.
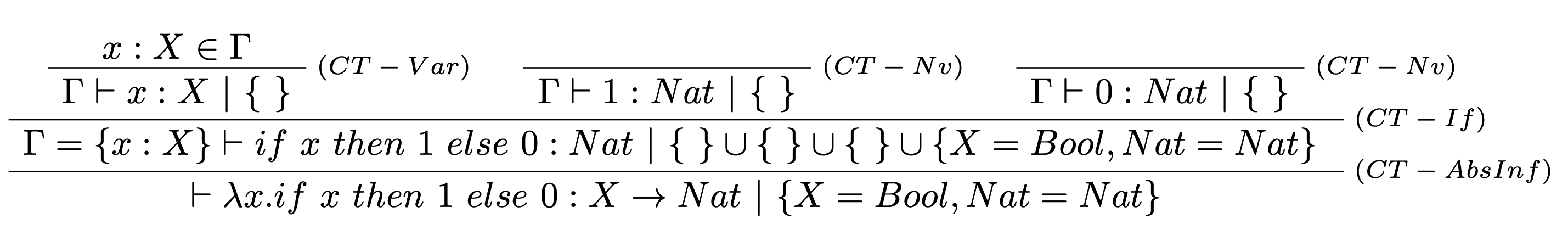
Následne z odvodenej množiny obmedzení $C=\{X=Bool, Nat=Nat\}$ určíme také riešenie $\sigma$, že jeho aplikácia na odvodený typ $S=X\rightarrow Nat$ poskytne taký typ $T$, že platí: $$\vdash \lambda x. if~x~then~1~else~0:T.$$
V tomto prípade je riešenie zjavné vzhľadom na odvodenú množinu obmedzení $$C=\{X=Bool, Nat=Nat\},$$ a odvodený typ $$S=X\rightarrow Nat,$$ je naše riešenie $\sigma$ nasledovné: $$\sigma=[X \mapsto Bool],$$ pričom:
$$ \begin{array}{lcl} \sigma S &=& [X \mapsto Bool](X\rightarrow Nat) \\ &=& [X \mapsto Bool]X \rightarrow [X \mapsto Bool]Nat \\ &=& Bool \rightarrow Nat\\ &=& T. \end{array} $$
Riešenie v jazyku OCaml:
utop # fun x -> if x then 1 else 0;;
- : bool -> int = <fun>
Najvšeobecnejší unifikátor a najvšeobecnejší typ
Majme danú identickú funkciu: $$id=\lambda x:T.x:T \rightarrow T.$$ Tento term je správne typovaný pre ľubovoľný typ $T$. Napríklad: $$\lambda x:Nat.x:Nat \rightarrow Nat,$$ pričom $\sigma=[T\mapsto Nat]$. Aj napriek tomu, že táto funkcia sa stále správa rovnako, v prípade potreby aplikácie tejto funkcie na argument iného typu, je nutné napísať vlastnú funkciu s príslušným typom: $$ \begin{array}{l} \lambda x:Bool.x:Bool \rightarrow Bool\\ \lambda x:Nat\rightarrow Bool.x:(Nat\rightarrow Bool) \rightarrow (Nat\rightarrow Bool)\\ ..., \end{array} $$ čo v konečnom dôsledku vytvára nekonečné množstvo unifikátorov: $$ \begin{array}{l} \sigma=[T\mapsto Bool]\\ \sigma=[T\mapsto Nat\rightarrow Bool]\\ .... \end{array} $$
Takéto riešenie z hľadiska softvérového inžinierstva nie je žiadúce. Tento problém je možné vyriešiť zavedením polymorfizmu, kde namiesto konkrétneho typu sa v typových anotáciách budú môcť vyskytovať typové premenné a typová rekonštrukcia odvodí konkrétny typ podľa potreby (napr. podľa typu argumentu).
Demonštrácia uvedeného v jazyku OCaml:
utop # let id : int -> int = fun x -> x;;
val id : int -> int = <fun>
utop # id 4;;
- : int = 4
utop # id "ahoj";;
Error: This expression has type string but an expression was expected of type
int
utop # let id_poly = fun x -> x;;
val id_poly : 'a -> 'a = <fun>
utop # id_poly 4;;
- : int = 4
utop # id_poly "ahoj";;
- : string = "ahoj"
Najvšeobecnejší unifikátor
Z vyššie uvedeného vyplýva, že našim cieľom nie len nájsť ľubovoľné riešenie ($\sigma$, $T$) aby platilo $\sigma S = T$, ale hľadáme najvšeobecnejšie riešenie (unifikátor) $\sigma_{mgu}$. Zároveň platí, že ak existuje také $\sigma$, že $\sigma S = T$, potom existuje aj najvšeobecnejší unifikátor.
Definícia: Unifikátor $\sigma$ je všeobecnejší (more general) ako unifikátor $\sigma_2$, ak existuje taký unifikátor $\sigma_1$, že platí: $$\sigma_1 \circ \sigma = \sigma_2.$$
Definícia: Najvšeobecnejší unifikátor (z ang. Most General Unifier (MGU)) dvoch typov $S,T$ je taký unifikátor $\sigma$, že platí:
- $\sigma$ je unifikátor typov ($S,T$),
- $\sigma$ je všeobecnejší ako ľubovoľný iný unifikátor ($S,T$).
Poznámka
Vo všeobecnosti najvšeobecnejší unifikátor nemusí byť jedinečný.
Príklad
Majme term $$\lambda x:T.x:T \rightarrow T.$$ Unifikátor $$\sigma_1=[T\mapsto X \rightarrow X],$$ je všeobecnejší ako $$\sigma_2=[T\mapsto Nat \rightarrow Nat],$$ avšak menej všeobecný ako najvšeobecnejší unifikátor: $$\sigma_{mgu}=[T\mapsto X].$$
Poznámka
Vlastnosť unifikátora byť "viac všeobecný" ako iný unifikátor, je možné chápať ako substitúciu, ktorá umožňuje vytvoriť väčšie množstvo typov.
Najvšeobecnejší typ
Ako je možné vidieť v predchádzajúcej kapitole, term $\lambda x.x$ má nekonečné množstvo inštancií typu, pri ktorých je správne typovaný. Avšak v takomto prípade naším cieľom pri typovom odvodení nie je len nájsť "nejaký" typ, ale nájsť najvšeobecnejší typ.
Najvšeobecnejší typ (z ang. principal type) je taký typ, ktorý povoľuje vytvorenie najväčšieho množstva typových inštancií, ktoré vznikajú aplikáciou substitúcie.
Príklad
Majme term $\lambda x.x$. Potom:
- Typ $Nat \rightarrow Nat$ nepovoľuje vytvorenie ďalších typových výrazov, keďže po aplikácií ľubovoľnej substitúcie výsledok vždy bude $Nat \rightarrow Nat$.
- Na typ $(X\rightarrow X) \rightarrow (X\rightarrow X)$ je možné aplikovať substitúciu a vytvoriť tak ďalšie typy, avšak tvar tohto typu obmedzuje možnosti aké typy môžu vzniknúť po aplikácii ľubovoľnej substitúcie. V tomto prípade napríklad nie je možné vytvoriť typ $Bool \rightarrow Bool$, ktorý je možné získať z typu $X\rightarrow X$.
Preto hovoríme, že typ $(X\rightarrow X) \rightarrow (X\rightarrow X)$ je viac všeobecný ako $Nat \rightarrow Nat$ avšak je menej všeobecný ako $(X\rightarrow X)$, ktorý je najvšeobecnejší typ pre term $\lambda x.x$.
Nájdenie najvšeobecnejšieho unifikátora prostredníctvom unifikačného algoritmu
Aby sme našli najvšeobecnejší typ potrebujeme nájsť najvšeobecnejšiu substitúciu (unifikátor) $\sigma$, ktorá bude spĺňať danú množinu obmedzení. Avšak nie vždy je množina obmedzení také prostá ako v predchádzajúcich príkladoch a nájdenie najvšeobecnejšieho unifikátora (ak vôbec existuje) sa stáva zložitým problémom.
Najvšeobecnejší unifikátor následne aplikujeme na odvodený typ a tým získame najvšeobecnejší typ.
Pre výpočet najvšeobecnejšieho unifikátora danej množiny obmedzení využijeme myšlienku Hindleyho a Milnera, ktorí na tento účel upravili Robinsonov unifikačný algoritmus.
Poznámka
Typová rekonštrukcia sa nazýva aj typový systém alebo algoritmus Hindleyho a Milnera (z ang. Hindley-Milner algorithm).
Unifikačný algoritmus
Algoritmus: Unifikačný algoritmus
Vstup: Množina obmedzení $C$
Výstup: Najvšeobecnejší unifikátor $\sigma_{mgu}$ (ak existuje), zlyhanie inak
$$ \begin{array}{lll} unify(C) &=& if~C=\{\}, ~then~[~] \\ & & else \\ & & \quad \quad let~ \{S=T\} \cup C'=C~in \\ & & \quad if~ S=T \\ & & \quad \quad then ~ unify(C')\\ & & \quad else~if~ S=X ~a~ X\notin T \\ & & \quad \quad then ~ unify([X\mapsto T]C') \circ [X\mapsto T]\\ & & \quad else~if~ T=X ~a~ X\notin S \\ & & \quad \quad then ~ unify([X\mapsto S]C') \circ [X\mapsto S]\\ & & \quad else~if~ S=S_1 \rightarrow S_2 ~~and~~ T = T_1 \rightarrow T_2 \\ & & \quad \quad then ~ unify(C' \cup \{S_1=T_1, S_2 = T_2\}) \\ & & \quad else ~ fail \end{array} $$
Unifikačný algoritmus slovne
- Rekurzívne voláme funkciu $unify(C)$ pokiaľ množina obmedzení $C$ nie je prázdna $C=\{~\}$. Možnosti:
- Priradenie novej substitúcie do $\sigma_{mgu}$.
- Priradenie nového obmedzenia do $C$.
- Fail, množina obmedzení $C$ je inkonzistentná.
- Vyberieme prvú rovnosť $S=T$ z množiny obmedzení $\{S=T\} \cup C'=C$ ($C'$ zvyšok množiny obmedzení).
- Ak zvolená rovnosť je v tvare $T=T$, napr. $X=X, Nat=Nat, Nat\rightarrow Nat = Nat\rightarrow Nat...$.
- Žiadne nové obmedzenie, ani substitúcia.
- Voláme rekurzívne funkciu $unify(C')$ so zvyškom množiny obmedzení.
- Ak vo zvolenej rovnosti $S=T$ je na pravej strane $X$ (*to znamená *$S=X$), a zároveň $X$ sa nenachádza v $T$, pričom $X$ je typová premenná:
- Substitúcia $T$ za $X$ v množine obmedzení $C'$ - eliminácia typovej premennej $X$.
- Rekurzívne volanie funkcie $unify([X\mapsto T]C') \circ [X\mapsto T]$ s aktualizovanou množinou obmedzení po substitúcii. Zároveň vzniká časť riešenia $unify(C) = \sigma_{mgu}= ... \circ [X\mapsto T]$.
- Ak vo zvolenej rovnosti $S=T$ je na ľavej strane $X$ (*to znamená *$T=X$) a zároveň $X$ sa nenachádza v $S$, pričom $X$ je typová premenná:
- Substitúcia $S$ za $X$ v množine obmedzení $C'$ - eliminácia typovej premennej $X$.
- Rekurzívne volanie funkcie $unify([X\mapsto S]C') \circ [X\mapsto S]$ s aktualizovanou množinou obmedzení po substitúcii. Zároveň vzniká časť riešenia $unify(C) = \sigma_{mgu}= ... \circ [X\mapsto S]$.
- Ak zvolená rovnosť je v tvare $T_1\rightarrow T_2 = S_1 \rightarrow S_2$
- Pridáme nové obmedzenia do množiny obmedzení $C'$ v tvare: $T_1=S_1, T_2=S_2$.
- Rekurzívne voláme $unify(C' \cup \{S_1=T_1, S_2 = T_2\})$.
- Ak zvolená rovnosť je v tvare $T=T$, napr. $X=X, Nat=Nat, Nat\rightarrow Nat = Nat\rightarrow Nat...$.
Poznámka
V prípade, že rovnosť je v tvare: $$T_1 \rightarrow T_2 = S_1 \rightarrow S_2,$$ podľa algoritmu postupujeme vytvorením dvoch nových obmedzení: $$S_1=T_1, S_2 = T_2.$$ V prípade ak v rovnosti: $$T_1 \rightarrow T_2 = S_1 \rightarrow S_2$$ sa nenachádza rovnaký počet typových konštruktorov funkčného typu: $$Nat \rightarrow Bool \rightarrow F = X \rightarrow Z,$$ je potrebné si uvedomiť, že konštruktor $\rightarrow$ je pravoasociatívny.
To znamená
$$ \begin{array}{l} Nat \rightarrow Bool \rightarrow F = X \rightarrow Z\\ Nat \rightarrow (Bool \rightarrow F) = X \rightarrow Z, \end{array} $$ pričom vznikajú nasledujúce dve rovnosti: $$ \begin{array}{l} Nat = X, \\ Bool \rightarrow F = Z. \end{array} $$
Príklad
Majme dané $\Gamma=\{~\}$ a $t=(\lambda x.x) (\lambda y.y)$. Nájdite najvšeobecnejší typ pre term $t$ v typovom prostredí $\Gamma$.
Riešenie
Máme daný sekvet: $$\vdash (\lambda x.x) (\lambda y.y): S~|~C.$$ V prvom kroku aplikáciou typových pravidiel zostrojíme typový strom pre $\Gamma, t$ bez typových anotácií a množiny obmedzení:
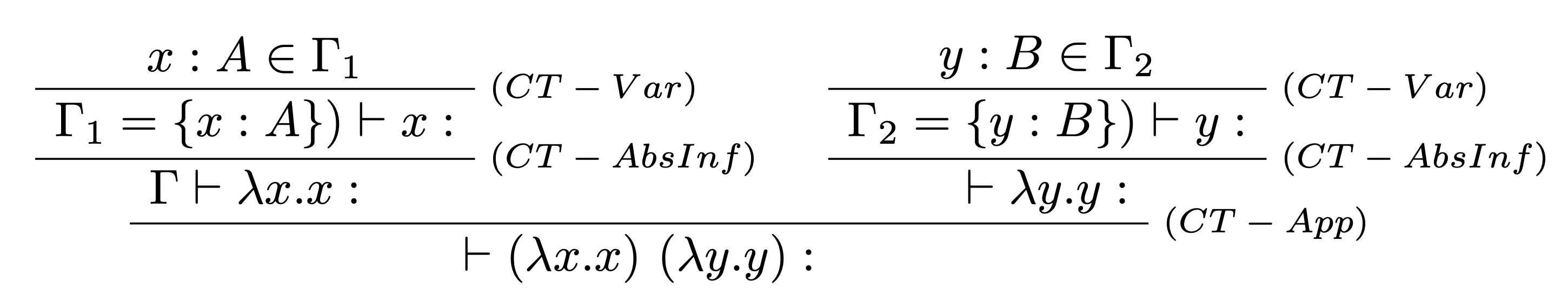
V druhom kroku podľa typových pravidiel odvodíme príslušný typ $S$ a množinu obmedzení $C$.
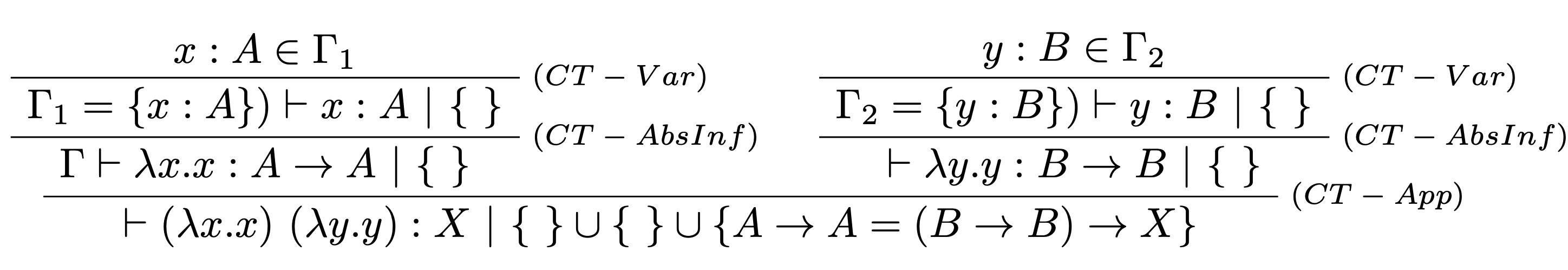
Odvodili sme typ $X$ a množinu obmedzení $C=\{A\rightarrow A = (B \rightarrow B) \rightarrow X\}$.
Vypočítame najvšeobecnejší unifikátor $\sigma_{mgu}$ využitím unifikačného algoritmu. $$ \begin{array}{lll} riadok & výpočet & \\ \hline 1 & unify(\{A\rightarrow A = (B \rightarrow B) \rightarrow X\}) &= \\ 2 & unify(\{A = B \rightarrow B, A = X\}\cup \{~\}) &= & \\ 3 & unify([A \mapsto B \rightarrow B] \{A = X\}) \circ [A \mapsto B \rightarrow B] &= & \\ 4 & unify(\{B \rightarrow B = X\}) \circ [A \mapsto B \rightarrow B] &= & \\ 5 & unify([X \mapsto B \rightarrow B]\{~\}) [X \mapsto B \rightarrow B] \circ [A \mapsto B \rightarrow B] &= & \\ 6 & unify(\{~\}) [X \mapsto B \rightarrow B] \circ [A \mapsto B \rightarrow B] &= & \\ 7 & [~] \circ [X \mapsto B \rightarrow B] \circ [A \mapsto B \rightarrow B] &= & \\ 8 & [X \mapsto B \rightarrow B] \circ [A \mapsto B \rightarrow B] &= & \\ 9 & \sigma_{mgu} & & \end{array} $$
Aplikujeme vypočítaný najvšeobecnejší unifikátor $\sigma_{mgu}$ na odvodený typ $X$:
$$ \begin{array}{lc} \sigma_{mgu} X & = \\ [X \mapsto B \rightarrow B] \circ [A \mapsto B \rightarrow B] X & = \\ [X \mapsto B \rightarrow B] X & = \\ B \rightarrow B & \end{array} $$ Náš term $t=(\lambda x.x) (\lambda y.y)$ je typu $B \rightarrow B$: $$(\lambda x:B.x) (\lambda y:B.y):B \rightarrow B.$$ V interpreteri jazykov Haskell a Ocaml je možné jednoducho overiť naše riešenie.
Haskell:
GHCi, version 9.4.7: https://www.haskell.org/ghc/ :? for help
ghci> term = (\x -> x) (\y -> y)
ghci> :t term
term :: p -> p
ghci> term 2
2
ghci> :t term 2
term 2 :: Num p => p
ghci> term "text"
"text"
ghci> :t term "text"
term "text" :: String
Ocaml:
utop # let term = (fun x -> x) (fun y -> y);;
val term : '_weak1 -> '_weak1 = <fun>
utop # let id = fun x -> x;;
val id : 'a -> 'a = <fun>
utop # term 2;;
- : int = 2
utop # term ;;
- : int -> int = <fun>
utop # let term = (fun x -> x) (fun y -> y);;
val term : '_weak2 -> '_weak2 = <fun>
utop # term "text";;
- : string = "text"
Príklad
Majme dané $$\Gamma=\{add: Nat \rightarrow Nat \rightarrow Nat\}$$ a $$t=\lambda f. \lambda x. f~(add ~x~1).$$ Nájdite najvšeobecnejší typ pre term $t$ v typovom prostredí $\Gamma$.
Riešenie
- Zostrojíme štruktúru typového stromu:
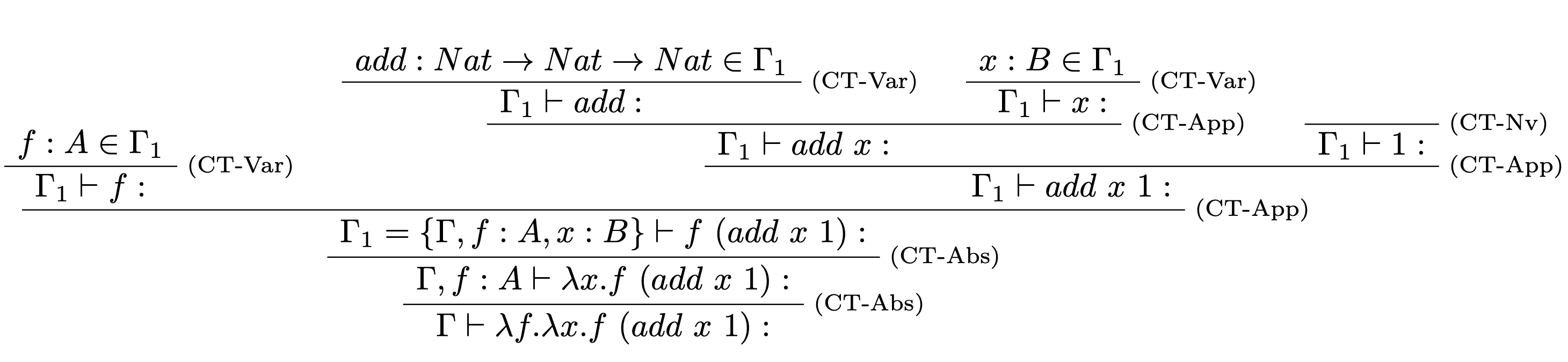
- Podľa pravidiel doplníme typy a obmedzenia:
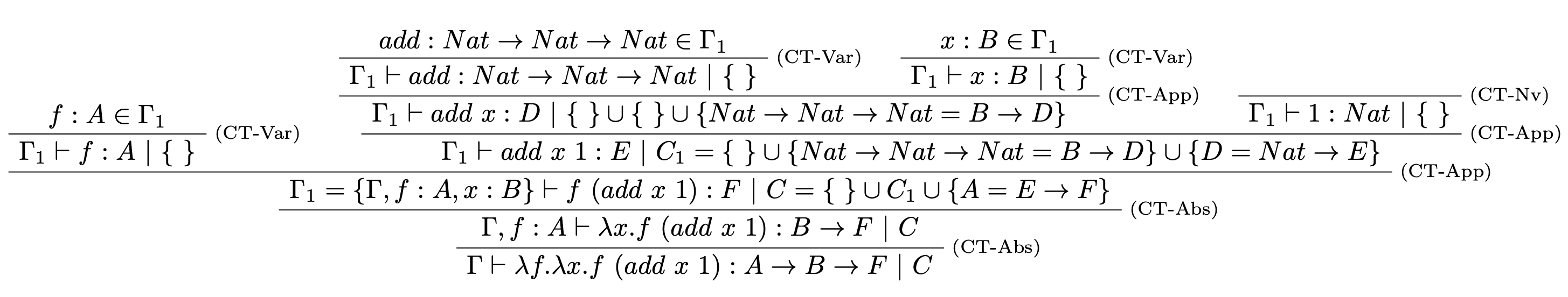
Z typového stromu sme získali nasledovné:
- Odvodený typ: $$S=A \rightarrow B \rightarrow F.$$
- Množina obmedzení: $$C=\{Nat \rightarrow Nat \rightarrow Nat = B \rightarrow D,~ D=Nat\rightarrow E,~ A=E \rightarrow F\}$$
Aplikujeme unifikačný algoritmus na množinu obmedzení $C$ a získame najvšeobecnejší unifikátor $\sigma_{mgu}$: $$unify(\{Nat \rightarrow Nat \rightarrow Nat = B \rightarrow D,~ D=Nat\rightarrow E,~ A=E \rightarrow F\})=\sigma_{mgu}$$
| $Unify$ Iterácia |
Množina obmedzení $C$ |
|---|---|
| 1. | $\{Nat \rightarrow Nat \rightarrow Nat = B \rightarrow D,~ D=Nat\rightarrow E,~ A=E \rightarrow F\}$ |
| 2. | $\{Nat = B,~ Nat \rightarrow Nat = D,~ D=Nat\rightarrow E,~ A=E \rightarrow F\}$ |
| 3. | $\{Nat \rightarrow Nat = D,~ D=Nat\rightarrow E,~ A=E \rightarrow F\}$ |
| 4. | $\{Nat \rightarrow Nat=Nat\rightarrow E,~ A=E \rightarrow F\}$ |
| 5. | $\{Nat=Nat,~ Nat = E,~ A=E \rightarrow F\}$ |
| 6. | $\{Nat = E,~ A=E \rightarrow F\}$ |
| 7. | $\{A=Nat \rightarrow F\}$ |
| 8. | $\{~\}$ |
Unifikáciou množiny obmedzení $C$ sme získali nasledujúci najvšeobecnejší unifikátor $\sigma_{mgu}$:
$$ \begin{array}{l} unify(\{Nat \rightarrow Nat \rightarrow Nat = B \rightarrow D,~ D=Nat\rightarrow E,~ A=E \rightarrow F\})= \\ [~]\circ [A \mapsto Nat \rightarrow F] \circ [E \mapsto Nat] \circ [D \mapsto Nat \rightarrow Nat] \circ [B \mapsto Nat]=\\ =\sigma_{mgu} \end{array} $$ Následne aplikujeme $\sigma_{mgu}$ na odvodený typ $S$ a získame najvšeobecnejší typ termu $t$ v typovom kontexte $\Gamma$:
$$\sigma_{mgu}(A \rightarrow B \rightarrow F)=(Nat \rightarrow F) \rightarrow Nat \rightarrow F.$$
Overíme naše riešenie prostredníctvom interpretéra jazyka OCaml:
utop # let add = fun x -> fun y -> x + y;;
val add : int -> int -> int = <fun>
utop # let t= fun f -> fun x -> f (add x 1);;
val t : (int -> 'a) -> int -> 'a = <fun>
Zdroje
- Benjamin C.Pierce, Types and programming languages. MIT press, 2002.
- Michael R. Clarkson et al., OCaml Programming: Correct + Efficient + Beautiful, Cornell University, 2023
- Lecture notes, CS 6110 - Advanced Programming Languages, Cornell University, 2019
- Lecture notes, CS 4110 - Programming Languages and Logics, Cornell University, 2021
- Valerie Novitzká, Daniel Mihályi: Teória typov, TU Košice, 2015