Rekurzia v typovanom $\lambda$-kalkule
V druhej prednáške sme zaviedli spôsob akým je možné vypočítať rekurzívne funkcie v netypovanom čistom $\lambda$-kalkule. Avšak daný spôsob sa nedá využiť v našom typovanom jazyku, keďže kombinátory fixného bodu využívajú princíp seba-aplikácie: $$\Omega = \omega\ \omega,$$ kde: $$\omega=\lambda x.\ x\ x$$ pričom takýto term nie je typovateľný, keďže ľavé $x$ musí byť funkčného typu $T_1 \to T_2$ a zároveň pravé $x$ by muselo byť typu $T_1$.
To znamená, že kombinátory fixného bodu nie je možné definovať ako termy v našom typovanom jazyku.
Fixný bod v typovanom $\lambda$-kalkule
Riešením vyššie uvedeného problému je zavedenie nového operátora $fix$ do syntaxe nášho jazyka, ktorý bude "imitovať" správanie sa kombinátora fixného bodu.
Rozšírime syntax nášho jazyka nasledovne:
$$t::= ... |\ fix\ t$$
Poznámka
Je potrebné si uvedomiť, že $fix\ v$ nie je hodnota.
Typovacie pravidlo:
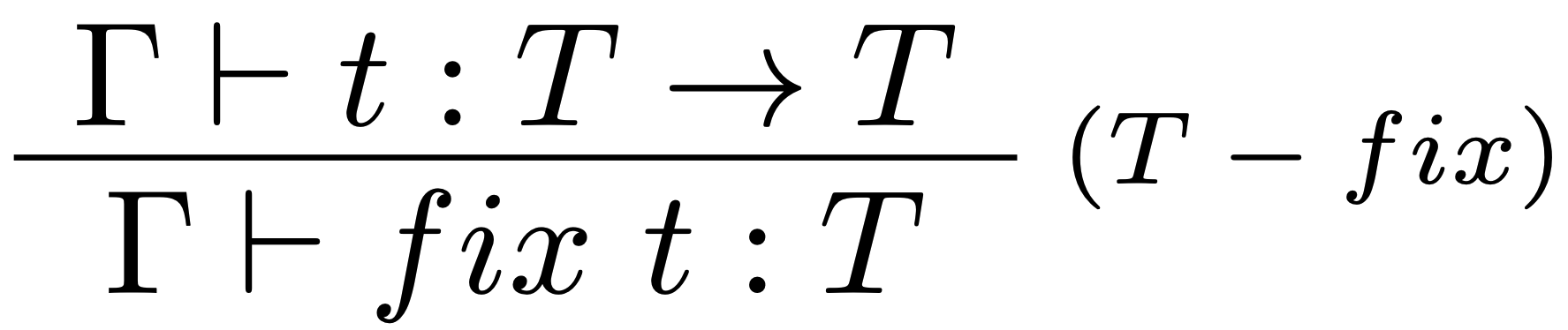
Vyhodnocovacie pravidlá:
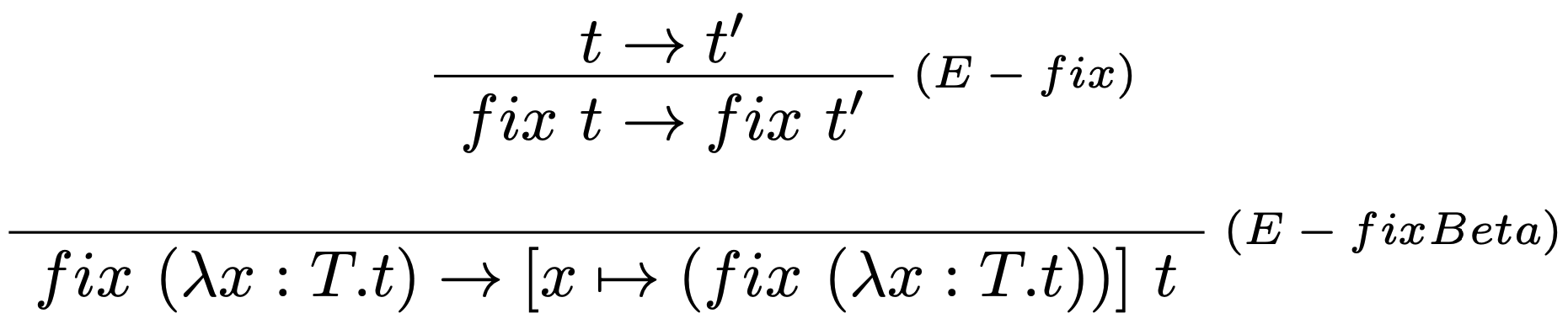
Príklad: Funkcia faktoriál
Majme funkciu faktoriál, ktorú opisuje nasledujúca rekurzívna definícia: $$ faktorial(n)= \begin{cases} 1 \quad \text{ak}~n=0,\\ ~ \\ n*faktorial(n-1) \end{cases} $$ kde $n \in \mathbf{N}$.
V našom jazyku je možné danú funkciu zapísať nasledovne: $$ faktorial = \lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n*faktorial(pred\ n), $$ pričom táto funkcia je typu: $$ faktorial: Nat \to Nat $$
Poznámka
Funkcia $faktorial$ obsahuje na pravej strane voľnú premennú $faktorial$. To znamená, že takáto funkcia nie je správne typovaná v prázdnom typovom kontexte $\Gamma$.
Pre vyriešenie tohto problému opäť využijeme trik na odstránenie rekurzívnej definície, jej prepisom na funkciu vyššieho rádu: $$ g = \lambda f:Nat \to Nat. \lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n*f(pred\ n), $$ pričom táto funkcia je typu: $$ g: (Nat \to Nat) \to Nat \to Nat $$
Dôkaz:
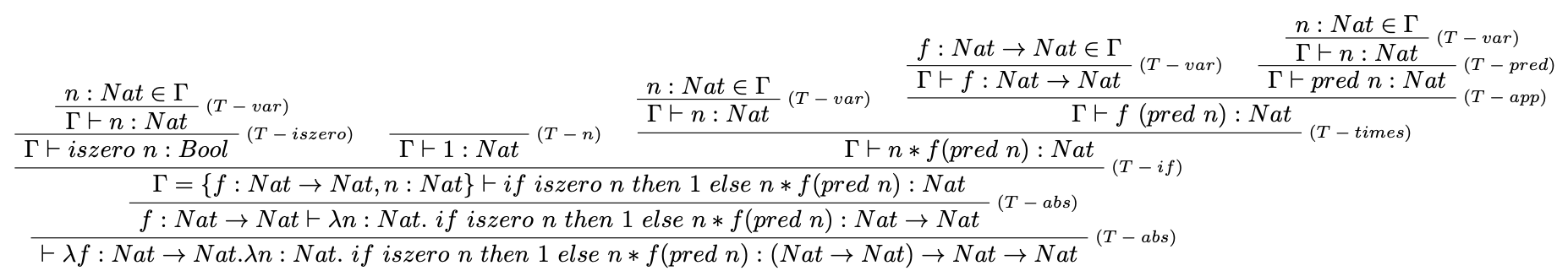
Poznámka
V typovej kontrole funkcie $g$ vyššie bolo využité nové typovacie pravidlo pre operáciu " * " násobenia, z dôvodu zníženia komplexnosti dôkazového stromu.
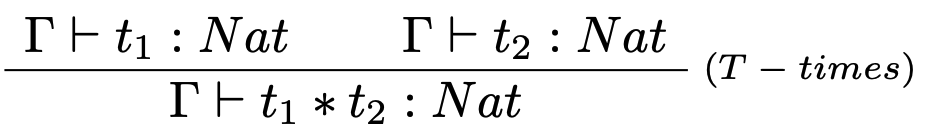
Následne stačí aplikovať operátor $fix$ na funkciu vyššieho rádu $g$ a získame funkciu, ktorá má žiadané vlastnosti: $$fakt = fix\ g$$
Príklad
Pre výpočet faktoriálu čísla $3$ použijeme funkciu $fakt$: $$fakt\ 3 = fix\ g\ 3.$$
V prvom kroku overíme, či je term $$fix\ g\ 3$$ správne typovaný v typovom kontexte $$\Gamma = \{g:(Nat \to Nat) \to Nat \to Nat\}.$$ Typová kontrola:
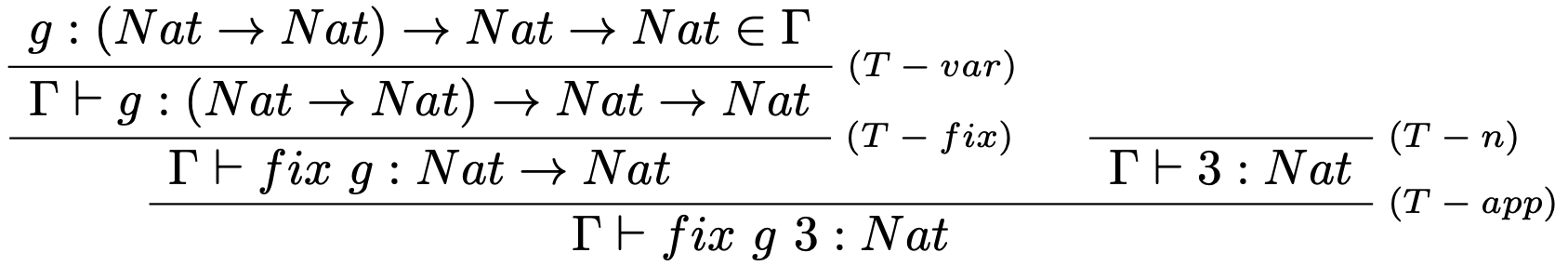
Pokračujeme vyhodnotením: $$ \begin{array}{l} fakt\ 3 = fix\ g\ 3 =\\ \underline{fix\ (\lambda f:Nat \to Nat. \lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n*f(pred\ n))}\ 3 \to \\ \underline{(\lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n* fix\ g\ (pred\ n))\ 3} \to\\ if\ iszero\ 3 \ then\ 1\ else\ 3* fix\ g\ (pred\ 3) \to^* \\ if\ false\ then\ 1\ else\ 3* fix\ g\ 2 \to \\ 3* fix\ g\ 2 = \\ 3* \underline{fix\ (\lambda f:Nat \to Nat. \lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n*f(pred\ n))}\ 2 \to \\ 3* \underline{(\lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n * fix\ g\ (pred\ n))\ 2} \to \\ 3* (if\ iszero\ 2 \ then\ 1\ else\ 2 * fix\ g\ (pred\ 2)) \to^* \\ 3* (if\ false\ then\ 1\ else\ 2 * fix\ g\ 1) \to \\ 3* 2 * fix\ g\ 1 = \\ 3*2* \underline{fix\ (\lambda f:Nat \to Nat. \lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n*f(pred\ n))}\ 1 \to \\ 3*2* \underline{(\lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n * fix\ g\ (pred\ n))\ 1} \to \\ 3*2* (if\ iszero\ 1\ then\ 1\ else\ 1 * fix\ g\ (pred\ 1)) \to^* \\ 3*2* (if\ false\ then\ 1\ else\ 1 * fix\ g\ 0) \to \\ 3*2*1* fix\ g\ 0 = \\ 3*2*1* \underline{fix\ (\lambda f:Nat \to Nat. \lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n*f(pred\ n))}\ 0 \to \\ 3*2*1* \underline{(\lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n * fix\ g\ (pred\ n))\ 0} \to \\ 3*2*1* (if\ iszero\ 0 \ then\ 1\ else\ 0 * fix\ g\ (pred\ 0)) \to^* \\ 3*2*1* (if\ true\ then\ 1\ else\ 0 * fix\ g\ 0) \to \\ 3*2*1*1 \to^* 6 \end{array} $$
Poznámka
Takéto rozšírenie jazyka spôsobilo stratu vlastnosti silnej normalizácie, keďže umožňuje písanie neterminujúcich programov, ktoré sú správne typované.
Príklad
Majme term: $$\lambda x:T.x: T \to T$$ na ktorý aplikujeme operátor $fix$: $$fix\ (\lambda x:T.x): T.$$ Takýto term je správne typovaný:
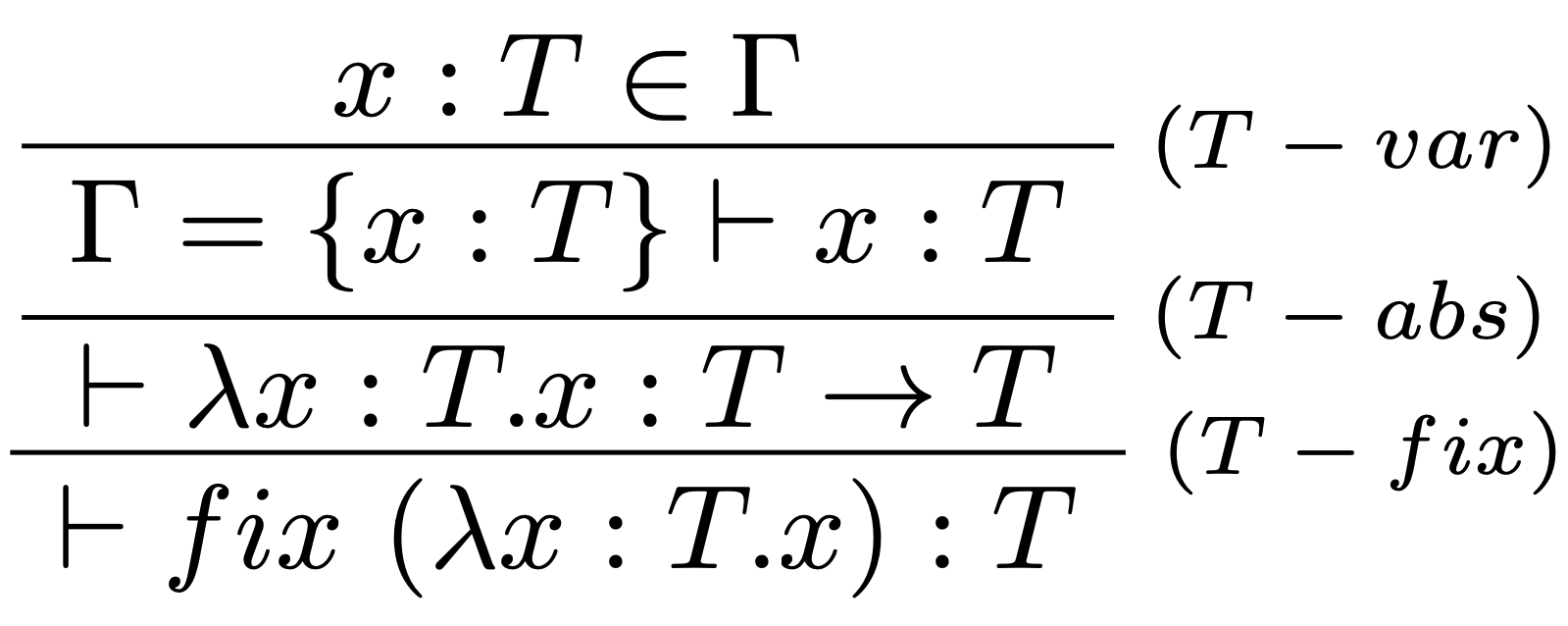
Avšak neterminuje: $$ \begin{array}{l} fix\ (\lambda x:T.x) \to \\ \lambda x:T.fix\ (\lambda x:T.x) \to \\ \lambda x:T.fix\ (\lambda x:T.fix\ (\lambda x:T.x)) \to \\ ... \end{array} $$
Nepriama rekurzia
Operátor $fix$ sa zvyčajne využíva na definíciu rekurzívnych funkcií funkčného typu, avšak môže byť využitý na nájdenie fixného bodu akéhokoľvek typu.
Poznámka
Všimnite si, že typ $T$ v typovaciom pravidle $(T-fix)$ nie je obmedzený na funkčný typ.
Táto vlastnosť umožňuje definíciu nepriamo rekurzívnych funkcií ako fixného bodu termu typu záznam, ktorý pozostáva z funkcií, ktoré sa na seba rekurzívne odkazujú.
Príklad
Definujme binárny záznam, ktorý bude obsahovať dve nepriamo rekurzívne funkcie pre overenie čí je číslo párne (isven), resp. nepárne (isodd): $$ \begin{array}{lcl} \mathbf{isevenisodd}= & & \langle\ iseven = \lambda n: Nat. if\ iszero\ n\ then\ true\ else\ \mathbf{isevenisodd}.isodd\ (pred\ n), \\ & & ~~isodd = \lambda n: Nat. if\ iszero\ n\ then\ false\ else\ \mathbf{isevenisodd}.iseven\ (pred\ n)\ \rangle \end{array} $$
Funkcia vyššieho rádu: $$ \begin{array}{lcl} g& = &\lambda ieio: \langle iseven:Nat \to Bool, isodd:Nat \to Bool \rangle\ . \\ & & \langle\ iseven = \lambda n: Nat. if\ iszero\ n\ then\ true\ else\ ieio.isodd\ (pred\ n), \\ & & ~~isodd = \lambda n: Nat. if\ iszero\ n\ then\ false\ else\ ieio.iseven\ (pred\ n)\ \rangle \end{array} $$ Pričom typ funkcie $g$: $$g:\langle iseven:Nat \to Bool, isodd:Nat \to Bool \rangle \to \langle iseven:Nat \to Bool, isodd:Nat \to Bool \rangle$$ Nasledne aplikujeme operátor $fix$ na funkciu $g$, čím získame binárny záznam, ktorý bude obsahovať dve návestia $iseven$ a $isodd$ s požadovanými rekurzívnymi funkciami: $$r_{ieio} = fix\ g: \langle iseven:Nat \to Bool, isodd:Nat \to Bool \rangle$$ Prístup k jednotlivým funkciám je možný prostredníctvom projekcií nad $r_{ieio}$ $$r_{ieio}\ .iseven:Nat \to Bool$$ $$r_{ieio}\ .isodd:Nat \to Bool$$
Odvodený tvar letrec
Väčšina vyššie-úrovňových jazykov zakrýva používanie operátorov ako je $fix$ do odvodených tvarov, ktoré sú pre programátora jednoduchšie na používanie.
Napríklad v programovacom jazyku OCaml je pri rekurzívnych funkciách využívaná konštrukcia let rec:
utop # let rec faktorial = fun n ->
if n = 0
then 1
else n*faktorial(n-1);;
val faktorial : int -> int = <fun>
utop # let rec faktorial = fun n ->
if n = 0
then 1
else n*faktorial(n-1)
in faktorial 5;;
- : int = 120
Odvodený tvar letrec je možné v našom jazyku zadefinovať nasledovne: $$ \begin{array}{c} letrec\ x:T=t_1\ \ in\ \ t_2 \\ \equiv \\ let\ x = fix\ (\lambda x:T. t_1)\ \ in\ \ t_2 \end{array} $$
Príklad
Funkciu $faktorial$ aplikovanú na argument $3$ $$faktorial = \lambda n:Nat.\ if\ iszero\ n\ then\ 1\ else\ n*faktorial(pred\ n)$$ je možné prepísať využitím $letrec$ následovne: $$ \begin{array}{l} \mathbf{letrec}\ faktorial:Nat\to Nat=\\ \quad \lambda n:Nat.\ \text{if}\ iszero\ n \ \text{then}\ 1\ \text{else}\ n * faktorial\ (pred\ n)\\ \mathbf{in}\ faktorial\ 3 \end{array} $$
Zoznamy
Ďalším užitočným typom, ktorý je možné zaviesť na základe doterajších vedomostí je typ zoznam (z ang. list).
Zoznam je najznámejší rekurzívny typ.
Poznámka
V tejto kapitole sa budeme venovať spôsobu ako zaviesť rekurzívny typ zoznam do jazyka ako jeho súčasť. Na to bude potrebné rozšíriť jazyk, definovať nové typovacie aj vyhodnocovacie pravidlá. V nasledujúcej kapitole rozoberieme spôsob ako zovšeobecniť zavedenie vlastných rekurzívnych typov do jazyka zavedením rekurzívnych typov.
Typový konštruktor pre zoznam označíme ako $List$.
Pre každý typ $T$ zápis $$ List~ T $$ konštruuje typ konečných zoznamov, ktorého prvky sú typu $T$.
Prvok typu $List~ T$ je buď:
- nil [T] - prázdny zoznam, alebo
- cons [T] $\ t_1$ $\ t_2$ - konštruktor, kde:
- $t_1$ je typu $T$,
- $t_2$ je typu $List~ T$.
Poznámka
Je potrebné si uvedomiť, že všetky prvky daného zoznamu musia byť toho istého typu, napríklad prirodzené čísla, záznamy, varianty a taktiež aj zoznamy a podobne.
Príklad
Majme typ zoznam prirodzených čísel: $$List\ Nat,$$ potom prvky takéhoto typu sú napríklad: $$ \begin{array}{l} nil\ [Nat] \\ cons\ [Nat]\ \ 3\ \ nil\ [Nat]\\ cons\ [Nat]\ \ 2\ \ (cons\ [Nat]\ \ 3\ \ nil\ [Nat])\\ cons\ [Nat]\ \ 1\ \ (cons\ [Nat]\ \ 2\ \ (cons\ [Nat]\ \ 3\ \ nil\ [Nat]))\\ ... \end{array} $$
Pre zvýšenie čitateľnosti zavedieme nasledujúce notácie využitím svorkových zátvoriek:
- nil [T] označíme ako $\{ \ \} [T]$,
- cons [T] $\ t_1$ $\ t_2$ označíme ako:
- $\{ t_1 \} [T]$ ak $t_2$ je $nil$,
- $\{ t_1,\ t_2 \} [T]$ ak $t_2$ je cons [T] $\ t_2$ $\ t_3$ a $t_3$ je $nil$,
- $\{ t_1, \ldots, t_n \}[T]$
Príklad
Majme typ zoznam prirodzených čísel: $$List\ Nat,$$ potom prvky takéhoto typu je možné zapísať využitím vyššie uvedenej notácie: $$ \begin{array}{lcl} \{ \ \}\ [Nat] & = & nil\ [Nat] \\ \{ 3 \}\ [Nat] & = & cons\ [Nat]\ \ 3\ \ nil\ [Nat]\\ \{ 2, 3 \}\ [Nat] & = & cons\ [Nat]\ \ 2\ \ (cons\ [Nat]\ \ 3\ \ nil\ [Nat])\\ \{ 1, 2, 3 \}\ [Nat] & = & cons\ [Nat]\ \ 1\ \ (cons\ [Nat]\ \ 2\ \ (cons\ [Nat]\ \ 3\ \ nil\ [Nat]))\\ ... \end{array} $$
Príklad
Vo všeobecnosti prvky typu zoznam môžu byť napríklad: $$ \begin{array}{l} \{ 1, 3, 5, 7, 9\}[Nat]: List~Nat, \\ \{true, false, false\}[Bool]: List~Bool, \\ \{ \langle 1, true \rangle, \langle 2, false \rangle, \langle 5, true \rangle \} [Nat \times Bool]: List ~ Nat \times Bool \\ \end{array} $$ Ako bolo spomenuté vyššie, je možne konštruovať aj zoznam zoznamov: $$\{ \{ 1, 3\}[Nat], \{ 7, 9\}[Nat], \{ 1, 3, 5, 7, 9\}[Nat]\}[Nat]: List~List~Nat,$$
Syntax
Rozšírime syntax nášho jazyka nasledovne:
$$ \begin{array}{lcl} t & ::= & \ldots~|~nil[T]~|~cons[T]~t~t~|~isnil[T]~t~|~head[T]~t~|~tail[T]~t \\ v & ::= & \ldots~|~nil[T]~|~cons[T]~v~v\\ T & ::= & \ldots~|~List~~T \end{array} $$ kde:
- $nil[T]$ označuje prázdny zoznam, ktorý očakáva len hodnoty typu $T$,
- $cons[T]~t_1~t_2$ je operácia, ktorá pridá hodnotu termu $t_1$ na začiatok zoznamu $t_2$,
- $isnil[T]~t$ je operácia, ktorá vráti $true$, ak je zoznam prázdny, v opačnom prípade je výsledok $false$,
- $head[T]~t$ vráti hlavičku zoznamu $t$, teda prvý člen zoznamu,
- $tail[T]~t$ vráti zvyšok zoznamu $t$ bez hlavičky.
Typovacie pravidlá
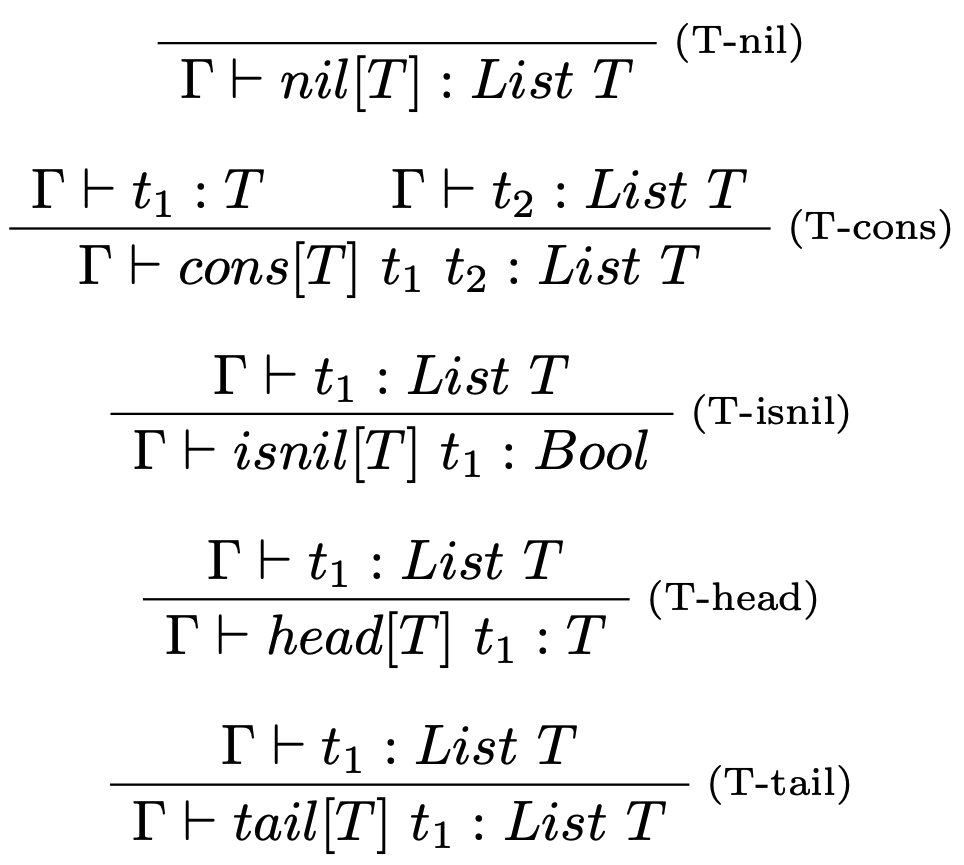
Vyhodnocovacie pravidlá
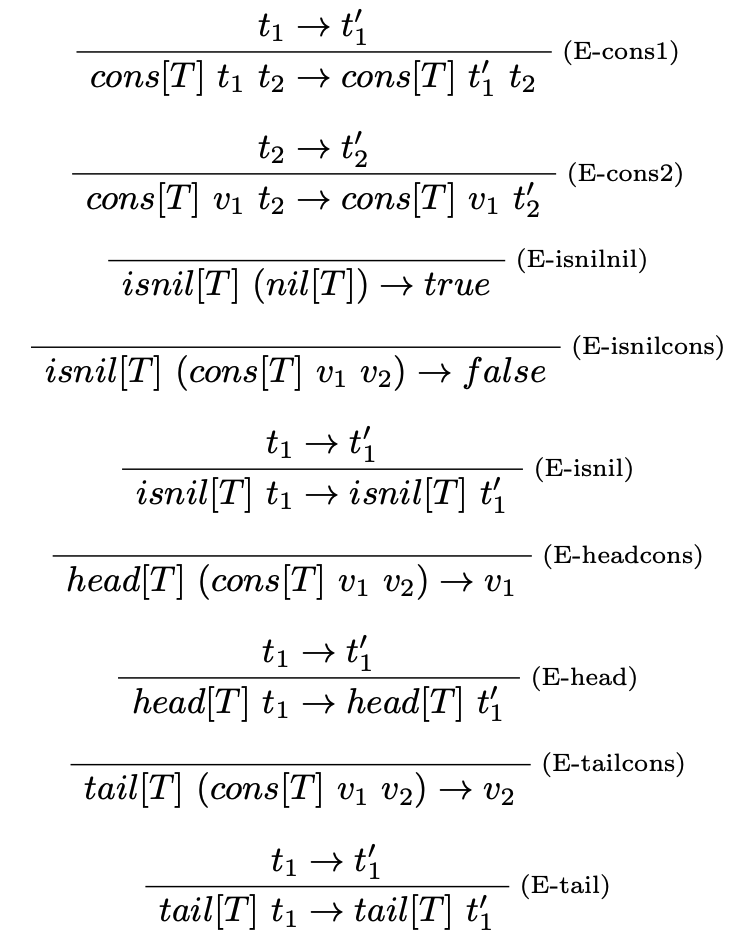
Príklad
Majme nasledujúci term: $$ \text{head}[Nat]\ \text{cons}[Nat]\ 3\ (\text{cons}[Nat]\ 8\ \text{nil}[Nat]):Nat $$ Overte či je správne typovaný, ak áno vyhodnoťte ho.
Riešenie
Typová kontrola:
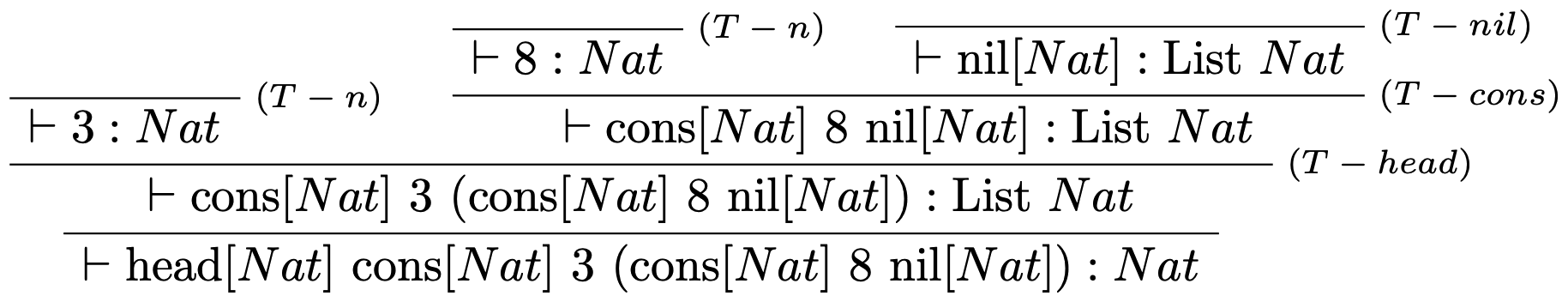
Vyhodnotenie: $$\text{head}[Nat]\ \text{cons}[Nat]\ 3\ (\text{cons}[Nat]\ 8\ \text{nil}[Nat]) \to 3$$
Príklad: Typ zoznam v OCaml
Aj ked programovací jazyk OCaml má vstavanú podporu pre zoznamy, pre demonštratívne účely zadefinujme vlastný typ zoznam celých čísel:
utop # type intlist = Nil | Cons of int*intlist;;
type intlist = Nil | Cons of int * intlist
(* Prvky takéhoto typu sú konštruované nasledovne *)
utop # Nil;;
- : intlist = Nil
utop # Cons (1,Nil);;
- : intlist = Cons (1, Nil)
utop # Cons (2,Cons (1,Nil));;
- : intlist = Cons (2, Cons (1, Nil))
(* Funkcie head a tail *)
utop # let head (l:intlist) : int = match l with
| Nil -> 0
| Cons(x,_) -> x ;;
val head : intlist -> int = <fun>
utop # let tail (l:intlist) : intlist = match l with
| Nil -> Nil
| Cons(_,x) -> x ;;
val tail : intlist -> intlist = <fun>
utop # head (Cons (2, Cons (1, Nil)));;
- : int = 2
utop # tail (Cons (2, Cons (1, Nil)));;
- : intlist = Cons (1, Nil)
utop # head (tail (Cons (2, Cons (1, Nil))));;
- : int = 1
Vstavaný typ zoznam v OCaml sa správa obdobne ako naša definícia, avšak jeho výpis prvkov je formátovaný kvôli čitateľnosti:
utop # #show list;;
type 'a list = [] | (::) of 'a * 'a list
(* Prvky typu zoznam sú uzavreté do hranatých zátvoriek
a oddelené bodkočiarkou *)
utop # [1;2;45;6];;
- : int list = [1; 2; 45; 6]
(* Operácie head a tail *)
utop # List.hd [1;2;45;6];;
- : int = 1
utop # List.tl [1;2;45;6];;
- : int list = [2; 45; 6]
(* prázdny zoznam *)
utop # [];;
- : 'a list = []
(* :: je infixný operátor cons *)
(* všimnite si výpis v druhom riadku *)
utop # 1::[];;
- : int list = [1]
utop # 2::1::[];;
- : int list = [2; 1]
utop # 2::(1::[]);;
- : int list = [2; 1]
utop # 3::(2::(1::[]));;
- : int list = [3; 2; 1]
utop # List.tl [1];;
- : int list = []
Rekurzívne typy
V predchádzajúcej kapitole bol do jazyka zavedený rekurzívny typ zoznam ako základná súčasť - primitívum jazyka (z ang. language primitives).
Zoznam je len jeden príklad triedy takýchto štruktúr, medzi ktoré patria: front, stromy, binárne stromy, abstraktné syntaktické stromy a mnoho ďalších.
Napríklad prvok typu zoznam prirodzených čísel je vždy buď prázdny zoznam alebo dvojica pozostávajúca z čísla a ďalšieho zoznamu prirodzených čísel. Pre zavedenie takéhoto typu do jazyka ako primitívum bolo potrebné rozšíriť syntax jazyka, definovať príslušné typovacie a vyhodnocovacie pravidlá pre všetky nové syntaktické tvary. V prípade potreby zavedenia inej štruktúry by bolo nutné celý tento proces opakovať.
Z tohto dôvodu namiesto zavádzania každej ďalšej štruktúry ako základnej časti jazyka, zovšeobecníme tento proces vytvorením mechanizmu, ktorý umožní definíciu takýchto štruktúr z jednoduchších elementov. Tento mechanizmus sa nazýva rekurzívne typy.
Rekurzívny operátor $\mu$
Rekurzívne typy sú najčastejšie využívané na definíciu rekurzívnych údajových štruktúr, ktoré špecifikujú nekonečné objekty, zväčša vo tvare stromov.
Takéto stromy vytvárajú špecifikáciu rekurzívnej rovnice a typ takéhoto stromu musí spĺňať túto rovnicu.
Rekurzívny operátor $\mu$ umožňuje definície takýchto typov.
Majme typy $T', T$ a typovú premennú $X$, potom $$T' = \mu X. T$$ hovorí, že rekurzívny typ $T'$ je definovaný rovnicou $X=T$. Zvyčajne $X$ sa nachádza voľne v $T$.
Rekurzívny operátor $\mu$ sa správa obdobne ako $\lambda$ pri $\lambda$-abstrakcii. V zápise: $$\mu X. T$$ $\mu$ viaže typovú premennú $X$ v type $T$.
Typ prirodzených čísel ako rekurzívny typ
Typ prirodzených čísel $Nat$, ktorý sme zaviedli ako primitívum jazyka je možné taktiež vyjadriť ako rekurzívny typ.
V programovacom jazyku OCaml je možné typ $Nat$ definovať ako variantový typ:
type nat = Zero | Succ of nat
Takýto typ je taktiež rekurzívny, keďže je definovaný sám sebou (nat sa nachádza na oboch stranách rovnice).
Majme typ prirodzených čísel $Nat$. Prvky takého typu sú buď nula alebo operátor nasledovníka prirodzeného čísla. Pokúsme sa tento typ reprezentovať ako variantový typ: $$Nat=[zero:Unit, succ: ...].$$ Hodnota $zero$ je triviálna, keďže návestie nám hovorí všetko čo potrebujeme vedieť o hodnote nula. Avšak hodnota ktorú môže nadobudnúť $succ$ je opäť prirodzené číslo: $$Nat=[zero:Unit, succ: Nat].$$ Takáto rovnica nie je definícia. Definícia je proste nové pomenovanie niečoho, čoho význam je už známy. V tomto prípade sa na oboch stranách sa nachádza $Nat$. Táto rovnica môže poslúžiť ako špecifikácia nekonečného stromu:
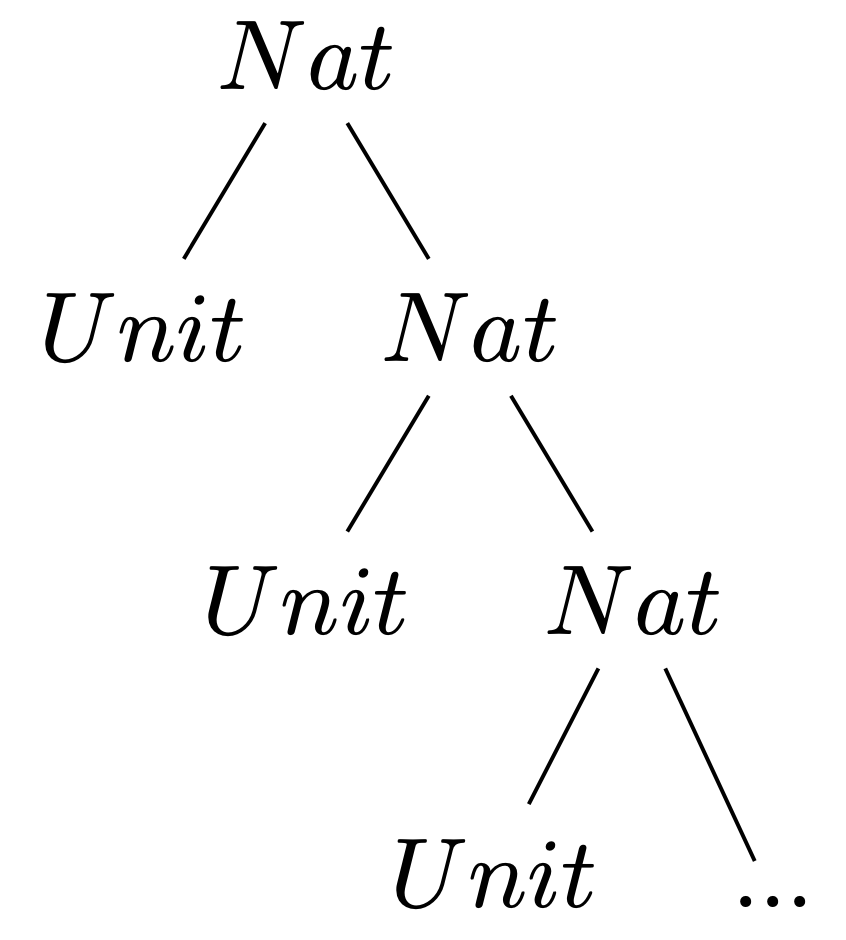
Inými slovami hľadáme riešenie rovnice rekurzívnej špecifikácie nekonečného stromu: $$X=[zero:Unit, succ: X].$$
Opäť využijeme trik na odstránenie rekurzie prostredníctvom rekurzívneho operátora $\mu$, a presunieme "cyklus" na pravú stranu: $$Nat= \mu X. [zero:Unit, succ: X].$$ Túto definíciu je možné prečítať ako: "Typ $Nat$ je nekonečný typ spĺňajúci rovnicu $X= [zero:Unit, succ: X]$".
Formalizácia rekurzívnych typov
Existujú dva základné spôsoby ako formalizovať rekurzívne typy:
- Ekvirekurzívne typy,
- Izorekurzívne typy.
Hlavným rozdielom je spôsob, akým je uvažované o relácii medzi typom $\mu X.T$ a jedným krokom jeho "rozbalenia": $$ \mu X.T \qquad \text{a} \qquad [X \mapsto \mu X.T]\ T $$
Pri type $Nat$ uvažujeme nad reláciou medzi: $$ Nat \qquad \text{ a } \qquad [zero:Unit, succ: Nat], $$ pričom po substitúcii $Nat$ definíciou vyššie získame: $$ \mu X. [zero:Unit, succ: X] \quad \text{ a } \quad [zero:Unit, succ: (\mu X. [zero:Unit, succ: X])] $$
- V ekvirekurzívnom prístupe je rekurzívny typ aj jeho rozbalený typ považovaný za ekvivalentný, keďže obidva opisujú ten istý nekonečný strom.
- Pri izorekurzívnom prístupe sú rekurzívne typy a ich rozbalené typy považované za rozdielne, avšak izomorfné typy.
Hlavnou výhodou ekvirekurzívneho prístupu je, že je koncepčne jednoduchý a možno ho priamo integrovať do existujúceho typového systému – stačí povoliť, aby typové výrazy mohli byť nekonečné.
Avšak na druhej strane, implementácia typovej kontroly pre ekvirekurzívne typy je komplikovaná, keďže prekladač musí sám odvodiť či daný typ potrebné rozbaliť, resp. zabaliť spať.
Jednoduchá implementovateľnosť je silnou stránkou izorekurzívneho prístupu. Aj keď na formálnej úrovni potreba explicitného izomorfizmu medzi rekurzívnym typom a jeho rozbalením robí typový systém komplikovanejším, tento izomorfizmus je možné často úplne skryť za iné jazykové konštrukcie v implementácii. Z tohto dôvodu sa budeme ďalej podrobnejšie venovať tomuto prístupu.
Poznámka
Ekvirekurzívny prístup využívajú jazyky ako je Java a Modula 3, pričom izorekurzívný prístup je využívaný napríklad v jazykoch C, rodina ML, medzi ktoré patrí aj OCaml.
Izorekurzívne typy
Pri tomto prístupe je výraz
$$
\mu X.T
$$
rekurzívny typ, pričom jeho rozbalený typ
$$[X \mapsto \mu X.T]\ T$$
je rozdielny, avšak izomorfný typ.
Formálne je rozbalenie rekurzívneho typu $\mu X.T$ substitúcia všetkých voľných premenných $X$ v type $T$ celým rekurzívnym typom $\mu X.T$: $$\mu X.T \to [X \mapsto \mu X.T]\ T $$ Napríklad rekurzívny typ prirodzených čísel $Nat$: $$\mu X. [zero:Unit, succ: X],$$ sa rozbalí na: $$[zero:Unit, succ: (\mu X. [zero:Unit, succ: X])].$$
V typovom systéme s izorekurzívnymi typmi zavedieme do jazyka pre každý typ $\mu X.T$ dvojicu funkcií, ktoré umožnia obojsmernú konverziu medzi rekurzívnym typom a jeho rozbalením: $$ \begin{array}{lcl} \mathbf{fold}_{\ \mu X.T} & : & [X \mapsto \mu X.T]\ T \to \mu X.T \\ \mathbf{unfold}_{\ \mu X.T} & : & \mu X.T \to [X \mapsto \mu X.T]\ T\\ \end{array} $$ Táto dvojica funkcií definuje izomorfizmus zobrazením hodnôt tam a späť medzi dvoma typmi:
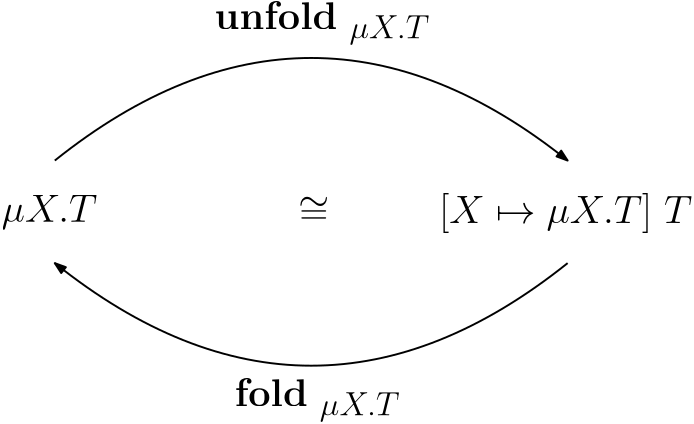
Poznámka
Dolný index pri funkciách fold a unfold môže byť vynechaný, ak je jasné o aký rekurzívny typ sa jedná.
Rozšírime syntax nášho jazyka nasledovne: $$ \begin{array}{lcl} t & ::= & \ldots~|~ \mathbf{fold}_{\ \mu X.T}\ \ t\ |\ \mathbf{unfold}_{\ \mu X.T}\ \ t \\ v & ::= & \ldots~|~ \mathbf{fold}_{\ \mu X.T}\ \ v\\ T & ::= & \ldots~|~ X\ \ |\ \mu X.T \end{array} $$
Poznámka
Syntax pre hodnoty bola rozšírená len o operáciu fold, keďže hodnota rekurzívneho typu $\mu X.T$ môže vzniknúť len zabalením konkrétnej hodnoty.
Typovacie pravidlá:
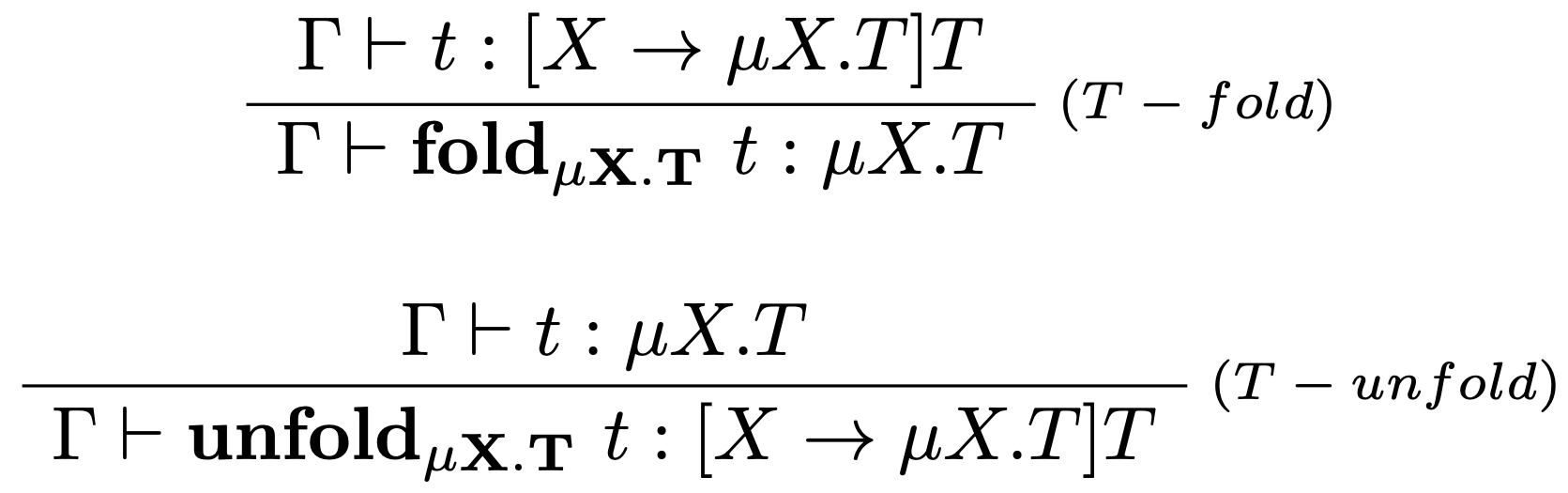
Vyhodnocovacie pravidlá
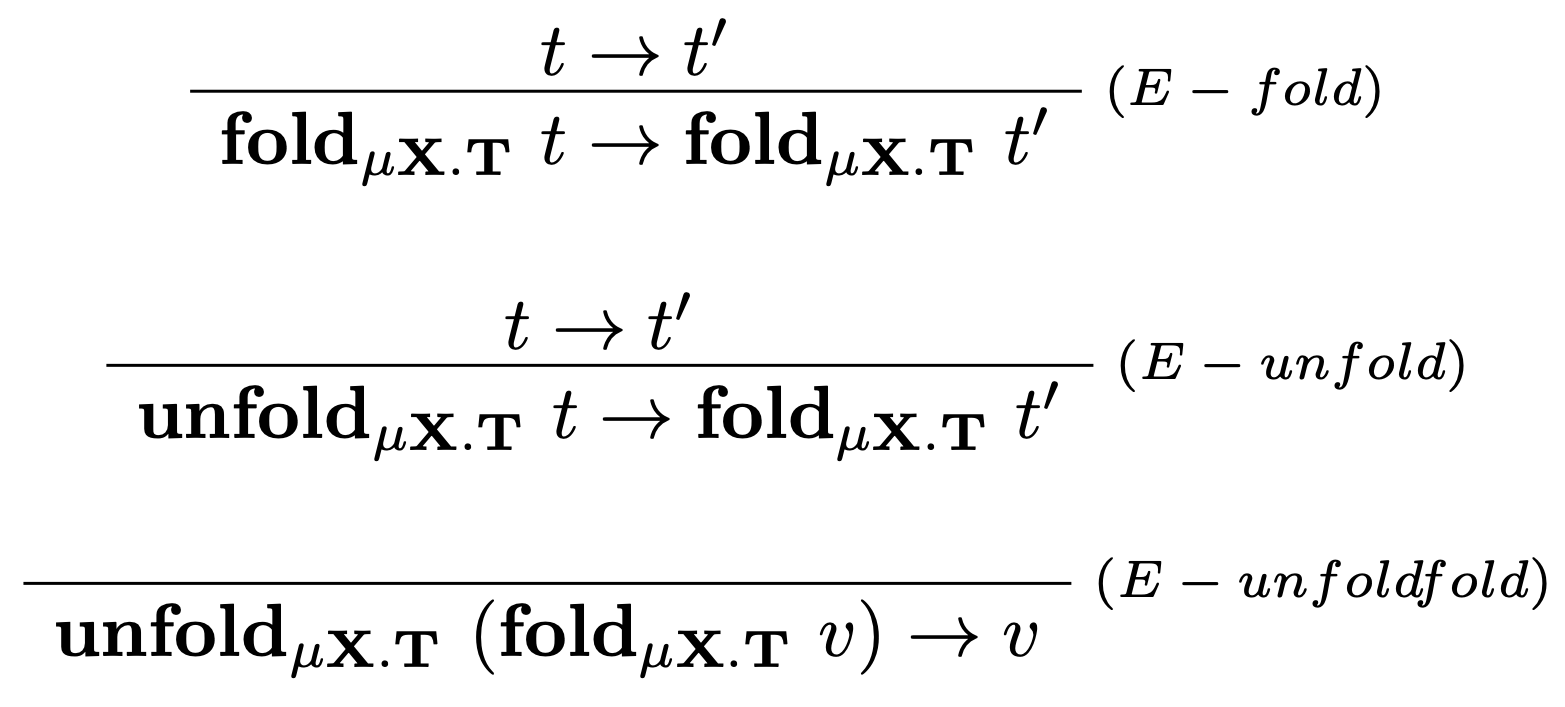
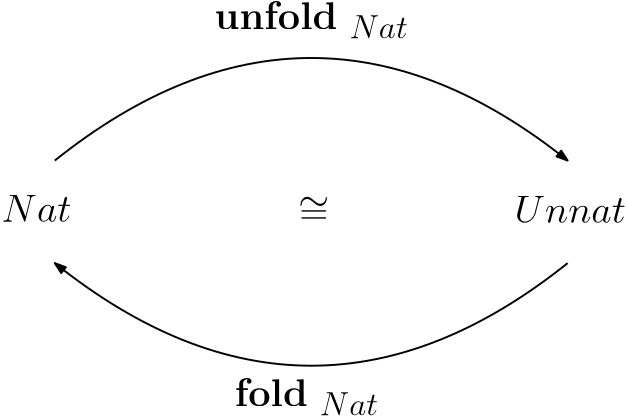
Pokračujme príkladom zavedenia rekurzívneho typu prirodzených čísel $Nat$ izorekurzívnym prístupom:
$$Nat= \mu X. [zero:Unit, succ: X]$$
Je užitočné zaviesť skratku pre jeho rozbalený tvar:
$$Unnat=[zero:Unit, succ: (\underbrace{\mu X. [zero:Unit, succ: X])}_{Nat}]$$
Potom izomorfizmus medzi $Nat$ a $Unnat$ je zobrazený na nasledujúcom obrázku:
Pričom po substitúcii skratiek ich definíciami je možné vidieť zabalenie a rozbalenie rekurzívneho typu $Nat$:
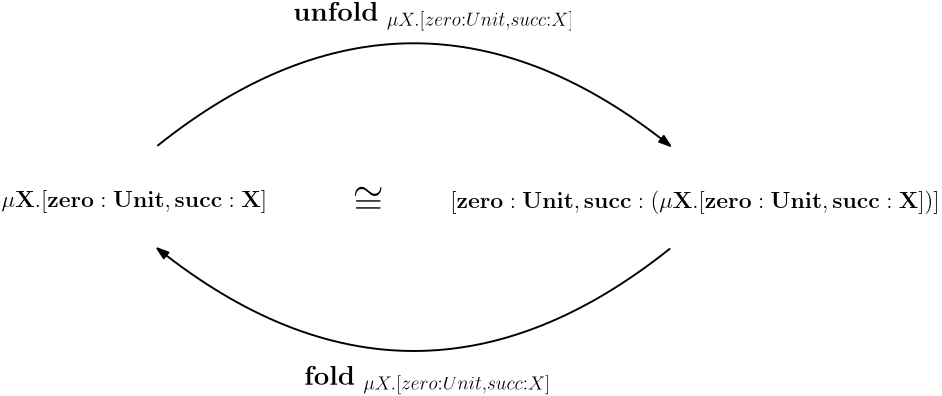
Hodnotu nula a operáciu nasledovníka je možné zaviesť nasledovne: $$ \begin{array}{ccl} 0 &=& \mathbf{fold_{nat}}\ [zero=unit]\ as\ Unnat \\ succ &=& \lambda n:Nat.\mathbf{fold_{nat}}\ [succ=n]\ as\ Unnat\\ \end{array} $$ kde: $$ \begin{array}{ccl} 0 & : & Nat\\ succ & : & Nat \to Nat \end{array} $$ Číslo $n$ takéhoto typu je možné vytvoriť $n$-násobnou aplikáciou operácie nasledovníka na nulu: $$ \begin{array}{lclcl} 1 &=& succ\ 0&=& \mathbf{fold_{nat}}\ [succ=0]\ as\ Unnat\\ 2 &=& succ\ 1&=& \mathbf{fold_{nat}}\ [succ=1]\ as\ Unnat\\ 3 &=& succ\ 2&=& \mathbf{fold_{nat}}\ [succ=2]\ as\ Unnat\\ \vdots \end{array} $$ kde: $$1,2,3,... : Nat.$$ Operácie $pred$ a $iszero$ nad typom $Nat$ je možné definovať nasledovne:
$$ \begin{array}{lcl} pred &=& \lambda x:Nat.\ \text{case}\ \mathbf{unfold_{nat}}\ x\ \text{of} \\ & & \ \ zero=x_1 \Rightarrow 0 \\ & & |\ succ=x_2 \Rightarrow x2\\ \end{array} $$ $$ \begin{array}{lcl} iszero &=& \lambda x:Nat.\ \text{case}\ \mathbf{unfold_{nat}}\ x\ \text{of} \\ & & \ \ zero=x_1 \Rightarrow true\\ & & |\ succ=x_2 \Rightarrow false\\ \end{array} $$ kde: $$ \begin{array}{ccl} iszero & : & Nat \to Nat\\ pred & : & Nat \to Nat \end{array} $$
Rekurzívny typ $Nat$ definovaný ako binárny súčtový typ
Rekurzívny typ $Nat$ je možné definovať aj prostredníctvom binárneho súčtového typu.
$$Nat \approx Unit + Nat, $$
to znamená, že je potrené nájsť riešenie nasledujúcej rovnice: $$X=Unit + X.$$ Využitím rekurzívneho operátora $\mu$ definujeme typ $Nat$ nasledovne: $$Nat = \mu X. Unit + X $$ Definujeme skratku pre jeho rozbalenie: $$ Unnat = Unit + (\underbrace{\mu X. Unit + X}_{Nat})$$
Potom izomorfizmus medzi $Nat$ a $Unnat$ je zobrazený na nasledujúcom obrázku:

Pričom po substitúcii skratiek ich definíciami je možné vidieť zabalenie a rozbalenie rekurzívneho typu $Nat$:
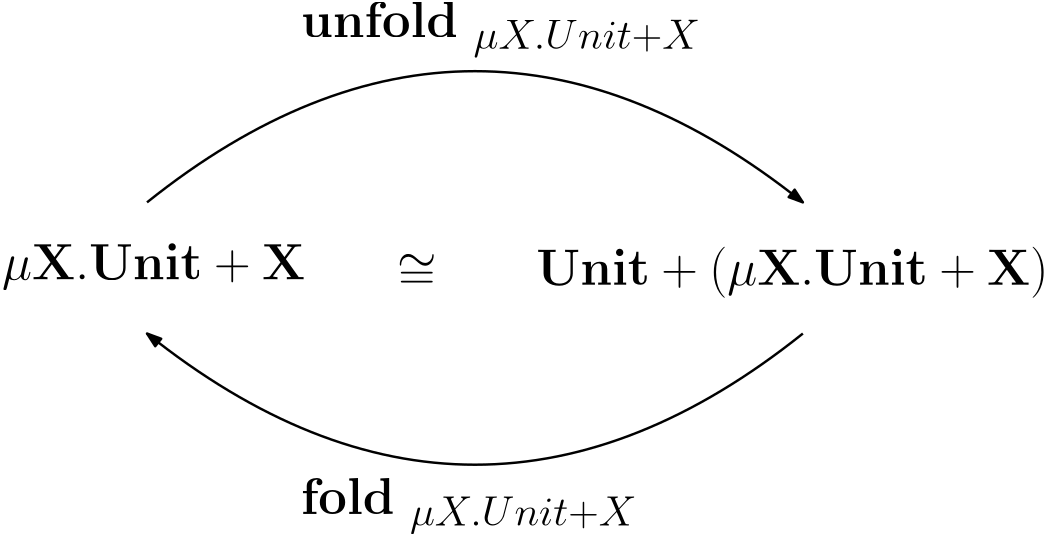
Hodnotu nula a operáciu nasledovníka je možné zadefinovať ako: $$ \begin{array}{ccl} 0 &=& \mathbf{fold}\ inl\ unit\ \text{as}\ Unnat\\ succ &=& \lambda n:Nat. \mathbf{fold}\ inr\ n\ \text{as}\ Unnat\\ \end{array} $$
Poznámka
V predchádzajúcej definícii pri operáciách fold, unfold bol zámerne vynechaný index s typom, keďže je jednoznačné o aký typ sa jedná.
Ďalšie hodnoty typu $Nat$ je možné definovať prostredníctvom operácie nasledovníka a nuly: $$ \begin{array}{lclcl} 1 &=& succ\ 0&=& \mathbf{fold_{nat}}\ inr\ 0\ as\ Unnat\\ 2 &=& succ\ 1&=& \mathbf{fold_{nat}}\ inr\ 1\ as\ Unnat\\ 3 &=& succ\ 2&=& \mathbf{fold_{nat}}\ inr\ 2\ as\ Unnat\\ \vdots \end{array} $$
Operácie pred, iszero je možné zadefinovať nasledovne:
$$ \begin{array}{lcl} pred &=& \lambda x:Nat.\ \text{case}\ \mathbf{unfold_{nat}}\ x\ \text{of} \\ & & \ \ inl\ x_1 \Rightarrow 0 \\ & & |\ inr\ x_2 \Rightarrow x2\\ \end{array} $$
$$ \begin{array}{lcl} iszero &=& \lambda x:Nat.\ \text{case}\ \mathbf{unfold_{nat}}\ x\ \text{of} \\ & & \ \ inl\ x_1 \Rightarrow true\\ & & |\ inr\ x_2 \Rightarrow false\\ \end{array} $$
Príklad
Overte, že hodnota nula je typu $Nat$: $$\vdash 0:Nat$$
Riešenie
Typová kontrola:
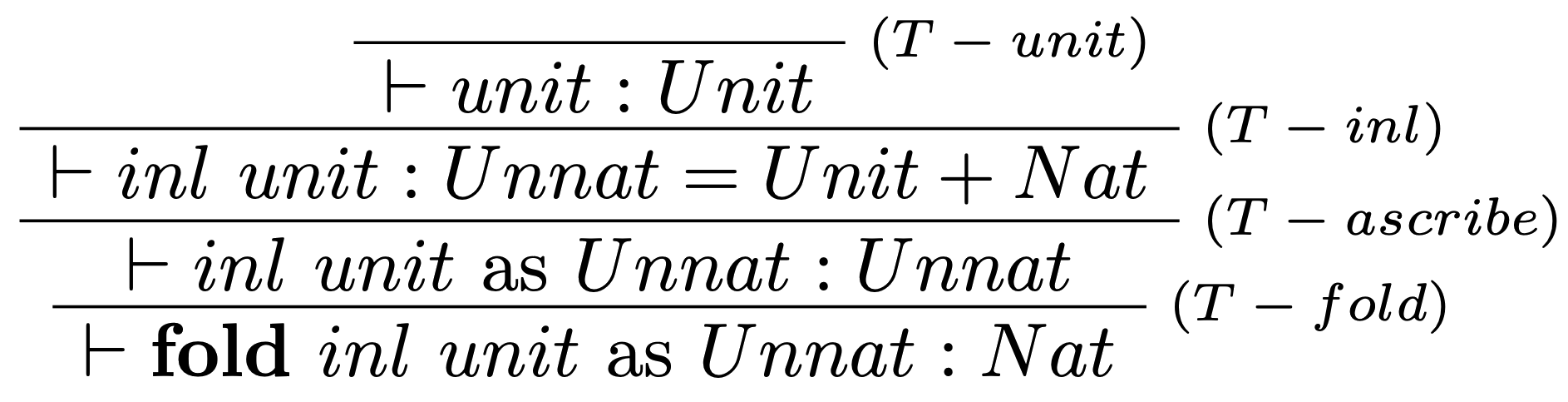
Príklad
Overte, že operácia nasledovníka je typu $Nat\to Nat$: $$\vdash succ:Nat\to Nat$$
Riešenie
Typová kontrola:

Riešenie
Typová kontrola:
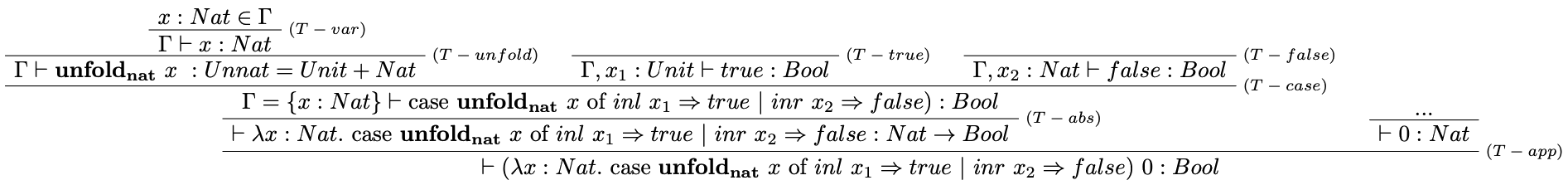
Vyhodnotenie:
$$ \begin{array}{l} iszero\ 0 = \\ (\lambda x:Nat.\ \text{case}\ \mathbf{unfold_{nat}}\ x\ \text{of}\ inl\ x_1 \Rightarrow true \ |\ inr\ x_2 \Rightarrow false)\ 0 \\ \text{case}\ \mathbf{unfold_{nat}}\ 0\ \text{of}\ inl\ x_1 \Rightarrow true \ |\ inr\ x_2 \Rightarrow false =\\ \text{case}\ \mathbf{unfold_{nat}}\ (\mathbf{fold}\ inl\ unit\ \text{as}\ Unnat)\ \text{of}\ inl\ x_1 \Rightarrow true \ |\ inr\ x_2 \Rightarrow false \to\\ \text{case}\ \mathbf{unfold_{nat}}\ (\mathbf{fold}\ inl\ unit)\ \text{of}\ inl\ x_1 \Rightarrow true \ |\ inr\ x_2 \Rightarrow false \to\\ \text{case}\ inl\ unit\ \text{of}\ inl\ x_1 \Rightarrow true \ |\ inr\ x_2 \Rightarrow false \to\\ true \end{array} $$
Implementácia izorekrzívnych typov v jazyku OCaml
Ako je možné vidieť, izorekurzívny prístup je z hľadiska notácie o niečo zložitejší, pretože vyžaduje, aby boli programy ozdobené funkciami fold a unfold všade, kde sa používajú rekurzívne typy.
V praxi však tieto anotácie je možné často „skryť” zlúčením s inými anotáciami. Jazyk OCaml využíva jednoduchý syntaktický trik vďaka ktorému nie je nutné explicitne uvádzať fold a unfold.
Napríklad majme typ:
type nat = Zero | Succ of nat
Kód:
Succ 5
sa v prekladači rozvinie na: \begin{flalign} \nonumber & \quad \mathbf{fold_{nat}}\ (inr\ 5) & \end{flalign}
Kód
match t with Zero -> ... | Succ x -> ...
sa v prekladači rozvinie na: \begin{flalign} \nonumber & \quad \text{match}\ \mathbf{unfold_{nat}}\ t\ \text{with}\ Zero\ \to\ ...\ |\ Succ\ x\ \to\ ... & \end{flalign}
Zdroje
- Pierce, Benjamin C. Types and programming languages. MIT press, Cambridge, 2001 (Перевод на русский язык: Бенджамин Пирс. Типы в языках программирования. — Добросвет, 2012. — ISBN 978-5-7913-0082-9)
- Lecture notes, CS ⅘110: Programming Languages and Logics, Cornell University — Department of Computer Science, 2024
- Lecture notes, 15-814: Types and Programming Languages, Carnegie Mellon University — School of Computer Science, 2024