Úvod
V teórii typov rozlišujeme dve základné kategórie kombinácií typov: súčinové typy a súčtové typy.
Zatiaľ čo súčinové typy (ako sme videli na predchádzajúcej prednáške) kombinujú hodnoty naraz (dvojica, n-tica, záznam), súčtové typy umožňujú, aby hodnota patrila k jednému z viacerých typov — teda predstavuje alternatívu medzi možnosťami.
Binárny súčtový typ
Základné pojmy súčtových typov zavedieme na príklade binárneho súčtového typu, ktorý je konštruovaný pomocou typového konštruktora ''$+$'': $$T_1 + T_2.$$
Formálne, nech $T_1$ a $T_2$ sú typy. Súčtový typ $T_1 + T_2$ je typ, ktorého termy sú buď typu $T_1$, alebo typu $T_2$, spolu s informáciou (návestím), ktorého typu je daný term.
Injekcie binárneho súčtového typu
Pre súčtový typ $T_1 + T_2$ zavádzame dve operácie ako konštruovať termy:
- $inl$ – ľavá injekcia - vloženie hodnoty typu $T_1$.
- $inr$ – pravá injekcia - vloženie hodnoty typu $T_2$.
Každý term typu $T_1 + T_2$ je jednoznačne identifikovaný, či patrí do $inl$ alebo $inr$.
Injekcie sú termové konštruktory, pomocou nich z termov typov $T_{1}$ a $T_{2}$ je možné konštruovať term súčtového typu $T_{1}+T_{2}$:
$$ \begin{array} ~ \mathtt{inl}:\ T_1 \to T_{1}+T_{2}\\ \mathtt{inr}:\ T_2 \to T_{1}+T_{2}\\ \end{array} $$
Poznámka
Vo všeobecnosti v súčtových typoch sa návestia nazývajú konštruktory. Keďže ich aplikáciou konštruujeme term daného súčtového typu.
Selektor $\mathtt{case}$
Jedinou operáciou nad termami súčtového typu je selektor: $$ \begin{array}{l} \mathtt{case}\ t\ \mathtt{of} \\ \qquad ~~~ \mathtt{inl}\ x_1 \Rightarrow t_1\\ \qquad ||\ \mathtt{inr}\ x_2 \Rightarrow t_2 \end{array} $$ kde:
- $t$ je term binárneho súčtového typu $T_1 + T_2$,
- $x_1:T_1$ a $x_2:T_2$ sú lokálne premenné, ktoré sa môžu nachádzať voľne v $t_1$ resp. $t_2$.
Pri vyhodnotení:
- Najprv sa term $t$ redukuje na hodnotu.
- Na základe toho, či je hodnota konštruovaná prostredníctvom $inl$ alebo $inr$, zvolí sa príslušná vetva.
- Všetky výskyty lokálnej premennej ($x_1$ alebo $x_2$) sa substituujú vo vetve hodnotou, ktorú viaže daný konštruktor.
Príklad
Nech $\mathtt{Nat}+\mathtt{Bool}$ je súčtový typ. Ak $t_{1}:\mathtt{Nat}$ a $t_{2}:\mathtt{Bool}$ sú termy, potom $$ \mathtt{inl}~ t_{1}: \mathtt{Nat}+ \mathtt{Bool}~~~~~~~\mathtt{inr}~ t_{2}: \mathtt{Nat}+ \mathtt{Bool} $$ sú termy súčtového typu $\mathtt{Nat}+\mathtt{Bool}$.
Súčinové a súčtové typy sú navzájom duálne:

Rozšírenie syntaxe jednoducho typovaného $\lambda$-kalkulu o binárny súčtový typ
Syntax jednoducho typovaného $\lambda$-kalkulu rozšírime o nové tvary termov, hodnôt a typu pre binárny súčtový typ:
$$ \begin{array}{ll} t::= & \ldots~|~\mathtt{inl}~t~|~\mathtt{inr}~t~|~\mathtt{case}~t~\mathtt{of~inl}~x\Rightarrow t ~ ||~\mathtt{inr}~ x\Rightarrow t \\ v::= & \ldots~|~\mathtt{inl}~v~|~\mathtt{inr}~v \\ T::= & \ldots~|~T + T \end{array} $$
Priorita a asociativita typových konštruktorov
Aktuálne máme v jazyku zavedené 3 binárne typové konštruktory. Pre jednoznačnosť je potrebné uviesť ich prioritu (kde 1 znamená najvyššiu prioritu) a asociativitu:
| Typový operátor | Priorita | Asociativita |
|---|---|---|
| $\times$ | 1 | (Ne)asociatívny |
| $+$ | 2 | (Ne)asociatívny |
| $\to$ | 3 | Pravo asociatívny |
Príklad
Do nasledujúcich typov doplníme zátvorky, tak aby sa nezmenil význam daných typov: $$ \begin{array}{lclcl} A \to B \to C &\equiv& A \to (B \to C)\\ A \times B \times C &\equiv& A \times (B \times C) &\equiv& (A \times B) \times C\\ A + B + C &\equiv& A + (B + C) &\equiv& (A + B) + C\\ A \times B + C &\equiv& (A \times B) + C \\ A \times B + C \to D &\equiv& ((A \times B) + C) \to D \\ A \times B \to C + D &\equiv& (A \times B) \to (C + D) \end{array} $$
Sumy a jednoznačnosť typov
Väčšina vlastností relácie typovania, ktoré platia pre jednoducho typovaný $\lambda$-kalkul, platia aj pre súčtové typy, s výnimkou vety o jednoznačnosti typov.
Veta o jednoznačnosti typov hovorí, že v danom typovom kontexte $\Gamma$ má term $t$ najviac jeden typ, čo pre súčtové typy to neplatí.
Majme term $t$ typu $Nat$. Po aplikácii ľubovoľného z termových konštruktorov $\mathtt{inl}$ resp. $\mathtt{inr}$ na term $t$ vznikne nasledujúci problém: $$ \begin{array} \quad \mathtt{inl}\ t:\ Nat\ +\ ? \\ \mathtt{inr}\ t:\ ?\ +\ Nat \end{array} $$
To znamená, že nie je jednoznačné akého typu je $\mathtt{inl}\ t$ resp. $\mathtt{inr}\ t$. Z tohto dôvodu algoritmus pre kontrolu typov nemožno konštruovať len aplikovaním typovacích pravidiel zdola nahor, ako to bolo doteraz.
Metódy kontroly typov pre súčtové typy
Aby bolo vykonať kontrolu typov v prípade súčtových typov, existujú rôzne prístupy. Najčastejšie sú to nasledujúce tri metódy:
- Upravíme algoritmus kontroly typov tak, že bude bude odhadovať, aký je typ $T_2$. Znamená to, že ponecháme $T_2$ ako neurčený typ a neskôr sa pokúšame zistiť, aká by mala byť jeho hodnota. Táto metóda sa používa pri rekonštrukcii typov (odvodení typov).
- Zjemníme jazyk typov tak, aby povoľoval všetky možné hodnoty pre typ $T_2$ a aby bol jednotne reprezentovaný. Táto metóda sa používa aj pri podtypoch;
- Požadujeme od programátora, aby poskytol explicitnú typovú anotáciu, ktorá indikuje, aký typ pre $T_2$ zamýšľa. Táto metóda je najjednoduchšia a je praktická: v úplnom návrhu jazyka sú tieto explicitné anotácie často umiestnené na iných jazykových konštrukciách, čím sa stanú neviditeľnými.
Poznámka
V rámci tohto predmetu budeme vyžadovať pri súčtových typoch explicitné uvádzanie typovej anotácie.
Pre zaručenie jednoznačnej kontroly typov teda rozšírime zápis termov binárneho súčtového typu o explicitnú typovú anotáciu, na ktorú použijeme odvodený tvar pripísanie.
Rozšírenú syntax pre termy a hodnoty modifikujeme nasledovne:
$$ \begin{array}{ll} t::= & \ldots~|~\mathtt{inl}~t~\mathtt{as}~T~|~\mathtt{inr}~t~\mathtt{as}~T \\ \\ v::= & \ldots~|~\mathtt{inl}~v~\mathtt{as}~T~|~\mathtt{inr}~v~\mathtt{as}~T \end{array} $$
Typovacie pravidlá
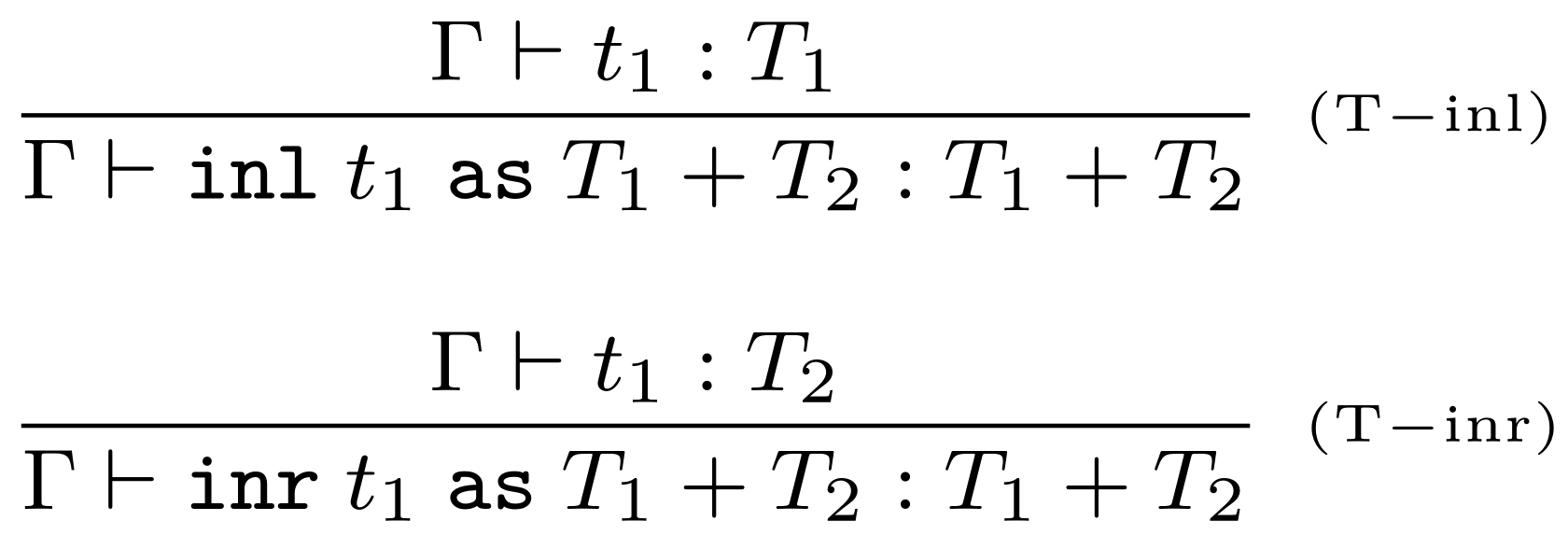
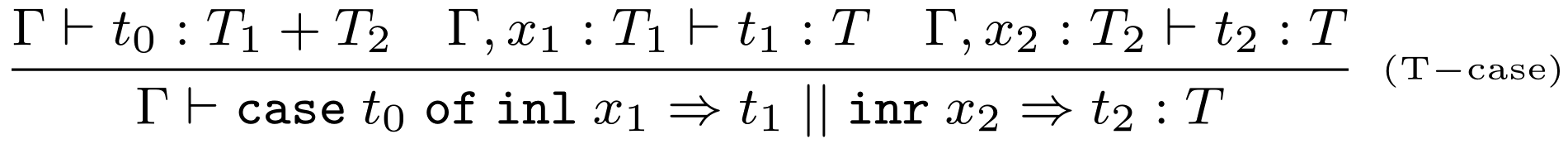
Vyhodnocovacie pravidlá
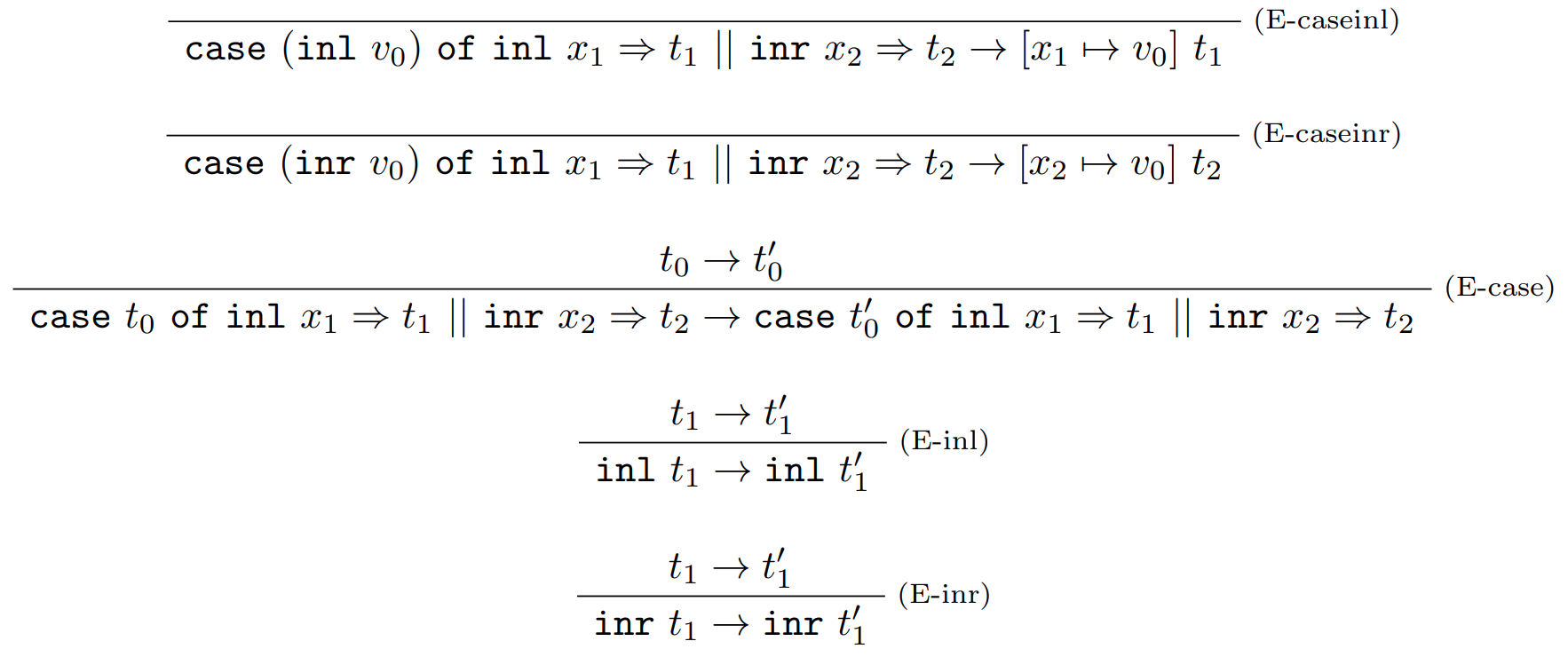
Príklad
Majme funkciu $getnat$ prijíma argument typu $Nat + Bool$, teda hodnotu, ktorá môže byť buď prirodzené číslo $(Nat)$, alebo booleovská hodnota $(Bool)$.
Pomocou selektora $case$ rozlíši, o ktorý variant ide, a vráti príslušnú číselnú hodnotu.
- V prípade, že vstup je $Inl\ n$, funkcia vráti samotné číslo $n$.
- Ak je vstup $Inr\ b$, prekonvertuje logickú hodnotu na číslo ($true \to 1$, $false \to 0$).
Overte typovú korektnosť a vyhodnoťte výraz: $$getnat\ \ (\texttt{Inr}\ true\ \texttt{as}\ Nat + Bool): Nat$$ kde: $$ \begin{array}{ll} getnat: Nat + Bool \to Nat \\ getnat = \lambda x: Nat + Bool . & \texttt{case} \ x \ \texttt{of} \\ & ~~ \ \texttt{Inl} \ n \ \Rightarrow n \\ & ||\ \texttt{Inr} \ b \ \Rightarrow \texttt{if}\ b\ \texttt{then}\ 1\ \texttt{else}\ 0. \end{array} $$
Riešenie
-
Typová kontrola:

Obr. 1: Typová kontrola |- getnat (Inr true as Nat + Bool): Nat -
Vyhodnotenie:
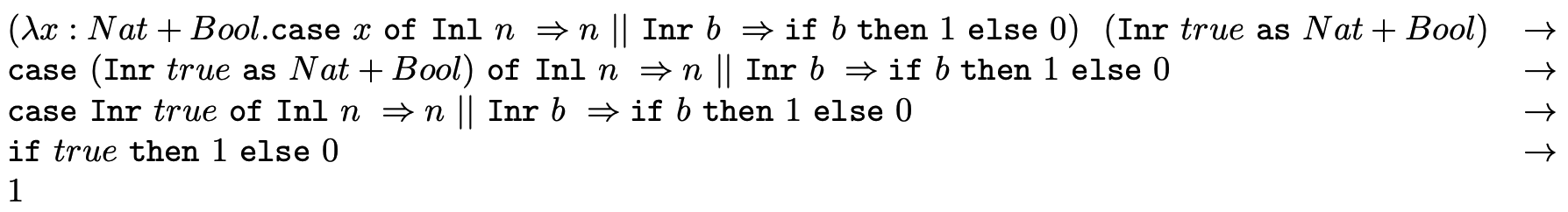
Obr. 2: Vyhodnotenie getnat (Inr true as Nat + Bool)
Riešenie
V jazyku OCaml je možné predchádzajúci príklad zapísať nasledovne: Funkcia getnat používa typ nat_or_bool, ktorý reprezentuje súčtový typ Nat + Bool. Pomocou konštruktorov Inl a Inr a match výrazu rozlišuje, či vstup obsahuje číslo alebo logickú hodnotu, a podľa toho vráti príslušnú číselnú hodnotu.
(* definícia "súčtového" typu Nat + Bool *)
type nat_or_bool = Inl of int | Inr of bool
(* getnat : nat_or_bool -> int *)
let getnat (x : nat_or_bool) : int =
match x with
| Inl n -> n
| Inr b -> if b then 1 else 0
(* príklady použitia *)
utop # getnat (Inr true);;
- : int = 1
utop # getnat (Inr false);;
- : int = 0
utop # getnat (Inl 5);;
- : int = 5
Varianty
Binárne súčty možno zovšeobecniť súčty $n$ typov, podobné ako bol rozšírený súčinový typ dvojica na typ n-tica a neskôr na záznam. Takto zovšeobecnené súčtové typy sa nazývajú varianty s návestiami.
Namiesto typu $ T_1 + T_2 $ je použitá notácia:
$$ [ lab_1: T_1,\ lab_2: T_2 ], $$
pričom $ lab_1,\ lab_2 $ sú návestia položiek variantu. Prostredníctvom návestí sú konštruované typy daného variantového typu.
Namiesto toho, aby vetvy termu case boli označené návesťami inl, inr, je možné použiť ľubovoľne pomenované návestia:
$$ \begin{array}{ll} \mathtt{inl}~t~\mathtt{as}~T_1 + T_2 & \text{používame}~~~[ lab_1 = t]~\mathtt{as}~[ lab_1: T_1,\ lab_2: T_2] \\ \mathtt{inr}~t~\mathtt{as}~T_1 + T_2 & \text{používame}~~~[ lab_2 = t]~\mathtt{as}~[ lab_1: T_1,\ lab_2: T_2] \end{array} $$
Poznámka
Každé návestie musí mať jedinečný názov.
Rozdiel medzi zápisom záznamu a variantu je v zátvorkách:
- pre záznamy používame zátvorky
⟨a⟩; - pre varianty používame zátvorky
[a].
Syntax jednoducho typovaného $\lambda$-kalkulu rozšírená o variantové typy
Formálna definícia rozšírenia jednoducho typovaného $\lambda$-kalkulu o variantové typy, zároveň zovšeobecňuje binárne súčtové typy na súčet $n$ typov.
Syntax je rozšírená o dva nové tvary termov a nový tvar pre variantový typ:
$$ \begin{array}{ll} t::= \ldots~|~~ [ lab = t]~\mathtt{as}~T ~~| ~~\mathtt{case}~t~\mathtt{of}~[ lab_i = x_i] \Rightarrow t_i^{~i\in 1..n} \\ T::= \ldots ~|~ [ lab_i: T_i^{~i\in 1..n}] \end{array} $$
Typovacie pravidlá
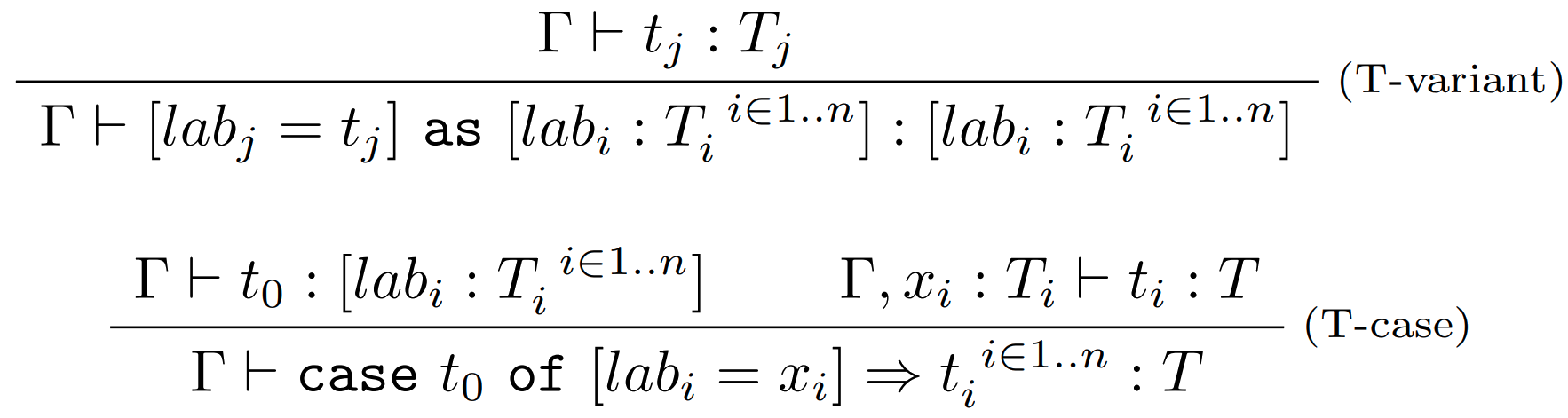
Vyhodnocovacie pravidlá
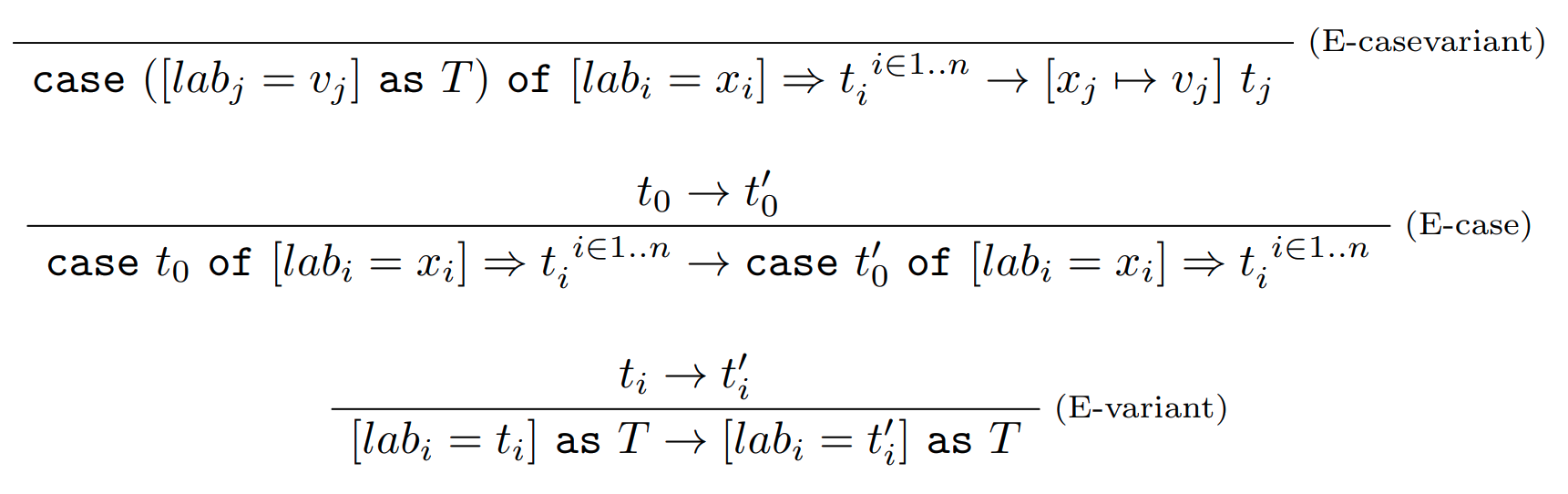
Príklad
Nasledujúci príklad ilustruje použitie variantových (súčtových) typov na reprezentáciu rôznych geometrických tvarov.
Definujeme typ $\mathtt{Tvar}$, ktorý môže nadobúdať tri varianty:
- $\mathtt{bod}$ reprezentujúci bod v 2D priestore,
- $\mathtt{kruh}$ reprezentujúci kruh zadaný stredom a polomerom,
- $\mathtt{obdl}$ reprezentujúci obdĺžnik daný dvoma bodmi — dolným ľavým a horným pravým rohom.
Každý z týchto variantov obsahuje inú kombináciu hodnôt, čím typ $\mathtt{Tvar}$ vyjadruje alternatívu rôznych dátových štruktúr v jednom spoločnom type.
$$ \begin{array}{l} \mathtt{Suradnica} = Float \times Float \\ \mathtt{Tvar} = [\ \mathtt{bod}: \mathtt{Suradnica},\ \mathtt{kruh}: \mathtt{Suradnica} \times Float,\ \mathtt{obdl}:\mathtt{Suradnica} \times \mathtt{Suradnica}\ ] \end{array} $$
Následne definujeme funkcie pre výpočet obsahu a stredu daného geometrického útvaru, ktoré s týmto variantovým typom pracujú prostredníctvom selektora (case), ktorý rozlišuje, o aký variant ide.
Funkcia pre výpočet obsahu:
$$ \begin{array}{l} abs: Float \to Float \\ abs = \lambda x:Float.\ if\ x < 0\ then\ 0-x\ else\ x \\ \mathtt{obsah}:\mathtt{Tvar} \to Float \\ \mathtt{obsah}:\lambda x: \mathtt{Tvar}. \mathtt{case}\ x\ \mathtt{of} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad ~~~\mathtt{bod}\ b \Rightarrow 0,0 \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad ||~\mathtt{kruh}\ k \Rightarrow 3.14 * k.2 * k.2 \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad ||~\mathtt{obdl}\ o \Rightarrow abs( o.1.1 - o.2.1 ) * abs(o.1.2 - o.2.2) \end{array} $$ Funkcia $\mathtt{obsah}$ vracia obsah geometrického tvaru podľa toho, o ktorý variant ide:
- Bod má nulovú plochu.
- Kruh má obsah $\pi r^2$.
- Obdĺžnik má obsah vypočítaný ako súčin šírky a výšky.
Funkcia pre výpočet stedu:
$$ \begin{array}{l} \mathtt{stred}:\mathtt{Tvar} \to \mathtt{Suradnica} \\ \mathtt{stred}:\lambda x: \mathtt{Tvar}. \mathtt{case}\ x\ \mathtt{of} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad ~~~\mathtt{bod}\ b \Rightarrow b \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad ||~\mathtt{kruh}\ k \Rightarrow k.1 \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad ||~\mathtt{obdl}\ o \Rightarrow \langle\ (o.1.1 + o.2.1)/2 , (o.1.2 + o.2.2)/2 \ \rangle \end{array} $$
Funkcia $\mathtt{stred}$ vracia stred tvaru:
- Pre bod je stred samotný bod.
- Pre kruh je to jeho stredový bod.
- Pre obdĺžnik ide o bod ležiaci v jeho geometrickom strede.
Vďaka použitiu variantového typu $\mathtt{Tvar}$ je možné jednoducho reprezentovať viacero rôznych typov geometrických objektov v jednom type.
Predchádzajúci príklad v jazyku OCaml.
(* Definícia typov *)
type suradnica = float * float
type tvar =
| Bod of suradnica
| Kruh of suradnica * float (* stred a polomer *)
| Obdl of suradnica * suradnica (* dolný ľavý a horný roh *)
(* výpočet obsahu tvaru *)
let obsah = function
| Bod _ -> 0.0
| Kruh (_, r) -> Float.pi *. (r ** 2.0)
| Obdl ((x1, y1), (x2, y2)) ->
let w = x2 -. x1 in
let h = y2 -. y1 in
w *. h
(* výpočet stredu tvaru *)
let stred = function
| Bod p -> p
| Kruh (p, _) -> p
| Obdl ((x1, y1), (x2, y2)) -> ((x2 +. x1) /. 2.0, (y2 +. y1) /. 2.0)
(* príklady použitia *)
utop # obsah (Kruh ((0.0, 0.0), 2.0));;
- : float = 12.5663706144
utop # obsah (Obdl ((0.0, 0.0), (3.0, 4.0)));;
- : float = 12.0
utop # stred (Obdl ((0.0, 0.0), (3.0, 4.0)));;
- : suradnica = (1.5, 2.)
Tento príklad demonštruje silu variantových typov pri modelovaní reálneho sveta – umožňujú zoskupiť rôzne formy dát (body, kruhy, obdĺžniky) do jednotnej štruktúry a pomocou selektorov nad nimi bezpečne vykonávať rôzne operácie.
Špeciálne variantové typy
Varianty môžeme využiť aj na definovanie niekoľkých špeciálnych, no veľmi užitočných typov.
Medzi ne patria:
- Voliteľné hodnoty — reprezentujú možnosť, že hodnota môže alebo nemusí existovať
(napr.Maybe,Optionv programovacích jazykoch). - Enumeračné typy — umožňujú vymenovať pevne danú množinu možností
(napr.Color = [ red, green, blue ]). - Jednopoložkové variantové typy — používajú sa na označenie špecifického prípadu alebo obalu hodnoty.
Poznámka
Je však dôležité uvedomiť si, že všetky tieto špeciálne typy sú založené na variante,
teda ide o súčtové typy, ktoré patria medzi jednoduché typy.
Enumeračné typy
Enumeračné typy sú variantové typy, kde každá položka má:
- návestie
lab, a - typ
Unit.
Príklad
Typ reprezentujúci dni v týždni je možné definovať ako enumeračný typ:
$$ \begin{array}{ll} \mathtt{Week} = & [\, monday: \mathtt{Unit},\; tuesday: \mathtt{Unit},\; wednesday: \mathtt{Unit},\; thursday: \mathtt{Unit},\; \\ & ~ friday: \mathtt{Unit},\; saturday: \mathtt{Unit},\; sunday: \mathtt{Unit} \,] \end{array} $$
Prvky tohto typu sú termy tvaru:
$$ [ monday = \mathtt{unit}]~\mathtt{as~Week} $$
Keďže typ $\mathtt{Unit}$ má jedinú hodnotu unit, typ Week má presne 7 hodnôt, zodpovedajúcich dňom v týždni.
Poznámka
Hodnota je vždy unit – podstatné je návestie, nie samotná hodnota.
K termom enumeračného typu Week je možné pristupovať prostredníctvom selektora case.
Majme funkciu, ktorá pre argument $ w : \mathtt{Week} $ vráti nasledujúci pracovný deň v týždni:
$$ \begin{aligned} nextWorkDay &= \lambda w: \mathtt{Week}. \\ &\quad \mathtt{case}~w~\mathtt{of} \\ &\quad\quad ~~~[monday = x] \Rightarrow [tuesday = \mathtt{unit}]~\mathtt{as~Week} \\ &\quad\quad ||~[tuesday = x] \Rightarrow [wednesday = \mathtt{unit}]~\mathtt{as~Week} \\ &\quad\quad ||~[wednesday = x] \Rightarrow [thursday = \mathtt{unit}]~\mathtt{as~Week} \\ &\quad\quad ||~[thursday = x] \Rightarrow [friday = \mathtt{unit}]~\mathtt{as~Week} \\ &\quad\quad ||~[friday = x] \Rightarrow [monday = \mathtt{unit}]~\mathtt{as~Week} \\ &\quad\quad ||~[saturday = x] \Rightarrow [monday = \mathtt{unit}]~\mathtt{as~Week} \\ &\quad\quad ||~[sunday = x] \Rightarrow [monday = \mathtt{unit}]~\mathtt{as~Week} \end{aligned} $$
Príklad použitia:
$$ nextWorkDay~ ([saturday = unit]~\mathtt{as~Week}) \rightarrow^{\star} [monday = \mathtt{unit}]~\mathtt{as~Week} $$
Predchádzajúci príklad v jazyku OCaml:
(* Definícia typu Week *)
type week =
| Monday
| Tuesday
| Wednesday
| Thursday
| Friday
| Saturday
| Sunday
(* Funkcia, ktorá vracia nasledujúci pracovný deň *)
let next_work_day w =
match w with
| Monday -> Tuesday
| Tuesday -> Wednesday
| Wednesday -> Thursday
| Thursday -> Friday
| Friday -> Monday
| Saturday -> Monday
| Sunday -> Monday
(* Príklad použitia *)
utop # next_work_day Saturday;;
- : week = Monday
Variantové typy s jednou položkou
Sú variantové typy, ktoré majú práve jedno návestie $lab$ a sú tvaru:
$$ V = [ lab: T ] $$
Prvky typu $V$ sú zapúzdrené a pomenované prvky typu $T$, každý prvok typu $V$ má tvar:
$$ [lab = t]~\mathtt{as}~V, \quad \text{pre } t:T $$
Na prvý pohľad nie je jasné, na čo by takýto typ mohol byť užitočný.
Často sa používa, aby sa zabránilo priamemu používaniu operácií typu $T$ na hodnoty typu $V$. Operácie typu $T$ nemôžu byť aplikované na prvky typu $V$ bez predchádzajúceho rozbalenia z variantu pomocou selektora case.
Teda hodnoty typu $V$ nemôžeme náhodne zameniť za hodnoty typu $T$.
Príklad
Majme program pre finančné výpočty a potrebujeme funkcie pre konverziu medzi menami dolár a euro.
Obidve meny budú typu $\mathtt{Real}$. Definujeme funkcie:
$$ \begin{aligned} & dollartoeuro = \lambda d:\mathtt{Real}.~times~d~0.8, \\ & dollartoeuro : \mathtt{Real} \rightarrow \mathtt{Real} \\[2mm] & eurotodollar = \lambda e:\mathtt{Real}.~times~e~1.25, \\ & eurotodollar : \mathtt{Real} \rightarrow \mathtt{Real} \end{aligned} $$
pričom
$$ times: \mathtt{Real}\rightarrow \mathtt{Real} \rightarrow \mathtt{Real} $$
je funkcia násobenia hodnôt typu $\mathtt{Real}$.
Majme teraz sumu v dolároch:
$$ mybalance = 39.50 $$
Konvertujeme ju do euro a späť:
$$ eurotodollar (dollartoeuro ~mybalance) \rightarrow^{\star} 39.50 $$
Nebráni nám ale konvertovať sumu na euro dvakrát:
$$ dollartoeuro (dollartoeuro~~ mybalance) \rightarrow^{\star} 25.28 $$
čo dáva nezmyselný výsledok.
Ak definujeme euro- a dolárové sumy ako rozdielne variantové typy:
$$ \begin{aligned} \mathtt{DollarAmount} &= [ dollars: \mathtt{Real} ] \\ \mathtt{EuroAmount} &= [ euros: \mathtt{Real} ] \end{aligned} $$
môžeme definovať bezpečné konverzie:
$$ \begin{aligned} dollartoeuro &= \lambda d: \mathtt{DollarAmount}.~ \mathtt{case}~d~\mathtt{of}~[ dollars = x ] \Rightarrow [ euros = times~x~0.8 ]~\mathtt{as~EuroAmount} \\ eurotodollar &= \lambda e: \mathtt{EuroAmount}.~ \mathtt{case}~e~\mathtt{of}~[ euros = x ] \Rightarrow [ dollars = times~x~1.25 ]~\mathtt{as~DollarAmount} \end{aligned} $$
ktoré majú typy:
$$ \begin{aligned} dollartoeuro &: \mathtt{DollarAmount} \rightarrow \mathtt{EuroAmount} \\ eurotodollar &: \mathtt{EuroAmount} \rightarrow \mathtt{DollarAmount} \end{aligned} $$
Teraz typová kontrola sleduje meny vo výpočtoch:
$$ \begin{array}{l} mybalance = [ dollars = 39.50 ]~\mathtt{as~DollarAmount} \\ eurotodollar(dollartoeuro~~mybalance) \rightarrow^{\star} 39.50 \end{array} $$
Ak napíšeme nezmyselnú dvojnásobnú konverziu, kontrola typov oznámi chybu:
$$ dollartoeuro(dollartoeuro~~mybalance) \rightarrow^{\star} \blacktriangleright \mathrm{Typing error} $$
Predchádzajúci príklad v jazyku OCaml:
(* Jednopoložkové varianty pre bezpečné meny *)
(* Definícia typov pre meny *)
type dollar_amount = Dollar of float
type euro_amount = Euro of float
(* Funkcia násobenia *)
let times x y = x *. y
(* Bezpečné konverzie medzi menami *)
let dollartoeuro (Dollar d) =
Euro (times d 0.8)
let eurotodollar (Euro e) =
Dollar (times e 1.25)
let mybalance = Dollar 39.50
(* Príklad použitia *)
utop # dollartoeuro mybalance;;
- : euro_amount = Euro 31.6
utop # eurotodollar (dollartoeuro mybalance);;
- : dollar_amount = Dollar 39.5
utop # dollartoeuro (dollartoeuro mybalance);;
Error: This expression has type euro_amount
but an expression was expected of type dollar_amount
Voliteľné hodnoty
Variantové typy umožňujú reprezentovať voliteľné hodnoty (optional values),
teda hodnoty, ktoré nemusia byť vždy prítomné.
Formálne je možné voliteľnú hodnotu pre ľubovoľný typ $T$ definovať ako variantový typ:
$$ \mathtt{Option}\;T = [\, none: \mathtt{Unit},\; some: T \,] $$
Tento typ vyjadruje, že hodnota typu $ \mathtt{Optional}\;T $ môže byť jednou z dvoch možností:
- $ [\, none = \mathtt{unit} \,] $ — prázdna hodnota, označujúca neprítomnosť hodnoty typu $ T $;
- $ [\, some = t \,] $ — hodnota typu $ T $, ktorá je prítomná.
Takto definovaný typ je analógiou známych konštrukcií v rôznych programovacích jazykoch:
| Jazyk | Typ / konštrukcia | Príklad použitia |
|---|---|---|
| OCaml | option |
Some 5 alebo None |
| Haskell | Maybe a |
Just 5 alebo Nothing |
| Rust | Option<T> |
Some(5) alebo None |
| Java | Optional<T> |
Optional.of(5) alebo Optional.empty() |
Príklad
Pre konkrétny typ, napríklad $ T = \mathtt{Nat} $, je typ volitelnej hodnoty definovaný: $$ \mathtt{OptionNat} = [\, none: \mathtt{Unit},\; some: \mathtt{Nat} \,] $$ V jazyku OCaml je možné tento typ zapísať ekvivalentne nasledovne:
type nat = Zero | S of nat
type natoption = None | Some of nat
V jednoducho typovanom $\lambda$-kalkule typ $Option$ umožňuje pracovať s čiastočnými funkciami alebo neúplnými dátami bez potreby špeciálnych chýb či výnimiek.
- Je možné jednoducho vyjadriť, že funkcia nemusí vždy vrátiť výsledok (napr.
find,lookup). - Typová kontrola musí ošetriť aj prípad, keď výsledok neexistuje.
- Jazyk zostáva čisto funkcionálny – žiadne vedľajšie účinky ani výnimky.
Príklad
Majem typ tabuľky ako funkciu z prirodzených čísel do voliteľných prirodzených čísel:
$$ \mathtt{Table} = \mathtt{Nat} \to \mathtt{OptionNat} $$
Teda ide o typ konečných funkcií z prirodzených čísel do prirodzených čísel rozšírených o hodnotu none.
- Definičný obor: množina indexov (napr. čísla buniek).
- Obor hodnôt: typ $\mathtt{OptionNat}$.
Hodnota v bunke môže byť:
-
prítomná:
$$ [some = n]~\mathtt{as~Table} \quad \text{pre určité } n $$ -
alebo prázdna:
$$ [none = \mathtt{unit}] $$
Ak by bol typ tabuľky definovaný ako
$$ \mathtt{Nat} \rightharpoonup \mathtt{Nat}, $$
funkcia by bola čiastočne definovaná.
Použitím typu $\mathtt{OptionNat}$ bol typ tabuľky rozšírený na úplne definovanú funkciu.
Majme funkciu lookup, ktorá vyhľadá hodnotu v tabuľke podľa daného indexu:
$$ \mathtt{lookup} : \mathtt{Nat} \to \mathtt{Table} \to \mathtt{OptionNat}. $$
Ak hodnota v tabuľke chýba, funkcia vráti none, inak some n.
Zdroje
- Pierce, Benjamin C. Types and programming languages. MIT press, Cambridge, 2001 (Перевод на русский язык: Бенджамин Пирс. Типы в языках программирования. — Добросвет, 2012. — ISBN 978-5-7913-0082-9)
- Lecture notes, CS ⅘110: Programming Languages and Logics, Cornell University — Department of Computer Science, 2024
- Lecture notes, 15-814: Types and Programming Languages, Carnegie Mellon University — School of Computer Science, 2024