01. Komplexné čísla
Riešené úlohy:
    Príklad: Vypočítajme \(i^{13},\ i^{22},\ i^{115},\ i^{-9},\ i^{-18}.\)
    Príklad: Nájdime reálne čísla \(x,y \def\a{&}\) tak, aby platilo \[(2-4i)(-2x+5iy)=8+34i.\]
    Príklad: Dané sú komplexné čísla \(z_1=3-4i,\ z_2=-2+3i\). Vypočítajme \(z_1+z_2,\ z_1.z_2,\) \(\frac{z_1}{z_2}\).
    Príklad: Dané sú komplexné čísla \(u=2-2i,\ v=-3+2i\). Vypočítajme \(u.\overline{v},\quad\frac{\overline{u}}{\overline{v}},\ \frac{u.\overline{v}}{v}\).
    Príklad: Komplexné číslo \(z=-1+i\) preveďte do goniometrického tvaru.
    Príklad: Vypočítajme \({\rm a)}\ (-1+i)^7,\qquad (-1+\sqrt{3}i)^{37}\).
    Príklad: Dané sú komplexné čísla \(z_1=\sqrt{2}-i\sqrt{2},\ z_2=-3\sqrt{3}+3i\). Vypočítajme v goniometrickom tvare a výsledok preveďme späť do algebraického tvatu, ak sa jedná o známe hodnoty goniometrických funkcií. \[{\rm a)}\ z_3=z_1\cdot z_2, \quad {\rm b)}\ z_4=\frac{z_1}{z_2}, \quad {\rm c)}\ z_5=z_1^4, \quad {\rm d)}\ z_6=\frac{z_2^4}{z_1^2}.\]
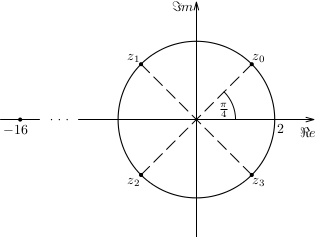
    Príklad: Vypočítajme všetky hodnoty \(\sqrt[4]{-16}\).
    Príklad: Vypočítajme všetky hodnoty \(\sqrt[3]{-i}.\)
    Príklad: V množine komplexných čísel riešme rovnicu \[z^2-(2+3i)z-1+3i=0.\]
Úlohy:
    Úloha: Dané komplexné čísla zapíšme v goniometrickom tvare a zobrazme ich v Gaussovej rovine:
    \(\quad {\rm a)} 3{\it i};\quad {\rm b)} -1-{\it i}; \quad {\rm c)} -4;\quad {\rm d)} -1+\sqrt 3{\it i};\quad {\rm e)} 3;\quad {\rm f)} \sqrt{12}-2{\it i}\).
    Úloha: Nájdite reálne čísla \(x,y\) tak, aby platilo: \[\begin{array}{ll} a)\a(3-2i)x+(5-7i)y=1-3i\\ b)\a(1-i)x+(4+2i)y=1+3i\\ c)\a(1+3i)(2x+iy)=1+i\\ d)\a\frac{x+iy}{1-i}=3+2i\\ e)\a(2+ix)(y+2i)=16-11i. \end{array} \]
    Úloha: Vypočítajte v algebraickom tvare: \[ \begin{array}{llcll} a)\a(2+4i)+(1+2i),\a\phantom{duchduchduch}\a b)\a(-2-i)-(4-6i),\\ c)\a -3(-5+4i)+5(6-3i),\a\a d)\a (3+2i)(2+i),\\ e)\a (2+3i)(4+5i),\a\a f)\a(2-i)(2+i)+(3-i)(4+2i),\\ g)\a \frac{2+i}{3-i},\a\a h)\a \left(\frac{1+2i}{3-i}\right)^2,\\ i)\a \frac{1+i}{1-i}-\frac{1+i}{1+i},\a\a j)\a \frac{(1-i)^3}{(2+i)(1+2i)}. \end{array} \]
    Úloha: Zjednodušte a vypočítajte: \[ \begin{array}{ll} a)\a i^{16};i^{29};i^{133};i^{-6};i^{-11}\\ b)\a 3-8i+3i^2+3i^3-6i^4\\ c)\a -5+4i^2-9i^6+7i^5. \end{array} \]
    Úloha: Vypočítajte komplexné číslo \(z=\frac{u.\overline{u}}{v}\), ak \[ \begin{array}{llcll} a)\a u=\sqrt{3}+i,\ v=1-i,\a\phantom{duchduch}\a b)\a u=-\sqrt{2}+i,\ v=\sqrt{2}-i,\\ c)\a u=2-3i,\ v=-1+2i,\a\a d)\a u=5+3i,\ v=-4-i. \end{array} \]
    Úloha: Napíšte v goniometrickom tvare komplexné čísla: \[ \begin{array}{llcll} a)\a 3,\a \phantom{duchduchduch} \a b)\a-2+2i\sqrt{3}\\ c)\a 2i,\a\a d)\a 1+i,\\ e)\a\sqrt{3}-i,\a\a f)\a 1-i\sqrt{3},\\ g)\a 1-\sqrt{3},\a\a h)\a 3-3i,\\ i)\a -\sqrt{2}-i\sqrt{2},\a\a j)\a -3i. \end{array} \]
    Úloha: V goniometrickom tvare vypočítajte súčin \(u.v\) a podiel \(\frac{u}{v}\), ak
    \( a) u=\sqrt{2}(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}),\ v=\sqrt{8}(\cos\frac{5}{6}\pi +i\sin\frac{5}{6}\pi)\)
    \( b) u=-1+i,\ v=3(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}),\)
    \( c) u=2(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi), v=\sqrt{2}(\cos\frac{1}{6}\pi+i\sin\frac{1}{6}\pi),\)
    \( d) u=\sqrt{3}-i,\ v=2+2i.\)
    Úloha: Pomocou Moivreovej vety vypočítajte a zapíšte v algebraickom tvare: \[ \begin{array}{llcll} a)\a(-1-i)^6,\a\phantom{duchduch}\a b)\a (\sqrt{3}-i)^{8},\\ c)\a\left( \frac{1-i\sqrt{3}}{1+i}\right)^{24},\a\a d)\a \left(\frac{1+i}{-\sqrt{3}+i}\right)^3. \end{array} \]
    Úloha: Dané sú komplexné čísla \(z_1=-\sqrt{3}+i,\ z_2=\sqrt{2}-\sqrt{2}i\). Vypočítajte:\[ \begin{array}{llcllcllcll} a)\a z_1^3.z_2^5,\a\phantom{duchduch}\a b)\a z_1^5.z_2^4,\a\phantom{duchduch}\a c)\a \frac{z_1^6}{z_2^3},\a\phantom{duchduch}\a d)\a\frac{z_2^6}{z_1^2}. \end{array} \]
    Úloha: Riešte binomické rovnice: \[ \begin{array}{llcllcllcll} a)\a z^2=-1,\a\phantom{duch}\a b)\a z^3=i,\a\phantom{duch}\a c)\a z^4=-16,\a\phantom{duch}\a d)\a z^5=32,\\ e)\a z^6=-729,\a\phantom{duch}\a f)\a z^4=-8+8\sqrt{3}i,\a\phantom{duch}\a g)\a z^3=-8i,\a\phantom{duch}\a h)\a z^8=256. \end{array} \]
    Úloha: V množine komplexných čísel vyriešte rovnicu:
    \( a)\ z^2-4z+8=0;\\ b)\ z^2-(2+3i)z-1+3i=0;\\ c))\ x^4+8x^2+16=0;\\ d) \ (x^4+16=0;\\ e) \ z^3+z^2+z+1=0;\\ f) \ z^6-4z^3+8=0;\\ g) \ \left(\dfrac{z-1}{z+1}\right)^2=2i.\)
02. Matice a determinanty
Riešené úlohy:
    Príklad: \(\def\a{&}\)\(\def\hod{{\rm h}}\) Utvorme lineárnu kombináciu vektorov \(\alpha \,\overline{x}_1+ \beta \, \overline{x}_2+ \gamma \, \overline{x}_3\), ak \[\overline{x}_1=(1,2,3),\ \overline{x}_2=(2,-1,1),\ \overline{x}_3=(1,7,9)\] pre \(\alpha =2,\ \beta =-3\) a \(\gamma =1\).
    Príklad: Zistime, či sú vektory \(\overline{x}_1\), \(\overline{x}_2\) a \(\overline{x}_3\) lineárne závislé alebo nezávislé, ak
    a) \( \overline{x}_1=(1,2,3),\ \overline{x}_2=(2,-1,1),\ \overline{x}_3=(1,7,9).\)
    b) \( \overline{x}_1=(1,2,3),\ \overline{x}_2=(2,-1,1),\ \overline{x}_3=(1,7,8).\)
    Príklad: Pre matice \[ A=\left[\begin{array}{rrr} 2\a0\a-1\\3\a2\a0 \end{array}\right] ,\qquad B=\left[\begin{array}{rrr} 5\a 2\a 1\\1\a 0\a -1\\ 0\a 2\a 3\\ \end{array}\right] ,\qquad C=\left[\begin{array}{rrr} 0\a2\a1\\-1\a0\a4 \end{array}\right] \] vypočítajme \[ \begin{array}{lclcl} a)\ 2A-B,\a\phantom{duchduch}\a b)\ 3A+2C,\a\phantom{duchduch}\a c)\ A\cdot B,\\ d)\ B\cdot A,\a\a e)\ B^2,\a\a f)\ A^\top. \end{array} \]
    Príklad: Určme hodnosť matice \[ A=\left[\begin{array}{rrrr} 2\a1\a3\a-1\\3\a-1\a2\a0\\1\a3\a4\a-2\\4\a-3\a1\a1 \end{array}\right]. \]
    Príklad: V závislosti na parametri \(\alpha\) určme hodnosť matice \[ A=\left[\begin{array}{rrrr} \alpha\a1\a0\a\alpha\\1\a\alpha\a\alpha\a0\\-1\a0\a0\a1\\0\a-1\a1\a0 \end{array}\right]. \]
    Príklad: Zistime, či sú vektory lineárne závislé alebo nezávislé \[ \begin{array}{lll} \overline{x}_1\a=\a(2,3,-1,4)\\ \overline{x}_2\a=\a(3,0,2,-2)\\ \end{array} \hspace{10mm}\begin{array}{lll} \overline{x}_3\a=\a(5,3,1,3)\\ \overline{x}_4\a=\a(4,6,-2,7). \end{array} \]
    Príklad: Vypočítajme determinanty matíc \[a)\ A=\left[\begin{array}{rr} 2\a3\\1\a4 \end{array}\right] ,\qquad b)\ B=\left[\begin{array}{rrr} 2\a3\a4\\1\a0\a2\\3\a1\a5 \end{array}\right], \] \[c)\ C=\left[\begin{array}{rrr} 1\a2\a3\\4\a5\a6\\7\a8\a9 \end{array}\right],\qquad d)\ D=\left[\begin{array}{rrrr} 0\a1\a1\a1\\1\a0\a1\a1\\1\a2\a3\a4\\4\a3\a1\a2 \end{array}\right]. \]
    Príklad: Vypočítajme inverznú maticu k matici \[ A=\left[\begin{array}{rr} 2\a3\\4\a5 \end{array}\right]. \]
    Príklad: Vypočítajme inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 1\a-4\a-3\\1\a-5\a-3\\-1\a6\a4 \end{array}\right]. \]
    Príklad: Vypočítajme inverznú maticu k matici \[ A=\left[\begin{array}{rrrr} 2\a1\a1\a1\\3\a2\a1\a1\\4\a3\a2\a1\\5\a4\a3\a2 \end{array}\right]. \]
    Príklad: Pomocou inverznej matice riešme maticovú rovnicu \[ \left[\begin{array}{rr} 2\a2\\3\a-1 \end{array}\right] X\left[\begin{array}{rr} 3\a5\\0\a1 \end{array}\right]= \left[\begin{array}{rr} 1\a1\\1\a1 \end{array}\right]\]
    Príklad: Pomocou inverznej matice riešme maticovú rovnicu \[ \left[\begin{array}{rrr} 1\a-4\a-3\\1\a-5\a-3\\-1\a6\a4 \end{array}\right]X- \left[\begin{array}{r} 1\\0\\1 \end{array}\right]= \left[\begin{array}{r} 0\\0\\0 \end{array}\right]. \]
    Príklad: Nájdime vektor \(\overline{c}\), ktorý je kolmý k obidvom vektorom \(\overline{a},\)\(\overline{b}\), ak \(\overline{a}=(3,1,-2),\,\overline{b}=(6,2,-1)\).
    Príklad: Vypočítajme obsah rovnobežníka \(ABCD\), ak \(A=(2,4,1),\ B=(3,-1,1),\ C=(1,0,5).\)
    Príklad: Vypočítajme objem štvorstena \(ABCD\), ak \(A=(1,3,1),\, B=(2,1,4),\, C=(3,1,0),\) \( D=(4,-3,5)\).
    Príklad: Objem štvorstena ABCD je \(V =3\). Tri jeho vrcholy sú \(A=(1,2,3),\ B=(-2,4,1),\ C=(6,2,1)\). Vypočítajme súradnice štvrtého vrchola \(D\), ktorý leží na osi \(o_x\).
    Príklad: Dané sú matice \[ A=\left[\begin{array}{rrr} 2\a0\a-1\\3\a2\a0\\5\a-4\a2 \end{array}\right] ,\qquad B=\left[\begin{array}{rrr} 5\a 2\a 1\\1\a 0\a -1\\ 0\a 2\a 3\\ \end{array}\right]. \] Vypočítajte \(A\cdot B,\,B\cdot A.\)
    Príklad: Určte hodnosť matice \(A\), ak \[ A=\left[\begin{array}{rrr} 0\a2\a-4\\-1\a-4\a5\\3\a1\a7\\0\a5\a-10\\2\a3\a0 \end{array}\right]. \]
    Príklad: Určte hodnosť matice \(A\) v závislosti od parametra \(\alpha\), ak \[ A=\left[\begin{array}{rrrr} 1\a1\a-2\a3 \\0\a4\a2\a-3\\3\a\alpha \a-4\a12\\2\a-1\a0\a3 \end{array}\right]. \]
    Príklad: Pomocou inverznej matice riešme maticovú rovnicu \[ \left[\begin{array}{rr} 2\a2\\3\a-1 \end{array}\right] X\left[\begin{array}{rr} 3\a5\\0\a1 \end{array}\right]= \left[\begin{array}{rr} 1\a1\\1\a1 \end{array}\right]\]
    Príklad: Pomocou inverznej matice riešme maticovú rovnicu \[ \left[\begin{array}{rrr} 1\a-4\a-3\\1\a-5\a-3\\-1\a6\a4 \end{array}\right]X- \left[\begin{array}{r} 1\\0\\1 \end{array}\right]= \left[\begin{array}{r} 0\\0\\0 \end{array}\right]. \]
    Príklad: V množine \(\mathbb{C}\) riešte rovnicu \[\left|\begin{array}{rrr} x\a0\a0\\0\a x-2\a4\\0\a-2\a x+2 \end{array}\right|=0\]
Úlohy:
    Úloha: Vypočítajte vektor \(\overline{x}=\alpha \,\overline{x}_1+ \beta \, \overline{x}_2+ \gamma \, \overline{x}_3\), ak \[\overline{x}_1=(3,-1,0,2),\ \overline{x}_2=(2,0,3,1),\ \overline{x}_3=(-2,2,0,3)\] pre nasledujúce hodnoty \(\alpha,\,\beta,\, \gamma\)
    a) \(\alpha =3,\ \beta =1,\ \gamma =-1,\)
    b) \(\alpha =1,\ \beta =1,\ \gamma =0,\)
    c) \(\alpha =2,\ \beta =0,\ \gamma =2,\)
    d) \(\alpha =0,\ \beta =1,\ \gamma =1\).
    Úloha: Zistite, či sú lineárne závislé alebo nezávislé vektory \[ \overline{x}_1=(-2,1,0),\quad \overline{x}_2=(1,2,0),\quad \overline{x}_3=(-1,3,0). \]
    Úloha: Zistite, či sú lineárne závislé alebo nezávislé vektory \[ \overline{x}_1=(1,2,0,3),\quad \overline{x}_2=(-1,-2,0,2),\quad \overline{x}_3=(2,4,0,11). \]
    Úloha: Zistite, či sú lineárne závislé alebo nezávislé vektory \[ \overline{x}_1=(-3,3,2),\quad \overline{x}_2=(2,1,0),\quad \overline{x}_3=(1,5,-2). \]
    Úloha: Zistite, či sú lineárne závislé alebo nezávislé vektory \[ \overline{x}_1=(-2,2,0,1),\quad \overline{x}_2=(-4,4,1,2),\quad \overline{x}_3=(2,-2,-1,1). \]
    Úloha: Vypočítajte determinanty matíc \[ A=\left[\begin{array}{rrr} 6\a3\a2\\1\a-3\a5\\2\a1\a9 \end{array}\right] ,\qquad B=\left[\begin{array}{rrr} 2\a-3\a1\\1\a2\a-1\\2\a1\a1 \end{array}\right]. \]
    Úloha: Vypočítajte determinanty matíc \[ C=\left[\begin{array}{rrrr} 2\a1\a-1\a2\\2\a3\a-3\a4\\6\a2\a1\a0\\2\a3\a0\a-5 \end{array}\right],\qquad D=\left[\begin{array}{rrrr} -1\a3\a2\a4\\2\a5\a1\a0\\2\a0\a-3\a1\\-2\a6\a8\a9 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrrr} 3\a1\a2\a-2\\4\a2\a1\a5\\1\a3\a-2\a18\\2\a1\a1\a1 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrrr} 2\a0\a2\a0\\0\a1\a0\a1\\2\a1\a0\a2\\0\a1\a-2\a2 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrr} 27\a26\a25\\19\a18\a17\\12\a11\a10 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrr} 1\a2\a3\\2\a-1\a1\\1\a7\a8 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrrr} 1\a0\a3\a2\\-2\a1\a0\a-1\\-1\a1\a3\a1\\-1\a2\a9\a4 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrrr} 1\a3\a5\a-1\\2\a-1\a-3\a4\\5\a1\a-1\a7\\7\a7\a9\a1 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrr} 0\a2\a-4\\-1\a-4\a5\\3\a1\a7\\0\a5\a-10\\2\a3\a0 \end{array}\right]. \]
    Úloha: Určte hodnosť matice \[ A=\left[\begin{array}{rrrrr} 4\a3\a-5\a2\a3\\8\a6\a-7\a4\a2\\4\a3\a-8\a2\a7\\4\a3\a1\a2\a-5\\8\a6\a-1\a4\a-6 \end{array}\right]. \]
    Úloha: Určte hodnosť matice v závislosti od parametra \(\alpha\) \[ A=\left[\begin{array}{rrrr} 3\a1\a2\a-2\\\alpha \a2\a1\a5\\1\a3\a-2\a18\\2\a1\a1\a1 \end{array}\right]. \]
    Úloha: Určte hodnosť matice v závislosti od parametra \(\alpha\) \[ A=\left[\begin{array}{rrrr} 3\a1\a1\a4 \\\alpha \a4\a10\a1\\1\a7\a17\a3\\2\a2\a4\a3 \end{array}\right]. \]
    Úloha: Určte hodnosť matice v závislosti od parametra \(\alpha\) \[ A=\left[\begin{array}{rrrr} 1\a1\a1\a\alpha \\1\a1\a\alpha \a1\\1\a\alpha \a1\a1\\\alpha \a1\a1\a1 \end{array}\right]. \]
    Úloha: Určte hodnosť matice v závislosti od parametra \(\alpha\) \[ A=\left[\begin{array}{rrrr} 1\a2\a-1\a1 \\4\a-1\a3\a0\\5\a1\a\alpha -1\a1\\3\a\alpha \a4\a-1 \end{array}\right]. \]
    Úloha: Určte hodnosť matice v závislosti od parametra \(\alpha\) \[ A=\left[\begin{array}{rrrr} 2\a2\a2\a-\alpha \\2\a2\a-\alpha \a2\\2\a-\alpha \a2\a2\\-\alpha \a2\a2\a2 \end{array}\right]. \]
    Úloha: Určte hodnosť matice v závislosti od parametra \(\alpha\) \[ A=\left[\begin{array}{rrrr} \alpha \a1\a2\a3 \\1\a2\a4\a0\\\alpha \a4\a-8\a10\\1\a1\a3\a2 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 1\a-2\a1\\3\a-5\a-2\\7\a-3\a1 \end{array}\right] \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 2\a5\a7\\6\a3\a4\\5\a-2\a-3 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rr} 3\a2\\6\a4 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rr} 3\a2\\6\a5 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rr} -3\a2\\-2\a4 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 3\a2\a-1\\-1\a3\a2\\2\a-1\a4 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 1\a1\a1\\6\a5\a4\\13\a10\a8 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 9\a17\a8\\18\a34\a17\\10\a19\a8 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 1\a1\a-1\\2\a1\a0\\1\a-1\a0 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrr} 2\a1\a4\\-5\a-2\a-1\\3\a1\a1 \end{array}\right]. \]
    Úloha: Vypočítajte inverznú maticu k matici \[ A=\left[\begin{array}{rrrr} 1\a1\a1\a1\\1\a1\a-1\a-1\\1\a-1\a1\a-1\\1\a-1\a-1\a1 \end{array}\right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ \left[\begin{array}{rr} 3\a2\\-1\a0 \end{array}\right] X= \left[\begin{array}{rr} -1\a2\\1\a4 \end{array}\right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ X \left[\begin{array}{rr} 2\a3\\1\a0 \end{array}\right]= \left[\begin{array}{rr} 2\a1\\1\a2 \end{array}\right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ \left[\begin{array}{rr} 3\a2\\-1\a0 \end{array}\right] X\left[\begin{array}{rr} 2\a0\\2\a1 \end{array}\right]= \left[\begin{array}{rr} 1\a1\\1\a1 \end{array}\right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ X\left[\begin{array}{rrr} 2\a1\a4\\-5\a-2\a-1\\3\a1\a1 \end{array}\right]= \left[\begin{array}{rrr} 10\a4\a6\\7\a3\a5 \end{array}\right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ \left[\begin{array}{rrr} 1\a-2\a1\\3\a-5\a-2\\7\a-3\a1 \end{array}\right] X= \left[\begin{array}{r} 0\\-3\\16 \end{array}\right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ X\left[\begin{array}{rrr} 1\a1\a-1\\2\a1\a0\\2\a-1\a0 \end{array}\right]= \left[\begin{array}{rrr} 1\a-1\a3\\4\a3\a4\\1\a-2\a5 \end{array}\right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ \left[\begin{array}{rrrr} 2 \a - 2 \a 0 \a 0\\ 0 \a 2 \a- 2 \a 0\\ 0 \a 0 \a 2 \a- 2\\ 0 \a 0 \a 0 \a 2 \end{array}\right]X = \left[ \begin{array}{rrrr} 1 \a 0 \a 1 \a 0\\ 0 \a 1 \a 0 \a 1\\ 1 \a 0 \a 1 \a 0\\ 0 \a 1 \a 0 \a 1 \end{array} \right]. \]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ \left[\begin{array}{rr} 3\a2\\-1\a0 \end{array}\right] X\left[\begin{array}{rr} 2\a0\\2\a1 \end{array}\right]- \left[\begin{array}{rr} 2\a0\\0\a2 \end{array}\right]= \left[\begin{array}{rr} -1\a1\\1\a-1 \end{array}\right].\]
    Úloha: Pomocou inverznej matice riešte maticovú rovnicu \[ \left[\begin{array}{rrr} 3\a2\a-1\\-1\a3\a2\\2\a-1\a4 \end{array}\right] X= \left[\begin{array}{r} 8\\3\\-4 \end{array}\right]. \]
    Úloha: Vypočítajte obsah rovnobežníka \(ABCD\), ak jeho tri za sebou idúce vrcholy sú
    a)\(\quad(A=(7,-5,6),\ B=(9,-4,8),\ C=(6,0,6)\),
    b)\(\quad(A=(-2,4,6),\ B=(2,5,4),\ C=(1,-5,3)\),
    c)\(\quad(A=(2,-1,7),\ B=(11,-5,8),\ C=(7,-4,-1)\),
    d)\(\quad (A=(-3,1,-2),\ B=(4,-4,2),\ C=(-2,1,0)\),
    e)\(\quad(A=(9,-4,-4),\ B=(11,-5,-4),\ C=(11,0,-9)\),
    f)\(\quad(A=(-1,9,0),\ B=(4,5,0),\ C=(0,0,0)\).
    Úloha: Vypočítajte objem štvorstena \(ABCD\), ak
    a)\(\quad A=(1,2,3),\ B=(-1,0,0),\ C=(0,-2,0),\ D=(0,0,-3)\),
    b)\(\quad A=(1,2,-1),\ B=(3,5,4),\ C=(-2,1,0),\ D=(4,2,3)\).
    Úloha: Objem štvorstena \(ABCD\) je \(V=5\). Tri jeho vrcholy sú \(A=(2,1,-1),\ B=(3,0,1),\ C=(2,-1,3)\). Vypočítajte súradnice vrchola \(D\), ktorý leží na osi \(o_y\).
    Úloha: Štvorsten \(ABCD\) má objem \(V=2\). Jeho tri vrcholy sú \(A=(2,1,3),\ B=(3,3,2),\ C=(1,2,4)\). Vypočítajte súradnice vrchola \(D\), ktorý leží na osi \(o_z\).
03. Sústavy lineárnych rovníc.
Riešené úlohy:
    Príklad: \(\def\a{&}\def\hod{\rm h}\) Pomocou Cramerovho pravidla riešme sústavu lineárnych algebraických rovníc nad \(\mathbb{R}\) \[ \begin{array}{rrrrrrl} 6x_1 \a \!+\! \a3x_2 \a \!-\! \a 2x_3 \a \!=\! \a 2\\ x_1 \a \!-\! \a 3x_2 \a \!+\! \a 2x_3 \a \!=\! \a 5\\ 2x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 9. \end{array} \]
    Príklad: Pomocou inverznej matice riešme nad \(\mathbb{R}\) sústavu lineárnych algebraických rovníc \[ \begin{array}{rrrrr} 2x_1 \a + \a 3x_2 \a \!=\! \a -4\\ 4x_1 \a + \a 5x_2 \a \!=\! \a -6. \end{array} \]
    Príklad: Pomocou inverznej matice riešme nad \(\mathbb{R}\) sústavu lineárnych algebraických rovníc \[ \begin{array}{rrrrrrl} x_1 \a - \a 4x_2 \a - \a 3x_3 \a \!=\! \a 1\\ x_1 \a - \a 5x_2 \a - \a 3x_3 \a \!=\! \a 0\\ -x_1 \a \!+\! \a 6x_2 \a \!+\! \a 4x_3 \a \!=\! \a 1. \end{array} \]
    Príklad: Pomocou Gaussovej eliminačnej metódy riešme sústavu lineárnych algebraických rovníc nad \(\mathbb{R}\) \[ \begin{array}{rrrrrrrrl} 2x_1 \a \!+\! \a 2x_2 \a \!-\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 4\\ 4x_1 \a \!+\! \a 3x_2 \a \!-\! \a x_3 \a \!+\! \a 2x_4 \a\!=\! \a 6\\ 8x_1 \a \!+\! \a 5x_2 \a \!-\! \a 3x_3 \a \!+\! \a 4x_4 \a\!=\! \a 12\\ 3x_1 \a \!+\! \a 3x_2 \a \!-\! \a 2x_3 \a \!+\! \a 2x_4 \a\!=\! \a 6. \end{array} \]
    Príklad: Pomocou Gaussovej eliminačnej metódy riešme sústavu lineár-nych algebraických rovníc nad \(\mathbb{R}\) \[ \begin{array}{rrrrrrrrl} 4x_1 \a \!-\! \a 3x_2 \a \!+\! \a 2x_3 \a \!-\! \a x_4 \a\!=\! \a 8\\ 3x_1 \a \!-\! \a 2x_2 \a \!+\! \a x_3 \a \!-\! \a 3x_4 \a\!=\! \a 7\\ 2x_1 \a \!-\! \a x_2 \a \a \a \!+\! \a 5x_4 \a\!=\! \a 6\\ 5x_1 \a \!-\! \a 3x_2 \a \!+\! \a x_3 \a \!-\! \a 8x_4 \a\!=\! \a 1. \end{array} \]
    Príklad: Pomocou Gaussovej eliminačnej metódy riešme sústavu lineárnych algebraických rovníc nad \(\mathbb{R}\) \[ \begin{array}{rrrrrrrrrrl} 2x_1 \a \!-\! \a x_2 \a \!+\! \a x_3 \a \!+\! \a 2x_4 \a \!+\! \a 3x_5 \a\!=\! \a 2\\ 6x_1 \a \!-\! \a 3x_2 \a \!+\! \a 2x_3 \a \!+\! \a 4x_4 \a \!+\! \a 5x_5 \a\!=\! \a 3\\ 6x_1 \a \!-\! \a 3x_2 \a \!+\! \a 4x_3 \a \!+\! \a 8x_4 \a \!+\! \a13x_5 \a\!=\! \a 9\\ 4x_1 \a \!-\! \a 2x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a \!+\! \a 2x_5 \a\!=\! \a 1. \end{array} \]
    Príklad: Pomocou Gaussovej eliminačnej metódy riešme sústavu lineárnych algebraických rovníc nad \(\mathbb{R}\) \begin{array}{rrrrrrrrrrr} 4x_1 \a \!+\! \a 3x_2 \a \!-\! \a x_3 \a \!+\! \a x_4 \a \!+\! \a x_5 \a \! =\! \a 15\\ x_1 \a \!-\! \a x_2 \a \!+\! \a x_3 \a \!-\! \a x_4 \a \! +\! \a x_5 \a \!=\! \a 2\\ 3x_1 \a \!-\! \a 2x_2 \a \!+\! \a x_3 \a \!-\! \a x_4 \a \!-\! \a 2x_5 \a \!=\! \a 5\\ 2x_1 \a \a \a \!+\! \a 3x_3 \a \a \a \a \a \!=\! \a 0\\ \a \a x_2 \a \a \a \!+\! \a x_4 \a \a \a \!=\! \a 0 \end{array}
    Príklad: Pomocou Gaussovej eliminačnej metódy riešme homogénnu sústavu lineárnych algebraických rovníc nad \(\mathbb{R}\) \[ \begin{array}{rrrrrrrrl} \!-\!x_1 \a \!+\! \a x_2 \a \!-\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 0\\ \!-\!2x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!-\! \a 3x_4 \a\!=\! \a 0\\ x_1 \a \!+\! \a 2x_2 \a \!-\! \a 3x_3 \a \!+\! \a x_4 \a\!=\! \a 0\\ 2x_1 \a \!+\! \a 3x_2 \a \!+\! \a 4x_3 \a \!-\! \a x_4 \a\!=\! \a 0. \end{array} \]
    Príklad: Pomocou Gaussovej eliminačnej metódy riešme homogénnu sústavu lineárnych algebraických rovníc nad \(\mathbb{R}\) \[ \begin{array}{rrrrrrrrrrl} 3x_1 \a \!-\! \a x_2 \a \!-\! \a 2x_3 \a \!+\! \a x_4 \a \!+\! \a 8x_5 \a\!=\! \a 0\\ 9x_1 \a \!-\! \a 3x_2 \a \!+\! \a 4x_3 \a \!+\! \a 8x_4 \a \!+\! \a 9x_5 \a\!=\! \a 0\\ 3x_1 \a \!-\! \a x_2 \a \!+\! \a 2x_3 \a \!+\! \a 3x_4 \a \!+\! \a 2x_5 \a\!=\! \a 0\\ 3x_1 \a \!-\! \a x_2 \a \!+\! \a 4x_3 \a \!+\! \a 4x_4 \a \!-\! \a x_5 \a\!=\! \a 0. \end{array} \]
    Príklad: Pomocou Cramerovho pravidla riešme nad \(\mathbb{R}\) sústavu lineárnych algebraických rovníc s parametrom \[ \begin{array}{rrrrrrl} x_1 \a \!+\! \a x_2 \a \!+\! \a ax_3 \a \!=\! \a 1\\ x_1 \a \!+\! \a ax_2 \a \!+\! \a x_3 \a \!=\! \a 1\\ ax_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 1. \end{array} \]
    Príklad: Pomocou Gaussovej eliminačnej metódy riešme nad \(\mathbb{R}\) sústavu lineárnych algebraických rovníc s parametrom \[ \begin{array}{rrrrrrrrl} 12x_1 \a \!-\! \a 6x_2 \a \!+\! \a 9x_3 \a \!+\! \a21x_4 \a \!=\! \a 3\!+\!a\\ 11x_1 \a \!-\! \a 5x_2 \a \!+\! \a10x_3 \a \!+\! \a24x_4 \a \!=\! \a 1\!+\!a\\ 7x_1 \a \!-\! \a 3x_2 \a \!+\! \a 7x_3 \a \!+\! \a17x_4 \a \!=\! \a a\\ 8x_1 \a \!-\! \a 6x_2 \a \!-\! \a x_3 \a \!-\! \a 5x_4 \a \!=\! \a 9. \end{array} \]
Úlohy:
    Úloha: Pomocou Cramerovho pravidla riešte sústavu rovníc \[ \begin{array}{rrrrrrr} x_1 \a \!+\! \a 3x_2 \a \!+\! \a 2x_3 \a \!=\! \a 4\\ 2x_1 \a \!+\! \a 6x_2 \a \!+\! \a x_3 \a \!=\! \a 2\\ 4x_1 \a \!+\! \a 8x_2 \a \!-\! \a x_3 \a \!=\! \a 2 \end{array} \]
    Úloha: Pomocou Cramerovho pravidla riešte sústavu rovníc \[ \begin{array}{rrrrrrr} x_1 \a \!-\! \a 2x_2 \a \!+\! \a 3x_3 \a \!=\! \a 9\\ \!-\!x_1 \a \!+\! \a 3x_2 \a \!-\! \a x_3 \a \!=\! \a -6\\ 2x_1 \a \!-\! \a 5x_2 \a \!+\! \a 5x_3 \a \!=\! \a 17 \end{array} \]
    Úloha: Pomocou Cramerovho pravidla riešte sústavu rovníc \[ \begin{array}{rrrrrrr} 3x_1 \a \!+\! \a 3x_2 \a \!+\! \a 5x_3 \a \!=\! \a 1\\ 3x_1 \a \!+\! \a 5x_2 \a \!+\! \a 9x_3 \a \!=\! \a 0\\ 5x_1 \a \!+\! \a 9x_2 \a \!+\! \a 17x_3 \a \!=\! \a 0 \end{array} \]
    Úloha: Pomocou Cramerovho pravidla riešte sústavu rovníc \[ \begin{array}{rrrrrrr} 2x_1 \a \!+\! \a 3x_2 \a \!+\! \a 3x_3 \a \!=\! \a 3\\ 6x_1 \a \!+\! \a 6x_2 \a \!+\! \a12x_3 \a \!=\! \a 13\\ 12x_1 \a \!+\! \a 9x_2 \a \!-\! \a x_3 \a \!=\! \a 2 \end{array} \]
    Úloha: Pomocou inverznej matice riešte sústavu rovníc \[ \begin{array}{rrrrrrr} 2x_1 \a \!+\! \a 3x_2 \a \!+\! \a x_3 \a \!=\! \a \!-\!1\\ 3x_1 \a \!+\! \a 3x_2 \a \!+\! \a x_3 \a \!=\! \a 1\\ 2x_1 \a \!+\! \a 4x_2 \a \!+\! \a x_3 \a \!=\! \a \!-\!2 \end{array} \]
    Úloha: Pomocou inverznej matice riešte sústavu rovníc \[ \begin{array}{rrrrrrr} 2x_1 \a \!+\! \a 3x_2 \a \!+\! \a x_3 \a \!=\! \a 4\\ 3x_1 \a \!+\! \a 3x_2 \a \!+\! \a x_3 \a \!=\! \a 8\\ 2x_1 \a \!+\! \a 4x_2 \a \!+\! \a x_3 \a \!=\! \a 5 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} 2x_1 \a \!+\! \a 5x_2 \a \!+\! \a 4x_3 \a \!+\! \a x_4 \a\!=\! \a 20\\ x_1 \a \!+\! \a 3x_2 \a \!+\! \a 2x_3 \a \!+\! \a x_4 \a\!=\! \a 11\\ 2x_1 \a \!+\! \a10x_2 \a \!+\! \a 9x_3 \a \!+\! \a 7x_4 \a\!=\! \a 40\\ 3x_1 \a \!+\! \a 8x_2 \a \!+\! \a 9x_3 \a \!+\! \a 2x_4 \a\!=\! \a 37 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} 2x_1 \a \!+\! \a 3x_2 \a \!+\! \a11x_3 \a \!+\! \a 5x_4 \a\!=\! \a 2\\ x_1 \a \!+\! \a x_2 \a \!+\! \a 5x_3 \a \!+\! \a 2x_4 \a\!=\! \a 1\\ 2x_1 \a \!+\! \a x_2 \a \!+\! \a 3x_3 \a \!+\! \a 2x_4 \a\!=\! \a-3\\ x_1 \a \!+\! \a x_2 \a \!+\! \a 3x_3 \a \!+\! \a 4x_4 \a\!=\! \a-3 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} 7x_1 \a \!+\! \a 9x_2 \a \!+\! \a 4x_3 \a \!+\! \a 2x_4 \a\!=\! \a 2\\ 2x_1 \a \!-\! \a 2x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 6\\ 5x_1 \a \!+\! \a 6x_2 \a \!+\! \a 3x_3 \a \!+\! \a 2x_4 \a\!=\! \a 3\\ 2x_1 \a \!+\! \a 3x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 0 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} 3x_1 \a \!+\! \a 4x_2 \a \!+\! \a x_3 \a \!+\! \a 2x_4 \a\!=\! \a -3\\ 3x_1 \a \!+\! \a 5x_2 \a \!+\! \a 3x_3 \a \!+\! \a 5x_4 \a\!=\! \a -6\\ 6x_1 \a \!+\! \a 8x_2 \a \!+\! \a x_3 \a \!+\! \a 5x_4 \a\!=\! \a -8\\ 3x_1 \a \!+\! \a 5x_2 \a \!+\! \a 3x_3 \a \!+\! \a 7x_4 \a\!=\! \a -8 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} x_1 \a \!+\! \a 2x_2 \a \!-\! \a x_3 \a \!-\! \a 2x_4 \a\!=\! \a -2\\ 2x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 8\\ x_1 \a \!-\! \a x_2 \a \!-\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 1\\ x_1 \a \!+\! \a 2x_2 \a \!+\! \a 2x_3 \a \!-\! \a x_4 \a\!=\! \a 4 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} 5x_1 \a \!+\! \a 3x_2 \a \!+\! \a 3x_3 \a \!+\! \a x_4 \a\!=\! \a 11\\ x_1 \a \!-\! \a x_2 \a \!+\! \a x_3 \a \a \a\!=\! \a -2\\ 3x_1 \a \!+\! \a 3x_2 \a \!+\! \a 2x_3 \a \!+\! \a x_4 \a\!=\! \a 10\\ 4x_1 \a \!+\! \a x_2 \a \!+\! \a 3x_3 \a \!+\! \a x_4 \a\!=\! \a 8\\ x_1 \a \!-\! \a 3x_2 \a \!+\! \a 2x_3 \a \a \a\!=\! \a -7 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrrrr} x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a \a \a\!=\! \a 1\\ 2x_1 \a \!+\! \a 2x_2 \a \!+\! \a 2x_3 \a \a \a \a \a\!=\! \a 1\\ x_1 \a \!+\! \a x_2 \a \!+\! \a 5x_3 \a \!-\! \a x_4 \a \!+\! \a 6x_5 \a\!=\! \a 1\\ x_1 \a \!+\! \a x_2 \a \!-\! \a 3x_3 \a \!+\! \a x_4 \a \!-\! \a 6x_5 \a\!=\! \a -1 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrrrr} 4x_1 \a \!+\! \a 3x_2 \a \!-\! \a x_3 \a \!+\! \a x_4 \a \!+\! \a x_5 \a\!=\! \a 15\\ x_1 \a \!-\! \a x_2 \a \!+\! \a x_3 \a \!-\! \a x_4 \a \!+\! \a x_5 \a\!=\! \a 2\\ 3x_1 \a \!-\! \a 2x_2 \a \!+\! \a x_3 \a \!-\! \a x_4 \a \!-\! \a 2x_5 \a\!=\! \a 5\\ 2x_1 \a \a \a \!+\! \a 3x_3 \a \a \a \a \a\!=\! \a 0\\ \a \a x_2 \a \a \a \!+\! \a x_4 \a \a \a\!=\! \a 0 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} x_1 \a \!+\! \a 2x_2 \a \!-\! \a 3x_3 \a \!+\! \a x_4 \a\!=\! \a -2\\ 3x_1 \a \!-\! \a 5x_2 \a \!+\! \a 2x_3 \a \!+\! \a x_4 \a\!=\! \a 3\\ 4x_1 \a \!+\! \a 3x_2 \a \!-\! \a 7x_3 \a \!+\! \a 2x_4 \a\!=\! \a -5\\ \!-\!x_1 \a \!+\! \a 2x_2 \a \!-\! \a x_3 \a \!+\! \a 3x_4 \a\!=\! \a 2\\ 3x_1 \a \!+\! \a x_2 \a \!-\! \a 4x_3 \a \!+\! \a 2x_4 \a\!=\! \a -2 \end{array} \]
    Úloha: Eliminačnou metódou riešte sústavu rovníc \[ \begin{array}{rrrrrrrrr} \!-\!2x_1 \a \!+\! \a 2x_2 \a \a \a \a \a\!=\! \a -6\\ x_1 \a \!+\! \a 8x_2 \a \!+\! \a 2x_3 \a \!+\! \a x_4 \a\!=\! \a -3\\ 3x_1 \a \!+\! \a10x_2 \a \!+\! \a 2x_3 \a \!-\! \a x_4 \a\!=\! \a -2\\ 2x_1 \a \a \a \a \a \!-\! \a x_4 \a\!=\! \a 1\\ 4x_1 \a \!+\! \a 3x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 5 \end{array} \]
    Úloha: Eliminačnou metódou riešte homogénnu sústavu rovníc \[ \begin{array}{rrrrrrr} x_1 \a \!+\! \a 3x_2 \a \!+\! \a 2x_3 \a \!=\! \a 0\\ 2x_1 \a \!-\! \a x_2 \a \!+\! \a 3x_3 \a \!=\! \a 0\\ 3x_1 \a \!-\! \a 5x_2 \a \!+\! \a 4x_3 \a \!=\! \a 0\\ x_1 \a \!+\! \a17x_2 \a \!+\! \a 4x_3 \a \!=\! \a 0 \end{array} \]
    Úloha: Eliminačnou metódou riešte homogénnu sústavu rovníc \[ \begin{array}{rrrrrrrrr} x_1 \a \!-\! \a 3x_2 \a \!-\! \a26x_3 \a \!+\! \a22x_4 \a\!=\! \a 0\\ x_1 \a \a \a \!-\! \a 8x_3 \a \!+\! \a 7x_4 \a\!=\! \a 0\\ x_1 \a \!+\! \a x_2 \a \!-\! \a 2x_3 \a \!+\! \a 2x_4 \a\!=\! \a 0\\ 4x_1 \a \!+\! \a 5x_2 \a \!-\! \a 2x_3 \a \!+\! \a 3x_4 \a\!=\! \a 0 \end{array} \]
    Úloha: Eliminačnou metódou riešte homogénnu sústavu rovníc \[ \begin{array}{rrrrrrrrrrrrr} \!-\!x_1 \a \!+\! \a x_2 \a \a \a \!+\! \a x_4 \a \a \a \a \a\!=\! \a 0\\ \a \a \a \a x_3 \a \a \a \!-\! \a x_5 \a \!+\! \a x_6 \a\!=\! \a 0\\ \a \!-\! \a x_2 \a \!+\! \a x_3 \a \!-\! \a x_4 \a \a \a \!-\! \a x_6 \a\!=\! \a 0\\ \a \a x_2 \a \a \a \!+\! \a x_4 \a \!-\! \a x_5 \a \a \a\!=\! \a 0\\ \!-\!x_1 \a \a \a \!+\! \a x_3 \a \a \a \a \a \!+\! \a x_6 \a\!=\! \a0 \end{array} \]
    Úloha: Eliminačnou metódou riešte homogénnu sústavu rovníc \[ \begin{array}{rrrrrrrrrrr} 3x_1 \a \a \a \!-\! \a x_3 \a \!-\! \a 2x_4 \a \!-\! \a 4x_5 \a\!=\! \a 0\\ 4x_1 \a \!+\! \a x_2 \a \!-\! \a 2x_3 \a \!-\! \a x_4 \a \!-\! \a 5x_5 \a\!=\! \a 0\\ 6x_1 \a \!-\! \a 3x_2 \a \a \a \!-\! \a 9x_4 \a \!-\! \a 3x_5 \a\!=\! \a 0\\ 10x_1 \a \!+\! \a x_2 \a \!-\! \a 4x_3 \a \!-\! \a 5x_4 \a \!-\! \a13x_5 \a\!=\! \a 0\\ x_1 \a \!+\! \a 4x_2 \a \!-\! \a 3x_3 \a \!+\! \a 6x_4 \a \a \a\!=\! \a 0 \end{array} \]
    Úloha: Eliminačnou metódou riešte homogénnu sústavu rovníc \[ \begin{array}{rrrrrrrrrrr} x_1 \a \!-\! \a x_2 \a \!+\! \a 2x_3 \a \!+\! \a 2x_4 \a \!+\! \a 6x_5 \a\!=\! \a 0\\ 3x_1 \a \!-\! \a 2x_2 \a \!+\! \a 4x_3 \a \!+\! \a 4x_4 \a \!+\! \a12x_5 \a\!=\! \a 0\\ \a \a x_2 \a \!-\! \a x_3 \a \!-\! \a x_4 \a \!-\! \a 3x_5 \a\!=\! \a 0\\ 2x_1 \a \!-\! \a 2x_2 \a \!+\! \a 4x_3 \a \!+\! \a 5x_4 \a \!+\! \a15x_5 \a\!=\! \a 0\\ 2x_1 \a \!-\! \a 2x_2 \a \!+\! \a 4x_3 \a \!+\! \a 4x_4 \a \!+\! \a13x_5 \a\!=\! \a 0 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 2\\ 2x_1 \a \!+\! \a 3x_2 \a \!+\! \a 4x_3 \a \!=\! \a 3\\ 3x_1 \a \!+\! \a 2x_2 \a \!+\! \a ax_3 \a \!=\! \a 6 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrrrr} 2x_1 \a \!-\! \a x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 1\\ x_1 \a \!+\! \a 2x_2 \a \!-\! \a x_3 \a \!+\! \a 4x_4 \a\!=\! \a 2\\ x_1 \a \!+\! \a 7x_2 \a \!-\! \a 4x_3 \a \!+\! \a11x_4 \a\!=\! \a a \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} ax_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 1\\ x_1 \a \!+\! \a ax_2 \a \!+\! \a x_3 \a \!=\! \a a\\ x_1 \a \!+\! \a x_2 \a \!+\! \a ax_3 \a \!=\! \a a^2 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrrrr} x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 4\\ 2x_1 \a \!-\! \a 3x_2 \a \!+\! \a x_3 \a \!-\! \a x_4 \a\!=\! \a -1\\ 3x_1 \a \!+\! \a 4x_2 \a \!-\! \a 2x_3 \a \!+\! \a 6x_4 \a\!=\! \a 11\\ 5x_1 \a \a \a \!+\! \a 4x_3 \a \!+\! \a 2x_4 \a\!=\! \a a \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrrrr} x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 4\\ 2x_1 \a \!-\! \a 3x_2 \a \!+\! \a x_3 \a \a \a\!=\! \a 0\\ 3x_1 \a \!+\! \a 4x_2 \a \!-\! \a 2x_3 \a \!+\! \a 6x_4 \a\!=\! \a 11\\ 5x_1 \a \a \a \!+\! \a 4x_3 \a \!+\! \a 3x_4 \a\!=\! \a a \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrrrr} x_1 \a \!-\! \a x_2 \a \!-\! \a x_3 \a \!-\! \a 3x_4 \a\!=\! \a 2\\ 4x_1 \a \!-\! \a 2x_2 \a \!+\! \a 3x_3 \a \!+\! \a 7x_4 \a\!=\! \a 1\\ x_1 \a \!-\! \a 3x_2 \a \!-\! \a 8x_3 \a \!-\! \a22x_4 \a\!=\! \a 9\\ 7x_1 \a \!-\! \a 3x_2 \a \!+\! \a 7x_3 \a \!+\! \a17x_4 \a\!=\! \a a \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrrrr} x_1 \a \!-\! \a x_2 \a \!+\! \a x_3 \a \!+\! \a x_4 \a\!=\! \a 0\\ 2x_1 \a \!+\! \a x_2 \a \!-\! \a x_3 \a \!-\! \a x_4 \a\!=\! \a 1\\ 3x_1 \a \!+\! \a 3x_2 \a \!-\! \a 3x_3 \a \!-\! \a 3x_4 \a\!=\! \a a\\ 4x_1 \a \!+\! \a 5x_2 \a \!-\! \a 5x_3 \a \!-\! \a 5x_4 \a\!=\! \a 3 \end{array} \]
    Úloha: \[ \begin{array}{rrrrrrr} (2\!-\!a)x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 0\\ x_1 \a \!+\! \a (a\!-\!2)x_2 \a \!+\! \a x_3 \a \!=\! \a 0\\ x_1 \a \!+\! \a x_2 \a \!+\! \a (a\!-\!2)x_3 \a \!=\! \a 0 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} x_1 \a \!+\! \a 2x_2 \a \!+\! \a 3x_3 \a \!=\! \a 4\\ 2x_1 \a \!+\! \a 5x_2 \a \!+\! \a 8x_3 \a \!=\! \a 6\\ \!-\!7x_1 \a \a \a \!+\! \a 7x_3 \a \!=\! \a 8\!-\!a \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} ax_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 1\\ x_1 \a \!+\! \a ax_2 \a \!+\! \a x_3 \a \!=\! \a 1\\ x_1 \a \!+\! \a x_2 \a \!+\! \a ax_3 \a \!=\! \a a^2 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} 4x_1 \a \!+\! \a 4x_2 \a \!+\! \a 4x_3 \a \!=\! \a 1\!+\!a\\ 8x_1 \a \!+\! \a 6x_2 \a \!+\! \a 4x_3 \a \!=\! \a 1\\ \!-\!3x_1 \a \!-\! \a 2x_2 \a \!-\! \a x_3 \a \!=\! \a 1 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} ax_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 0\\ x_1 \a \!+\! \a ax_2 \a \!+\! \a x_3 \a \!=\! \a 0\\ x_1 \a \!+\! \a x_2 \a \!+\! \a ax_3 \a \!=\! \a 0 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} ax_1 \a \!-\! \a 2x_2 \a \!+\! \a x_3 \a \!=\! \a 0\\ 3x_1 \a \!+\! \a2ax_2 \a \!-\! \a x_3 \a \!=\! \a 0\\ \!-\!a^2x_1 \a \!-\! \a x_2 \a \!+\! \a (1\!-\!a)x_3 \a \!=\! \a 0 \end{array} \]
    Úloha: Riešte sústavu lineárnych rovníc s parametrom \[ \begin{array}{rrrrrrr} x_1 \a \!+\! \a x_2 \a \!+\! \a x_3 \a \!=\! \a 1\\ x_1 \a \!+\! \a x_2 \a \!+\! \a ax_3 \a \!=\! \a a\\ x_1 \a \!+\! \a ax_2 \a \!+\! \a x_3 \a \!=\! \a a \end{array} \]
04. Polynómy a racionálne funkcie
Riešené úlohy:
    Príklad: Vykonajme delenie polynómu \(2\,x^4-11\,x^3-15\,x^2+95\,x+9\) polynómom \(x^3-5\,x^2-9\,x+45\).
    Ďalej sa budeme venovať rozkladu rýdzoracionálnej funkcie \[R_1(x)={{-2\,x^2-4\,x+54}\over{x^3-5\,x^2-9\,x+45}}\] na súčet elementárnych zlomkov.
    Príklad: Rozložme polynóm \(x^3-5\,x^2-9\,x+45\) na súčin koreňových činiteľov.
    Príklad: Rozložme rýdzoracionálnu funkciu \[R_1(x)= {{-2\,x^2-4\,x+54}\over{x^3-5\,x^2-9\,x+45}}\] na súčet elementárnych zlomkov.
    Poznámka: Je zrejmé, že v tomto prípade sú obidve metódy ekvivalentné, dosadzovacia metóda je však vhodná na použitie aj v prípade viacnásobných alebo komplexných koreňov.
    Príklad: Racionálnu funkciu \[ R(x)={{2\,x^4-11\,x^3-15\,x^2+95\,x+9}\over{x^3-5\,x^2-9\,x+45}} \] rozložme na súčet parciálnych (elementárnych) zlomkov nad poľom \(\mathbb{R}\), teda v rámci množiny reálnych čísel.
    Príklad: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \begin{equation}\label{RF2} {{2\,x^4+13\,x^3+4\,x^2-60\,x+4}\over{x^3+6\,x^2-32}}\cdot \end{equation}
    Poznámka: Koeficient \(C\) sme mohli určiť aj pomocou ďalšej modifikácie dosadzovacej metódy, keď v rovnici \eqref{RZ2} dosadíme za \(x\) nejaké vhodné číslo, napríklad \(x=0\): \[ \frac{36}{-32}=-\frac{1}{2}+\frac{2}{16}+\frac{C}{4} \qquad\Rightarrow\qquad C=\frac{-36+16-4}{8}=\frac{-24}{8}=-3. \]
    Príklad: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \begin{equation}\label{RF3} {{-x^4-7\,x^3-12\,x^2+4\,x+18}\over{x^3+7\,x^2+17\,x+15}}\,\cdot \end{equation}
    Príklad: Rozložme nad \(\mathbb{R}\) funkciu \begin{equation}\label{RF4} {{240\,x^2+86}\over{48\,x^3+40\,x^2-21\,x-18}} \end{equation}
Úlohy:
    Úloha: Racionálnu funkciu \begin{equation}\label{RF} R(x)={{2\,x^4-11\,x^3-15\,x^2+95\,x+9}\over{x^3-5\,x^2-9\,x+45}} \end{equation} rozložme na súčet parciálnych (elementárnych) zlomkov nad poľom \(\mathbb{R}\), teda v rámci množiny reálnych čísel.
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ {{2\,x^4+3\,x^3-52\,x^2-115\,x+34}\over{x^3+2\,x^2-23\,x-60}}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ {{x-1}\over{x^5+5\,x^4+9\,x^3+5\,x^2-8\,x-12}}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ \frac{2p^3+6p^2+p-11}{p^3+3p^2-4}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ \frac{z-4}{z^3+3z^2-9z-27}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ \frac{2s^2-1}{s^3-7s^2+32s-60} \cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ \frac{4-3x^2}{x^3-12x^2+48x-64} \cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ \frac{p(2p+9)}{p^3+4p^2-12p-80} \cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ \frac{(z+3)(2z+6)}{z^3+15z^2+79z+145}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ \frac{s^4+3s^3-3s-3}{s^3+3s^2-4}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ {{33\,x-51-3\,x^2}\over{x^3+4\,x^2-9\,x+18}}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ {{p^2+2\,p-7}\over{p^3+17\,p^2+95\,p+175}}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ {{s^4-9\,s^3+57\,s^2-133\,s+198}\over{s^3-8\,s^2+46\,s-68}}\cdot \]
    Úloha: Rozložte v \(\mathbb{R}\) na parciálne zlomky výraz \[ {{3x^4+x^3+7\,x^2-16\,x+13}\over{x^3+x^2+3\,x-5}}\cdot \]
05. Definičný obor, grafy a základné vlastnosti funkcií
Riešené úlohy:
    Príklad: Určme definičný obor funkcie \[ f(x)=\frac{1}{2+\sqrt{3x+4}}. \]
    Príklad: Určme definičný obor funkcie \[ h(x)=\frac{1}{2+\sqrt[3]{x+4}}. \]
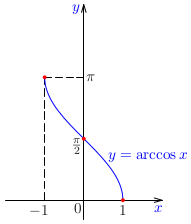
    Príklad: Určme definičný obor funkcie \[ g(x)=\log\left(\arccos\frac{x}{2x+3}\right). \]
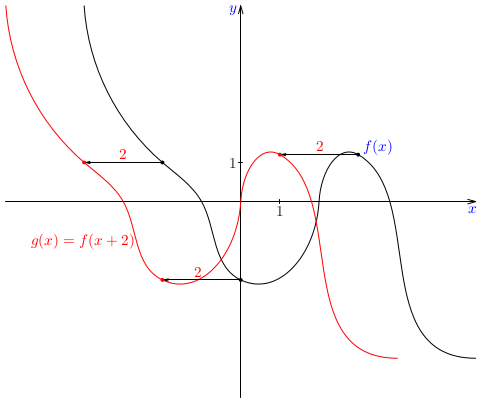
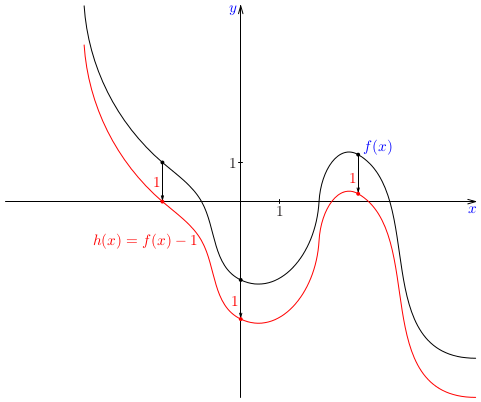
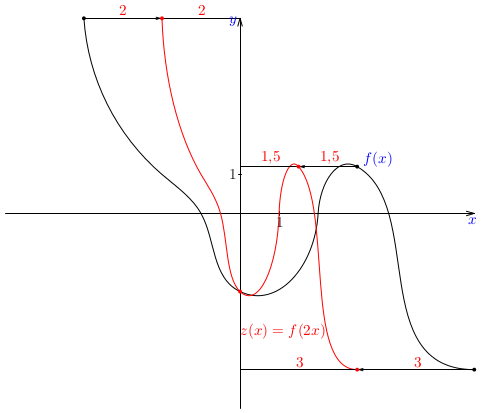
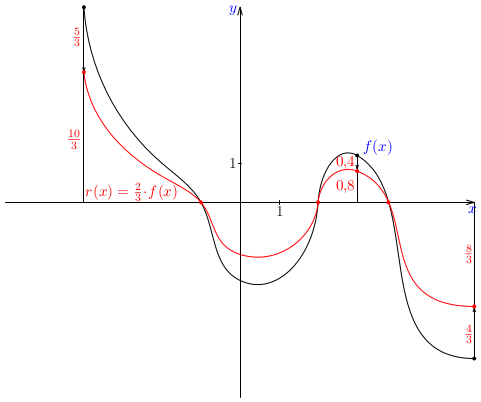
    Príklad: Na základe daného grafu funkcie \(f(x)\) zostrojte náčrt grafu funkcií \(f(x+2)\), \(f(x)-1\), \(f(2x)\) a \(\frac23\cdot f(x)\).
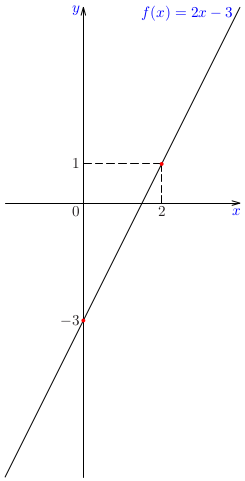
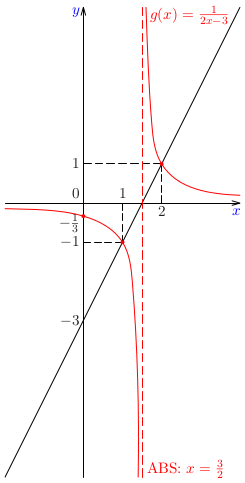
    Príklad: Zostrojte graf funkcie \(f(x)=2x-3\) a na základe náčrtu grafu zostrojte náčrt grafu funkcie \(g(x)=1/f(x)\).
    Poznámka: Funkcia \(g(x)=1/(2x-3)\) patrí do triedy funkcií, ktoré nazývame lineárne lomené funkcie. Sú to funkcie, ktorých predpis je podiel dvoch lineárnych funkcií, t. j. funkcie tvaru \[ r(x)=\frac{ax+b}{cx+d}. \] V našom prípade je \(a=0\), \(b=1\), \(c=2\) a \(d=-3\). Lineárne lomené funkcie patria ďalej do triedy racionálnych funkcií, ktorým sa budeme venovať v nasledujúcom cvičení.
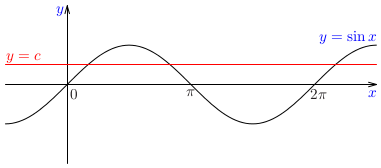
    Príklad: Na základe náčrtu grafu funkcie \(f(x)=\sin x\) posúďme, či má funkcie \(\sin x\) inverznú funkciu.
    Poznámka: Je zrejmé, že žiadna periodická funkcia nemôže mať inverznú funkciu!!!
    Poznámka: Je známe, že inverzná funkcia k funkcii \(\sin x\) sa nazýva \(\arcsin x\). Ako je to možné, ak funkcia \(\sin x\) nemôže mať inverznú funkciu? Vysvetlenie podáva riešenie nasledujúcej úlohy.
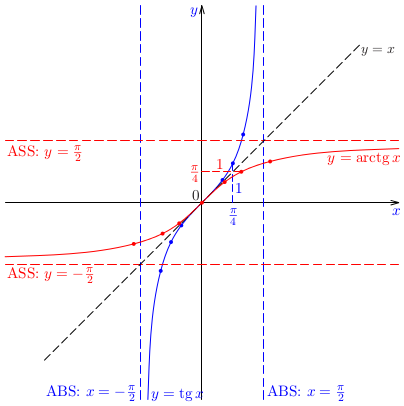
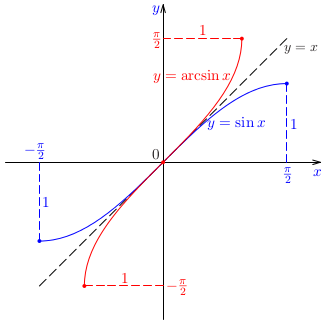
    Príklad: Určme takú časť grafu funkcie \(\sin x\), ktorá reprezentuje graf prostej funkcie. Pre túto časť načrtnime graf inverznej funkcie.
    Poznámka: Ako sme už vyššie konštatovali, funkcia \(\sin x\) nemá inverznú funkciu. Funkcia \(\arcsin x\) je inverzná funkcia k tzv. zúženiu funkcie \(\sin x\) na interval \(\langle-\pi /2;\pi /2\rangle\), ktoré označujeme ako \(\sin|_{\langle-\pi /2;\pi /2\rangle}\, x\).
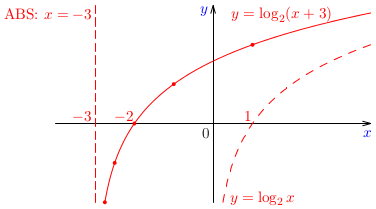
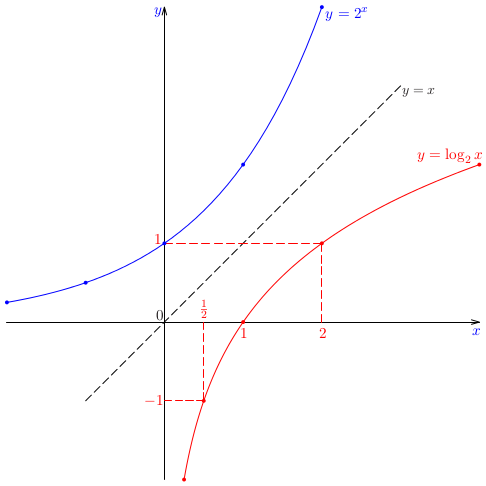
    Príklad: Načrtnime graf logaritmickej funkcie \(\log_2(x+3)\). Posúďte, či je táto funkcia párna alebo nepárna.
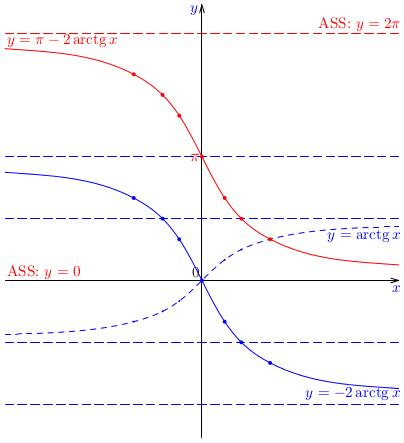
    Príklad: Načrtnime graf funkcie \(f(x)=\pi-2\arctg x\). Posúďte, či je táto funkcia párna alebo nepárna, rastúca alebo klesajúca.
Úlohy:
    Úloha: Načrtnite graf funkcie \(h(x)=2\arccotg x\).
    Úloha: Určte definičný obor funkcie \[ f(x)=\sqrt[3]{x^3+2x+3}-\frac{\arccos(x^2)}{3+\sqrt{1-x-x^2}}+\mathrm{e}^{-4x}\cdot\sin(3+2x). \]
    Úloha: Určte definičný obor funkcie \[ f(x)=\arcsin(\log_2(x+3))-\frac{x^2+5}{x^2-5}+\mathrm{e}^{-x}\cdot\cos(\pi x). \]
    Úloha: Určte definičný obor funkcie \[ f(x)=\arccotg(x+\pi^2)\cdot\sqrt[3]{x^6+\ln x-7}+\frac{11}{(3-2x)\cdot\ln(x^2+2x-3)}. \]
    Úloha: Určte definičný obor funkcie \[ f(x)=\mathrm{e}^x\cdot\sin(3x)-\frac{\arctg(x^2)}{x\cdot\sqrt{20-x-x^2}}+\sqrt[3]{x^3+2\cotg x+3}. \]
    Úloha: Určte definičný obor funkcie \[ f(x)=\frac{x}{2-\sqrt{x^2-4}}+\arccos\left(2^{-x}\right)+(x+\pi)\cdot\sqrt[5]{x^2-7}. \]
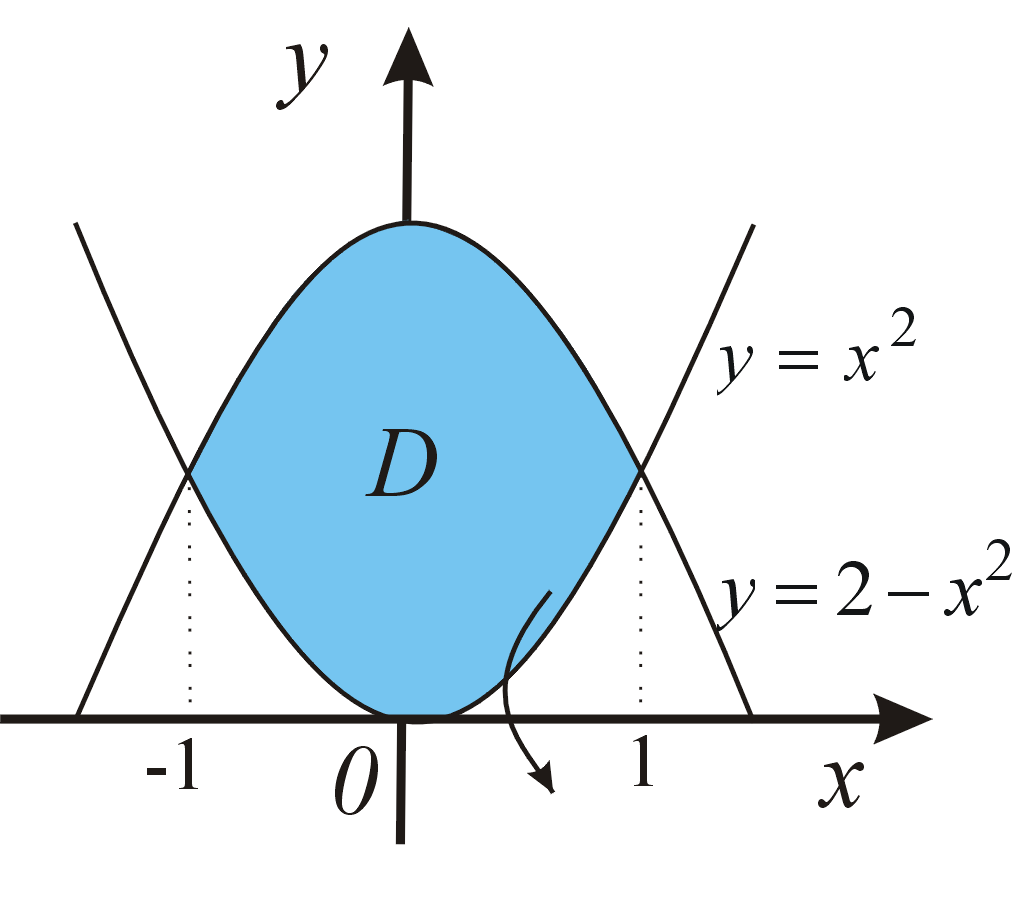
    Úloha: Určte definičný obor a načrtnite graf funkcie \(h(x)=2-x-x^2\). Zistite, či je funkcia párna alebo nepárna.
    Úloha: Určte definičný obor a načrtnite graf funkcie \(g(x)=2\cdot \cos(3x)+4\). Zistite, či je funkcia párna alebo nepárna.
    Úloha: Určte definičný obor a načrtnite graf funkcie \(f(x)=\mathrm{e}^{\sin (2x)}\). Zistite, či je funkcia párna alebo nepárna.
    Úloha: Určte definičný obor a načrtnite graf funkcie \(h(x)=\mathrm{e}^{-x}\cdot \cos (2x)\). Zistite, či je funkcia párna alebo nepárna.
06. Náčrt grafov jednoduchých racionálnych funkcií
Riešené úlohy:
    Príklad: Určme definičný obor funkcie \begin{equation}\label{cv61} f(x)=\frac{x}{x^2+1}. \end{equation}
    Príklad: Určme definičný obor funkcie \begin{equation}\label{cv62} g(x)=\frac{x^2+1}{x+1}. \end{equation}
    Príklad: Určme definičný obor funkcie \begin{equation}\label{cv63} h(x)=\frac{x^2-x-2}{x^3-7x-6}. \end{equation}
    Príklad: Určme všetky jednostranné limity v bodoch nespojitosti funkcie \begin{equation}\label{cv64} f(x)=\frac{x^2-4}{x^3-4x^2-3x+18}. \end{equation}
    Príklad: Určme všetky jednostranné limity v bodoch nespojitosti funkcie \begin{equation}\label{cv66} g(x)=\frac{x+4}{x^3}. \end{equation}
    Príklad: Určme asymptoty so smernicou funkcie funkcie \[ f(x)=\frac{x^2-x+5}{x+3}. \]
    Príklad: Určme ASS funkcie \[ r(x)=\frac{3-2x^3}{x^2+2x-4}. \]
    Príklad: Určme asymptoty so smernicou funkcie \[ g(x)=\frac{x^3}{x-5}. \]
    Príklad: Určme všetky nulové body funkcie (\ref{cv64}) \[ R(x)=\frac{P(x)}{Q(x)}=\frac{x^2-4}{x^3-4x^2-3x+18}. \]
    Príklad: Určme všetky nulové body funkcie \[ f(x)=\frac{x^3+10\,x^2+33\,x+36}{x} \] a skúmajme ich charakter, t. j. správanie sa funkcie v blízkosti nulových bodov.
    Poznámka: Môžeme si všimnúť, že ak je násobnosť bodu \(x_0\) nepárna (za predpokladu, že patrí do definičného oboru), bude nulový bod \((x_0;0)\) pretínať os \(o_x\) – vtedy budeme hovoriť o pretínacom nulovom bode – pri prechode cez tento bod sa mení znamienko funkčných hodnôt. Ak je násobnosť párna, budeme hovoriť o odrážacom nulovom bode – pri prechode cez tento bod sa zachováva znamienko funkčných hodnôt.
    Poznámka: Aj v prípade určovania asymptot bez smernice rozhoduje o zmene znamienka pri prechode cez bod nespojitosti jeho násobnosť v menovateli (za predpokladu, že nie je zároveň koreňom čitateľa). V prípade párnej násobnosti sa znamienka nemenia, v prípade nepárnej násobnosti sa znamienka menia. Tento fakt je možné efektívne využiť pri konštrukcii nárčtu grafu racionálnych (ale nielen racionálnych) funkcií.
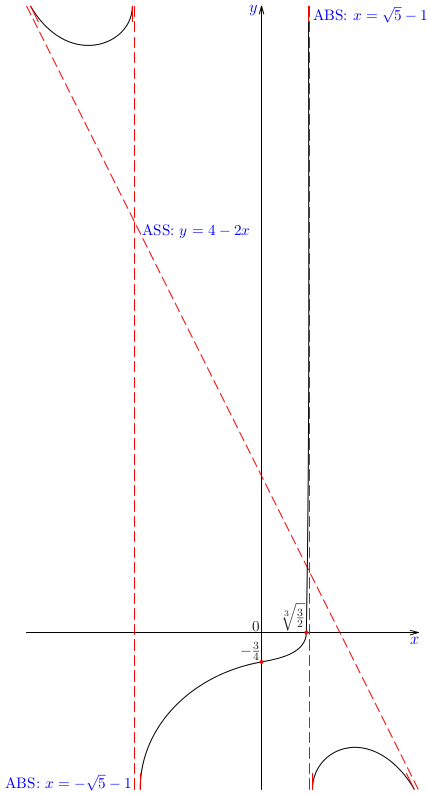
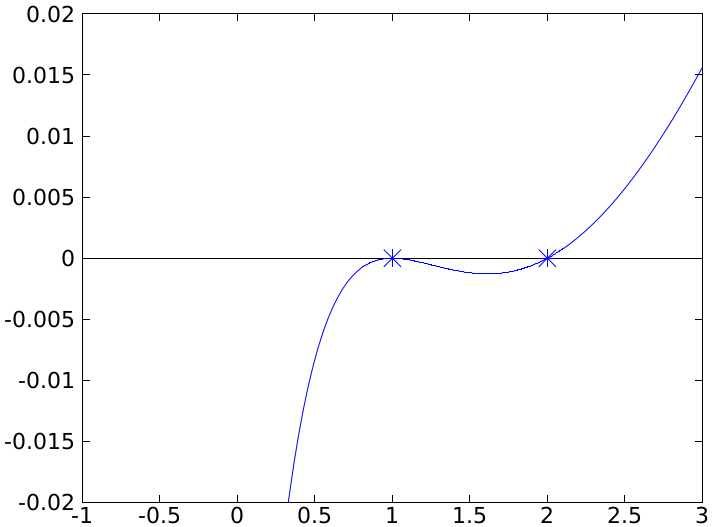
    Príklad: Načrtnime graf funkcie \[ g(x)={{x^3-4\,x^2+5\,x-2}\over{x^3+11\,x^2+35\,x+25}} \]
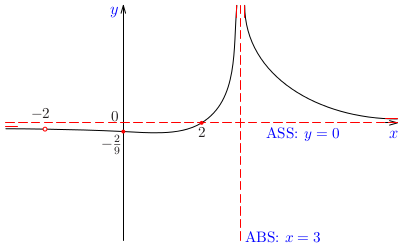
    Príklad: Načrtnime graf funkcie \[ h(x)={{x^2-x-6}\over{x^2}} \]
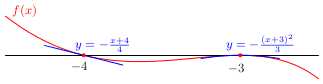
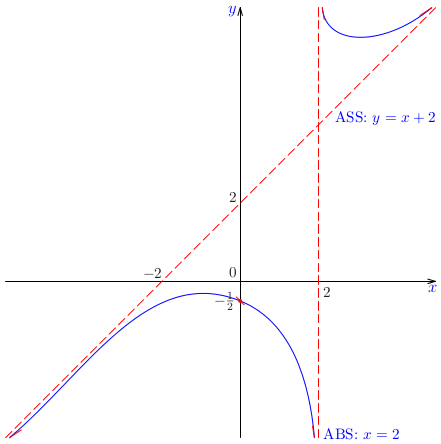
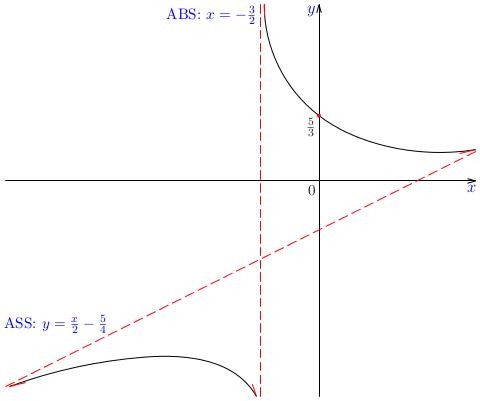
    Poznámka: V tomto prípade sa ukazuje, že hypotéza náčrtu grafu je nesprávna, t. j. nevystihuje všetky kvalitatívne vlastnosti samotného grafu. Napríklad funkcia \(h(x)\) má lokálne maximum, hypotéza grafu nie. Presnejší náčrt grafu vidíte na nasledujúcom obrázkoch.
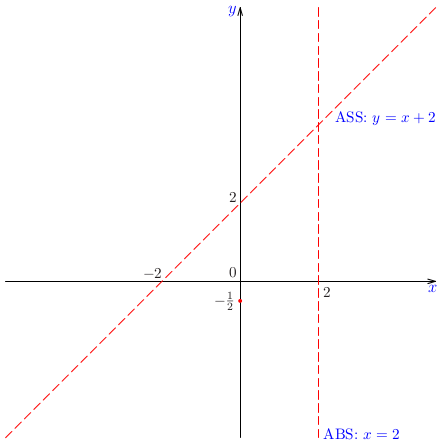
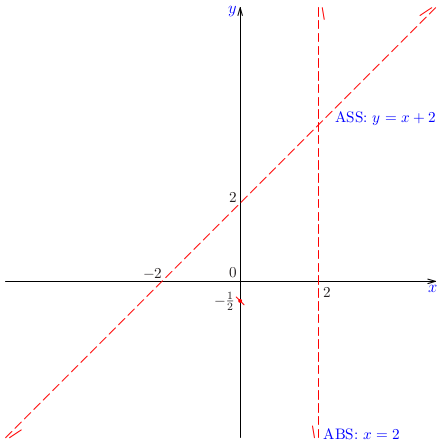
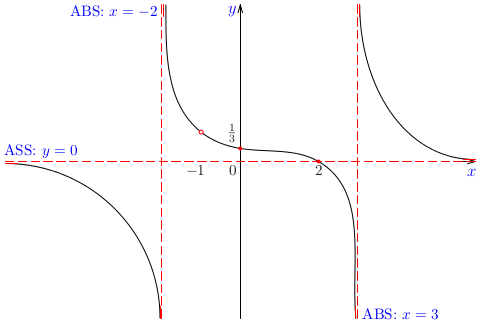
    Príklad: Načrtnime graf funkcie \[ f(x)={{x^2+1}\over{x-2}} \]
Úlohy:
    Úloha: Určte asymptoty so smernicou funkcie \[ f(x)=\frac{x^2-x+5}{x+3} \] metódou delenia polynómov.
    Úloha: Určte asymptoty so smernicou a bez smernice, nulové body a vytvorte hypotézu náčrtu grafu funkcie \[ f(x)=\frac{x}{x^2+1}. \]
    Úloha: Určte asymptoty so smernicou a bez smernice, nulové body a vytvorte hypotézu náčrtu grafu funkcie \[ g(x)=\frac{x^2+1}{x+1}. \]
    Úloha: Určte asymptoty so smernicou a bez smernice, nulové body a vytvorte hypotézu náčrtu grafu funkcie \[ h(x)=\frac{x^2-x-2}{x^3-7x-6}. \]
    Úloha: Určte asymptoty so smernicou a bez smernice, nulové body a vytvorte hypotézu náčrtu grafu funkcie \[ f(x)=\frac{x^2-4}{x^3-4x^2-3x+18} \]
    Úloha: Určte asymptoty so smernicou a bez smernice, nulové body a vytvorte hypotézu náčrtu grafu funkcie \[ g(x)=\frac{(x+4)^2}{x^4}. \]
    Úloha: Určte asymptoty so smernicou a bez smernice, nulové body a vytvorte hypotézu náčrtu grafu funkcie \[ f(x)=\frac{x^2-x+5}{2x+3}. \]
    Úloha: Určte asymptoty so smernicou a bez smernice, nulové body a vytvorte hypotézu náčrtu grafu funkcie \[ r(x)=\frac{3-2x^3}{x^2+2x-4}. \]
07. Tu napíšte názov cvičenia.
Riešené úlohy:
    Príklad: Vypočítajme deriváciu funkcie \(f(x)=x^4-2x+3\sqrt{x} +4 \sqrt[3]{x^4}-5\).
    Riešenie: Najprv prepíšeme odmocniny pomocou mocnín, \[f(x)=x^4-2x+3x^{\frac{1}{2}} +4 x^{\frac{4}{3}}-5.\] Využijeme vzťahy (1), (2), (3) a vzorce čísla 1. a 2. Dostávame \[f^\prime(x)=4x^3-2+\frac{3}{2}x^{-\frac{1}{2}} +\frac{16}{3} x^{\frac{1}{3}}.\]
    Príklad: Vypočítajme deriváciu funkcie \(f(x)=2^x \sin x\).
    Riešenie: Použijeme vzťah (4) a vzorce 4. a 7. Potom \[f^\prime(x)=2^x \ln 2 \sin x+2^x \cos x.\]
    Príklad: Vypočítajme deriváciu funkcie
    1. \(f(x)=(\tg x + \e^x - \log_2 x)^{11}\)
    2. \(f(x)=11^{\cos x+2\arctg x}\).
    Riešenie: Obidve funkcie sú zložené funkcie. \begin{itemize} \item[\emph{a)}] Zložky funkcie \(f(x)=(\tg x + \e^x - \log_2 x)^{11}\) sú \(u=g(x)\) a \(g(x)=\tg x + \e^x - \log_2 x\) a \(f(u)=u^{11}\). Podľa vzorca 15., dostaneme \[f^\prime(x)=(u^{11})^\prime_{u=g(x)}g^\prime(x) = (11u^{10})_{u=\tg x + \e^x - \log_2 x}(\tg x + \e^x - \log_2 x)^\prime=\] \[=11(\tg x + \e^x - \log_2 x)^{10}) \Big(\frac{1}{\cos^2 x}+\e^x-\frac{1}{x\ln 2}\Big).\] \item[\emph{b)}] Zložky funkcie \(f(x)=11^{\cos x+2\arctg x}\) sú \(u=g(x)\) a \(g(x)=\cos x+2\arctg x\) a \(f(u)=11^u\). Podľa vzorca 15., dostaneme \[f^\prime(x)=(11^u)^\prime_{u=g(x)}g^\prime(x) = (11^u\ln 11)_{u=\cos x+2\arctg x}(\cos x+2\arctg x)^\prime=\]\[= 11^{\cos x+2\arctg x}\ln 11 \Big(-\sin x+2\frac{1}{1+x^2}\Big) .\] \end{itemize}
    Príklad: Vypočítajme deriváciu funkcie \(f(x)=(\sin x)^{\ln x}\).
    Riešenie: Použijeme vzťah číslo 16. Upravíme funkciu \[f(x)=(\sin x)^{\ln x}=\e^{(\sin x)^{\ln x}} = \e^{\ln x \ln \sin x}\] a derivujeme ju pomocou vzorca 15., \[f^\prime(x)=(\e^{\ln x \ln \sin x})^\prime = \e^{\ln x \ln \sin x}(\ln x \ln \sin x)^\prime = \e^{\ln x \ln \sin x}\Big(\frac{1}{x} \ln \sin x+ \ln x \frac{1}{\sin x}\cos x\Big)= \]\[= (\sin x)^{\ln x}\Big(\frac{ \ln \sin x}{x}+ \ln x \tg x\Big).\]
    Príklad: Nájdime rovnicu dotyčnice a normály ku grafu funkcie \(y=x^2 +4x+1\) v bode \(A=[0, ?]\).
    Riešenie: Vypočítame \(y\)-ovú súradnicu bodu \(A\), \(y_0=1\). Teda \(A=[0,1]\). Funkciu \(f(x)=x^2 +4x+1\) zderivujeme, máme \(f^\prime(x)=2x +4\). Potom \(f^\prime(0)=4\), čo je smernica hľadanej dotyčnice. Podľa vzťahu pre výpočet rovnice dotyčnice ku grafu funkcie \(y=f(x)\) v bode \(A=[x_0, f(x_0)]\), dostávame rovnicu tejto dotyčnice: \[y-1=4(x-0),\] teda \[4x-y-1=0.\] Rovnica normály ku grafu funkcie \(y=f(x)\) v bode \(A\) je \[y-1=-\frac{1}{4}(x-0),\] teda \[x+4y-4=0.\]
    Príklad: Nájdime rovnicu dotyčnice a normály ku grafu funkcie \(y=\ln x\), pričom dotyčnica je rovnobežná s priamkou \(p:\ 2x -y-3=0\).
    Riešenie: Keďže dotyčnica je rovnobežná s priamkou \(p\), obe priamky majú rovnaké normálové vektory \(\vec{n}_p=(2,-1)=\vec{n}_t\), rovnica dotyčnice \(t\) je \[2x-y+c=0,\] t. j. \[y=2x+c.\] Teda má smernicu 2. Ale jej smernica je tiež \(f^\prime(x_0)=\frac{1}{x_0} \), odtiaľ získame \(x_0=\frac{1}{4}\). Potom \(y_0=f(x_0)=\ln \frac{1}{4}\). Máme \(A=[\frac{1}{4},\ln \frac{1}{4}]\). Vypočítame neznámu konštantu \(c\) dosadením súradníc dotykového bodu do rovnice dotyčnice, \(2\frac{1}{4}-\ln \frac{1}{4}+c=0\), odtiaľ dostávame \(c=\ln \frac{1}{4}- \frac{1}{2}\). Rovnica dotyčnice je: \[y=2x+\ln \frac{1}{4}+\frac{1}{2}.\] Rovnica normály ku grafu funkcie \(y=\ln x\) v bode \(A=[\frac{1}{4},\ln \frac{1}{4}]\) je \[y-\ln \frac{1}{4}=-\frac{1}{2}(x-\frac{1}{4}),\] teda \[4x+8y-8\ln \frac{1}{4}-1=0.\]
    Príklad: Nájdime rovnicu dotyčnice a normály ku grafu funkcie \(y=x^2 -2x+3\), ak dotyčnica je kolmá na priamku \(q:\ x +y-1=0\).
    Riešenie: Keďže dotyčnica je kolmá na priamku \(q\), skalárny súčin ich normálových vektorov je nula. Z rovnice priamky \(q\) vieme určiť jej normálový vektor \(\vec{n}_q=(1,1)\). Potom normálový vektor hľadanej dotyčnice \(t\) je \(\vec{n}_t=(1,-1)\). Rovnica dotyčnice \(t\) je \[x-y+c=0,\] t. j. \[y=x+c.\] Teda jej smernica je 1. Ale jej smernica je tiež \(f^\prime(x_0)=2x_0-2 \), odtiaľ získame \(x_0=\frac{3}{2}\), potom \(y_0=f(x_0)=(\frac{3}{2})^2 -2\frac{3}{2}+3=\frac{9}{4}\), máme \(A=[\frac{3}{2}, \frac{9}{4}]\). Vypočítame neznámu konštantu \(c\) dosadením súradníc dotykového bodu do rovnice dotyčnice, \(\frac{3}{2}- \frac{9}{4}+c=0\). Odtiaľ dostávame \(c=\frac{3}{4}\). Rovnica dotyčnice je: \[y=x+ \frac{3}{4}.\] Rovnica normály ku grafu funkcie \(y=x^2 -2x+3\) v bode \(A=[\frac{3}{2}, \frac{9}{4}]\) je \[y- \frac{9}{4}=-(x-\frac{3}{2}),\] teda \[4x+4y-15=0.\]
    Príklad: Vypočítajme \(y^{\prime\prime}\), ak \(y=\frac{x}{\sqrt{1+x^2}}\).
    Riešenie: Vypočítajme najprv prvú deriváciu \(y^\prime\). Máme \[y^\prime=\frac{\sqrt{1+x^2}-x\frac{1}{2}\frac{2x}{\sqrt{1+x^2}}}{1+x^2}=\frac{\frac{1+x^2-x^2}{\sqrt{1+x^2}}}{1+x^2}=\frac{1}{\sqrt{(1+x^2)^3}}\] Podľa definície druhej derivácie je \[y^{\prime\prime}=(y^\prime)^\prime=\left((1+x^2)^{-\frac{3}{2}}\right)^\prime=-\frac{3}{2}(1+x^2)^{-\frac{5}{2}}2x=-\frac{3x}{\sqrt{(1+x^2)^5}}\].
    Príklad: Daná je funkcia \(y=x\e^{-x^2}\). Vypočítajme \(y^{\prime\prime}(1)\).
    Riešenie: Vypočítajme najprv prvú deriváciu \(y^\prime\). Dostávame \[y^\prime=\e^{-x^2}+x\e^{-x^2}(-2x)=\e^{-x^2}(1-2x^2)\] Potom druhá derivácia je \[y^{\prime\prime}=\left(\e^{-x^2}(1-2x^2)\right)^\prime=\e^{-x^2}(-2x)(1-2x^2)+\e^{-x^2}(-4x)=\e^{-x^2}(-2x+4x^3-4x)=\e^{-x^2}(4x^3-6x).\] Pre \(x=1\) platí \(y^{\prime\prime}(1)=\e^{-1^2}(4-6)=-2\e^{-1}\).
    Príklad: Vypočítajme deriváciu štvrtého rádu \(y^{(4)}\) funkcie \(y=\frac{2}{(3x+4)^5}\).
    Riešenie: Platí \[y^\prime=\left(\frac{1}{(2x+3)^4}\right)^\prime=((2x+3)^{-4})^\prime=-8(2x+3)^{-5}=\frac{-8}{(2x+3)^5 }\] \[y^{\prime\prime}=(y^\prime)^\prime=\left(\frac{-8}{(2x+3)^5}\right)^\prime=-8\cdot (-10)\cdot (2x+3)^{-6}=\frac{80}{(2x+3)^6}\] \[y^{\prime\prime\prime}=(y^{\prime\prime})^\prime=\left(\frac{80}{(2x+3)^6}\right)^\prime=80\cdot (-12)\cdot (2x+3)^{-7}=\frac{-960}{(2x+3)^7}\] \[y^{(4)}=(y^{\prime\prime\prime})^\prime=\left(\frac{-960}{(2x+3)^7}\right)^\prime=-960\cdot (-14)\cdot (2x+3)^{-8}=\frac{13440}{(2x+3)^8}\]
Úlohy:
    Úloha: Vypočítajme deriváciu funkcie \(f(x)=\frac{\ln x}{x^3}.\)
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
08. L'Hospitalovo pravidlo
Riešené úlohy:
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow 1}\frac{x^2-1}{x^3-2x^2+2x-1}\).
    Riešenie: Položme \(f(x)=x^2-1\) a \(g(x)=x^3-2x^2+2x-1\). Potom \(\lim\limits_{x\rightarrow 1} f(x)=\lim\limits_{x\rightarrow 1} g(x)=0\). Použitím L'Hospitalovho pravidla dostaneme \[\lim\limits_{x\rightarrow 1}\frac{x^2-1}{x^3-2x^2+2x-1}=\lim\limits_{x\rightarrow 1}\frac{2x}{3x^2-4x+2}=2.\]
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow \infty}\frac{\e^{2x}}{x^2}\).
    Riešenie: Položme \(f(x)=\e^{2x}\) a \(g(x)=x^2\). Potom \(\lim\limits_{x\rightarrow \infty} f(x)=\lim\limits_{x\rightarrow \infty} g(x)=\infty\). Keďže aj \(\lim\limits_{x\rightarrow \infty} f^\prime(x)=\lim\limits_{x\rightarrow \infty}g^\prime(x)=\infty\), použitím L'Hospitalovho pravidla dostaneme \[\lim\limits_{x\rightarrow \infty}\frac{\e^{2x}}{x^2}=\lim\limits_{x\rightarrow \infty}\frac{2\e^{2x}}{2x}=\lim\limits_{x\rightarrow \infty}\frac{4\e^{2x}}{2}=\infty.\]
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow 0^+}\frac{\ln x}{\cotg x}\).
    Riešenie: Táto limita je tvaru \(\frac{-\infty}{\infty}\), pričom \(f(x)=\ln x\) a \(g(x)=\cotg x\). Potom platí \[\lim\limits_{x\rightarrow 0^+}\frac{\ln x}{\cotg x}=\lim\limits_{x\rightarrow 0^+}\frac{\frac{1}{x}}{-\frac{1}{\sin^2 x}}=\lim\limits_{x\rightarrow 0^+}\frac{-\sin^2 x}{ x}=\lim\limits_{x\rightarrow 0^+}\frac{-2\sin x \cos x}{ 1}=0.\]
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow 0^+}\left(\frac{1}{2x}-\frac{1}{\sin x}\right)\).
    Riešenie: Daná limita je typu \(\infty - \infty\). Úpravou dostaneme \[\lim\limits_{x\rightarrow 0^+}\left(\frac{1}{2x}-\frac{1}{\sin x}\right)=\lim\limits_{x\rightarrow 0^+}\frac{\sin x - 2x}{2x\ \sin x}.\] Táto limita je typu \(\frac{0}{0}\), pričom \(f(x)=\sin x - 2x\) a \(g(x)=2x\ \sin x\). Potom použitím L'Hospitalovho pravidla dostaneme \[\lim\limits_{x\rightarrow 0^+}\frac{\sin x - 2x}{2x\ \sin x}=\lim\limits_{x\rightarrow 0^+}\frac{\cos x - 2}{2\sin x\ +2x\cos x}=\frac{-1}{\lim\limits_{x\rightarrow 0^+}(2\sin x\ +2x\cos x)}=-\infty.\] Teda \[\lim\limits_{x\rightarrow 0^+}\left(\frac{1}{2x}-\frac{1}{\sin x}\right)=-\infty.\]
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow 0^+}x\ln x\).
    Riešenie: Daná limita je typu \(0\cdot (- \infty)\). Úpravou dostaneme \[\lim\limits_{x\rightarrow 0^+}x\ln x=\lim\limits_{x\rightarrow 0^+}\frac{\ln x}{x^{-1}}.\] Táto limita je typu \(\frac{0}{0}\), pričom \(f(x)=\ln x\) a \(g(x)=x^{-1}\). Potom použitím L'Hospitalovho pravidla dostaneme \[\lim\limits_{x\rightarrow 0^+}\frac{\ln x}{x^{-1}}=\lim\limits_{x\rightarrow 0^+}\frac{\frac{1}{x}}{-x^{-2} }=\lim\limits_{x\rightarrow 0^+}(-x )=0.\] Teda \[\lim\limits_{x\rightarrow 0^+}x\ln x=0.\]
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow 0^+}x^x\).
    Riešenie: Daná limita je typu \(0^0\). Úpravou dostaneme \[\lim\limits_{x\rightarrow 0^+}x^ x=\lim\limits_{x\rightarrow 0^+}\e^{\ln x^x}=\lim\limits_{x\rightarrow 0^+}\e^{x\ln x}.\] Keďže táto limita je limitou zloženej funkcie, platí \[\lim\limits_{x\rightarrow 0^+}\e^{x\ln x}=\e^{\lim\limits_{x\rightarrow 0^+}x\ln x}.\] Teraz využijeme výsledok predchádzajúceho príkladu, máme \[\e^{\lim\limits_{x\rightarrow 0^+}x\ln x}=\e^0=1.\] Teda \[\lim\limits_{x\rightarrow 0^+} x^x=1.\]
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow \infty}x^{\frac{1}{x}}\).
    Riešenie: Daná limita je typu \(\infty^0\). Úpravou dostaneme \[\lim\limits_{x\rightarrow \infty}x^{\frac{1}{x}}=\lim\limits_{x\rightarrow \infty}\e^{\ln {x^{\frac{1}{x}}}}=\lim\limits_{x\rightarrow \infty}\e^{\frac{\ln x}{x}}.\] Opäť sa jedná o limitu zloženej funkcie, teda \[\lim\limits_{x\rightarrow \infty}\e^{\frac{\ln x}{x}}=\e^{\lim\limits_{x\rightarrow \infty}\frac{\ln x}{x}}=\e^{\lim\limits_{x\rightarrow \infty}\frac{\frac{1}{x}}{1}}=\e^0=1.\] Teda \[\lim\limits_{x\rightarrow \infty}x^{\frac{1}{x}}=1.\]
    Príklad: Vypočítajme \(\lim\limits_{x\rightarrow 1^-}x^{\frac{1}{1-x}}\).
    Riešenie: Daná limita je typu \(1^\infty\). Úpravou dostaneme \[\lim\limits_{x\rightarrow 1^-}x^{\frac{1}{1-x}}=\lim\limits_{x\rightarrow 1^-}\e^{\ln {x^{\frac{1}{1-x}}}}=\lim\limits_{x\rightarrow 1^-}\e^{\frac{\ln x}{1-x}}.\] Opäť sa jedná o limitu zloženej funkcie, teda \[\lim\limits_{x\rightarrow 1^-}\e^{\frac{\ln x}{1-x}}=\e^{\lim\limits_{x\rightarrow 1^-}\frac{\ln x}{1-x}}=\e^{\lim\limits_{x\rightarrow 1^-}\frac{\frac{1}{x}}{-1}}=\e^{\lim\limits_{x\rightarrow 1^-}\frac{-1}{x}}=\e^{-1}.\] Teda \[\lim\limits_{x\rightarrow 1^-}x^{\frac{1}{1-x}}=\frac{1}{\e}.\]
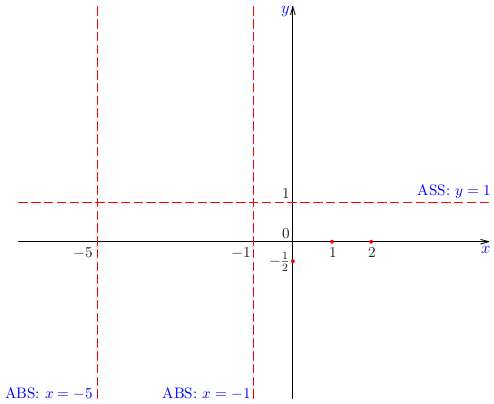
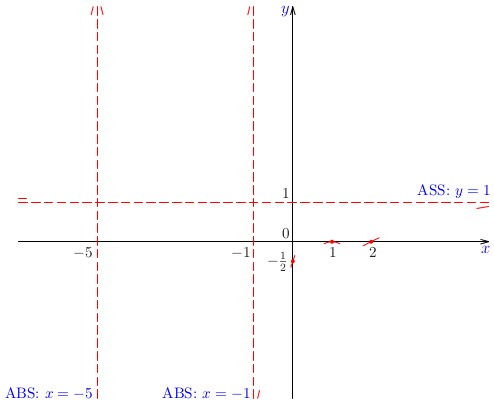
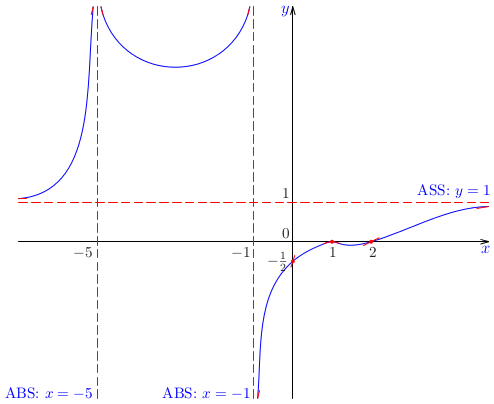
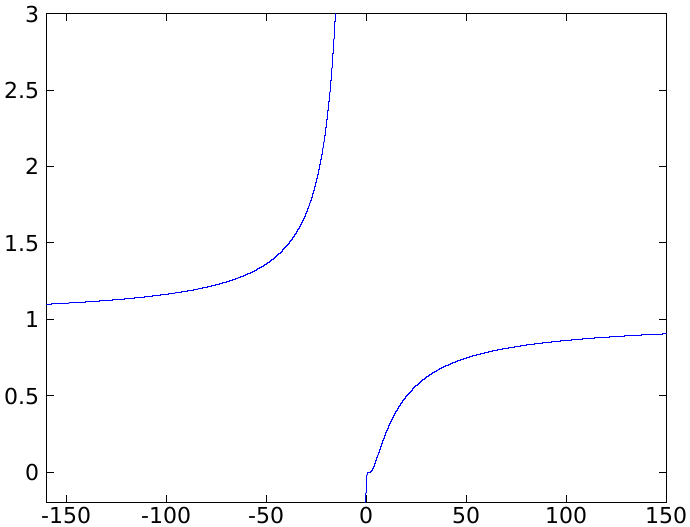
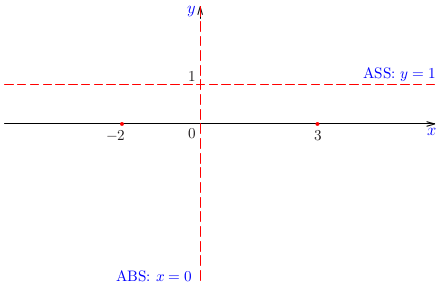
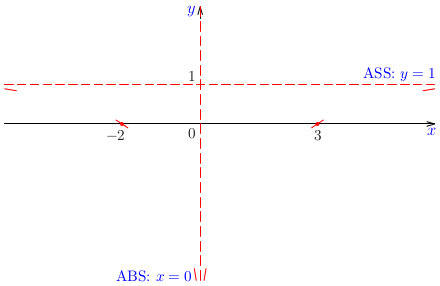
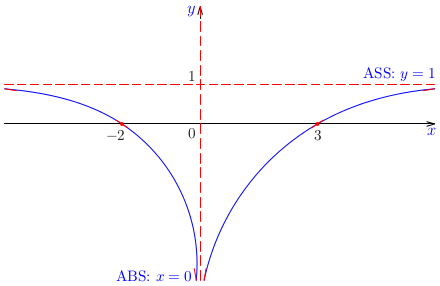
    Príklad: Nájdime asymptoty grafu funkcie \(y=\frac{x}{x-1}\).
    Riešenie: Keďže platí \[\lim\limits_{x\rightarrow 1^+}\frac{x}{x-1}=\infty,\] priamka \(y=1\) je asymptotou bez smernice danej funkcie. Iné asymptoty bez smernice neexistujú, lebo daná funkcia je spojitá pre každé \(x\neq 1\). Teraz hľadajme asymptoty so smernicou. Vypočítajme limity
    \(\qquad a=\displaystyle\lim\limits_{x\rightarrow \infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow \infty}\frac{1}{x-1}=0,\)

    \(\qquad b=\displaystyle\lim\limits_{x\rightarrow \infty}(f(x)-ax)=\lim\limits_{x\rightarrow \infty}\left(\frac{x}{x-1}-0\cdot x\right)=1,\)

    \(\qquad \displaystyle a=\lim\limits_{x\rightarrow -\infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow -\infty}\frac{1}{x-1}=0,\)

    \(\qquad b=\displaystyle\lim\limits_{x\rightarrow -\infty}(f(x)-ax)=\lim\limits_{x\rightarrow -\infty}\left(\frac{x}{x-1}-0\cdot x\right)=1.\)

    Teda priamka \(y=1\) je asymptotou so smernicou grafu danej funkcie.
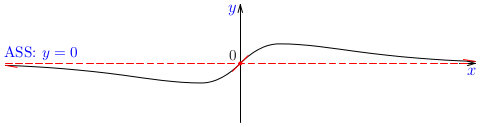
    Príklad: Nájdime asymptoty grafu funkcie \(y=x\cdot \arctg x\).
    Riešenie: Daná funkcia je spojitá pre každé \(x\), asymptotou bez smernice danej funkcie neexistuje. Hľadajme asymptoty so smernicou. Vypočítame limity
    \(\qquad a=\lim\limits_{x\rightarrow \infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow \infty} \arctg x=\frac{\pi}{2}, \)

    \(\qquad b=\lim\limits_{x\rightarrow \infty}(f(x)-ax)=\lim\limits_{x\rightarrow \infty}\left(x \arctg x - \frac{\pi}{2} x\right)= \lim\limits_{x\rightarrow \infty}x \left(\arctg x - \frac{\pi}{2}\right)= \)

    \( \qquad \phantom{b}=\lim\limits_{x\rightarrow \infty}\frac{\arctg x - \frac{\pi}{2}}{ x^{-1}}=\lim\limits_{x\rightarrow \infty}\frac{\frac{1}{1+x^2}}{-x^{-2}}= \lim\limits_{x\rightarrow \infty}\frac{-x^2}{1+x^2}=-1, \)

    \( \qquad a=\lim\limits_{x\rightarrow -\infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow -\infty} \arctg x=-\frac{\pi}{2}, \)

    \( \qquad b=\lim\limits_{x\rightarrow -\infty}(f(x)-ax)=\lim\limits_{x\rightarrow -\infty}\left(x \arctg x + \frac{\pi}{2} x\right)= \lim\limits_{x\rightarrow -\infty}x \left(\arctg x - \frac{\pi}{2}\right)= \)

    \( \qquad \phantom{b}=\lim\limits_{x\rightarrow -\infty}\frac{\arctg x - \frac{\pi}{2}}{ x^{-1}}=\lim\limits_{x\rightarrow -\infty}\frac{\frac{1}{1+x^2}}{-x^{-2}}=\lim\limits_{x\rightarrow -\infty}\frac{-x^2}{1+x^2}=-1. \)

    Teda priamky \(y=\frac{\pi}{2}x-1\) a \(y=-\frac{\pi}{2}x-1\) sú asymptotami so smernicou grafu danej funkcie.
Úlohy:
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
09. Priebeh funkcie\(\def\a{&}\def\e{\mathrm{e}}\)
Riešené úlohy:
    Príklad: Zistime priebeh funkcie \(f(x)=\frac{x^2+1}{x}\).
    Riešenie: \
    1. Funkcia \(f\) je definovaná pre všetky \(x\neq 0\), t. j. definičný obor funkcie je \(D(f)=(-\infty,0)\cup (0,\infty)\).
    2. Pre každé \(x\in D(f)\) existuje \((-x)\in D(f)\) a platí \(f(-x)=\frac{(-x)^2+1}{-x}=-\frac{x^2+1}{x}=-f(x)\). Funkcia \(f\) je nepárna.
    3. Keďže rovnica \(x^2+1=0\) nemá riešenie, nulové body funkcie \(f\) neexistujú.
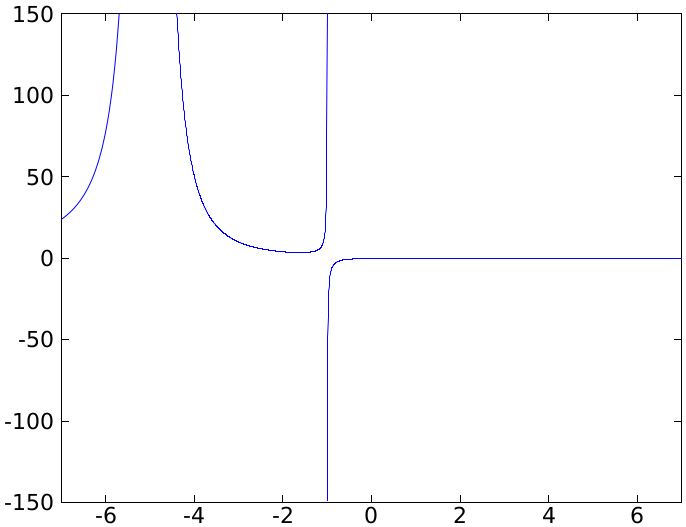
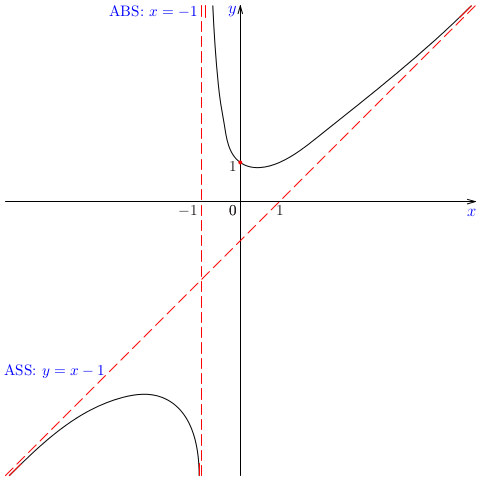
    4. Funkcie \(x^2+1\) aj \(x\) sú spojité, teda aj funkcia \(f(x)=\frac{x^2+1}{x}\) je spojitá v každom čísle \(x\in D(f)\). Je nespojitá v čísle \(x=0\). Pre limity funkcie \(f\) v čísle \(x=0\) platí \[\lim\limits_{x\rightarrow 0^+}\frac{x^2+1}{x}=\infty,\ \ \ \ \ \ \lim\limits_{x\rightarrow 0^+}\frac{x^2+1}{x}=-\infty.\] Teda priamka \(x=1\) je asymptotou bez smernice danej funkcie. Určme, či existujú asymptoty so smernicou \(y=ax+b\) ku grafu funkcie \(f\). Vypočítame limity \[a=\lim\limits_{x\rightarrow \infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow \infty}\frac{\frac{x^2+1}{x}}{x}=\lim\limits_{x\rightarrow \infty}\frac{x^2+1}{x^2}=1\] \[b=\lim\limits_{x\rightarrow \infty}(f(x)-ax)=\lim\limits_{x\rightarrow \infty}\left(\frac{x^2+1}{x}-x\right)=\lim\limits_{x\rightarrow \infty}\frac{1}{x}=0\] Podobne vypočítame \[a=\lim\limits_{x\rightarrow -\infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow -\infty}\frac{\frac{x^2+1}{x}}{x}=\lim\limits_{x\rightarrow -\infty}\frac{x^2+1}{x^2}=1\] \[b=\lim\limits_{x\rightarrow -\infty}(f(x)-ax)=\lim\limits_{x\rightarrow -\infty}\left(\frac{x^2+1}{x}-x\right)=\lim\limits_{x\rightarrow -\infty}\frac{1}{x}=0\] Teda priamka \(y=x\) je asymptota so smernicou.
    5. Vypočítajme deriváciu \[f^\prime(x)=\left(\frac{x^2+1}{x}\right)^\prime=\frac{2x\cdot x -(x^2+1)}{x^2}=\frac{x^2-1}{x^2}.\] Derivácia \(f^\prime\) sa rovná nule práve vtedy, keď \(x^2-1=0\), t. j. keď \(x=1\) alebo \(x=-1\). Derivácia \(f^\prime\) je definovaná pre každé \(x\in D(f)\). Stacionárnymi bodmi funkcie \(f\) sú čísla 1, -1.
    6. Stacionárne body a číslo 0, kde nie je funkcia definovaná, rozdeľujú definičný obor \(D(f)\) na intervaly \[ (-\infty,-1),\ (-1,0), \ (0,1),\ (1,-\infty).\] Zistime znamienka derivácie v jednotlivých intervaloch a tak určíme monotónnosť funkcie. Urobme tabuľku \[ \begin{array}{r|c|c|c|c|} x \a (-\infty,-1) \a (-1,0) \a (0,1) \a (1,\infty)\\ \hline f^\prime(x) \a + \a - \a - \a + \\ \hline f(x) \a \nearrow \a \searrow \a \searrow \a \nearrow\\ \hline \end{array} \] Funkcia \(f\) je klesajúca na intervaloch \((-1,0),\ (0,1)\) a rastúca na intervaloch \((-\infty,-1),\ (1,\infty)\).
    7. Na základe monotónnosti funkcie \(f\) určíme jej lokálne extrémy. V čísle \(x=-1\) funkcia nadobúda lokálne maximum, v čísle \(x=1\) nadobúda lokálne minimum a v čísle \(x=0\) funkcia nemôže nadobúdať extrém, keďže v ňom nie je definovaná.
    8. Vypočítajme druhú deriváciu \[f^{\prime\prime}(x)=\left(\frac{x^2-1}{x^2}\right)^\prime=\frac{2x\cdot x^2-(x^2-1)2x}{x^4}=\frac{2}{x^3}.\] Derivácia \(f^{\prime\prime}\) je definovaná pre každé \(x\in D(f)\) a je vždy nenulová, pretože \(\frac{2}{x^3}\neq 0\). Teda inflexné body neexistujú.
    9. Zistime znamienka druhej derivácie v jednotlivých intervaloch definičného oboru a potom určme konkávnosť a konvexnosť. Urobme tabuľku \[ \begin{array}{r|c|c|} x \a (-\infty,0)\a (0,\infty)\\ \hline f^{\prime\prime}(x) \a - \a + \\ \hline f(x) \a \cap \a \cup\\ \hline \end{array} \] Funkcia je konkávna na intervale \((-\infty,0)\) a konvexná na intervale \((0,\infty)\).
    Príklad: Zistime priebeh funkcie \(f(x)=x \ln x\).
    Riešenie: \
    1. Funkcia \(f\) je definovaná pre všetky \(x> 0\), t. j. definičný obor funkcie je \(D(f)=(0,\infty)\).
    2. Keďže neplatí, že pre každé \(x\in D(f)\) existuje \((-x)\in D(f)\), funkcia \(f(x)\) nie je ani párna ani nepárna.
    3. Rovnica \(x \ln x=0\) má riešenie \(x=1\), je to nulový bod funkcie \(f\).
    4. Funkcie \(x\) aj \(\ln x\) sú spojité, teda aj funkcia \(f(x)=x\ln x\) je spojitá v každom čísle \(x\in D(f)\). Vypočítajme jednostrannú limitu funkcie \(f\) v čísle \(x=0\). \[\lim\limits_{x\rightarrow 0^+}x\ln x=\lim\limits_{x\rightarrow 0^+}\frac{\ln x}{\frac{1}{x}}=\lim\limits_{x\rightarrow 0^+}\frac{\frac{1}{x}}{-\frac{1}{x^{2}}}=0.\] Limita nie je nevlastné číslo, teda priamka \(x=0\) nie je asymptotou bez smernice danej funkcie. Určme, či existujú asymptoty so smernicou \(y=ax+b\) ku grafu funkcie \(f\). Vypočítame najprv limitu \[a=\lim\limits_{x\rightarrow \infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow \infty}\ln x=\infty\] Teda asymptota so smernicou neexistuje.
    5. Vypočítajme deriváciu \[f^\prime(x)=\left(x\ln x\right)^\prime=\ln x+x\frac{1}{x}=\ln +1.\] Derivácia \(f^\prime\) sa rovná nule práve vtedy, keď \(\ln x=-1\), t. j. keď \(x=\frac{1}{\e}\). Funkcia \(f^\prime\) je definovaná pre každé \(x\in D(f)\). Stacionárnym bodom funkcie \(f\) je číslo \(\frac{1}{\e}\).
    6. Číslo \(\frac{1}{\e}\) rozdeľuje definičný obor \(D(f)\) na intervaly \[ \left(0, \frac{1}{\e}\right),\ \left( \frac{1}{\e},\infty\right).\] Zistime znamienka derivácie v týchto intervaloch. Urobme tabuľku \[ \begin{array}{r|c|c|} x \a (0,\frac{1}{\e}) \a (\frac{1}{\e},\infty)\\ \hline f^\prime(x) \a - \a + \\ \hline f(x) \a \searrow \a \nearrow\\ \hline \end{array} \] Funkcia \(f\) je klesajúca na intervale \((0,\frac{1}{\e})\) a rastúca na intervale \((\frac{1}{\e},\infty)\).
    7. Na základe predchádzajúcej tabuľky vieme, že v čísle \(x=\frac{1}{\e}\) funkcia \(f\) nadobúda lokálne minimum.
    8. Vypočítajme druhú deriváciu \[f^{\prime\prime}(x)=\frac{1}{x}.\] Derivácia \(f^{\prime\prime}\) je definovaná pre každé \(x\in D(f)\) a je vždy kladná. Teda inflexné body funkcie \(f\) neexistujú.
    9. Druhá derivácia \(f^{\prime\prime}\) je vždy kladná, funkcia \(f\) je na celom definičnom obore konvexná.
    Príklad: Zistime priebeh funkcie \(f(x)=x^2 \e ^{\frac{1}{x}}\).
    Riešenie: \
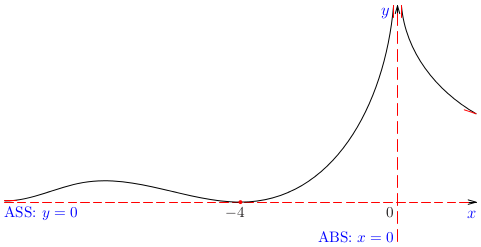
    1. Funkcia \(f\) je definovaná pre všetky \(x\neq 0\), t. j. definičný obor funkcie je \(D(f)=(-\infty,0)\cup (0,\infty)\).
    2. Keďže pre každé \(x\in D(f)\) existuje \((-x)\in D(f)\), pre ktoré \(f(-x)=(-x)^2\e^{\frac{1}{-x}}=x^2\e^{-\frac{1}{x}}\). Nakoľko \(f(-x)\neq f(x)\) a tiež \(f(-x)\neq -f(x)\), funkcia \(f\) nie je ani je párna ani nepárna.
    3. Vieme, že \(x^2 \e ^{\frac{1}{x}}\neq 0\), nulové body funkcie \(f\) neexistujú.
    4. Funkcie \(x^2\) aj \( \e ^{\frac{1}{x}}\) sú spojité, teda aj funkcia \(f(x)=x^2 \e ^{\frac{1}{x}}\) je spojitá v každom čísle \(x\in D(f)\). V čísle \(x=0\) je funkcia \(f\) nespojitá. Pre limity funkcie \(f\) v čísle \(x=0\) platí \[\lim\limits_{x\rightarrow 0^-}x^2 \e ^{\frac{1}{x}}=0\] \[\lim\limits_{x\rightarrow 0^+}x^2 \e ^{\frac{1}{x}}=\lim\limits_{x\rightarrow 0^+} \frac{\e ^{\frac{1}{x}}}{\frac{1}{x^2}}=\lim\limits_{x\rightarrow 0^+} \frac{-\frac{1}{x^2}\e ^{\frac{1}{x}}}{-2\frac{1}{x^3}}=\lim\limits_{x\rightarrow 0^+} \frac{\e ^{\frac{1}{x}}}{2\frac{1}{x}}=\lim\limits_{x\rightarrow 0^+} \frac{-\frac{1}{x^2}\e ^{\frac{1}{x}}}{-2\frac{1}{x^2}}=\lim\limits_{x\rightarrow 0^+} \frac{1}{2}\e ^{\frac{1}{x}}=\infty.\] Priamka \(x=0\) je asymptotou bez smernice danej funkcie. Určme, či existujú asymptoty so smernicou \(y=ax+b\) ku grafu funkcie \(f\). Vypočítame najprv limity \[a=\lim\limits_{x\rightarrow \infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow \infty}x\e ^{\frac{1}{x}}=\infty.\] \[a=\lim\limits_{x\rightarrow -\infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow -\infty}x\e ^{\frac{1}{x}}=-\infty.\] Teda asymptota so smernicou neexistuje.
    5. Vypočítajme deriváciu \[f^\prime(x)=\left(x^2 \e ^{\frac{1}{x}}\right)^\prime=2x\e ^{\frac{1}{x}}+x^2\e ^{\frac{1}{x}}\left(-\frac{1}{x^2}\right)=\e ^{\frac{1}{x}}(2x-1).\] Derivácia \(f^\prime\) sa rovná nule práve vtedy, keď \(2x-1=0\), t. j. keď \(x=\frac{1}{2}\) a \(f^\prime\) je definovaná pre každé \(x\in D(f)\). Stacionárnym bodom funkcie \(f\) je číslo \(\frac{1}{2}\).
    6. Stacionárny bod funkcie \(f\) a číslo 0, kde nie je funkcia \(f\) definovaná, rozdeľujú definičný obor \(D(f)\) na intervaly \[ \left(-\infty,0\right),\ \left(0,\frac{1}{2}\right), \ \left(\frac{1}{2},\infty\right).\] Zistime znamienka derivácie \(f^\prime\) v jednotlivých intervaloch a tak určíme monotónnosť funkcie. Urobme tabuľku \[ \begin{array}{r|c|c|c|} x \a (-\infty,0) \a (0,\frac{1}{2}) \a (\frac{1}{2},\infty)\\ \hline f^\prime(x)\a - \a - \a + \\ \hline f(x) \a \searrow \a \searrow \a \nearrow\\ \hline \end{array} \] Funkcia \(f\) je klesajúca na intervaloch \((-\infty,0),\ (0,\frac{1}{2})\) a rastúca na intervale \((\frac{1}{2},\infty)\).
    7. V čísle \(x=\frac{1}{2}\) funkcia nadobúda lokálne minimum.
    8. Vypočítajme druhú deriváciu \[f^{\prime\prime}(x)=\left(\e ^{\frac{1}{x}}(2x-1)\right)^\prime=2\e ^{\frac{1}{x}}+(2x-1)\e^{\frac{1}{x}}(-\frac{1}{x^2})=\e ^{\frac{1}{x}}\left(2-\frac{2x-1}{x^2}\right)=\e ^{\frac{1}{x}}\frac{2x^2-2x+1}{x^2}.\] Derivácia \(f^{\prime\prime}\) je definovaná pre každé \(x\in D(f)\) a keďže \(2x^2-2x+1\neq 0\), je vždy nenulová. Teda inflexné body funkcie \(f\) neexistujú.
    9. Zistime znamienka druhej derivácie v jednotlivých intervaloch definičného oboru a tak určíme konkávnosť a konvexnosť. Urobme tabuľku \[ \begin{array}{r|c|c|} x \a (-\infty,0)\a (0,\infty)\\ \hline f^{\prime\prime}(x) \a - \a + \\ \hline f(x) \a \cap \a \cup\\ \hline \end{array} \] Funkcia \(f\) je konkávna na intervale \((-\infty,0)\) a konvexná na intervale \((0,\infty)\).
    Príklad: Zistime priebeh funkcie \(f(x)=\sqrt[3]{1-x^3}\).
    Riešenie: \
    1. Definičný obor funkcie \(f\) je množina reálnych čísel \(\mathbb R\).
    2. Keďže pre každé \(x\in \mathbb R\) existuje \((-x)\in \mathbb R\), pre ktoré \(f(-x)=\sqrt[3]{1-(-x)^3}=\sqrt[3]{1+x^3}\). Keďže \(f(-x)\neq f(x)\) ani \(f(-x)\neq -f(x)\), funkcia \(f\) nie je ani je párna ani nepárna.
    3. Nulový bod funkcie \(f\) je bod \(x=1\).
    4. Funkcie \(\sqrt[3]{1-x^3}\) je spojitá v každom čísle \(x\in \mathbb R\). Asymptoty bez smernice danej funkcie neexistujú. Určme, či existujú asymptoty so smernicou \(y=ax+b\) ku grafu funkcie \(f\). Vypočítame limity \[a=\lim\limits_{x\rightarrow \infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow \infty}\frac{\sqrt[3]{1-x^3}}{x}=\lim\limits_{x\rightarrow \infty}\sqrt[3]{\frac{1-x^3}{x^3}}=\sqrt[3]{\lim\limits_{x\rightarrow \infty}\frac{1-x^3}{x^3}}=\sqrt[3]{-1}=-1\] \[b=\lim\limits_{x\rightarrow \infty}(f(x)-ax)=\lim\limits_{x\rightarrow \infty}(\sqrt[3]{1-x^3}+x)=\]\[=\lim\limits_{x\rightarrow \infty}\frac{(\sqrt[3]{1-x^3}+x)(\sqrt[3]{(1-x^3)^2}-x\sqrt[3]{1-x^3}+x^2)}{\sqrt[3]{(1-x^3)^2}-x\sqrt[3]{1-x^3}+x^2}=\]\[=\lim\limits_{x\rightarrow \infty}\frac{(1-x^3)+x^3}{\sqrt[3]{(1-x^3)^2}-x\sqrt[3]{1-x^3}+x^2}=0\] Podobne vypočítame \[a=\lim\limits_{x\rightarrow -\infty}\frac{f(x)}{x}=\lim\limits_{x\rightarrow -\infty}\frac{\sqrt[3]{1-x^3}}{x}=\lim\limits_{x\rightarrow -\infty}\sqrt[3]{\frac{1-x^3}{x^3}}=\sqrt[3]{\lim\limits_{x\rightarrow -\infty}\frac{1-x^3}{x^3}}=\sqrt[3]{-1}=-1\] \[b=\lim\limits_{x\rightarrow -\infty}(f(x)-ax)=\lim\limits_{x\rightarrow -\infty}(\sqrt[3]{1-x^3}+x)=\]\[=\lim\limits_{x\rightarrow \infty}\frac{(\sqrt[3]{1-x^3}+x)(\sqrt[3]{(1-x^3)^2}-x\sqrt[3]{1-x^3}+x^2)}{\sqrt[3]{(1-x^3)^2}-x\sqrt[3]{1-x^3}+x^2}=\]\[=\lim\limits_{x\rightarrow \infty}\frac{(1-x^3)+x^3}{\sqrt[3]{(1-x^3)^2}-x\sqrt[3]{1-x^3}+x^2}=0\] Teda priamka \(y=-x\) je asymptota so smernicou.
    5. Derivácia \[f^\prime(x)=\left(\sqrt[3]{1-x^3}\right)^\prime=\frac{1}{3}(1-x^3)^{-\frac{2}{3}}(-3x^2)=\frac{-x^2}{\sqrt[3]{(1-x^3)^2}}.\] Derivácia \(f^\prime\) je definovaná pre každé \(x\in \mathbb R-\{1\}\) a je rovná nule práve vtedy, keď \(x=0\). Stacionárnymi bodmi funkcie \(f\) sú čísla \( 0, 1\).
    6. Stacionárne body rozdeľujú množinu reálnych čísel \(\mathbb R\) na intervaly \[ (-\infty,0),\ (0,1), \ (1,\infty).\] Zistime znamienka derivácie \(f^\prime\) v jednotlivých intervaloch. Urobme tabuľku \[ \begin{array}{r|c|c|c|} x \a (-\infty,0) \a (0,1) \a (1,\infty)\\ \hline f^\prime(x)\a - \a - \a - \\ \hline f(x) \a \searrow \a \searrow \a \searrow\\ \hline \end{array} \] Funkcia \(f\) je klesajúca na celom definičnom obore \(\mathbb R\).
    7. Z monotónnosti vyplýva, že lokálny extrém funkcie \(f\) neexistuje.
    8. Vypočítajme druhú deriváciu \[f^{\prime\prime}(x)=\left(\frac{-x^2}{\sqrt[3]{(1-x^3)^2}}\right)^\prime=\frac{-2x\sqrt[3]{(1-x^3)^2}+x^2\frac{2}{3}(1-x^3)^{-\frac{1}{3}}(-3x^2)}{\sqrt[3]{(1-x^3)^4}}=\] \[=\frac{-2x(1-x^3)-2x^4}{\sqrt[3]{(1-x^3)^5}}=\frac{-2x}{\sqrt[3]{(1-x^3)^5}}.\] Derivácia \(f^{\prime\prime}\) je rovná nule práve vtedy, keď \(x=0\) a je definovaná pre všetky \(x\in \mathbb R-\{1\}\) . Teda inflexné body funkcie \(f\) sú body \(x=0\) a \(x=1\).
    9. Inflexné body rozdeľujú množinu reálnych čísel \(\mathbb R\) na intervaly \[ (-\infty,0),\ (0,1), \ (1,\infty).\] Zistime znamienka derivácie \(f^{\prime\prime}\) v jednotlivých intervaloch. Urobme tabuľku. \[ \begin{array}{r|c|c|c|} x \a (-\infty,0)\a (0,1)\a (1,\infty)\\ \hline f^{\prime\prime}(x) \a + \a - \a +\\ \hline f(x) \a \cap \a \cup\ \a \cup\\ \hline \end{array} \] Funkcia \(f\) je konkávna na intervale \((0,1)\) a konvexná na intervaloch \((-\infty,0),\ (1,\infty)\).
Úlohy:
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
10. Neurčitý integrál
Riešené úlohy:
    Príklad: Vypočítajme integrál \(\displaystyle\myint{\left(\frac{2}{x}-\frac{3}{x^2}+\sqrt[3]{x^2}-\frac{2}{\sqrt x}\right)}\).
    Príklad: Vypočítajme integrál \(\myint{x\left( {x+1} \right)\left( {x-2} \right)}\).
    Príklad: Vypočítajme integrál \(\displaystyle\myint{\frac{x^2-2x+6}{\sqrt x }}\).
    Príklad: Vypočítajme integrál \(\myint{2x\cdot \e^{x^2+3}}\).
    Príklad: Vypočítajme integrál \(\myint{\frac{\sqrt {2+\ln x} }{x}}\).
    Príklad: Vypočítajme integrál \(\myint{\frac{\sqrt {2+\ln x} }{x}} \).
    Príklad: Vypočítajme integrál \(\myint{\frac{x-1}{\sqrt[3]{x+1}}} \).
    Príklad: Vypočítajme integrál \(\myint{\e^{4x}} \).
    Príklad: Vypočítajme integrál\(\myint{\left( {3x-5} \right) \cdot \e^x}\).
    Príklad: Vypočítajme integrál \(\myint{\left( {x^2-1} \right) \cdot \sin 4x}\).
    Príklad: Vypočítajme neurčitý integrál \(\myint{\arctg x}\).
    Príklad: Vypočítajme integrál \(\myint{\e^{2x+3}\cdot\cos\left(1-\frac{x}{2}\right)}\).
Úlohy:
    Úloha: Vypočítajte neurčité integrály:
    1. \(\myint{ (5x^5+6x^2-7x+12)}\).
    2. \(\myint{\left( {\frac{1}{3}\cdot x^4+\frac{x^2}{2}+\frac{3}{5}} \right)}\).
    3. \(\myint{\left( {\frac{2}{x}-\frac{3}{x^2}+\frac{2}{3x^3}} \right)}\).
    4. \(\myint{\left( {\sqrt {x^3} +2\sqrt x -3\sqrt[4]{x^5}} \right)}\).
    5. \(\myint{\left( {\frac{1}{3}\sqrt[3]{x^2}+3x^2\cdot \sqrt x } \right)}\).
    6. \(\myint{\left( {\frac{x^2}{\sqrt x }-\frac{\sqrt x }{\sqrt[3]{x}}} \right)}\).
    7. \(\myint{\left( {5e^x-\sqrt 3 \cdot x^5+\frac{3}{1-x^2}} \right)}\).
    8. \(\myint{x\left( {x+1} \right)\left( {x-2} \right)}\).
    9. \(\myint{\left( {3\sqrt x -2x} \right)^2}\).
    10. \(\myint{\frac{\left( {x+1} \right)^2}{x^3}}\).
    11. \(\myint{\frac{\sqrt[3]{x}-2\sqrt x +x^2-2}{x^2}}\).
    12. \(\myint{\frac{x^2-5x+6}{x-2}}\).
    13. \(\myint{\frac{x^3-1}{x-1}}\).
    14. \(\myint{\mathrm{e}^x\left( 2-\frac{\mathrm{e}^{-x}}{x}\right)}\).
    15. \(\myint{\frac{5}{8x^2-32}}\).
    16. \(\myint{\frac{3}{9-3x^2}}\).
    17. \(\myint{\frac{x^2}{x^3+1}}\).
    18. \(\myint{\frac{\mathrm{e}^x}{3+\mathrm{e}^x}}\).
    19. \(\myint{\frac{1}{x\left(4+\ln x\right)}}\).
    20. \(\myint{\cotg x}\).
    21. \(\myint{\frac{1}{\arcsin x \cdot\sqrt {\strut 1-x^2} }}\).
    Úloha: Pomocou substitúcií vypočítajte neurčité integrály:
    1. \(\myint{\left(4x-2\right)^{13}}\).
    2. \(\myint{\frac{2}{\left( {x+17} \right)^5}}\).
    3. \(\myint{\sqrt {3x-2}}\).
    4. \(\myint{\sqrt[3]{\left( {2x+1} \right)^4}}\).
    5. \(\myint{\frac{1}{\sqrt {2-5x} }}\).
    6. \(\myint{x^2\cdot \,\left( {x^3+4} \right)^6}\).
    7. \(\myint{x\,\cdot \sqrt {x^2+5}}\).
    8. \(\myint{x^2\cdot \sqrt[6]{x^3+2}}\).
    9. \(\myint{\frac{x}{\sqrt {4-5x^2}}}\).
    10. \(\myint{\mathrm{e}^{4x}}\).
    11. \(\myint{\mathrm{e}^{\frac{x}{3}}}\).
    12. \(\myint{x\,\mathrm{e}^{1+x^2}}\).
    13. \(\myint{5x^2\,\mathrm{e}^{x^3-2}}\).
    14. \(\myint{\frac{\mathrm{e}^{1+\sqrt x }}{\sqrt x }}\).
    15. \(\myint{\frac{dx}{x\,\left( {3+\ln x} \right)^2}}\).
    16. \(\myint{\frac{\sqrt {2+\ln x} }{x}}\).
    17. \(\myint{\frac{\ln x-2}{x\sqrt {\ln x} }}\).
    18. \(\myint{\frac{\ln x}{x}\cdot\mathrm{e}^{\,\ln^2x-1}}\).
    19. \(\myint{\frac{\ln \left( {\arctg x} \right)}{\left( {1+x^2} \right)\,\arctg x}}\).
    Úloha: Pomocou metódy per partes vypočítajte neurčité integrály:
    1. \(\myint{\left( {3x-1} \right)\,\mathrm{e}^x}\).
    2. \(\myint{\left( {3x+1} \right)\,\mathrm{e}^{3x}}\).
    3. \(\myint{\left( {2x+3} \right)\,\mathrm{e}^{\frac{x}{4}}}\).
    4. \(\myint{\left( {x^2-4x} \right)\cdot\mathrm{e}^x}\).
    5. \(\myint{\left( {3x-4} \right)\cdot\sin x}\).
    6. \(\myint{\left( {x-3} \right)\,\cos (4x)}\).
    7. \(\myint{\left( {3-x} \right)\,\sin \frac{x}{2}}\).
    8. \(\myint{\left( {x^2+1} \right)\,\sin x}\).
    9. \(\myint{\ln x}\).
    10. \(\myint{x^2\cdot\ln x}\).
    11. \(\myint{x\cdot\arctg x}\).
    12. \(\myint{x^2\cdot\arctg x}\).
    13. \(\myint{\arcsin x}\).
    14. \(\myint{x\cdot\ln ^2x }\).
    15. \(\myint{x\cdot\ln \left( {x^2+3} \right) }\).
    16. \(\myint{\frac{\ln x}{x^2} }\).
11. Integrovanie racionálnych funkcií
Riešené úlohy:
    Príklad: Vypočítajme integrál \(\myint {\frac{1}{x+5}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{3}{2x+5}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{1}{\left({x+5} \right)^3}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{3}{\left( {2x+5} \right)^4}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{2x-4}{x^2+x+1}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{2x^2+3x-23}{x^3-4x^2+x+6}} \).
    Príklad: Vypočítajme integrál \(\myint{\frac{x^3-2x+1}{x^2+x}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{-x^2+5}{x^3-x^2-x+1}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{5x^2-7x+9}{x^3-3x^2+2x-6}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{4x^2+8x+16}{x^3+4x^2+9x+6}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{\sqrt[3]{x}}{x+\sqrt[6]{x^5}}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{\sqrt {x-2} -\sqrt[4]{x-2}}{4x-8}}.\)
    Príklad: Vypočítajme neurčitý integrál \(\myint{\sqrt{\frac{x+1}{x-1}}}\).
Úlohy:
    Úloha: Vypočítajte nasledujúce integrály racionálnych funkcií:
    1. \(\myint{\frac{1}{x(x+1)(x+2)}} \)
    2. \(\myint{\frac{ 5-x}{x^2-1 }} \)
    3. \(\myint{\frac{4x+2 }{ x^2-2x-8}} \)
    4. \(\myint{\frac{ 7x+7}{ x^2+x-12}} \)
    5. \(\myint{\frac{-x-1 }{ x^2-7x+10}} \)
    6. \(\myint{\frac{2x+13 }{x62+9x+20 }} \)
    7. \(\myint{\frac{4x^2+8x-8 }{x^3-4x }} \)
    8. \(\myint{\frac{ x-1}{(x+1)(x+2)^2 }} \)
    9. \(\myint{\frac{6x^2-22x+18 }{(x-1)(x^2-5x+6) }} \)
    10. \(\myint{\frac{2x^2+3x+3 }{(x+2)(x^2-9) }} \)
    11. \(\myint{\frac{-2x+12 }{(x-2)(x^2-4) }} \)
    12. \(\myint{\frac{-2x^2+3x-9 }{x^3-3x^2 }} \)
    13. \(\myint{\frac{ x^2+4x-2}{ x^3-x^2}} \)
    14. \(\myint{\frac{4x^2+6x+4 }{x^3+2x^2+x }} \)
    15. \(\myint{\frac{x^2-1 }{x^3+x }} \)
    16. \(\myint{\frac{5x^2-4x+2 }{(x-1)(x^2+2) }} \)
    17. \(\myint{\frac{3x^2+6 }{x^3+3x }} \)
    18. \(\myint{\frac{(x+1)^3 }{x^2-x }} \)
    19. \(\myint{\frac{2x^3-x^2-3x+6 }{x^2-1 }} \)
    20. \(\myint{\frac{x^3+3x^2-3x-17 }{x^2+x-12 }} \)
    21. \(\myint{\frac{ x^2+11x+33}{x^2+9x+20 }} \)
    22. \(\myint{\frac{x^4+8x-8 }{x^3-4x }} \)
    23. \(\myint{\frac{-x^3+12x+21 }{(x+2)(x^2-9) }} \)
    24. \(\myint{\frac{x^4-5x^3+4x^2+3x-9 }{x^3-3x^2 }} \)
    25. \(\myint{\frac{9x-14 }{ 9x^2-24x+16}} \)
    26. \(\myint{\frac{5x^3+9x^2-22x-8 }{x^3-4x }} \)
    27. \(\myint{\frac{1 }{x^2-x+1 }} \)
    28. \(\myint{\frac{ 1}{x^2+x+2 }} \)
    29. \(\myint{\frac{ 1}{x^2+x+1 }} \)
    30. \(\myint{\frac{1 }{x^2-2x+2 }} \)
    31. \(\myint{\frac{ 1}{x^2-2x+5 }} \)
    32. \(\myint{\frac{1 }{x^3+1 }} \)
    33. \(\myint{\frac{x^3+x-1 }{x(x^2+1) }} \)
    34. \(\myint{\frac{1 }{x^3+x^2+x }} \)
    35. \(\myint{\frac{x^4+1 }{x^3-x^2+x-1 }} \)
    36. \(\myint{\frac{x }{x^3+9x^2+23x+15 }} \)
    37. \(\myint{\frac{x^4+1 }{x^2(x-1)(x+1)^2 }} \)
    38. \(\myint{\frac{x^4+1 }{x^3-x^2+x-1 }} \)
    39. \(\myint{\frac{x^2+3x+2 }{x^2+x+2 }} \)
    40. \(\myint{\frac{x^2-2x+1 }{(x^2-2x+2)(x^2-2x+5) }} \)
    Úloha: Vypočítajte nasledujúce integrály funkcií obsahujúcich lineárnu iracionalitu:
    1. \(\myint{\frac{\sqrt{1-x}}{x}} \)
    2. \(\myint{\frac{ x}{ \sqrt{2x+1}}} \)
    3. \(\myint{\frac{x-1 }{\sqrt[3]{x+1} }} \)
    4. \(\myint{\frac{3x+1 }{\sqrt[3]{3x-2} }} \)
    5. \(\myint{\frac{\sqrt{x+1} }{x }} \)
    6. \(\myint{\frac{1 }{\sqrt{x}+\sqrt[4]{x} }} \)
    7. \(\myint{\frac{\sqrt[3]{x} }{x(\sqrt{x}+\sqrt[3]{x}) }} \)
    8. \(\myint{\frac{ \sqrt{2x-1}}{3-\sqrt{2x-1} }} \)
    9. \(\myint{\frac{\sqrt[3]{3x+4} }{1+\sqrt[3]{3x+4} }} \)
    10. \(\myint{\frac{4x+5\sqrt{x+2} }{\sqrt[3]{ (x+2)^2} }} \)
    11. \(\myint{\frac{ x}{x+\sqrt{x} }} \)
    12. \(\myint{\frac{1-\sqrt{x} }{\sqrt{x}(1+\sqrt{x}) }} \)
    13. \(\myint{\frac{1 }{1+\sqrt[3]{x} }} \)
    14. \(\myint{\frac{ \sqrt[3]{x}}{x+\sqrt[6]{ x^5} }} \)
    15. \(\myint{\frac{\sqrt[6]{x}-1 }{\sqrt[3]{ x^4}+\sqrt[4]{ x^5} }} \)
    16. \(\myint{\frac{\sqrt{x}+\sqrt[4]{x}+\sqrt[3]{x} }{x+\sqrt[6]{x^7} }} \)
    17. \(\myint{\frac{(x-1)\sqrt[3]{x+1} }{x-1+\sqrt[3]{x+1} }} \)
    18. \(\myint{\frac{x^2 }{(5x+2)\sqrt{ 5x+2} }} \)
12. Integrovanie niektorých funkcií obsahujúcich racionálne výrazy
Riešené úlohy:
    Príklad: Vypočítajme integrál \(\myint {\frac{1}{\sqrt{2x^2-x+3}}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{x^2}{\sqrt{2x^2-4x+1} }}\).
    Príklad: Vypočítajme neurčitý integrál \(\myint{\sqrt{1-x^2}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{\e^x}{\sqrt {\e^{2x}-4} }}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{1}{\e^x+2}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{\left({1+\sin x} \right)\cos x}{\sin ^6x}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{\sin^3x}{\cos ^2x}}\).
    Príklad: Vypočítajme integrál \(\myint{\frac{1}{2\cos x+\sin x+5}}\).
    Príklad: Vypočítajme integrál \(\myint {\frac{1}{\tg x\cdot \cos 2x}}\).
Úlohy:
    Úloha: Vypočítajte neurčité integrály s kvadratickou iracionalitou:
    1. \(\myint{\frac{1}{\sqrt {x^2+4x+5} }}\).
    2. \(\myint{\frac{1}{\sqrt {x^2-2x+4} } }\).
    3. \(\myint{\frac{1}{\sqrt {2x-x^2} } }\).
    4. \(\myint{\frac{2}{\sqrt {4x^2-8x+12} }}\).
    5. \(\myint{\frac{1}{\sqrt {x^2+10x-5} } }\).
    6. \(\myint{\frac{1}{\sqrt {2x^2-5x+3} } }\).
    7. \(\myint{\frac{x+7}{\sqrt {x^2+4x+5} } }\).
    8. \(\myint{\frac{3x-2}{\sqrt{x^2-2x+4}} }\).
    9. \(\myint{\frac{3-x}{\sqrt {x^2-2x+3} } }\).
    10. \(\myint{\frac{2x+5}{\sqrt {x^2+10x-5} } }\).
    11. \(\myint{\frac{4x^2-x}{\sqrt {x^2+4x+5} } }\).
    12. \(\myint{\frac{2x^2-3x+5}{\sqrt {x^2-2x+4} } }\).
    13. \(\myint{\frac{x^2+2x+1}{\sqrt {x^2-2x+3} } }\).
    14. \(\myint{\frac{-2x^2-20x+30}{\sqrt {x^2+10x-5} } }\).
    15. \(\myint{\frac{x^3+2}{\sqrt {x^2+1} } }\).
    16. \(\myint{\sqrt {x^2-2x-1} }\).
    Úloha: Vypočítajte neurčité integrály s exponenciálnymi funkciami:
    1. \(\myint{\frac{\mathrm{e}^x}{1-\mathrm{e}^{2x}} }\).
    2. \(\myint{\frac{2\mathrm{e}^x}{\mathrm{e}^{2x}-9} }\).
    3. \(\myint{\mathrm{e}^x\cdot\frac{5-\mathrm{e}^x}{\mathrm{e}^{2x}-1} }\).
    4. \(\myint{\frac{2\mathrm{e}^{2x}+13e^x}{\mathrm{e}^{2x}+9\mathrm{e}^x+20} }\).
    5. \(\myint{\frac{\mathrm{e}^{3x}}{\mathrm{e}^x+1} }\).
    6. \(\myint{\frac{\mathrm{e}^{4x}-\mathrm{e}^{2x}}{\mathrm{e}^{2x}-16} }\).
    7. \(\myint{\frac{4}{\mathrm{e}^x+2} }\).
    8. \(\myint{\frac{1}{\mathrm{e}^x-7} }\).
    9. \(\myint{\frac{1}{(\mathrm{e}^x-3)(\mathrm{e}^x-2)} }\).
    10. \(\myint{\frac{1}{\mathrm{e}^{2x}+2\mathrm{e}^x+1} }\).
    Úloha: Vypočítajte neurčité integrály s goniometrickými funkciami:
    1. \(\myint{\left( {3-2\sin x+3\sin ^2x} \right)\cos x }\).
    2. \(\myint{\frac{\cos x}{\sqrt {\sin ^2x-4} } }\).
    3. \(\myint{\frac{\sin x}{\sqrt {\strut\cos ^2x+3} } }\).
    4. \(\myint{\frac{\sin 2x}{\strut\sin ^2x-6} }\).
    5. \(\myint{\frac{\cos 2x}{\cos x-\sin x} }\).
    6. \(\myint{\frac{\cos 2x}{\sin ^2x} }\).
    7. \(\myint{\frac{\sin x-5}{\sin ^2x}\cdot\cos x }\).
    8. \(\myint{\cos x\cdot\sqrt {2+\sin x} }\).
    9. \(\myint{\frac{\cos x}{\sin ^2x+8\sin x+6} }\).
    10. \(\myint{\left( {2-\cos x} \right)^4\sin x }\).
    11. \(\myint{\frac{\sin x}{\cos ^2x-4\cos x+3} }\).
    12. \(\myint{\frac{\sin 2x}{1-\sin ^2x} }\).
    13. \(\myint{\frac{\cos x\sin 2x}{6-2\cos x} }\).
    14. \(\myint{\frac{9-\cos^2x}{3+\cos x}\;\sin (2x) }\).
    15. \(\myint{\frac{\sin ^3x}{1+\cos x} }\).
    16. \(\myint{\cos ^3x }\).
    17. \(\myint{\cos ^5x }\).
    18. \(\myint{\cotg x\cdot \ln(\sin x )}\).
    19. \(\myint{\tg x\cdot \ln(\cos x) }\).
    20. \(\myint{\frac{5-\sin x}{\sin ^2x-1}\cdot\cos x }\).
    21. \(\myint{\frac{2\cos x}{\sin ^2x-9} }\).
    22. \(\myint{\frac{2\sin x}{\cos ^2x-9} }\).
    23. \(\myint{\frac{\cos x}{1-\sin ^2x} }\).
    24. \(\myint{\frac{2+4\sin x}{\sin ^2x-2\sin x-8}\cdot\cos x }\).
    25. \(\myint{\frac{-\cos x-1}{\cos ^2x-7\cos x+10}\cdot\sin x }\).
    26. \(\myint{\frac{2\cos x+13}{\cos ^2x+9\cos x+20}\cdot\sin x }\).
    27. \(\myint{\frac{1}{3+5\cos x} }\).
    28. \(\myint{\frac{\cos x}{1+\cos x} }\).
    29. \(\myint{\frac{1}{\cos x+2\sin x+3} }\).
    30. \(\myint{\frac{2-\sin x}{2+\cos x} }\).
    31. \(\myint{\frac{1+\sin x+\cos x}{1-\sin x-\cos x} }\).
    32. \(\myint{\frac{1+\tg x}{1-\tg x} }\).
    33. \(\myint{\frac{1}{3\sin ^2x+5\cos ^2x} }\).
    34. \(\myint{\frac{1}{\sin ^2x+3\cos ^2x+2} }\).
    35. \(\myint{\frac{\sin ^2x}{1-\tg x} }\).
    36. \(\myint{\frac{\sin x}{\sqrt {2\sin x+1} }\cdot\cos x }\).
    37. \(\myint{\frac{\sin x-1}{\sqrt[3]{\sin x+1}}\cdot\cos x }\).
    38. \(\myint{\frac{3\sin x+1}{\sqrt[3]{3\sin x-2}}\cdot\cos x }\).
    39. \(\myint{\frac{\sqrt {\cos x+1} }{\cos x}\cdot\sin x }\).
    40. \(\myint{\frac{1}{\sqrt {\cos x} +\sqrt[4]{\cos x}}\cdot\sin x }\).
13. Určitý a nevlastný integrál a ich aplikácie
Riešené úlohy:
    Príklad: Vypočítajme integrál \(\displaystyle\int_1^2 \left(4x^{{3}}+2x\right)\,\mathrm{d}x\).
    Príklad: Vypočítajme integrál \(\displaystyle\int_1^{\mathrm{e}} \frac{3+\ln x}{x}\,\mathrm{d}x\).
    Príklad: Vypočítajme integrál \(\displaystyle\int_0^1\left(x+1\right)\;\e^{2x}\,\mathrm{d}x\).
    Príklad: Vypočítajme integrál \(\displaystyle\int_0^{\infty}\frac{1}{1+x^2} \, \mathrm{d}x\).
    Príklad: Vypočítajme integrál \(\displaystyle\int^0_{-\infty} \frac{1}{1+x^2}\,\mathrm{d}x\).
    Príklad: Vypočítajme integrál \(\displaystyle\int^{\infty}_{-\infty}\frac{1}{1+x^2}\,\mathrm{d}x\).
    Príklad: Vypočítajme určitý integrál \(\displaystyle\int_0^1{\frac{1}{\sqrt{1-x^2}}}\,\mathrm{d}x\).
    Poznámka: Podobne sa definujú nevlastné integrály funkcií, ktoré sú neohraničené v pravom okolí nejakého bodu. Integrál funkcie, ktorá je neohraničená v okolí viacerých bodov intervalu integrovania sa rozdelí na integrály na intervaloch obsahujúcich len jeden ľavostranný alebo pravostranný problém, pričom konvergencia každého takého integrálu sa podudzuje samostatne.
    Poznámka: V niektorých prípadoch, keď nevlastný integrál rozdelený na dve časti diverguje, uvažuje sa spoločná konvergencia, keď sa hranice integrálov volia symetricky. Tak sú definované tzv. hlavné hodnoty integrálov.
    Príklad: Vypočítajme obsah časti roviny ohraničenej krivkami \(y=-x\) a \(y=2x-x^{{2}}\).
    Príklad: Vypočítajme obsah časti roviny ohraničenej krivkami \(y=x-2\) a \(x=y^2\).
    Príklad: Vypočítajme objem telesa, ktoré vznikne rotáciou oblasti ohraničenej krivkami \(y=x^2\), \(y=2-x^2\) okolo osi \(o_x\).
    Príklad: Vypočítajme objem telesa, ktoré vznikne rotáciou oblasti ohraničenej krivkami \(x=y^2\), \(y=x-2\) okolo osi \(o_y\).
    Príklad: Vypočítajme dĺžku danej krivky \(C\): \(y=\ln\sin x\), \(x\in \langle \frac{\pi }{3};\frac{2\pi }{3}\rangle.\)
Úlohy:
    Úloha: Vypočítajte určité integrály:
    1. \(\myint{_0^1 \left(x^{{2}}+x+1\right)}\)
    2. \(\myint{_1^4 \left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)}\)
    3. \(\myint{_{-1}^1 \frac{x^{{2}}-5x+6}{x-2}}\)
    4. \(\myint{_0^1 \frac{\mathrm{e}^x}{3+\mathrm{e}^x}}\)
    5. \(\myint{_0^{\pi /2} \left(3-2\sin x+3\sin ^2 x\right)\cdot\cos x}\)
    6. \(\myint{_2^3 \left(1-x\right)^{-3}}\)
    7. \(\myint{_0^1 2x\;\left(x^2+2\right)^3}\)
    8. \(\myint{_0^1 x\,\mathrm{e}^{1+x^2}}\)
    9. \(\myint{_1^{\mathrm{e}} \frac{\sqrt{2+\ln x}}{x} }\)
    10. \(\myint{_0^{\pi /2} \left(2-\cos x\right)^4\sin x}\)
    11. \(\myint{_1^2 \left(3x-1\right)\;\mathrm{e}^x}\)
    12. \(\myint{_2^{\mathrm{e}} x\cdot\ln x}\)
    13. \(\myint{_5^6 \frac{4x+2}{x^{{2}}-2x-8}}\)
    14. \(\myint{_0^7 \frac{x-1}{\sqrt[{{3}}]{x+1}}}\)
    15. \(\myint{_0^1 \frac{1}{\sqrt{x^{{2}}+4x+5}}}\)
    16. \(\myint{_1^2 \frac{\mathrm{e}^x}{1-\mathrm{e}^{2x}}}\)
    17. \(\myint{_0^1 \frac{4}{2+\mathrm{e}^x}}\)
    Úloha: Vypočítajte nevlastné integrály:
    1. \(\myint{_2^{\infty} \left(\frac{3}{x}+\frac{2}{x^2}\right)^2}\)
    2. \(\myint{_2^{\infty} \left(\frac{3}{x}+\frac{2}{x^2}\right)}\)
    3. \(\myint{_3^{\infty} \frac{1}{\left(x-2\right)^2}}\)
    4. \(\myint{_0^{\infty} \mathrm{e}^{-3x}}\)
    5. \(\myint{_1^{\infty} \frac{\mathrm{e}^{1/x}}{x^2}}\)
    6. \(\myint{_2^{\infty} \frac{\ln x}{x}}\)
    7. \(\myint{_2^{\infty} \frac{1}{x\,\ln x}}\)
    8. \(\myint{_2^{\infty} \frac{1}{x\,\ln^2 x}}\)
    9. \(\myint{_1^{\infty} \frac{x}{\sqrt{x^2+1}}}\)
    10. \(\myint{_1^{\infty} \frac{x}{\mathrm{e}^x}}\)
    11. \(\myint{_0^{\infty} x\cdot \mathrm{e}^{-x^2}}\)
    12. \(\myint{_{-\infty}^{-0{,}5} \frac{1}{x^2+x+1}}\)
    13. \(\myint{_{-\infty}^{\infty} \frac{1}{x^2+2x+2}}\)
    14. \(\myint{_{-\infty}^{\infty} \frac{\arctg^2 x}{1+x^2}}\)
    Úloha: Vypočítajte obsah časti roviny ohraničenej krivkami:
    1. \(y=2x,\;y=x,\;x=5 \)
    2. \( y=5-2x,\;y=2+x,\;x=0\)
    3. \(y=x^2-2x,\;y=0 \)
    4. \( y=x^2-2x,\;y=x\)
    5. \(y=6x-x^2,\;y=0 \)
    6. \(y=-x^2+4x-2,\;y+x=2 \)
    7. \(y=x^2-3x+10,\;y=2x+4 \)
    8. \(y=x^2+x,\;y=2x+2 \)
    9. \(y=-x^{{2}}+2,\;y=-3x+4 \)
    10. \(y=x^2-x-6,\;y=-x^2+5x+14 \)
    11. \(y=x^2+2x+10,\;y=-x^2-4x+18 \)
    12. \(y=x^2-x,\;y=-x^2+3x \)
    13. \(y=2x^2-x-2,\;y=x^2+2x+2 \)
    14. \( y=x^2,\;y^2=x\)
    15. \(xy=4,\;x+y=5 \)
    16. \(xy=5,\;y=6-x \)
    17. \(y=\dfrac{4}{x},\;y=6-2x \)
    18. \( y=x^3,\;y=4x\)
    19. \(y=\mathrm{e}^x,\;y=0,\;x=0,\;x=1 \)
    20. \(y=\mathrm{e}^{2x},\;y=\mathrm{e}^x+2,\;x=0 \)
    21. \(y=\mathrm{e}^{2x}-3,\;y=\mathrm{e}^x-1,\;x=0 \)
    22. \(y=2\mathrm{e}^x+3,\;y=\mathrm{e}^{2x},\;x=0 \)
    23. \( y=3-x,\;y=x,\;y=0\)
    24. \( y=x+1,\;y=7-x,\;y=0\)
    25. \(x=4,\;y^2=x \)
    26. \(x=6,\;x=y^2-3 \)
    27. \(y=x-2,\;y^2=x \)
    28. \( x=y^2,\;x+y-6=0\)
    29. \(x=y^2,\;x-3y-4=0 \)
    30. \( y^2=x+1,\;x+2y-2=0\)
    31. \(x=y^2-2,\;x-y-4=0 \)
    32. \( y=x+1,\;\left(y-1\right)^2=x\)
    33. \(y=\dfrac{8}{x},\;y=2x,\;y=6 \)
    34. \(y=\dfrac{8}{x},\;y=\dfrac{x}{2},\;y=5 \)
    35. \( y=\dfrac{6}{x},\;y=\dfrac{x}{6},\;y=3\)
    36. \(y=\ln x,\;y=0,\;y=\mathrm{e},\;x=0 \)
    Úloha: Vypočítajte objem telesa, ktoré vznikne rotáciou okolo osi \(o_x\) oblasti ohraničenej krivkami:
    1. \(y=2x,\;y=x,\;x=5 \)
    2. \(y=5-2x,\;y=2+x,\;x=0\)
    3. \( y=3x+1,\;y=0,\;x=0,\;x=1\)
    4. \(y=2x-x^2,\;y=0 \)
    5. \(y=x^2+2,\;y=2x^2+1 \)
    6. \( y=x^2,\;y=1-x^2\)
    7. \(y=x^2+2,\;y=0,\;x=-1,\;x=3 \)
    8. \(y=6x-x^{{2}},\;y=0 \)
    9. \(y=x^2,\;y^2=x \)
    10. \(xy=4,\;x+y=5 \)
    11. \(xy=5,\;y=6-x \)
    12. \( y=\dfrac{4}{x},\;y=6-2x\)
    13. \( y=x^3,\;y=4x,\;x\ge 0\)
    14. \(y=\mathrm{e}^x,\;y=0,\;x=0,\;x=1 \)
    15. \(y=\mathrm{e}^{-x/10},\;y=0,\;x=0,\;x=10 \)
    16. \(y=\mathrm{e}^{x/2},\;y=e,\;x=0 \)
    17. \( y=\mathrm{e}^{2x},\;y=1,\;x=4\)
    18. \(y=\mathrm{e}^x,\;y=\dfrac{1}{x},\;x=2,\;x=3 \)
    19. \(y=\mathrm{e}^{-x},\;y=x+1,\;x=2 \)
    20. \(y=3-x,\;y=x,\;y=0 \)
    21. \(y=x+1,\;y=7-x,\;y=0 \)
    22. \(x=4,\;y^2=x \)
    23. \(x=6,\;x=y^2-3 \)
    24. \( y=\dfrac{8}{x},\;y=2x,\;y=6\)
    25. \(y=\dfrac{8}{x},\;y=\dfrac{x}{2},\;y=5 \)
    26. \( y=\dfrac{6}{x},\;y=\dfrac{x}{6},\;y=3\)
    Úloha: Vypočítajte objem telesa, ktoré vznikne rotáciou okolo osi \(o_{{y}}\) oblasti ohraničenej krivkami:
    1. \( y=3-x,\;y=x,\;y=0\)
    2. \( x=4,\;y^2=x\)
    3. \( y=x-2,\;y^{{2}}=x\)
    4. \( x=y^2,\;x+y-6=0\)
    5. \(x=y^2,\;x-3y-4=0 \)
    6. \( y=x+1,\;\left(y-1\right)^2=x\)
    7. \( y=\dfrac{8}{x},\;y=2x,\;y=6\)
    8. \(y=\dfrac{8}{x},\;y=\dfrac{x}{2},\;y=5 \)
    9. \(y=\dfrac{6}{x},\;y=\dfrac{x}{6},\;y=3 \)
    10. \(y=\ln x,\;y=0,\;y=\mathrm{e},\;x=0 \)
    Úloha: Vypočítajte dĺžku krivky:
    1. \( C:\;y=\dfrac{\mathrm{e}^x+\mathrm{e}^{-x}}{2},\;x\in \langle 0;3\rangle \)
    2. \(C:\;y=\dfrac{x^2}{4}-\dfrac{\ln x}{2},\;x\in \langle 1;4\rangle \)
    3. \(C:\;y=1-\ln(\cos x),\;x\in \left\langle 0;\dfrac{\pi }{4}\right\rangle \)
    4. \( C:\;y=2\sqrt{x^3},\;x\in \langle 0;2\rangle\)
    5. \(C:\;y=2\sqrt{x},\;x\in \langle 1;2\rangle \)
    6. \(C:\;y=\ln \dfrac{\mathrm{e}^x+1}{\mathrm{e}^x-1},\;x\in \langle \ln 2;\ln 5\rangle \)
    7. \(C:\;y=\mathrm{e}^x,\;x\in \langle 0;1\rangle \)