Určitý a nevlastný integrál a ich aplikácie

Ciele

Naučiť študentov počítať určitý integrál pomocou Newtonovho-Leibnizovho vzorca
Naučiť študentov počítať určitý integrál pomocou substitučnej metódy
Naučiť študentov počítať určitý integrál metódou per-partes
Naučiť študentov počítať nevlastný integrál
Naučiť študentov využívať geometrické aplikácie určitého integrálu (plošný obsah rovinného útvaru, objem rotačného telesa, dĺžka krivky)

Úvod

\(\def\myint#1{\displaystyle\int #1 \,\mathrm{d}x} \def\arctg{\mathop{\rm arctg}}\def\tg{\mathop{\mathrm{tg}}} \def\arccotg{\mathop{\mathrm{arccotg}}} \def\cotg{\mathop{\mathrm{cotg}}}\def\e{\mathrm{e}}\def\a{&} \)Výpočet úrčitého integrálu patrí medzi najdôležitejšie inžinierske aplikácie a využíva sa na riešenie veľkého množstva praktických úloh. Na tomto cvičení sa oboznámime so základnými metódami výpočtu určitého integrálu.

Postup

Výpočet určitého integrálu pomocou Newtonovho-Leibnizovho vzorca

Určitý integrál v prípade, ak funkcia \(f\) je integrovateľná na intervale \(\langle a;b\rangle\) a má na intervale \(\langle a;b\rangle\) primitívnu funkciu \(F\), počítame pomocou Newtonovho-Leibnizovho vzorca: \[ \int_a^b f\left(x\right)\;\,\mathrm{d}x=\left[F\left(x\right)\right]_{a}^{b}=F\left(b\right)-F\left(a\right). \]
Príklad: Vypočítajme integrál \(\displaystyle\int_1^2 \left(4x^{{3}}+2x\right)\,\mathrm{d}x\).

Riešenie: Integrál vypočítame využitím Newtonovho-Leibnizovho vzorca: \[ \int_1^2 \left(4x^3+2x\right) \,\mathrm{d}x=\left[x^4+x^2\right]_1^2=\left(2^4+2^2\right)-\left(1^4+1^2\right)=18. \]
Výpočet určitého integrálu substitučnou metódou

Nech \(\varphi :\;\langle a,\;b\rangle \rightarrow \langle \alpha ,\;\beta \rangle \) má spojitú deriváciu. Nech \(F\) je primitívna funkcia k funkcii \(f(t)\) na \(\langle \alpha ,\;\beta \rangle \). Potom funkcia \(F\left[\varphi \left(x\right)\right]\) je primitívna k \(f\left[\varphi \left(x\right)\right]\cdot \varphi ^{'}\left(x\right)\) na \(\langle a,\;b\rangle \) a platí \[ \int_a^b f\left[\varphi \left(x\right)\right]\cdot \varphi ^{'}\left(x\right)\;\,\mathrm{d}x=\int_{\alpha}^{\beta} f\left(t\right)\;\,\mathrm{d}t. \]
Príklad: Vypočítajme integrál \(\displaystyle\int_1^{\mathrm{e}} \frac{3+\ln x}{x}\,\mathrm{d}x\).

Riešenie: Integrál vypočítame využitím substitúcie a Newtonovho-Leibnizovho vzorca: \[ \int_1^{\mathrm{e}}\frac{3+\ln x}{x}\,\mathrm{d}x=\left|\begin{array}{c}3+\ln x=t\\ \dfrac{\mathrm{d}x}{x}=\mathrm{d}t\\a=1\rightarrow \alpha =3+\ln 1=3\\b=e\rightarrow \beta =3+\ln \mathrm{e}=4\end{array}\right|=\int_3^4 t\,\mathrm{d}t =\left[\frac{t^2}{2}\right]_3^4=8-\frac{9}{2}=\frac{7}{2}. \]
Výpočet určitého integrálu pomocou metódy per partes

Nech funkcie \(u\left(x\right),\;v\left(x\right)\) majú spojité derivácie na intervale \(\langle a;b\rangle\). Potom platí \[ \int _a^b u(x)\cdot v^{'}(x)\,\mathrm{d}x =\left[u(x)\cdot v(x)\right]_a^b-\int_a^b u^{'} (x)\cdot v(x)\,\mathrm{d}x. \]
Príklad: Vypočítajme integrál \(\displaystyle\int_0^1\left(x+1\right)\;\e^{2x}\,\mathrm{d}x\).

Riešenie: Integrál vypočítame využitím metódy per partes a Newtonovho-Leibnizovho vzorca: \[ \int^1_0 \left(x+1\right)\;\mathrm{e}^{2x}\,\mathrm{d}x= \left|\begin{array}{ll}u=x+1 \a v^{'}=\mathrm{e}^{2x}\\ u^{'}=1\a v=\dfrac{\mathrm{e}^{2x}}{2}\end{array}\right| =\left[\left(x+1\right)\frac{\mathrm{e}^{{2x}}}{2}\right]_0^1-\frac{1}{2}\int^1_0 \mathrm{e}^{2x}\,\mathrm{d}x= \] \[ =\left[\left(x+1\right)\dfrac{\mathrm{e}^{2x}}{2}-\dfrac{\mathrm{e}^{2x}}{4}\right]_{{0}}^{{1}}=\frac{3}{4}\,\mathrm{e}^{{2}}+\frac{1}{4}. \]
Nevlastný integrál

Integrál funkcie na neohraničenom intervale

Počítame integrály, v ktorých hociktorá z hraníc môže byť nevlastné číslo.
Príklad: Vypočítajme integrál \(\displaystyle\int_0^{\infty}\frac{1}{1+x^2} \, \mathrm{d}x\).

Riešenie: Počítame nevlastný integrál, pričom z definície platí, že \[ \int^{\infty}_{0} \frac{1}{1+x^2}\,\mathrm{d}x=\lim_{b\rightarrow\infty }\int^{b}_0 \frac{1}{1+x^2}\,\mathrm{d}x=\lim_{b\rightarrow\infty } \left[\arctg x\right]_0^b=\lim_{b\rightarrow\infty } \left(\arctg b-\arctg 0\right)=\frac{\pi }{2}. \] Keďže limita je vlastná, daný integrál existuje (konverguje).

Príklad: Vypočítajme integrál \(\displaystyle\int^0_{-\infty} \frac{1}{1+x^2}\,\mathrm{d}x\).

Riešenie: Počítame nevlastný integrál, pričom z definície platí, že \[ \int^0_{-\infty}\frac{1}{1+x^2}\,\mathrm{d}x=\lim_{a\rightarrow-\infty}\int^0_a\frac{1}{1+x^2}\,\mathrm{d}x= \lim_{a\rightarrow -\infty}\left[\arctg x\right]_a^0=\lim_{a\rightarrow -\infty}\left(\arctg 0-\arctg a\right)=\frac{\pi}{2}. \] Keďže limita je vlastná, daný integrál existuje (konverguje).

Príklad: Vypočítajme integrál \(\displaystyle\int^{\infty}_{-\infty}\frac{1}{1+x^2}\,\mathrm{d}x\).

Riešenie: Počítame nevlastný integrál, pričom \(\displaystyle\int^{\infty}_{-\infty} \frac{1}{1+x^2}\,\mathrm{d}x\) sa dá prepísať napríklad takto \[ \displaystyle\int^{\infty}_{-\infty}\frac{1}{1+x^2}\,\mathrm{d}x= \int^{0}_{-\infty}\frac{1}{1+x^2}\,\mathrm{d}x+\int^{\infty}_0 \frac{1}{1+x^2}\,\mathrm{d}x, \] preto na základe výsledkov predchádzajúcich úloh platí \[ \int^{\infty}_{-\infty} \frac{1}{1+x^2}\,\mathrm{d}x= \int^{0}_{-\infty}\frac{1}{1+x^2}\,\mathrm{d}x+\int^{\infty}_0\frac{1}{1+x^2}\,\mathrm{d}x= 2\cdot\frac{\pi }{2}=\pi. \] Aj tento integrál existuje (konverguje).

Integrál funkcie neohraničenej na uzavretom intervale

Príklad: Vypočítajme určitý integrál \(\displaystyle\int_0^1{\frac{1}{\sqrt{1-x^2}}}\,\mathrm{d}x\).

Riešenie: Pri pohľade na podintegrálnu funkciu a na hranice integrovania si môžeme všimnúť, že menovateľ funkcie sa v bode \(x=1\) rovná \(0\), a teda funkcia nie je definovaná na celom uzavretom intervale \(\langle 0;1\rangle\). Funkciu by sme mohli dodefinovať v bode \(x=1\), avšak v ľavom okolí bodu \(x=1\) ostane funkcia neohraničenou. Aj tento typ integrálu sa nazýva nevlastný integrál. Počítame ho na základe nasledujúcej definície: \[ \int_0^1 \frac{1}{\sqrt{1-x^2}}\,\mathrm{d}x\stackrel{\mathrm{def}}{=} \lim_{\varepsilon\to0^+} \int_0^{1-\varepsilon} \frac{1}{\sqrt{1-x^2}}\,\mathrm{d}x= \lim_{\varepsilon\to0^+} [\arcsin x]_0^{1-\varepsilon}= \] \[ =\lim_{\varepsilon\to0^+} [\arcsin (1-\varepsilon) - \arcsin 0]=\arcsin 1 -\arcsin0 =\frac{\pi}2. \] Integrál konverguje.

Poznámka: Podobne sa definujú nevlastné integrály funkcií, ktoré sú neohraničené v pravom okolí nejakého bodu. Integrál funkcie, ktorá je neohraničená v okolí viacerých bodov intervalu integrovania sa rozdelí na integrály na intervaloch obsahujúcich len jeden ľavostranný alebo pravostranný problém, pričom konvergencia každého takého integrálu sa podudzuje samostatne.

Poznámka: V niektorých prípadoch, keď nevlastný integrál rozdelený na dve časti diverguje, uvažuje sa spoločná konvergencia, keď sa hranice integrálov volia symetricky. Tak sú definované tzv. hlavné hodnoty integrálov.
Geometrické aplikácie určitého integrálu

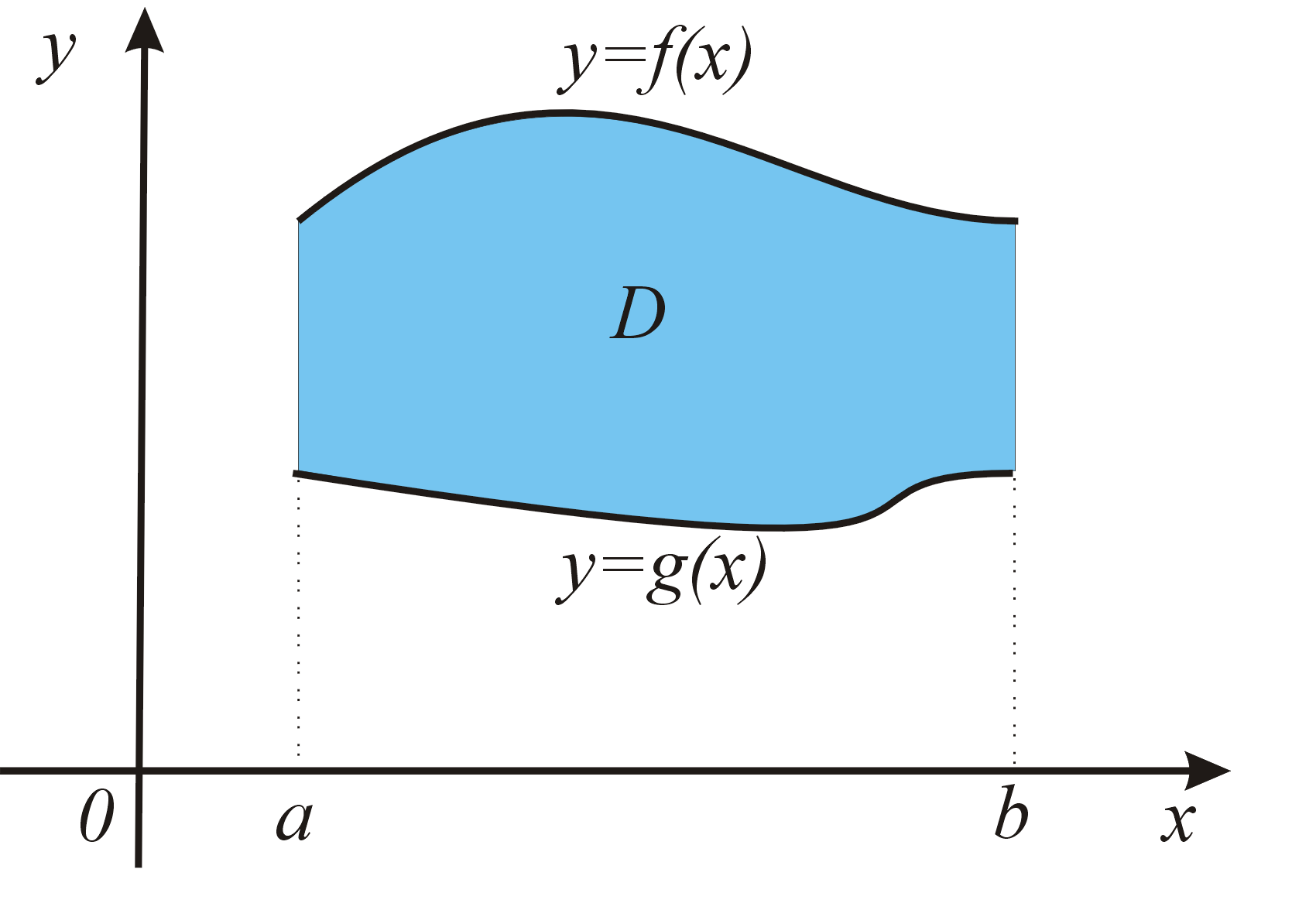
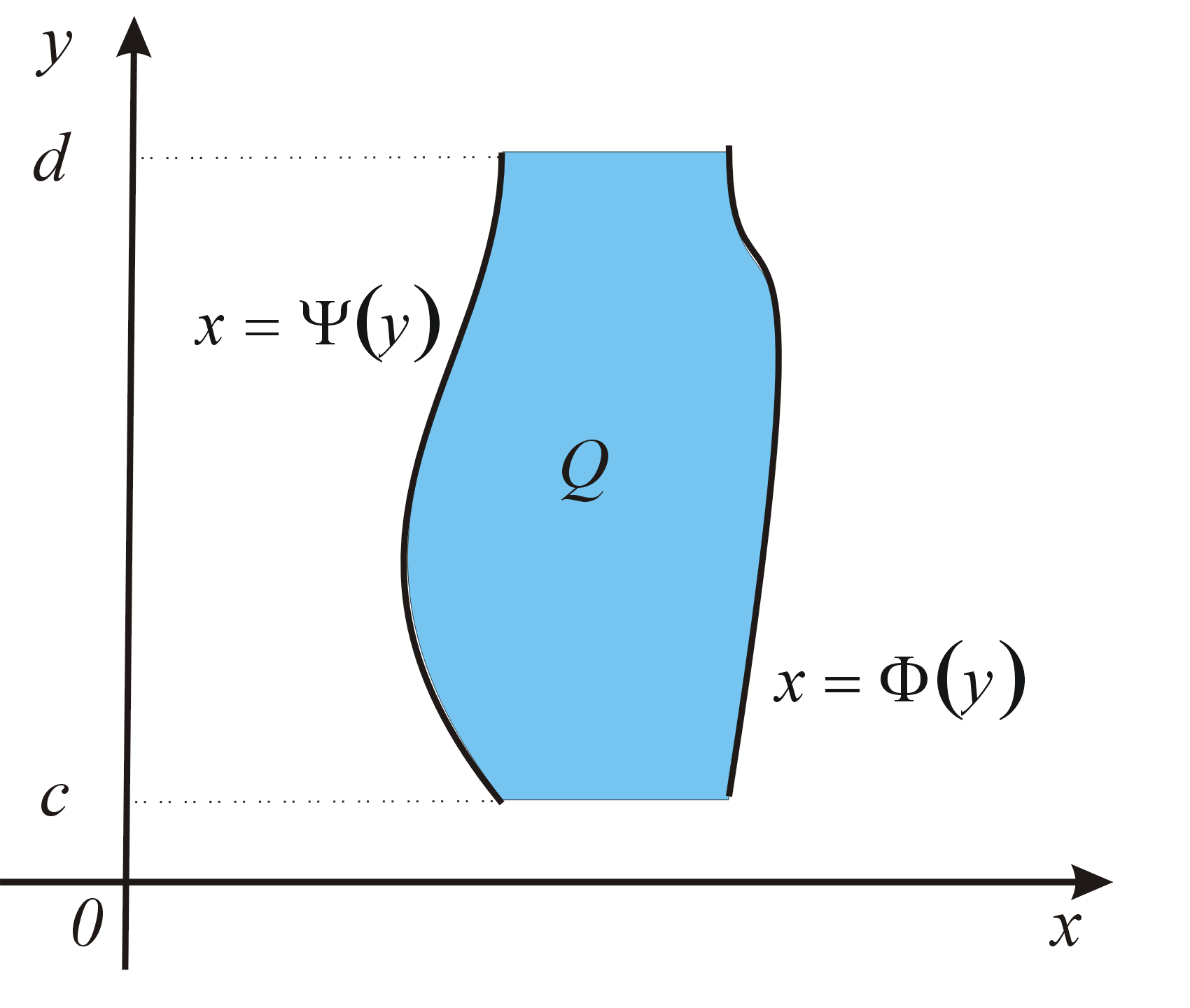
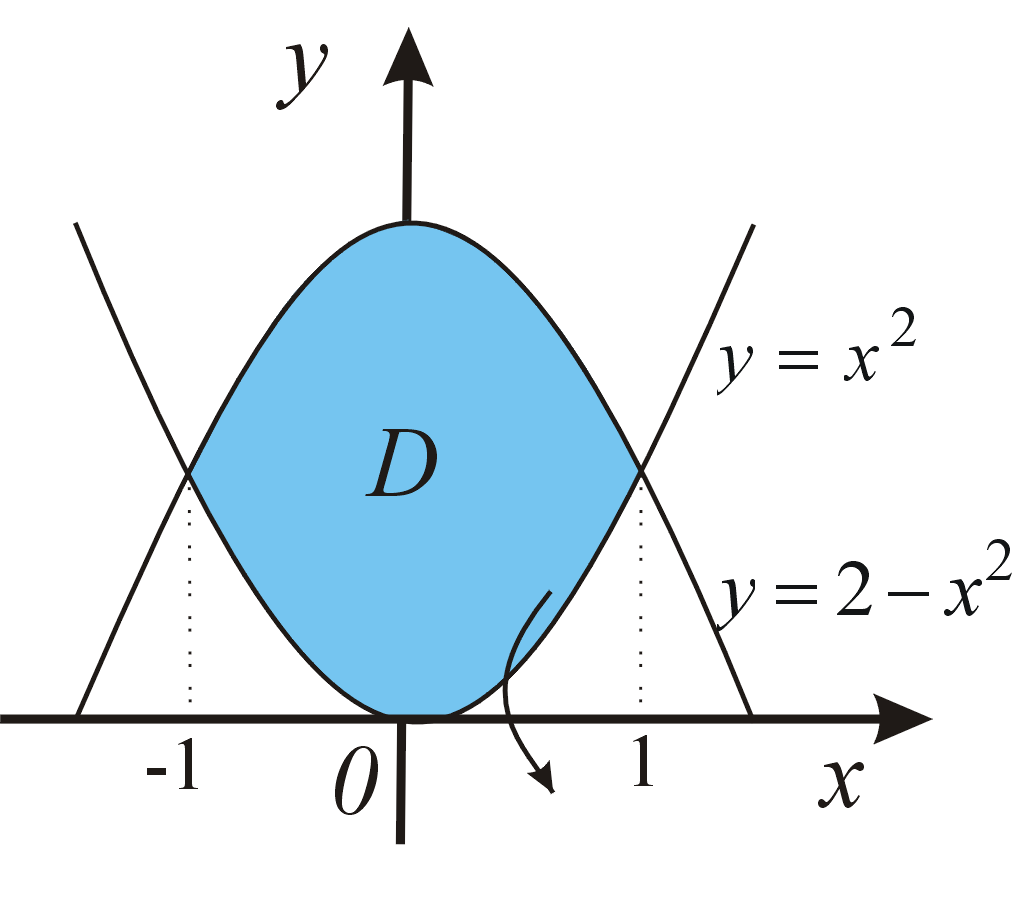
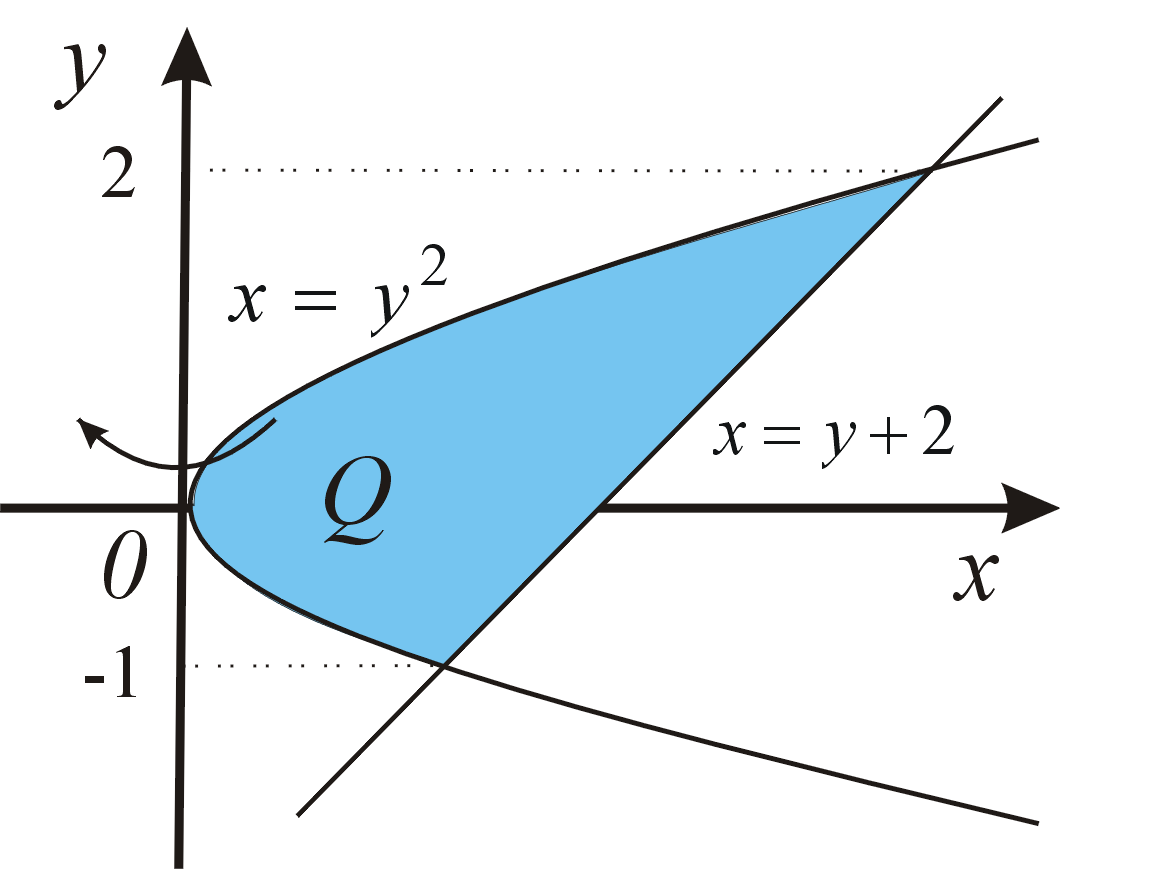
Množina \(D=\left\{\;\left(x,y\right)\in R^{{2}},\;a\leqq x\leqq b,\;g\left(x\right)\leqq y\leqq f\left(x\right)\;\right\}\) popisuje elementárnu oblasť vzhľadom na os \(O_x\) (elementárnu oblasť typu \([x,y]\)).

Množina \(Q=\left\{\;\left(x,y\right)\in R^{{2}},\;c\leqq y\leqq d,\;\Phi \left(y\right)\leqq x\leqq \Psi \left(y\right)\;\right\}\) popisuje elementárnu oblasť vzhľadom na os \(O_y\) (elementárnu oblasť typu \([y,x]\)).

Plošný obsah rovinného útvaru

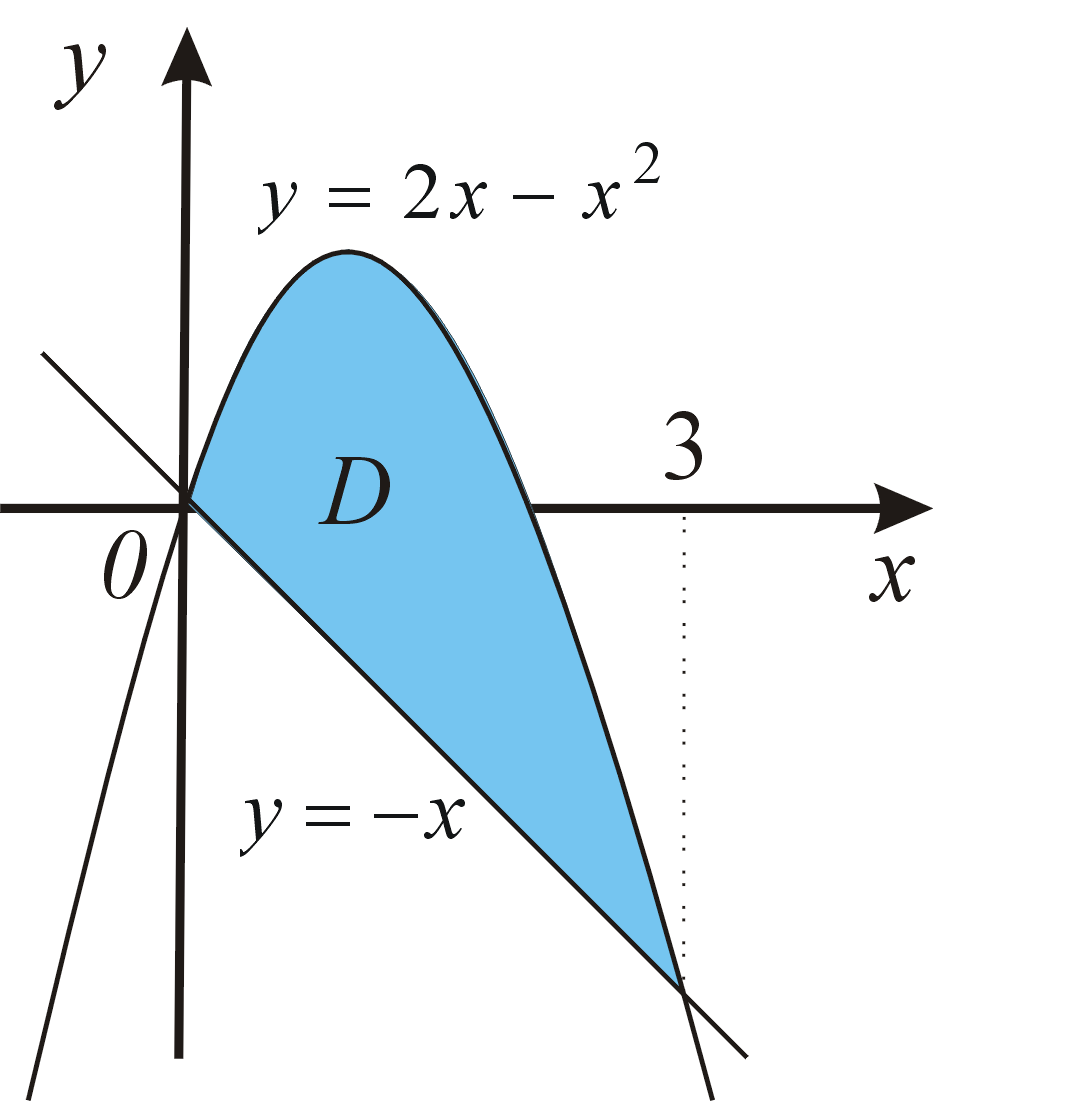
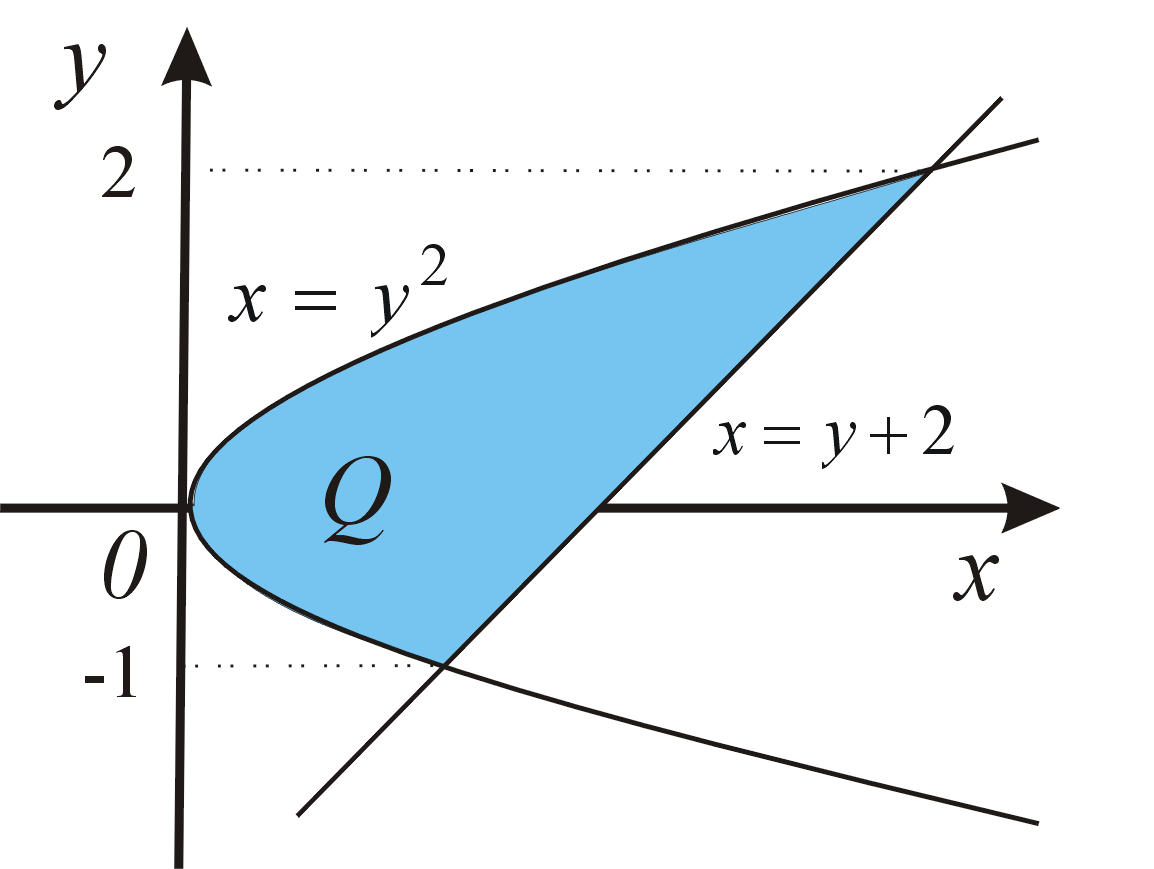
Plošný obsah elementárnej oblasti \(D\) typu \([x,y]\) vypočítame podľa vzorca \[ P=\int ^b_a \left[f(x)-g(x)\right]\,\mathrm{d}x . \] Plošný obsah elementárnej oblasti \(Q\) typu \(\left[y,x\right]\) vypočítame podľa vzorca \[ P=\int^d_c\left[\Phi(y)-\Psi(y)\right] \,\mathrm{d}y. \]
Príklad: Vypočítajme obsah časti roviny ohraničenej krivkami \(y=-x\) a \(y=2x-x^{{2}}\).

Riešenie: Načrtnime dané krivky a množinu nimi určenú označme \(D\).

Aby sme množinu \(D\) popísali, potrebujeme vypočítať priesečníky daných kriviek: \[ -x=2x-x^2\Leftrightarrow x=0\vee x=3. \] Množina \(D\) je elementárna oblasť typu \(\left[x,y\right]\), a preto ju môžeme vyjadriť nerovnosťami: \[ \begin{matrix}{\;\;\;0\leqq x\leqq 3,} \\{-x\leqq y\leqq 2x-x^{{2}}.} \end{matrix} \] Pre obsah množiny \(D\) platí: \[ P=\int^3_0 \left(2x-x^2-\left(-x\right)\right)\,\mathrm{d}x=\int^3_0 \left(3x-x^2\right) \,\mathrm{d}x=\left[\frac{3}{2}x^2-\frac{x^3}{3}\right]_0^2=\frac{9}{2}. \]

Príklad: Vypočítajme obsah časti roviny ohraničenej krivkami \(y=x-2\) a \(x=y^2\).

Riešenie: Načrtnime dané krivky a nimi ohraničenú oblasť označme \(Q\).

Aby sme množinu \(Q\) popísali, potrebujeme vypočítať priesečníky daných kriviek: \[ y^2=y+2\Leftrightarrow y=-1\vee y=2. \] Množina \(Q\) je elementárna oblasť typu \(\left[y,x\right]\), a preto ju môžeme popísať nerovnosťami: \[ \begin{matrix}{\;\;\;-1\leqq y\leqq 2,} \\{y^2\leqq x\leqq y+2\;.} \end{matrix} \] Pre obsah množiny \(Q\) platí: \[P=\int^2_{-1} \left(y+2-y^2\right) \,\mathrm{d}y=\left[\frac{y^2}{2}+2y-\frac{y^3}{3}\right]_{-1}^2=\frac{9}{2}. \]

Objem rotačného telesa

Objem rotačného telesa, ktoré vznikne rotáciou elementárnej oblasti \(D\) okolo osi \(o_x\), vypočítame podľa vzorca \[ V=\pi \int^b_a \left[f^{2}(x)-g^2(x)\right]\,\mathrm{d}x. \]
Príklad: Vypočítajme objem telesa, ktoré vznikne rotáciou oblasti ohraničenej krivkami \(y=x^2\), \(y=2-x^2\) okolo osi \(o_x\).

Riešenie: Načrtnime dané krivky a nimi ohraničenú oblasť označme napr. \(D\).

Aby sme množinu \(D\) popísali, potrebujeme vypočítať priesečníky daných kriviek: \[ x^2=2-x^2\Leftrightarrow x=-1\vee x=1. \] Množina \(D\) je elementárna oblasť typu \(\left[x,y\right]\), a preto ju môžeme popísať nerovnosťami: \[ \begin{matrix}{\;\;\;-1\leqq x\leqq 1,} \\x^2\leqq y\leqq 2-x^2. \end{matrix} \] Pre objem telesa platí: \[V=\pi \int^1_{-1} \left[\left(2-x^2\right)^2-\left(x^2\right)^2\right] \,\mathrm{d}x= \pi\int^1_{-1} \left(4-4x^2\right) \,\mathrm{d}x=4\pi \left[x-\frac{x^3}3\right]_{-1}^1= \frac{16}{3}\cdot\pi . \]

Objem rotačného telesa, ktoré vznikne rotáciou elementárnej oblasti \(Q\) okolo osi \(o_y\), vypočítame podľa vzorca \[ V=\pi \int^d_c \left[\Phi^2(y)-\Psi^2(y)\right] \,\mathrm{d}y . \]
Príklad: Vypočítajme objem telesa, ktoré vznikne rotáciou oblasti ohraničenej krivkami \(x=y^2\), \(y=x-2\) okolo osi \(o_y\).

Riešenie: Načrtnime dané krivky a nimi ohraničenú oblasť označme \(Q\).

Pre ohraničenie elementárnej oblasti použijeme postup ako v predchádzajúcej úlohe. Pre objem telesa platí: \[ V=\pi \int^2_{-1} \left[\left(y+2\right)^2-\left(y^2\right)^2\right] \,\mathrm{d}y=\pi \int^2_{-1} \left(y^2+4y+4-y^4\right) \,\mathrm{d}y=\pi \left[\frac{y^3}{3}+2y^{{2}}+4y-\frac{y^5}{5}\right]_{-1}^2=\frac{72}{5}\cdot\pi. \]

Dĺžka krivky

Dĺžku krivky \(C\) danej funkciou \(y=f(x)\) na intervale \(\langle a;b\rangle\), pričom \(f(x)\) má spojitú deriváciu, vypočítame takto: \[ L=\int_{a}^{b}\sqrt{1+[f^{\prime}(x)]^2}\,\mathrm{d}x. \]
Príklad: Vypočítajme dĺžku danej krivky \(C\): \(y=\ln\sin x\), \(x\in \langle \frac{\pi }{3};\frac{2\pi }{3}\rangle.\)

Riešenie: Kedže \(f(x)=\ln\sin x\), \(f^{'}(x)=\dfrac{\cos x}{\sin x}\). Po dosadení do vzťahu na výpočet dĺžky krivky dostávame: \[ L=\int^{\frac{2\pi }{3}}_{\frac{\pi }{3}} \sqrt{1+\frac{\cos^2x}{\sin^2x}}\,\mathrm{d}x= \int^{\frac{2\pi}{3}}_{\frac{\pi }{3}}\frac{1}{\sin x}\,\mathrm{d}x= \int^{\frac{2\pi}{3}}_{\frac{\pi }{3}}\frac{\sin x}{1-\cos^2x}\,\mathrm{d}x= \] \[ = \int^{\frac{1}{2}}_{-{\frac{1}{2}}}\,\frac{\mathrm{d}t}{1-t^{{2}}}=\left[\frac{1}{2}\ln\left|\frac{1+t}{1-t}\right|\right]_{-{\frac{1}{2}}}^{\frac{1}{2}}=\ln 3. \]

Doplňujúce úlohy

Úloha: Vypočítajte určité integrály:

\(\myint{_0^1 \left(x^{{2}}+x+1\right)}\)

Výsledok: \(\frac{11}{6} \)
\(\myint{_1^4 \left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)}\)

Výsledok: \(\frac{8}{3} \)
\(\myint{_{-1}^1 \frac{x^{{2}}-5x+6}{x-2}}\)

Výsledok: \(-6 \)
\(\myint{_0^1 \frac{\mathrm{e}^x}{3+\mathrm{e}^x}}\)

Výsledok: \(\ln\dfrac{3+\mathrm{e}}{4} \)
\(\myint{_0^{\pi /2} \left(3-2\sin x+3\sin ^2 x\right)\cdot\cos x}\)

Výsledok: \( 3\)
\(\myint{_2^3 \left(1-x\right)^{-3}}\)

Výsledok: \(-\frac{3}{8} \)
\(\myint{_0^1 2x\;\left(x^2+2\right)^3}\)

Výsledok: \( \frac{65}{4}\)
\(\myint{_0^1 x\,\mathrm{e}^{1+x^2}}\)

Výsledok: \(\frac{1}{2}\left(\mathrm{e}^{2}-\mathrm{e}\right) \)
\(\myint{_1^{\mathrm{e}} \frac{\sqrt{2+\ln x}}{x} }\)

Výsledok: \( \)
\(\myint{_0^{\pi /2} \left(2-\cos x\right)^4\sin x}\)

Výsledok: \(\frac{2}{3}\left(\sqrt{27}-\sqrt{8}\right) \)
\(\myint{_1^2 \left(3x-1\right)\;\mathrm{e}^x}\)

Výsledok: \(2\mathrm{e}^{{2}}+\mathrm{e} \)
\(\myint{_2^{\mathrm{e}} x\cdot\ln x}\)

Výsledok: \(\frac{1}{4}\mathrm{e}^{{2}}-\ln 4+1 \)
\(\myint{_5^6 \frac{4x+2}{x^{{2}}-2x-8}}\)

Výsledok: \(\ln \frac{64}{7} \)
\(\myint{_0^7 \frac{x-1}{\sqrt[{{3}}]{x+1}}}\)

Výsledok: \(\frac{48}{5} \)
\(\myint{_0^1 \frac{1}{\sqrt{x^{{2}}+4x+5}}}\)

Výsledok: \(\ln \dfrac{3+\sqrt{10}}{2+\sqrt{5}} \)
\(\myint{_1^2 \frac{\mathrm{e}^x}{1-\mathrm{e}^{2x}}}\)

Výsledok: \(\frac{1}{2}\ln \dfrac{1+\mathrm{e}^2}{\left(1+\mathrm{e}\right)^2} \)
\(\myint{_0^1 \frac{4}{2+\mathrm{e}^x}}\)

Výsledok: \(2-2\ln \dfrac{2+\mathrm{e}}{3} \)

Úloha: Vypočítajte nevlastné integrály:

\(\myint{_2^{\infty} \left(\frac{3}{x}+\frac{2}{x^2}\right)^2}\)

Výsledok: \(\frac{37}{6} \)
\(\myint{_2^{\infty} \left(\frac{3}{x}+\frac{2}{x^2}\right)}\)

Výsledok: \(\infty\)
\(\myint{_3^{\infty} \frac{1}{\left(x-2\right)^2}}\)

Výsledok: \(1 \)
\(\myint{_0^{\infty} \mathrm{e}^{-3x}}\)

Výsledok: \(\frac{1}{3} \)
\(\myint{_1^{\infty} \frac{\mathrm{e}^{1/x}}{x^2}}\)

Výsledok: \(\mathrm{e}-1 \)
\(\myint{_2^{\infty} \frac{\ln x}{x}}\)

Výsledok: \(\infty \)
\(\myint{_2^{\infty} \frac{1}{x\,\ln x}}\)

Výsledok: \(\infty \)
\(\myint{_2^{\infty} \frac{1}{x\,\ln^2 x}}\)

Výsledok: \(\dfrac{1}{\ln 2} \)
\(\myint{_1^{\infty} \frac{x}{\sqrt{x^2+1}}}\)

Výsledok: \(\infty \)
\(\myint{_1^{\infty} \frac{x}{\mathrm{e}^x}}\)

Výsledok: \(2\mathrm{e}^{-1} \)
\(\myint{_0^{\infty} x\cdot \mathrm{e}^{-x^2}}\)

Výsledok: \(\frac{1}{2} \)
\(\myint{_{-\infty}^{-0{,}5} \frac{1}{x^2+x+1}}\)

Výsledok: \(\dfrac{\pi}{\sqrt{3}} \)
\(\myint{_{-\infty}^{\infty} \frac{1}{x^2+2x+2}}\)

Výsledok: \(\pi \)
\(\myint{_{-\infty}^{\infty} \frac{\arctg^2 x}{1+x^2}}\)

Výsledok: \(\dfrac{\pi^3}{12} \)

Úloha: Vypočítajte obsah časti roviny ohraničenej krivkami:

\(y=2x,\;y=x,\;x=5 \)

Výsledok: \(\dfrac{25}{2} \)
\( y=5-2x,\;y=2+x,\;x=0\)

Výsledok: \(\dfrac{3}{2} \)
\(y=x^2-2x,\;y=0 \)

Výsledok: \(\dfrac{4}{3} \)
\( y=x^2-2x,\;y=x\)

Výsledok: \(\dfrac{9}{2} \)
\(y=6x-x^2,\;y=0 \)

Výsledok: \(36 \)
\(y=-x^2+4x-2,\;y+x=2 \)

Výsledok: \(\dfrac{9}{2} \)
\(y=x^2-3x+10,\;y=2x+4 \)

Výsledok: \(\dfrac{1}{6} \)
\(y=x^2+x,\;y=2x+2 \)

Výsledok: \( \dfrac{9}{2}\)
\(y=-x^{{2}}+2,\;y=-3x+4 \)

Výsledok: \(\dfrac{1}{6} \)
\(y=x^2-x-6,\;y=-x^2+5x+14 \)

Výsledok: \(\dfrac{343}{3} \)
\(y=x^2+2x+10,\;y=-x^2-4x+18 \)

Výsledok: \(\dfrac{125}{3} \)
\(y=x^2-x,\;y=-x^2+3x \)

Výsledok: \(\dfrac{8}{3} \)
\(y=2x^2-x-2,\;y=x^2+2x+2 \)

Výsledok: \(\dfrac{125}{6} \)
\( y=x^2,\;y^2=x\)

Výsledok: \( \dfrac{1}{3}\)
\(xy=4,\;x+y=5 \)

Výsledok: \(\dfrac{15}{2}-8\ln 2 \)
\(xy=5,\;y=6-x \)

Výsledok: \(12-5\ln 5 \)
\(y=\dfrac{4}{x},\;y=6-2x \)

Výsledok: \(3-4\ln 2 \)
\( y=x^3,\;y=4x\)

Výsledok: \( 8\)
\(y=\mathrm{e}^x,\;y=0,\;x=0,\;x=1 \)

Výsledok: \(\mathrm{e}-1 \)
\(y=\mathrm{e}^{2x},\;y=\mathrm{e}^x+2,\;x=0 \)

Výsledok: \(2\ln 2-\dfrac{1}{2} \)
\(y=\mathrm{e}^{2x}-3,\;y=\mathrm{e}^x-1,\;x=0 \)

Výsledok: \(2\ln 2-\dfrac{1}{2} \)
\(y=2\mathrm{e}^x+3,\;y=\mathrm{e}^{2x},\;x=0 \)

Výsledok: \(3\ln 3 \)
\( y=3-x,\;y=x,\;y=0\)

Výsledok: \(\dfrac{9}{4} \)
\( y=x+1,\;y=7-x,\;y=0\)

Výsledok: \(16 \)
\(x=4,\;y^2=x \)

Výsledok: \(\dfrac{32}{3} \)
\(x=6,\;x=y^2-3 \)

Výsledok: \(36 \)
\(y=x-2,\;y^2=x \)

Výsledok: \(\dfrac{9}{2} \)
\( x=y^2,\;x+y-6=0\)

Výsledok: \(\dfrac{125}{6} \)
\(x=y^2,\;x-3y-4=0 \)

Výsledok: \(\dfrac{125}{6} \)
\( y^2=x+1,\;x+2y-2=0\)

Výsledok: \(\dfrac{32}{3} \)
\(x=y^2-2,\;x-y-4=0 \)

Výsledok: \(\dfrac{125}{6} \)
\( y=x+1,\;\left(y-1\right)^2=x\)

Výsledok: \( \dfrac{1}{6}\)
\(y=\dfrac{8}{x},\;y=2x,\;y=6 \)

Výsledok: \(5-8\ln \dfrac{3}{2} \)
\(y=\dfrac{8}{x},\;y=\dfrac{x}{2},\;y=5 \)

Výsledok: \(21-8\ln \dfrac{5}{2} \)
\( y=\dfrac{6}{x},\;y=\dfrac{x}{6},\;y=3\)

Výsledok: \(24-6\ln 3 \)
\(y=\ln x,\;y=0,\;y=\mathrm{e},\;x=0 \)

Výsledok: \(\mathrm{e}^{\mathrm{e}}-1 \)

Úloha: Vypočítajte objem telesa, ktoré vznikne rotáciou okolo osi \(o_x\) oblasti ohraničenej krivkami:

\(y=2x,\;y=x,\;x=5 \)

Výsledok: \(125\pi \)
\(y=5-2x,\;y=2+x,\;x=0\)

Výsledok: \( 10\pi\)
\( y=3x+1,\;y=0,\;x=0,\;x=1\)

Výsledok: \(7\pi \)
\(y=2x-x^2,\;y=0 \)

Výsledok: \(\dfrac{16}{15}\,\pi \)
\(y=x^2+2,\;y=2x^2+1 \)

Výsledok: \(\dfrac{24}{5}\,\pi \)
\( y=x^2,\;y=1-x^2\)

Výsledok: \(\dfrac{2}{3}\,\sqrt{2}\pi \)
\(y=x^2+2,\;y=0,\;x=-1,\;x=3 \)

Výsledok: \( \dfrac{1532}{15}\,\pi\)
\(y=6x-x^{{2}},\;y=0 \)

Výsledok: \(\dfrac{1296}{5}\,\pi \)
\(y=x^2,\;y^2=x \)

Výsledok: \(\dfrac{3}{10}\,\pi \)
\(xy=4,\;x+y=5 \)

Výsledok: \( 9\pi\)
\(xy=5,\;y=6-x \)

Výsledok: \( \frac{64}{3}\,\pi\)
\( y=\dfrac{4}{x},\;y=6-2x\)

Výsledok: \(\dfrac{4}{3}\,\pi \)
\( y=x^3,\;y=4x,\;x\ge 0\)

Výsledok: \(\dfrac{512}{21}\,\pi \)
\(y=\mathrm{e}^x,\;y=0,\;x=0,\;x=1 \)

Výsledok: \(\dfrac{\pi}{2}\cdot\left(\mathrm{e}^2-1\right) \)
\(y=\mathrm{e}^{-x/10},\;y=0,\;x=0,\;x=10 \)

Výsledok: \(5\pi \left(1-\mathrm{e}^{-2}\right) \)
\(y=\mathrm{e}^{x/2},\;y=e,\;x=0 \)

Výsledok: \(\pi \left(\mathrm{e}^2+1\right) \)
\( y=\mathrm{e}^{2x},\;y=1,\;x=4\)

Výsledok: \(\dfrac{\pi }{4}\,\left(\mathrm{e}^{16}-17\right) \)
\(y=\mathrm{e}^x,\;y=\dfrac{1}{x},\;x=2,\;x=3 \)

Výsledok: \(\dfrac{\pi }{6}\,\left(3\mathrm{e}^6-3\mathrm{e}^4-1\right) \)
\(y=\mathrm{e}^{-x},\;y=x+1,\;x=2 \)

Výsledok: \(\dfrac{\pi }{6}\left(49+3\mathrm{e}^{-4}\right) \)
\(y=3-x,\;y=x,\;y=0 \)

Výsledok: \(\dfrac{9}{4}\,\pi \)
\(y=x+1,\;y=7-x,\;y=0 \)

Výsledok: \( \dfrac{128}{3}\,\pi\)
\(x=4,\;y^2=x \)

Výsledok: \(8\pi \)
\(x=6,\;x=y^2-3 \)

Výsledok: \( \dfrac{81}{2}\,\pi\)
\( y=\dfrac{8}{x},\;y=2x,\;y=6\)

Výsledok: \(\dfrac{56}{3}\,\pi \)
\(y=\dfrac{8}{x},\;y=\dfrac{x}{2},\;y=5 \)

Výsledok: \(108\pi \)
\( y=\dfrac{6}{x},\;y=\dfrac{x}{6},\;y=3\)

Výsledok: \(80\pi \)

Úloha: Vypočítajte objem telesa, ktoré vznikne rotáciou okolo osi \(o_{{y}}\) oblasti ohraničenej krivkami:

\( y=3-x,\;y=x,\;y=0\)

Výsledok: \(\dfrac{27}{4}\,\pi \)
\( x=4,\;y^2=x\)

Výsledok: \( \dfrac{256}{5}\,\pi\)
\( y=x-2,\;y^{{2}}=x\)

Výsledok: \( \dfrac{72}{5}\,\pi\)
\( x=y^2,\;x+y-6=0\)

Výsledok: \(\dfrac{500}{3}\,\pi \)
\(x=y^2,\;x-3y-4=0 \)

Výsledok: \(250\pi \)
\( y=x+1,\;\left(y-1\right)^2=x\)

Výsledok: \(\dfrac{2}{15}\,\pi \)
\( y=\dfrac{8}{x},\;y=2x,\;y=6\)

Výsledok: \(\dfrac{22}{3}\,\pi \)
\(y=\dfrac{8}{x},\;y=\dfrac{x}{2},\;y=5 \)

Výsledok: \( \dfrac{684}{5}\,\pi\)
\(y=\dfrac{6}{x},\;y=\dfrac{x}{6},\;y=3 \)

Výsledok: \(288\pi \)
\(y=\ln x,\;y=0,\;y=\mathrm{e},\;x=0 \)

Výsledok: \(\dfrac{\pi}{2}\,\left(\mathrm{e}^{2\mathrm{e}}-1\right) \)

Úloha: Vypočítajte dĺžku krivky:

\( C:\;y=\dfrac{\mathrm{e}^x+\mathrm{e}^{-x}}{2},\;x\in \langle 0;3\rangle \)

Výsledok: \(\dfrac{1}{2}\left(\mathrm{e}^3-\mathrm{e}^{-3}\right) \)
\(C:\;y=\dfrac{x^2}{4}-\dfrac{\ln x}{2},\;x\in \langle 1;4\rangle \)

Výsledok: \(\dfrac{15}{4}+\ln 2 \)
\(C:\;y=1-\ln(\cos x),\;x\in \left\langle 0;\dfrac{\pi }{4}\right\rangle \)

Výsledok: \(\dfrac{1}{2}\ln \left|\dfrac{2+\sqrt{2}}{2-\sqrt{2}}\right| \)
\( C:\;y=2\sqrt{x^3},\;x\in \langle 0;2\rangle\)

Výsledok: \(\dfrac{2}{27}\left(19\,\sqrt{19}-1\right) \)
\(C:\;y=2\sqrt{x},\;x\in \langle 1;2\rangle \)

Výsledok: \(\sqrt{6}-\sqrt{2}+\dfrac{1}{2}\,\ln\dfrac{2\sqrt{6}+5}{2\sqrt{2}+3} \)
\(C:\;y=\ln \dfrac{\mathrm{e}^x+1}{\mathrm{e}^x-1},\;x\in \langle \ln 2;\ln 5\rangle \)

Výsledok: \(\ln\dfrac{16}{5} \)
\(C:\;y=\mathrm{e}^x,\;x\in \langle 0;1\rangle \)

Výsledok: \(\sqrt{\strut1+\mathrm{e}^2}+\frac{1}{2}\,\ln \left|\dfrac{1+\sqrt{1+\mathrm{e}^2}}{1-\sqrt{1+\mathrm{e}^2}}\,\right|-\sqrt{2}-\frac{1}{2}\,\ln\left|\dfrac{1+\sqrt{2}}{1-\sqrt{2}}\right| \)

Určitý a nevlastný integrál a ich aplikácie

Ciele

Úvod

Postup

Doplňujúce úlohy

Doplňujúce zdroje