Definičný obor, grafy a základné vlastnosti funkcií

Ciele

1. Naučiť sa určovať definičný obor funkcií.
2. Naučiť sa uskutočňovať základné operácie s grafmi funkcií.
3. Naučiť sa určovať, či je funkcia prostá a či existuje inverzná funkcia k funkcii zadanej graficky.
4. Zopakovať si elementárne funkcie a naučiť sa načrtávať ich grafy. Dokazovanie párnosti/nepárnosti jednoduchých funkcií.

Úvod

\(\def\a{&}\def\arctg{\mathop{\mathrm{arctg}}} \def\tg{\mathop{\mathrm{tg}}} \def\arccotg{\mathop{\mathrm{arccotg}}} \def\cotg{\mathop{\mathrm{cotg}}}\) Určenie definičného oboru a náčrt grafov funkcií tvorí súčasť skúmania priebehu funkcií. Graf funkcie slúži na zistenie základných informácií o funkcii, akými sú, napríklad, ohraničenosť/neohraničenosť, párnosť/nepárnosť, monotónnosť, periodicita, spojitosť/nespojitosť alebo znalosť toho, či je funkcia prostá alebo nie. Schopnosť určovať definičný obor a načrtávať grafy elementárnych funkcií sú dobrým predpokladom na zvládnutie riešenia úlohy o priebehu funkcie aj v prípade zložitejších funkcií. V inžinierskej praxi sa stretávame s rôznymi funkciami a ich vlastnosti sú dôležité pri riešení množstva inžinierskych úloh.

Postup

1. Budeme predpokladať, že funkcia \(f(x)\) je zadaná pravidlom alebo vzorcom, napríklad \[ f(x)=\frac{1}{2+\sqrt{3x+4}}. \] Pod prirodzeným definičným oborom funkcie \(\mathcal{D}(f)\) budeme rozumieť množinu všetkých reálnych hodnôt \(x\), ktoré je možné dosadiť do výrazu, t. j. pre ktoré má daný výraz zmysel. Ďalej prívlastok prirodzený nebudeme písať.

   Poznámka: Definičný obor je možné umelo zúžiť, alebo naopak, často je vhodné rozšírenie definičného oboru dodefinovaním funkčných hodnôt v problematických bodoch.

   Pri určovaní problematických bodov sa budeme venovať nasledujúcim problémom, ktoré zapíšeme symbolicky:

   1. \(\dfrac{1}{\ne 0}\) – menovateľ sa nesmie rovnať nule;
   2. \(\sqrt[2n]{\strut\geqq0}\) – výraz pod párnou (\(2n\), \(n\in\mathbb{N}\)) odmocninou musí byť nezáporný;
   3. \(\log(>0)\) – výraz vnútri logaritmu musí byť kladný;
   4. \(\arcsin(\langle-1;1\rangle)\) – hodnoty výrazu vnútri funkcie arkussínus musia byť z intervalu \(\langle-1;1\rangle\) a
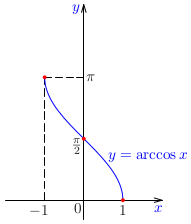
   5. \(\arccos(\langle-1;1\rangle)\) – hodnoty výrazu vnútri funkcie arkuskosínus musia byť z intervalu \(\langle-1;1\rangle\).

   Poznámka: Vyššie uvedené problémy sú typické pri skúmaní väčšiny funkcií, ale nie sú jediné. Napríklad funkcia \(g(x)=\log_x 7\) má aj iné problémy. Mu sa ohraničíme týmito piatimi, ktoré sme uviedli vyššie.

   Poznámka: Ak funkcia nebude obsahovať menovateľ, odmocnicu, logaritmus, arkussínus alebo arkuskosínus, definičným oborom bude množina všetkých reálnych čísel – \(\mathbb{R}\).

   Príklad: Určme definičný obor funkcie \[ f(x)=\frac{1}{2+\sqrt{3x+4}}. \]

   Riešenie: Pri riešení danej úlohy si všimneme, že výraz určujúci danú funkciu obsahuje menovateľ a párnu (druhú) odmocninu. Preto vypíšeme podmienky, týkajúce sa týchto problémov – pričom obsah menovateľa a odmocniny len skopírujeme a pridáme vyššie uvedené značky: \[ 2+\sqrt{3x+4}\ne0\qquad \wedge\qquad 3x+4\geqq0. \] Obidve podmienky musia platiť súčasne, preto sme použili znak konjunkcie. V prípade nerovnosti \(2+\sqrt{3x+4}\ne0\) namiesto bodov, ktoré ju spĺňajú je jednoduchšie určiť problematické body, ktoré bude potrebné vylúčiť z definičného oboru. Teda v obore reálnych čísel riešime rovnicu \[ 2+\sqrt{3x_m+4}=0 \qquad \Longleftrightarrow \qquad \sqrt{3x_m+4}=-2. \] Je zrejmé, že v obore reálnych čísel nemôže odmocnina nadobúdať záporné hodnoty, odkiaľ dedukujeme, že sa menovateľ v obore reálnych čísel nemôže nikdy rovnať nule (vieme dokonca povedať, že menovateľ bude vždy kladný – prečo?). Druhú nerovnicu môžeme v tomto prípade vyriešiť jednoducho: \[ 3x+4\geqq0\qquad \Longleftrightarrow\qquad x\geqq-\frac43. \] Teda definičným oborom zadanej funkcie je \(\mathcal{D}(f)=\big\{x\in\mathbb{R}\,|\,x\geqq-\frac43\big\}=\big\langle\!-\frac43;\infty\big)\).

   Zobraziť riešenieSkryť riešenie

   Príklad: Určme definičný obor funkcie \[ h(x)=\frac{1}{2+\sqrt[3]{x+4}}. \]

   Riešenie: V zadaní funkcie sa len trojka presunula na trochu inú pozíciu. Z možných problémov tentoraz registrujeme len prítomnosť menovateľa a podmienku: \[ 2+\sqrt[3]{x+4}\ne0. \] Podobne ako v predchádzajúcej úlohe, snažíme sa určiť problematické body menovateľa, t. j. vyriešiť rovnicu \[ 2+\sqrt[3]{x_m+4}=0\qquad \Longleftrightarrow \qquad \sqrt[3]{x_m+4}=-2\qquad \Longleftrightarrow \qquad x_m+4=(-2)^3. \] Teda \(x_m=-12\) je jediným riešením danej rovnice a súčasne jediným problémovým bodom definičného oboru. Preto prichádzame k záveru, že \[ \mathcal{D}(h)=\{x\in\mathbb{R}\,|\,x\ne-12\}=\mathbb{R}\backslash\{-12\}=(-\infty;-12)\cup(-12;\infty). \]

   Zobraziť riešenieSkryť riešenie

   Príklad: Určme definičný obor funkcie \[ g(x)=\log\left(\arccos\frac{x}{2x+3}\right). \]

   Riešenie: V tomto prípade sa v zadaní funkcie objavila kombinácia troch možných problémov. Napíšeme príslušné podmienky (vnútra jednotlivých funkcií presne odpíšeme), pričom zachováme vyššie uvedené poradie podmienok: \[ 2x+3\ne0\qquad \wedge \qquad \arccos\frac{x}{2x+3}>0 \qquad \wedge \qquad -1\leqq \frac{x}{2x+3} \leqq 1. \] Pri riešení tejto úlohy využijeme náčrt grafu funkcie \(\arccos x\) (graf zložitejšej funkcie \(\arccos \big(x/(2x+3)\big)\) nebudeme potrebovať).

   

   Obr.: : Graf funkcie \(\arccos x\)

   Z nárčtu grafu je zrejmé, že funkčné hodnoty funkcie \(\arccos x\) sú vždy nezáporné, pričom len v bode \(x=1\) je hodnota arkuskosínusu nulová. Preto strednú podmienku môžeme nahradiť podmienkou \begin{equation}\label{eq:51} -1\leqq \frac{x}{2x+3} \lt 1 \end{equation} (porozmýšľajte prečo). Ak správne vyriešime túto nerovnicu (\ref{eq:51}), vybavíme tým súčasne ľavú aj pravú podmienku. (\ref{eq:51}) v skutočnosti predstavuje sústavu dvoch nerovníc: \begin{equation}\label{eq:52} -1\leqq \frac{x}{2x+3} \qquad \wedge \qquad \frac{x}{2x+3} \lt 1. \end{equation} Ďalej budeme postupne riešiť jednotlivé nerovnice tejto sústavy.

   Poznámka: Na riešenie nerovníc je dobré použiť postup, ktorý je ekvivalentný so známou metódou nulových bodov. Spočíva v tom, že namiesto nerovníc riešime najprv rovnice, pričom tieto riešenia nanášame na časť číselnej osi, zobrazujúcu definičný obor nerovnice. Aj je nerovnica neostrá, riešenie rovnice vyznačíme plným krúžkom, riešenie ostrej rovnice vyznačíme prázdnym krúžkom, Na záver overíme platnosť nerovnice vo ľubovoľnom zvolenom vnútornom bode každého intervalu, ktorý vznikol delením definičného oboru nerovnice zakrúžkovanými bodmi.

   Začneme ľavou nerovnicou (\ref{eq:52}), ktorej definičný obor je \(\mathbb{R}\backslash\big\{-\frac{3}{2}\big\}\). Nerovnicu prepíšeme na rovnicu a vyriešime: \[ -1= \frac{x}{2x+3} \qquad \Rightarrow \qquad -2x-3=x \qquad \Leftrightarrow \qquad -3=3x \qquad \Leftrightarrow \qquad x=-1. \] Po vyznačení plného krúžku v bode \(x=-1\) dostávame nasledujúci obrázok pre ľavú nerovnicu.

   

   Obr.: : Vyznačenie riešení ľavej rovnice

   Platnosť ľavej nerovnice (\ref{eq:52}) overíme dosadením, napríklad, bodov \(x=-2\); \(x=-1{,}1\) a \(x=0\): \[ -1\leqq \frac{-2}{-4+3}=2 \qquad \wedge \qquad -1\not\leqq \frac{-1{,}1}{-2{,}2+3}=\frac{-1{,}1}{0{,}8}=-\frac{11}{8} \qquad \wedge \qquad -1\leqq \frac{0}{3}=0. \] Riešením ľavej nerovnice je teda množina zobrazená na nasledujúcom obrázku.

   

   Obr.: : Vyznačenie riešení ľavej nerovnice

   Aj pravú nerovnicou (\ref{eq:52}), ktorá má rovnaký definičný obor ako ľavá, prepíšeme na rovnicu a vyriešime: \[ \frac{x}{2x+3}= 1 \qquad \Rightarrow \quad x=2x+3 \qquad \Leftrightarrow \qquad -3=x \qquad \Leftrightarrow \qquad x=-3. \] Po vyznačení prázdneho krúžku v bode \(x=-3\) dostávame nasledujúci obrázok pre pravú nerovnicu.

   

   Obr.: : Vyznačenie riešení pravej rovnice

   Platnosť pravej nerovnice (\ref{eq:52}) overíme dosadením, napríklad, bodov \(x=-4\); \(x=-2\) a \(x=0\): \[ \frac{-4}{-8+3}=\frac45\lt1 \qquad \wedge \qquad \frac{-2}{-4+3}=2\not\lt1 \qquad \wedge \qquad \frac{0}{3}=0\lt1. \] Riešením pravej nerovnice je teda množina zobrazená na nasledujúcom obrázku.

   

   Obr.: : Vyznačenie riešení pravej nerovnice

   Riešenie sústavy nerovníc (\ref{eq:52}) získame, keď urobíme prienik množín obsahujúcich riešenia ľavej a pravej nerovnosti, čo môžeme znázorniť graficky.

   

   Obr.: : Obor pravdivosti sústavy nerovníc

   Teda definičným oborom funkcie \(g(x)\) (oborom pravdivosti sústavy nerovníc (\ref{eq:52})) je množina \(\mathcal{D}(g)=(\infty;-3)\cup\langle-1;\infty)\).

   Poznámka: Ak by sme sústavu (\ref{eq:52}) riešili nasledujúcim nesprávnym spôsobom (prečo nesprávnym?), dostali by sme: \[ -1\leqq \frac{x}{2x+3} \lt 1 \qquad\not\Rightarrow\qquad -2x-3\leqq x \lt 2x+3\qquad\Leftrightarrow\qquad -3x-3\leqq 0 \lt x+3 \qquad\Leftrightarrow\qquad \] \[ \qquad\Leftrightarrow\qquad -3\lt x \quad\wedge\quad -1\leqq x\qquad\Rightarrow\qquad -1\leqq x. \] Interval \(\langle-1;\infty)\) je nesprávny obor pravdivosti. O nesprávnosti tohoto riešenia sa ľahko presvedčíme, napríklad, dosadením hodnoty \(x=-4\), ktorá patrí do definičného oboru, pretože \(-1\leqq4/5\lt1\), ale ktorá nepatrí do intervalu \(\langle-1;\infty)\).

   Poznámka: Pri týchto úlohách sa dosť často stáva, že nesprávnym postupom riešenia získame správny obor pravdivosti!

   Zobraziť riešenieSkryť riešenie
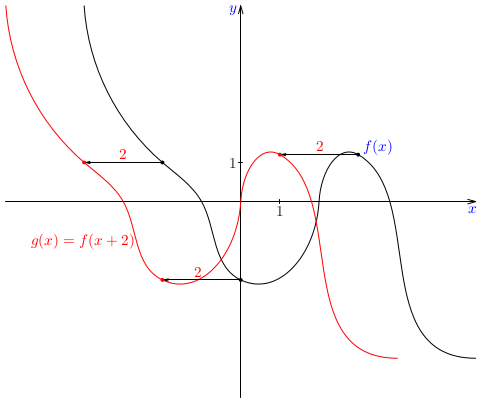
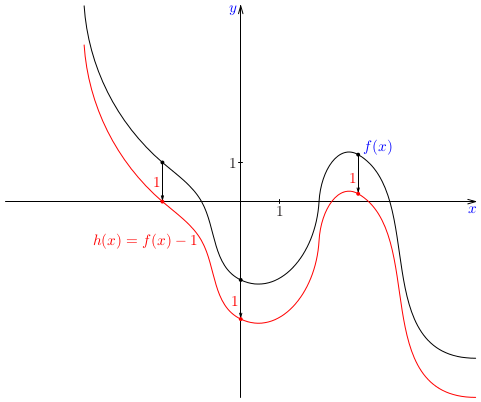
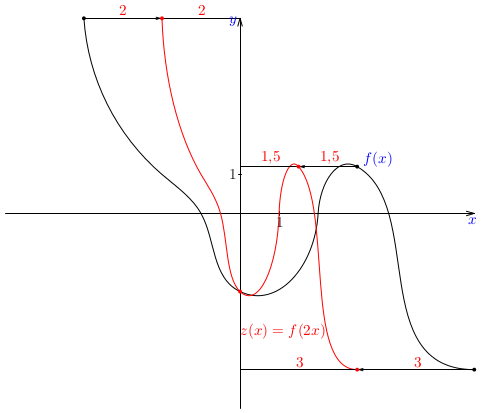
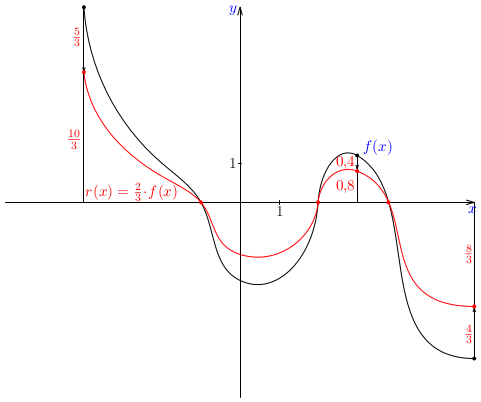
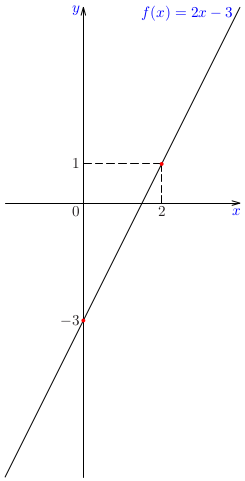
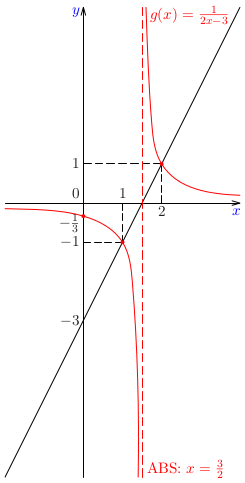
2. Pri práci s grafmi funkcií je užitočné ovládať zopár základných trikov, t. j. základných manipulácií s grafmi. Niektoré si teraz precvičíme.

   Poznámka: Je zrejmé, že pre funkciu, ktorej definičným oborom je celá množina reálnych čísel, nie sme schopní načrtnúť jej celý graf. Preto v podobných úlohách implicitne predpokladáme, že sa budeme zaoberať len príslušnými časťami grafov.

   Poznámka: Budeme sa najprv venovať grafom funkcií, ktorých pravidlo je zadané ako \(a\cdot f(b\cdot x+c)+d\) za predpokladu, že je známa funkcia \(f(x)\). Každý z koeficientov \(a\), \(b\), \(c\) a \(d\) má svoj význam.

   Príklad: Na základe daného grafu funkcie \(f(x)\) zostrojte náčrt grafu funkcií \(f(x+2)\), \(f(x)-1\), \(f(2x)\) a \(\frac23\cdot f(x)\).

   Riešenie: Na začiatok zvolíme nejaký graf funkcie, pretože riešenie úlohy neovplyvňuje konkrétny tvar funkcie. Predpokladáme, že poznáme polohu súradnicových osí (v 3. a vo 4. prípade), ako aj hodnoty jednotiek (v 1. a v 2. prípade). Označme prvú funkciu \(g(x)=f(x+2)\) a vypočítajme jej funkčné hodnoty v niektorých zvolených bodoch. Napríklad \(g(-4)=f(-4+2)=f(-2)\), \(g(-2)=f(-2+2)=f(0)\) alebo \(g(1)=f(1+2)=f(3)\). Takto môžeme naniesť 3 body grafu funkcie \(g\): \(\big(-4;f(-2)\big)\); \(\big(-2;f(0)\big)\) a \(\big(1;f(3)\big)\). Potrebné funkčné hodnoty \(f(-2)\); \(f(0)\) a \(f(3)\) môžeme odmerať na grafe funkcie \(f(x)\). Pri pohľade na graf je zrejmé, že všetky tri body vznikajú horizontálnym posunutím bodov grafu funkcie \(f(x)\) o 2 jednotky vľavo. Je jasné, že takýmto spôsobom môžeme získať aj ďalšie body, t. j. celý graf funkcie \(g(x)=f(x+2)\) získame horizontálnym posunutím bodov grafu funkcie \(f(x)\) o 2 jednotky vľavo tak, ako je to znázornené na obrázku.

   

   Obr.: : Graf funkcie \(f(x-c)\)

   Poznámka: Horizontálny posun o \(-2\) jednotky, t. j. o \(2\) jednotky vľavo súvisí s tým, že funkciu \(g\) môžeme zapísať v tvare \(g(x)=f\big(x-(-2)\big)\). Graf funkcie \(f(x+c)=f\big(x-(-c)\big)\) získame podobne posunutím grafu funkcie \(f(x)\) o \(c\) jednotiek doľava.

   Druhú funkciu označme \(h(x)=f(x)-1\). Je zrejmé, že všetky funkčné hodnoty funkcie \(h(x)\) sú o 1 menšie ako odpovedajúce funkčné hodnoty funkcie \(f(x)\), preto sa body grafu \(\big(x;f(x)\big)\) posunú do bodov \(\big(x;f(x)\big)\), teda o 1 jednotku dole. Vo všeobecnosti graf funkcie \(f(x)+d\) získame vertikálnym posunutím grafu funkcie \(f(x)\) o \(d\) jednotiek dohora (viď obrázok, na ktorom sa nezdá, že všade je posun rovnaký o 1 jednotku dole).

   

   Obr.: : Graf funkcie \(f(x)+d\)

   Tretiu funkciu označme, napríklad, \(z(x)=f(2x)\). Podobne, ako v prvom prípade, môžeme určiť funkčné hodnoty v niekoľkých zvolených bodoch: napríklad \(z(0)=f(2\cdot0)=f(0)\); \(z(-2)=f\big(2\cdot(-2)\big)=f(-4)\) alebo \(z(1{,}5)=f(2\cdot1{,}5)=f(3)\). Teda bod grafu \(\big(0;z(0)\big)\) bude totožný s bodom zadaného grafu \(\big(0;z(0)\big)\), bod grafu \(\big(-2;z(-2)\big)=(-2;f(-4)\big)\) vznikne posunutím bodu \((-4;f(-4)\big)\) smerom ku osi \(o_y\) (presne do polovice!) a bod \(\big(1{,}5;z(1{,}5)\big)=(1{,}5;f(3)\big)\) vznikne rovnako posunutím bodu \((3;f(3)\big)\) smerom ku osi \(o_y\) (presne do polovice!). Ak rovnakú operáciu vykonáme s každým bodom zadaného grafu, t. j. presunieme ho smerom kolmo ku osi \(o_y\) do polovičnej vzdialenosti, získame graf funkcie \(z(x)\) (pozri obrázok). Teda graf funkcie \(f(2x)\) získame 2-násobným horizontálnym stlačením (ako keď stláčame akordeón). Všimnime si tiež, že priesečník s osou \(o_y\) – nulový bod funkcie \(f(x)\) – ostáva na mieste.

   

   Obr.: : Graf funkcie \(f(b\cdot x)\)

   Štvrtú funkciu označme, napríklad, \(r(x)=\frac23\cdot f(x)\). Každá funkčná hodnota \(f(x)\) sa vynásobí koeficientom \(2/3\), t. j. spojnica bodu grafu \(\big(x;f(x)\big)\) s osou \(x\) sa rozdelí v tomto prípade v pomere 1:2. Graf funkcie \(r(x)\) získame z grafu funkcie \(f(x)\) vertikálnym stlačením tak, ako je to znázornené na obrázku.

   

   Obr.: : Graf funkcie \(a\cdot f(x)\)

   V tomto prípade ostávajú na mieste nulové body – priesečníky grafu s osou \(o_x\).

   Zobraziť riešenieSkryť riešenie

   Príklad: Zostrojte graf funkcie \(f(x)=2x-3\) a na základe náčrtu grafu zostrojte náčrt grafu funkcie \(g(x)=1/f(x)\).

   Riešenie: Funkcia \(f(x)=2x-3\) je lineárna funkcia, preto jej grafom je priamka. Na jej určenie stačí určiť dvojicu bodov, ktoré na nej ležia. Tieto body môžeme určiť, napríklad, tak, že zvolíme dve hodnoty \(x\) a určíme im prislúchajúce funkčné hodnoty: \[ x_1=0 \quad \Rightarrow f(x_1)=-3, \qquad x_2=2 \quad \Rightarrow f(x_2)=4-3=1. \] Teda body \((0;-3)\) a \((2;1)\) ležia na grafe, ktorý získame, ak nimi prevedieme priamku tak, ako je to znázornené na obrázku.

   

   Obr.: : Grafom lineárnej funkcie \(f(x)=2x-3\) je priamka

   Pri konštrukcii náčrtu grafu funkcie \(g(x)=1/f(x)\) si najprv všimnime, že body, v ktorých sú nulové funkčné hodnoty funkcie \(f(x)\), nepatria do definičného oboru funkcie \(g(x)\). Presnejšie, budú to jej body nespojitosti, v ktorých má funkcia \(g(x)\) asymptoty bez smernice. V našom prípade (ako je to evidentné z náčrtu grafu funkcie \(f(x)\) existuje jeden takýto bod. Pri náčrte grafu prevrátenej funkcie nie je nutné tento bod vypočítať, stačí len v tomto bode načrtnúť asymptotu bez smernice. V našom konkrétnom prípade však určenie nulového bodu nie je zložité: \(2x_0-3=0\), a teda \(x_0=3/2\). Na náčrt grafu funkcie \(g(x)\) stačí určiť jej hodnoty v niekoľkých bodoch (ak by bol zadaný len náčrt grafu funkcie \(f(x)\), mohli by sme, napríklad, odhadnúť, v ktorom bode \(x\) nadobúda funkcia \(f\) hodnotu 1, \(-2\) atď, v tých bodoch by sme potom dokázali určiť prevrátené hodnoty \(g(x)\)).

   

   Obr.: : Graf lineárne lomenej funkcie \(g(x)=1/(2x-3)\)

   V našom príklade sme využili nasledujúce informácie: \(f(-2)=-7\);\(f(0)=-3\); \(f(1)=-1\); \(f(2)=1\) a \(f(4)=5\). Prevrátené hodnotu sú teda \(g(-2)=-1/7\); \(g(0)=-1/3\); \(g(1)=-1\); \(g(2)=1\) a \(g(4)=1/5\). Tieto body nám úplne postačili na to, aby sme načrtli graf funkcie \(g(x)\).

   Zobraziť riešenieSkryť riešenie

   Poznámka: Funkcia \(g(x)=1/(2x-3)\) patrí do triedy funkcií, ktoré nazývame lineárne lomené funkcie. Sú to funkcie, ktorých predpis je podiel dvoch lineárnych funkcií, t. j. funkcie tvaru \[ r(x)=\frac{ax+b}{cx+d}. \] V našom prípade je \(a=0\), \(b=1\), \(c=2\) a \(d=-3\). Lineárne lomené funkcie patria ďalej do triedy racionálnych funkcií, ktorým sa budeme venovať v nasledujúcom cvičení.

   Poznámka: Podobne môžeme postupovať pri náčrtoch grafov funkcií tvaru \(f(x)\pm g(x)\), resp. \(f(x)\cdot g(x)\) alebo \(f(x)/g(x)\). Napríklad, môžeme využiť nulové body niektorej zo zložiek na určenie funkčnej hodnoty súčtu, rozdielu, súčinu alebo podielu, prípadne iné zaujímavé funkčné hodnoty: \(\pm1\), \(\pm2\) a pod.
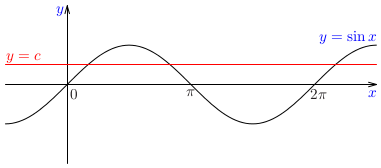
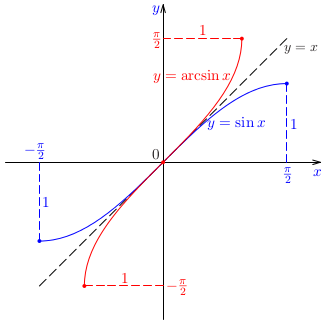
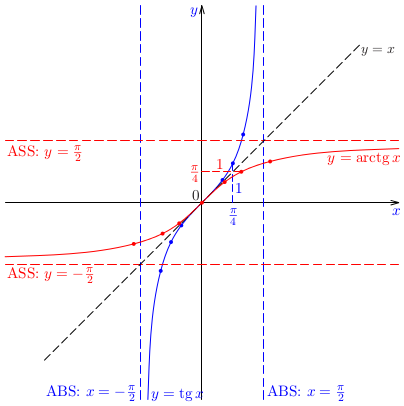
3. V praxi je veľmi dôležité posudzovanie, či má určitá funkcia inverznú funkciu, t. j., či na základe znalosti funkčnej hodnoty \(y=f(x)\) funkcie \(f\) sme schopní identifikovať odpovedajúcu hodnotu nezávisle premennej \(x\). Náčrt grafu funkcie nám často umožní odpovedať na podobné otázky.

   Príklad: Na základe náčrtu grafu funkcie \(f(x)=\sin x\) posúďme, či má funkcie \(\sin x\) inverznú funkciu.

   Riešenie: Načrtneme graf funkcie \(\sin x\) napríklad na intervale obsahujúcom interval \(\langle0;2\pi\rangle\), t. j. na intervale obsahujúcom aspoň jednu periódu funkcie \(\sin x\). Ďalej si predstavíme množinu horizontálnych priamok zadaných rovnicami \(y=c\), kde \(c\) sú reálne konštanty. Ak niektorá z týchto priamok pretína graf funkcie \(f(x)\) v aspoň dvoch bodoch, tak funkcia \(f(x)\) nie je prostá, a teda nemôže mať inverznú funkciu.

   

   Obr.: : Graf funkcie \(\sin x\)

   Je zrejmé, že funkcia \(\sin x\) nie je prostá, keďže sa nám podarilo nájsť takú priamku \(y=c\) (samotná hodnota \(c\) pritom nie je dôležitá), ktorá pretína graf funkcie \(\sin x\) vo viacerých bodoch (na obrázku sú znázornené 3 priesečníky, ale je zrejmé, že priesečníkov je nekonečne veľa). Teda funkcia \(\sin x\) nemá inverznú funkciu!

   Zobraziť riešenieSkryť riešenie

   Poznámka: Je zrejmé, že žiadna periodická funkcia nemôže mať inverznú funkciu!!!

   Poznámka: Je známe, že inverzná funkcia k funkcii \(\sin x\) sa nazýva \(\arcsin x\). Ako je to možné, ak funkcia \(\sin x\) nemôže mať inverznú funkciu? Vysvetlenie podáva riešenie nasledujúcej úlohy.

   Príklad: Určme takú časť grafu funkcie \(\sin x\), ktorá reprezentuje graf prostej funkcie. Pre túto časť načrtnime graf inverznej funkcie.

   Riešenie: Pri pohľade na graf uvedený vyššie je zrejmé, že daná úloha nemá jednoznačné riešenie. Intervalov, na ktorých horizontálne priamky pretínajú graf funkcie \(\sin x\) najviac v jednom bode je nekonečne veľa. Zvoľme teda taký čo najširší interval obsahujúci bod \(x=0\), na ktorom bude funkcia \(\sin x\) prostá. Je zrejmé, že takýmto intervalom je interval \(\langle-\pi /2;\pi /2\rangle\). Ak odpovedajúcu časť grafu funkcie \(\sin x\) na intervale \(\langle-\pi /2;\pi /2\rangle\) zobrazíme symetricky voči osi \(y=x\), získame graf inverznej funkcie, ktorá sa nazýva \(\arcsin(x)\). Pozrite sa na nasledujúci obrázok.

   

   Obr.: : Graf zúženej funkcie \(\sin|_{\langle-\pi /2;\pi /2\rangle}\, x\) a jej inverznej funkcie \(\arcsin x\)

   Symetrické zobrazenie spôsobuje výmenu súradníc jednotlivých bodov grafu: bod \((\pi /2;1)\) grafu funkcie \(\sin x\) sa vymení za bod \((1;\pi /2)\) grafu funkcie \(\arcsin x\), podobne sa bod \((-\pi /2;-1)\) vymení za bod \((-1;-\pi /2)\), v bode \((0;0)\) výmena súradníc nespôsobí žiadnu zmenu.

   Zobraziť riešenieSkryť riešenie

   Poznámka: Ako sme už vyššie konštatovali, funkcia \(\sin x\) nemá inverznú funkciu. Funkcia \(\arcsin x\) je inverzná funkcia k tzv. zúženiu funkcie \(\sin x\) na interval \(\langle-\pi /2;\pi /2\rangle\), ktoré označujeme ako \(\sin|_{\langle-\pi /2;\pi /2\rangle}\, x\).
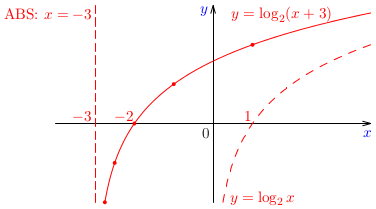
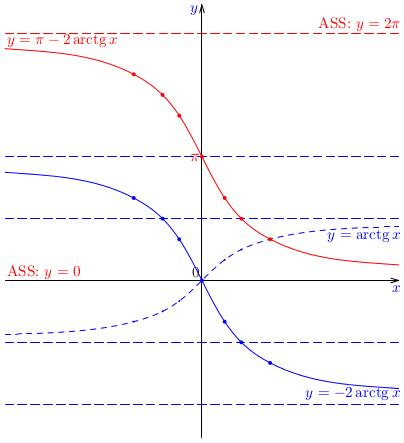
4. Medzi elementárne funkcie zaraďujeme lineárne, kvadratické, mocninové, lineárne-lomené, exponenciálne, logaritmické, goniometrické a cyklometrické funkcie. Ich význam spočíva aj v tom, že pomocou nich vyjadrujeme celý rad zložitejších funkcií, ktoré majú praktické použitie, aj keď sa občas stáva, že je potrebné/vhodné zaviesť ďalšie funkcie, ktoré nedokážeme pomocou elementárnych vyjadriť. Preto sa od študentov požaduje dobrá znalosť vlastností elementárnych funkcií a tiež schopnosť načrtávať ich grafy (pri zadaní funkcií v základnom tvare).

   Príklad: Načrtnime graf logaritmickej funkcie \(\log_2(x+3)\). Posúďte, či je táto funkcia párna alebo nepárna.

   Riešenie: Logaritmická funkcia \(\log_2 x\) je inverzná funkcia ku exponenciálnej funkcii so základom 2, t. j. ku funkcii \(f(x)=2^x\). Na načrtnutie jej grafu postačujú znalosti elementárnej matematiky. Vypočítajme jej funkčné hodnoty v bodoch \(x=-2\); \(-1\); 0; 1; 2 (nie je nutné dodržať toto poradie). Výsledok zapíšme do nasledujúcej tabuľky: \[ \begin{array}{|c||c|c|c|c|c|} \hline x \a -2 \a -1 \a 0 \a 1 \a 2 \\ \hline 2^x \a 1/4 \a 1/2 \a 1 \a 2 \a 4 \\ \hline \end{array} \] Vypočítané hodnoty využijeme na náčrt grafu exponenciálnej funkcie \(f(x)=2^x\) tak, ako je to znázornené na nasledujúcom obrázku.

   

   Obr.: : Graf exponenciálnej funkcie \(2^x\)

   Z obrázku je zrejmé, že exponenciálna funkcia \(2^x\) je prostá. Predstavte si množinu horizontálnych priamok a porozmýšľajte o možnom počte priesečníkov s grafom.

   Poznámka: Iným spôsobom zdôvodnenia faktu, že exponenciálna funkcia je prostá je aj to, že je rastúca (preto nemôže nadobúdať tú istú funkčnú hodnotu v dvoch rôznych bodoch).

   Prostá funkcia má inverznú funkciu, ktorou je pre exponenciálnu funkciu \(2^x\) logaritmická funkcia \(log_2 x\) (pripomíname, že číslo 2 sa nazýva základ logaritmu). Ako sme uviedli vyššie, na náčrt grafu funkcie \(g(x)=\log_2 x\) stačí vymeniť súradnice bodov grafu, teda v našom prípade vymeníme riadky vyššie uvedenej tabuľky (s výnimkou 1. stĺpca): \[ \begin{array}{|c||c|c|c|c|c|} \hline x \a 1/4 \a 1/2 \a 1 \a 2 \a 4 \\ \hline \log_2 x \a -2 \a -1 \a 0 \a 1 \a 2 \\ \hline \end{array} \]

   Poznámka: Ak zmeníme základ 2 na všeobecné číslo \(a\), \(1\not=a\in(0;\infty)\), získame tabuľku funkčných hodnôt pre funkciu \(\log_a x\): \[ \begin{array}{|c||c|c|c|c|c|} \hline x \a a^{-2} \a a^{-1} \a 1 \a a \a a^2 \\ \hline \log_a x \a -2 \a -1 \a 0 \a 1 \a 2 \\ \hline \end{array} \] Na náčrt logaritmickej funkcie často postačujú 3., 4. a 5. stĺpec.

   Graf funkcie \(g(x)=\log_2 x\) je znázornený na nasledujúcom obrázku:

   

   Obr.: : Konštrukcia graf logaritmickej funkcie \(\log_2 x\) na základe jej inverznej exponenciálnej funkcie

   Graf funkcie \(\log_2(x+3)\) teraz získame jednoduchým posunutím grafu funkcie \(\log_2 x\) o 3 jednotky vľavo. Náčrt je zobrazený na nasledujúcom obrázku:

   

   Obr.: : Graf funkcie \(h(x)=\log_2(x+3)\) získaný posunom logaritmickej funkcie \(\log_2 x\)

   Na záver ešte posúďme, či je funkcia \(h(x)=\log_2(x+3)\) párna (\(h(-x)=h(x)\)) alebo nepárna (\(h(-x)=-h(x)\)). Párnosť znamená symetriu grafu funkcie voči osi \(o_y\), nepárnosť znamená symetriu grafu funkcie voči bodu \((0;0)\). Pri pohľade na graf je zrejmé, že funkcia nie je ani párna ani nepárna. Aby sme toto tvrdenie dokázali, využijeme, napríklad, nulový bod funkcie: \[ 0= h(-2) \ne \pm h(2) \ne 0. \]

   Poznámka: Využili sme fakt, že v prípade párnej aj nepárnej funkcie musia byť nulové body grafu – priesečníky s osou \(o_x\) – rozložené symetricky voči bodu \(x=0\).

   Zobraziť riešenieSkryť riešenie

   Príklad: Načrtnime graf funkcie \(f(x)=\pi-2\arctg x\). Posúďte, či je táto funkcia párna alebo nepárna, rastúca alebo klesajúca.

   Riešenie: Na vytvorenie náčrtu grafu danej funkcie je postačujúce načrtnúť graf funkcie \(\arctg x\) a použiť transformácie grafov opísané vyššie v cieli 2. Ako nasvedčuje názov funkcie \(\arctg x\), súvisí táto funkcia s funkciou \(\tg x\), ktorá je však periodická, a preto k nej neexistuje inverzná funkcia. Podobne, ako je to v prípade funkcií arkuskosínus a arkussínus, je potrebné zvoliť len tú časť grafu funkcie tangens, ktorá reprezentuje prostú funkciu. Funkcia \(\arctg x\) je definovaná ako inverzná funkcia ku funkcii \(\tg|_{(-\pi /2;\pi /2)}\, x\), t. j. k zúženiu funkcie tangens. Náčrt funkcie \(\arctg x\) získame, ak symetricky znázorníme vetvu grafu funkcie \(\tg x\). Pripomeňme si základné hodnoty goniometrických funkcií (\(\tg x=\sin x /\cos x\) a \(\cotg x=\cos x /\sin x\)): \[ \begin{array}{c||c|c|c|c} \alpha \a \sin \alpha \a \cos \alpha \a \tg \alpha \a \cotg \alpha\\ \hline\hline 0 \a 0 \a 1 \a 0 \a -\\ \hline \frac{\pi}{6} \a \frac{1}{2} \a \frac{\sqrt3}{2} \a \frac{\sqrt3}{3} \a \sqrt3\\\hline \frac{\pi}{4} \a \frac{\sqrt2}{2} \a \frac{\sqrt2}{2} \a 1 \a 1\\ \hline \frac{\pi}{3} \a \frac{\sqrt3}{2} \a \frac{1}{2} \a \sqrt3 \a \frac{\sqrt3}{3}\\ \hline \frac{\pi}{2} \a 1 \a 0 \a - \a 0\\ \hline\hline \end{array} \] Funkčné hodnoty tangensu pre záporné hodnoty premennej \(x\) získame na základe nepárnosti tangensu: \(\tg(-x)=-\tg(x)\).

   Poznámka: Vzhľadom na menovateľ \(\cos x\) funkcia \(\tg x\) nie je definovaná v bode \(\pi /2\). Dá sa však ukázať, že priamky \(x=\pm \pi /2\) sú asymptoty bez smernice funkcie tangens, pričom ak sa hodnoty \(x\) blížia k \(\pi /2\) zľava, funkčné hodnoty neohraničene narastajú, resp. ak sa hodnoty \(x\) blížia k \(-\pi /2\) zprava, funkčné hodnoty neohraničene klesajú.

   Na základe uvedených informácií načrtneme jednu vetvu grafu funkcie \(\tg x\) a pomocou zobrazenia symetrie okolo osi \(y=x\) získame náčrt grafu funkcie \(\arctg x\).

   

   Obr.: : Grafy funkcií \(\tg x\) a \(\arctg x\)

   Poznámka: Poznamenajme, že pri symetrickom zobrazení voči osi \(y=x\) sa vertikálne priamky (asymptoty bez smernice) zobrazujú do horizontálnych priamok (asymptot so smernicou rovnou nule) a naopak.

   Náčrt zadanej funkcie ľahko dokončíme, ak si uvedomíme, že náčrt grafu arkustangensu stačí prevrátiť a vertikálne dvojnásobne roztiahnuť (koeficient \(-2\)) a posunúť o \(\pi\) jednotiek nahor. Tieto transformácie sú znázornené na nasledujúcom obrázku.

   

   Obr.: : Nárčt grafu funkcie \(f(x)=\pi-2\arctg x\) na základe grafu funkcie \(\arctg x\)

   Na záver si všimnime, že výsledná funkcia je klesajúca. Jej graf nie je symetrický ani voči osi \(o_y\) (funkcia nie je párna), ani voči bodu \((0;0)\) (funkcia nie je nepárna), hoci je symetrický voči bodu \((0;\pi)\). Na vyvrátenie párnosti môžeme napísať \(f(-1)\ne f(1)\) a na vyvrátenie nepárnosti môžeme napísať \(0\lt f(-1)\ne -f(1)\lt 0\).

   Zobraziť riešenieSkryť riešenie

   Úloha: Načrtnite graf funkcie \(h(x)=2\arccotg x\).

   Výsledok: Graf je totožný s grafom funkcie \(h(x)=\pi-2\arctg x\).

   Zobraziť výsledokSkryť výsledok

Doplňujúce úlohy

Úloha: Určte definičný obor funkcie \[ f(x)=\sqrt[3]{x^3+2x+3}-\frac{\arccos(x^2)}{3+\sqrt{1-x-x^2}}+\mathrm{e}^{-4x}\cdot\sin(3+2x). \]
Výsledok: \[ -1\leqq x^2\leqq1 \quad\mbox{t. j.}\quad -1\leqq x\leqq1 \quad \wedge\quad 1-x-x^2\geqq0 \qquad \Rightarrow \qquad x\in \langle-1;(\sqrt{5}-1)/2\rangle \]
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor funkcie \[ f(x)=\arcsin(\log_2(x+3))-\frac{x^2+5}{x^2-5}+\mathrm{e}^{-x}\cdot\cos(\pi x). \]
Výsledok: \[ -1\leqq \log_2(x+3)\leqq1\quad\mbox{t. j.}\quad\frac12\leqq x+3\leqq2 \quad \wedge\quad x^2-5\ne 0 \qquad \Rightarrow \] \[ \Rightarrow \qquad x\in \langle-5/2;-\sqrt{5}) \cup (-\sqrt{5};-1\rangle \]
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor funkcie \[ f(x)=\arccotg(x+\pi^2)\cdot\sqrt[3]{x^6+\ln x-7}+\frac{11}{(3-2x)\cdot\ln(x^2+2x-3)}. \]
Výsledok: \[ x>0\quad \wedge\quad x\ne \frac32\quad \wedge\quad x^2+2x-3>0\quad \wedge\quad x^2+2x-3\ne1 \quad \Rightarrow \] \[ \Rightarrow\quad x\in(1;\sqrt5-1)\cup(\sqrt5-1;3/2)\cup(3/2;\infty) \]
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor funkcie \[ f(x)=\mathrm{e}^x\cdot\sin(3x)-\frac{\arctg(x^2)}{x\cdot\sqrt{20-x-x^2}}+\sqrt[3]{x^3+2\cotg x+3}. \]
Výsledok: \[ x\ne0\quad \wedge\quad \sin x\ne 0\quad \wedge\quad 20-x-x^2>0 \qquad \Rightarrow \qquad x\in(-5;0)\cup(0;\pi)\cup(\pi;4) \]
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor funkcie \[ f(x)=\frac{x}{2-\sqrt{x^2-4}}+\arccos\left(2^{-x}\right)+(x+\pi)\cdot\sqrt[5]{x^2-7}. \]
Výsledok: \[ x^2-4\ne4\quad \wedge\quad x^2-4\geqq 0\quad \wedge\quad -1\leqq 2^{-x}\leqq1\quad\mbox{t. j.}\quad x\geqq0 \qquad \Rightarrow \] \[ \Rightarrow\qquad x\in\big(2;2\sqrt2\big)\cup\big(2\sqrt2;\infty\big) \]
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor a načrtnite graf funkcie \(h(x)=2-x-x^2\). Zistite, či je funkcia párna alebo nepárna.
Výsledok: \(h(0)=2\ne0\quad\Rightarrow\quad\) funkcia nie je nepárna.
Poznámka: Pre nepárnu funkciu definovanú v bode \(x=0\) musí platiť: \(h(0)=h(-0)=-h(0)\), t. j. \(h(0)=0\,\)!
\(2=h(-1)\ne h(1) =0\quad\Rightarrow\quad\) funkcia nie je párna.
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor a načrtnite graf funkcie \(g(x)=2\cdot \cos(3x)+4\). Zistite, či je funkcia párna alebo nepárna.
Výsledok: \(g(0)=6\ne0\quad\Rightarrow\quad\) funkcia nie je nepárna.
\(g(-x)=2\cdot \cos(-3x)+4\stackrel{\cos\ \mathrm{je\ párna}}{=}2\cdot \cos(3x)+4=g(x)\quad\Rightarrow\quad\) funkcia je párna.
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor a načrtnite graf funkcie \(f(x)=\mathrm{e}^{\sin (2x)}\). Zistite, či je funkcia párna alebo nepárna.
Výsledok: \(f(0)=\mathrm{e}^{0}=1\ne0 \quad\Rightarrow\quad\) funkcia nie je nepárna.
\(1>\mathrm{e}^{-1}=f(-\pi /4)\ne f(\pi /4)=\mathrm{e}^{1}>1 \quad\Rightarrow\quad\) funkcia nie je párna.
Zobraziť výsledokSkryť výsledok
Úloha: Určte definičný obor a načrtnite graf funkcie \(h(x)=\mathrm{e}^{-x}\cdot \cos (2x)\). Zistite, či je funkcia párna alebo nepárna.
Výsledok: \(h(0)=\mathrm{e}^{0}\cdot1=1\ne0 \quad\Rightarrow\quad\) funkcia nie je nepárna.
\(1\lt \mathrm{e}^{\pi}=h(-\pi)\ne h(\pi)=\mathrm{e}^{-\pi}\lt 1 \quad\Rightarrow\quad\) funkcia nie je párna.
Zobraziť výsledokSkryť výsledok

Doplňujúce zdroje

1. Stránka predmetu Matematika 1 .
2. Učebnica Úvod do predmetu Matematika 1 .