Komplexné čísla

Ciele

1. Precvičiť operácie s komplexnými číslami v algebrickom tvare.
2. Vysvetliť a precvičiť prevod komlexného čísla z algebrického do goniometrického tvaru.
3. Vysvetliť a precvičiť operácie s komplexnými číslami v goniometrickom tvare.
4. Odvodiť a precvičiť riešenie binomickej rovnice.
5. Precvičiť riešenie rovníc v množine komplexných čísel.

Úvod

Je všeobecne známe, že druhá mocnina každého reálneho čísla je nezáporné reálne číslo. Túto základnú vlastnosť reálnych čísel nemajú komplexné čísla, definované pomocou tzv. imaginárnej jednotky, ktorú označíme symbolom \(i\) a pre ktorú platí \[i^2=-1.\]

Postup

1. Precvičiť operácie s komplexnými číslami v algebrickom tvare.
   Mocniny imaginárnej jednotky definujeme rovnako, ako mocniny reálnych čísel. Potom dostávame \[i^3=i^2\cdot i=-i,\quad i^4=i^3\cdot i=-i^2=1,\quad i^5=i^4\cdot i=i,\dots.\] Ľahko zistíme, že pre každé prirodzené číslo \(n\) platí \[i^{n+4}=i^n.\]
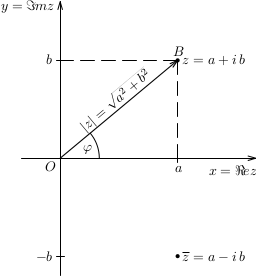
   Komplexné číslo je v algebrickom tvare, ak je v tvare \(z=a+b\cdot i\), kde \(a,\, b\) sú reálne čísla. Číslo \(a\in \mathbb{R}\) nazývame reálna časť komplexného čísla a číslo \(b\in\mathbb{R}\) imaginárna časť komplexného čísla. Každému komplexnému číslu \(z=a+b{\it i}\) v~algebrickom tvare zodpovedá práve jedna usporiadaná dvojica \((a,b)\) reálnych čísel. Zvoľme v rovine bežnú pravouhlú súradnicovú sústavu a v nej bod \(B=[a;b].\) Jeho prvá súradnica sa rovná reálnej časti a druhá súradnica imaginárnej časti komplexného čísla \(z\). Toto priradenie je vzájomne jednoznačné, lebo ku každému bodu roviny existuje jediné komplexné číslo, ktoré je tzv. vzorom tohto bodu pri danom priradení.
   Bodom osi \(x\) je priradená usporiadaná dvojica \((x,0)\), ktorej zodpovedá číslo \(x+0{\it i}=x\), kde \(x\in\mathbb{R}\). To ale znamená, že body osi \(x\) reprezentujú reálne čísla. Podobnou úvahou dostaneme, že body osi \(y\) znázorňujú čísla typu \(0+y{\it i}=y{\it i}\), kde \(y\in\mathbb{R}\). To sú komplexné čísla s nulovou reálnou časťou -- hovoríme im rýdzo imaginárne čísla. Rovine, v ktorej sú uvedeným spôsobom znázorňované komplexné čísla, hovoríme Gaussova rovina, osi \(x\) hovoríme reálna os a osi \(y\) imaginárna os.

   

   Obr.: : Zobrazenie v Gaussovej rovine

   Príklad: Vypočítajme \(i^{13},\ i^{22},\ i^{115},\ i^{-9},\ i^{-18}.\)

   Riešenie: Využitím vzťahu \(i^{n+4}=i^n\) dostávame: \[i^{13}=i^1=i,\quad i^{22}=i^2=-1,\quad i^{115}=i^3=-i,\quad i^{-9}=i^3=-i,\quad i^{-18}=i^2=-1.\]

   Zobraziť riešenieSkryť riešenie

   Príklad: Nájdime reálne čísla \(x,y \def\a{&}\) tak, aby platilo \[(2-4i)(-2x+5iy)=8+34i.\]

   Riešenie: Dve komplexné čísla sa rovnajú, ak majú rovnakú reánu aj imaginárnu časť.
   Roznásobíme výrazy na ľavej strane rovnice a vyjadríme ľavú rovnicu v tvare \(a+bi\): \[-4x+20y+i(8x+10y)=8+34i.\] Porovnaním reálnych a imaginárnych zložiek na oboch stranách rovnice dostávame sústavu rovníc: \[ \begin{array}{rrl} -4x+20y\a=\a 8\\8x+10y\a=\a 34. \end{array} \] Jej riešenie je \(x=3, y=1.\)

   Zobraziť riešenieSkryť riešenie

   Príklad: Dané sú komplexné čísla \(z_1=3-4i,\ z_2=-2+3i\). Vypočítajme \(z_1+z_2,\ z_1.z_2,\) \(\frac{z_1}{z_2}\).

   Riešenie: \[z_1+z_2=(3-4i)+(-2+3i)=1-i, \], \[z_1.z_2=(3-4i)(-2+3i)=-6+9i+8i-12i^2=-6+17i+12=6+17i, \] \[\frac{z_1}{z_2}=\frac{(3-4i)(-2-3i)}{(-2+3i)(-2-3i)}=\frac{-6-9i+8i-12}{4+9}=\frac{-18-i}{13}= -\frac{18} {13}-\frac{1}{13}i.\]

   Zobraziť riešenieSkryť riešenie

   Príklad: Dané sú komplexné čísla \(u=2-2i,\ v=-3+2i\). Vypočítajme \(u.\overline{v},\quad\frac{\overline{u}}{\overline{v}},\ \frac{u.\overline{v}}{v}\).

   Riešenie: Komplexne združené číslo k číslu \(z=a+bi\) je číslo \(\overline{z}=a-bi\). Teda komplexne združené čísla k číslam \(u,\,v\) sú čísla: \[\overline{u}=2+2i,\ \overline{v}=-3-2i.\] Potom \[u.\overline{v}=(2-2i)(-3-2i)=-6-4i+6i-4=-10+2i,\] \[\frac{\overline{u}}{\overline{v}}=\frac{\overline{u}\cdot v}{\overline{v}\cdot v}=\frac{(2+2i)(-3+2i)}{(-3-2i)(-3+2i)}= \frac{-6+4i-6i-4}{9+4}=\frac{-10-2i}{13}=-\frac{10}{13}-\frac{2}{13},\] \[\frac{u.\overline{v}}{v}=\frac{-10+2i}{-3+2i}=\frac{(-10+2i)(-3-2i)}{(-3+2i)(-3-2i)}= \frac{30+20i-6i+4}{9+4}=\frac{34+14i}{13}=\frac{34}{13}+\frac{14}{13}.\]

   Zobraziť riešenieSkryť riešenie
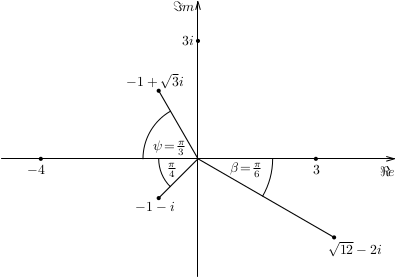
2. Prevod komplexného čísla z algebrického do goniometrického tvaru.

   Príklad: Komplexné číslo \(z=-1+i\) preveďte do goniometrického tvaru.

   Riešenie: Goniometrický tvar komplexného čísla je tvar \[ z=|z|\cdot(\cos\varphi+i\cdot\sin\varphi). \] Najprv vypočítame \(|z|\) podľa vzťahu \(|z|=\sqrt{a^2+b^2}\).
   Dostávame \[|z|=\sqrt{(-1)^2+1^2}=\sqrt{2}.\] Pre určenie argumentu \(\varphi\) vypočítame hodnoty goniometrických funkcíí podľa vzťahov \[ \cos\varphi=\frac{a}{|z|},\quad \sin\varphi=\frac{b}{|z|}. \] Dostávame \[\cos\varphi =-\frac{1}{\sqrt{2}}=-\frac{\sqrt{2}}{2},\ \ \sin \varphi=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2},\] potom \[\varphi=\frac{3\pi}{4}.\] Goniometrický tvar je:\[z=\sqrt{2}(\cos\frac{3\pi}{4}+i \sin\frac{3\pi}{4}).\]

   Zobraziť riešenieSkryť riešenie

   Úloha: Dané komplexné čísla zapíšme v goniometrickom tvare a zobrazme ich v Gaussovej rovine:
   \(\quad {\rm a)} 3{\it i};\quad {\rm b)} -1-{\it i}; \quad {\rm c)} -4;\quad {\rm d)} -1+\sqrt 3{\it i};\quad {\rm e)} 3;\quad {\rm f)} \sqrt{12}-2{\it i}\).

   Riešenie: a) Zrejme \(\vert 3{\it i}\vert=\sqrt{0^2+3^2}=3\) a dostávame \[ \cos\varphi=\frac{0}{3}\qquad\mbox{a}\qquad \sin\varphi=\frac{3}{3}=1.\] Jej riešením je množina \(\varphi=\pi/2+2k\pi,k \in\mathbb{Z}.\) Za argument čísla \(3i\) zvolíme hodnotu \(\varphi=\pi/2.\) Potom \[ 3{\it i}=3(\cos\tfrac{\pi}{2} +{\it i}\sin\tfrac{\pi}{2}). \]
   b) Tentoraz \(\vert\! -1-{\it i}\vert =\sqrt{(-1)^2+(-1)^2}=\sqrt 2.\) Komplexné číslo \(-1-{\it i}\) leží v~Gaussovej rovine na osi tretieho kvadrantu. Odtiaľ ľahko vidno, že \(\varphi=\pi +\pi/4=5\pi/4.\quad\) Potom \[ -1-{\it i}=\sqrt 2(\cos\tfrac{5\pi}{4} +{\it i}\sin\tfrac{5\pi}{4}). \]
   c) Číslo -4 leží v Gaussovej rovine na zápornej časti reálnej osi. To znamená, že \(\varphi=\pi\) a keďže \(\vert -4\vert=4\), tak \[ -4=4(\cos\pi +{\it i}\sin\pi). \]
   d) Máme \(\vert\! -1+\sqrt 3{\it i}\vert =\sqrt{(-1)^2+(\sqrt 3)^2}=2.\quad\) Argument \(\varphi\) získame vyriešením sústavy rovníc \[ \cos\varphi=-\frac{1}{2}\qquad\mbox{a}\qquad \sin\varphi=\frac{\sqrt3}{2}. \] Obraz komplexného čísla \(-1+\sqrt 3{\it i}\) leží v druhom kvadrante Gaussovej roviny. Uvažujme uhol \(\psi\): pre ktorý platí \({\rm tg}\,\psi=\sqrt3:1=\sqrt3.\) Odtiaľ \(\psi=\pi/3\) a teda \(\varphi=\pi -\pi/3=2\pi/3.\) Potom \[ -1+\sqrt3{\it i}= 2(\cos\tfrac{2\pi}{3} +{\it i}\sin\tfrac{2\pi}{3}). \]
   e) Pre číslo 3 je situácia jednoduchá: \(\vert 3\vert=3\) a \(\varphi =0\). Teda \[ 3= 3(\cos 0 +{\it i}\sin 0). \]
   f) Najprv určíme modul \(\vert\sqrt{12}-2{\it i}\vert =\sqrt{(\sqrt{12})^2+(-2)^2}=4.\quad\) Máme \[ \cos\varphi=\frac{\sqrt{12}}{4}=\frac{\sqrt 3}{2} \qquad\mbox{a}\qquad \sin\varphi=-\frac{2}{4}=-\frac{1}{2}. \] Teda \[ \sqrt{12}-2{\it i}= 4(\cos\tfrac{11\pi}{6} +{\it i}\sin\tfrac{11\pi}{6}). \]

   

   Obr.: : Zobrazenie komplexných čísel v Gaussovej rovine

   Zobraziť riešenieSkryť riešenie
3. Precvičiť operácie s komplexnými číslami v goniometrickom tvare.

   Príklad: Vypočítajme \({\rm a)}\ (-1+i)^7,\qquad (-1+\sqrt{3}i)^{37}\).

   Riešenie: Komplexné čísla v goniometrickom tvare umocňujeme podľa Moivreovej vety: \[ z^n=|z|\cdot(\cos(n\varphi)+i\sin(n\varphi)). \] a) Označme \(z=-1+i\ \). Komplexné číslo \(z^7\) vypočítame pomocou Moivreovej vety. Goniometrický tvar komplexného čísla \(z\) sme vypočítali v predchádzajúcej časti. Dostávame: \[z^7=(-1+i)^7=[\sqrt{2}(\cos\frac{3\pi}{4}+i\sin\frac{3\pi}{4})]^7=\left(\sqrt{2}\right)^7(\cos 7.\frac{3\pi}{4}+i\sin 7.\frac{3\pi}{4})=\\= 8\sqrt{2}(\cos\frac{21\pi}{4}+i\sin\frac{21\pi}{4}) =8\sqrt{2}(\cos\frac{5\pi}{4}+i\sin\frac{5\pi}{4})=8\sqrt{2}(-\frac{\sqrt{2}}{2} -i\frac{\sqrt{2}}{2})=-8-8i.\]
   b) Označme \(z=-1+\sqrt{3}i\ \). Komplexné číslo \(z^{37}\) vypočítame pomocou Moivreovej vety. Goniometrický tvar komplexného čísla \(z\) sme vypočítali v predchádzajúcej časti. Dostávame: \[z^7=(-1+\sqrt{3})^{37}=[2(\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3})]^{37}=2^{37}(\cos 37.\frac{2\pi}{3}+i\sin 37.\frac{2\pi}{3})=\\= 2^{37}(\cos\frac{74\pi}{3}+i\sin\frac{74\pi}{3}) =2^{37}(\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3})=2^{37}(-\frac{1}{2} +i\frac{\sqrt{3}}{2})=-2^{36}+2^{36}\sqrt{2}i.\]

   Zobraziť riešenieSkryť riešenie

   Príklad: Dané sú komplexné čísla \(z_1=\sqrt{2}-i\sqrt{2},\ z_2=-3\sqrt{3}+3i\). Vypočítajme v goniometrickom tvare a výsledok preveďme späť do algebraického tvatu, ak sa jedná o známe hodnoty goniometrických funkcií. \[{\rm a)}\ z_3=z_1\cdot z_2, \quad {\rm b)}\ z_4=\frac{z_1}{z_2}, \quad {\rm c)}\ z_5=z_1^4, \quad {\rm d)}\ z_6=\frac{z_2^4}{z_1^2}.\]

   Riešenie: Nech komplexné čísla \(z_1,\,z_2\) majú goniometrický tvar \[ z_1=|z_1|\cdot(\cos\varphi_1+i\sin\varphi_1),\qquad z_2=|z_2|\cdot(\cos\varphi_2+i\sin\varphi_2).\] Pre násobenie a delenie komplexných čísel v goniometrickom tvare platia nasledujúce vzťahy: \[ z_1\cdot z_2=|z_1|\cdot|z_2|\cdot(\cos(\varphi_1+\varphi_2)+i\sin(\varphi_1+\varphi_2)),\] \[ \frac{z_1}{z_2}= \frac{|z_1|}{|z_2|}\cdot(\cos(\varphi_1-\varphi_2)+i\sin(\varphi_1-\varphi_2)) .\] pre umocňovanie komplexných čísel platí Moivreova veta: \[ z^n=|z|^n\cdot(\cos\, n\varphi+i\sin\,n\varphi). \] Komplexné čísla \(z_1,\,z_2\) zapíšeme v goniometrickom tvare postupom uvedeným v predchádzajúcom príklade. Dostaneme: \[z_1=2(\cos\frac{7}{4}\pi+i\sin\frac{7}{4}\pi),\ z_2=6(\cos\frac{5}{6}\pi+i\sin\frac{5}{6}\pi).\] Potom \({\rm a)}\ z_3=2(\cos\frac{7}{4}\pi+i\sin\frac{7}{4}\pi)\cdot 6(\cos\frac{5}{6}\pi+i\sin\frac{5}{6}\pi) = 2\cdot 6\cdot(\cos (\frac{7\pi}{4}+\frac{5\pi}{6})+i\sin( \frac{7\pi}{4}+\frac{5\pi}{6}))=\\12\cdot(\cos \frac{31\pi}{12}+i\sin \frac{31\pi}{12})= 12\cdot(\cos \frac{7\pi}{12}+i\sin \frac{7\pi}{12}),\)
   
   \({\rm b)} z_4={\large\dfrac{2(\cos\frac{7}{4}\pi+i\sin\frac{7}{4}\pi)}{ 6(\cos\frac{5}{6}\pi+i\sin\frac{5}{6}\pi)}} = \frac{2}{6}\cdot(\cos (\frac{7\pi}{4}-\frac{5\pi}{6})+i\sin( \frac{7\pi}{4}-\frac{5\pi}{6}))=\frac{1}{3}\cdot(\cos \frac{11\pi}{12}+i\sin \frac{11\pi}{12}),\)
   
   \({\rm c)} z_5=2^4(\cos 4\cdot\frac{7\pi}{4}+i\sin 4\cdot\frac{7\pi}{4}) = 2^4(\cos\,7\pi+i\sin\,7\pi)=16\cdot(\cos\,\pi+i\sin\,\pi)=\\=16\cdot(-1+0i)=-16, \)
   
   \({\rm d)} z_6={\large\dfrac{6^4.(\cos\frac{20}{6}\pi+i\sin\frac{20}{6}\pi)} {2^2.(\cos\frac{7}{2}\pi+i\sin\frac{7}{2}\pi)}}=324(\cos(\frac{10}{3}\pi-\frac{7}{2}\pi)+ i\sin(\frac{10}{3}\pi-\frac{7}{2}\pi))=\\324(\cos(-\frac{1}{6}\pi)+i\sin(-\frac{1}{6}\pi))=324(\cos\frac{1}{6}\pi-i\sin\frac{1}{6}\pi)=324(\frac{\sqrt{3}}{2}-\frac{1}{2}i)=162\sqrt{3} -162i.\)

   Zobraziť riešenieSkryť riešenie
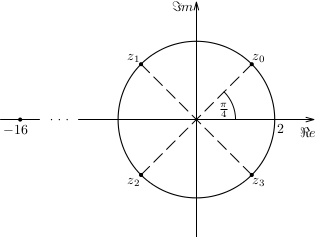
4. Odmocnina komplexného čísla.

   Príklad: Vypočítajme všetky hodnoty \(\sqrt[4]{-16}\).

   Riešenie: Binomická rovnica je rovnica v tvare \[z^n=a,\] kde \(a\) je komplexné číslo. ktorého goniometrický tvar je \(a=|a|(\cos\alpha+i\sin\alpha)\).
   Odvodíme riešenie binomickej rovnice. Nech goniometrický tvar komplexného čísla \(a\) je \(a=|a|(\cos\alpha+i\sin\alpha)\). Dosadíme \(z^n,\ a\) v goniometrickom tvare do binomickej rovnice. Dostávame: \[|z|^n(\cos(n\varphi)+i\sin(n\varphi))=|a|(\cos\alpha+i\sin\alpha).\] Z rovnosti modulov \(|z|^n=|a|\) dostávame \(|z|=\sqrt[n]{|a|}\)a z rovnosti hodnôt goniometrických funkcií vzhľadom na ich periodičnosť vyplýva \(n\varphi=\alpha+k\pi\), teda \(\varphi={\large\frac{\alpha+2k\pi}{n}}.\)
   Riešenia binomickej rovnice môžeme teda zapísať v tvare \[ z_k=\sqrt[n]{|a|}(\cos\frac{\alpha+2k\pi}{n}+i\sin\frac{\alpha+2k\pi}{n}), \ k=1,2,...,n-1 . \] V našom príklade máme \(|a|=|-4|=2, \ \alpha =\pi,\ n=4\), teda riešením binomickej rovnice sú komplexné čísla v tvare: \[z_k=\sqrt[4]{16}\cdot\left(\cos\frac{\pi +2k\pi}{4}+i\sin\frac{\pi+2k\pi}{4}\right),\ \ k=0,1,2,3.\] Dostávame\[ \begin{array}{r@{\!}l} z_0=\a 2\cdot(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4})=\sqrt{2}+i\sqrt{2},\\ z_1=\a 2\cdot(\cos\frac{3\pi}{4}+i\sin\frac{3\pi}{4})=-\sqrt{2}+i\sqrt{2},\\ z_3=\a 2\cdot(\cos\frac{5\pi}{4}+i\sin\frac{5\pi}{4})=-\sqrt{2}-i\sqrt{2},\\ z_4=\a 2\cdot(\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4})=\sqrt{2}-i\sqrt{2}. \end{array} \]

   

   Obr.: : Zobrazenie všetkých hodnôt \(\sqrt[4]{-16}\).

   Na obrázku sú znázornené čísla \(z_0,\,z_1,\,z_2,\,z_3\) v Gaussovej rovine. Vidíme, že všetky hodnoty \(z_k\) ležia na kružnici s polomerom 2. Komplexné číslo \(z_0\) má argument \(\alpha/n=\pi/4\). Rozdiel argumentov ľubovoľných dvoch "na kružnici susedných bodov}" je \(2\pi/n=\pi/2\). Dôsledkom toho je, že obrazy komplexných čísel \(z_0,\,z_1,\,z_2,\,z_3\) tvoria vrcholy pravidelného štvoruholníka, t.j. štvorca, vpísaného kružnici s polomerom 2.
   Vo všeobecnosti, obrazy \(n\)-tých odmocnín komplexného čísla \(a\) tvoria vrcholy pravidelného \(n\)-uholníka vpísaného kružnici s polomerom \(\sqrt[n]|a|\), pričom argument čísla \(z_0\) je \(\alpha/n\).

   Zobraziť riešenieSkryť riešenie

   Príklad: Vypočítajme všetky hodnoty \(\sqrt[3]{-i}.\)

   Riešenie: Z geometrického významu \(|a|\) a \(\alpha\) vyplýva, že pre \(a=-i\) máme \(|a|=1,\ \alpha=\frac{3\pi}{2}\). Teda \[a=1(\cos \frac{3\pi}{2} +{\it i}\sin \frac{3\pi}{2})\] Teda \(n=3\), \(\vert z\vert=1\) a \(\alpha =\frac{3\pi}{2}\). Dostávame: \[z_0=\sqrt[3]1\left(\cos\frac{\frac{3\pi}{2}+0\cdot 2\pi}{3}+i\sin\frac{\frac{3\pi}{2}+0\cdot 2\pi}{3} \right) =\cos 90^{\circ}+i\sin 90^{\circ}=i,\] \[z_1=\sqrt[3]1\left(\cos\frac{\frac{3\pi}{2}+1\cdot 2\pi}{3}+i\sin\frac{\frac{3\pi}{2}+1\cdot 2\pi}{3} \right)= \cos \frac{7\pi}{6}+i\sin \frac{7\pi}{6}=-\frac{\sqrt3}{2}-\frac{1}{2}i,\] \[z_2=\sqrt[3]1\left(\cos\frac{\frac{3\pi}{2}+2\cdot 2\pi}{3}+i\sin\frac{\frac{3\pi}{2}+2\cdot 2\pi}{3} \right)= \cos \frac{11\pi}{6}+i\sin \frac{11\pi}{6}=\frac{\sqrt3}{2}-\frac{1}{2}i.\]

   Zobraziť riešenieSkryť riešenie
5. Riešenie rovníc v množine komplexných čísel.

   Príklad: V množine komplexných čísel riešme rovnicu \[z^2-(2+3i)z-1+3i=0.\]

   Riešenie: Máme kvadratickú rovnicu s komplexnými koeficientami. Budeme ju riešiť obdobne ako kvadratickú rovnicu v množine reálnych čísel. Najprv vypočítame diskriminant. Máme \[ D=(2+3i)^2-4(-1+3i)=4+12i+9i^2+4-12i=-1. \] Nájdeme hodnoty \(\sqrt{-1}\). Z definície čísla \(i\) vyplýva, že sú to hodnoty \(i,\,-i\). Riešenia danej rovnice sú \[z_1=\frac{(2+3i)+i}{2}=1+2i,\quad z_2=\frac{(2+3i)-i}{2}=1+i.\]

   Zobraziť riešenieSkryť riešenie

Zdroje

1. M. Molnárová, H.Myšková: Úvod do lineárnej algebry.
2. J. Buša, Š. Schrotter: Komplexné čísla

Doplňujúce úlohy

Úloha: Nájdite reálne čísla \(x,y\) tak, aby platilo: \[\begin{array}{ll} a)\a(3-2i)x+(5-7i)y=1-3i\\ b)\a(1-i)x+(4+2i)y=1+3i\\ c)\a(1+3i)(2x+iy)=1+i\\ d)\a\frac{x+iy}{1-i}=3+2i\\ e)\a(2+ix)(y+2i)=16-11i. \end{array} \]
Výsledok: \(a)\,x=-\frac{8}{11},\ y=\frac{7}{11},\quad b)\,x=-\frac{5}{3},\ y=\frac{2}{3},\quad c)\,x=-\frac{1}{5},\ y=-\frac{1}{5},\quad \\ d)\, x=5,\ y=-1,\quad e)\,[x,y]\in\{[-3,5],[-5,3]\} \)
Zobraziť výsledokSkryť výsledok
Úloha: Vypočítajte v algebraickom tvare: \[ \begin{array}{llcll} a)\a(2+4i)+(1+2i),\a\phantom{duchduchduch}\a b)\a(-2-i)-(4-6i),\\ c)\a -3(-5+4i)+5(6-3i),\a\a d)\a (3+2i)(2+i),\\ e)\a (2+3i)(4+5i),\a\a f)\a(2-i)(2+i)+(3-i)(4+2i),\\ g)\a \frac{2+i}{3-i},\a\a h)\a \left(\frac{1+2i}{3-i}\right)^2,\\ i)\a \frac{1+i}{1-i}-\frac{1+i}{1+i},\a\a j)\a \frac{(1-i)^3}{(2+i)(1+2i)}. \end{array} \]
Výsledok: \( a)\,3+6i,\quad b)\,-6+5i,\quad c)\,45-27i,\quad d)\,4+7i,\quad e)\,-7+22i,\quad f)\,19+2i,\\ g)\,\frac{1}{2}+\frac{1}{2}i,\quad h)\,-\frac{12}{25}+\frac{7}{10}i,\quad i)\,2i,\quad j)\,-\frac{2}{5}+\frac{2}{5}i. \)
Zobraziť výsledokSkryť výsledok
Úloha: Zjednodušte a vypočítajte: \[ \begin{array}{ll} a)\a i^{16};i^{29};i^{133};i^{-6};i^{-11}\\ b)\a 3-8i+3i^2+3i^3-6i^4\\ c)\a -5+4i^2-9i^6+7i^5. \end{array} \]
Výsledok: \(a)\,1,\,i,\,i,\,-1,\,i,\quad b)\,-6-11i,\quad c)\,7i.\)
Zobraziť výsledokSkryť výsledok
Úloha: Vypočítajte komplexné číslo \(z=\frac{u.\overline{u}}{v}\), ak \[ \begin{array}{llcll} a)\a u=\sqrt{3}+i,\ v=1-i,\a\phantom{duchduch}\a b)\a u=-\sqrt{2}+i,\ v=\sqrt{2}-i,\\ c)\a u=2-3i,\ v=-1+2i,\a\a d)\a u=5+3i,\ v=-4-i. \end{array} \]
Výsledok: \(a)\,z=2+2i,\quad b)\,z=\sqrt{2}+1,\quad c)\,z=-\frac{13}{3}-\frac{26}{5}i,\quad d)\,z=-8+2i.\)
Zobraziť výsledokSkryť výsledok
Úloha: Napíšte v goniometrickom tvare komplexné čísla: \[ \begin{array}{llcll} a)\a 3,\a \phantom{duchduchduch} \a b)\a-2+2i\sqrt{3}\\ c)\a 2i,\a\a d)\a 1+i,\\ e)\a\sqrt{3}-i,\a\a f)\a 1-i\sqrt{3},\\ g)\a 1-\sqrt{3},\a\a h)\a 3-3i,\\ i)\a -\sqrt{2}-i\sqrt{2},\a\a j)\a -3i. \end{array} \]
Výsledok: \(a)\,3\,\cdot\,(\cos 0+i\sin 0),\quad b)\,4\cdot(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi),\quad c)\,2\cdot(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}),\\ d)\,\sqrt{2}\cdot(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}),\quad e)\,2\cdot(\cos\frac{13}{6}\pi+i\sin\frac{13}{6}\pi),\quad f)\,2\cdot(\cos\frac{5}{3}\pi+i\sin\frac{5}{3}\pi)\\ g)\,(\sqrt{3}-1)\cdot(\cos\pi+i\sin\pi),\quad h)\,3\sqrt{2}\cdot(\cos\frac{7}{4}\pi+i\sin\frac{7}{4}\pi),\quad i)\,2\cdot(\cos\frac{5}{4}\pi+i\sin\frac{5}{4}\pi),\quad \\j)\,3\cdot(\cos\frac{3}{2}\pi+i\sin\frac{3}{2}\pi) \)
Zobraziť výsledokSkryť výsledok
Úloha: V goniometrickom tvare vypočítajte súčin \(u.v\) a podiel \(\frac{u}{v}\), ak
\( a) u=\sqrt{2}(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}),\ v=\sqrt{8}(\cos\frac{5}{6}\pi +i\sin\frac{5}{6}\pi)\)
\( b) u=-1+i,\ v=3(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}),\)
\( c) u=2(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi), v=\sqrt{2}(\cos\frac{1}{6}\pi+i\sin\frac{1}{6}\pi),\)
\( d) u=\sqrt{3}-i,\ v=2+2i.\)

Výsledok: \( a)\,u\cdot v=4\cdot(\cos\frac{13}{12}\pi+i\sin\frac{13}{12}\pi),\quad\frac{u}{v}=\frac{1}{2}\cdot(\cos\frac{17}{12}\pi+i\sin\frac{17}{12}\pi),\\ b)\,u\cdot v=3\sqrt{2}\cdot(\cos\frac{13}{12}\pi+i\sin\frac{13}{12}\pi),\quad\frac{u}{v}=\frac{\sqrt{2}}{3}\cdot(\cos\frac{5}{12}\pi+i\sin\frac{5}{12}\pi),\\ c)\,u\cdot v=2\sqrt{2}\cdot(\cos\frac{5}{6}\pi+i\sin\frac{5}{6}\pi),\quad\frac{u}{v}=\sqrt{2}\cdot(\cos\frac{1}{2}\pi+i\sin\frac{1}{2}\pi),\\ d)\,u\cdot v=4\sqrt{2}\cdot(\cos\frac{1}{12}\pi+i\sin\frac{1}{12}\pi),\quad\frac{u}{v}=\frac{\sqrt{2}}{2}\cdot(\cos\frac{19}{12}\pi+i\sin\frac{19}{12}\pi). \)
Zobraziť výsledokSkryť výsledok
Úloha: Pomocou Moivreovej vety vypočítajte a zapíšte v algebraickom tvare: \[ \begin{array}{llcll} a)\a(-1-i)^6,\a\phantom{duchduch}\a b)\a (\sqrt{3}-i)^{8},\\ c)\a\left( \frac{1-i\sqrt{3}}{1+i}\right)^{24},\a\a d)\a \left(\frac{1+i}{-\sqrt{3}+i}\right)^3. \end{array} \]
Výsledok: \( a)\,-8i,\quad b)\,-128-128\sqrt{3}i,\quad c)\,4096,\quad d)\,\frac{1}{4}+\frac{1}{4}i. \)
Zobraziť výsledokSkryť výsledok
Úloha: Dané sú komplexné čísla \(z_1=-\sqrt{3}+i,\ z_2=\sqrt{2}-\sqrt{2}i\). Vypočítajte:\[ \begin{array}{llcllcllcll} a)\a z_1^3.z_2^5,\a\phantom{duchduch}\a b)\a z_1^5.z_2^4,\a\phantom{duchduch}\a c)\a \frac{z_1^6}{z_2^3},\a\phantom{duchduch}\a d)\a\frac{z_2^6}{z_1^2}. \end{array} \]
Výsledok: \( a)\,-16\sqrt{2}-16\sqrt{2}\,i,\quad b)\,-256\sqrt{3}-256i,\quad c)\,4\sqrt{2}-4\sqrt{2}\,i,\quad d)\,8\sqrt{3}-8i. \)
Zobraziť výsledokSkryť výsledok
Úloha: Riešte binomické rovnice: \[ \begin{array}{llcllcllcll} a)\a z^2=-1,\a\phantom{duch}\a b)\a z^3=i,\a\phantom{duch}\a c)\a z^4=-16,\a\phantom{duch}\a d)\a z^5=32,\\ e)\a z^6=-729,\a\phantom{duch}\a f)\a z^4=-8+8\sqrt{3}i,\a\phantom{duch}\a g)\a z^3=-8i,\a\phantom{duch}\a h)\a z^8=256. \end{array} \]
Výsledok: \( a)\,z_0=i,\ z_1=-1;\\ b)\,z_k=\cos\frac{\frac{\pi}{2}+2k\pi}{3}+i\sin\frac{\frac{\pi}{2}+2k\pi}{3},\ k=0,1,2;\\ c)\,z_k=2\cdot(\cos\frac{\pi+2k\pi}{4}+i\sin\frac{\pi+2k\pi}{4}),\ k=0,1,2,3;\\ d)\,z_k=2\cdot(\cos\frac{2k\pi}{5}+i\sin\frac{2k\pi}{5}),\ k=0,1,2,3,4;\\ e)\,z_k=3\cdot(\cos\frac{\pi+2k\pi}{6}+i\sin\frac{\pi+2k\pi}{6}),\ k=0,1,\dots,5;\\ f)\,z_k=2\cdot(\cos\frac{\frac{2\pi}{3}+2k\pi}{4}+i\sin\frac{\frac{2\pi}{3}+2k\pi}{4}),\ k=0,1,2,3;\\ g)\,z_k=2\cdot(\cos\frac{\frac{3\pi}{2}+2k\pi}{3}+i\sin\frac{\frac{3\pi}{2}+2k\pi}{3}),\ k=0,1,2;\\ h)\,z_k=2\cdot(\cos\frac{2k\pi}{8}+i\sin\frac{2k\pi}{8}),\ k=0,1,2,\dots,7. \)
Zobraziť výsledokSkryť výsledok
Úloha: V množine komplexných čísel vyriešte rovnicu:
\( a)\ z^2-4z+8=0;\\ b)\ z^2-(2+3i)z-1+3i=0;\\ c))\ x^4+8x^2+16=0;\\ d) \ (x^4+16=0;\\ e) \ z^3+z^2+z+1=0;\\ f) \ z^6-4z^3+8=0;\\ g) \ \left(\dfrac{z-1}{z+1}\right)^2=2i.\)
Výsledok: \( a) \ {\cal K}=\{2+2i;2-2i\}\\ b) \ {\cal K}=\{1+i;1+2i\}\\ c) \ {\cal K}=\{2i;-2i\}\\ d) \ {\cal K}=\{\sqrt2\pm\sqrt2i;-\sqrt2\pm\sqrt2i\}\\ e) \ {\cal K}=\{-1;i;-i\}\\ f) \ {\cal K}=\{\sqrt2\big(\!\cos\frac{(8k\pm 1)\pi}{12}+i\sin\frac{(8k\pm 1)\pi}{12}\big),\: k\in\{0,1,2\}\}\\ g) \ {\cal K}=\{-1+2i;(-1-2i)/5\}\)
Zobraziť výsledokSkryť výsledok

Doplňujúce zdroje

1. M. Bučko, J. Buša, Š. Schrotter: Lineárna algebra