Ciele
- Pomocou Greenovej vety transformovať dvojný integrál na krivkový.
Úvod
- Vyjadrenie funkcie \(g(t,s)\) (rovnosť \(\stackrel{2}{=} \))
- Voľba funkcií \(P(t,s)\) a \(Q(t,s)\) (rovnosť \(\stackrel{3}{=} \))
- Voľba funkcií \(P(t,s)\) a \(Q(t,s)\) (rovnosť \(\stackrel{3}{=} \))
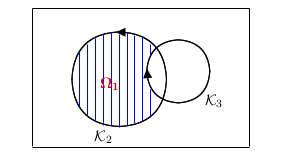
Cieľom tejto kapitoly je vypočítať \[ \iint\limits_{P(G_1)} z\,\textrm{d}{x}\,\textrm{d}{y}, \] pričom \(P(G_1)\) je orientovaná normálou von. Použitím vety o výpočte plošného integrálu dostávame \[ \iint\limits_{P(G_1)} z\,\textrm{d}{x}\,\textrm{d}{y}= \pm \iint\limits_{\Omega_1}\left| \begin{array}{lll} \,\, 0 \qquad 0 \quad\,\, z_1+r_1-\frac{8r_1^{\, 3}}{t^2+s^2+4r_1^{\, 2}}\\ \frac{\partial x}{\partial t} \quad\frac{\partial y}{\partial t} \qquad\qquad\frac{\partial z}{\partial t}\\ \frac{\partial x}{\partial s} \quad\frac{\partial y}{\partial s} \qquad\qquad\frac{\partial z}{\partial s} \end{array} \right|\,\textrm{d}{t}\,\textrm{d}{s}= -\iint\limits_{\Omega_1}\left( z_1+r_1-\frac{8r_1^{\, 3}}{t^2+s^2+4r_1^{\, 2}} \right)J(t,s)\,\textrm{d}{t}\,\textrm{d}{s} \] pričom použitím parametrického vyjadrenia dostávame \[ J(t,s)=\left|\begin{array}{cc} \frac{\partial x}{\partial t} \quad\frac{\partial y}{\partial t}\\ \quad\quad\\ \frac{\partial x}{\partial s} \quad\frac{\partial y}{\partial s} \end{array}\right| =16r_1^4\frac{4r_1^2-t^2-s^2}{(t^2+s^2+4r_1^2)^3}. \] Keďže \(P(G_1)\) je orientovaná normálou von, znamená to, že normálový vektor zvierá s vektorom \(\vec{\pmb{k}}\) na severnej pologuli ostrý uhol a na južnej pologuli tupý uhol. Pre body severnej polgule parametre \((t,s)\) spĺňajú nerovnosť \(t^2+s^2\geq 4r_1^2\) a teda pre nami použitý normálový vektor \(\vec{\pmb{n}}_p=\vec{\pmb{r}}'_t \times\vec{\pmb{r}}'_s\) je skalárný súčin \(\vec{\pmb{n}}_p\circ \vec{\pmb{k}}= J(t,s)\lt 0\), t.j. uhol \(\vec{\pmb{n}}_p, \vec{\pmb{k}}\) je tupý. Zatiaľ čo pre body južnej polgule, t.j. \(t^2+s^2\leq 4r_1^2\) je skalárný súčin \(\vec{\pmb{n}}_p\circ \vec{\pmb{k}}= J(t,s)>0\).
A teda v oboch prípadoch je orientácia plochy nesúhlasná s použitým parametrickým vyjadrením, preto sme pri použití vety o výpočte plošného integrálu použili znamienko "\(-\)".
Použitím elementárných úprav dostávame nasledujúci vzťah pre výpočet plošného integrálu (rovnosť \(\stackrel{2}{=} \)) \[ \iint\limits_{P(G_1)} z\,\textrm{d}{x}\,\textrm{d}{y}\stackrel{2}{=} \iint\limits_{\Omega_1}g(t,s)\,\textrm{d}{t}\,\textrm{d}{s}= \] \[ =128r_1^7\iint\limits_{\Omega_1}\frac{8r_1^2}{\left(t^2+s^2+4r_1^{\, 2}\right)^4} -\frac{2+\frac{z_1}{r_1}}{\left(t^2+s^2+4r_1^{\, 2}\right)^3} -\frac{\frac{z_1+r_1}{8r_1^3}}{\left(t^2+s^2+4r_1^{\, 2}\right)^2} \,\textrm{d}{t}\,\textrm{d}{s}. \]
Pomocou Greenovej vety potrebujeme transformovať dvojný integrál na krivkový, t. j. potrebujeme nájsť funkcie \(P(t,s)\) a \(Q(t,s)\), také aby platilo \begin{equation}\label{gv} g(t,s)=\frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}. \end{equation} Na základe istej symetrie parametrov \(t,s\) vo funkcii \(g(t,s)\) a skúsenosti z kapitoly xy budeme funkcie \(P(t,s)\) a \(Q(t,s)\) hľadať v tvare \[ Q(t,s)=\frac{Dt}{(t^2+s^2+4r_1^2)^3}+\frac{Et}{(t^2+s^2+4r_1^2)^2}+\frac{Ft}{(t^2+s^2+4r_1^2)} \] \[ P(t,s)=\frac{-Ds}{(t^2+s^2+4r_1^2)^3}+\frac{-Es}{(t^2+s^2+4r_1^2)^2}+\frac{-Fs}{(t^2+s^2+4r_1^2)} \] kde konštanty \(D,E,F\) vypočítame dosadením do \eqref{gv}. Upravíme pravú stranu \[ \frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}= \] \[ =\frac{D}{(t^2+s^2+4r_1^2)^3}-\frac{6Dt^2}{(t^2+s^2+4r_1^2)^4}+\frac{E}{(t^2+s^2+4r_1^2)^2}= \] \[ =-\frac{4Et^2}{(t^2+s^2+4r_1^2)^3}+\frac{F}{(t^2+s^2+4r_1^2)}-\frac{2Ft^2}{(t^2+s^2+4r_1^2)^2}+ \] \[ +\frac{D}{(t^2+s^2+4r_1^2)^3}-\frac{6Ds^2}{(t^2+s^2+4r_1^2)^4}+\frac{E}{(t^2+s^2+4r_1^2)^2}- \] \[ -\frac{4Es^2}{(t^2+s^2+4r_1^2)^3}+\frac{F}{(t^2+s^2+4r_1^2)}-\frac{2Fs^2}{(t^2+s^2+4r_1^2)^2} \] Po združení členov máme \[ \frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}= \] \[ =\frac{2D}{(t^2+s^2+4r_1^2)^3}+\frac{2E}{(t^2+s^2+4r_1^2)^2}+\frac{2F}{(t^2+s^2+4r_1^2)}- \] \[ -\frac{6D\left(t^2+s^2\right)}{(t^2+s^2+4r_1^2)^4}- \frac{4E\left(t^2+s^2\right)}{(t^2+s^2+4r_1^2)^3}- \frac{2F\left(t^2+s^2\,{\color{red1}{+\,4r_1^2-4r_1^2}}\right)}{(t^2+s^2+4r_1^2)^2} \] Po zjednodušení a dosadení do \eqref{gv} dostávame \[ 128r_1^7\left(\frac{8r_1^2}{\left(t^2+s^2+4r_1^{\, 2}\right)^4} -\frac{2+\frac{z_1}{r_1}}{\left(t^2+s^2+4r_1^{\, 2}\right)^3} -\frac{\frac{z_1+r_1}{8r_1^3}}{\left(t^2+s^2+4r_1^{\, 2}\right)^2}\right)= \] \[ =\frac{24Dr_1^2}{(t^2+s^2+4r_1^2)^4}+\frac{16Er_1^2-4D}{(t^2+s^2+4r_1^2)^3}+ \frac{8Fr_1^2-2E}{(t^2+s^2+4r_1^2)^2} \] Porovnaním koeficientov \[ \begin{array}{ccc} 128r_1^78r_1^2=24Dr_1^2 \Rightarrow D=\frac{128}{3}r_1^7 \\ 128r_1^7\left(-2-\frac{z_1}{r_1}\right)=16Er_1^2-4D \Rightarrow E=\frac{8r_1^4(3z_1+2r_1)}{3} \\ 128r_1^7\left(\frac{z_1+r_1}{r_1^3}\right)=8Fr_1^2-4E \Rightarrow F=\frac{2}{3}r_1^3 \end{array} \] Našli sme teda konkrétne vyjadrenie funkcií \(P(t,s)\) a \(Q(t,s)\), ktoré potrebujeme k použitiu Greenovej vety. Teda \begin{equation}\label{kriv} \iint\limits_{\Omega_1}g(t,s)\,\textrm{d}{t}\,\textrm{d}{s} =\frac{128r_1^7}{3} \oint\limits_{H(\Omega_1)}\frac{t\,\textrm{d}{s}-s\,\textrm{d}{t}}{(t^2+s^2+4r_1^2)^3}+ \frac{8r_1^4(3z_1+2r_1)}{3} \oint\limits_{H(\Omega_1)}\frac{t\,\textrm{d}{s}-s\, \textrm{d}{t}}{(t^2+s^2+4r_1^2)^2}+\frac{2r_1^3}{3} \oint\limits_{H(\Omega_1)}\frac{t\,\textrm{d}{s}-s\,\textrm{d}{t}}{(t^2+s^2+4r_1^2)}, \end{equation} pričom predpokladáme, že \(\Omega_1\) je ohraničená množina a jej hranicu tvorí krivka \(H(\Omega_1)\). Neskôr sa budeme zaoberať aj prípadom, ak oblasť \(\Omega_1\) je neohraničená.
Postup
-
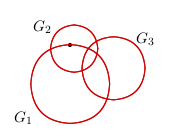
Príklad: Zakrelite množinu \(\Omega_1\) ktorá je priemetom \(P(G_1)\) pričom pozícia gúľ \(G_1\), \(G_2\) a \(G_3\) je daná nasledujúcim obrázkom
Zdroje
comments powered by Disqus