Ciele
- Výpočet krivkového integrálu po uzavretej krivke prevodomna dvojný integrál -- aplikácie Greenovej vety.
- Výpočet dvojného integrálu v prípade nezávislosti od integračnej cesty.
- Výpočet dvojného integrálu prevodom krivky -- aplikácie Greenovej vety.
Úvod
- Greenova veta.
- Dôsledky Greenovej vety, nezávislosť od integračnej cesty.
V prípade, ak je krivka C uzavretá, kladne orientovaná, môžeme krivkový integrál pocítat prevodom na dvojný integrál, o com hovorí nasledujúca veta.
\(\mathbf{Veta.}\) Nech \(C\) je uzavretá, jednoduchá, hladká, kladne, orientovaná krivka. Nech \(D\) je rovinná oblast ohranicená krivkou \(C\). Nech \(\displaystyle\frac{\partial Q}{\partial x}\), \(\displaystyle\frac{\partial P} {\partial y}\) sú spojité na \(D\). Potom. \[ \oint\limits_{C} P(x,y)\, \mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} = \iint\limits_{D} \left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right)\,\mathrm{d}{x}\,\mathrm{d}{y} \]
\({\mathit{Dôkaz.}}\) Ukážeme, že platia nasledujúce rovnosti. \[ \oint\limits_{C} P(x,y)\, \mathrm{d}{x} = -\iint\limits_{D} \frac{\partial P(x,y)}{\partial y}\,\mathrm{d}{x}\,\mathrm{d}{y} \] \[ \oint\limits_{C} Q(x,y)\,\mathrm{d}{y} = \iint\limits_{D} \frac{\partial Q(x,y)}{\partial x} \,\mathrm{d}{x}\,\mathrm{d}{y} \] Predpokladáme, že \(D\) je elementárna oblasť typu \([x,y]\) aj \([y,x]\) (ak nie, tak oblasť \(D\) vyjadríme ako zjednotenie viacerých elementárnych oblastí. )
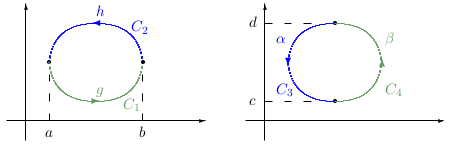
Nech \(C\) je uzavretá, jednoduchá hladká, kladne orientovaná krivka, ktorá tvorí hranicu oblasti \(D\). Ak na oblasti \(D\) platí \[ \frac{\partial Q(x,y)}{\partial x} =\frac{\partial P(x,y)}{\partial y}, \] potom \[ \oint\limits_{C} P(x,y)\, \mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} =0. \] Táto vlastnosť je bezprostredným dôsledkom Greenovej vety a využijeme ho pri nasledujúcich úvahách.
Nech na oblasti \(D\) platí \[ \frac{\partial Q(x,y)}{\partial x} =\frac{\partial P(x,y)}{\partial y}. \] Nech jednoduché krivky \(C_1\) a \(C_2\) ležia v oblasti \(D\) a majú spoločný začiatočný aj koncový bod.
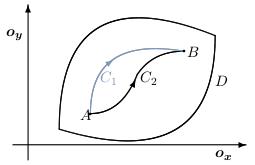
Ďalej zadefinujeme potenciál silového poľa a ukážeme jeho použitie pri výpočte krivkového integrálu. Majme jednoduchú hladkú krivku $C$ určenú parametrickým vyjadrením \[ C:\quad \vec{\pmb{r}}(t)=\varphi(t)\vec{\pmb{i}}+ \psi(t)\vec{\pmb{j}},\qquad t\in[a,b], \] a jej orientácia je súhlasná s daným parametrickým vyjadrením, t.j. \(A=[\varphi(a),\psi(a)]\) je jej začiatočný bod a \(B=[\varphi(b),\psi(b)]\) je jej koncový bod. Krivka leží v oblasti \(D\).
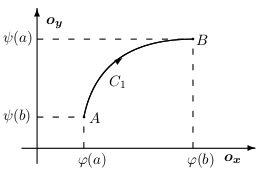
Krivkový integrál nezávisí od integračnej cesty práve vtedy ak existuje potenciál jeho silového poľa.
Ukážeme, že pomocou potenciálu silového poľa môžeme jednoducho vypočítať krivkový integrál. \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}= \] použitím vety o výpočte \[ =\int\limits_a^b P(\varphi(t),\psi(t))\varphi'(t)+Q(\varphi(t), \psi(t))\psi'(t)\,\mathrm{d}{t}= \] keďže \[ \frac{\mathrm{d}V(\varphi(t),\psi(t))}{\mathrm{d}t}= \frac{\partial V(\varphi(t),\psi(t))}{\partial x} \frac{\mathrm{d}\varphi(t)}{\mathrm{d}t} +\frac{\partial V(\varphi(t),\psi(t))}{\partial y} \frac{\mathrm{d}\psi(t)}{\mathrm{d}t}= P(\varphi(t),\psi(t))\varphi'(t)+Q(\varphi(t),\psi(t))\psi'(t)= \] \[ =\int\limits_a^b \frac{\mathrm{d}}{\mathrm{d}t}\big(V(\varphi(t),\psi(t))\big) {\mathrm{d}{t}}=\Big[V(\varphi(t),\psi(t))\Big]_{a}^{b}=V(B)-V(A). \] Uvedené možno zhrnúť do nasledujúceho tvrdenia
Ak existuje potenciál silového poľa \(V\) (krivkový integrál nezávisí od integračnej cesty), potom \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}=V(B)-V(A), \] kde \(A\) a \(B\) sú prvý a posledný bod krivky.
Postup
-
Greenova veta
Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C} (x+y)\,\mathrm{d}{x}- (x-y)\,\mathrm{d}{y}, \] ak krivka ak \(C\) je kladne orientovaná elipsa \( \displaystyle{\frac{x^2}{4}+\frac{y^2}{9}=1}, \)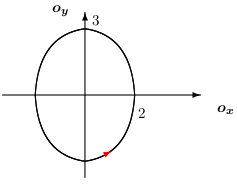 Riešenie: Použitím Greenovej vety dostávame \[ \int\limits_{C} (x+y)\,\mathrm{d}{x}- (x-y)\,\mathrm{d}{y}=-2\iint\limits_{D} 1 \, \mathrm{d}{x}\,\mathrm{d}{y}=-2P(D)=-12\pi \]Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C}\frac{y^2}{2}\,\mathrm{d}{x}+\frac{x^2}{2}\,\mathrm{d}{y}, \] ak \(C\) je kladne orientovaná hranica oblasti ohraničenej krivkami \(y=\ln x\), \(y=1\), \(y=2\), \(x=0\).Riešenie: Načrtneme si kontúry oblasti ohraničenej krivkou \(C\).Množina \(D\) vyjadríme nasledovne \[\begin{split} D: \quad 1 \leq y\leq 2\quad\\ \qquad 0 \leq x\leq \mathrm{e}^y\quad \end{split} \] Použitím Greenovej vety dostávame \[ \begin{split} \int\limits_{C}\frac{y^2}{2}\,\mathrm{d}{x}+\frac{x^2}{2}\,\mathrm{d}{y}= \iint\limits_{D} (x-y) \,\mathrm{d}{x}\,\mathrm{d}{y}= \int\limits_1^2 \left(\, \int\limits_{0}^{\mathrm{e}^y} (x-y)\,\mathrm{d}{x} \right)\mathrm{d}{y}=\left[ \frac{\mathrm{e}^{2y}}{4}-y\mathrm{e}^y+ \mathrm{e}^y\right]_1^2=\frac{\mathrm{e}^4}{4}-\frac{5\mathrm{e}^2}{4}. \end{split} \]
Riešenie: Použitím Greenovej vety dostávame \[ \int\limits_{C} (x+y)\,\mathrm{d}{x}- (x-y)\,\mathrm{d}{y}=-2\iint\limits_{D} 1 \, \mathrm{d}{x}\,\mathrm{d}{y}=-2P(D)=-12\pi \]Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C}\frac{y^2}{2}\,\mathrm{d}{x}+\frac{x^2}{2}\,\mathrm{d}{y}, \] ak \(C\) je kladne orientovaná hranica oblasti ohraničenej krivkami \(y=\ln x\), \(y=1\), \(y=2\), \(x=0\).Riešenie: Načrtneme si kontúry oblasti ohraničenej krivkou \(C\).Množina \(D\) vyjadríme nasledovne \[\begin{split} D: \quad 1 \leq y\leq 2\quad\\ \qquad 0 \leq x\leq \mathrm{e}^y\quad \end{split} \] Použitím Greenovej vety dostávame \[ \begin{split} \int\limits_{C}\frac{y^2}{2}\,\mathrm{d}{x}+\frac{x^2}{2}\,\mathrm{d}{y}= \iint\limits_{D} (x-y) \,\mathrm{d}{x}\,\mathrm{d}{y}= \int\limits_1^2 \left(\, \int\limits_{0}^{\mathrm{e}^y} (x-y)\,\mathrm{d}{x} \right)\mathrm{d}{y}=\left[ \frac{\mathrm{e}^{2y}}{4}-y\mathrm{e}^y+ \mathrm{e}^y\right]_1^2=\frac{\mathrm{e}^4}{4}-\frac{5\mathrm{e}^2}{4}. \end{split} \]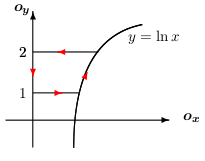 Príklad: Pomocou krivkového integrálu odvoďte vzorec pre výpočet obsahu elipsy danej: \(\displaystyle{\quad\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}\).Riešenie: Vieme, že plochu vieme vyjadriť pomocou dvojného integrálu, na ktorý aplikujeme Greenovu vetu:Teda \[ \begin{split} \text{Plocha }=\iint\limits_{D} 1 \,\mathrm{d}{x}\,\mathrm{d}{y}= \iint\limits_{D} \left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right)\,\mathrm{d}{x}\,\mathrm{d}{y}= \oint\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} \end{split} \] Potrebujeme nájsť také funkcie \(P\), \(Q\), aby platilo \[ 1=\left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right). \] Možnosti na zvolenie funkcií \(P\), \(Q\) je samozrejme viacej. My použijeme \[ P(x,y)=-\frac{y}{2}\qquad Q(x,y)=\frac{x}{2} \] A teda odvodili sme všeobecný vzorec pre výpočet obsahu rovinného telesa \[ P(D)=\oint\limits_{C} -\frac{y}{2}\,\mathrm{d}{x}+\frac{x}{2}\,\mathrm{d}{y}, \] kde \(C\) je kladne orientovaná hranica \(D\). Aplikáciou tohto vzorca na náš príklad, použitím nasledujúcich parametrických rovníc pre elipsu \[ \begin{split} C: \quad x =\cos t,\quad \\ \qquad\qquad y = \sin t,\quad t\in[0,2\pi], \end{split} \] dostávame \[ P(D)=\oint\limits_{C} -\frac{y}{2}\,\mathrm{d}{x}+\frac{x}{2}\,\mathrm{d}{y} = \int\limits_0^{2\pi}(-b\sin t)(-a\sin t)+(a\cos t)(b\cos t)\,\mathrm{d}{t}=\pi ab \]
Príklad: Pomocou krivkového integrálu odvoďte vzorec pre výpočet obsahu elipsy danej: \(\displaystyle{\quad\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}\).Riešenie: Vieme, že plochu vieme vyjadriť pomocou dvojného integrálu, na ktorý aplikujeme Greenovu vetu:Teda \[ \begin{split} \text{Plocha }=\iint\limits_{D} 1 \,\mathrm{d}{x}\,\mathrm{d}{y}= \iint\limits_{D} \left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right)\,\mathrm{d}{x}\,\mathrm{d}{y}= \oint\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} \end{split} \] Potrebujeme nájsť také funkcie \(P\), \(Q\), aby platilo \[ 1=\left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right). \] Možnosti na zvolenie funkcií \(P\), \(Q\) je samozrejme viacej. My použijeme \[ P(x,y)=-\frac{y}{2}\qquad Q(x,y)=\frac{x}{2} \] A teda odvodili sme všeobecný vzorec pre výpočet obsahu rovinného telesa \[ P(D)=\oint\limits_{C} -\frac{y}{2}\,\mathrm{d}{x}+\frac{x}{2}\,\mathrm{d}{y}, \] kde \(C\) je kladne orientovaná hranica \(D\). Aplikáciou tohto vzorca na náš príklad, použitím nasledujúcich parametrických rovníc pre elipsu \[ \begin{split} C: \quad x =\cos t,\quad \\ \qquad\qquad y = \sin t,\quad t\in[0,2\pi], \end{split} \] dostávame \[ P(D)=\oint\limits_{C} -\frac{y}{2}\,\mathrm{d}{x}+\frac{x}{2}\,\mathrm{d}{y} = \int\limits_0^{2\pi}(-b\sin t)(-a\sin t)+(a\cos t)(b\cos t)\,\mathrm{d}{t}=\pi ab \]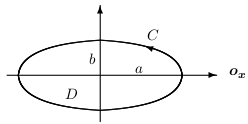 Úloha: Vypočítajte \[ \oint\limits_{C}y^2\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(C\) je kladne orientovaný obvod štvorca ohraničený priamkami \(x=1\), \(x=-1\), \(y=1\), \(y=-1\).Riešenie: \(\displaystyle\left[4\right]\)Úloha: Vypočítajte \[ \oint\limits_{C}\frac{1}{x}\mathrm{arctg}\frac{y}{x} \,\mathrm{d}{x}+ \frac{2}{x}\mathrm{arctg}\frac{x}{y} \,\mathrm{d}{y}, \] ak \(C\) je hranica oblasti \(1\leq x^2+y^2\leq 4\), \(x\leq y\leq \sqrt{3}x\).Riešenie: \(\displaystyle\left[\frac{\pi}{12}\ln 2\right]\)Úloha: Vypočítajte \[ \oint\limits_{C}y^2\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(C\) je kružnica s polomerom 2 a so stredom v bode \([0,0]\) kladne orientovaná.Riešenie: \(\displaystyle\left[4\pi\right]\)
Úloha: Vypočítajte \[ \oint\limits_{C}y^2\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(C\) je kladne orientovaný obvod štvorca ohraničený priamkami \(x=1\), \(x=-1\), \(y=1\), \(y=-1\).Riešenie: \(\displaystyle\left[4\right]\)Úloha: Vypočítajte \[ \oint\limits_{C}\frac{1}{x}\mathrm{arctg}\frac{y}{x} \,\mathrm{d}{x}+ \frac{2}{x}\mathrm{arctg}\frac{x}{y} \,\mathrm{d}{y}, \] ak \(C\) je hranica oblasti \(1\leq x^2+y^2\leq 4\), \(x\leq y\leq \sqrt{3}x\).Riešenie: \(\displaystyle\left[\frac{\pi}{12}\ln 2\right]\)Úloha: Vypočítajte \[ \oint\limits_{C}y^2\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(C\) je kružnica s polomerom 2 a so stredom v bode \([0,0]\) kladne orientovaná.Riešenie: \(\displaystyle\left[4\pi\right]\)
2. Dôsledky Greenovej vety, nezávislosť od integračnej cesty.
Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C} y\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(A=[1,1]\) a \(B=[2,4]\) sú prvý a posledný bod krivky.Riešenie: Keďže \[ \frac{\partial Q(x,y)}{\partial x} =1=\frac{\partial P(x,y)}{\partial y}, \] uvedený integrál nezávisí od integračnej cesty a môžeme ho rátať pomocou potenciálu \(V(x,y)\), kde \[ \begin{split} \frac{\partial V(x,y)}{\partial x} = P(x,y)=y,\\ \frac{\partial V(x,y)}{\partial y} = Q(x,y)=x. \end{split} \] Očividne \(V(x,y)=xy\) vyhovuje týmto podmienkam, a preto \[ \int\limits_{C} y\,\mathrm{d}{x}+x\,\mathrm{d}{y}=\Big[xy\Big]_{A= [1,1]}^{B=[2,4]}=8-1=7. \]Úloha: Vypočítajte \[ \int\limits_{C}(2y-6xy^3)\,\mathrm{d}{x}+(2x-9x^2y^2)\,\mathrm{d}{y}, \] ak prvý bod krivky je \(A=[0,0]\) a posledný bod je \(B=[2,2]\)Riešenie: \(\displaystyle\left[-88\right]\)Úloha: Vypočítajte \[ \int\limits_{C}(2x+3y)\,\mathrm{d}{x}+(3x-3y)\,\mathrm{d}{y}, \] ak prvý bod krivky je \(A=[1,1]\) a posledný bod je \(B=[3,3]\)Riešenie: \(\displaystyle\left[16\right]\)
Príklad: Nech \(C\) je uzavretá, jednoduchá hladká, kladne orientovaná krivka, ktorá tvorí hranicu oblasti \(\Omega\). Vyjadrite dvojný integrál \[ \iint\limits_{\Omega} ts \,\mathrm{d}{t}\,\mathrm{d}{s} \] pomocou krivkového integrálu.Riešenie: Greenova veta vyžaduje funkcie \(P(t,s)\), \(Q(t,s)\), také,že \[ ts=\left(\frac{\partial Q(t,s)}{\partial t}-\frac{\partial P(t,s)}{\partial s}\right). \] Existuje nekonečne veľa variant pre ich výber. My urobíme jeden konkrétny založený na zameniteľnosti premenných \(t\), \(s\) vo funkcii \(ts\), a teda \[ ts=\frac{ts}{2}-\frac{-ts}{2}=\left(\frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}\right). \] Funkciu \(Q(t,s)\) nájdeme z podmienky \(\displaystyle\frac{\partial Q(t,s)} {\partial t}=\frac{ts}{2}\) a využitím symetrie medzi \(t\) a \(s\) stačí potom položiť \(P(t,s)=-Q(s,t)\). A teda v našom prípade bude \[ Q(t,s)=\frac{t^2s}{4} \quad\text{a následne}\quad P(t,s)=-\frac{ts^2}{4}. \] Preto \[ \iint\limits_{\Omega} ts\,\mathrm{d}{t}\,\mathrm{d}{s}=\oint\limits_{C}- \frac{ts^2}{4}\,\mathrm{d}{t}+ \frac{t^2s}{4} \,\mathrm{d}{s}. \]Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť. -
Napíšte ďalší krok.
-
Napíšte ďalší krok.
Zdroje
Doplňujúce úlohy
Úloha:
Vypočítajte \(\displaystyle\quad\int\limits_{C}x^2\,\mathrm{d}{x}-xy\mathrm{d}{y}\),
ak \(C\) je štvrťkružnica \(x=\cos t\), \(y=\sin t\), pričom \(t\in\langle0,\pi/2\rangle\)
Úloha:
Vypočítajte \(\displaystyle\quad\int\limits_{C}3x^2y\,\mathrm{d}{x}+
\left(x^3+1\right)\,\mathrm{d}{y}\), ak \(C\) je časť oblúka paraboly \(y=x^2\)
od bodu \(A=[0,0]\) po bod \(B=[1,1]\)
Úloha:
Vypočítajte \(\displaystyle\quad\int\limits_{C} x\,\mathrm{d}{y}\), ak \(C\) je
kladne orientovaný obvod trojuholníka tvorený súradnicovými osami a priamkou \(x+y=3\).
Úloha:
Vypočítajte \(\displaystyle\quad\int\limits_{C}\left(x^2-y^2\right)\mathrm{d}{x}\),
ak \(C\) je časť oblúka paraboly \(y=x^2\) od bodu \(A=[0,0]\) po bod \(B=[2,4]\).
Úloha:
Vypočítajte \(\displaystyle\quad\int\limits_{C} xy\,\mathrm{d}{x}+(y-x)\,
\mathrm{d}{y}\), ak \(C\) je krivka \(a)\,\,y=x\), \(b)\,\,y=x^2\),
\(c)\,\,y=x^3\), \(d)\,\,y^2=x\) od bodu \(A=[0,0]\) po bod \(B=[1,1]\).
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Doplňujúce zdroje
- Tu vložte doplňujúce odporúčané zdroje.
- Tu vložte doplňujúce odporúčané zdroje.


