Ciele
- Aplikácia vety o výpočte dvojného integrálu -- praktický výpočet.
- Tu napíšte aspoň jeden cieľ.
Úvod
-
Výpočet dvojného integrálu.
Ukážeme ako vypočítať dvojný integrál prevodom na dvojnásobný. Ak množina \(A\) je elementárna oblasť typu \([x,y]\), t.j. \[ A=\big\{[x,y]\in \Bbb R^2; a\leq x\leq b,\ g(x)\leq y\leq h(x)\big\}, \] kde \(g\), \(h\) sú spojité na intervale \(\langle a,b\rangle\),potom \[ \iint\limits_{A} f(x,y)\, \mathrm{d}{x}\mathrm{d}{y}= \int\limits_{a}^b\left[ \int\limits_{g(x)}^{h(x)} f(x,y)\,\mathrm{d}{y}\right]\mathrm{d}{x}. \] Ak množina \(A\) je elementárna oblasť typu \([y,x]\), t.j. \[ A=\big\{[x,y]\in \Bbb R^2; c\leq y\leq d, \ \alpha(y)\leq x\leq \beta(y)\big\}, \] kde \(\alpha\), \(\beta\) sú spojité na intervale \(\langle c,d\rangle\), potom \[ \iint\limits_{A} f(x,y)\, \mathrm{d}{x}\mathrm{d}{y}= \int\limits_{c}^d\left[\ \int\limits_{\alpha(y)}^{\beta(y)} f(x,y)\, \mathrm{d}{x}\right]\mathrm{d}{y}. \]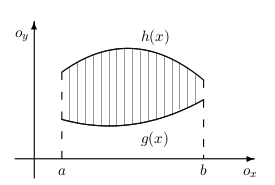
Príklad: Vypočítajme integrál \[ \iint\limits_{A} \left(x^2+y^2\right)\, \mathrm{d}{x}\mathrm{d}{y}, \] kde množina \(A\) je ohraničená priamkami \(y=x\), \(y=-x\), \(y=3\).Riešenie:Množina \(A\) je elementárna oblasť \([y,x]\) a môžeme ju zapísať nasledujúcimi nerovnosťami \begin{array}{ccc} A: 0\a\leq y\leq\a 3\\ -y\a\leq x\leq\a y. \end{array} Teda \begin{equation*} \iint\limits_{A} \left(x^2+y^2\right)\, \mathrm{d}{x}\mathrm{d}{y}= \int\limits_{0}^3\left[\ \int\limits_{-y}^{y} \left(x^2+y^2\right)\, \mathrm{d}{x}\right]\mathrm{d}{y}= \int\limits_{0}^3 \left[\frac{x^3}{3}+y^2x\right]_{-y}^{y}\,\mathrm{d}{x}=\frac{8}{3} \int\limits_{0}^3 {y^3}\,\mathrm{d}{x}=54. \end{equation*}
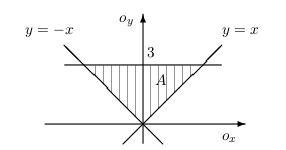Poznámka: Vypočítali sme vlastne objem valcovitého telesa zdola ohraničeného množinou \(A\) a zhora časťou paraboloidu \(z=x^2+y^2\). -
Základné vlastnosti dvojného integrálu.
-
lineárnosť
Nech funkcie \(f\) a \(g\) sú spojité na \(A\), \(a,b\in \Bbb R\). Potom \[ \iint\limits_{A} af(x,y)+bg(x,y)\,\mathrm{d}{x}\mathrm{d}{y}=a\iint\limits_{A} f(x,y)\, \mathrm{d}{x}\mathrm{d}{y} +b\iint\limits_{A} g(x,y)\, \mathrm{d}{x}\mathrm{d}{y}. \] -
delenie
Nech množiny \(B\) a \(D\) tvoria delenie \(A\), potom \[ \iint\limits_{A} f(x,y)\, \mathrm{d}{x}\mathrm{d}{y}= \iint\limits_{B} f(x,y)\, \mathrm{d}{x}\mathrm{d}{y} +\iint\limits_{D} f(x,y)\, \mathrm{d}{x}\mathrm{d}{y}. \]
-
lineárnosť
-
Výpočet dvojného integrálu transformáciou do polárnych súradníc.
Niektoré typy príkladov je výhodnejšie pocítat pomocou transformácie súradníc. Ak napr. pocítame integrál na množine, ktorej hranicu tvorí kružnica alebo jej cast je vhodné použit na popis oblasti polárne súradnice. Vztah medzi polárnymi a pravouhlými súradnicami je vyjadrený rovnicami\begin{equation*} x=\rho\cos\varphi\\ y=\rho\sin\varphi,\qquad\text{kde}\quad\varphi\in\langle0,2\pi\rangle, \rho\geq0. \end{equation*} Dvojný integrál potom počítame \[ \iint\limits_{A} f(x,y)\, \mathrm{d}{x}\mathrm{d}{y}=\iint\limits_{B} f(\rho\cos\varphi,\rho\sin\varphi)\rho\, \mathrm{d}{\rho}\mathrm{d}{\varphi}, \] kde množina \(B\) vznikne transformáciou množiny \(A\) do polárnych súradníc.
Príklad: Vypočítajme integrál \[ \iint\limits_{A} \frac{1}{\left(x^2+y^2\right)^2}\, \mathrm{d}{x}\mathrm{d}{y} \] ak \(A\) je ohraničená krivkami \(x^2+y^2=4x\), \(x^2+y^2=4x\), \(y=x\), \(y=\sqrt{3}x\).Riešenie: Nacrtneme si hranice množiny \(A\).Ak by sme vyjadrili množinu \(A\) pomocou pravouhlých súradníc bol by výpočet veľmi komplikovaný, preto použijeme polárne súradnice a využijeme jednoduchšie vyjadrenie kružníc v polárnych súradniciach. \[ A: \quad \displaystyle\frac{\pi}{4} \leq \varphi\leq \frac{\pi}{3}\quad\\ 4\cos\varphi \leq \rho\leq 8\cos\varphi \] Preto \[ \iint\limits_{A} \frac{1}{\left(x^2+y^2\right)^2}\, \mathrm{d}x\mathrm{d}y = \int\limits_{\pi/4}^{\pi/3} \left[\ \int\limits_{4\cos\varphi}^{8\cos\varphi} \frac{1}{\left(\rho^2\cos^2\varphi+\rho^2\sin^2\varphi\right)^2}\,\rho\, \mathrm{d}\rho \right]\mathrm{d}\varphi = \] \[ =\int\limits_{\pi/4}^{\pi/3} \left[-\frac{1}{2\rho^2}\right]_{4\cos\varphi}^{8\cos\varphi}\,\mathrm{d}\varphi =\frac{3}{128}\int\limits_{\pi/4}^{\pi/3} \frac{1}{\cos^2\varphi}\,\mathrm{d} \varphi=\frac{3}{128}(\sqrt{3}-1). \]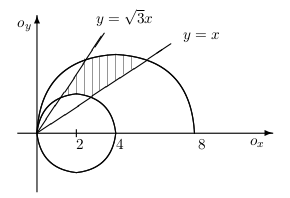
Postup
-
Zopakovanie pojmu elementárna oblasť vzhľadom na \(o_x\) a vzhľadom na \(o_x\).
- Hovoríme, že množina \(A\) je elementárna oblasť typu \([x,y]\) ak \[ A=\big\{[x,y]\in \Bbb R^2; a\leq x\leq b,\ g(x)\leq y\leq h(x)\big\}, \] kde \(g\), \(h\) sú spojité na intervale \(\langle a,b\rangle\).
- Hovoríme, že množina \(A\) je elementárna oblasť typu \([y,x]\) ak \[ A=\big\{[x,y]\in \Bbb R^2; c\leq y\leq d,\ \alpha(y)\leq x\leq \beta(y)\big\}, \] kde \(\alpha\), \(\beta\) sú spojité na intervale \(\langle c,d\rangle\).
Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{}xy\, \mathrm{d}x\mathrm{d}y,\qquad A:\quad y=2x-x^2,\,y=-x. \]Riešenie: \(\displaystyle\left[ -\frac{243}{40}\right]\)Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{} \sqrt{xy-y^2}\,\mathrm{d}x\mathrm{d}y,\qquad A:\quad 0\leq x y\leq x,\, y\leq x\leq 10y. \]Riešenie: \(\displaystyle \left[ 48\right] \)Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{} \mathrm{e}^{\frac{x}{y}}\,\mathrm{d}x\mathrm{d}y,\qquad A:\quad y^2=x,\,x=0,\,y=1,\,y=2. \]Riešenie: \(\displaystyle \left[ \mathrm{e}^2-\frac{3}{2}\right]\)Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{} \frac{x^2}{y^2}\,\mathrm{d}x\mathrm{d}y,\qquad A:\quad\frac{1}{x}, \,y=4x,\,x=3. \]Riešenie: \(\displaystyle \left[ \frac{125}{64}\right]\)Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{} \frac{x}{3}\,\mathrm{d}x\mathrm{d}y,\qquad A:\quad x=2+\sin y,\, x=0,\,y=0,\,y=2\pi. \]Riešenie: \(\displaystyle \left[ \frac{3}{2}\pi\right]\)Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{} (1-2x-3y)\,\mathrm{d}x\mathrm{d}y,\qquad A:\quad x^2+y^2=2 \]Riešenie: \(\displaystyle \left[ 2\pi\right]\)Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{} \mathrm{arctg}\frac{y}{x}\,\mathrm{d}x\mathrm{d}y,\qquad A:\quad 1=x^2+y^2=9,\,y=\sqrt{3}x,\,y=\frac{x}{\sqrt{3}},\,x\geq 0,\,y\geq 0. \]Riešenie: \(\displaystyle \left[ \frac{\pi^2}{6}\right]\)Poznámka:Príklad: Vypočítajte dvojný integrál, ak množina \(A\) je ohraničená danými krivkami \[ \iint_{A}^{} (x^2+y^2)\,\mathrm{d}x\mathrm{d}y,\qquad A:\quad x^2+y^2=2x,\, x^2+y^2=2x,\,y=0,\,(y>0) \]Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.Riešenie: \(\displaystyle \left[ \frac{45}{4}\pi\right]\)Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť. -
Napíšte ďalší krok.
-
Napíšte ďalší krok.
Zdroje
Doplňujúce úlohy
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{M}
(2x+y)\,\mathrm{d}x\mathrm{d}y\), ak \(M\) je ohraničená
krivkami \(y=x^2-4\), \(y=x+2\).
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{M}
2xy\,\mathrm{d}x\mathrm{d}y\), ak \(M\) je ohraničená krivkami
\(y^2=x\), \(y=x\), \(x=2\), pričom \(y^2\leq x\).
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{M}
\left( x^2-2y^2+4xy-6x-1\right)\,\mathrm{d}x\mathrm{d}y\), ak \(M\) je ohraničená
krivkami \(y=0\), \(x=0\), \(x+y=3\).
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{M}
\left( x^2+y\right)\,\mathrm{d}{x}\mathrm{d}{y}\), ak \(M\) je ohraničená parabolami \(y=x^2\), \(y^2=x\).
Úloha:
ypočítajte \(\displaystyle\quad\iint\limits_{M}
\frac{x^2}{y^2}\,\mathrm{d}{x}\mathrm{d}{y}\), ak \(M\) je ohraničená priamkami
\(y=x\), \(x=2\) a hyperbolou \(xy=1\).
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{M}
\sqrt{xy-y^2}\,\mathrm{d}{x}\mathrm{d}{y}\), ak \(M\) je ohraničená priamkami
\(y=5\), \(y=x\), \(y=x/10\).
Úloha:
Doplňujúce zdroje
- Tu vložte doplňujúce odporúčané zdroje.
- Tu vložte doplňujúce odporúčané zdroje.