Ciele
- Fyzikálne aplikácie trojného integrálu - hmotnosť telesa, statické momenty, súradnice ťažiska.
- Objem telesa.
- Hmotnosť telesa.
- Statické momenty. Ťažisko
Úvod
- Vzťahy pre výpočet hmotnosti homogenného a nehomogenného telesa, statických momentov a súradníc ťažiska telesa.
- Objem telesa.
- Hmotnosť telesa.
- Statické momenty. Ťažisko
- Využitie súradníc ťažiska pri výpočte niektorých typov trojných integrálov.
Priamo z definície trojného integrálu vyplýva, že vzorec pre objem telesa je \[ V(A)= \iiint\limits_{A} 1\, \textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z} \]
Uvažujme priestorové teleso \(A\), s hotnosťou \(m\) a objemom \(V\). V prípade, že teleso je homogénne, tak jeho hustotu vieme vyjadriť \(\displaystyle{\sigma=\frac{m}{V}}\). Predpokladajme, že teleso \(A\) nie je homogénne a jeho hustota v bode \([x,y,z]\) je daná funkciou \(\sigma(x,y,z)\). Otázka je ako vypočítať hmotnosť takéhoto telesa \(A\).
Pomocou delenia (ako pri definícii trojného integrálu) rozdelíme teleso \(A\). na hranolčeky \(A_{ijk}\). Segment \(A_{ijk}\) môžeme vďaka použitiu normálnej postupnosti delení \(A\) považovať za tak malý, že jeho hustota je konštantná a je reprezentovaná hustotou vo zvolenom bode \(T_{ijk}=[x_i^*,y_j^*,z_k^*]\in A_{ijk}\) a teda na \(A_{ijk}\) je \[ \sigma(x,y,z)=\sigma(x_i^*,y_j^*,z_k^*). \] Preto hotnosť segmentu \(A_{ijk}\) môžeme vyjadriť \( m(A_{ijk})\approx \sigma(x_i^*,y_i^*,z_k^*)V(A_{ijk})=\sigma(x_i^*,y_i^*,z_k^*)\Delta x_i \Delta y_j \Delta z_k \) Hmotnosť celého telesa \(A\) aproximujeme súčtom hmotností homogénnych segmentov \(A_{ij}\), preto \[ m(A)\approx \sum\limits_{i,j,k}m(A_{ijk}) \approx\sum\limits_{i,j,k}\sigma(x_i^*,y_i^*,z_k^*)\Delta x_i \Delta y_j \Delta z_k. \] Keďže uvažujeme normálnu postupnosť delení množiny \(A\), limitným prechodom dostávame \[ m(A)= \iiint\limits_{A}\sigma(x,y,z)\, \mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}. \]
Statické momenty priestorového telesa \(A\) s hustotou \(\sigma(x,y,z)\) vzhľadom na roviny \(\rho_{xy}\), \(\rho_{xy}\), \(\rho_{xy}\) počítame analogicky ako pri rovinnej oblasti \[ S_{xz}=\iiint\limits_{A}\sigma(x,y,z)\,y\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}\\ \] \[ S_{xy}=\iiint\limits_{A}\sigma(x,y,z)\,z\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}\\ \] \[ S_{yz}=\iiint\limits_{A}\sigma(x,y,z)\,x\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}. \] Pre súradnice ťažiska \(T=[x_{T},y_{T},z_{T}]\) platia nasledovné vzťahy \[ x_T= \frac{1}{m}\iiint\limits_{A}x\,\sigma(x,y,z)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}\\ \] \[ y_T= \frac{1}{m}\iiint\limits_{A}y\,\sigma(x,y,z)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}\\ \] \[ z_T= \frac{1}{m}\iiint\limits_{A}z\,\sigma(x,y,z)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z} \] Rovnako ako pri dvojnom integráli, aj pri trojnom vieme súradnice ťažiska využiť pri výpočte trojných integrálov z lineárnej funkcie \[ \iiint\limits_{A}\big(ax+by+cz+d\big)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z} =\big(ax_T+by_T+cz_T+d\big)V(A), \] pričom \(V(A)\) je objem homogenného telesa \(A\) hustotou \(\sigma(x,y,z)=1\) pričom \(T=(x_T,y_T,z_T)\) sú súradnice jeho ťažiska. V nasledujúcom príklade ukážeme použitie tohto výpočtu.
Príklad:
Vypočítajte hmotnosť telesa
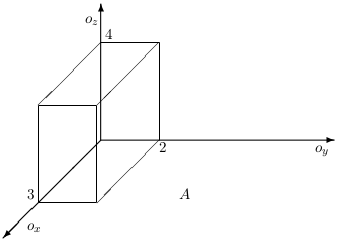
\(A=\langle0,2\rangle\times\langle0,3\rangle\times\langle0,4\rangle\),
ktorého hustota je \(\sigma(x,y,z)=3x-2y+z+5\).
Riešenie:
Načrtneme si množinu \(A\).
 \[
m =\iiint\limits_{A}\sigma(x,y,z)\,\mathrm{d}{y}\,\mathrm{d}{z}=\iiint\limits_{A}
\left(3x-2y+z+5\right)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}
=(3x_T-2y_T+z_T +5)V(A)=228.
\]
\[
m =\iiint\limits_{A}\sigma(x,y,z)\,\mathrm{d}{y}\,\mathrm{d}{z}=\iiint\limits_{A}
\left(3x-2y+z+5\right)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}
=(3x_T-2y_T+z_T +5)V(A)=228.
\]

Poznámka:
Tento integrál môžeme rátať pomocou súradníc ťažiska \(T=[1.5;1;2]\),
teraz už homogénneho hranola \(A\)
Príklad:
Vypočítajte súradnice ťažiska homogénneho telesa ohraničeného plochami
\(y^2=x\), \(z=0\), \(x+z=2\).
Riešenie:
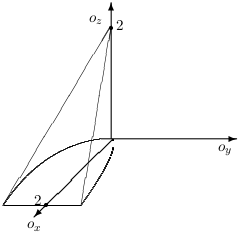 Zo symetrie telesa plynie, že pre ťažisko platí \(T=[x_T,0,z_T]\).
Náčrtok nám pomôže popísať množinu \(A\) ako oblasť typu \([x,y,z]\), t.j.
\[
\begin{array}
0\leq x\leq 2\\
-\sqrt{x}\leq y\leq \sqrt{x}\\
0\leq z\leq 2-\sqrt{x}.
\end{array}
\]
Môžeme položiť \(\sigma(x,y,z)=1\), a preto
\[
m=\iiint\limits_{A}\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}=\int\limits_{0}^{2}
\left[ \int\limits_{-\sqrt{x}}^{\sqrt{x}}\left( \int\limits_{0}^{2-x}\,\mathrm{d}{z}
\right)\,\mathrm{d}{y} \right]\,\mathrm{d}{x}=\int\limits_{0}^{2} \Big[ 2y-xy
\Big]_{-\sqrt{x}}^{\sqrt{x}}\,\mathrm{d}{x}=\int\limits_{0}^{2}2\left(
2\sqrt{x} -x^{3/2}\right)\,\mathrm{d}{x}=\frac{32\sqrt{2}}{15}.
\]
Pre statické momenty platí
\[
S_{yz}=\iiint\limits_{A}x\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}=
\int\limits_{0}^{2}\left[ \int\limits_{-\sqrt{x}}^{\sqrt{x}}\left(
\int\limits_{0}^{2-x}x\,\mathrm{d}{z} \right)\,\mathrm{d}{y} \right]\,\mathrm{d}{x}
=\int\limits_{0}^{2} \Big[ (2x-x^2)y \Big]_{-\sqrt{x}}^{\sqrt{x}}\,\mathrm{d}{x}
=\int\limits_{0}^{2}2\left( 2x^{3/2} -x^{5/2}\right)\,\mathrm{d}{x}=\frac{64\sqrt{2}}{35}.
\]
\[
S_{xy}=\iiint\limits_{A}z\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}=
\int\limits_{0}^{2} \left[ \int\limits_{-\sqrt{x}}^{\sqrt{x}}\left(
\int\limits_{0}^{2-x}z\,\mathrm{d}{z} \right)\,\mathrm{d}{y} \right]\,\mathrm{d}{x}
=\frac{1}{2}\int\limits_{0}^{2} \Big[ (4-4x-x^2)y \Big]_{-\sqrt{x}}^{\sqrt{x}}\,\mathrm{d}{x}
=\int\limits_{0}^{2}\left( (4-4x-x^2)\sqrt{x}\right)\,\mathrm{d}{x}=\frac{128\sqrt{2}}{105}.
\]
Preto \(\displaystyle T=\left[\frac{6}{7},0,\frac{4}{7}\right]\).
Zo symetrie telesa plynie, že pre ťažisko platí \(T=[x_T,0,z_T]\).
Náčrtok nám pomôže popísať množinu \(A\) ako oblasť typu \([x,y,z]\), t.j.
\[
\begin{array}
0\leq x\leq 2\\
-\sqrt{x}\leq y\leq \sqrt{x}\\
0\leq z\leq 2-\sqrt{x}.
\end{array}
\]
Môžeme položiť \(\sigma(x,y,z)=1\), a preto
\[
m=\iiint\limits_{A}\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}=\int\limits_{0}^{2}
\left[ \int\limits_{-\sqrt{x}}^{\sqrt{x}}\left( \int\limits_{0}^{2-x}\,\mathrm{d}{z}
\right)\,\mathrm{d}{y} \right]\,\mathrm{d}{x}=\int\limits_{0}^{2} \Big[ 2y-xy
\Big]_{-\sqrt{x}}^{\sqrt{x}}\,\mathrm{d}{x}=\int\limits_{0}^{2}2\left(
2\sqrt{x} -x^{3/2}\right)\,\mathrm{d}{x}=\frac{32\sqrt{2}}{15}.
\]
Pre statické momenty platí
\[
S_{yz}=\iiint\limits_{A}x\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}=
\int\limits_{0}^{2}\left[ \int\limits_{-\sqrt{x}}^{\sqrt{x}}\left(
\int\limits_{0}^{2-x}x\,\mathrm{d}{z} \right)\,\mathrm{d}{y} \right]\,\mathrm{d}{x}
=\int\limits_{0}^{2} \Big[ (2x-x^2)y \Big]_{-\sqrt{x}}^{\sqrt{x}}\,\mathrm{d}{x}
=\int\limits_{0}^{2}2\left( 2x^{3/2} -x^{5/2}\right)\,\mathrm{d}{x}=\frac{64\sqrt{2}}{35}.
\]
\[
S_{xy}=\iiint\limits_{A}z\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}=
\int\limits_{0}^{2} \left[ \int\limits_{-\sqrt{x}}^{\sqrt{x}}\left(
\int\limits_{0}^{2-x}z\,\mathrm{d}{z} \right)\,\mathrm{d}{y} \right]\,\mathrm{d}{x}
=\frac{1}{2}\int\limits_{0}^{2} \Big[ (4-4x-x^2)y \Big]_{-\sqrt{x}}^{\sqrt{x}}\,\mathrm{d}{x}
=\int\limits_{0}^{2}\left( (4-4x-x^2)\sqrt{x}\right)\,\mathrm{d}{x}=\frac{128\sqrt{2}}{105}.
\]
Preto \(\displaystyle T=\left[\frac{6}{7},0,\frac{4}{7}\right]\).

Postup
-
Výpočet príkladov na fyzikálne aplikácie dvojného integrálu.Úloha: Výpočítajte hnmotnosť telesa ohraničeného plochami \[ \begin{array} z = 8-x^2-y^2\\ z = x^2+y^2, \end{array} \] ak hustota v každom jeho bode je \(\rho(x,y,z)=z\).Úloha: Výpočítajte hnmotnosť telesa ohraničeného plochami \[ \begin{array} z^2 = x^2+y^2\\ z = x^2+y^2, \end{array} \] ak hustota v každom jeho bode je \(\rho(x,y,z)=k\,z\).Úloha: Výpočítajte ťažisko homogenného telesa ohraničeného plochami \[ z = 1-\sqrt{x^2+y^2},\quad z=0. \]Úloha: Výpočítajte ťažisko homogenného telesa ohraničeného plochami \[ x^2+y^2+z^2=1,\quad z=0, \quad (z\ge 0). \]Úloha: Výpočítajte \[ \iiint\limits_{A}(7x-6y+4z+8)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}, \] kde \( A: x^2+y^2+z^2\le 4\,\quad z\le 0\)Úloha: Výpočítajte \[ \iiint\limits_{A}(3x-2y+4z-8)\,\mathrm{d}{x}\,\mathrm{d}{y}\,\mathrm{d}{z}, \] kde \( A: z = 1-\sqrt{x^2+y^2},\quad z=0.\)Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť.
-
Napíšte ďalší krok.
-
Napíšte ďalší krok.
Zdroje
Doplňujúce úlohy
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Doplňujúce zdroje
- Tu vložte doplňujúce odporúčané zdroje.
- Tu vložte doplňujúce odporúčané zdroje.


