Ciele
- Aplikácia vzťahov pre výpočet hmotnosti a ťažiska rovinných homogénnych a nehomogénnych telies.
- Zrýchlený výpočet niektorých typov dvojných integrálov pomocou súradníc a ťažiska.
Úvod
- Vzťahy pre výpočet hmotnosti, statických momentov a súradníc ťažiska rovinných útvarov:
- Statické momenty. Ťažisko.
- Využitie súradníc ťažiska pri výpočte niektorých typov integrálov:
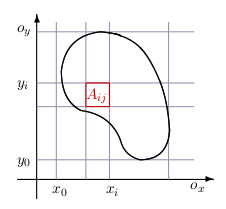
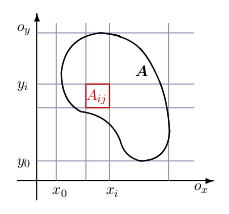
Uvažujme priestorové teleso \(A\), ktorého jeden rozmer môžeme zanedbať (napr. kus plechu), teda v podstate skúmame rovinné teleso. Uvažujme na úvod jednoduchší prípad, ak teleso \(A\) je homogénne s hmotnosťou \(m\) a plochou \(S\). Plošná hustota tohto telesa je \(\displaystyle{\sigma=\frac{m}{S}}\) (t.j. hmotnosť jednotkovej plochy). Uvažujme ďalej všeobecnejší prípad. Teleso \(A\) nie je homogénne, pričom plošná hustota v jeho ľubovoľnom bode \([x,y]\) je určená funkciou \(\sigma(x,y)\). Zaujíma nás aká je teraz hmotnosť tohto nehomogénneho telesa \(A\). Hmotnosť telesa vyjadríme pomocou dvojného integrálu. Začneme delením rovinného telesa \(A\), rovnako ako pri definícii dvojného integrálu.
Príklad:
Polkruh \(x^2+y^2\leq r_2, y\geq 0\) má hustotu v každom bode priamo úmernú
vzdialenosti bodu od osi \(o_x\). Vypočítajte jeho hmotnosť.
Riešenie:
Načrtneme si množinu \(A\).
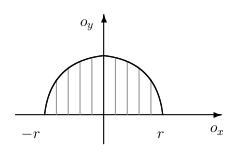 Využitím vzťahov pre výpočet hmotnosti rovinného telesa
dostávame
\(
m(A)= \iint\limits_{A}\sigma(x,y)\, \mathrm{d}{x}\mathrm{d}{y}=
\iint\limits_{A}ky\, \mathrm{d}{x}\mathrm{d}{y}.
\)
Polkruh \(A\) môžeme popísať aj pomocou
pravouhlých súradníc aj polárnych súradníc.
\[
\begin{array}{ccc}
A: \quad -r \leq x\leq r\\
\quad 0 \leq y\leq \sqrt{r^2-x^2}
\end{array}
\qquad\qquad
\begin{split}
A: \quad 0 \leq \varphi\leq \pi\\
0 \leq \rho\leq r
\end{split}
\]
Výpočet integrálu urobíme v pravouhlých súradniciach
\begin{equation*}
\begin{split}
m(A) = \iint\limits_{A}ky\, \mathrm{d}{x}\mathrm{d}{y} = \int\limits_{-r}^{r}
\left[\ \int\limits_{0}^{\sqrt{r^2-x^2}}ky\,\mathrm{d}{y} \right]\mathrm{d}{x}=
\frac{k}{2}\int\limits_{-r}^{r}\left(r^2-x^2\right)\,\mathrm{d}{x}=
\frac{k}{2}\left[r^2x-\frac{x^3}{3} \right]_{-r}^{r}=\frac23 kr^3.
\end{split}
\end{equation*}
Využitím vzťahov pre výpočet hmotnosti rovinného telesa
dostávame
\(
m(A)= \iint\limits_{A}\sigma(x,y)\, \mathrm{d}{x}\mathrm{d}{y}=
\iint\limits_{A}ky\, \mathrm{d}{x}\mathrm{d}{y}.
\)
Polkruh \(A\) môžeme popísať aj pomocou
pravouhlých súradníc aj polárnych súradníc.
\[
\begin{array}{ccc}
A: \quad -r \leq x\leq r\\
\quad 0 \leq y\leq \sqrt{r^2-x^2}
\end{array}
\qquad\qquad
\begin{split}
A: \quad 0 \leq \varphi\leq \pi\\
0 \leq \rho\leq r
\end{split}
\]
Výpočet integrálu urobíme v pravouhlých súradniciach
\begin{equation*}
\begin{split}
m(A) = \iint\limits_{A}ky\, \mathrm{d}{x}\mathrm{d}{y} = \int\limits_{-r}^{r}
\left[\ \int\limits_{0}^{\sqrt{r^2-x^2}}ky\,\mathrm{d}{y} \right]\mathrm{d}{x}=
\frac{k}{2}\int\limits_{-r}^{r}\left(r^2-x^2\right)\,\mathrm{d}{x}=
\frac{k}{2}\left[r^2x-\frac{x^3}{3} \right]_{-r}^{r}=\frac23 kr^3.
\end{split}
\end{equation*}

Motivácia: Statický moment chápeme ako silu potrebnú na udržanie hmotného bodu (telesa) v rovnováhe.
\[ \hline \]
Dvojný integrál má rozmanité geometrické a fyzikálne aplikácie, napríklad v predchádzajúcej časti spomínané ťažisko. Ale aj naopak, pomocou súradníc ťažiska vieme šikovne vypočítať isté typy dvojných integrálov, konkrétne integrál z lineárnej funkcie. Vyplýva to z nasledujúcich úvah. Vieme, že \[ x_T = \frac{1}{m}\iint\limits_{A}\sigma(x,y)\,x\,\mathrm{d}{x}\mathrm{d}{y}. \] Predpokladajme, že teleso \(A\) je homogénne s hustotou \(\sigma(x,y)=1\). Potom \(m= P(A)\cdot 1\) a teda \[ \iint\limits_{A}x\,\mathrm{d}{x}\mathrm{d}{y}=x_T P(A). \] Analogicky \[ \iint\limits_{A} y\,\mathrm{d}{x}\mathrm{d}{y}=y_T P(A). \] Preto \[ \iint\limits_{A}\big(ax+by+c\big)\,\mathrm{d}{x}\mathrm{d}{y}= \] využitím lineárnosti pre dvojný integrál \[ =a\iint\limits_{A}x\,\mathrm{d}{x}\mathrm{d}{y}+b\iint\limits_{A}y\, \mathrm{d}{x}\mathrm{d}{y}+c\iint\limits_{A}\,\mathrm{d}{x}\mathrm{d}{y}= \big(ax_T+by_T+c\big)P(A). \] V nasledujúcom príklade ukážeme použitie tohto výpočtu.
Príklad:
Vypočítajte
\[
\iint\limits_{A} \left(2x+3y-5\right)\, \mathrm{d}{x}\mathrm{d}{y},
\]
kde množina \(A\) je ohraničená krivkou
\(\displaystyle{\frac{(x-1)^2}{4}+\frac{(y-2)^2}{9}=1}\)
Riešenie:
Načrtneme si množinu \(A\).
 Ak sa na množinu \(A\) pozrieme ako na homogénne rovinné teleso, tak
potom súradnice jeho ťažiska sú \(T=[1,2]\). Obsah množiny \(A\) je
\(P(A)=6\pi\). Preto
\[
\iint\limits_{A} \left(2x+3y-5\right)\, \mathrm{d}{x}\mathrm{d}{y}=(
2x_T+3y_T-5)P(A)=18\pi.
\]
Ak sa na množinu \(A\) pozrieme ako na homogénne rovinné teleso, tak
potom súradnice jeho ťažiska sú \(T=[1,2]\). Obsah množiny \(A\) je
\(P(A)=6\pi\). Preto
\[
\iint\limits_{A} \left(2x+3y-5\right)\, \mathrm{d}{x}\mathrm{d}{y}=(
2x_T+3y_T-5)P(A)=18\pi.
\]

Postup
-
Výpočet príkladov na fyzikálne aplikácie dvojného integrálu.Príklad: Vypočítajte hmotnosť homogénnej rovinnej oblasti ohraničenej danými krivkami: \(y^2=x\), \(y=1\), \(x=0\).Riešenie: \(\displaystyle\left[\frac{1}{3}\right]\)Príklad: Vypočítajte hmotnosť homogénnej rovinnej oblasti ohraničenej danými krivkami: \[x^2+y^2=2x\] \[x^2+y^2=2y\].Riešenie: \(\displaystyle\left[\frac{1}{2},\frac{1}{2}\right]\)Príklad: Vypočítajte hmotnosť homogénnej rovinnej oblasti ohraničenej danými krivkami: \[y^2=4x\] \[x=4\].Riešenie: \(\displaystyle\left[\frac{12}{5},0\right]\)Príklad: Vypočítajte súradnice ťažiska homogénnej rovinnej oblasti ohraničenej': kruhobý výsek medzikružia s polomermi 2 a 4 a \(\varphi\in\left\langle 0,2\pi\right\rangle\).Riešenie: \(\displaystyle\left[\frac{59}{9\pi},\frac{56}{9\pi}\right]\)Príklad: Vypočítajte dvojný integrál využitím súradnic ťažiska \[\iint_A(4x+2y+5)\,{\rm d}x\,{\rm d}y,\quad A:\,\,\frac{(x-3)^2}{4}+\frac{y^2}{1}=1\].Riešenie: \(\left[ 34\pi\right]\)
Zdroje
Doplňujúce úlohy
Úloha:
Vypočítajte súradnice ťažiska homogénnej rovinnej oblasti ohraničenej kružnicou
\(\displaystyle x^2-2x+y^2=0\) a priamkou \(y=x\) ak naviac \(y\geq x\).
Úloha:
Vypočítajte súradnice ťažiska homogénnej rovinnej oblasti ohraničenej parabolou
\(\displaystyle 2y=x^2\) a priamkou ak \(x+y=2\).
Úloha:
Vypočítajte súradnice ťažiska homogénnej rovinnej oblasti ohraničenej krivkami
\(\displaystyle y=\sin x \), \(y=0\), \(x=\pi/4\) ak \(0\leq x\leq \pi/4\).
Doplňujúce zdroje
- Tu vložte doplňujúce odporúčané zdroje.
- Tu vložte doplňujúce odporúčané zdroje.


