Ciele
- Nájst aj parametrické vyjadrenie prístupného povrchu gule.
- Výpočet objemu molekuly.
Úvod
- Molekula zložená z \(n\) atómov.
- Parametrizácia guľovej plochy (rovnosť \(\stackrel{2}{=}\))
- južný pól sa zobrazí sám do seba t.j. \(J=[x_1,y_1,z_1-r_1]\mapsto (0,0)\).
- "rovník" (v geografickom význame) sa zobrazí na kružnicu so stredom v \((0,0)\) a polomerom \(2r_1\) a teda s rovnicou \(t^2+s^2=4r_1^2\) (pozri obrázok)
- "južná pologuľa" (v geografickom význame) sa zobrazí na kruh daný nerovnicou \(t^2+s^2\leq4r_1^2\).
- jednotlivé "rovnobežky" (v geografickom význame) sa zobrazia na sústredné kružnice so stredom v \((0,0)\) aplatí, čím je rovnobežka bližšie k severnému pólu, tým má odpovedajúca kružnica väčší polomer.
- severný pól sa zobrazí do "kružnice" s nekonečne veľkým polomerom.
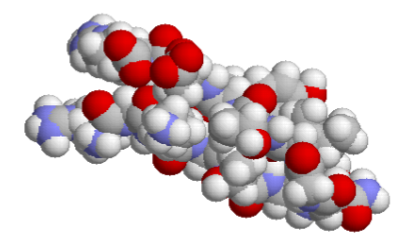
Pre molekulu \(M\) skladajúcu sa z atómov \(G_i\) tvaru guličiek (viď obrázok) \[ M=G_1\cup G_2\cup \dots \cup G_n:\quad n\in N \] je treba vypočítať objem, pričom \[ G_i:\qquad (x-x_i)^2+(y-y_i)^2+(z-z_i)^2= r_i^{\, 2} \] Z teórie trojného integrálu vieme, že \[ V(M)= \iiint\limits_{M}1\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}. \] Pre praktický výpočet tohto integrálu je už pre \(n=3\) nemožné na popis molekuly \(M\) použiť sférické súradnice (nie je totiž možné zistiť potrebné uhly súvisiace s prienikmi jednotlivých gúľ)
Tieto problémy je možné odstráníť prevodom trojného integrálu na plošný použitím Gauss - Ostrogradského vety. A teda pre výpočet objemu máme \[ V(M)= \iiint\limits_{M}1\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}= \iint\limits_{P(M)} z\,\textrm{d}{x}\,\textrm{d}{y} = \sum\limits_{i=1}^n \iint\limits_{P(G_i)} z\,\textrm{d}{x}\,\textrm{d}{y}, \] kde \(P(M)\) je povrch molekuly \(M\) orientovaný normálou von, \(P(G_i)\) je prístupný povrch guličky \(G_i\) (takisto orientovaný normálou von), t.j. ide o tú časť povrchu \(G_i\), ktorá leží zvonku všetkých susedov \(G_i\), t.j. je prístupná, narozdiel od časti povrchu, ktorý je "pohltený" susedmi a je teda neprístupný.
Na vyjadrenie trojného integrálu pomocou plošného môžeme použiť napríklad nasledujúce vyjadrenie \[ \iiint\limits_{M}\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}\stackrel{G.O.}{=} \frac{1}{3}\iint\limits_{P(M)} x\,\textrm{d}{y}\,\textrm{d}{z} + y\,\textrm{d}{x}\,\textrm{d}{z} +z\,\textrm{d}{x}\,\textrm{d}{y} \] Ukážme, ako vypočítať jeden z plošných integrálov \[ \iint\limits_{P(G_i)} z\,\textrm{d}{x}\,\textrm{d}{y};\quad i=1,\dots,n. \] Počítajme integrál pre \(i=1\). Na základe vety o výpočte plošného integrálu je potrebné vyjadriť plochu pomocou vhodného parametrického vyjadrenia. \[ P(G_i):\quad \vec{\pmb{r}}(t,s)= x(t,s)\vec{\pmb{i}}+y(t,s)\vec{\pmb{j}}+z(t,s)\vec{\pmb{k}},\qquad (t,s)\in\Omega_1. \] Teda počítame plošný integrál prevodom na dvojný integrál \[ \iint\limits_{P(G_1)} z\,\textrm{d}{x}\,\textrm{d}{y}= \iint\limits_{\Omega_1}g(t,s)\,\textrm{d}{t}\,\textrm{d}{s}, \] kde funkcia \(g(t,s)\) závisí od parametrického vyjadrenia plochy \(P(G_1)\).
Pre jednoduchosť predpokladajme najprv, že \(\Omega_1\) je ohraničená oblasť, a preto tento dvojný integrál môžeme vypočítať prevodom na krivkový integrál využitím Greenovej vety. Vyjadrime funkciu \(g(t,s)\) v tvare \[ g(t,s)=\frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}. \] Greenova veta teda dáva \[ \iint\limits_{\Omega_1}\left(\frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}\right)\,\textrm{d}{t}\,\textrm{d}{s}= \oint\limits_{H(\Omega_1)} P(t,s)\,\textrm{d}{t}+Q(t,s)\,\textrm{d}{s}, \] kde \(H(\Omega_1)\) je označenie pre hranicu \(\Omega_1\). V našom prípade hranicu \(\Omega_1\) tvoria oblúky kružníc.
Krivkový integrál vypočítame na základe vety o výpočte krivkového integrálu prevodom na určitý, čo môžeme zapísať: \[ \oint\limits_{H(\Omega_1)} P(t,s)\,\textrm{d}{t}+Q(t,s)\,\textrm{d}{s}= \sum\limits_{j=1}^m\int_{a_j}^{b_j} f(\varphi) z\,\textrm{d}{\varphi}, \] kde počet určitých integrálov \(m\) sa rovná počtu oblúkov kružníc tvoriacich \(H(\Omega_1)\). Záverom dostávame nasledujúcu schému pre výpočet objemu molekuly \(M\): \[ V(M)= \iiint\limits_{M}1\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}\stackrel{1}{=} \iint\limits_{P(M)} z\,\textrm{d}{x}\,\textrm{d}{y} = \sum\limits_{i=1}^n\iint\limits_{P(G_i)} z\,\textrm{d}{x}\,\textrm{d}{y}, \] \[ \iint\limits_{P(G_1)}z\,\textrm{d}{x}\,\textrm{d}{y}\stackrel{2}{=} \iint\limits_{\Omega_1}g(t,s)\,\textrm{d}{t}\,\textrm{d}{s}\stackrel{3}{=} \iint\limits_{\Omega_1}\left(\frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}\right)\,\textrm{d}{t}\,\textrm{d}{s}\stackrel{4}{=} \oint\limits_{H(\Omega_1)} P(t,s)\,\textrm{d}{t}+Q(t,s)\,\textrm{d}{s}\stackrel{5}{=} \sum\limits_{j=1}^m\int_{a_j}^{b_j} f(\varphi) z\,\textrm{d}{\varphi} \]
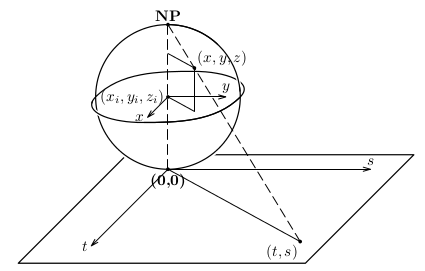
Takýmto spôsobom je celá guľová plocha zobrazená (transformovaná) do celej roviny \(\varrho_{t,s}\). Našou úlohou je nájsť vzťah (transformačné rovnice) medzi súradnicami bodu \(Q=[x,y,z]\) súradnicami bodu \(A=[t,s]\).
Predtým ale je zaujímavé všimnúť si nasledujúce detaily:
Vektor \(\overrightarrow{NA}\) je násobkom vektora \(\overrightarrow{NQ}\), t.j. \(\overrightarrow{NA}=k \overrightarrow{NQ}\), kde \(k\in \Bbb R\), pričom \[ \overrightarrow{NA}=A-N=(t,s,-2r_1) \] \[ \overrightarrow{NQ}=Q-N=(x-x_1,y-y_1,z-z_1-r_1) \] a preto \[ t=k(x-x_1) \] \[ s=k(y-y_1) \] \[ -2r_1=k(z-z_1-r_1) \] Vyjadrime \(x,y,z\) pomocou parametrov \(t,s\), čím získame parametrické vyjadrenie guľovej plochy. Eliminovaním konštanty \(k\) dostávame: \begin{equation}\label{ts} t=\frac{-2r_1}{z-z_1-r_1}(x-x_1)\\ s=\frac{-2r_1}{z-z_1-r_1}(y-y_1). \end{equation} Využitím faktu, že bod \(Q=[x,y,z]\) leží na guľovej ploche \(G_1: (x-x_1)^2+(y-y_1)^2+(z-z_1)^2= r_1^{\, 2}\) dostávame \[ \frac{t^2\left(z-z_1-r_1\right)^2}{4r_1^2}+\frac{s^2\left(z-z_1-r_1\right)^2} {4r_1^2}+\left(z-z_1\right)^2=r_1^2 \] Jednoduchou úpravou dostávame \[ \left(z-z_1-r_1\right)^2\left[\frac{t^2}{4r_1^2}+\frac{s^2}{4r_1^2}+1\right] + 2r_1\left(z-z_1-r_1\right)=0 \] a preto \[ z-z_1-r_1=\frac{-8r_1^{\, 3}}{t^2+s^2+4r_1^{\, 2}} \] Využitím vzťahov \eqref{ts} dostávame hľadané parametrické vyjadrenie guľovej plochy \(G_1\) \begin{equation}\label{transfeq} x=x_1+\frac{4r_1^{\, 2}t}{t^2+s^2+4r_1^{\, 2}},\\ y=y_1+\frac{4r_1^{\, 2}s}{t^2+s^2+4r_1^{\, 2}},\\ z=z_1+r_1-\frac{8r_1^{\, 3}}{t^2+s^2+4r_1^{\, 2}},\quad (t,s)\in \Bbb R \end{equation} respektíve \begin{equation}\label{transfeq2} \vec{\pmb{r}}(t,s)=\left(x_1+\frac{4r_1^{\, 2}t}{t^2+s^2+4r_1^{\, 2}}\right) \vec{\pmb{i}}+\left(y_1+\frac{4r_1^{\, 2}s}{t^2+s^2+4r_1^{\, 2}}\right)\vec{\pmb{j}} +\left(z_1+r_1-\frac{8r_1^{\, 3}}{t^2+s^2+4r_1^{\, 2}}\right)\vec{\pmb{k}}, \quad (t,s)\in \Bbb R.\tag{$2^*$} \end{equation}
Poznámka:
Spätným dosadením vzťahov \eqref{transfeq} do rovnice guľovej plochy \(G_1\)
môžeme overiť správnosť odvodeneného parametrického vyjadrenia.
Postup
-
V krokoch opíšte postup cvičenia. Krok definuje množinu súvisiacich úloh, ktoré vedú k napĺňaniu aspoň jedného cieľa.Príklad: Nájdite parametrické vyjadrenie prístupného povrchu gule \(G_1\) pri dvoch pretínajúcich sa guliach.Riešenie: Budeme zaoberať parametrizáciou prístupného povrchu \(P(G_1)\) pomocou transformačných rovníc \eqref{transfeq}, t.j. budeme hľladať obmedzujúcu množinu \(\Omega_1\) z ktorej sú parametre \(t,s\).
Začneme najjednoduchším prípadom keď uvažujeme len dve pretínajúce sa gule \(G_1\) a \(G_2\) (viď obrázok).Zaujíma nás priemet tej čati guľovej plochy \[ G_1:\qquad (x-x_1)^2+(y-y_1)^2+(z-z_1)^2= r_1^{\, 2}, \] ktorá leží zvonku guľovej plochy $G_2$ t.j. splňa \[ G_2^V:\qquad (x-x_2)^2+(y-y_2)^2+(z-z_2)^2\geq r_2^{\, 2}, \] Hľadaný priemet nájdeme dosadením parametrických rovníc \eqref{transfeq} gule \(G_1\) do vzťahu \(G_1^V\) \[ \left( x_1+\frac{4r_i^{\, 2}t}{t^2+s^2+4r_i^{\, 2}}-x_2\right)^2+ \left( y_1+\frac{4r_i^{\, 2}s}{t^2+s^2+4r_i^{\, 2}}-y_2\right)^2+ \left( z_1+r_1+\frac{4r_i^{\, 2}t}{t^2+s^2+4r_i^{\, 2}}-z_2\right)^2\geq r_2^{\, 2} \] Použitím označenia \begin{equation}\label{oznac} \begin{array}{l} a=(x_1-x_2)^2+(y_1-y_2)^2+(z_1+r_1-z_2)^2-r_2^{\, 2}\\ b=8r_1^{\, 2}(x_1-x_2)\\ a=8r_1^{\, 2}(y_1-y_2)\\ d=a4r_1^{\, 2}-16r_1^{\, 3}(z_1+r_1-z_2)+16r_1^{\, 4}. \end{array} \end{equation} dostávame \begin{equation}\label{omega} {\Omega}_1:\qquad a(t^2+s^2)+bt+cs+d\geq 0, \end{equation} čo vyjadruje hľadaný priemet prístupnej oblasti do roviny \(\varrho_{t,s}\). Urobíme analýzu hranice \(H(\Omega_1)\), ktorá je teda vyjadrená príslušnou rovnicou \begin{equation}\label{kruz1} \mathcal{K}_2:\qquad a(t^2+s^2)+bt+cs+d= 0. \end{equation}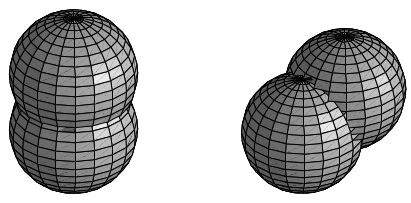
-
Ak \(a=0\), tak rovnica \eqref{kruz1} má tvar
\[
bt+cs+d= 0
\]
čo je rovnica priamky a množina \(\Omega_1\) t.j. priemet prístupného povrchu
je polrovina. Z geometrického hľadiska tento veľmi špecifický prípad nastáva ak
guľová plocha \(G_2\) prechádza práve "severným pólom" guľovej plochy \(G_1\).
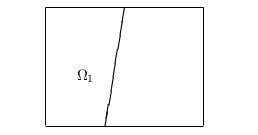
- Ak \(a\not=0\), tak rovnica \eqref{kruz1} má tvar \begin{equation}\label{kruz} \mathcal{K}_2:\qquad \left(t+\frac{b}{2a}\right)^2+ \left(s+\frac{c}{2a}\right)^2= \frac{b^2}{4a^2}+ \frac{c^2}{4a^2}- \frac{d}{a}. \end{equation} a teda \(\mathcal{K}_2\) predstavuje rovnicu kružnice v \(\varrho_{t,s}\), t.j. priemet priesečnice gulí \(G_1\) a \(G_2\) je kružnica. Rozlíšime dva prípady.
-
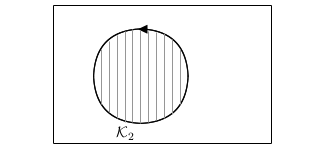
Ak \(A\lt 0\), tak v tomto prípade nerovnica \eqref{omega} nadobúda tvar
\[
{\Omega}_1:\qquad \left(t+\frac{b}{2a}\right)^2+
\left(s+\frac{c}{2a}\right)^2\leq \frac{b^2}{4a^2}+ \frac{c^2}{4a^2}- \frac{d}{a}
\]
a teda prístupný povrch gule \(G_1\) sa zobrazí a zobrazí do vnútra kružnice
\(\mathcal{K}_2\). Z geometrického hľadiska tento prípad nastáva ak
"severný pól" guľovej plochy \(G_1\) leží vo vnútri guľovej plochy \(G_2\).
-
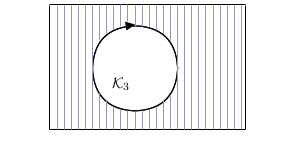
Ak \(A>0\), v tomto prípade nerovnica \eqref{omega} má tvar
\[
{\Omega}_1:\qquad \left(t+\frac{b}{2a}\right)^2+
\left(s+\frac{c}{2a}\right)^2\geq \frac{b^2}{4a^2}+
\frac{c^2}{4a^2}- \frac{d}{a}
\]
a teda prístupný povrch gule \(G_1\) sa zobrazí do vonkajška kružnice
\(\mathcal{K}_2\). Z geometrického hľadiska tento prípad nastáva ak
"severný pól" guľovej plochy \(G_1\) leží vo mimoguľovej plochy \(G_2\).
Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť. -
Ak \(a=0\), tak rovnica \eqref{kruz1} má tvar
\[
bt+cs+d= 0
\]
čo je rovnica priamky a množina \(\Omega_1\) t.j. priemet prístupného povrchu
je polrovina. Z geometrického hľadiska tento veľmi špecifický prípad nastáva ak
guľová plocha \(G_2\) prechádza práve "severným pólom" guľovej plochy \(G_1\).
-
Napíšte ďalší krok.
-
Napíšte ďalší krok.
Zdroje
Doplňujúce úlohy
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Doplňujúce zdroje
- Tu vložte doplňujúce odporúčané zdroje.
- Tu vložte doplňujúce odporúčané zdroje.


