01.
Numerické riešenie nelineárnych rovníc \(f(x)=0\)
Riešené úlohy:
Príklad:
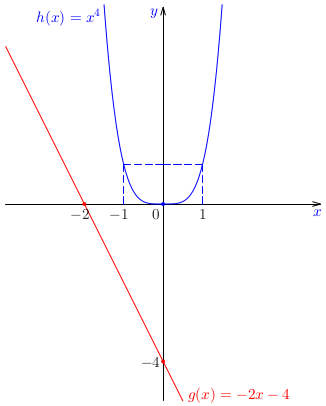
Určme počet reálnych riešení nelineárnej rovnice
\[
x^4+2x+4=0
\]
a separujme všetky reálne korene.
Príklad:
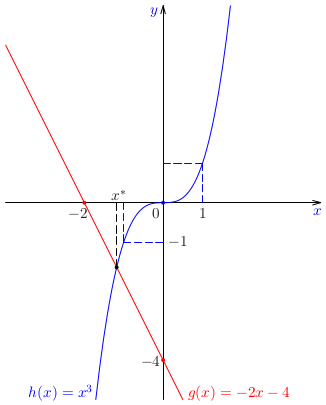
Určme počet reálnych riešení nelineárnej rovnice
\[
x^3+2x+4=0
\]
a separujme všetky reálne korene.
Poznámka:
Uvedené dve podmienky intervalu separácie sú postačujúce podmienky existencie riešenia
vnútri intervalu, ale nie sú nutné, t. j. korene rovnice môžu ležať aj vnútri intervalu, na
ktorom tieto podmienky nie sú splnené. To je prípad
všetkých dvoj-, štvornásobných a pod. koreňov rovníc (napríklad pre riešenie \(x=0\)
rovnice \(x^2=0\)).
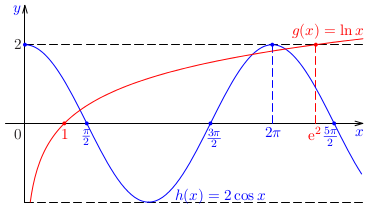
Príklad:
Určme počet reálnych riešení nelineárnej rovnice
\[
2\cos x -\ln x=0
\]
a separujme všetky reálne korene.
Príklad:
Určme, akej chyby sa dopustíme, ak za približné riešenie rovnice
\(x^3+2x+4=0\) vezmeme hodnotu \(x_p=-1{,}2\).
Príklad:
Metódou bisekcie určme približné riešenie rovnice \(x^3+2x+4=0\) s presnosťou \(\varepsilon=0{,}01\).
Poznámka:
Programy Matlab a Octave majú zabudovanú funkciu na riešenie algebrických rovníc, ktorá je samozrejme
tiež numerická.
Príkaz roots([1 0 2 4]) dáva odpoveď v nasledujúcom tvare:
ans =
0.589754512301458 + 1.744543250922657i
0.589754512301458 - 1.744543250922657i
-1.179509024602917 + 0.000000000000000i
Odchýlka nášho numerického riešenia od numerického riešenia určeného funkciou roots je \(|-1{,}179509024602917-(-1{,}18125)|\lt 0{,}001741\) je blízka skutočnej absolútnej chybe.
Príkaz roots([1 0 2 4]) dáva odpoveď v nasledujúcom tvare:
ans =
0.589754512301458 + 1.744543250922657i
0.589754512301458 - 1.744543250922657i
-1.179509024602917 + 0.000000000000000i
Odchýlka nášho numerického riešenia od numerického riešenia určeného funkciou roots je \(|-1{,}179509024602917-(-1{,}18125)|\lt 0{,}001741\) je blízka skutočnej absolútnej chybe.
Príklad:
Newtonovou metódou určme približné reálne riešenie rovnice \(x^3+2x+4=0\) na intervale separácie
\(\langle-2;-1\rangle\) s presnosťou \(\varepsilon=10^{-6}\).
Príklad:
Newtonovou metódou určme približne najväčšie reálne riešenie rovnice \(2\cos x-\ln x=0\)
s presnosťou \(\varepsilon=10^{-6}\).
Úlohy:
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte najmenší reálny koreň rovnice
\(x^3 + 2 x^2 - 4 x - 5 = 0\) s presnosťou \(0{,}005.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte najväčší reálny koreň rovnice
\(x^3 + 0{,}9 x^2 + 1{,}1 x - 7{,}8 = 0\) s presnosťou \(0{,}005.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte najmenší reálny koreň rovnice
\(x^3 -12 x + 1 = 0\) s presnosťou \(0{,}000001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(2 x^5 + 5 x^4 -10 x^2 + 10x - 3 = 0\) s presnosťou \(0{,}000001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte kladný koreň rovnice
\(2 x^4 + 6 x^3 + 5 x^2 - 0{,}5 = 0\) s presnosťou \(0{,}0001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(\sin x + 2 x - 2 = 0\) s presnosťou \(0{,}000001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(2 x\cdot \ln x - 4 x + 5{,}3 = 0\) s presnosťou \(0{,}00001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(x^3 - 8 x + 15 = 0\) s presnosťou \(0{,}0001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(x^3 + 3 x^2 - 3 = 0\) s presnosťou \(0{,}001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte najväčší reálny koreň rovnice
\(5 x^3 + 2 x^2 - 15 x - 6 = 0\) s presnosťou \(0{,}0001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(x^3 - 7 x - 7 = 0\) s presnosťou \(0{,}001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(x^4-3 x^2+4 x-1 = 0\) s presnosťou \(0{,}001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(x^5 - x^4 + 2 x^3 - 3 x^2 + 4 x - 5 = 0\) s presnosťou \(0{,}0001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte záporný koreň rovnice
\(x^6 - 3 x^2 + x - 1 = 0\) s presnosťou \(0{,}0001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(x - \sin x = 0{,}25\) s presnosťou \(0{,}00001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(2{,}2 x - 2^x = 0\) s presnosťou \(0{,}00001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(2 \,\mathrm{ln} x - 1/x = 0\) s presnosťou \(0{,}00001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(\mathrm{e}^{-x} + x^2 - 2 = 0\) s presnosťou \(0{,}00001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(\mathrm{e}^x + x^2 - 2 = 0\) s presnosťou \(0{,}00001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice
\(2 x - \mathrm{log} x - 7 = 0\) väčšie ako 3 s presnosťou \(0{,}00001.\)
Úloha:
Pomocou metódy bisekcie a Newtonovej metódy určte kladné korene rovnice
\(\mathrm{e}^x + \mathrm{e}^{-3x} = 4\) s presnosťou \(0{,}00001.\)
02.
Banachova veta o konvergencii iteračných procesov
Riešené úlohy:
Príklad:
Metódou prostých iterácií určme približné reálne riešenie nelineárnej rovnice
\[
x^3+2x+4=0
\]
s presnosťou \(\varepsilon=10^{-6}\).
Poznámka:
Výpočty v Matlabe/Octave sa dajú realizovať nastavením štartovacej hodnoty
x=-1.25
a následným opakovaním trojice príkazov umiestnených do jedného riadku:
xn=-(2*x+4)^(1/3), 2*abs(x-xn), x=xn;
Podobne efektívne sa však dá v Matlabe/Octave realizovať aj výpočet pomocou Newtonovej metódy.
x=-1.25
a následným opakovaním trojice príkazov umiestnených do jedného riadku:
xn=-(2*x+4)^(1/3), 2*abs(x-xn), x=xn;
Podobne efektívne sa však dá v Matlabe/Octave realizovať aj výpočet pomocou Newtonovej metódy.
Poznámka:
Dá sa ukázať, že ak je \(|\varphi^{\prime}(x)|\leqq \lambda\lt1\) na intervale separácie
\(\langle a;b\rangle\) , tak iteračný proces skonverguje z bodu \(x_0=a\) alebo \(x_0=b\)
aj bez overenia podmienky \(\varphi(x)\in\langle a;b\rangle\).
Príklad:
Určme riadkové normy nasledujúcich matíc:
\[
\mbf{x}=(\begin{array}{rrr}1\a -2\a 3\end{array}), \qquad \mbf{y}=\left(\begin{array}{r}-4 \\5\\-6 \end{array}\right),
\qquad \mbf{A}=\left(\begin{array}{rrr}7 \a -8 \a 9 \\-10 \a 11 \a -12 \end{array}\right).
\]
Poznámka:
Riadková norma sa zvykne označovať tiež ako tzv. nekonečno-norma:
\(\Vert\mbf{A}\Vert_{\mathrm{r}}=\Vert\mbf{A}\Vert_{\mathrm{\infty}}\). Táto maticová norma je
zosúladená s riadkovou normou stĺpcového vektora
\(\Vert\mbf{x}\Vert_{\infty}=\max\limits_{1\leqq i\leqq m}|x_i|\).
Príklad:
Overme, či je matica
\[
\mbf{A}=\left(\begin{array}{rrr}7 \a -8 \a 9 \\-10 \a 11 \a -12\\ 13 \a -14 \a 15 \end{array}\right)
\]
riadkovo diagonálne dominantná, prípadne či sa dá výmenami riadkov pretransformovať na riadkovo diagonálne dominantnú.
Príklad:
Overme, či je matica
\[
\mbf{A}=\left(\begin{array}{rrr}3 \a -4 \a 9 \\5 \a 2 \a 1\\ -3 \a -10 \a 6 \end{array}\right)
\]
riadkovo diagonálne dominantná, prípadne či sa dá výmenami riadkov pretransformovať na riadkovo diagonálne dominantnú.
Príklad:
Sústavu lineárnych algebrických rovníc
\[
\begin{array}{rcr}
2x-3y+7z\a=\a-11\\
10x-2y+\phantom{1}z\a=\a5\\
-3x+8y-2z\a=\a15
\end{array}
\]
riešme Jacobiovou iteračnou metódou. Najprv overme splnenie postačujúcich podmienok
konvergencie, potom uskutočnime 3 iterácie a odhadnime chybu.
Úlohy:
Úloha:
Metódou prostej iterácie určte približné reálne riešenie rovnice \(\mathrm{e}^{x}+x=0\)
s presnosťou \(\varepsilon=0{,}0001\).
Overte, že navrhnuté zobrazenie \(\varphi\) je kontraktívne a dosiahnutú presnosť overte
na základe vzťahu (\ref{qodhad}).
Úloha:
Metódou prostej iterácie určte všetky približné reálne riešenia rovnice \(5\cdot x\cdot \mathrm{e}^{x}+1=0\)
s presnosťou \(\varepsilon=0{,}001\).
Pre každý koreň overte, že navrhnuté zobrazenie \(\varphi\) je kontraktívne a dosiahnutú presnosť overte
na základe vzťahu (\ref{qodhad}).
Úloha:
Metódou prostej iterácie určte približné reálne riešenie rovnice \(\sin(x)+2x/2=0\)
s presnosťou \(\varepsilon=0{,}0001\).
Overte, že navrhnuté zobrazenie \(\varphi\) je kontraktívne a dosiahnutú presnosť overte
na základe vzťahu (\ref{qodhad}).
Úloha:
Metódou prostej iterácie určte približné reálne riešenie rovnice \(2\cdot\ln x-\dfrac1x=0\)
s presnosťou \(\varepsilon=0{,}0001\).
Overte, že navrhnuté zobrazenie \(\varphi\) je kontraktívne a dosiahnutú presnosť overte
na základe vzťahu (\ref{qodhad}).
Úloha:
S presnosťou \(0{,}001\) riešte sústavu rovníc
\(\begin{array}[t]{rcr}
2 x_2 - 4 x_3 + 2 x_4 \a = \a 5,\\
5 x_1 - 4 x_2 + 3 x_3 + 6 x_4 \a = \a - 2, \\
x_1 + 4 x_2 - 2 x_3 + 3 x_4 \a = \a 6, \\
3 x_1 - 5 x_2 + x_3 + 4 x_4 \a = \a 7.\\
\end{array}\)
Úloha:
S presnosťou \(0{,}001\) riešte sústavu rovníc
\(\begin{array}[t]{rcr}
2 x_1 - 4 x_2 + 5 x_3 + 6 x_4 \a =\a -7,\\
3 x_1 - 6 x_2 + 4 x_3 - 3 x_4 \a =\a 5,\\
4 x_1 + 2 x_2 - 2 x_3 + 5 x_4 \a =\a 3,\\
2 x_1 - x_2 + 3 x_3 - 4 x_4 \a =\a 6.\\
\end{array}\)
Úloha:
S presnosťou \(0{,}001\) riešte sústavu rovníc
\(\begin{array}[t]{rcr}
x_1 - 2 x_2 + 3 x_3 - 12 x_4 \a =\a -4, \\
9 x_1 - x_2 + 3 x_3 + 2 x_4 \a =\a 6,\\
-9 x_1 + 10 x_2 - 2 x_3 + x_4 \a =\a -2, \\
2 x_1 - x_2 + 8 x_3 - x_4 \a =\a 5 . \\
\end{array}\)
Úloha:
S presnosťou \(0{,}001\) riešte sústavu rovníc
\(\begin{array}[t]{rcr}
2 x_1 - 3 x_2 + x_3 - 12 x_4 \a =\a 24,\\
x_1 + 10 x_2 - 2 x_3 + 3 x_4 \a =\a 8,\\
13 x_1 - x_2 + 3 x_3 - 4 x_4 \a =\a -5,\\
2 x_1 - 2 x_2 + 10 x_3 + x_4 \a =\a -7 .\\
\end{array}\)
Úloha:
S presnosťou \(0{,}001\) riešte sústavu rovníc
\(\begin{array}[t]{rcr}
15 x_1 - 2 x_2 + 3 x_3 + 2 x_4 \a =\a 10,\\
x_1 + 12 x_2 - x_3 + 2 x_4 \a =\a -13,\\
2 x_1 - x_2 + 17 x_3 - 3 x_4 \a =\a 12, \\
-3 x_1 + x_2 + 2 x_3 -13 x_4 \a =\a 14 .\\
\end{array}\)
03.
Newtonova metóda riešenia sústav nelineárnych rovníc
Riešené úlohy:
Príklad:
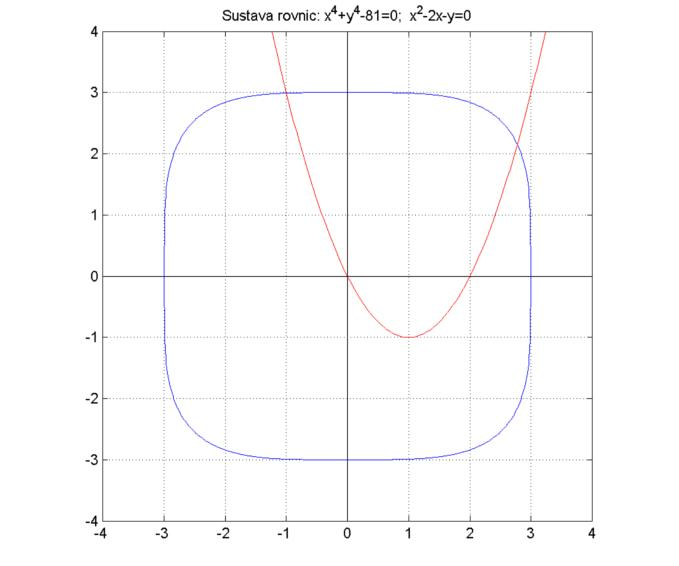
Určme počet riešení sústavy nelineárnych rovníc
\[
\begin{array}{r}
x^4+y^4-81=0,\\
x^2-2x-y=0.
\end{array}
\]
a separujme všetky korene.
Príklad:
Pre sústavu nelineárnych rovníc
\[
\begin{array}{r}
x^4+y^4-81=0,\\
x^2-2x-y=0.
\end{array}
\]
upresnite pomocou jedného kroku Newtonovej metódy odhadnuté začiatočné hodnoty všetkých koreňov.
Poznámka:
Newtonova metóda sa v prípade dobrej začiatočnej aproximácie prejavuje ako rýchle konvergujúca
(jedná sa o metódu s tzv. kvadratickou rýchlosťou konvergencie). V nasledujúcich dvoch tabuľkách
uvádzame výsledky, ktoré sme získali v Matlabe/Octave pomocou opakovania nasledujúcich príkazov
umiestnených na jeden riadok:
J=[4*x(1)^3, 4*x(2)^3;2*x(1)-2,-1], f=[x(1)^4+x(2)^4-81; x(1)^2-2*x(1)-x(2)], dx=-inv(J)*f, x=x+dx \[ \begin{array}{|r|c|c|c|c|} \hline k\a x_{1}^{[k]} \a y_{1}^{[k]} \a f_1(\vec{x}_{1}^{[k]}) \a f_2(\vec{x}_{1}^{[k]}) \\ \hline 0\a 2{,}700000000000000 \a 2{,}200000000000000 \a -4{,}4303 \a -0{,}31 \\ \hline 1\a 2{,}778882711653324 \a 2{,}158201219621302 \a 0{,}327608523 \a 0{,}006222482 \\ \hline 2\a 2{,}776358337288419 \a 2{,}155442569988142 \a 0{,}000507577 \a 0{,}000006372 \\ \hline 3\a 2{,}776354990216047 \a 2{,}155437051254248 \a 1{,}367 \cdot 10^{-9} \a 0{,}011 \cdot 10^{-9}\\ \hline 4\a 2{,}776354990208079 \a 2{,}155437051237144 \a 1{,}421 \cdot 10^{-14} \a 0 \\ \hline \end{array} \] \[ \begin{array}{|r|c|c|c|c|} \hline k\a x_{2}^{[k]} \a y_{2}^{[k]} \a f_1(\vec{x}_{2}^{[k]}) \a f_2(\vec{x}_{2}^{[k]}) \\ \hline 0\a -1 \a 3 \a 1 \a 0 \\ \hline 1\a -0{,}997706422018349 \a 2{,}990825688073394 \a 0{,}004567328 \a 0{,}000005260 \\ \hline 2\a -0{,}997694533482717 \a 2{,}990783448965392 \a 9{,}660 \cdot 10^{-8}\a 0{,}014 \cdot 10^{-8} \\ \hline 3\a -0{,}997694533223806 \a 2{,}990783448072278 \a 2{,}842 \cdot 10^{-14} \a 0 \\ \hline \end{array} \] Nuly v pravom dolnom rohu obidvoch tabuliek sú výsledky, ktoré vypísal použitý program. Je pravdepodobné, že odpovedajúce hodnoty ľavých strán druhej rovnice sústavy sú malé nenulové hodnoty.
J=[4*x(1)^3, 4*x(2)^3;2*x(1)-2,-1], f=[x(1)^4+x(2)^4-81; x(1)^2-2*x(1)-x(2)], dx=-inv(J)*f, x=x+dx \[ \begin{array}{|r|c|c|c|c|} \hline k\a x_{1}^{[k]} \a y_{1}^{[k]} \a f_1(\vec{x}_{1}^{[k]}) \a f_2(\vec{x}_{1}^{[k]}) \\ \hline 0\a 2{,}700000000000000 \a 2{,}200000000000000 \a -4{,}4303 \a -0{,}31 \\ \hline 1\a 2{,}778882711653324 \a 2{,}158201219621302 \a 0{,}327608523 \a 0{,}006222482 \\ \hline 2\a 2{,}776358337288419 \a 2{,}155442569988142 \a 0{,}000507577 \a 0{,}000006372 \\ \hline 3\a 2{,}776354990216047 \a 2{,}155437051254248 \a 1{,}367 \cdot 10^{-9} \a 0{,}011 \cdot 10^{-9}\\ \hline 4\a 2{,}776354990208079 \a 2{,}155437051237144 \a 1{,}421 \cdot 10^{-14} \a 0 \\ \hline \end{array} \] \[ \begin{array}{|r|c|c|c|c|} \hline k\a x_{2}^{[k]} \a y_{2}^{[k]} \a f_1(\vec{x}_{2}^{[k]}) \a f_2(\vec{x}_{2}^{[k]}) \\ \hline 0\a -1 \a 3 \a 1 \a 0 \\ \hline 1\a -0{,}997706422018349 \a 2{,}990825688073394 \a 0{,}004567328 \a 0{,}000005260 \\ \hline 2\a -0{,}997694533482717 \a 2{,}990783448965392 \a 9{,}660 \cdot 10^{-8}\a 0{,}014 \cdot 10^{-8} \\ \hline 3\a -0{,}997694533223806 \a 2{,}990783448072278 \a 2{,}842 \cdot 10^{-14} \a 0 \\ \hline \end{array} \] Nuly v pravom dolnom rohu obidvoch tabuliek sú výsledky, ktoré vypísal použitý program. Je pravdepodobné, že odpovedajúce hodnoty ľavých strán druhej rovnice sústavy sú malé nenulové hodnoty.
Poznámka:
V tomto prípade sme mohli namiesto sústavy nelineárnych rovníc prejsť na riešenie nasledujúcej
algebrickej rovnice 8. rádu:
\[
x^8-8x^7+24x^6-32x^5+17x^4-81=0,
\]
ktorú môžeme získať tak, že z druhej rovnice sústavy vyjadríme \(y=x^2-2x\) a tento výraz
dosadíme do prvej rovnice.
V prípade zložitejších nelineárnych sústav však je takýto postup možný len výnimočne.
Pri pohľade na algebrickú rovnicu tiež nie je jasné, koľko reálnych koreňov má a kde sa nachádzajú. Použitím príkazu
roots([1 -8 24 -32 17 0 0 0 -81])
v programe Matlab/Octave dostaneme nasledujúce výsledky: \[ \begin{array}{l} \phantom{-} 2.776354990208112 \\ \phantom{-} 2.568708345457808 + 0.978208721044785i\\ \phantom{-} 2.568708345457808 - 0.978208721044785i\\ \phantom{-} 0.981203232720892 + 1.436060637512282i\\ \phantom{-} 0.981203232720892 - 1.436060637512282i\\ -0.439241806670853 + 1.042383788608000i\\ -0.439241806670853 - 1.042383788608000i\\ -0.997694533223805 \end{array} \] Algebrická rovnica má práve 2 reálne korene, ktoré sa s vysokou presnosťou zhodujú s hodnotami \(x_{1}^{[4]}\) a \(x_{2}^{[3]}\) získanými Newtonovou metódou na riešenie sústav nelineárnych rovníc.
V prípade zložitejších nelineárnych sústav však je takýto postup možný len výnimočne.
Pri pohľade na algebrickú rovnicu tiež nie je jasné, koľko reálnych koreňov má a kde sa nachádzajú. Použitím príkazu
roots([1 -8 24 -32 17 0 0 0 -81])
v programe Matlab/Octave dostaneme nasledujúce výsledky: \[ \begin{array}{l} \phantom{-} 2.776354990208112 \\ \phantom{-} 2.568708345457808 + 0.978208721044785i\\ \phantom{-} 2.568708345457808 - 0.978208721044785i\\ \phantom{-} 0.981203232720892 + 1.436060637512282i\\ \phantom{-} 0.981203232720892 - 1.436060637512282i\\ -0.439241806670853 + 1.042383788608000i\\ -0.439241806670853 - 1.042383788608000i\\ -0.997694533223805 \end{array} \] Algebrická rovnica má práve 2 reálne korene, ktoré sa s vysokou presnosťou zhodujú s hodnotami \(x_{1}^{[4]}\) a \(x_{2}^{[3]}\) získanými Newtonovou metódou na riešenie sústav nelineárnych rovníc.
Príklad:
S presnosťou \(\varepsilon=0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc
\[\begin{array}{l}
x^2+ y^2 -1 = 0,\\
x\cdot\cos x - y = 0. \\
\end{array}\]
Úlohy:
Úloha:
S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc
\[\begin{array}{l}
x^2 y^2 - 3x^3 - 6 y^3 + 8 = 0,\\
x^4 - 9 y + 2 = 0. \\
\end{array}\]
Úloha:
S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc
\[\begin{array}{l}
\sin x - y = 1{,}32,\\
\cos y - x = -0{,}85. \\
\end{array}\]
Úloha:
S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc
\[\begin{array}{l}
(x - 1{,}2)^2 + (y - 0{,}6)^2 = 1,\\
4{,}2 x^2 + 8{,}8 y^2 = 1{,}42. \\
\end{array}\]
Úloha:
S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc
\[\begin{array}{l}
x^3 - y^2 - 1 = 0,\\
x y^3 - y - 4 = 0. \\
\end{array}\]
Úloha:
S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc
\[\begin{array}{l}
\mathrm{e}^{xy} - x^2 + y = 0,\\
x^2 + y^2 = 4. \\
\end{array}\]
04. Lagrangeov interpolačný polynóm a metóda najmenších štvorcov
Riešené úlohy:
Príklad:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\), ktorá je zadaná tabuľkou svojich funkčných hodnôt \(y_i=f(x_i)\) v uzlových bodoch \(x_i\). \[\begin{array}{|c|c|c|c|} \def\a{&} \hline x_i\a 0 \a 1{,}5 \a 6{,}8 \\ \hline y_i \a 1{,}45 \a 3{,}14 \a 4{,}11 \\ \hline \end{array} \]
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\), ktorá je zadaná tabuľkou svojich funkčných hodnôt \(y_i=f(x_i)\) v uzlových bodoch \(x_i\). \[\begin{array}{|c|c|c|c|} \def\a{&} \hline x_i\a 0 \a 1{,}5 \a 6{,}8 \\ \hline y_i \a 1{,}45 \a 3{,}14 \a 4{,}11 \\ \hline \end{array} \]
Príklad:
Funkcia \(f(x)\) je zadaná tabuľkou svojich funkčných hodnôt \(y_i=f(x_i)\) v uzlových bodoch \(x_i\).
\[\begin{array}{|c|c|c|c|c|}
\def\a{&}
\hline
x_i\a 0 \a 1 \a 3 \a 5 \\ \hline
y_i \a -6 \a -3 \a 0 \a 1 \\ \hline
\end{array}
\]
Pomocou Lagrangeovho interpolačného polynómu vypočítajte približnú hodnotu
funkcie \(f(x)\) v bode \(x=2\).
Príklad:
Funkcia \(f(x)\) je zadaná tabuľkou svojich funkčných hodnôt \(y_i=f(x_i)\) v uzlových bodoch \(x_i\).
\[\begin{array}{|c|c|c|c|c|}
\def\a{&}
\hline
x_i\a 1{,}462 \a 1{,}491 \a 2{,}247 \a 3{,}490 \\ \hline
y_i \a 0{,}38 \a 0{,}40 \a 0{,}81 \a 1{,}25 \\ \hline
\end{array}
\]
Pomocou inverzného Lagrangeovho interpolačného polynómu určte približné riešenie rovnice
\( f(x)=0,53
\).
Príklad:
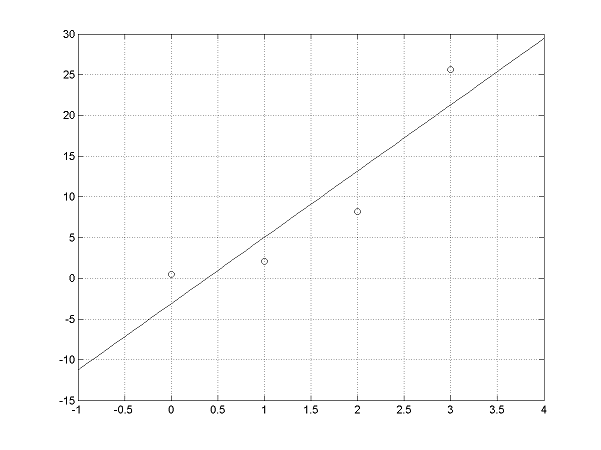
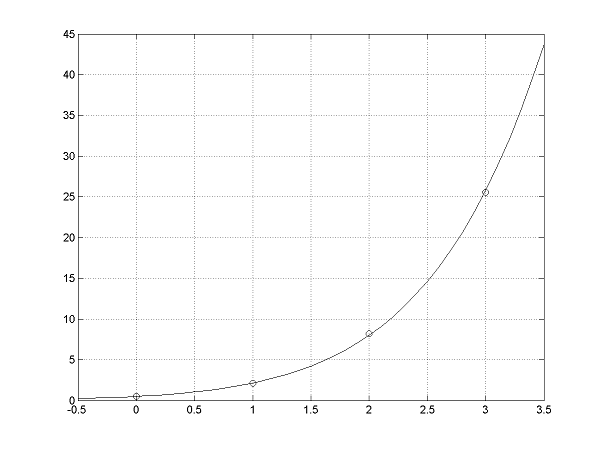
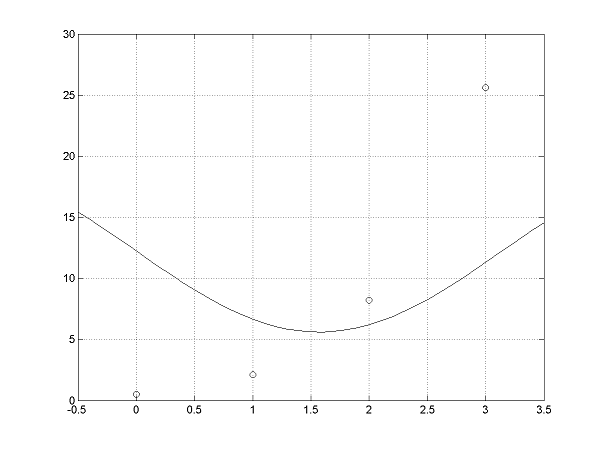
Funkcia \(f\left(x\right)\) je zadaná tabuľkou svojich funkčných hodnôt \(y_{i}=f\left(x_{i}\right)\) v uzlových bodoch \(x_{i}\) \[ \begin{array}{|c|c|c|c|c|} \def\a{&} \hline x_i\a 0 \a 1 \a 2\a 3 \\ \hline y_i \a 0{,}5 \a 2{,}1 \a 8{,}2\a 25{,}6 \\ \hline \end{array} \] Určte, ktorá z funkcií \(g_{1}\left(x\right)=ax+b,\) \(g_{2}\left(x\right)=e^{ax^{2}+bx+c},\) a \(g_{3}\left(x\right)=b+a\sin x\) najlepšie aproximuje v zmysle MNŠ funkciu \(f\left(x\right).\)
Funkcia \(f\left(x\right)\) je zadaná tabuľkou svojich funkčných hodnôt \(y_{i}=f\left(x_{i}\right)\) v uzlových bodoch \(x_{i}\) \[ \begin{array}{|c|c|c|c|c|} \def\a{&} \hline x_i\a 0 \a 1 \a 2\a 3 \\ \hline y_i \a 0{,}5 \a 2{,}1 \a 8{,}2\a 25{,}6 \\ \hline \end{array} \] Určte, ktorá z funkcií \(g_{1}\left(x\right)=ax+b,\) \(g_{2}\left(x\right)=e^{ax^{2}+bx+c},\) a \(g_{3}\left(x\right)=b+a\sin x\) najlepšie aproximuje v zmysle MNŠ funkciu \(f\left(x\right).\)
Úlohy:
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|} \hline x_i \a 0 \a 1 \a 5\\ \hline y_i \a 2 \a 3 \a 147\\ \hline \end{array} \]
Výsledok:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|} \hline x_i \a 0 \a 1 \a 5\\ \hline y_i \a 2 \a 3 \a 147\\ \hline \end{array} \]
Výsledok:
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\\ \hline y_i \a 3 \a -5 \a 4\\ \hline \end{array} \]
Výsledok:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\\ \hline y_i \a 3 \a -5 \a 4\\ \hline \end{array} \]
Výsledok:
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 11 \a 13 \a 14\a 18\\ \hline y_i \a 1342 \a 2210 \a 2758\a 5850\\ \hline \end{array} \]
Výsledok:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 11 \a 13 \a 14\a 18\\ \hline y_i \a 1342 \a 2210 \a 2758\a 5850\\ \hline \end{array} \]
Výsledok:
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a -2 \a 1 \a 2\a 4\\ \hline y_i \a 25 \a -8 \a -15\a -23\\ \hline \end{array} \]
Výsledok:
\
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a -2 \a 1 \a 2\a 4\\ \hline y_i \a 25 \a -8 \a -15\a -23\\ \hline \end{array} \]
Výsledok:
\
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a -1 \a 0 \a 2\a 4\\ \hline y_i \a 5 \a 2 \a -4\a -10\\ \hline \end{array} \]
Výsledok:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a -1 \a 0 \a 2\a 4\\ \hline y_i \a 5 \a 2 \a -4\a -10\\ \hline \end{array} \]
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 1 \a 3\a 5 \\ \hline y_i \a -6 \a -3 \a 0\a 1 \\ \hline \end{array} \] \(z=4.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 1 \a 3\a 5 \\ \hline y_i \a -6 \a -3 \a 0\a 1 \\ \hline \end{array} \] \(z=4.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\a 8 \\ \hline y_i \a 0 \a 1 \a 2\a 3 \\ \hline \end{array} \] \(z=2,5.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\a 8 \\ \hline y_i \a 0 \a 1 \a 2\a 3 \\ \hline \end{array} \] \(z=2,5.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0{,}89 \a 1{,}14 \a 1{,}50\a 1{,}62 \\ \hline y_i \a 2{,}435 \a 3{,}126 \a 4{,}481\a 5{,}053 \\ \hline \end{array} \] \(z=1,35.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0{,}89 \a 1{,}14 \a 1{,}50\a 1{,}62 \\ \hline y_i \a 2{,}435 \a 3{,}126 \a 4{,}481\a 5{,}053 \\ \hline \end{array} \] \(z=1,35.\)
Výsledok:
Úloha:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 3{,}287 \a 4{,}055 \a 5{,}528\a 5{,}584 \\ \hline y_i \a 1{,}19 \a 1{,}40 \a 1{,}71\a 1{,}72 \\ \hline \end{array} \] \(v=1,55.\)
Výsledok:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 3{,}287 \a 4{,}055 \a 5{,}528\a 5{,}584 \\ \hline y_i \a 1{,}19 \a 1{,}40 \a 1{,}71\a 1{,}72 \\ \hline \end{array} \] \(v=1,55.\)
Výsledok:
Úloha:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1{,}462 \a 1{,}491 \a 2{,}247\a 3{,}490 \\ \hline y_i \a 0{,}38 \a 0{,}40 \a 0{,}81\a 1{,}25 \\ \hline \end{array} \] \(v=0,53.\)
Výsledok:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1{,}462 \a 1{,}491 \a 2{,}247\a 3{,}490 \\ \hline y_i \a 0{,}38 \a 0{,}40 \a 0{,}81\a 1{,}25 \\ \hline \end{array} \] \(v=0,53.\)
Výsledok:
Úloha:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|} \hline x_i \a 8{,}935 \a 11{,}473 \a 18{,}356 \\ \hline y_i \a 2{,}190 \a 2{,}440 \a 2{,}910 \\ \hline \end{array} \] \(v=2,49.\)
Výsledok:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|} \hline x_i \a 8{,}935 \a 11{,}473 \a 18{,}356 \\ \hline y_i \a 2{,}190 \a 2{,}440 \a 2{,}910 \\ \hline \end{array} \] \(v=2,49.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 1 \a 3\a 5 \\ \hline y_i \a -6 \a -3 \a 0\a 1 \\ \hline \end{array} \] \(z=4.\)
Výsledok:
\(0,6\).
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 1 \a 3\a 5 \\ \hline y_i \a -6 \a -3 \a 0\a 1 \\ \hline \end{array} \] \(z=4.\)
Výsledok:
\(0,6\).
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\a 8 \\ \hline y_i \a 0 \a 1 \a 2\a 3 \\ \hline \end{array} \] \(z=2,5.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\a 8 \\ \hline y_i \a 0 \a 1 \a 2\a 3 \\ \hline \end{array} \] \(z=2,5.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0 \a 2\a 4\a 6 \a 8 \\ \hline y_i \a 2{,}1 \a 3{,}5 \a 5\a 6{,}7 \a 8 \\ \hline \end{array} \] \(g(x)=ax+b.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0 \a 2\a 4\a 6 \a 8 \\ \hline y_i \a 2{,}1 \a 3{,}5 \a 5\a 6{,}7 \a 8 \\ \hline \end{array} \] \(g(x)=ax+b.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0 \a 2\a 4\a 6 \a 8 \\ \hline y_i \a 2{,}1 \a 3{,}5 \a 5\a 7{,}2 \a 9 \\ \hline \end{array} \] \(g(x)=ax+b.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0 \a 2\a 4\a 6 \a 8 \\ \hline y_i \a 2{,}1 \a 3{,}5 \a 5\a 7{,}2 \a 9 \\ \hline \end{array} \] \(g(x)=ax+b.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0{,}78 \a 1{,}56\a 2{,}34\a 3{,}12 \a 3{,}81 \\ \hline y_i \a 2{,}5 \a 1{,}2 \a 1{,}12\a 2{,}25 \a 4{,}28 \\ \hline \end{array} \] \(g(x)=ax^2+bx+c.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0{,}78 \a 1{,}56\a 2{,}34\a 3{,}12 \a 3{,}81 \\ \hline y_i \a 2{,}5 \a 1{,}2 \a 1{,}12\a 2{,}25 \a 4{,}28 \\ \hline \end{array} \] \(g(x)=ax^2+bx+c.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0{,}78 \a 1{,}56\a 2{,}34\a 3{,}12 \\ \hline y_i \a 2{,}5 \a 1{,}2 \a 1{,}12\a 2{,}25 \\ \hline \end{array} \] \(g(x)=ax^2+bx+c.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0{,}78 \a 1{,}56\a 2{,}34\a 3{,}12 \\ \hline y_i \a 2{,}5 \a 1{,}2 \a 1{,}12\a 2{,}25 \\ \hline \end{array} \] \(g(x)=ax^2+bx+c.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a -0{,}53 \a 0{,}25\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+b\sin x+c\cos x.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a -0{,}53 \a 0{,}25\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+b\sin x+c\cos x.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a -0{,}53 \a 0{,}25\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+b\sin x.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a -0{,}53 \a 0{,}25\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+b\sin x.\)
Výsledok:
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a 0{,}53 \a 0{,}95\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+be^x.\)
Výsledok:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a 0{,}53 \a 0{,}95\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+be^x.\)
Výsledok:
05. Numerický výpočet určitého integrálu
Riešené úlohy:
Príklad:
Vypočítajme lichobežníkovou metódou približnú hodnotu integrálu
\(\int_{0}^{1}\cos x^{2}dx
\) pre
\(n=10
\) a odhadnime chybu výpočtu.
Príklad:
Vypočítajte lichobežníkovou metódou približnú hodnotu integrálu
\(\int_{1}^{4}\sqrt{x}\;dx\) s presnosťou \( \epsilon=10^{-2}\).
Príklad:
Vypočítajte Simpsonovou metódou približnú hodnotu integrálu
\(\int_{0}^{1}\cos x^{2}dx
\) pre
\(n=10
\) a odhadnite chybu výpočtu.
Príklad:
Vypočítajte Simpsonovou metódou približnú hodnotu integrálu
\(\int_{1}^{4}\sqrt{x}\;dx\) s presnosťou \( \epsilon=10^{-3}\).
Úlohy:
Úloha:
Pre zadaný počet \( \ n=10 \ \) delení vypočítajte lichobežníkovou metódou približnú hodnotu integrálu \[ \int^{5}_{1} \frac{dx}{x} \] a odhadnite chybu výpočtu.
Výsledok:
Pre zadaný počet \( \ n=10 \ \) delení vypočítajte lichobežníkovou metódou približnú hodnotu integrálu \[ \int^{5}_{1} \frac{dx}{x} \] a odhadnite chybu výpočtu.
Výsledok:
Úloha:
Pre zadaný počet \(\ n=10 \ \) delení vypočítajte lichobežníkovou metódou približnú hodnotu integrálu \[ \int^{10}_{1} \frac{dx}{1+x^2} \] a odhadnite chybu výpočtu.
Výsledok:
Pre zadaný počet \(\ n=10 \ \) delení vypočítajte lichobežníkovou metódou približnú hodnotu integrálu \[ \int^{10}_{1} \frac{dx}{1+x^2} \] a odhadnite chybu výpočtu.
Výsledok:
Úloha:
Lichobežníkovou metódou vypočítajte približnú hodnotu integrálu \[ \int^{1}_{0}e^{x^2}dx \] tak, ste dosiahli presnosť výpočtu \(\epsilon =0{,}05\).
Výsledok:
Lichobežníkovou metódou vypočítajte približnú hodnotu integrálu \[ \int^{1}_{0}e^{x^2}dx \] tak, ste dosiahli presnosť výpočtu \(\epsilon =0{,}05\).
Výsledok:
Úloha:
Lichobežníkovou metódou vypočítajte približnú hodnotu integrálu \[ \int^{1}_{0}\sin{x^2}dx \] tak, ste dosiahli presnosť výpočtu \(\epsilon =0{,}01\).
Výsledok:
Lichobežníkovou metódou vypočítajte približnú hodnotu integrálu \[ \int^{1}_{0}\sin{x^2}dx \] tak, ste dosiahli presnosť výpočtu \(\epsilon =0{,}01\).
Výsledok:
Úloha:
Pre zadaný počet \( \ n=10 \ \) delení vypočítajte Simpsonovou metódou približnú hodnotu integrálu \[ \int^{5}_{0} \frac{dx}{1+x} \] a odhadnite chybu výpočtu.
Výsledok:
Pre zadaný počet \( \ n=10 \ \) delení vypočítajte Simpsonovou metódou približnú hodnotu integrálu \[ \int^{5}_{0} \frac{dx}{1+x} \] a odhadnite chybu výpočtu.
Výsledok:
Úloha:
Pre zadaný počet \( \ n=10 \ \) delení vypočítajte Simpsonovou metódou približnú hodnotu integrálu \[ \int^{1}_{0} \frac{\sin x}{1+x}dx \] a odhadnite chybu výpočtu.
Výsledok:
Pre zadaný počet \( \ n=10 \ \) delení vypočítajte Simpsonovou metódou približnú hodnotu integrálu \[ \int^{1}_{0} \frac{\sin x}{1+x}dx \] a odhadnite chybu výpočtu.
Výsledok:
Úloha:
Simpsonovou metódou vypočítajte približnú hodnotu integrálu
\[
\int^{1}_{0}e^{x^2}dx
\]
tak, ste dosiahli presnosť výpočtu \(\epsilon =0{,}01\).
Výsledok:
Výsledok:
Úloha:
Simpsonovou metódou vypočítajte približnú hodnotu integrálu
\[
\int^{1}_{0}\cos {x^2}dx
\]
tak, ste dosiahli presnosť výpočtu \(\epsilon =0{,}0001\).
Výsledok:
Výsledok:
06. Numerické riešenie diferenciálnych rovníc
Riešené úlohy:
Príklad:
Cauchyho úlohu
\[y'=1+2\left(y-x\right),\ y\left(0\right)=1
\]
riešte približne na intervale
\[\left\langle 0;0,2\right\rangle
\]
najprv Eulerovou a potom Heunovou metódou s krokom
\(h=0,1.
\)
Výsledky porovnajte s hodnotami presného riešenia danej úlohy.
Poznámka:
V tomto prípade vieme vypočítať hodnoty presného riešenia Cauchyho úlohy, takže bez väčších problémov
sa nám podarí porovnať v tabuľke približné a presné riešenie. V bežnej praxi však vo
väčšine prípadov nevieme nájsť presné riešenie Cauchyho úlohy.
Príklad:
Cauchyho úlohu
\[y'=\left(xy-5\right)e^{2x+3}, \qquad y\left(0\right)=1\]
riešte približne na intervale\( \left\langle 0;0,2\right\rangle \) s krokom \( h=0,1 \)
Rungeho-Kuttovou metódou 4. rádu.
Úlohy:
Úloha:
Cauchyho úlohu \[ y'=xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,5\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,5\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=\frac{x}{y},\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,5\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=\frac{x}{y},\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,5\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=\frac{x}{y^{2}}-1,\ y(0)=1 \] riešte na intervale \(\left\langle 1;1,4\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=\frac{x}{y^{2}}-1,\ y(0)=1 \] riešte na intervale \(\left\langle 1;1,4\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=\frac{\cos y}{1,5+x}+0,1y^{2},\ y(0)=0 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=\frac{\cos y}{1,5+x}+0,1y^{2},\ y(0)=0 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Eulerovou metódou s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Heunovou metódou s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Heunovou metódou s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=y^{2}e^{x}-2y,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Heunovou metódou s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=y^{2}e^{x}-2y,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Heunovou metódou s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=x^{2}(1+y),\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Heunovou metódou s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=x^{2}(1+y),\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) Heunovou metódou s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=x^{2}(1+y),\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=x^{2}(1+y),\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=y^{2}-3xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=y^{2}-3xy,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=2xy-1,\ y(1)=0 \] riešte na intervale \(\left\langle 1;1,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=2xy-1,\ y(1)=0 \] riešte na intervale \(\left\langle 1;1,3\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=-y+\ln x,\ y(1)=1 \] riešte na intervale \(\left\langle 1;1,4\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,2\).
Výsledok:
Cauchyho úlohu \[ y'=-y+\ln x,\ y(1)=1 \] riešte na intervale \(\left\langle 1;1,4\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,2\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=-(y+1)\cos x,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,2\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Cauchyho úlohu \[ y'=-(y+1)\cos x,\ y(0)=1 \] riešte na intervale \(\left\langle 0;0,2\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,1\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=2x^{2}-y,\ y(0,5)=1 \] riešte na intervale \(\left\langle 0,5;0,6\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,05\).
Výsledok:
Cauchyho úlohu \[ y'=2x^{2}-y,\ y(0,5)=1 \] riešte na intervale \(\left\langle 0,5;0,6\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,05\).
Výsledok:
Úloha:
Cauchyho úlohu \[ y'=x^{2}-y,\ y(0,5)=1 \] riešte na intervale \(\left\langle 0,5;0,6\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,05\).
Výsledok:
Cauchyho úlohu \[ y'=x^{2}-y,\ y(0,5)=1 \] riešte na intervale \(\left\langle 0,5;0,6\right\rangle \) štandardnou metódou Rungeho-Kutta 4.rádu s krokom \(h=0,05\).
Výsledok:
07. Kombinatorika a pravdepodobnosť
Riešené úlohy:
Príklad:
Určme pravdepodobnosť toho, že pri jednom hode bežnou hracou kockou:
a) padne číslo \(6\);
b) padne nepárne číslo;
c) nepadne číslo \(4\);
d) nepadne číslo väčšia ako \(4\).
a) padne číslo \(6\);
b) padne nepárne číslo;
c) nepadne číslo \(4\);
d) nepadne číslo väčšia ako \(4\).
Riešenie:
Nech \(E_k\) je jav, ktorý spočíva v tom, že pri hode hracou kockou padne číslo \(k\). Je zrejmé, že množina šiestich javov \(\gamma=\{E_1,E_2,E_3,E_4,E_5,E_6\}\) je množinou elementárnych javov pre daný pokus. Teda podľa (\ref{kp}) \(n=6\). Nech \(A\) je jav, ktorého pravdepodobnosť chceme určiť. Potom na základe (\ref{kk}) a (\ref{kp}) dostaneme:
a) \(A=E_6\), čo znamená, že \(m=1\) a \(P(A)=\frac{1}{6}\);
b) \(A=E_1\cup E_3\cup E_5\), a preto \(m=3\) a \(P(A)=\frac{3}{6}=\frac{1}{2};\)
c) pre opačný jav \(\overline{A}=E_5\) je \(m=1\) a \(P(\overline{A})=\frac{1}{6}\). Teda \(P(A)=1-P(\overline{A})=\frac{5}{6};\)
d) zrejme \(A=E_1\cup E_2\cup E_3\cup E_4\), a teda \(m=4\) a \(P(A)=\frac{4}{6}=\frac{2}{3}.\)
Nech \(E_k\) je jav, ktorý spočíva v tom, že pri hode hracou kockou padne číslo \(k\). Je zrejmé, že množina šiestich javov \(\gamma=\{E_1,E_2,E_3,E_4,E_5,E_6\}\) je množinou elementárnych javov pre daný pokus. Teda podľa (\ref{kp}) \(n=6\). Nech \(A\) je jav, ktorého pravdepodobnosť chceme určiť. Potom na základe (\ref{kk}) a (\ref{kp}) dostaneme:
a) \(A=E_6\), čo znamená, že \(m=1\) a \(P(A)=\frac{1}{6}\);
b) \(A=E_1\cup E_3\cup E_5\), a preto \(m=3\) a \(P(A)=\frac{3}{6}=\frac{1}{2};\)
c) pre opačný jav \(\overline{A}=E_5\) je \(m=1\) a \(P(\overline{A})=\frac{1}{6}\). Teda \(P(A)=1-P(\overline{A})=\frac{5}{6};\)
d) zrejme \(A=E_1\cup E_2\cup E_3\cup E_4\), a teda \(m=4\) a \(P(A)=\frac{4}{6}=\frac{2}{3}.\)
Príklad:
Neštandardná spoločenská hra domino pozostáva z obdĺžnikových doštičiek, ktoré sú uprostred rozdelené
a každej polovičke doštičky je počtom bodiek priradená jedna z číselných hodnôt od nuly
do deväť (napr. na jednej z doštičiek je na jednej jej polovičke šesť bodiek a na
druhej polovičke osem bodiek - takejto doštičke môžeme priradiť neusporiadanú dvojicu
\(\{6;8\}\)). Z úplnej sady domina náhodne vyberieme
bez vrátenia tri doštičky. Určme pravdepodobnosť toho, že na každej
vybranej doštičke je na oboch jej polovičkách rovnaký počet bodiek (napr. doštičky
\(\{7;7\}\) a \(\{0;0\}\)).
Riešenie:
Najprv zistíme, koľko doštičiek obsahuje úplná sada domina. Pre počet bodiek na každej
polovičke doštičky máme \(9\) možností (\(0,1,2,\ldots, 7,8\) bodiek). Počet bodiek
môže byť na oboch polovičkách doštičky rovnaký, čo znamená výber s opakovaním dvoch
číselných hodnôt z deviatich, pričom poradie nie je rozhodujúce. Ide teda o kombinácie
druhej triedy z deviatich prvkov s opakovaním - na základe (\ref{kombop}) dostaneme,
že úplná sada nášho domina obsahuje práve
\[C^{\prime}_9(2)={9+2-1 \choose 2}={10 \choose 2}=45\,\mbox{doštičiek}\]
(skúste dôjsť k tomuto záveru aj bez poznatkov o \(C^{\prime}_9(2)\)).
Teda náhodne vyberáme tri doštičky domina zo \(45\) doštičiek bez vrátenia. Zrejme na poradí vyberaných doštičiek nezáleží. Doštičky úplnej sady domina môžeme rozdeliť do dvoch disjunktných množín: doštičky, ktoré majú na oboch ich polovičkách rovnaký počet bodiek (tých je \(9\)) a doštičky, ktoré majú na oboch ich polovičkách odlišný počet bodiek (tých je zrejme \(36\)).
Z formulácie úlohy vyplýva, že \(3\) doštičky z úplnej sady \(45\) doštičiek domina môžeme vybrať \({45 \choose 3}\) spôsobmi (čo je počet všetkých možných výsledkov daného pokusu), pričom každý výber je rovnako pravdepodobný. Tri doštičky s rovnakým počtom bodiek na oboch ich polovičkách môžeme vybrať \({9 \choose 3}\) spôsobmi (čo je počet všetkých priaznivých výsledkov daného pokusu). Z klasickej definície pravdepodobnosti dostaneme \[p=\frac{\displaystyle{{9 \choose 3}}}{\displaystyle{{45 \choose 3}}}=\frac{84}{14\,190}\approx 0{,}00592.\] Poznamenávame, že k tomuto záveru sme mohli dospieť aj na základe (\ref{phyge}), kde \(N=45\), \(K=9\), \(n=3\) a \(k=3\).
Teda náhodne vyberáme tri doštičky domina zo \(45\) doštičiek bez vrátenia. Zrejme na poradí vyberaných doštičiek nezáleží. Doštičky úplnej sady domina môžeme rozdeliť do dvoch disjunktných množín: doštičky, ktoré majú na oboch ich polovičkách rovnaký počet bodiek (tých je \(9\)) a doštičky, ktoré majú na oboch ich polovičkách odlišný počet bodiek (tých je zrejme \(36\)).
Z formulácie úlohy vyplýva, že \(3\) doštičky z úplnej sady \(45\) doštičiek domina môžeme vybrať \({45 \choose 3}\) spôsobmi (čo je počet všetkých možných výsledkov daného pokusu), pričom každý výber je rovnako pravdepodobný. Tri doštičky s rovnakým počtom bodiek na oboch ich polovičkách môžeme vybrať \({9 \choose 3}\) spôsobmi (čo je počet všetkých priaznivých výsledkov daného pokusu). Z klasickej definície pravdepodobnosti dostaneme \[p=\frac{\displaystyle{{9 \choose 3}}}{\displaystyle{{45 \choose 3}}}=\frac{84}{14\,190}\approx 0{,}00592.\] Poznamenávame, že k tomuto záveru sme mohli dospieť aj na základe (\ref{phyge}), kde \(N=45\), \(K=9\), \(n=3\) a \(k=3\).
Príklad:
O javoch \(A\) a \(B\) je známe, že \(P(A)=0{,}4\), \(P(\overline{B})=0{,}45\) a
\(P(\,\overline{\!A}\cap B)=0{,}2\) (\(\overline{\!A}\) je opačný jav k javu
\(A\)). Určme
a) \(P(\,\overline{\!A}\cap \overline{B}\,)\);
b) \(P(A\cup B)\);
c) \(P(A\cap B)\);
d) \(P(\,\overline{\!A}\cup \overline{B}\,)\);
e) \(P(B-A)\);
f) \(P(A-B)\).
a) \(P(\,\overline{\!A}\cap \overline{B}\,)\);
b) \(P(A\cup B)\);
c) \(P(A\cap B)\);
d) \(P(\,\overline{\!A}\cup \overline{B}\,)\);
e) \(P(B-A)\);
f) \(P(A-B)\).
Riešenie:
Viackrát použijeme poznatok, že ak javy \(C\) a \(D\) sú disjunktné (nezlučiteľné),
tak pravdepodobnosť javu \(C\cup D\) je rovná súčtu pravdepodobností javov \(C\) a \(D\), t. j.
\begin{equation}\label{pdj}
C\cap D=\emptyset \quad \Longrightarrow\quad P(C\cup D)=P(C)+P(D).
\end{equation}
a) Keby boli javy \(A\) a \(B\) nezávislé (nezávislými javmi sa budeme zaoberať
na budúcom cvičení), tak by platila rovnosť
\(P(\,\overline{\!A}\cap B)=P(\,\overline{\!A})\cdot P(B)=0{,}33.\) My musíme
určiť požadovanú pravdepodobnosť pre ľubovoľné javy \(A\) a \(B\): pre ne platí
\[\overline{\!A}=\overline{\!A}\cap I\stackrel{\star}{=}\overline{\!A}\cap(B\cup \overline{B}\,)\stackrel{\star\star}{=}(\,\overline{\!A}\cap
B)\cup(\,\overline{\!A}\cap\overline{B}\,),\]
kde v rovnosti \(\stackrel{\star}{=}\) sme vyjadrili istý jav \(I\) ako zjednotenie
javu \(B\) a javu, ktorý je k nemu opačný a v rovnosti \(\stackrel{\star\star}{=}\)
sme použili distributívny zákon. Teda
\[\overline{\!A}=(\,\overline{\!A}\cap B)\cup(\,\overline{\!A}\cap\overline{B}\,).\]
Je evidentné, že javy \((\,\overline{\!A}\cap B)\) a \((\,\overline{\!A}\cap\overline{B}\,)\)
sú disjunktné, a preto
na základe (\ref{pdj}) je
\[P(\overline{A})=P(\,\overline{\!A}\cap B)+P(\,\overline{\!A}\cap\overline{B}\,).\]
Odtiaľ vzhľadom na to, že \(P(A)=0{,}4\) a \(P(\,\overline{\!A}\cap B)=0{,}2\) dostaneme
\[0{,}6=0{,}2+P(\,\overline{\!A}\cap\overline{B}\,), \]
a teda \(P(\,\overline{\!A}\cap\overline{B}\,)=0{,}4.\)
b) Z výsledku časti a) vyplýva, že \(P(\overline{\,\overline{\!A}\cap\overline{B}\,})=0{,}6\) (ide o pravdepodobnosť opačného javu). Z de Morganovho pravidla je \(\overline{\,\overline{\!A}\cap\overline{B}\,}=A\cup B,\) a preto \(P(A\cup B)=0{,}6.\)
c) Pre ľubovoľné javy \(A\) a \(B\) platí \[P(A\cup B)=P(A)+P(B)-P(A\cap B),\] čo v našom prípade znamená, že (pozri výsledok časti b) a dané pravdepodobnosti v znení príkladu) \[0{,}6=0{,}4+0{,}55-P(A\cap B),\] a preto \(P(A\cap B)=0{,}35.\)
d) Pokúste sa vysvetliť každú z nasledujúcich rovností: \[P(\,\overline{\!A}\cup \overline{B}\,)=1-P(\overline{\,\overline{\!A}\cup \overline{B}\,})=1-P(A\cap B)=1-0{,}35=0{,}65.\]
e) Je zrejmé, že pre ľubovoľné javy \(A\) a \(B\) platí \[B-A=B\cap\overline{\!A}=\overline{\!A}\cap B.\] Keďže \(P(\,\overline{\!A}\cap B)=0{,}2\) (pozri text daného príkladu), tak \(P(B-A)=0{,}2\).
f) Požadovanú pravdepodobnosť by sme mohli získať napr. z nasledujúceho rozkladu javu \(A\cup B\) na zjednotenie troch po dvojiciach disjunktných javov: \[A\cup B=(A-B)\cup(A\cap B)\cup(B-A),\] pričom by sme využili výsledky častí b), c) a e). Ukážeme iný postup: obdobnou úvahou ako v časti a) dostaneme \[A=A\cap I=A\cap(B\cup \overline{B}\,)=(A\cap B)\cup(A\cap\overline{B}\,).\] Keďže javy \((A\cap B)\) a \((A\cap\overline{B}\,)\) sú disjunktné, tak na základe (\ref{pdj}) je \[P(A)=P(A\cap B)+P(A\cap\overline{B}\,).\] Ale \(P(A)=0{,}4\) a z časti c) je \(P(A\cap B)=0{,}35\), a teda \[0{,}4=0{,}35+P(A\cap\overline{B}\,).\] To znamená, že \(P(A\cap\overline{B}\,)=0{,}05\). Keďže \(A\cap\overline{B}=A-B\), tak \(P(A-B)=0{,}05\).
b) Z výsledku časti a) vyplýva, že \(P(\overline{\,\overline{\!A}\cap\overline{B}\,})=0{,}6\) (ide o pravdepodobnosť opačného javu). Z de Morganovho pravidla je \(\overline{\,\overline{\!A}\cap\overline{B}\,}=A\cup B,\) a preto \(P(A\cup B)=0{,}6.\)
c) Pre ľubovoľné javy \(A\) a \(B\) platí \[P(A\cup B)=P(A)+P(B)-P(A\cap B),\] čo v našom prípade znamená, že (pozri výsledok časti b) a dané pravdepodobnosti v znení príkladu) \[0{,}6=0{,}4+0{,}55-P(A\cap B),\] a preto \(P(A\cap B)=0{,}35.\)
d) Pokúste sa vysvetliť každú z nasledujúcich rovností: \[P(\,\overline{\!A}\cup \overline{B}\,)=1-P(\overline{\,\overline{\!A}\cup \overline{B}\,})=1-P(A\cap B)=1-0{,}35=0{,}65.\]
e) Je zrejmé, že pre ľubovoľné javy \(A\) a \(B\) platí \[B-A=B\cap\overline{\!A}=\overline{\!A}\cap B.\] Keďže \(P(\,\overline{\!A}\cap B)=0{,}2\) (pozri text daného príkladu), tak \(P(B-A)=0{,}2\).
f) Požadovanú pravdepodobnosť by sme mohli získať napr. z nasledujúceho rozkladu javu \(A\cup B\) na zjednotenie troch po dvojiciach disjunktných javov: \[A\cup B=(A-B)\cup(A\cap B)\cup(B-A),\] pričom by sme využili výsledky častí b), c) a e). Ukážeme iný postup: obdobnou úvahou ako v časti a) dostaneme \[A=A\cap I=A\cap(B\cup \overline{B}\,)=(A\cap B)\cup(A\cap\overline{B}\,).\] Keďže javy \((A\cap B)\) a \((A\cap\overline{B}\,)\) sú disjunktné, tak na základe (\ref{pdj}) je \[P(A)=P(A\cap B)+P(A\cap\overline{B}\,).\] Ale \(P(A)=0{,}4\) a z časti c) je \(P(A\cap B)=0{,}35\), a teda \[0{,}4=0{,}35+P(A\cap\overline{B}\,).\] To znamená, že \(P(A\cap\overline{B}\,)=0{,}05\). Keďže \(A\cap\overline{B}=A-B\), tak \(P(A-B)=0{,}05\).
Príklad:
a) Určme pravdepodobnosť toho, že medzi \(n\) náhodne vybranými osobami budú aspoň
dve osoby, ktoré oslavujú svoje narodeniny v ten istý deň v roku (pre zjednodušenie
predpokladajme, že každý rok má \(365\) dní - osoby, ktoré sa narodili 29. februára
môžeme zaradiť medzi tých, ktorí sa narodili 28. februára).
b) Pri akom minimálnom počte osôb je pravdepodobnosť toho, že sú medzi nimi aspoň dve osoby oslavujúce svoje narodeniny v ten istý deň, väčšia ako pravdepodobnosť toho, že takéto osoby medzi nimi nie sú?
c) Urobme diskusiu o vypočítaných pravdepodobnostiach.
b) Pri akom minimálnom počte osôb je pravdepodobnosť toho, že sú medzi nimi aspoň dve osoby oslavujúce svoje narodeniny v ten istý deň, väčšia ako pravdepodobnosť toho, že takéto osoby medzi nimi nie sú?
c) Urobme diskusiu o vypočítaných pravdepodobnostiach.
Riešenie:
a) Nech
\(\bullet\) \(A_n\) je jav, ktorý spočíva v tom, že medzi \(n\) náhodne vybranými osobami budú aspoň dve osoby, ktoré oslavujú svoje narodeniny v ten istý deň v roku a
\(\bullet\) \(\overline{A_n}\) je opačný jav k javu \(A_n\) (teda \(\overline{A_n}\) je jav, ktorý spočíva v tom, že každá z \(n\) náhodne vybraných osôb oslavuje svoje narodeniny v odlišných dňoch).
Je evidentné, že pre \(n\gt 365\) je \(P(A_n)=1\) a \(P(\overline{A_n})=0\).
Ak \(n\le 365\), tak každá osoba má \(365\) možných dní na oslavu svojich narodenín. Je zrejmé, že pre \(n\) osôb existuje práve \(365^n\) rovnako pravdepodobných možností pre oslavu ich narodenín.
Pre \(n=2\) máme \(365\cdot 364\) priaznivých možností pre jav \(\overline{A_2}\), lebo prvá osoba má \(365\) možností, ale druhá osoba už len \(364\) možností. Potom \[P(\overline{A_2})=\frac{365\cdot 364}{365^2}\quad \Longrightarrow\quad P(A_2)=1-P(\overline{A_2})=1-\frac{365\cdot 364}{365^2}\approx 0{,}0027.\] Pre \(n=3\) máme \(365\cdot 364\cdot 363\) priaznivých možností pre jav \(\overline{A_3}\). Preto \[P(\overline{A_3})=\frac{365\cdot 364\cdot 363}{365^3}\approx 0{,}9918\quad \Longrightarrow\quad P(A_3)=1-P(\overline{A_3})\approx 0{,}0082.\] Je zrejmé, že v prípade \(n\) osôb \((n\ge 2)\) máme \(365\cdot 364\cdot\ldots\cdot (365-(n-1))\) priaznivých možností pre jav \(\overline{A_n}\) (skúste sa zamyslieť nad prípadom \(n=1\)). Potom \[P(\overline{A_n})=\frac{365\cdot 364\cdot\ldots\cdot (365-n+1)}{365^n},\] a teda \begin{equation}\label{p365} P(A_n)=1-P(\overline{A_n})=1-\frac{365\cdot 364\cdot\ldots\cdot (366-n)}{365^n} \end{equation} b) Je potrebné určiť najmenšie \(n\), pre ktoré platí \(P(A_n)\gt P(\overline{A_n})\). Ak prihliadneme na to, že \(P(A_n)=1- P(\overline{A_n})\), tak posledná nerovnosť je ekvivalentná s nerovnosťou \begin{equation}\label{n365} P(A_n)\gt 0{,}5 \end{equation} Dá sa ukázať, že postupnosť pravdepodobností \(\big\{P(A_n)\big\}_{n=2}^{365}\) je rastúca. V nasledujúcej tabuľke sú uvedené niektoré jej členy: \[ \begin{array}{c||c|c|c|c|c|c|c} n \a 5 \a 15 \a 20 \a 22 \a 23 \a 50\a 70 \\ \hline P(A_n) \a 0{,}0271 \a0{,}2529 \a 0{,}4114 \a 0{,}4757 \a 0{,}5072\a 0{,}9704 \a 0{,}9992 \end{array} \] Z uvedených pravdepodobností vyplýva, že \(P(A_{22})\lt 0{,}5\), ale \(P(A_{23})\gt 0{,}5\). To znamená, že odpoveď na položenú otázku znie: stačí minimálne \(23\) osôb. Nie je to prekvapujúce?
c) V praxi je jav, ktorého pravdepodobnosť je väčšia ako \(0{,}97\) považovaný za "temer istý jav". Z tabuľky, ktorá je uvedená v časti b) vidno, že je temer isté, že medzi \(50\) osobami sa nájdu aspoň dve osoby, ktoré oslavujú svoje narodeniny v ten istý deň v roku. A to sme asi nečakali! V literatúre sa tento fakt zvykne označovať ako paradox spoločných narodenín. Zaujímavé je aj to, že napríklad pri \(70\) osobách je uvažovaná pravdepodobnosť dokonca \(0{,}9992\) - a to reprezentuje "ešte istejší jav".
\(\bullet\) \(A_n\) je jav, ktorý spočíva v tom, že medzi \(n\) náhodne vybranými osobami budú aspoň dve osoby, ktoré oslavujú svoje narodeniny v ten istý deň v roku a
\(\bullet\) \(\overline{A_n}\) je opačný jav k javu \(A_n\) (teda \(\overline{A_n}\) je jav, ktorý spočíva v tom, že každá z \(n\) náhodne vybraných osôb oslavuje svoje narodeniny v odlišných dňoch).
Je evidentné, že pre \(n\gt 365\) je \(P(A_n)=1\) a \(P(\overline{A_n})=0\).
Ak \(n\le 365\), tak každá osoba má \(365\) možných dní na oslavu svojich narodenín. Je zrejmé, že pre \(n\) osôb existuje práve \(365^n\) rovnako pravdepodobných možností pre oslavu ich narodenín.
Pre \(n=2\) máme \(365\cdot 364\) priaznivých možností pre jav \(\overline{A_2}\), lebo prvá osoba má \(365\) možností, ale druhá osoba už len \(364\) možností. Potom \[P(\overline{A_2})=\frac{365\cdot 364}{365^2}\quad \Longrightarrow\quad P(A_2)=1-P(\overline{A_2})=1-\frac{365\cdot 364}{365^2}\approx 0{,}0027.\] Pre \(n=3\) máme \(365\cdot 364\cdot 363\) priaznivých možností pre jav \(\overline{A_3}\). Preto \[P(\overline{A_3})=\frac{365\cdot 364\cdot 363}{365^3}\approx 0{,}9918\quad \Longrightarrow\quad P(A_3)=1-P(\overline{A_3})\approx 0{,}0082.\] Je zrejmé, že v prípade \(n\) osôb \((n\ge 2)\) máme \(365\cdot 364\cdot\ldots\cdot (365-(n-1))\) priaznivých možností pre jav \(\overline{A_n}\) (skúste sa zamyslieť nad prípadom \(n=1\)). Potom \[P(\overline{A_n})=\frac{365\cdot 364\cdot\ldots\cdot (365-n+1)}{365^n},\] a teda \begin{equation}\label{p365} P(A_n)=1-P(\overline{A_n})=1-\frac{365\cdot 364\cdot\ldots\cdot (366-n)}{365^n} \end{equation} b) Je potrebné určiť najmenšie \(n\), pre ktoré platí \(P(A_n)\gt P(\overline{A_n})\). Ak prihliadneme na to, že \(P(A_n)=1- P(\overline{A_n})\), tak posledná nerovnosť je ekvivalentná s nerovnosťou \begin{equation}\label{n365} P(A_n)\gt 0{,}5 \end{equation} Dá sa ukázať, že postupnosť pravdepodobností \(\big\{P(A_n)\big\}_{n=2}^{365}\) je rastúca. V nasledujúcej tabuľke sú uvedené niektoré jej členy: \[ \begin{array}{c||c|c|c|c|c|c|c} n \a 5 \a 15 \a 20 \a 22 \a 23 \a 50\a 70 \\ \hline P(A_n) \a 0{,}0271 \a0{,}2529 \a 0{,}4114 \a 0{,}4757 \a 0{,}5072\a 0{,}9704 \a 0{,}9992 \end{array} \] Z uvedených pravdepodobností vyplýva, že \(P(A_{22})\lt 0{,}5\), ale \(P(A_{23})\gt 0{,}5\). To znamená, že odpoveď na položenú otázku znie: stačí minimálne \(23\) osôb. Nie je to prekvapujúce?
c) V praxi je jav, ktorého pravdepodobnosť je väčšia ako \(0{,}97\) považovaný za "temer istý jav". Z tabuľky, ktorá je uvedená v časti b) vidno, že je temer isté, že medzi \(50\) osobami sa nájdu aspoň dve osoby, ktoré oslavujú svoje narodeniny v ten istý deň v roku. A to sme asi nečakali! V literatúre sa tento fakt zvykne označovať ako paradox spoločných narodenín. Zaujímavé je aj to, že napríklad pri \(70\) osobách je uvažovaná pravdepodobnosť dokonca \(0{,}9992\) - a to reprezentuje "ešte istejší jav".
Príklad:
O javoch \(A\) a \(B\) je známe, že \(P(A-B)=0{,}3\), \(P(\overline{A})=0{,}3\) a
\(P(\,\overline{\!A}\cap \overline{B}\,)=0{,}1\). Určte
a) \(P(A)\);
b) \(P(A\cap B)\);
c) \(P(B)\);
d) \(P(B-A)\);
e) \(P(\overline{B}\cup A)\);
f) \(P(A-\overline{B}\,)\).
a) \(P(A)\);
b) \(P(A\cap B)\);
c) \(P(B)\);
d) \(P(B-A)\);
e) \(P(\overline{B}\cup A)\);
f) \(P(A-\overline{B}\,)\).
Príklad:
Dvaja hráči \({\cal H}_A\) a \({\cal H}_B\) budú striedavo hádzať mincou a zvíťazí
ten, komu ako prvému padne rub mince. Hráč \({\cal H}_A\) hádže prvý, pričom
dohromady budú hádzať najviac štyrikrát. Ak nepadne rub mince v žiadnom zo štyroch
hodov, tak hra skončí remízou. Je to spravodlivá hra?
Riešenie:
Kedy je hra spravodlivá? Zrejme vtedy, ak pravdepodobnosť (t. j. šanca) výhry je
u oboch hráčov rovnaká.
Na ohodnotenie šancí u oboch hráčov je nevyhnutné zobrať do úvahy tieto dva javy:
- jav \(A\), ktorý spočíva v tom, že rub mince padne prvýkrát v prvom alebo v druhom hode;
- jav \(B\), ktorý spočíva v tom, že rub mince padne prvýkrát v druhom alebo vo štvrtom hode.
Ak nastane jav \(A\), tak zvíťazí hráč \({\cal H}_A\) a pokiaľ nastane jav \(B\), tak zvíťazí hráč \({\cal H}_B\). Skúsme stanoviť \(\gamma \) - množinu elementárnych javov daného pokusu. Ľahko vidieť, že pre daný pokus máme päť elementárnych javov: \begin{equation}\label{ej} \gamma=\{r,\ell r, \ell\ell r, \ell\ell\ell r,\ell\ell\ell\ell\}, \end{equation} kde \(r\) znamená padnutie rubu mince a \(\ell\) padnutie líca mince (napr. \(\ell\ell r\) označuje postupnosť líce, líce a rub mince - vtedy vyhráva hráč \({\cal H}_A\)). Teda v definícii (\ref{kp}) je \(n=5\). Je evidentné, že \(A= r\cup \ell\ell r\), a teda podľa (\ref{kk}) je \(m=2\). Na základe (\ref{kp}) dostávame \[P(A)=\frac{2}{5}.\] Obdobnou úvahou dospejeme k týmto záverom: \(B= \ell r\cup \ell\ell\ell r\), čo znamená, že aj pre jav \(B\) je \[P(B)=\frac{2}{5}.\] Teda šance na výhru sú u oboch hráčov rovnaké. Nie je to pravda! V definícii (\ref{kp}) sa predpokladá, že každý elementárny jav je rovnako možný. A to v našom prípade nie je splnené! Overíme to. Zoberme napr jav \(\ell\ell r\), ktorý je výsledkom troch hodov mincou. Množina elementárnych javov má teraz tvar \[\gamma_3=\{\ell\ell\ell, \ell\ell r,\ell r\ell,r\ell\ell,\ell rr,r\ell r,rr\ell,rrr\}\] a podľa (\ref{kp}) je \(n=8\) a pre jav \(\ell\ell r\) je \(m=1\). Teda \[P(\ell\ell r)=\frac{1}{8}.\] Pre jav \(\ell r\) je \(\gamma_2=\{\ell\ell, \ell r, r\ell,rr\}\), a teda \(P(\ell r)=\frac{1}{4}\). Presvedčte sa, že pre elementárne javy (\ref{ej}) platí: \[P(r)=\frac{1}{2}, \quad P(\ell r)=\frac{1}{4}, \quad P(\ell\ell r)=\frac{1}{8}, \quad P(\ell\ell\ell r)=\frac{1}{16}, \quad P(\ell\ell\ell\ell)=\frac{1}{16}.\] Teda elementárne javy z (\ref{ej}) nie sú rovnako možné (pozri predpoklady v definícii (\ref{kp})), a preto naše predchádzajúce úvahy boli chybné! Tu je správny výpočet požadovaných pravdepodobností: \[P(A)=P(r)+P(\ell\ell r)=\frac{1}{2}+\frac{1}{8}=\frac{5}{8}\quad \mbox{a} \quad P(B)=P(\ell r)+P(\ell\ell\ell r)=\frac{1}{4}+\frac{1}{16}=\frac{5}{16}. \] Hra teda nie je spravodlivá: šanca na výhru je u hráča \({\cal H}_A\) dvakrát väčšia ako u hráča \({\cal H}_B\). Pravdepodobnosť remízy je \(\frac{1}{16}.\)
Touto úlohou sme chceli ukázať, že je dôležité uvedomiť si v (\ref{kp}) predpoklady klasickej definície pravdepodobnosti. V tomto príklade neplatil predpoklad o tom, že všetky elementárne javy sú rovnako možné.
Na ohodnotenie šancí u oboch hráčov je nevyhnutné zobrať do úvahy tieto dva javy:
- jav \(A\), ktorý spočíva v tom, že rub mince padne prvýkrát v prvom alebo v druhom hode;
- jav \(B\), ktorý spočíva v tom, že rub mince padne prvýkrát v druhom alebo vo štvrtom hode.
Ak nastane jav \(A\), tak zvíťazí hráč \({\cal H}_A\) a pokiaľ nastane jav \(B\), tak zvíťazí hráč \({\cal H}_B\). Skúsme stanoviť \(\gamma \) - množinu elementárnych javov daného pokusu. Ľahko vidieť, že pre daný pokus máme päť elementárnych javov: \begin{equation}\label{ej} \gamma=\{r,\ell r, \ell\ell r, \ell\ell\ell r,\ell\ell\ell\ell\}, \end{equation} kde \(r\) znamená padnutie rubu mince a \(\ell\) padnutie líca mince (napr. \(\ell\ell r\) označuje postupnosť líce, líce a rub mince - vtedy vyhráva hráč \({\cal H}_A\)). Teda v definícii (\ref{kp}) je \(n=5\). Je evidentné, že \(A= r\cup \ell\ell r\), a teda podľa (\ref{kk}) je \(m=2\). Na základe (\ref{kp}) dostávame \[P(A)=\frac{2}{5}.\] Obdobnou úvahou dospejeme k týmto záverom: \(B= \ell r\cup \ell\ell\ell r\), čo znamená, že aj pre jav \(B\) je \[P(B)=\frac{2}{5}.\] Teda šance na výhru sú u oboch hráčov rovnaké. Nie je to pravda! V definícii (\ref{kp}) sa predpokladá, že každý elementárny jav je rovnako možný. A to v našom prípade nie je splnené! Overíme to. Zoberme napr jav \(\ell\ell r\), ktorý je výsledkom troch hodov mincou. Množina elementárnych javov má teraz tvar \[\gamma_3=\{\ell\ell\ell, \ell\ell r,\ell r\ell,r\ell\ell,\ell rr,r\ell r,rr\ell,rrr\}\] a podľa (\ref{kp}) je \(n=8\) a pre jav \(\ell\ell r\) je \(m=1\). Teda \[P(\ell\ell r)=\frac{1}{8}.\] Pre jav \(\ell r\) je \(\gamma_2=\{\ell\ell, \ell r, r\ell,rr\}\), a teda \(P(\ell r)=\frac{1}{4}\). Presvedčte sa, že pre elementárne javy (\ref{ej}) platí: \[P(r)=\frac{1}{2}, \quad P(\ell r)=\frac{1}{4}, \quad P(\ell\ell r)=\frac{1}{8}, \quad P(\ell\ell\ell r)=\frac{1}{16}, \quad P(\ell\ell\ell\ell)=\frac{1}{16}.\] Teda elementárne javy z (\ref{ej}) nie sú rovnako možné (pozri predpoklady v definícii (\ref{kp})), a preto naše predchádzajúce úvahy boli chybné! Tu je správny výpočet požadovaných pravdepodobností: \[P(A)=P(r)+P(\ell\ell r)=\frac{1}{2}+\frac{1}{8}=\frac{5}{8}\quad \mbox{a} \quad P(B)=P(\ell r)+P(\ell\ell\ell r)=\frac{1}{4}+\frac{1}{16}=\frac{5}{16}. \] Hra teda nie je spravodlivá: šanca na výhru je u hráča \({\cal H}_A\) dvakrát väčšia ako u hráča \({\cal H}_B\). Pravdepodobnosť remízy je \(\frac{1}{16}.\)
Touto úlohou sme chceli ukázať, že je dôležité uvedomiť si v (\ref{kp}) predpoklady klasickej definície pravdepodobnosti. V tomto príklade neplatil predpoklad o tom, že všetky elementárne javy sú rovnako možné.
Príklad:
V číselnej lotérii sa losuje šesť čísel zo \(49\) čísel \(\{1,2, 3,\ldots , 49\}\).
Určme pravdepodobnosť toho, že budú vylosované
a) dve po sebe idúce čísla (napr. \(17\) a \(18\));
b) práve dve po sebe idúce čísla;
c) práve štyri po sebe idúce čísla (napr. \(17,\) \(18,\) \(19,\) a \(20\));
d) dve trojice po sebe idúcich čísel.
a) dve po sebe idúce čísla (napr. \(17\) a \(18\));
b) práve dve po sebe idúce čísla;
c) práve štyri po sebe idúce čísla (napr. \(17,\) \(18,\) \(19,\) a \(20\));
d) dve trojice po sebe idúcich čísel.
Riešenie:
Predstavme si \(49\) bielych guliek, ktoré sú očíslované v jednom rade v poradí od
\(1\) po \(49\). Po vylosovaní šiestich čísel zmeníme farby vylosovaných guliek
na zelenú farbu. Teda po vylosovaní šiestich čísel bude mať \(6\) guliek zelenú farbu
a \(43\) nevylosované guľky budú biele. Pri losovaní guliek na ich poradí nezáleží
(rozhodujúce je to, že aké guľky sa vylosovali) a guľky sa losujú bez návratu (ľubovoľná
guľka môže byť vylosovaná maximálne raz). Na základe (\ref{komb}) dostaneme počet
všetkých možných výsledkov \(|\Omega|\) losovania (pokusu):
\[|\Omega|={49 \choose 6}=13\,983\,816,\]
pričom všetky výsledky losovania sú rovnako pravdepodobné.
a) Nech \(A\) je jav, ktorý spočíva v tom, že budú vylosované dve po sebe idúce čísla. Zrejme k nemu opačný jav \(\overline{\!A}\) znamená, že medzi \(6\) vylosovanými číslami nebudú dve po sebe idúce čísla. To znamená, že zelené guľky sú v uvažovanom rade umiestnené tak, že medzi \(43\) bielymi guľkami žiadne dve zelené nie sú vedľa seba. Uložme \(43\) bielych guliek do radu a skúmajme počet miest, na ktorých môžu byť umiestnené zelené guľky tak, aby žiadne dve zelené neboli vedľa seba. Jedno miesto môže byť na začiatku radu, jedno na konci radu a \(42\) miest medzi bielymi guľkami - spolu \(44\) miest. Na tých \(44\) miest môžeme \(6\) zelených guliek umiestniť \({44 \choose 6}\) spôsobmi. Teda javu \(\overline{\!A}\) zodpovedá \({44 \choose 6}\) priaznivých výsledkov. Teda \[P(\overline{\!A})=\frac{\displaystyle{{44 \choose 6}} }{\displaystyle{{49 \choose 6}}}=\frac{7\,059\,052}{13\,983\,816}\approx 0{,}5048\quad\Longrightarrow\quad P(A)=1-0{,}5048=0{,}4952.\] b) Nech \(B\) je jav, ktorý spočíva v tom, že budú vylosované práve dve po sebe idúce čísla. Opäť uvažujme \(43\) bielych guliek a \(6\) zelených. Vzhľadom na to, že chceme, aby bola vylosovaná práve jedna dvojica po sebe idúcich čísel, tak "spojíme" dve zelené guľky do jednej trebárs červenej guľky (takto budeme mať jednu červenú guľku a štyri zelené guľky).
Teraz stačí zistiť, koľkými spôsobmi môžeme \(5\) farebných guliek (červenú alebo zelené) umiestniť k bielym guľkám tak, aby ľubovoľné dve farebné neboli vedľa seba. Je zrejmé, že tak ako v časti a) máme k dispozícii \(44\) miest:
- najprv umiestnime červenú guľku - na to máme k dispozícii \(44\) miest;
- pre zvyšné \(4\) zelené nám zostalo \(43\) miest, na ktoré ich môžeme umiestniť \({43 \choose 4}\) spôsobmi.
Teda máme \(44\cdot{43 \choose 4}\) priaznivých prípadov, kedy nastáva jav \(B\). Potom \[P(B)=\frac{44\cdot \displaystyle{{43 \choose 4}} }{\displaystyle{{49 \choose 6}}}=\frac{5\,430\,040}{13\,983\,816}\approx 0{,}3883.\] c) Nech \(C\) je jav, ktorý spočíva v tom, že budú vylosované práve štyri po sebe idúce čísla.Obdobne ako v časti b) "spojíme" štyri zelené guľky do jednej červenej guľky (takto budeme mať jednu červenú guľku a dve zelené guľky). Pre červenú guľku máme takisto \(44\) možných umiestnení a pre zvyšné dve zelené guľky zostane \(43\) pozícií, na ktoré ich môžeme umiestniť \({43 \choose 2}\) spôsobmi. Takto získame \(44\cdot{43 \choose 2}\) priaznivých prípadov, kedy nastáva jav \(C\). Teda \[P(C)=\frac{44\cdot \displaystyle{{43 \choose 2}} }{\displaystyle{{49 \choose 6}}}=\frac{39\,732}{13\,983\,816}\approx 0{,}002\,841.\] d) Nech \(D\) je jav, ktorý spočíva v tom, že budú vylosované dve trojice po sebe idúcich čísel. Teraz spojíme každú zodpovedajúcu trojicu zelených guliek do jednej červenej guľky - týmto dostaneme dve červené guľky. Je evidentné, že tieto červené guľky môžeme umiestniť na \(44\) miest, a to \({44 \choose 2}\) rôznymi spôsobmi, čo je vlastne počet priaznivých prípadov, kedy nastáva jav \(D\). Potom \[P(D)=\frac{\displaystyle{{44 \choose 2}} }{\displaystyle{{49 \choose 6}}}=\frac{946}{13\,983\,816}\approx 0{,}000\,067\,65.\]
a) Nech \(A\) je jav, ktorý spočíva v tom, že budú vylosované dve po sebe idúce čísla. Zrejme k nemu opačný jav \(\overline{\!A}\) znamená, že medzi \(6\) vylosovanými číslami nebudú dve po sebe idúce čísla. To znamená, že zelené guľky sú v uvažovanom rade umiestnené tak, že medzi \(43\) bielymi guľkami žiadne dve zelené nie sú vedľa seba. Uložme \(43\) bielych guliek do radu a skúmajme počet miest, na ktorých môžu byť umiestnené zelené guľky tak, aby žiadne dve zelené neboli vedľa seba. Jedno miesto môže byť na začiatku radu, jedno na konci radu a \(42\) miest medzi bielymi guľkami - spolu \(44\) miest. Na tých \(44\) miest môžeme \(6\) zelených guliek umiestniť \({44 \choose 6}\) spôsobmi. Teda javu \(\overline{\!A}\) zodpovedá \({44 \choose 6}\) priaznivých výsledkov. Teda \[P(\overline{\!A})=\frac{\displaystyle{{44 \choose 6}} }{\displaystyle{{49 \choose 6}}}=\frac{7\,059\,052}{13\,983\,816}\approx 0{,}5048\quad\Longrightarrow\quad P(A)=1-0{,}5048=0{,}4952.\] b) Nech \(B\) je jav, ktorý spočíva v tom, že budú vylosované práve dve po sebe idúce čísla. Opäť uvažujme \(43\) bielych guliek a \(6\) zelených. Vzhľadom na to, že chceme, aby bola vylosovaná práve jedna dvojica po sebe idúcich čísel, tak "spojíme" dve zelené guľky do jednej trebárs červenej guľky (takto budeme mať jednu červenú guľku a štyri zelené guľky).
Teraz stačí zistiť, koľkými spôsobmi môžeme \(5\) farebných guliek (červenú alebo zelené) umiestniť k bielym guľkám tak, aby ľubovoľné dve farebné neboli vedľa seba. Je zrejmé, že tak ako v časti a) máme k dispozícii \(44\) miest:
- najprv umiestnime červenú guľku - na to máme k dispozícii \(44\) miest;
- pre zvyšné \(4\) zelené nám zostalo \(43\) miest, na ktoré ich môžeme umiestniť \({43 \choose 4}\) spôsobmi.
Teda máme \(44\cdot{43 \choose 4}\) priaznivých prípadov, kedy nastáva jav \(B\). Potom \[P(B)=\frac{44\cdot \displaystyle{{43 \choose 4}} }{\displaystyle{{49 \choose 6}}}=\frac{5\,430\,040}{13\,983\,816}\approx 0{,}3883.\] c) Nech \(C\) je jav, ktorý spočíva v tom, že budú vylosované práve štyri po sebe idúce čísla.Obdobne ako v časti b) "spojíme" štyri zelené guľky do jednej červenej guľky (takto budeme mať jednu červenú guľku a dve zelené guľky). Pre červenú guľku máme takisto \(44\) možných umiestnení a pre zvyšné dve zelené guľky zostane \(43\) pozícií, na ktoré ich môžeme umiestniť \({43 \choose 2}\) spôsobmi. Takto získame \(44\cdot{43 \choose 2}\) priaznivých prípadov, kedy nastáva jav \(C\). Teda \[P(C)=\frac{44\cdot \displaystyle{{43 \choose 2}} }{\displaystyle{{49 \choose 6}}}=\frac{39\,732}{13\,983\,816}\approx 0{,}002\,841.\] d) Nech \(D\) je jav, ktorý spočíva v tom, že budú vylosované dve trojice po sebe idúcich čísel. Teraz spojíme každú zodpovedajúcu trojicu zelených guliek do jednej červenej guľky - týmto dostaneme dve červené guľky. Je evidentné, že tieto červené guľky môžeme umiestniť na \(44\) miest, a to \({44 \choose 2}\) rôznymi spôsobmi, čo je vlastne počet priaznivých prípadov, kedy nastáva jav \(D\). Potom \[P(D)=\frac{\displaystyle{{44 \choose 2}} }{\displaystyle{{49 \choose 6}}}=\frac{946}{13\,983\,816}\approx 0{,}000\,067\,65.\]
Príklad:
V urne je \(190\) guliek, z ktorých každá je očíslovaná práve jedným z čísel
\(1,2,\dots , 190\). Náhodne z nej vytiahneme jednu guľku. Určme pravdepodobnosť
toho, že vytiahnutá guľka je označená číslom, ktoré je deliteľné
a) tromi;
b) štyrmi alebo šiestimi;
c) štyrmi alebo šiestimi alebo deviatimi;
a) tromi;
b) štyrmi alebo šiestimi;
c) štyrmi alebo šiestimi alebo deviatimi;
Riešenie:
Je zrejmé, že počet všetkých možných výsledkov daného pokusu je vo všetkých troch úlohách \(n=190\). Nech \(A_k\) je jav, ktorý spočíva vo vytiahnutí guľky označenej číslom, ktoré je deliteľné číslom \(k\).
a) Je potrebné určiť \(P(A_3)\). Ľahko zistíme, že z čísel \(1,2,\dots , 190\) je deliteľných číslom \(3\) práve \(63=m\) (počet priaznivých prípadov). Preto \[P(A_3)=\frac{m}{n}=\frac{63}{190}.\] b) Tentoraz nás zaujíma \(P(A_4\cup A_6)\). Je známe, že pre pravdepodobnosť zjednotenia dvoch javov platí \begin{equation}\label{a} P(A_4\cup A_6)=P(A_4)+P(A_6)-P(A_4\cap A_6). \end{equation} Obdobným spôsobom ako v časti a) ľahko zistíme, že \[P(A_4)=\frac{47}{190} \qquad \mbox{a} \qquad P(A_6)=\frac{31}{190}.\] Jav \(A_4\cap A_6\) spočíva v tom, že číslo na vytiahnutej guľke je deliteľné súčasne číslom \(4\) a aj číslom \(6\). Je evidentné, že tento jav nastane práve vtedy, keď to číslo je deliteľné najmenším spoločným násobkom čísel \(4\) a \(6\), teda číslom \(12\). Preto \(A_4\cap A_6=A_{12}\). Keďže \(P(A_{12})=\frac{15}{190}\), tak na základe (\ref{a}) dostaneme \[P(A_4\cup A_6)=\frac{47}{190}+\frac{31}{190}-\frac{15}{190}=\frac{63}{190}.\] c) Máme určiť \(P(A_4\cup A_6\cup A_9)\). Pre pravdepodobnosť zjednotenia troch javov platí \begin{equation}\label{b} P(A_4\cup A_6\cup A_9)=P(A_4)+P(A_6)+P(A_9)-P(A_4\cap A_6)-P(A_4\cap A_9)-P(A_6\cap A_9)+P(A_4\cap A_6\cap A_9). \end{equation} Je zrejmé, že \(P(A_4)=\frac{47}{190}\), \(P(A_6)=\frac{31}{190}\), \(P(A_9)=\frac{21}{190}\), Využijúc najmenšie spoločné násobky dostaneme, že pre pravdepodobnosti prienikov javov v (\ref{b}) platí (overte!):
\(A_4\cap A_6=A_{12}\) a \(P(A_4\cap A_6)=P(A_{12})=\frac{15}{190}\) (pozri časť b))
\(A_4\cap A_9=A_{36}\) a \(P(A_4\cap A_9)=P(A_{36})=\frac{5}{190}\)
\(A_6\cap A_9=A_{18}\) a \(P(A_6\cap A_9)=P(A_{18})=\frac{10}{190}\)
a nakoniec
\(A_4\cap A_6\cap A_9=A_{36}\) a \(P(A_4\cap A_6\cap A_9)=P(A_{36})=\frac{5}{190}\).
Napokon podľa (\ref{b}) dostaneme \[P(A_4\cup A_6\cup A_9)=\frac{47}{190}+\frac{31}{190}+\frac{21}{190}-\frac{15}{190}-\frac{5}{190}-\frac{10}{190}+\frac{5}{190}=\frac{74}{190}. \]
Je zrejmé, že počet všetkých možných výsledkov daného pokusu je vo všetkých troch úlohách \(n=190\). Nech \(A_k\) je jav, ktorý spočíva vo vytiahnutí guľky označenej číslom, ktoré je deliteľné číslom \(k\).
a) Je potrebné určiť \(P(A_3)\). Ľahko zistíme, že z čísel \(1,2,\dots , 190\) je deliteľných číslom \(3\) práve \(63=m\) (počet priaznivých prípadov). Preto \[P(A_3)=\frac{m}{n}=\frac{63}{190}.\] b) Tentoraz nás zaujíma \(P(A_4\cup A_6)\). Je známe, že pre pravdepodobnosť zjednotenia dvoch javov platí \begin{equation}\label{a} P(A_4\cup A_6)=P(A_4)+P(A_6)-P(A_4\cap A_6). \end{equation} Obdobným spôsobom ako v časti a) ľahko zistíme, že \[P(A_4)=\frac{47}{190} \qquad \mbox{a} \qquad P(A_6)=\frac{31}{190}.\] Jav \(A_4\cap A_6\) spočíva v tom, že číslo na vytiahnutej guľke je deliteľné súčasne číslom \(4\) a aj číslom \(6\). Je evidentné, že tento jav nastane práve vtedy, keď to číslo je deliteľné najmenším spoločným násobkom čísel \(4\) a \(6\), teda číslom \(12\). Preto \(A_4\cap A_6=A_{12}\). Keďže \(P(A_{12})=\frac{15}{190}\), tak na základe (\ref{a}) dostaneme \[P(A_4\cup A_6)=\frac{47}{190}+\frac{31}{190}-\frac{15}{190}=\frac{63}{190}.\] c) Máme určiť \(P(A_4\cup A_6\cup A_9)\). Pre pravdepodobnosť zjednotenia troch javov platí \begin{equation}\label{b} P(A_4\cup A_6\cup A_9)=P(A_4)+P(A_6)+P(A_9)-P(A_4\cap A_6)-P(A_4\cap A_9)-P(A_6\cap A_9)+P(A_4\cap A_6\cap A_9). \end{equation} Je zrejmé, že \(P(A_4)=\frac{47}{190}\), \(P(A_6)=\frac{31}{190}\), \(P(A_9)=\frac{21}{190}\), Využijúc najmenšie spoločné násobky dostaneme, že pre pravdepodobnosti prienikov javov v (\ref{b}) platí (overte!):
\(A_4\cap A_6=A_{12}\) a \(P(A_4\cap A_6)=P(A_{12})=\frac{15}{190}\) (pozri časť b))
\(A_4\cap A_9=A_{36}\) a \(P(A_4\cap A_9)=P(A_{36})=\frac{5}{190}\)
\(A_6\cap A_9=A_{18}\) a \(P(A_6\cap A_9)=P(A_{18})=\frac{10}{190}\)
a nakoniec
\(A_4\cap A_6\cap A_9=A_{36}\) a \(P(A_4\cap A_6\cap A_9)=P(A_{36})=\frac{5}{190}\).
Napokon podľa (\ref{b}) dostaneme \[P(A_4\cup A_6\cup A_9)=\frac{47}{190}+\frac{31}{190}+\frac{21}{190}-\frac{15}{190}-\frac{5}{190}-\frac{10}{190}+\frac{5}{190}=\frac{74}{190}. \]
-
Výber bez návratu:
v krabici je spolu \(18\) guliek. Keďže guľky vyberáme bez návratu, tak \(9\) guliek môžeme vybrať \(r=\displaystyle{{18 \choose 9}}\) rôznymi spôsobmi, pričom požadovaná konštelácia farieb sa dá dosiahnuť \(m=\displaystyle{{5 \choose 2}{6 \choose 3}{7 \choose 4}}\) spôsobmi. Preto hľadaná pravdepodobnosť je \[P=\frac{m}{r}=\frac{\displaystyle{{5 \choose 2}{6 \choose 3}{7 \choose 4}}}{\displaystyle{{18 \choose 9}}}=\frac{10\cdot 20\cdot 35}{48620}=0{,}1440.\] Tento výsledok sme mohli dostať aj na základe (\ref{pkombsa}), kde \(s=3\), \(K_1=5\), \(K_2=6\), \(K_3=7\), \(N=18\), \(k_1=2\), \(k_2=3\), \(k_3=4\) a \(n=9\). -
Výber s návratom:
podľa (\ref{pkombsan}) je \[P=\frac{9!}{2!\cdot 3!\cdot 4!}\!\cdot\left(\frac{5}{18}\right)^{\!\!2}\!\cdot\left(\frac{6}{18}\right)^{\!\!3}\!\!\cdot\left(\frac{7}{18}\right)^{\!\!4}\approx0{,}0824.\]
Príklad:
V krabici je \(5\) bielych, \(6\) modrých a \(7\) červených guliek. Náhodne z nej
(bez vrátenia do krabice) vyberieme \(9\) guliek. Aká je pravdepodobnosť toho,
že sme vybrali \(2\) biele, \(3\) modré a \(4\) červené guľky?
Riešenie:
Z textu úlohy vyplýva, že pri výbere guliek nezáleží na poradí. Je potrebné rozlišovať
dva prípady: či guľky vyberáme z urny bez návratu alebo s návratom.
Príklad:
V urne je \(b\) bielych guliek a \(c\) červených guliek (\(b\ge 1\), \(c\ge 1\)).
Náhodne z nej postupne vyberáme po jednej guľke
a) s návratom vytiahnutej guľky do urny;
b) bez návratu.
Určme pravdepodobnosť toho, že \(j\)-tá vytiahnutá guľka bude biela.
a) s návratom vytiahnutej guľky do urny;
b) bez návratu.
Určme pravdepodobnosť toho, že \(j\)-tá vytiahnutá guľka bude biela.
Riešenie:
Nech \(B_j\) je jav, ktorý spočíva v tom, že \(j\)-tá vytiahnutá guľka bude biela.
V oboch prípadoch a) a b) je pred vytiahnutím prvej guľky konštelácia guliek v urne rovnaká:
-
- jav \(B_1\) nastane práve v \(b\) možnostiach - toľko je bielych guliek v urne.
Preto \[P(B_1)=\frac{b}{b+c}.\] Konštelácia guliek v urne pred vytiahnutím druhej guľky nebude v prípadoch a) a b) rovnaká. Preto sa musíme prípadmi zaoberať osobitne.
a) Keďže prvú vytiahnutú guľku vrátime späť do urny, tak zloženie guliek v urne pred vytiahnutím druhej guľky bude rovnaké ako pred vytiahnutím prvej guľky. To znamená, že pravdepodobnosť toho, že druhá vytiahnutá guľka bude biela je rovnaká ako bola pre prvú guľku, t. j. \[P(B_2)=\frac{b}{b+c}.\] Ľahko nahliadneme, že pravdepodobnosť toho, že \(j\)-tá vytiahnutá guľka bude biela je \begin{equation}\label{a1} P(B_j)=\frac{b}{b+c}, \qquad j=1,2,3,\dots . \end{equation} b) Ak prvú vytiahnutú guľku nevrátime späť do urny, tak konštelácia guliek v urne pred vytiahnutím druhej guľky bude iná: jednak tam bude už len \(b+c-1\) guliek a čo je horšie, nevieme koľko guliek bude bielych, resp. čiernych. Úlohu by sme mohli vyriešiť pomocou podmienenej pravdepodobnosti, ale to je náplň budúceho cvičenia (navyše tento prístup by bol komplikovanejší).
Očíslujme biele guľky číslami od \(1\) do \(b\) a červené guľky číslami od \(b+1\) do \(b+c\). Pretože postupne vyberáme po jednej guľke bez návratu guľky do urny, tak môžeme vytiahnuť maximálne \(b+c\) guliek. Je zrejmé, že existuje práve \((b+c)!\) možností výberu očíslovaných guliek (ide o permutácie množiny \(\{1,2, \dots ,b+c\}\)). V koľkých prípadoch bude \(j\)-tá vytiahnutá guľka biela? Tu si stačí uvedomiť, že
- na to, aby \(j\)-tá guľka bola biela máme \(b\) možností;
- pre zvyšné \(b+c-1\) miesta máme \((b+c-1)!\) možností.
Teda existuje práve \(b\cdot (b+c-1)!\) prípadov, keď na \(j\)-tom mieste bude biela guľka. A teraz pomocou klasickej definície pravdepodobnosti ľahko určíme \(P(B_j)\): \begin{equation}\label{b1} P(B_j)=\frac{b\cdot (b+c-1)!}{(b+c)!}=\frac{b}{b+c}, \qquad j=1,2,3,\dots , b+c. \end{equation} Ak porovnáme výsledky (\ref{a1}) a (\ref{b1}), tak zistíme, že pre \(j\in\{1,2,3,\dots , b+c\}\) sú pravdepodobnosti toho, že \(j\)-tá vytiahnutá guľka bude biela, prekvapujúco v oboch prípadoch rovnaké.
-
- jav \(B_1\) nastane práve v \(b\) možnostiach - toľko je bielych guliek v urne.
Preto \[P(B_1)=\frac{b}{b+c}.\] Konštelácia guliek v urne pred vytiahnutím druhej guľky nebude v prípadoch a) a b) rovnaká. Preto sa musíme prípadmi zaoberať osobitne.
a) Keďže prvú vytiahnutú guľku vrátime späť do urny, tak zloženie guliek v urne pred vytiahnutím druhej guľky bude rovnaké ako pred vytiahnutím prvej guľky. To znamená, že pravdepodobnosť toho, že druhá vytiahnutá guľka bude biela je rovnaká ako bola pre prvú guľku, t. j. \[P(B_2)=\frac{b}{b+c}.\] Ľahko nahliadneme, že pravdepodobnosť toho, že \(j\)-tá vytiahnutá guľka bude biela je \begin{equation}\label{a1} P(B_j)=\frac{b}{b+c}, \qquad j=1,2,3,\dots . \end{equation} b) Ak prvú vytiahnutú guľku nevrátime späť do urny, tak konštelácia guliek v urne pred vytiahnutím druhej guľky bude iná: jednak tam bude už len \(b+c-1\) guliek a čo je horšie, nevieme koľko guliek bude bielych, resp. čiernych. Úlohu by sme mohli vyriešiť pomocou podmienenej pravdepodobnosti, ale to je náplň budúceho cvičenia (navyše tento prístup by bol komplikovanejší).
Očíslujme biele guľky číslami od \(1\) do \(b\) a červené guľky číslami od \(b+1\) do \(b+c\). Pretože postupne vyberáme po jednej guľke bez návratu guľky do urny, tak môžeme vytiahnuť maximálne \(b+c\) guliek. Je zrejmé, že existuje práve \((b+c)!\) možností výberu očíslovaných guliek (ide o permutácie množiny \(\{1,2, \dots ,b+c\}\)). V koľkých prípadoch bude \(j\)-tá vytiahnutá guľka biela? Tu si stačí uvedomiť, že
- na to, aby \(j\)-tá guľka bola biela máme \(b\) možností;
- pre zvyšné \(b+c-1\) miesta máme \((b+c-1)!\) možností.
Teda existuje práve \(b\cdot (b+c-1)!\) prípadov, keď na \(j\)-tom mieste bude biela guľka. A teraz pomocou klasickej definície pravdepodobnosti ľahko určíme \(P(B_j)\): \begin{equation}\label{b1} P(B_j)=\frac{b\cdot (b+c-1)!}{(b+c)!}=\frac{b}{b+c}, \qquad j=1,2,3,\dots , b+c. \end{equation} Ak porovnáme výsledky (\ref{a1}) a (\ref{b1}), tak zistíme, že pre \(j\in\{1,2,3,\dots , b+c\}\) sú pravdepodobnosti toho, že \(j\)-tá vytiahnutá guľka bude biela, prekvapujúco v oboch prípadoch rovnaké.
Príklad:
Určte pravdepodobnosť toho, že náhodne zvolené kladné trojciferné číslo je deliteľné
a) ôsmimi;
b) štyrmi alebo šiestimi;
c) štyrmi alebo ôsmimi alebo dvanástimi.
a) ôsmimi;
b) štyrmi alebo šiestimi;
c) štyrmi alebo ôsmimi alebo dvanástimi.
Príklad:
V číselnej lotérii sa losuje šesť čísel zo \(49\) čísel \(\{1,2, 3,\ldots , 49\}\).
Určme pravdepodobnosť toho, že budú vylosované
a) šesť po sebe idúce čísla;
b) práve tri po sebe idúce čísla;
c) práve päť po sebe idúcich čísel (napr. \(17,\) \(18,\) \(19,\) a \(20\));
d) tri dvojice po sebe idúcich čísel;
e) jedna dvojica a jedna štvorica po sebe idúcich čísel.
a) šesť po sebe idúce čísla;
b) práve tri po sebe idúce čísla;
c) práve päť po sebe idúcich čísel (napr. \(17,\) \(18,\) \(19,\) a \(20\));
d) tri dvojice po sebe idúcich čísel;
e) jedna dvojica a jedna štvorica po sebe idúcich čísel.
Príklad:
Výrobca ponúka kódovacie zámky pre zabezpečenie bytu. Kód zámku tvorí postupnosť
\(n\) číslic z množiny \(\{0,1,2,\dots ,9\}\) (napríklad pre \(n=7\) kódom môže
byť postupnosť \(1108841\)). Ak niekto trikrát po sebe zle vyťuká kód, tak sa spustí alarm.
a) Určte pravdepodobnosť toho, že sa zlodejovi (ten samozrejme nepozná kód zámku, ale pozná typ zámku, t. j. vie koľkomiestny je kód) podarí bez spustenia alarmu otvoriť byt.
b) Minimálne z koľkých číslic musí pozostávať kód zámku, aby pravdepodobnosť toho, že sa zlodejovi podarí otvoriť byt, bola menšia ako \(0{,}000\,25\)?
a) Určte pravdepodobnosť toho, že sa zlodejovi (ten samozrejme nepozná kód zámku, ale pozná typ zámku, t. j. vie koľkomiestny je kód) podarí bez spustenia alarmu otvoriť byt.
b) Minimálne z koľkých číslic musí pozostávať kód zámku, aby pravdepodobnosť toho, že sa zlodejovi podarí otvoriť byt, bola menšia ako \(0{,}000\,25\)?
Poznámka:
Túto úlohu môžeme vyriešiť viacerými spôsobmi. Efektívne je využiť závery predchádzajúceho
riešeného príkladu.
V tejto úlohe máme \(10^n\) možností pre \(n\)-miestny kód. Pre zlodeja, ktorý chce otvoriť byt, je to v podstate ťahanie guľky z urny bez vrátenia, v ktorej je \(10^n\) guliek, z ktorých je \(10^n-1\) červených a jedna biela (kód bytu). Toľkokrát (ale maximálne trikrát) náhodne vyberá po jednej guľke bez vrátenia z tejto urny, kým nevytiahne bielu.
V tejto úlohe máme \(10^n\) možností pre \(n\)-miestny kód. Pre zlodeja, ktorý chce otvoriť byt, je to v podstate ťahanie guľky z urny bez vrátenia, v ktorej je \(10^n\) guliek, z ktorých je \(10^n-1\) červených a jedna biela (kód bytu). Toľkokrát (ale maximálne trikrát) náhodne vyberá po jednej guľke bez vrátenia z tejto urny, kým nevytiahne bielu.
Príklad:
V urne je osem gulí očíslovaných od \(1\) do \(8\). Aká je pravdepodobnosť toho,
že pri prvých piatich náhodne vytiahnutých guliach bude poradové číslo ťahanej gule
vždy totožné s číslom na vytiahnutej guli?
08. Podmienená pravdepodobnosť. Nezávislé javy
Riešené úlohy:
Príklad:
Isté zariadenie je v bezporuchovej prevádzke aspoň dva roky s pravdepodobnosťou
\(0{,}8\) a aspoň tri roky s pravdepodobnosťou \(0{,}5\). Je známe, že toto
zariadenie bolo dva roky v bezporuchovej prevádzke. Určme pravdepodobnosť toho,
že bude v bezporuchovej prevádzke ešte aspoň rok.
Riešenie:
Nech \(B\) je jav, ktorý spočíva v tom, že zariadenie je v bezporuchovej prevádzke
aspoň dva roky a nech \(A\) je jav, že zariadenie je v bezporuchovej prevádzke
aspoň tri roky. V úlohe žiadame určiť pravdepodobnosť toho, že nastal jav \(A\)
za predpokladu, že nastal jav \(B\), t. j. \(P(A/B)\). Všimnime si, že \(A\subset B\),
a teda \(A\cap B=A\), čo znamená, že \(P(A\cap B)=P(A)\). Z týchto poznatkov pre
požadovanú podmienenú pravdepodobnosť dostaneme
\[P(A/B)=\frac{P(A\cap B)}{P(B)}=\frac{P(A)}{P(B)}=\frac{0{,}5}{0{,}8}=0{,}625.\]
Príklad:
\(\def\a{&}\)
Máme tri urny \({\cal U}_1\), \({\cal U}_2\) a \({\cal U}_3\). Počet bielych a
červených guliek v jednotlivých urnách je uvedený v nasledujúcej tabuľke:
\[
\begin{array}{|c|c|c|c|}
\hline
\a {\cal U}_1 \a {\cal U}_2 \a {\cal U}_3 \\ \hline
\mbox{počet bielych guliek}\a 6 \a 5 \a 3 \\ \hline
\mbox{počet červených guliek} \a 4 \a 5 \a 5 \\ \hline
\end{array}
\]
a) Z urny \({\cal U}_1\) náhodne bez vrátenia vytiahneme štyri guľky. Aká je
pravdepodobnosť toho, že všetky vytiahnuté guľky nebudú mať rovnakú farbu?
b) S rovnakou pravdepodobnosťou siahneme do jednej z troch urien a náhodne z nej bez vrátenia vytiahneme štyri guľky. Aká je pravdepodobnosť toho, že všetky vytiahnuté guľky nebudú mať rovnakú farbu?
c) Náhodne sme siahli do jednej z urien a náhodne bez vrátenia sme vytiahli štyri guľky. Zistili sme, že vytiahnuté guľky nemajú rovnakú farbu. Aká je pravdepodobnosť toho, že sme siahli do druhej urny?
b) S rovnakou pravdepodobnosťou siahneme do jednej z troch urien a náhodne z nej bez vrátenia vytiahneme štyri guľky. Aká je pravdepodobnosť toho, že všetky vytiahnuté guľky nebudú mať rovnakú farbu?
c) Náhodne sme siahli do jednej z urien a náhodne bez vrátenia sme vytiahli štyri guľky. Zistili sme, že vytiahnuté guľky nemajú rovnakú farbu. Aká je pravdepodobnosť toho, že sme siahli do druhej urny?
Riešenie:
Nech \(B_j\), resp. \(C_j\), \(j\in\{0,1,2,3,4\}\), je jav, ktorý spočíva v tom,
že medzi štyrmi vytiahnutými guľkami je \(j\) bielych, resp. \(j\) červených, guliek
a) Tu nám postačia poznatky z minulého cvičenia. Nech \(N\) je jav, ktorý znamená, že všetky štyri vytiahnuté guľky nebudú mať rovnakú farbu. Zrejme jav \(N\) môžeme rozložiť na zjednotenie týchto troch disjunktných javov:
- vytiahli sme jednu bielu guľku a tri červené, t. j. nastal jav \(B_1\cap C_3\);
- vytiahli sme dve biele guľky a dve červené, t. j. nastal jav \(B_2\cap C_2\);
- vytiahli sme tri biele guľky a jednu červenú, t. j. nastal jav \(B_3\cap C_1\).
Potom platí: \[P(N)= P(B_1\cap C_3)+P(B_2\cap C_2)+P(B_3\cap C_1).\] Skúste si vyčísliť tieto pravdepodobnosti. My na to pôjdeme cez opačný jav: nech \(R=\overline{N}\), t. j. jav \(R\) znamená, že všetky štyri vytiahnuté guľky majú rovnakú farbu. Jav \(R\) môžeme rozložiť na zjednotenie týchto dvoch disjunktných javov:
- vytiahli sme len biele guľky, t. j. nastal jav \(B_4\cap C_0\);
- vytiahli sme len červené guľky, t. j. nastal jav \(B_0\cap C_4\).
Preto \begin{equation}\label{rr} P(R)= P(B_4\cap C_0)+P(B_0\cap C_4). \end{equation} Z minulého cvičenia je známe, že \[ P(B_4\cap C_0)=\frac{{6 \choose 4}{4 \choose 0}}{{10 \choose 4}}=\frac{1}{14}\qquad \mbox{a}\qquad P(B_0\cap C_4)=\frac{{6 \choose 0}{4 \choose 4}}{{10 \choose 4}}=\frac{1}{210}.\] Odtiaľ na základe (\ref{rr}) dostaneme \[P(R)=\frac{1}{14}+\frac{1}{210}=\frac{8}{105}.\] Teda \begin{equation}\label{rrr} P(N)=1-P(R)=\frac{97}{105}. \end{equation}
b) Teraz pravdepodobnosť toho, že všetky vytiahnuté guľky nebudú mať rovnakú farbu závisí od toho, z ktorej urny sme guľky vybrali. Nech \(H_i\) je jav (hypotéza), že sme štyri guľky vybrali z \(i\)-tej urny \({\cal U}_i\), \(i\in\{1,2,3\}\). Potom z vety o úplnej pravdepodobnosti dostaneme (pozri (\ref{vup})) \begin{equation}\label{rrrr} P(N)=P(H_1)\cdot P(N/H_1)+P(H_2)\cdot P(N/H_2)+P(H_3)\cdot P(N/H_3). \end{equation} Keďže sme náhodne siahli do jednej z troch urien, tak \[P(H_1)=P(H_2)=P(H_3)=\frac{1}{3}.\] \(P(N/H_1)\) je pravdepodobnosť toho, že sme vytiahli guľky rovnakej farby za predpokladu, že sme guľky vyberali z prvej urny - podľa (\ref{rrr}) je \[P(N/H_1)=\frac{97}{105}.\] Teraz, obdobným spôsobom ako v časti a) určíme \(P(N/H_2)\). Ľahko vidno, že tentoraz \[ P(B_4\cap C_0)=\frac{{5 \choose 4}{5 \choose 1}}{{10 \choose 4}}=\frac{5}{42}\qquad \mbox{a}\qquad P(B_0\cap C_4)=\frac{{5 \choose 1}{5 \choose 4}}{{10 \choose 4}}=\frac{5}{42},\] a preto \[P(R/H_2)=\frac{5}{42}+\frac{5}{42}=\frac{5}{21}.\] Teda \begin{equation}\label{oo} P(N/H_2)=1-P(R/H_2)=\frac{16}{21}. \end{equation} Ak siahneme do tretej urny (v nej je osem guliek) a chceme z nej vybrať guľky jednej farby, tak to môžu byť len červené guľky (biele sú tamlen tri). Takto \[P(R/H_3)=\frac{{3 \choose 0}{5 \choose 4}}{{8 \choose 4}}=\frac{1}{14}.\] Potom \[P(N/H_3)=1-P(R/H_3)=\frac{13}{14}\] a na základe (\ref{rrrr}) dostaneme \begin{equation}\label{rb} P(N)=\frac{1}{3}\cdot \frac{97}{105}+\frac{1}{3}\cdot \frac{16}{21}+\frac{1}{3}\cdot \frac{13}{14}=\frac{183}{210}. \end{equation} Je potrebné uvedomiť si, že jav \(N\) v (\ref{rrr}) a v (\ref{rb}) je výsledkom dvoch pokusov za odlišného systému podmienok.
c) Nech \(N\) je jav z časti b), ktorý spočíva v tom, že sme po náhodnom výbere jednej z troch urien náhodne z nej bez vrátenia vytiahli štyri guľky nerovnakej farby. V úlohe máme určiť pravdepodobnosť toho, že sme za predpokladu nastatia javu \(N\) vytiahli guľky z druhej urny (t. j. že nastala hypotéza \(H_2\)). V krátkosti, pýtame sa na \(P(H_2/N)\). Tu nám pomôže Bayesov vzorec: podľa (\ref{bv}) je pre \(k=2\) a \(A=N\) \[ P(H_2/N)=\frac{P(H_2)\cdot P(N/H_2)}{P(N)}.\] Na základe (\ref{oo}) a (\ref{rb}) dostaneme \[P(H_2/N)=\frac{\frac{1}{3}\cdot \frac{16}{21}}{\frac{183}{210}}=\frac{160}{549}.\]
a) Tu nám postačia poznatky z minulého cvičenia. Nech \(N\) je jav, ktorý znamená, že všetky štyri vytiahnuté guľky nebudú mať rovnakú farbu. Zrejme jav \(N\) môžeme rozložiť na zjednotenie týchto troch disjunktných javov:
- vytiahli sme jednu bielu guľku a tri červené, t. j. nastal jav \(B_1\cap C_3\);
- vytiahli sme dve biele guľky a dve červené, t. j. nastal jav \(B_2\cap C_2\);
- vytiahli sme tri biele guľky a jednu červenú, t. j. nastal jav \(B_3\cap C_1\).
Potom platí: \[P(N)= P(B_1\cap C_3)+P(B_2\cap C_2)+P(B_3\cap C_1).\] Skúste si vyčísliť tieto pravdepodobnosti. My na to pôjdeme cez opačný jav: nech \(R=\overline{N}\), t. j. jav \(R\) znamená, že všetky štyri vytiahnuté guľky majú rovnakú farbu. Jav \(R\) môžeme rozložiť na zjednotenie týchto dvoch disjunktných javov:
- vytiahli sme len biele guľky, t. j. nastal jav \(B_4\cap C_0\);
- vytiahli sme len červené guľky, t. j. nastal jav \(B_0\cap C_4\).
Preto \begin{equation}\label{rr} P(R)= P(B_4\cap C_0)+P(B_0\cap C_4). \end{equation} Z minulého cvičenia je známe, že \[ P(B_4\cap C_0)=\frac{{6 \choose 4}{4 \choose 0}}{{10 \choose 4}}=\frac{1}{14}\qquad \mbox{a}\qquad P(B_0\cap C_4)=\frac{{6 \choose 0}{4 \choose 4}}{{10 \choose 4}}=\frac{1}{210}.\] Odtiaľ na základe (\ref{rr}) dostaneme \[P(R)=\frac{1}{14}+\frac{1}{210}=\frac{8}{105}.\] Teda \begin{equation}\label{rrr} P(N)=1-P(R)=\frac{97}{105}. \end{equation}
b) Teraz pravdepodobnosť toho, že všetky vytiahnuté guľky nebudú mať rovnakú farbu závisí od toho, z ktorej urny sme guľky vybrali. Nech \(H_i\) je jav (hypotéza), že sme štyri guľky vybrali z \(i\)-tej urny \({\cal U}_i\), \(i\in\{1,2,3\}\). Potom z vety o úplnej pravdepodobnosti dostaneme (pozri (\ref{vup})) \begin{equation}\label{rrrr} P(N)=P(H_1)\cdot P(N/H_1)+P(H_2)\cdot P(N/H_2)+P(H_3)\cdot P(N/H_3). \end{equation} Keďže sme náhodne siahli do jednej z troch urien, tak \[P(H_1)=P(H_2)=P(H_3)=\frac{1}{3}.\] \(P(N/H_1)\) je pravdepodobnosť toho, že sme vytiahli guľky rovnakej farby za predpokladu, že sme guľky vyberali z prvej urny - podľa (\ref{rrr}) je \[P(N/H_1)=\frac{97}{105}.\] Teraz, obdobným spôsobom ako v časti a) určíme \(P(N/H_2)\). Ľahko vidno, že tentoraz \[ P(B_4\cap C_0)=\frac{{5 \choose 4}{5 \choose 1}}{{10 \choose 4}}=\frac{5}{42}\qquad \mbox{a}\qquad P(B_0\cap C_4)=\frac{{5 \choose 1}{5 \choose 4}}{{10 \choose 4}}=\frac{5}{42},\] a preto \[P(R/H_2)=\frac{5}{42}+\frac{5}{42}=\frac{5}{21}.\] Teda \begin{equation}\label{oo} P(N/H_2)=1-P(R/H_2)=\frac{16}{21}. \end{equation} Ak siahneme do tretej urny (v nej je osem guliek) a chceme z nej vybrať guľky jednej farby, tak to môžu byť len červené guľky (biele sú tamlen tri). Takto \[P(R/H_3)=\frac{{3 \choose 0}{5 \choose 4}}{{8 \choose 4}}=\frac{1}{14}.\] Potom \[P(N/H_3)=1-P(R/H_3)=\frac{13}{14}\] a na základe (\ref{rrrr}) dostaneme \begin{equation}\label{rb} P(N)=\frac{1}{3}\cdot \frac{97}{105}+\frac{1}{3}\cdot \frac{16}{21}+\frac{1}{3}\cdot \frac{13}{14}=\frac{183}{210}. \end{equation} Je potrebné uvedomiť si, že jav \(N\) v (\ref{rrr}) a v (\ref{rb}) je výsledkom dvoch pokusov za odlišného systému podmienok.
c) Nech \(N\) je jav z časti b), ktorý spočíva v tom, že sme po náhodnom výbere jednej z troch urien náhodne z nej bez vrátenia vytiahli štyri guľky nerovnakej farby. V úlohe máme určiť pravdepodobnosť toho, že sme za predpokladu nastatia javu \(N\) vytiahli guľky z druhej urny (t. j. že nastala hypotéza \(H_2\)). V krátkosti, pýtame sa na \(P(H_2/N)\). Tu nám pomôže Bayesov vzorec: podľa (\ref{bv}) je pre \(k=2\) a \(A=N\) \[ P(H_2/N)=\frac{P(H_2)\cdot P(N/H_2)}{P(N)}.\] Na základe (\ref{oo}) a (\ref{rb}) dostaneme \[P(H_2/N)=\frac{\frac{1}{3}\cdot \frac{16}{21}}{\frac{183}{210}}=\frac{160}{549}.\]
Príklad:
Je známe, že v Morseovej abecede pomer priemerného počtu vyslaných bodiek
k počtu vyslaných čiarok je \(5:3\). Pri prenose sa skreslí v priemere päť percent
bodiek (t. j. vyslaná bodka je prijatá ako čiarka) a skreslenie u čiarok je sedem
percent. Určme pravdepodobnosť toho, že bola
a) vyslaná čiarka, ak bola prijatá bodka;
b) vyslaná bodka, ak bola prijatá bodka.
a) vyslaná čiarka, ak bola prijatá bodka;
b) vyslaná bodka, ak bola prijatá bodka.
Riešenie:
Nech \(H_{\scriptsize \mbox{b}}\), resp. \(H_{\scriptsize \mbox{č}}\) je jav spočívajúci
v tom, že bola vyslaná bodka, resp. čiarka. Tieto javy zrejme tvoria hypotézy a vzhľadom
na daný pomer počtov vysielaných bodiek a čiarok je \(P(H_{\scriptsize \mbox{b}})=\frac{5}{8}\)
a \(P(H_{\scriptsize \mbox{č}})=\frac{3}{8}\).
Nech \(A\) je označenie javu, že je prijatá bodka. Z formulácie príkladu vyplýva:
- pravdepodobnosť toho, že ak bola vyslaná bodka, tak bolo prijatá bodka je \(P(A/H_{\scriptsize \mbox{b}})=0{,}95\) (\(95\,\%\) vyslaných bodiek sa neskreslí)
- pravdepodobnosť toho, že ak bola vyslaná čiarka, tak bolo prijatá bodka je \(P(A/H_{\scriptsize \mbox{č}})=0{,}07\) (vyslaná čiarka sa skreslila).
Z vety o úplnej pravdepodobnosti (\ref{vup}) máme \[P(A)= P(H_{\scriptsize \mbox{b}})\cdot P(A/H_{\scriptsize \mbox{b}})+ P(H_{\scriptsize \mbox{č}})\cdot P(A/H_{\scriptsize \mbox{č}})=\] \[=\frac{5}{8}\cdot 0{,}95+\frac{3}{8}\cdot 0{,}07=0{,}62.\]
a) Žiada sa určiť pravdepodobnosť toho, že bola vyslaná čiarka, ak bola prijatá bodka, t.j. \(P(H_{\scriptsize \mbox{č}}/A)\). Podľa Bayesovho vzorca (\ref{bv}) je \[P(H_{\scriptsize \mbox{č}}/A)=\frac{P(H_{\scriptsize \mbox{č}})\cdot P(A/H_{\scriptsize \mbox{č}})}{P(A)}=\frac{\frac{3}{8}\cdot 0{,}07}{0{,}62}=0{,}0423.\]
b) Tu chceme vypočítať \(P(H_{\scriptsize \mbox{b}}/A)\). Opäť podľa (\ref{bv}) je \[P(H_{\scriptsize \mbox{b}}/A)=\frac{P(H_{\scriptsize \mbox{b}})\cdot P(A/H_{\scriptsize \mbox{b}})}{P(A)}=\frac{\frac{5}{8}\cdot 0{,}95}{0{,}62}=0{,}9577.\] Všimnime si, že v časti b) sme určovali pravdepodobnosť javu, ktorý je opačným javom k javu z časti a).
Nech \(A\) je označenie javu, že je prijatá bodka. Z formulácie príkladu vyplýva:
- pravdepodobnosť toho, že ak bola vyslaná bodka, tak bolo prijatá bodka je \(P(A/H_{\scriptsize \mbox{b}})=0{,}95\) (\(95\,\%\) vyslaných bodiek sa neskreslí)
- pravdepodobnosť toho, že ak bola vyslaná čiarka, tak bolo prijatá bodka je \(P(A/H_{\scriptsize \mbox{č}})=0{,}07\) (vyslaná čiarka sa skreslila).
Z vety o úplnej pravdepodobnosti (\ref{vup}) máme \[P(A)= P(H_{\scriptsize \mbox{b}})\cdot P(A/H_{\scriptsize \mbox{b}})+ P(H_{\scriptsize \mbox{č}})\cdot P(A/H_{\scriptsize \mbox{č}})=\] \[=\frac{5}{8}\cdot 0{,}95+\frac{3}{8}\cdot 0{,}07=0{,}62.\]
a) Žiada sa určiť pravdepodobnosť toho, že bola vyslaná čiarka, ak bola prijatá bodka, t.j. \(P(H_{\scriptsize \mbox{č}}/A)\). Podľa Bayesovho vzorca (\ref{bv}) je \[P(H_{\scriptsize \mbox{č}}/A)=\frac{P(H_{\scriptsize \mbox{č}})\cdot P(A/H_{\scriptsize \mbox{č}})}{P(A)}=\frac{\frac{3}{8}\cdot 0{,}07}{0{,}62}=0{,}0423.\]
b) Tu chceme vypočítať \(P(H_{\scriptsize \mbox{b}}/A)\). Opäť podľa (\ref{bv}) je \[P(H_{\scriptsize \mbox{b}}/A)=\frac{P(H_{\scriptsize \mbox{b}})\cdot P(A/H_{\scriptsize \mbox{b}})}{P(A)}=\frac{\frac{5}{8}\cdot 0{,}95}{0{,}62}=0{,}9577.\] Všimnime si, že v časti b) sme určovali pravdepodobnosť javu, ktorý je opačným javom k javu z časti a).
Príklad:
V krabici sú dve nové a tri už použité tenisové loptičky. K prvej hre si hráči
náhodne z nej vyberú dve loptičky a s oboma si zahrajú. Po hre ich vrátia
naspäť do krabice. K druhej hre si vyberú tri loptičky. Určme pravdepodobnosť
toho, že to budú už použité loptičky.
Riešenie:
Nech \(H_i\), \(i\in\{0,1,2\}\) je jav, ktorý spočíva v tom, že k prvej hre si
hráči vybrali \(i\) nových loptičiek. Tieto javy tvoria hypotézy, pričom
\[P(H_0)=\frac{{2 \choose 0}{3 \choose 2}}{{5 \choose 2}}=\frac{3}{10}, \quad P(H_1)=\frac{{2 \choose 1}{3 \choose 1}}{{5
\choose 2}}=\frac{6}{10}\]
\[ P(H_2)=\frac{{2 \choose 2}{3 \choose 0}}{{5 \choose 2}}=\frac{1}{10}.\]
Všimnime si konšteláciu loptičiek v krabici pred výberom loptičiek k druhej hre:
ak nastala hypotéza
-\(H_0,\) tak v krabici sú dve nové a tri už použité tenisové loptičky;
-\(H_1,\) tak v krabici je jedna nová a štyri už použité tenisové loptičky;
-\(H_2,\) tak v krabici sú už len použité tenisové loptičky.
Nech \(A\) je jav, ktorý spočíva v tom, že k druhej hre budú vytiahnuté tri už použité loptičky. Potom \[P(A/H_0)=\frac{{3 \choose 3}{2 \choose 0}}{{5 \choose 3}}=\frac{1}{10}\] \[P(A/H_1)=\frac{{4 \choose 3}{1 \choose 0}}{{5 \choose 3}}=\frac{4}{10}, \quad P(A/H_2)=1.\] Podľa vety o úplnej pravdepodobnosti (\ref{vup}) je \[P(A)=\frac{3}{10}\cdot\frac{1}{10}+\frac{6}{10}\cdot\frac{4}{10}+\frac{1}{10}\cdot 1=\frac{37}{100}.\]
-\(H_0,\) tak v krabici sú dve nové a tri už použité tenisové loptičky;
-\(H_1,\) tak v krabici je jedna nová a štyri už použité tenisové loptičky;
-\(H_2,\) tak v krabici sú už len použité tenisové loptičky.
Nech \(A\) je jav, ktorý spočíva v tom, že k druhej hre budú vytiahnuté tri už použité loptičky. Potom \[P(A/H_0)=\frac{{3 \choose 3}{2 \choose 0}}{{5 \choose 3}}=\frac{1}{10}\] \[P(A/H_1)=\frac{{4 \choose 3}{1 \choose 0}}{{5 \choose 3}}=\frac{4}{10}, \quad P(A/H_2)=1.\] Podľa vety o úplnej pravdepodobnosti (\ref{vup}) je \[P(A)=\frac{3}{10}\cdot\frac{1}{10}+\frac{6}{10}\cdot\frac{4}{10}+\frac{1}{10}\cdot 1=\frac{37}{100}.\]
- troch hodoch bežnou hracou kockou padne šestka práve dvakrát;
- šiestich hodoch bežnou hracou kockou padne šestka a) práve štyrikrát;
Príklad:
Určme pravdepodobnosť toho, že pri
b) aspoň štyrikrát;
c) najviac štyrikrát.
Riešenie:
1. Nech jav \(B_i\), \(i\in\{1,2,3\},\) znamená, že v \(i\)-tom hode padne šestka.
Zrejme tieto javy sú nezávislé a \(P(B_i)=\frac{1}{6}\) a \(P(\overline{B}_i)=\frac{5}{6}.\)
Pri troch hodoch kockou má padnúť šestka práve dvakrát a práve raz nemá padnúť:
to nastane len vtedy, keď šestka nepadne pri prvom alebo druhom alebo treťom hode.
Tento jav \(D\) môžeme zapísať takto:
\[D=(\overbrace{\overline{B}_1\cap B_2\cap B_3}^{C_1})\cup (\overbrace{B_1\cap
\overline{B}_2\cap B_3}^{C_2})\cup (\overbrace{B_1\cap B_2\cap \overline{B}_3}^{C_3}).\]
Zátvorkové javy \(C_1,C_2,C_3\) sú disjunktné, a preto
\[P(D)=P(\overline{B}_1\cap B_2\cap B_3)+P(B_1\cap \overline{B}_2\cap B_3)+P(B_1\cap B_2\cap \overline{B}_3).\]
Z nezávislosti javov \(B_1,B_2\) a \(B_3\) plynie:
\(P(\overline{B}_1\cap B_2\cap B_3)=\frac{5}{6}\cdot \frac{1}{6}\cdot \frac{1}{6}
=\frac{5}{216}\), \(P(B_1\cap \overline{B}_2\cap B_3)=\frac{1}{6}\cdot \frac{5}{6}
\cdot \frac{1}{6}=\frac{5}{216}\) a \(P(B_1\cap B_2\cap \overline{B}_3)=
\frac{1}{6}\cdot \frac{1}{6}\cdot \frac{5}{6}=\frac{5}{216}.\)
Teda
\[P(D)=\frac{5}{216}+\frac{5}{216}+\frac{5}{216}=\frac{5}{72}.\]
Poznamenávame, že túto úlohu sme mohli rýchlejšie vyriešiť pomocou Bernoulliho
vzorca (\ref{bev}): ide o trojnásobné nezávislé opakovanie pokusu, v ktorom pod
javom \(A\) rozumieme padnutie šestky pri jednom hode kockou. Teda \(n=3\),
\(p=P(A)=\frac{1}{6}\) a chceme určiť pravdepodobnosť toho, že jav \(A\) nastal
práve dvakrát (\(k=2\)), teda máme určiť \(P_3(2)\). Podľa (\ref{bev}) dostaneme
\[P(D)=P_3(2)={3 \choose 2}\cdot \Big(\frac{1}{6}\Big)^2\!\cdot\!\Big(1-\frac{1}{6}\Big)^{3-2}=3\cdot \frac{1}{36}\cdot \frac{5}{6}=\frac{5}{72}.\]
2. Úlohy a) až c) by sme mohli riešiť, podobne ako v časti 1., výpisom všetkých možnosti nastatia javov, ktorých pravdepodobnosť máme určiť. To by bolo prácne. Jednoduchšie to pôjde pomocou Bernoulliho vzorca (\ref{bev}), v ktorom \(n=6\) a \(p=\frac{1}{6}\).
a) Pýtame sa na pravdepodobnosť toho, že jav \(A\) - padnutie šestky - nastal v sérii šiestich nezávislých pokusov práve štyrikrát. Na základe Bernoulliho vzorca (\ref{bev}) dostaneme (\(k=4\)): \[P_6(4)={6 \choose 4}\cdot \Big(\frac{1}{6}\Big)^4\!\cdot\!\Big(1-\frac{1}{6} \Big)^{6-4}=15\cdot \frac{1}{6^4}\cdot \frac{5^2}{6^2}=\frac{125}{15\,552} \approx 0{,}000\,804.\]
Nech \(m\) je počet padnutých šestiek pri šiestich hodoch kockou.
b) Máme určiť pravdepodobnosť javu, ktorý spočíva v tom, že \(m\ge 4\), t. j. \(P_6(m\ge 4)\). Javy \(m= 4\), \(m= 5\) a \(m=6\) sú disjunktné, a preto \[P_6(m\ge 4)=P_6(m= 4)+P_6(m=5)+P_6(m=6).\] Z Bernoulliho vzorca (\ref{bev}) pre \(n=6\) a \(p=\frac{1}{6}\) dostaneme \[P_6(m\ge 4)={6 \choose 4}\cdot \Big(\frac{1}{6}\Big)^4\!\cdot\!\Big(\frac{5}{6} \Big)^{6-4}+{6 \choose 5}\cdot \Big(\frac{1}{6}\Big)^5\!\cdot\!\Big(\frac{5}{6} \Big)^{6-5}+{6 \choose 6}\cdot \Big(\frac{1}{6}\Big)^6\!\cdot\!\Big(\frac{5}{6} \Big)^{6-6}\] a po jednoduchých výpočtoch \[P_6(m\ge 4)=\frac{125}{15\,552}+\frac{5}{7\,776}+\frac{1}{46\,656}= \frac{203}{23\,328}\approx 0{,}0087.\] Poznamenávame, že v MATLABe môžeme tieto výpočty realizovať pomocou príkazu \(sum(binopdf(4:6,6,1/6))\).
c) Ak použijeme označenia z časti b) tejto úlohy, tak máme určiť \(P_6(m\le 4)\). Zrejme \[P_6(m\le 4)=P_6(m=0)+P_6(m=1)+P_6(m=2)+P_6(m=3)+P_6(m=4)\] a ďalej by sme mohli postupovať ako v časti b). Tu je výhodnejšie použiť opačný jav: ľahko vidieť, že \[P_6(m\le 4)=1-P_6(m\gt 4)=1-[P_6(m=5)+P_6(m=6)].\] Z výpočtov v časti b) dostaneme \[P_6(m\le 4)=1-\Big[\frac{5}{7\,776}+\frac{1}{46\,656}\Big]=\frac{46\,625} {46\,656}\approx 0{,}9993.\] Tieto výsledky dostaneme v MATLABe pomocou príkazu \(sum(binopdf(0:4,6,1/6))\) alebo \(1-sum(binopdf(5:6,6,1/6))\).
2. Úlohy a) až c) by sme mohli riešiť, podobne ako v časti 1., výpisom všetkých možnosti nastatia javov, ktorých pravdepodobnosť máme určiť. To by bolo prácne. Jednoduchšie to pôjde pomocou Bernoulliho vzorca (\ref{bev}), v ktorom \(n=6\) a \(p=\frac{1}{6}\).
a) Pýtame sa na pravdepodobnosť toho, že jav \(A\) - padnutie šestky - nastal v sérii šiestich nezávislých pokusov práve štyrikrát. Na základe Bernoulliho vzorca (\ref{bev}) dostaneme (\(k=4\)): \[P_6(4)={6 \choose 4}\cdot \Big(\frac{1}{6}\Big)^4\!\cdot\!\Big(1-\frac{1}{6} \Big)^{6-4}=15\cdot \frac{1}{6^4}\cdot \frac{5^2}{6^2}=\frac{125}{15\,552} \approx 0{,}000\,804.\]
Nech \(m\) je počet padnutých šestiek pri šiestich hodoch kockou.
b) Máme určiť pravdepodobnosť javu, ktorý spočíva v tom, že \(m\ge 4\), t. j. \(P_6(m\ge 4)\). Javy \(m= 4\), \(m= 5\) a \(m=6\) sú disjunktné, a preto \[P_6(m\ge 4)=P_6(m= 4)+P_6(m=5)+P_6(m=6).\] Z Bernoulliho vzorca (\ref{bev}) pre \(n=6\) a \(p=\frac{1}{6}\) dostaneme \[P_6(m\ge 4)={6 \choose 4}\cdot \Big(\frac{1}{6}\Big)^4\!\cdot\!\Big(\frac{5}{6} \Big)^{6-4}+{6 \choose 5}\cdot \Big(\frac{1}{6}\Big)^5\!\cdot\!\Big(\frac{5}{6} \Big)^{6-5}+{6 \choose 6}\cdot \Big(\frac{1}{6}\Big)^6\!\cdot\!\Big(\frac{5}{6} \Big)^{6-6}\] a po jednoduchých výpočtoch \[P_6(m\ge 4)=\frac{125}{15\,552}+\frac{5}{7\,776}+\frac{1}{46\,656}= \frac{203}{23\,328}\approx 0{,}0087.\] Poznamenávame, že v MATLABe môžeme tieto výpočty realizovať pomocou príkazu \(sum(binopdf(4:6,6,1/6))\).
c) Ak použijeme označenia z časti b) tejto úlohy, tak máme určiť \(P_6(m\le 4)\). Zrejme \[P_6(m\le 4)=P_6(m=0)+P_6(m=1)+P_6(m=2)+P_6(m=3)+P_6(m=4)\] a ďalej by sme mohli postupovať ako v časti b). Tu je výhodnejšie použiť opačný jav: ľahko vidieť, že \[P_6(m\le 4)=1-P_6(m\gt 4)=1-[P_6(m=5)+P_6(m=6)].\] Z výpočtov v časti b) dostaneme \[P_6(m\le 4)=1-\Big[\frac{5}{7\,776}+\frac{1}{46\,656}\Big]=\frac{46\,625} {46\,656}\approx 0{,}9993.\] Tieto výsledky dostaneme v MATLABe pomocou príkazu \(sum(binopdf(0:4,6,1/6))\) alebo \(1-sum(binopdf(5:6,6,1/6))\).
Príklad:
Do siete je zapojených \(9\) odporov. Ľubovoľný z nich je v bezchybnom stave
s pravdepodobnosťou \(0{,}8.\) Stav ľubovoľného z odporov nezávisí na stave ostatných.
Určte pravdepodobnosť toho, že:
a) aspoň jeden z odporov je pokazený;
b) najmenej päť a nie viac ako sedem odporov je v bezchybnom stave;
c) najmenej päť alebo nie viac ako sedem odporov je v bezchybnom stave;
d) pravdepodobnosť najpravdepodobnejšieho počtu bezchybných odporov.
a) aspoň jeden z odporov je pokazený;
b) najmenej päť a nie viac ako sedem odporov je v bezchybnom stave;
c) najmenej päť alebo nie viac ako sedem odporov je v bezchybnom stave;
d) pravdepodobnosť najpravdepodobnejšieho počtu bezchybných odporov.
Riešenie:
Zrejme ide o deväťnásobné opakovanie nezávislých pokusov na jednotlivých odporoch -
výsledkom každého pokusu sú dva disjunktné javy:
\(\bullet\) jav \(A\), ktorý spočíva v tom, že konkrétny odpor je v bezchybnom stave;
\(\bullet\) a jav \(\overline{\!A}\), ktorý spočíva v tom, že konkrétny odpor nie je v bezchybnom stave.
Ide teda o Bernoulliho schému, v ktorej \(n=9\) a \(p=P(A)=0{,}8.\) Na základe Bernoulliho vzorca (\ref{bev}) je práve \(k\) odporov v bezchybnom stave s pravdepodobnosťou \begin{equation}\label{bevp} P_9(k)={9 \choose k}0{,}8^k0{,}2^{9-k}\qquad \mbox{pre }k\in\{0,1,2,\dots ,9\}. \end{equation} a) Pýtame sa na pravdepodobnosť javu \(B,\) ktorý spočíva v tom, že aspoň jeden z odporov je pokazený. Túto pravdepodobnosť by sme mohli dostať ako súčet pravdepodobností \(P_9(k)\) zo vzťahu (\ref{bevp}) pre \(k\) od nuly po osem (lebo pre tieto hodnoty \(k\) je aspoň jeden odpor nie v bezchybnom stave). Jednoduchšie to pôjde cez jav opačný: je evidentné, že jav \(\overline{B}\) spočíva v tom, že všetky odpory sú v bezchybnom stave, t. j. \(k=9\). Teda \[P(\overline{B})=P_9(9)=0{,}8^9,\] čo znamená, že \(P(B)=1-0{,}8^9\approx 0{,}8658.\)
b) Z textu úlohy vidno, že ak \(k\) je počet bezchybných odporov, tak nás zaujíma prípad, keď \(5\le k\) a súčasne \(k \le 7\). Ak použijeme označenie z Bernoulliho vzorca (\ref{bevp}), tak je potrebné určiť \(P_9(5\le k \le 7)\). Keďže javy \(k=5\), \(k=6\) a \(k=7\) sú disjunktné, tak \[P_9(5\le k \le 7)=P_9(5)+P_9(6)+P_9(7). \] Odtiaľ na základe (\ref{bevp}) je \[P_9(5\le k \le 7)={9 \choose 5}0{,}8^50{,}2^{4}+{9 \choose 6}0{,}8^60{,}2^{3}+{9 \choose 7}0{,}8^70{,}2^{2}\approx 0{,}5442.\] Poznamenávame, že v .MATLABe. môžeme uvedený výsledok získať pomocou sum(binopdf(5:7,9,.8)).
c) Tentoraz má počet bezchybných odporov spĺňať nerovnosť \(5\le k\) alebo nerovnosť \(k \le 7\). Je zrejmé, že ide o istý jav, a preto jeho pravdepodobnosť je rovná jednej.
d) Najprv určíme najpravdepodobnejší počet \(k_0\) bezchybných odporov: na základe (\ref{k0}) dostaneme (\(n=9\), \(p=0{,}8\) a \(q=0{,}2\)) \[k_0\in \langle np-q;\,np+p\rangle=\langle 9\!\cdot\! 0{,}8-0{,}2\;;\; 9\!\cdot\! 0{,}8+0{,}8\rangle=\langle 7 ;8\rangle.\] To ale znamená, že postupnosť pravdepodobností \(P_9(0), P_9(1),P_9(2),\ldots ,P_9(9)\) (pozri (\ref{bevp})) nadobúda maximálne hodnoty pre \(k=7\) a \(k=8\), pričom \(P_9(7)=P_9(8).\) Preto požadovaná pravdepodobnosť je \[P_9(7)+P_9(8)={9 \choose 7}0{,}8^70{,}2^{2}+{9 \choose 8}0{,}8^80{,}2^{1}\approx0{,}3020+0{,}3020=0{,}6040.\]
\(\bullet\) jav \(A\), ktorý spočíva v tom, že konkrétny odpor je v bezchybnom stave;
\(\bullet\) a jav \(\overline{\!A}\), ktorý spočíva v tom, že konkrétny odpor nie je v bezchybnom stave.
Ide teda o Bernoulliho schému, v ktorej \(n=9\) a \(p=P(A)=0{,}8.\) Na základe Bernoulliho vzorca (\ref{bev}) je práve \(k\) odporov v bezchybnom stave s pravdepodobnosťou \begin{equation}\label{bevp} P_9(k)={9 \choose k}0{,}8^k0{,}2^{9-k}\qquad \mbox{pre }k\in\{0,1,2,\dots ,9\}. \end{equation} a) Pýtame sa na pravdepodobnosť javu \(B,\) ktorý spočíva v tom, že aspoň jeden z odporov je pokazený. Túto pravdepodobnosť by sme mohli dostať ako súčet pravdepodobností \(P_9(k)\) zo vzťahu (\ref{bevp}) pre \(k\) od nuly po osem (lebo pre tieto hodnoty \(k\) je aspoň jeden odpor nie v bezchybnom stave). Jednoduchšie to pôjde cez jav opačný: je evidentné, že jav \(\overline{B}\) spočíva v tom, že všetky odpory sú v bezchybnom stave, t. j. \(k=9\). Teda \[P(\overline{B})=P_9(9)=0{,}8^9,\] čo znamená, že \(P(B)=1-0{,}8^9\approx 0{,}8658.\)
b) Z textu úlohy vidno, že ak \(k\) je počet bezchybných odporov, tak nás zaujíma prípad, keď \(5\le k\) a súčasne \(k \le 7\). Ak použijeme označenie z Bernoulliho vzorca (\ref{bevp}), tak je potrebné určiť \(P_9(5\le k \le 7)\). Keďže javy \(k=5\), \(k=6\) a \(k=7\) sú disjunktné, tak \[P_9(5\le k \le 7)=P_9(5)+P_9(6)+P_9(7). \] Odtiaľ na základe (\ref{bevp}) je \[P_9(5\le k \le 7)={9 \choose 5}0{,}8^50{,}2^{4}+{9 \choose 6}0{,}8^60{,}2^{3}+{9 \choose 7}0{,}8^70{,}2^{2}\approx 0{,}5442.\] Poznamenávame, že v .MATLABe. môžeme uvedený výsledok získať pomocou sum(binopdf(5:7,9,.8)).
c) Tentoraz má počet bezchybných odporov spĺňať nerovnosť \(5\le k\) alebo nerovnosť \(k \le 7\). Je zrejmé, že ide o istý jav, a preto jeho pravdepodobnosť je rovná jednej.
d) Najprv určíme najpravdepodobnejší počet \(k_0\) bezchybných odporov: na základe (\ref{k0}) dostaneme (\(n=9\), \(p=0{,}8\) a \(q=0{,}2\)) \[k_0\in \langle np-q;\,np+p\rangle=\langle 9\!\cdot\! 0{,}8-0{,}2\;;\; 9\!\cdot\! 0{,}8+0{,}8\rangle=\langle 7 ;8\rangle.\] To ale znamená, že postupnosť pravdepodobností \(P_9(0), P_9(1),P_9(2),\ldots ,P_9(9)\) (pozri (\ref{bevp})) nadobúda maximálne hodnoty pre \(k=7\) a \(k=8\), pričom \(P_9(7)=P_9(8).\) Preto požadovaná pravdepodobnosť je \[P_9(7)+P_9(8)={9 \choose 7}0{,}8^70{,}2^{2}+{9 \choose 8}0{,}8^80{,}2^{1}\approx0{,}3020+0{,}3020=0{,}6040.\]
Príklad:
Pravdepodobnosť toho, že pri štyroch nezávislých pokusoch nastane jav \(A\) práve
dvakrát je \(0{,}2646\). Určme pravdepodobnosť toho, že v sérii tých istých šiestich
nezávislých pokusov nastane jav \(A\) najviac štyrikrát, ak je známe, že
\(P(A)\gt P(\overline{\!A})\).
Riešenie:
Najprv určíme pravdepodobnosť toho, že jav \(A\) nastane v jednom pokuse: nech \(P(A)=p\).
Na základe Bernoulliho vzorca (\ref{bev}) dostaneme, že pre pravdepodobnosť toho,
že pri štyroch nezávislých pokusoch nastane jav \(A\) práve dvakrát platí (\(n=4\) a \(k=2\))
\[P_4(2)={4 \choose 2}p^2(1-p)^{4-2}\stackrel{\star}{=}0{,}2646.\]
Keďže \({4 \choose 2}=6\), tak \(\stackrel{\star}{=}\) nadobudne tvar
\[p^2(1-p)^2=0{,}0441.\]
Odtiaľ \(p(1-p)=\sqrt{0{,}0441}=0{,}21\) (treba si uvedomiť, že \(p\) a \(1-p\)
sú nezáporné). Ľahko sa presvedčíme, že riešením vzniknutej kvadratickej rovnice
\(p(1-p)=0{,}21\) je \(p\in\{0{,}3;\,0{,}7\}\). Ak zoberieme do úvahy požiadavku
\(p=P(A)\gt P(\overline{\!A})\), tak \(p=0{,}7\).
Chceme určiť pravdepodobnosť toho, že v sérii tých istých šiestich nezávislých pokusov nastane jav \(A\) najviac štyrikrát. Ak označíme písmenom \(k\) počet pokusov, v ktorých jav \(A\) nastal, tak je potrebné vypočítať \(P_6(k\le 4)\). Je zrejmé, že \[P_6(k\le 4)=P_6(0)+P_6(1)+P_6(2)+P_6(3)+P_6(4).\] Tu by sme päťkrát použili Bernoulliho vzorec (\ref{bev}). Rýchlejšie sa dopracujeme k požadovanej pravdepodobnosti pomocou opačného javu: v našom prípade opačným javom k javu \(k\le4\) je jav \(4\lt k\le 6\). Teda \[P_6(k\le 4)=1-P_6(4\lt k\le 6)=1-[P_6(5)+P_6(6)]=\spadesuit\] Z Bernoulliho vzorca (\ref{bev}) dostaneme \[P_6(5)+P_6(6)={6 \choose 5}0{,}7^5\cdot 0{,}3^1+{6 \choose 6}0{,}7^6\cdot 0{,}3^0=0{,}420175\] a teda \[\spadesuit =1-0{,}420175=0{,}579825.\] V MATLABe by sme tento výsledok získali pomocou \(1-sum(binopdf(5:6,6,.7))\) alebo pomocou \(sum(binopdf(0:4,6,.7))\).
Chceme určiť pravdepodobnosť toho, že v sérii tých istých šiestich nezávislých pokusov nastane jav \(A\) najviac štyrikrát. Ak označíme písmenom \(k\) počet pokusov, v ktorých jav \(A\) nastal, tak je potrebné vypočítať \(P_6(k\le 4)\). Je zrejmé, že \[P_6(k\le 4)=P_6(0)+P_6(1)+P_6(2)+P_6(3)+P_6(4).\] Tu by sme päťkrát použili Bernoulliho vzorec (\ref{bev}). Rýchlejšie sa dopracujeme k požadovanej pravdepodobnosti pomocou opačného javu: v našom prípade opačným javom k javu \(k\le4\) je jav \(4\lt k\le 6\). Teda \[P_6(k\le 4)=1-P_6(4\lt k\le 6)=1-[P_6(5)+P_6(6)]=\spadesuit\] Z Bernoulliho vzorca (\ref{bev}) dostaneme \[P_6(5)+P_6(6)={6 \choose 5}0{,}7^5\cdot 0{,}3^1+{6 \choose 6}0{,}7^6\cdot 0{,}3^0=0{,}420175\] a teda \[\spadesuit =1-0{,}420175=0{,}579825.\] V MATLABe by sme tento výsledok získali pomocou \(1-sum(binopdf(5:6,6,.7))\) alebo pomocou \(sum(binopdf(0:4,6,.7))\).
Príklad:
Štyria študenti sa nezávisle jeden od druhého snažia vyriešiť úlohu. Prvý študent
vyrieši úlohu s pravdepodobnosťou \(0{,}6\) a pre ďalších študentov sú pravdepodobnosti
úspešného vyriešenia úlohy (v poradí druhý, tretí a štvrtý študent) takéto:
\(0{,}55\), \(0{,}45\) a \(0{,}5.\) Aká je pravdepodobnosť toho, že úloha bude vyriešená:
a) všetkými študentami;
b) práve troma študentami;
c) aspoň dvoma študentami.
a) všetkými študentami;
b) práve troma študentami;
c) aspoň dvoma študentami.
Riešenie:
Nech \(A_i\) je jav, že \(i\)-tý študent vyrieši úlohu. Potom z textu príkladu máme
\begin{equation}\label{nn}
P(A_1)=0{,}6;\qquad P(A_2)=0{,}55;\qquad P(A_3)=0{,}45\qquad \mbox{a} \qquad P(A_4)=0{,}5.
\end{equation}
a) Všetci študenti vyriešia úlohu práve vtedy, ak nastane jav \(A_1\cap A_2\cap A_3\cap A_4\).
Keďže riešia úlohu nezávisle jeden od druhého, tak z vety o pravdepodobnosti prieniku
celkove nezávislých javov (\ref{nz}) dostaneme
\[P(A_1\cap A_2\cap A_3\cap A_4)=P(A_1)\cdot P(A_2)\cdot P(A_3)\cdot P(A_3)\]
a odtiaľ na základe (\ref{nn})
\begin{equation}\label{nm}
P(A_1\cap A_2\cap A_3\cap A_4)=0{,}6\cdot 0{,}55\cdot 0{,}45\cdot 0{,}5=0{,}074\,25.
\end{equation}
b) Máme určiť pravdepodobnosť toho, že traja študenti úlohu vyriešia a jeden študent
ju nevyrieši. Je zrejmé, že \(i\)-tý študent úlohu nevyrieši s pravdepodobnosťou
\(P(\overline{A_i})=1-P(A_i)\). Nech \(A\) je jav, ktorý znamená, že práve traja
študenti vyriešia úlohu. Je zrejmé, že jav \(A\) je zjednotením štyroch disjunktných javov:
\begin{equation}\label{m}
A\!=\!(\overline{A_1}\cap A_2\cap A_3\cap A_4) \cup (A_1\cap \overline{A_2}\cap A_3\cap A_4) \cup (A_1\cap A_2\cap \overline{A_3}\cap
A_4) \cup (A_1\cap A_2\cap A_3\cap \overline{A_4}),
\end{equation}
a preto \(P(A)\) je súčtom pravdepodobností týchto javov. Určíme napr.
\(P(\overline{A_1}\cap A_2\cap A_3\cap A_4)\). Je známe, že javy \(A_1,\) \(A_2,\) \(A_3,\) \(A_4\)
sú celkovo nezávislé práve vtedy, keď sú celkovo nezávislé javy \(\overline{A_1},\) \(A_2,\) \(A_3,\) \(A_4\).
Teda na výpočet \(P(\overline{A_1}\cap A_2\cap A_3\cap A_4)\) môžeme opäť použiť
vetu o pravdepodobnosti prieniku celkove nezávislých javov (\ref{nz}). Dostaneme
\[P(\overline{A_1}\cap A_2\cap A_3\cap A_4)\!=\!P\!(\overline{A_1})\cdot P(A_2)\cdot P(A_3)\cdot P(A_4)\!=\!(1-0{,}6)\cdot
0{,}55\cdot 0{,}45\cdot 0{,}5=0{,}0495.\]
Obdobnými úvahami získame
\[P(A_1\cap \overline{A_2}\cap A_3\cap A_4)=0{,}6\cdot (1-0{,}55)\cdot 0{,}45\cdot 0{,}5=0{,}06075;\]
\[P(A_1\cap A_2\cap \overline{A_3}\cap A_4)=0{,}6\cdot 0{,}55\cdot (1-0{,}45)\cdot 0{,}5=0{,}09075;\]
\[P(A_1\cap A_2\cap A_3\cap \overline{A_4})=0{,}6\cdot 0{,}55\cdot 0{,}45\cdot (1-0{,}5)=0{,}07425.\]
Ak teraz aplikujeme na rovnosť (\ref{m}) poznatok o pravdepodobnosti zjednotenia
systému disjunktných javov, tak dostaneme
\[P(A)=0{,}0495+ 0{,}06075+ 0{,}09075+0{,}07425=0{,}27525.\]
c) Jav \(B\), ktorý spočíva v tom, že úlohu vyriešia aspoň dvaja študenti môžeme
rozložiť na zjednotenie týchto troch disjunktných javov:
- úlohu vyriešia práve dvaja študenti (tento jav môžeme rozložiť na zjednotenie šiestich disjunktných javov - skúste ich vypísať);
- úlohu vyriešia práve traja študenti (čomu zodpovedá rozklad na zjednotenie štyroch disjunktných javov);
- úlohu vyriešia štyria študenti.
Teda jav \(B\) môžeme rozložiť na zjednotenie až jedenástich disjunktných javov. Poďme na to cez jav opačný: zrejme jav \(\overline{B}\) spočíva v tom, že úlohu vyrieši maximálne jeden študent. Tento jav môžeme rozložiť na zjednotenie týchto dvoch disjunktných javov:
- jav \(C\), ktorý spočíva v tom, že úlohu vyrieši len jeden študent;
- jav \(D\), ktorý spočíva v tom, že úlohu nevyrieši nikto.
Analogickým spôsobom ako v časti b) určíme \(P(C)\). Je evidentné, že \[C\!=\!(\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}\cap A_4) \cup (\overline{A_1}\cap \overline{A_2}\cap A_3\cap \overline{A_4}) \cup (\overline{A_1}\cap A_2\cap \overline{A_3}\cap \overline{A_4}) \cup (A_1\cap \overline{A_2}\cap \overline{A_3}\cap \overline{A_4}).\] Potom \[P(C)=(1-0{,}6)\cdot (1-0{,}55)\cdot (1-0{,}45)\cdot 0{,}5+ (1- 0{,}6)\cdot (1-0{,}55)\cdot 0{,}45\cdot (1-0{,}5)+\] \[+(1-0{,}6)\cdot 0{,}55\cdot (1-0{,}45)\cdot (1-0{,}5)+0{,}6\cdot (1-0{,}55)\cdot (1-0{,}45)\cdot (1-0{,}5)=0{,}22475.\] Zrejme \(D=\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}\cap \overline{A_4}\), a preto \[P(D)=(1-0{,}6)\cdot (1-0{,}55)\cdot (1-0{,}45)\cdot (1-0{,}5)=0{,}0495.\] Takto \[P(\overline{B})=P(C)+P(D=0{,}22475+0{,}0495=0{,}27425\] a \[P(B)=1-0{,}27425=0{,}72575.\]
- úlohu vyriešia práve dvaja študenti (tento jav môžeme rozložiť na zjednotenie šiestich disjunktných javov - skúste ich vypísať);
- úlohu vyriešia práve traja študenti (čomu zodpovedá rozklad na zjednotenie štyroch disjunktných javov);
- úlohu vyriešia štyria študenti.
Teda jav \(B\) môžeme rozložiť na zjednotenie až jedenástich disjunktných javov. Poďme na to cez jav opačný: zrejme jav \(\overline{B}\) spočíva v tom, že úlohu vyrieši maximálne jeden študent. Tento jav môžeme rozložiť na zjednotenie týchto dvoch disjunktných javov:
- jav \(C\), ktorý spočíva v tom, že úlohu vyrieši len jeden študent;
- jav \(D\), ktorý spočíva v tom, že úlohu nevyrieši nikto.
Analogickým spôsobom ako v časti b) určíme \(P(C)\). Je evidentné, že \[C\!=\!(\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}\cap A_4) \cup (\overline{A_1}\cap \overline{A_2}\cap A_3\cap \overline{A_4}) \cup (\overline{A_1}\cap A_2\cap \overline{A_3}\cap \overline{A_4}) \cup (A_1\cap \overline{A_2}\cap \overline{A_3}\cap \overline{A_4}).\] Potom \[P(C)=(1-0{,}6)\cdot (1-0{,}55)\cdot (1-0{,}45)\cdot 0{,}5+ (1- 0{,}6)\cdot (1-0{,}55)\cdot 0{,}45\cdot (1-0{,}5)+\] \[+(1-0{,}6)\cdot 0{,}55\cdot (1-0{,}45)\cdot (1-0{,}5)+0{,}6\cdot (1-0{,}55)\cdot (1-0{,}45)\cdot (1-0{,}5)=0{,}22475.\] Zrejme \(D=\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}\cap \overline{A_4}\), a preto \[P(D)=(1-0{,}6)\cdot (1-0{,}55)\cdot (1-0{,}45)\cdot (1-0{,}5)=0{,}0495.\] Takto \[P(\overline{B})=P(C)+P(D=0{,}22475+0{,}0495=0{,}27425\] a \[P(B)=1-0{,}27425=0{,}72575.\]
Príklad:
V urne je \(b\) bielych a \(m\) modrých guliek (\(b\ge 2\) a \(m\ge 2\)). Náhodne
z nej vylosujeme bez návratu dve guľky. Nech \(\overline{\!A}_i\) je jav, ktorý
spočíva v tom, že \(i\)-tá vylosovaná guľka je biela (\(i\in\{1,2\}\)). Určte tieto
pravdepodobnosti: a) \(P(A_1)\); b) \(P(A_1/A_2)\); c) \(P(A_2/A_1)\);
d) \(P(A_2/\overline{\!A}_1)\); e) \(P(\overline{\!A}_2/\overline{\!A}_1)\); f) \(P(A_2)\).
Úlohy:
Úloha:
Z urny, ktorá obsahuje \(6\) čiernych a \(9\) bielych guliek, náhodne vyberieme
jednu guľku. Guľku vrátime naspäť do urny a pridáme ešte \(9\) guliek tej istej
farby, akej bola vytiahnutá guľka. Potom z urny náhodne vyberieme jednu guľku.
Aká je pravdepodobnosť toho, že bude biela?
Úloha:
Z urny, ktorá obsahuje \(2\) čierne, \(3\) červené a \(5\) bielych guliek, náhodne
vyberieme jednu guľku. Ak sme vytiahli
- čiernu guľku, tak ju vrátime naspäť do urny;
- červenú guľku, tak ju nevrátime naspäť do urny;
- bielu guľku, tak ju vrátime naspäť do urny a pridáme do urny ešte jednu bielu guľku.
V druhom ťahu z urny náhodne vyberieme tri guľky bez návratu. Určte pravdepodobnosť toho, že všetky vytiahnuté guľky budú odlišnej farby.
- čiernu guľku, tak ju vrátime naspäť do urny;
- červenú guľku, tak ju nevrátime naspäť do urny;
- bielu guľku, tak ju vrátime naspäť do urny a pridáme do urny ešte jednu bielu guľku.
V druhom ťahu z urny náhodne vyberieme tri guľky bez návratu. Určte pravdepodobnosť toho, že všetky vytiahnuté guľky budú odlišnej farby.
Úloha:
Z urny, ktorá obsahuje \(6\) čiernych a \(9\) bielych guliek, náhodne vyberieme
jednu guľku. Guľku vrátime naspäť do urny a pridáme ešte \(9\) guliek tej istej
farby, akej bola vytiahnutá guľka. Potom z urny náhodne vyberieme jednu guľku.
Aká je pravdepodobnosť toho, že bude biela?
Úloha:
Pravdepodobnosť toho, že basketbalista trafí do koša je \(0{,}7\). Určte pravdepodobnosť
toho, že basketbalista pri šiestich nezávislých hodoch:
a) aspoň raz trafí do koša;
b) práve dvakrát trafí do koša;
c) aspoň dvakrát trafí do koša.
d) Stanovte najpravdepodobnejší počet trafení do koša v sérii dvadsiatich nezávislých hodov.
a) aspoň raz trafí do koša;
b) práve dvakrát trafí do koša;
c) aspoň dvakrát trafí do koša.
d) Stanovte najpravdepodobnejší počet trafení do koša v sérii dvadsiatich nezávislých hodov.
Úloha:
Pravdepodobnosť toho, že pri piatich nezávislých pokusoch nastane jav \(A\) aspoň
raz je \(0{,}98976\). Určte pravdepodobnosť toho, že v sérii tých istých šiestich
nezávislých pokusov jav \(A\) aspoň raz nenastane.
Úloha:
Aká je pravdepodobnosť toho, že pri nezávislom hode štyrmi bežnými hracími kockami
padne na prvej kocke párne číslo, na druhej kocke nepárne číslo a na zvyšných dvoch
kockách padne súčet \(6\)?
Úloha:
V prvej urne je \(1\) biela a \(2\) čierne guľky, v druhej urne sú \(3\) biele a
\(1\) čierna guľka a v tretej urne sú \(2\) biele a \(3\) čierne guľky. Z každej
urny náhodne vytiahneme po jednej guľke. Určte pravdepodobnosť toho, že:
a) všetky tri vytiahnuté guľky budú rovnakej farby;
b) \(2\) guľky budú biele a \(1\) čierna.
a) všetky tri vytiahnuté guľky budú rovnakej farby;
b) \(2\) guľky budú biele a \(1\) čierna.
09. Náhodná premenná
Riešené úlohy:
Príklad:
V urne sú \(3\) biele guľky a \(5\) čiernych guliek. Náhodne z nej vyberáme po
jednej guľke bez návratu dovtedy, kým nevytiahneme prvú bielu guľku. Určme
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu vytiahnutých guliek (t. j., ktorá sa rovná počtu vytiahnutých guliek);
b) priemerný počet vytiahnutých guliek;
c) disperziu počtu vytiahnutých guliek;
d) pravdepodobnosť toho, že sme vytiahli viac guliek ako je smerodajná odchýlka počtu vytiahnutých guliek;
e) najpravdepodobnejší počet vytiahnutých guliek.
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu vytiahnutých guliek (t. j., ktorá sa rovná počtu vytiahnutých guliek);
b) priemerný počet vytiahnutých guliek;
c) disperziu počtu vytiahnutých guliek;
d) pravdepodobnosť toho, že sme vytiahli viac guliek ako je smerodajná odchýlka počtu vytiahnutých guliek;
e) najpravdepodobnejší počet vytiahnutých guliek.
Riešenie:
a) Určíme zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda
hodnoty počtu vytiahnutých guliek. Náhodná premenná \(X\) nadobudne hodnotu \(1\),
ak prvá vytiahnutá guľka bude biela. Všetkých guliek v urne je osem, z toho sú tri
biele. Preto
\[P(X\!=\!1)=\frac{3}{8}.\]
Náhodná premenná \(X\) nadobudne hodnotu \(2\), ak prvá vytiahnutá guľka bude
čierna a druhá biela. Pravdepodobnosť toho, že prvá guľka bude čierna je \(\frac{5}{8}\).
Ak prvá guľka bola čierna, tak v urne zostali tri biele a štyri čierne guľky. Preto
pravdepodobnosť toho, že druhá vytiahnutá bude biela je \(\frac{3}{7}\). Takto
\[P(X\!=\!2)=\frac{5}{8}\cdot \frac{3}{7}= \frac{15}{56}.\]
Náhodná premenná \(X\) nadobudne hodnotu \(3\), ak prvé dve vytiahnuté guľky budú
čierne a tretia biela. Pravdepodobnosť toho, že prvé dve guľky budú čierne je
\(\frac{5}{8}\cdot \frac{4}{7}\). Ak prvé dve guľky boli čierne, tak v urne zostali
tri biele a tri čierne guľky. Preto pravdepodobnosť toho, že tretia vytiahnutá
bude biela je \(\frac{3}{6}\). Potom
\[P(X\!=\!3)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}= \frac{5}{28}.\]
Obdobnou úvahou dostaneme
\[P(X\!=\!4)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}\cdot \frac{3}{5}= \frac{3}{28}.\]
a
\[P(X\!=\!5)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}\cdot \frac{2}{5}\cdot \frac{3}{4}= \frac{3}{56}.\]
Je evidentné, že náhodná premenná \(X\) nadobudne hodnotu \(6\), ak prvé päť
vytiahnuté guľky budú čierne. Potom v urne zostali už len tri biele guľky a tak
šiesta vytiahnutá guľka musí byť biela. Preto
\[P(X\!=\!6)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}\cdot \frac{2}{5}\cdot \frac{1}{4}= \frac{1}{56}.\]
Je zrejmé, že tým sme vyčerpali všetky možné hodnoty, ktoré náhodná premenná
\(X\) nadobúda s nenulovou pravdepodobnosťouu. Naše výpočty sú zhrnuté v nasledujúcej
tabuľke pravdepodobností náhodnej premennej \(X\):
\[
\begin{array}{c||c|c|c|c|c|c}
x_i \a 1 \a 2 \a 3 \a 4 \a 5 \a 6 \\ \hline
P(X\!=\!x_i) =p_i\a \frac{3}{8} \a \frac{15}{56} \a \frac{5}{28} \a \frac{3}{28} \a \frac{3}{56} \a \frac{1}{56}
\end{array}
\]
Pre náhodnú premennú \(X\) by mal byť súčet pravdepodobností \(P(X\!=\!x_i)\)
v druhom riadku tejto tabuľky rovný jednej (presvedčte sa o tom).
b) Priemerný počet vytiahnutých guliek reprezentuje stredná hodnota \(E(X)\) náhodnej premennej. Na základe (\ref{sh}) dostaneme \[E(X)= 1\!\cdot \!\frac{3}{8} +2\!\cdot\! \frac{15}{56} +3\!\cdot\! \frac{5}{28} +4\!\cdot\! \frac{3}{28}+5\!\cdot\! \frac{3}{56}+6\!\cdot\! \frac{1}{56}=\frac{9}{4}.\]
c) Disperziu náhodnej premennej \(X\) určíme podľa (\ref{dis}). Dostaneme \[D(X)= (1-\tfrac{9}{4})^2\tfrac{3}{8} +(2-\tfrac{9}{4})^2 \tfrac{15}{56} +(3-\tfrac{9}{4})^2 \tfrac{5}{28} +(4-\tfrac{9}{4})^2\tfrac{3}{28}+(5-\tfrac{9}{4})^2 \tfrac{3}{56}+(6-\tfrac{9}{4})^2 \tfrac{1}{56}=\frac{27}{16}.\]
d) Smerodajnú odchýlku \(\sigma (X)\) náhodnej premennej \(X\) dostaneme z jej disperzie podľa vzťahu \[\sigma (X)=\sqrt{D(X)}. \] V našom prípade je \[\sigma (X)=\sqrt{\frac{27}{16}}=\frac{3\sqrt 3}{4}\approx 1{,}299. \] Keďže náhodná premenná \(X\) nadobúda hodnoty počtu vytiahnutých guliek, tak máme určiť pravdepodobnosť toho, že nastane jav \(X\gt 1{,}299\). Na základe toho, že \(X\) je diskrétna náhodná premenná s oborom hodnôt \({\cal H}=\{1,2,3,4,5,6\}\) dostávame (pri výpočte je výhodnejšie použiť opačný jav): \[P(X\!\gt\! \sigma (X))= P(X\!\gt\! 1{,}299)=1-P(X\!\leqq \!1{,}299)=1-P(X\!=\!1)=1-\frac{3}{8}=\frac{5}{8}. \]
e) Najpravdepodobnejší počet vytiahnutých guliek (t. j. modus náhodnej premennej \({\cal M}o(X)\)) určíme z pravdepodobnostnej tabuľky náhodnej premennej \(X\): ľahko vidno, že maximum z hodnôt \(p_i\) je
\(p_1=\frac{3}{8},\) a preto \({\cal M}o(X)=1.\)
b) Priemerný počet vytiahnutých guliek reprezentuje stredná hodnota \(E(X)\) náhodnej premennej. Na základe (\ref{sh}) dostaneme \[E(X)= 1\!\cdot \!\frac{3}{8} +2\!\cdot\! \frac{15}{56} +3\!\cdot\! \frac{5}{28} +4\!\cdot\! \frac{3}{28}+5\!\cdot\! \frac{3}{56}+6\!\cdot\! \frac{1}{56}=\frac{9}{4}.\]
c) Disperziu náhodnej premennej \(X\) určíme podľa (\ref{dis}). Dostaneme \[D(X)= (1-\tfrac{9}{4})^2\tfrac{3}{8} +(2-\tfrac{9}{4})^2 \tfrac{15}{56} +(3-\tfrac{9}{4})^2 \tfrac{5}{28} +(4-\tfrac{9}{4})^2\tfrac{3}{28}+(5-\tfrac{9}{4})^2 \tfrac{3}{56}+(6-\tfrac{9}{4})^2 \tfrac{1}{56}=\frac{27}{16}.\]
d) Smerodajnú odchýlku \(\sigma (X)\) náhodnej premennej \(X\) dostaneme z jej disperzie podľa vzťahu \[\sigma (X)=\sqrt{D(X)}. \] V našom prípade je \[\sigma (X)=\sqrt{\frac{27}{16}}=\frac{3\sqrt 3}{4}\approx 1{,}299. \] Keďže náhodná premenná \(X\) nadobúda hodnoty počtu vytiahnutých guliek, tak máme určiť pravdepodobnosť toho, že nastane jav \(X\gt 1{,}299\). Na základe toho, že \(X\) je diskrétna náhodná premenná s oborom hodnôt \({\cal H}=\{1,2,3,4,5,6\}\) dostávame (pri výpočte je výhodnejšie použiť opačný jav): \[P(X\!\gt\! \sigma (X))= P(X\!\gt\! 1{,}299)=1-P(X\!\leqq \!1{,}299)=1-P(X\!=\!1)=1-\frac{3}{8}=\frac{5}{8}. \]
e) Najpravdepodobnejší počet vytiahnutých guliek (t. j. modus náhodnej premennej \({\cal M}o(X)\)) určíme z pravdepodobnostnej tabuľky náhodnej premennej \(X\): ľahko vidno, že maximum z hodnôt \(p_i\) je
\(p_1=\frac{3}{8},\) a preto \({\cal M}o(X)=1.\)
- Kocka \({\cal K}_1\) a kocka \({\cal K}_2\).
Ľahko nahliadneme, že v tomto súboji kocka \({\cal K}_1\) vyhráva, ak výsledkom pokusu je jav \(21\) alebo \(61\) alebo jav \(65\). Tieto javy sú disjunktné, a preto \[P(X_1\gt X_2)=P(21)+P(61)+P(65)=\frac{4}{6}\cdot\frac{2}{6}+\frac{2}{6}\cdot\frac{2}{6}+\frac{2}{6}\cdot\frac{4}{6}=\frac{5}{9}\gt 0{,}5.\] To znamená, že kocka \({\cal K}_1\) je lepšia ako kocka \({\cal K}_2\), a teda \begin{equation}\label{k12} {\cal K}_1\succ {\cal K}_2. \end{equation} - Kocka \({\cal K}_2\) a kocka \({\cal K}_3\).
V tomto prípade kocka \({\cal K}_2\) vyhráva, ak výsledkom pokusu je jav \(53\) alebo jav \(54\). Potom \[P(X_2\gt X_3)=P(53)+P(54)=\frac{4}{6}\cdot\frac{2}{6}+\frac{4}{6}\cdot\frac{4}{6}=\frac{2}{3}\gt 0{,}5.\] Teda kocka \({\cal K}_2\) je lepšia ako kocka \({\cal K}_3\), čo môžeme zapísať takto \begin{equation}\label{k23} {\cal K}_2\succ {\cal K}_3. \end{equation} - Kocka \({\cal K}_3\) a kocka \({\cal K}_1\).
V tomto prípade kocka \({\cal K}_3\) vyhráva, ak výsledkom pokusu je jav \(32\) alebo jav \(42\). Potom \[P(X_3\gt X_1)=P(32)+P(42)=\frac{2}{6}\cdot\frac{4}{6}+\frac{4}{6}\cdot\frac{4}{6}=\frac{2}{3}\gt 0{,}5.\] Takto kocka \({\cal K}_3\) je lepšia ako kocka \({\cal K}_1\), čo znamená, že \begin{equation}\label{k31} {\cal K}_3\succ {\cal K}_1. \end{equation}
Príklad:
Uvažujme tri neštandardné hracie kocky, pričom na ich stenách sú počty bodiek od
\(1\) do \(6\), ale počty bodiek sa na jednej kocke môžu aj opakovať. Nech sú to
kocky \({\cal K}_1=\{2,2,2,2,6,6\}\), \({\cal K}_2=\{1,1,5,5,5,5\}\) a \({\cal K}_3=\{3,3,4,4,4,4\}\)
(t. j. napr. štyri steny kocky \({\cal K}_1\) majú po dvoch bodkách a na zvyšných
dvoch stenách je po šesť bodiek).
Máte si zvoliť jednu z tých kociek a váš súper si potom vyberie jednu zo zvyšných dvoch kociek. Obaja hodíte svojou kockou a vyhráva ten, komu padlo väčšie číslo (t. j. stena s väčším počtom bodiek). Akú stratégiu voľby kocky by ste zvolili?
Máte si zvoliť jednu z tých kociek a váš súper si potom vyberie jednu zo zvyšných dvoch kociek. Obaja hodíte svojou kockou a vyhráva ten, komu padlo väčšie číslo (t. j. stena s väčším počtom bodiek). Akú stratégiu voľby kocky by ste zvolili?
Riešenie:
Je evidentné, že vašou snahou bude zvoliť takú stratégiu, aby pravdepodobnosť vašej
výhry bola väčšia ako pravdepodobnosť výhry súpera.
Urobíme rozbor toho, ktorú z kociek je najvýhodnejšie zvoliť. Nech \(X_k\) je náhodná premenná, ktorá nadobúda hodnoty počtu padnutých bodiek na \(k\)-tej kocke (\(k\in\{1,2,3\}\)) a nech \(X_i\gt X_j\) je jav, ktorý spočíva v tom, že na \(i\)-tej kocke padne viac bodiek ako na \(j\)-tej kocke. Uvažujme dva prípady:
\(\bullet\) ak \(P(X_i\gt X_j)=0{,}5\), tak kocky \({\cal K}_i\) a \({\cal K}_j\) nazveme rovnocennými;
\(\bullet\) ak \(P(X_i\gt X_j)\gt\ 0{,}5\), tak kocku \({\cal K}_i\) nazveme lepšou ako kocka \({\cal K}_j\), čo označíme zápisom \({\cal K}_i\succ {\cal K}_j\).
Pre zjednodušenie výkladu urobíme túto dohodu: ak na prvej kocke \({\cal K}_i\) padlo \(x\) bodiek a na druhej kocke \({\cal K}_j\) padlo \(y\) bodiek, tak tento jav môžeme jednoznačne interpretovať dvojciferným číslom \(10x+y\) (napr. javu, ktorý spočíva v padnutí \(2\) bodiek na prvej kocke a \(5\) bodiek na druhej kocke priradíme číslo \(25\)).
Poďme porovnať jednotlivé kocky:
Na základe týchto poznatkov skúste sformulovať vašu stratégiu voľby kocky (samozrejme, že chcete si vybrať takú kocku, aby pravdepodobnosť vašej výhry bola väčšia ako pravdepodobnosť výhry vášho súpera).
Urobíme rozbor toho, ktorú z kociek je najvýhodnejšie zvoliť. Nech \(X_k\) je náhodná premenná, ktorá nadobúda hodnoty počtu padnutých bodiek na \(k\)-tej kocke (\(k\in\{1,2,3\}\)) a nech \(X_i\gt X_j\) je jav, ktorý spočíva v tom, že na \(i\)-tej kocke padne viac bodiek ako na \(j\)-tej kocke. Uvažujme dva prípady:
\(\bullet\) ak \(P(X_i\gt X_j)=0{,}5\), tak kocky \({\cal K}_i\) a \({\cal K}_j\) nazveme rovnocennými;
\(\bullet\) ak \(P(X_i\gt X_j)\gt\ 0{,}5\), tak kocku \({\cal K}_i\) nazveme lepšou ako kocka \({\cal K}_j\), čo označíme zápisom \({\cal K}_i\succ {\cal K}_j\).
Pre zjednodušenie výkladu urobíme túto dohodu: ak na prvej kocke \({\cal K}_i\) padlo \(x\) bodiek a na druhej kocke \({\cal K}_j\) padlo \(y\) bodiek, tak tento jav môžeme jednoznačne interpretovať dvojciferným číslom \(10x+y\) (napr. javu, ktorý spočíva v padnutí \(2\) bodiek na prvej kocke a \(5\) bodiek na druhej kocke priradíme číslo \(25\)).
Poďme porovnať jednotlivé kocky:
Na základe týchto poznatkov skúste sformulovať vašu stratégiu voľby kocky (samozrejme, že chcete si vybrať takú kocku, aby pravdepodobnosť vašej výhry bola väčšia ako pravdepodobnosť výhry vášho súpera).
Príklad:
Terč tvorí kruh \(K\) a dve medzikružia \(M\) a \(N\). Zásah do kruhu \(K\)
je dosiahnutý pri každom výstrele s pravdepodobnosťou \(P(K)=0{,}7\) a je
hodnotený \(10\) bodmi, pre medzikružia \(M\), resp. \(N\) je pravdepodobnosť
zásahu \(P(M)=0{,}2\), resp. \(P(N)=0{,}1\) s ohodnotením \(5\), resp. \(0\)
bodov. Nech \(X\) je náhodná premenná, ktorá nadobúda hodnoty dosiahnutého súčtu
bodov pri troch nezávislých výstreloch na terč. Určme:
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X;\)
b) priemerný počet dosiahnutého súčtu bodov;
c) \(P(E(X)\lt X \leqq {\cal M}o(X))\).
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X;\)
b) priemerný počet dosiahnutého súčtu bodov;
c) \(P(E(X)\lt X \leqq {\cal M}o(X))\).
Riešenie:
a) Najprv určíme obor hodnôt \({\cal H}(X)\) danej náhodnej premennej \(X\): je
zrejmé, že pri troch výstreloch môžeme získať práve jeden z týchto súčtov bodov
\[\{0,5,10,15,20,25, 30\}={\cal H}(X)\] (pozri pravdepodobnostnú tabuľku (\ref{cc})).
Na určenie zákona rozdelenia pravdepodobnosti náhodnej premennej \(X\) je potrebné vyčísliť pravdepodobnosti nadobudnutia jednotlivých hodnôt z množiny \({\cal H}(X)\). Nech pre \(i=1,2,3\)
- \(K_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli kruh \(K\) - zrejme \(P(K_i)=0{,}7\);
- \(M_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli medzikružie \(M\), teda \(P(M_i)=0{,}2\);
- \(N_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli medzikružie \(N\), t. j. \(P(N_i)=0{,}1\).
Zoberme napr. jav \(X\!=\!0\). Tento jav nastane práve vtedy, ak všetky tri výstrely skončili v medzikruží \(N\), čo symbolicky môžeme zapísať takto: \(N_1\cap N_2\cap N_3\). Keďže ide o nezávislé výstrely, tak \[P(X\!=\!0)=P(N_1\cap N_2\cap N_3)=P(N_1)\cdot P(N_2)\cdot P(N_3)=0{,}1\cdot0{,}1\cdot0{,}1=0{,}001. \] Tento výsledok zapíšeme do pravdepodobnostnej tabuľky (\ref{cc}).
Jav \(X\!=\!5\) nastane práve vtedy, ak dva výstrely skončili v medzikruží \(N\) (dve nuly) a jeden výstrel v medzikruží \(M\) (jedna päťka). Tento jav mohol nastať v troch prípadoch (k zásahu medzikružia \(M\) mohlo dôjsť v prvom alebo druhom alebo treťom výstrele), čo môžeme zapísať takto \[(M_1\cap N_2\cap N_3)\cup (N_1\cap M_2\cap N_3)\cup (N_1\cap N_2\cap M_3).\] Javy \(M_1\cap N_2\cap N_3\), \(N_1\cap M_2\cap N_3\) a \(N_1\cap N_2\cap M_3\) sú disjunktné, a preto \[P(X\!=\!5)=P((M_1\cap N_2\cap N_3)\cup (N_1\cap M_2\cap N_3)\cup (N_1\cap N_2\cap M_3))=\] \[\qquad \qquad=P(M_1\cap N_2\cap N_3)+ P(N_1\cap M_2\cap N_3)+ P(N_1\cap N_2\cap M_3).\] Výstrely sú nezávislé, a preto \[P(X\!=\!5)=0{,}2\cdot0{,}1\cdot0{,}1+0{,}1\cdot0{,}2\cdot0{,}1+0{,}1\cdot0{,}1\cdot0{,}2=0{,}006.\]
Súčet desať sa mohol dosiahnuť dvoma spôsobmi:
-- jav \(A\): dve päťky a jedna nula (dvakrát medzikružie \(M\) a raz \(N\)) alebo
-- jav \(B\): dve nuly a jedna desiatka (dvakrát medzikružie \(N\) a raz kruh \(K\)).
Je zrejmé, že javy \(A\) a \(B\) sú disjunktné, a preto \begin{equation}\label{ab} P(X\!=\!10)=P(A\cup B)=P(A)+P(B). \end{equation} Pravdepodobnosti \(P(A)\) a \(P(B)\) určíme obdobným spôsobom ako pri výpočte \(P(X\!=\!5)\): \[P(A)=0{,}2\cdot0{,}2\cdot0{,}1+0{,}2\cdot0{,}1\cdot0{,}2+0{,}1\cdot0{,}2\cdot0{,}2=0{,}012.\] Presvedčte sa, že pre \(P(B)\) môžeme použiť túto skrátenú verziu: \[P(B)=3\cdot 0{,}7\cdot0{,}1\cdot0{,}1=0{,}021.\] Na základe (\ref{ab}) dostaneme \[P(X\!=\!10)=0{,}012+0{,}021=0{,}033\] (pozri pravdepodobnostnú tabuľku (\ref{cc})).
Súčet pätnásť dosiahneme tiež dvoma spôsobmi:
-- jav \(C\): tri päťky (trikrát medzikružie \(M\)) alebo
-- jav \(D\): jednou desiatkou, jednou päťkou a jednou nulou (raz kruh \(K\), raz medzikružie \(M\) a raz \(N\)).
Javy \(C\) a \(D\) sú disjunktné, a preto \begin{equation}\label{aa} P(X\!=\!15)=P(C\cup D)=P(C)+P(D). \end{equation} Obdobným spôsobom ako pre \(P(X\!=\!0)\) dostaneme \[P(C)=P(M_1\cap M_1\cap M_1)=P(M_1)\cdot P(M_1)\cdot P(M_1)=0{,}2\cdot0{,}2\cdot0{,}2=0{,}008. \] Jav \(D\) (jedna desiatka, jedna päťka a jedna nula) môžeme rozložiť na zjednotenie týchto šiestich disjunktných javov: \begin{equation}\label{bb} \left. \begin{array}{ccc} (M_1\cap N_2\cap K_3);\quad\a (M_1\cap K_2\cap N_3);\quad\a (N_1\cap K_2\cap M_3);\quad\\ (N_1\cap M_2\cap K_3);\quad\a (K_1\cap M_2\cap N_3);\quad\a (K_1\cap N_2\cap M_3). \end{array} \right\} \end{equation} (tí, čo sú zručnejší v kombinatorike, si určite uvedomili, že ide o permutácie troch množín \(M\), \(N\) a \(K\), pričom tých permutácii je \(3!=6\)).
\(P(D)\) je preto súčtom pravdepodobností týchto šiestich javov. Keďže výstrely sú nezávislé, tak napr. pre prvý jav z (\ref{bb}) platí \[P(M_1\cap N_2\cap K_3)= P(M_1)\cdot P(N_2)\cdot P(K_3)=0{,}2\cdot0{,}1\cdot0{,}7=0{,}014.\] Je zrejmé, že pravdepodobnosti zvyšných piatich javov z (\ref{bb}) sú také isté, a preto \[P(D)=6\cdot 0{,}014=0{,}084.\] Takto na základe (\ref{aa}) dostaneme \[P(X\!=\!15)=0{,}008+0{,}084=0{,}092. \]
Súčet dvadsať dosiahneme taktiež dvoma spôsobmi:
-- jav \(E\): dve desiatky a jedna nula alebo
-- jav \(F\): dve päťky a jedna desiatka, pričom \begin{equation}\label{dd} P(X\!=\!20)=P(E\cup F)=P(E)+P(F). \end{equation} Ak použijeme predchádzajúce poznatky, tak dostaneme \[P(E)=3\cdot 0{,}7\cdot0{,}7\cdot0{,}1=0{,}147 \] a \[P(F)=3\cdot 0{,}2\cdot0{,}2\cdot0{,}7=0{,}084. \] Takto podľa (\ref{dd}) je \[P(X\!=\!20)=0{,}147+0{,}084=0{,}231\] (pozri tabuľku (\ref{cc})).
\(X\!=\!25\) práve vtedy, keď dvakrát sa dosiahla desiatka a raz päťka. Preto \[P(X\!=\!25)=3\cdot 0{,}7\cdot 0{,}7\cdot 0{,}2=0{,}294.\]
Je zrejmé, že \(X\!=\!30\) práve vtedy, keď trikrát sa dosiahla desiatka. Teda \[P(X\!=\!30)=0{,}7\cdot 0{,}7\cdot 0{,}7=0{,}343.\]
Požadovaný zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\) dostaneme zhrnutím predchádzajúcich výsledkov, ktoré sú zapísané v nižšie uvedenej pravdepodobnostnej tabuľke: \begin{equation}\label{cc} \begin{array}{c||c|c|c|c|c|c|c} x_i \a 0 \a 5 \a 10 \a 15 \a 20 \a 25 \a 30\\ \hline P(X\!=\!x_i) =p_i\a 0{,}001 \a 0{,}006 \a 0{,}033 \a 0{,}092 \a 0{,}231 \a 0{,}294 \a 0{,}343 \end{array} \end{equation}
b) Priemerný počet dosiahnutého súčtu bodov je určený strednou hodnotou \(E(X)\) náhodnej premennej \(X\). Podľa (\ref{sh}) a (\ref{cc}) je \[E(X)=0 \cdot 0{,}001+ 5\cdot 0{,}006+ 10 \cdot 0{,}033+15\cdot 0{,}092+20\cdot 0{,}231+ 25\cdot 0{,}294+30\cdot 0{,}343,\] čo po vyčíslení dáva \(E(X)= 24\).
c) Z časti b) je známe, že \(E(X)=24\). \({\cal M}o(X)\) je najpravdepodobnejšia hodnota náhodnej premennej \(X\). Z pravdepodobnostnej tabuľky (\ref{cc}) je vidieť, že hodnota \(X\!=\!30\) je nadobúdaná s najväčšiou pravdepodobosťou \(0{,}343\). Preto \({\cal M}o(X)=30\). Našou úlohou je teda určiť \(P(24\lt X \leqq 30)\). Z tabuľky (\ref{cc}) dostaneme \[P(24\lt X \leqq 30)=P(X\!=\!25)+ P(X\!=\!30)= 0{,}294 + 0{,}343= 0{,}637.\]
Na určenie zákona rozdelenia pravdepodobnosti náhodnej premennej \(X\) je potrebné vyčísliť pravdepodobnosti nadobudnutia jednotlivých hodnôt z množiny \({\cal H}(X)\). Nech pre \(i=1,2,3\)
- \(K_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli kruh \(K\) - zrejme \(P(K_i)=0{,}7\);
- \(M_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli medzikružie \(M\), teda \(P(M_i)=0{,}2\);
- \(N_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli medzikružie \(N\), t. j. \(P(N_i)=0{,}1\).
Zoberme napr. jav \(X\!=\!0\). Tento jav nastane práve vtedy, ak všetky tri výstrely skončili v medzikruží \(N\), čo symbolicky môžeme zapísať takto: \(N_1\cap N_2\cap N_3\). Keďže ide o nezávislé výstrely, tak \[P(X\!=\!0)=P(N_1\cap N_2\cap N_3)=P(N_1)\cdot P(N_2)\cdot P(N_3)=0{,}1\cdot0{,}1\cdot0{,}1=0{,}001. \] Tento výsledok zapíšeme do pravdepodobnostnej tabuľky (\ref{cc}).
Jav \(X\!=\!5\) nastane práve vtedy, ak dva výstrely skončili v medzikruží \(N\) (dve nuly) a jeden výstrel v medzikruží \(M\) (jedna päťka). Tento jav mohol nastať v troch prípadoch (k zásahu medzikružia \(M\) mohlo dôjsť v prvom alebo druhom alebo treťom výstrele), čo môžeme zapísať takto \[(M_1\cap N_2\cap N_3)\cup (N_1\cap M_2\cap N_3)\cup (N_1\cap N_2\cap M_3).\] Javy \(M_1\cap N_2\cap N_3\), \(N_1\cap M_2\cap N_3\) a \(N_1\cap N_2\cap M_3\) sú disjunktné, a preto \[P(X\!=\!5)=P((M_1\cap N_2\cap N_3)\cup (N_1\cap M_2\cap N_3)\cup (N_1\cap N_2\cap M_3))=\] \[\qquad \qquad=P(M_1\cap N_2\cap N_3)+ P(N_1\cap M_2\cap N_3)+ P(N_1\cap N_2\cap M_3).\] Výstrely sú nezávislé, a preto \[P(X\!=\!5)=0{,}2\cdot0{,}1\cdot0{,}1+0{,}1\cdot0{,}2\cdot0{,}1+0{,}1\cdot0{,}1\cdot0{,}2=0{,}006.\]
Súčet desať sa mohol dosiahnuť dvoma spôsobmi:
-- jav \(A\): dve päťky a jedna nula (dvakrát medzikružie \(M\) a raz \(N\)) alebo
-- jav \(B\): dve nuly a jedna desiatka (dvakrát medzikružie \(N\) a raz kruh \(K\)).
Je zrejmé, že javy \(A\) a \(B\) sú disjunktné, a preto \begin{equation}\label{ab} P(X\!=\!10)=P(A\cup B)=P(A)+P(B). \end{equation} Pravdepodobnosti \(P(A)\) a \(P(B)\) určíme obdobným spôsobom ako pri výpočte \(P(X\!=\!5)\): \[P(A)=0{,}2\cdot0{,}2\cdot0{,}1+0{,}2\cdot0{,}1\cdot0{,}2+0{,}1\cdot0{,}2\cdot0{,}2=0{,}012.\] Presvedčte sa, že pre \(P(B)\) môžeme použiť túto skrátenú verziu: \[P(B)=3\cdot 0{,}7\cdot0{,}1\cdot0{,}1=0{,}021.\] Na základe (\ref{ab}) dostaneme \[P(X\!=\!10)=0{,}012+0{,}021=0{,}033\] (pozri pravdepodobnostnú tabuľku (\ref{cc})).
Súčet pätnásť dosiahneme tiež dvoma spôsobmi:
-- jav \(C\): tri päťky (trikrát medzikružie \(M\)) alebo
-- jav \(D\): jednou desiatkou, jednou päťkou a jednou nulou (raz kruh \(K\), raz medzikružie \(M\) a raz \(N\)).
Javy \(C\) a \(D\) sú disjunktné, a preto \begin{equation}\label{aa} P(X\!=\!15)=P(C\cup D)=P(C)+P(D). \end{equation} Obdobným spôsobom ako pre \(P(X\!=\!0)\) dostaneme \[P(C)=P(M_1\cap M_1\cap M_1)=P(M_1)\cdot P(M_1)\cdot P(M_1)=0{,}2\cdot0{,}2\cdot0{,}2=0{,}008. \] Jav \(D\) (jedna desiatka, jedna päťka a jedna nula) môžeme rozložiť na zjednotenie týchto šiestich disjunktných javov: \begin{equation}\label{bb} \left. \begin{array}{ccc} (M_1\cap N_2\cap K_3);\quad\a (M_1\cap K_2\cap N_3);\quad\a (N_1\cap K_2\cap M_3);\quad\\ (N_1\cap M_2\cap K_3);\quad\a (K_1\cap M_2\cap N_3);\quad\a (K_1\cap N_2\cap M_3). \end{array} \right\} \end{equation} (tí, čo sú zručnejší v kombinatorike, si určite uvedomili, že ide o permutácie troch množín \(M\), \(N\) a \(K\), pričom tých permutácii je \(3!=6\)).
\(P(D)\) je preto súčtom pravdepodobností týchto šiestich javov. Keďže výstrely sú nezávislé, tak napr. pre prvý jav z (\ref{bb}) platí \[P(M_1\cap N_2\cap K_3)= P(M_1)\cdot P(N_2)\cdot P(K_3)=0{,}2\cdot0{,}1\cdot0{,}7=0{,}014.\] Je zrejmé, že pravdepodobnosti zvyšných piatich javov z (\ref{bb}) sú také isté, a preto \[P(D)=6\cdot 0{,}014=0{,}084.\] Takto na základe (\ref{aa}) dostaneme \[P(X\!=\!15)=0{,}008+0{,}084=0{,}092. \]
Súčet dvadsať dosiahneme taktiež dvoma spôsobmi:
-- jav \(E\): dve desiatky a jedna nula alebo
-- jav \(F\): dve päťky a jedna desiatka, pričom \begin{equation}\label{dd} P(X\!=\!20)=P(E\cup F)=P(E)+P(F). \end{equation} Ak použijeme predchádzajúce poznatky, tak dostaneme \[P(E)=3\cdot 0{,}7\cdot0{,}7\cdot0{,}1=0{,}147 \] a \[P(F)=3\cdot 0{,}2\cdot0{,}2\cdot0{,}7=0{,}084. \] Takto podľa (\ref{dd}) je \[P(X\!=\!20)=0{,}147+0{,}084=0{,}231\] (pozri tabuľku (\ref{cc})).
\(X\!=\!25\) práve vtedy, keď dvakrát sa dosiahla desiatka a raz päťka. Preto \[P(X\!=\!25)=3\cdot 0{,}7\cdot 0{,}7\cdot 0{,}2=0{,}294.\]
Je zrejmé, že \(X\!=\!30\) práve vtedy, keď trikrát sa dosiahla desiatka. Teda \[P(X\!=\!30)=0{,}7\cdot 0{,}7\cdot 0{,}7=0{,}343.\]
Požadovaný zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\) dostaneme zhrnutím predchádzajúcich výsledkov, ktoré sú zapísané v nižšie uvedenej pravdepodobnostnej tabuľke: \begin{equation}\label{cc} \begin{array}{c||c|c|c|c|c|c|c} x_i \a 0 \a 5 \a 10 \a 15 \a 20 \a 25 \a 30\\ \hline P(X\!=\!x_i) =p_i\a 0{,}001 \a 0{,}006 \a 0{,}033 \a 0{,}092 \a 0{,}231 \a 0{,}294 \a 0{,}343 \end{array} \end{equation}
b) Priemerný počet dosiahnutého súčtu bodov je určený strednou hodnotou \(E(X)\) náhodnej premennej \(X\). Podľa (\ref{sh}) a (\ref{cc}) je \[E(X)=0 \cdot 0{,}001+ 5\cdot 0{,}006+ 10 \cdot 0{,}033+15\cdot 0{,}092+20\cdot 0{,}231+ 25\cdot 0{,}294+30\cdot 0{,}343,\] čo po vyčíslení dáva \(E(X)= 24\).
c) Z časti b) je známe, že \(E(X)=24\). \({\cal M}o(X)\) je najpravdepodobnejšia hodnota náhodnej premennej \(X\). Z pravdepodobnostnej tabuľky (\ref{cc}) je vidieť, že hodnota \(X\!=\!30\) je nadobúdaná s najväčšiou pravdepodobosťou \(0{,}343\). Preto \({\cal M}o(X)=30\). Našou úlohou je teda určiť \(P(24\lt X \leqq 30)\). Z tabuľky (\ref{cc}) dostaneme \[P(24\lt X \leqq 30)=P(X\!=\!25)+ P(X\!=\!30)= 0{,}294 + 0{,}343= 0{,}637.\]
Príklad:
Daná je funkcia \(F\) predpisom
\[F(x)=\left\{ \begin{array}{ll} a\a \mbox{pre } x\lt 4\\ b-\frac{64}{x^3} \a\mbox{pre } x\geqq 4, \end{array} \right. \] kde \(a, b\in R \).
a) Pre aké hodnoty \(a, b\in R \) je funkcia \(F\) distribučnou funkciou náhodnej premennej \(X\)?
b) Určte predpis hustoty pravdepodobnosti tejto náhodnej premennej \(X\).
c) Vypočítajte strednú hodnotu a smerodajnú odchýlku tejto náhodnej premennej.
d) určte \(P(E(X)\leqq X\lt D(X))\), kde \(E(X)\) je stredná hodnota a \(D(X)\) je disperzia náhodnej premennej \(X\).
\[F(x)=\left\{ \begin{array}{ll} a\a \mbox{pre } x\lt 4\\ b-\frac{64}{x^3} \a\mbox{pre } x\geqq 4, \end{array} \right. \] kde \(a, b\in R \).
a) Pre aké hodnoty \(a, b\in R \) je funkcia \(F\) distribučnou funkciou náhodnej premennej \(X\)?
b) Určte predpis hustoty pravdepodobnosti tejto náhodnej premennej \(X\).
c) Vypočítajte strednú hodnotu a smerodajnú odchýlku tejto náhodnej premennej.
d) určte \(P(E(X)\leqq X\lt D(X))\), kde \(E(X)\) je stredná hodnota a \(D(X)\) je disperzia náhodnej premennej \(X\).
Riešenie:
a) Je známe, že ak \(F\) je distribučná funkcia náhodnej premennej, tak
\begin{equation}\label{df}
\lim_{x\to-\infty}F(x)=0\qquad \mbox{a}\qquad \lim_{x\to\infty}F(x)=1.
\end{equation}
Je zrejmé, že pre danú funkciu \(F\) platí:
\[\lim_{x\to-\infty}F(x)=a\qquad \mbox{a}\qquad \lim_{x\to\infty}F(x)=b. \]
Odtiaľ na základe (\ref{df}) dostávame \(a=0\) a \(b=1.\) Je potrebné sa presvedčiť o tom, či získaná funkcia
\[F(x)=\left\{ \begin{array}{ll}
0\a \mbox{pre } x\lt 4\\
1-\frac{64}{x^3} \a\mbox{pre } x\geqq 4,
\end{array} \right. \]
spĺňa ďalšie poodmienky, ktoré sú kladené na distribučnú funkciu. Ľahko vidieť (znázornite si graf funkcie \(F\)), že
- funkcia \(F\) je neklesajúca a spojitá na množine reálnych čísel;
- oborom hodnôt funkcie \(F\) je množina \(\langle 0;1)\).
Získaná funkcia \(F\) je teda distribučnou funkciou spojitej náhodnej premennej.
b) Ak \(F\) je distribučnou funkciou náhodnej premennej \(X\), tak pre hustotu pravdepodobnosti \(f\) tejto náhodnej premennej platí: \[f(x)=F^{\prime}(x)\] (samozrejme, ak \(F^{\prime}(x)\) existuje). V našom prípade dostávame tak predpis hustoty pravdepodobnosti tejto náhodnej premennej \[f(x)=F^{\prime}(x)=\left\{ \begin{array}{ll} 0\a \mbox{pre } x\lt 4\\ \frac{192}{x^4} \a\mbox{pre } x\gt 4, \end{array} \right. \] Poznamenávame, že \(F^{\prime}(4)\) neexistuje.
c) Stredná hodnota \(E(X)\) náhodnej premennej \(X\) s hustotou pravdepodobnosti \(f\) je definovaná vzťahom \[E(X)=\int\limits_{-\infty}^{\infty }\!\!x\cdot f(x)\,\md x.\] V našom prípade je hustota pravdepodobnosti na intervale \((-\infty ; 4)\) rovná nule, a preto \[E(X)=\int\limits_{4}^{\infty }\!\!x\cdot \frac{192}{x^4}\,\md x= \int\limits_{4}^{\infty }\frac{192}{x^3}\,\md x=\Bigg[ \frac{-96}{x^2}\Bigg]_4^{\infty }= 6.\] Pre smerodajnú odchýlku \(\sigma(X)\) náhodnej premennej platí: \[\sigma(X)=\sqrt{D(X)},\] kde \(D(X)\) je disperzia náhodnej premennej, ktorá je je definovaná vzťahom \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] V našom prípade dostávame (opäť si treba všimnúť, že hustota pravdepodobnosti \(f\) je na intervale \((-\infty ; 4)\) rovná nule) \[D(X)=\int\limits_{4}^{\infty } \!\big[x-6\big]^2\cdot \frac{192}{x^4}\,\md x\stackrel{\star}{=}12\] (presvedčte sa o správnosti rovnosti označenej symbolom \(\star\)). Odtiaľ \(\sigma(X)=\sqrt{12}=2\sqrt3\).
d) Vzhľadom na výsledky z časti c) tejto úlohy, máme učiť \(P(6\leqq X\lt 12)\). Túto pravdepodobnosť môžeme stanoviť napr. podľa základnej vlastnosti distribučnej funkcie \(F\) spojitej náhodnej premennej \(X\): pre ľubovoľné reálne čísla \(a \lt b\) platí: \[P(a\leqq X\lt b)=F(b)-F(a),\] čo v našom prípade dáva \[P(6\leqq X\lt 12)=F(12)-F(6)=\Big(1-\frac{64}{12^3} \Big)-\Big(1-\frac{64}{6^3} \Big)=\frac{7}{27}.\] Túto úlohu sme mohli vyriešiť aj pomocou hustoty pravdepodobnosti \(f\) tejto náhodnej premennej \(X\), to takto: \[P(6\leqq X\lt 12)=\int\limits_{4}^{12} \! f(x)\md x=\int\limits_{4}^{12} \! \frac{192}{x^4}\md x=\Bigg[ \frac{-64}{x^3}\Bigg]_4^{12}=\frac{7}{27}.\]
- funkcia \(F\) je neklesajúca a spojitá na množine reálnych čísel;
- oborom hodnôt funkcie \(F\) je množina \(\langle 0;1)\).
Získaná funkcia \(F\) je teda distribučnou funkciou spojitej náhodnej premennej.
b) Ak \(F\) je distribučnou funkciou náhodnej premennej \(X\), tak pre hustotu pravdepodobnosti \(f\) tejto náhodnej premennej platí: \[f(x)=F^{\prime}(x)\] (samozrejme, ak \(F^{\prime}(x)\) existuje). V našom prípade dostávame tak predpis hustoty pravdepodobnosti tejto náhodnej premennej \[f(x)=F^{\prime}(x)=\left\{ \begin{array}{ll} 0\a \mbox{pre } x\lt 4\\ \frac{192}{x^4} \a\mbox{pre } x\gt 4, \end{array} \right. \] Poznamenávame, že \(F^{\prime}(4)\) neexistuje.
c) Stredná hodnota \(E(X)\) náhodnej premennej \(X\) s hustotou pravdepodobnosti \(f\) je definovaná vzťahom \[E(X)=\int\limits_{-\infty}^{\infty }\!\!x\cdot f(x)\,\md x.\] V našom prípade je hustota pravdepodobnosti na intervale \((-\infty ; 4)\) rovná nule, a preto \[E(X)=\int\limits_{4}^{\infty }\!\!x\cdot \frac{192}{x^4}\,\md x= \int\limits_{4}^{\infty }\frac{192}{x^3}\,\md x=\Bigg[ \frac{-96}{x^2}\Bigg]_4^{\infty }= 6.\] Pre smerodajnú odchýlku \(\sigma(X)\) náhodnej premennej platí: \[\sigma(X)=\sqrt{D(X)},\] kde \(D(X)\) je disperzia náhodnej premennej, ktorá je je definovaná vzťahom \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] V našom prípade dostávame (opäť si treba všimnúť, že hustota pravdepodobnosti \(f\) je na intervale \((-\infty ; 4)\) rovná nule) \[D(X)=\int\limits_{4}^{\infty } \!\big[x-6\big]^2\cdot \frac{192}{x^4}\,\md x\stackrel{\star}{=}12\] (presvedčte sa o správnosti rovnosti označenej symbolom \(\star\)). Odtiaľ \(\sigma(X)=\sqrt{12}=2\sqrt3\).
d) Vzhľadom na výsledky z časti c) tejto úlohy, máme učiť \(P(6\leqq X\lt 12)\). Túto pravdepodobnosť môžeme stanoviť napr. podľa základnej vlastnosti distribučnej funkcie \(F\) spojitej náhodnej premennej \(X\): pre ľubovoľné reálne čísla \(a \lt b\) platí: \[P(a\leqq X\lt b)=F(b)-F(a),\] čo v našom prípade dáva \[P(6\leqq X\lt 12)=F(12)-F(6)=\Big(1-\frac{64}{12^3} \Big)-\Big(1-\frac{64}{6^3} \Big)=\frac{7}{27}.\] Túto úlohu sme mohli vyriešiť aj pomocou hustoty pravdepodobnosti \(f\) tejto náhodnej premennej \(X\), to takto: \[P(6\leqq X\lt 12)=\int\limits_{4}^{12} \! f(x)\md x=\int\limits_{4}^{12} \! \frac{192}{x^4}\md x=\Bigg[ \frac{-64}{x^3}\Bigg]_4^{12}=\frac{7}{27}.\]
Príklad:
Pre funkciu, ktorá je daná predpisom \(f(x)=\mathrm{e}^{k|x|}\), \(x\in R,\) určme:
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) \(P(E(X)\lt X \lt D(X))\);
c) \({\cal M}o(X).\)
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) \(P(E(X)\lt X \lt D(X))\);
c) \({\cal M}o(X).\)
Riešenie:
a) Najprv overíme podmienky, ktoré musí spĺňať hustota pravdepodobnosti náhodnej premennej.
1. Daná funkcia nadobúda len kladné hodnoty, a teda je na svojom definičnom obore nezáporná.
2. Z normalizačnej podmienky (\ref{np}) pre hustotu \(f\) danej náhodnej premennej dostaneme \[\int\limits_{-\infty}^{\infty } \!\mathrm{e}^{k|x|}\,\md x=2\cdot \int\limits_{0}^{\infty } \!\mathrm{e}^{kx}\,\md x=2\cdot \Bigg[ \frac{\mathrm{e}^{kx}}{k}\Bigg]_0^{\infty}\stackrel{\star}{=}\frac{-2}{k}=1,\] pričom rovnosť \((\star)\) platí len pre \(k\lt 0\) (pre \(k\geqq 0\) integrál diverguje). Odtiaľ \(k=-2\) (overte, že \(k=-2\) vyhovuje všetkým požiadavkám hustoty).
b) Keďže získaná hustota pravdepodobnosti je párna funkcia, tak pre strednú hodnotu náhodnej premennej \(X\) je \(E(X)=0\) a na základe definície jej disperzie \(D(X)\) \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] je \[D(X)=\int\limits_{-\infty}^{\infty } \!x^2\cdot \mathrm{e}^{-2|x|}\,\md x=2\cdot \int\limits_{0}^{\infty } \!x^2\cdot \mathrm{e}^{-2x}\,\md x=\Bigg[ \frac{(-2x^2-2x-1)\mathrm{e}^{-2x}}{2}\Bigg]_0^{\infty }=0{,}5.\] Na základe známeho vzťahu \[P(a\lt X\lt b)=\int\limits_{a}^{b} \! f(x)\md x,\] kde \(a\lt b\) a \(f\) je hustota, dostaneme \[P(E(X)\lt X\lt D(X))=P(0\lt X\lt 0{,}5)=\int\limits_{0}^{0{,}5 } \! \mathrm{e}^{-2x}\,\md x= \Bigg[ \frac{\mathrm{e}^{-2x}}{-2}\Bigg]_0^{0{,}5}\!\!\!=\frac{\mathrm{e}-1}{2\mathrm{e}}\approx 0{,}31606.\] c) Uvažovaná hustota pravdepodobnosti má jediné lokálne maximum v bode \(0\) (znázornite si graf získanej hustoty \(f\)), a preto \({\cal M}o(X)=0.\)
1. Daná funkcia nadobúda len kladné hodnoty, a teda je na svojom definičnom obore nezáporná.
2. Z normalizačnej podmienky (\ref{np}) pre hustotu \(f\) danej náhodnej premennej dostaneme \[\int\limits_{-\infty}^{\infty } \!\mathrm{e}^{k|x|}\,\md x=2\cdot \int\limits_{0}^{\infty } \!\mathrm{e}^{kx}\,\md x=2\cdot \Bigg[ \frac{\mathrm{e}^{kx}}{k}\Bigg]_0^{\infty}\stackrel{\star}{=}\frac{-2}{k}=1,\] pričom rovnosť \((\star)\) platí len pre \(k\lt 0\) (pre \(k\geqq 0\) integrál diverguje). Odtiaľ \(k=-2\) (overte, že \(k=-2\) vyhovuje všetkým požiadavkám hustoty).
b) Keďže získaná hustota pravdepodobnosti je párna funkcia, tak pre strednú hodnotu náhodnej premennej \(X\) je \(E(X)=0\) a na základe definície jej disperzie \(D(X)\) \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] je \[D(X)=\int\limits_{-\infty}^{\infty } \!x^2\cdot \mathrm{e}^{-2|x|}\,\md x=2\cdot \int\limits_{0}^{\infty } \!x^2\cdot \mathrm{e}^{-2x}\,\md x=\Bigg[ \frac{(-2x^2-2x-1)\mathrm{e}^{-2x}}{2}\Bigg]_0^{\infty }=0{,}5.\] Na základe známeho vzťahu \[P(a\lt X\lt b)=\int\limits_{a}^{b} \! f(x)\md x,\] kde \(a\lt b\) a \(f\) je hustota, dostaneme \[P(E(X)\lt X\lt D(X))=P(0\lt X\lt 0{,}5)=\int\limits_{0}^{0{,}5 } \! \mathrm{e}^{-2x}\,\md x= \Bigg[ \frac{\mathrm{e}^{-2x}}{-2}\Bigg]_0^{0{,}5}\!\!\!=\frac{\mathrm{e}-1}{2\mathrm{e}}\approx 0{,}31606.\] c) Uvažovaná hustota pravdepodobnosti má jediné lokálne maximum v bode \(0\) (znázornite si graf získanej hustoty \(f\)), a preto \({\cal M}o(X)=0.\)
Príklad:
Pre funkciu \(f\), ktorej graf je načrtnutý na obrázku, určme:
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie \(F\) tejto náhodnej premennej \(X\) a načrtnime jej graf;
c) strednú hodnotu náhodnej premennej \(X\);
d) smerodajnú odchýlku náhodnej premennej \(X\);
e) \(P(-0{,}5\leqq X\leqq 1)\).
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie \(F\) tejto náhodnej premennej \(X\) a načrtnime jej graf;
c) strednú hodnotu náhodnej premennej \(X\);
d) smerodajnú odchýlku náhodnej premennej \(X\);
e) \(P(-0{,}5\leqq X\leqq 1)\).
Riešenie:
a) Z uvedeného grafu je vidieť, že funkcia \(f\) je nezáporná na množine reálnych
čísel, a teda je splnená prvá požiadavka, ktorú musí spĺňať hustota pravdepodobnosti
náhodnej premennej. Druhú, tzv. normalizačnú podmienku pre hustotu \(f\)
\[\int\limits_{-\infty}^{\;\infty } \!\!\!f(x),\md x=1,\]
môžeme zabezpečiť z geometrickej interpretácie tohto integrálu: obsah útvaru, ktorý
je ohraničený grafom hustoty a osou \(x\) je rovný jednej. V našom prípade uvažovaný
útvar pozostáva z obdĺžnika so stranami veľkostí \(1\) a \(k\) a pravouhlého trojuholníka
s odvesnami veľkostí \(2\) a \(k\). Súčet ich obsahov musí byť rovný jednej:
\[1\cdot k+\frac{2\cdot k}{2}=1\]
a odtiaľ \(k=0{,}5.\)
b) Je známe, že ak \(f\) je hustota pravdepodobnosti a \(F\) je distribučná funkcia náhodnej premennej \(X\), tak platí \begin{equation}\label{husdf} F(x)=\int\limits_{-\infty}^{\,x} \!\!\!f(t)\md t. \end{equation} Často sa robia chyby pri použití uvedeného vzťahu. Tu si musíme uvedomiť, že funkcia \(f\) je v našom prípade definovaná na jednotlivých intervaloch odlišnými predpismi. Presvedčte sa, že je daná týmto zápisom (všimnite si obrázok grafu funkcie \(f\)): \begin{equation}\label{huspr} f(x)=\left\{ \begin{array}{ll} 0{,}5 \a \mbox{pre } x\in(-1; 0),\\ \dfrac{2-x}{4} \a\mbox{pre } x\in (0;2),\\ 0 \a\mbox{pre } x\in (-\infty ;-1)\cup(2;\infty ). \end{array} \right. \end{equation} V bodoch \(-1\), \(0\) a \(2\) nie je definovaná -- to pri výpočte integrálu (\ref{husdf}) nie je podstatné. Na základe (\ref{husdf}) a (\ref{huspr}) dostaneme
\(\bullet\) ak \(x\in (-\infty ;-1\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,x} \!\!\!f(t)\md t=\int\limits_{-\infty\;\;}^{\,x} \!\!\!0\md t=0;\] \(\bullet\) ak \(x\in (-1 ;0\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t=0+\bigg[0{,}5t\bigg]^x_{-1}=\frac{x+1}{2}\,;\] \(\bullet\) ak \(x\in (0 ;2\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t+\int\limits_{0}^{\,x} \!\frac{2-t}{4}\md t= 0+0{,}5+\bigg[\frac{2t-\frac{t^2}{2}}{4}\bigg]^{\!x}_{\!0}=\frac{-x^2+4x+4}{8}\,;\] \(\bullet\) ak \(x\in (2 ;\infty)\), tak by malo byť \(F(x)=1\). Skutočne \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t+\int\limits_{0}^{\;2} \!\frac{2-t}{4}\md t+\int\limits_{2}^{\;x} \!\!0\md t= 0+0{,}5+0{,}5+0=1.\] Zhrnutím týchto výpočtov dostaneme predpis distribučnej funkcie náhodnej premennej \(X\): \begin{equation}\label{dfpr} F(x)=\left\{ \begin{array}{ll} 0 \a \mbox{pre } x\in(-1; 0\rangle,\\ \dfrac{x+1}{2} \a\mbox{pre } x\in (-1;0\rangle,\\[2.5mm] \dfrac{-x^2+4x+4}{8}\a\mbox{pre } x\in (0 ;2\rangle,\\ 1\a\mbox{pre } x\in (2;\infty ). \end{array} \right. \end{equation} Jej graf je načrtnutý na nasledujúcom obrázku. Odporúčame si na ňom overiť platnosť základných vlastností distribučnej funkcie náhodnej premennej.
c) Na základe definície strednej hodnoty \(E(X)\) náhodnej premennej \(X\) je \[E(X)=\int\limits_{-\infty}^{\infty } \!x\cdot f(x)\,\md x, \] kde \(f\) je jej hustota pravdepodobnosti. Vzhľadom na (\ref{huspr}) dostaneme \[E(X)=\int\limits_{-\infty}^{-1} \!x\cdot 0\,\md x+ \int\limits_{-1}^{\;0} \!x\cdot 0{,}5 \,\md x+ \int\limits_{0}^{\;2} \!x\cdot \frac{2-x}{4}\,\md x+ \int\limits_{2}^{\infty} \!x\cdot 0 \,\md x= \frac{1}{12}.\]
d) Na určenie smerodajnej odchýlky \(\sigma(X)=\sqrt{D(X)}\) náhodnej premennej \(X\) potrebujeme najskôr vypočítať jej disperziu \(D(X)\), pre ktorú platí vzorec \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] kde \(f\) je jej hustota pravdepodobnosti. Keďže \(E(X)=1/12\), tak na základe (\ref{huspr}) dostaneme \[D(X)=\int\limits_{-\infty}^{-1 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot 0\md x+ \int\limits_{-1}^{\,0 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot \frac{1}{2}\,\md x+ \int\limits_{0}^{\,2 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot \frac{2-x}{4}\,\md x+\] \[+\int\limits_{2}^{\infty } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot 0\,\md x=0+\frac{61}{288}+\frac{9}{32}+0=\frac{71}{144}\,.\phantom{aaaaaaaaaamm}\] Teda \[\sigma(X)=\sqrt{\frac{71}{144}}=\frac{\sqrt{71}}{12}\,.\]
e) Požadovanú pravdepodobnosť by sme mohli získať zo vzťahu \[P(-0{,}5\leqq X\leqq 1)=\int\limits_{\!\!-0{,}5}^{\,1} \!\! f(x)\md x\,,\] kde \(f\) je hustota danej náhodnej premennej \(X\) (pozri jej predpis (\ref{huspr})). Keďže z časti b) poznáme predpis distribučnej funkcie \(F\), tak môžeme využiť aj vzorec \[P(-0{,}5\leqq X\leqq 1)=F(1)-F(-0{,}5).\] Odtiaľ vzhľadom na (\ref{dfpr}) dostaneme \[P(-0{,}5\leqq X\le 1)=F(1)-F(-0{,}5)=\dfrac{-1^2+4\cdot 1+4}{8}-\dfrac{-0{,}5+1}{2}=\frac{5}{8}\,.\]
b) Je známe, že ak \(f\) je hustota pravdepodobnosti a \(F\) je distribučná funkcia náhodnej premennej \(X\), tak platí \begin{equation}\label{husdf} F(x)=\int\limits_{-\infty}^{\,x} \!\!\!f(t)\md t. \end{equation} Často sa robia chyby pri použití uvedeného vzťahu. Tu si musíme uvedomiť, že funkcia \(f\) je v našom prípade definovaná na jednotlivých intervaloch odlišnými predpismi. Presvedčte sa, že je daná týmto zápisom (všimnite si obrázok grafu funkcie \(f\)): \begin{equation}\label{huspr} f(x)=\left\{ \begin{array}{ll} 0{,}5 \a \mbox{pre } x\in(-1; 0),\\ \dfrac{2-x}{4} \a\mbox{pre } x\in (0;2),\\ 0 \a\mbox{pre } x\in (-\infty ;-1)\cup(2;\infty ). \end{array} \right. \end{equation} V bodoch \(-1\), \(0\) a \(2\) nie je definovaná -- to pri výpočte integrálu (\ref{husdf}) nie je podstatné. Na základe (\ref{husdf}) a (\ref{huspr}) dostaneme
\(\bullet\) ak \(x\in (-\infty ;-1\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,x} \!\!\!f(t)\md t=\int\limits_{-\infty\;\;}^{\,x} \!\!\!0\md t=0;\] \(\bullet\) ak \(x\in (-1 ;0\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t=0+\bigg[0{,}5t\bigg]^x_{-1}=\frac{x+1}{2}\,;\] \(\bullet\) ak \(x\in (0 ;2\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t+\int\limits_{0}^{\,x} \!\frac{2-t}{4}\md t= 0+0{,}5+\bigg[\frac{2t-\frac{t^2}{2}}{4}\bigg]^{\!x}_{\!0}=\frac{-x^2+4x+4}{8}\,;\] \(\bullet\) ak \(x\in (2 ;\infty)\), tak by malo byť \(F(x)=1\). Skutočne \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t+\int\limits_{0}^{\;2} \!\frac{2-t}{4}\md t+\int\limits_{2}^{\;x} \!\!0\md t= 0+0{,}5+0{,}5+0=1.\] Zhrnutím týchto výpočtov dostaneme predpis distribučnej funkcie náhodnej premennej \(X\): \begin{equation}\label{dfpr} F(x)=\left\{ \begin{array}{ll} 0 \a \mbox{pre } x\in(-1; 0\rangle,\\ \dfrac{x+1}{2} \a\mbox{pre } x\in (-1;0\rangle,\\[2.5mm] \dfrac{-x^2+4x+4}{8}\a\mbox{pre } x\in (0 ;2\rangle,\\ 1\a\mbox{pre } x\in (2;\infty ). \end{array} \right. \end{equation} Jej graf je načrtnutý na nasledujúcom obrázku. Odporúčame si na ňom overiť platnosť základných vlastností distribučnej funkcie náhodnej premennej.
c) Na základe definície strednej hodnoty \(E(X)\) náhodnej premennej \(X\) je \[E(X)=\int\limits_{-\infty}^{\infty } \!x\cdot f(x)\,\md x, \] kde \(f\) je jej hustota pravdepodobnosti. Vzhľadom na (\ref{huspr}) dostaneme \[E(X)=\int\limits_{-\infty}^{-1} \!x\cdot 0\,\md x+ \int\limits_{-1}^{\;0} \!x\cdot 0{,}5 \,\md x+ \int\limits_{0}^{\;2} \!x\cdot \frac{2-x}{4}\,\md x+ \int\limits_{2}^{\infty} \!x\cdot 0 \,\md x= \frac{1}{12}.\]
d) Na určenie smerodajnej odchýlky \(\sigma(X)=\sqrt{D(X)}\) náhodnej premennej \(X\) potrebujeme najskôr vypočítať jej disperziu \(D(X)\), pre ktorú platí vzorec \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] kde \(f\) je jej hustota pravdepodobnosti. Keďže \(E(X)=1/12\), tak na základe (\ref{huspr}) dostaneme \[D(X)=\int\limits_{-\infty}^{-1 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot 0\md x+ \int\limits_{-1}^{\,0 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot \frac{1}{2}\,\md x+ \int\limits_{0}^{\,2 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot \frac{2-x}{4}\,\md x+\] \[+\int\limits_{2}^{\infty } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot 0\,\md x=0+\frac{61}{288}+\frac{9}{32}+0=\frac{71}{144}\,.\phantom{aaaaaaaaaamm}\] Teda \[\sigma(X)=\sqrt{\frac{71}{144}}=\frac{\sqrt{71}}{12}\,.\]
e) Požadovanú pravdepodobnosť by sme mohli získať zo vzťahu \[P(-0{,}5\leqq X\leqq 1)=\int\limits_{\!\!-0{,}5}^{\,1} \!\! f(x)\md x\,,\] kde \(f\) je hustota danej náhodnej premennej \(X\) (pozri jej predpis (\ref{huspr})). Keďže z časti b) poznáme predpis distribučnej funkcie \(F\), tak môžeme využiť aj vzorec \[P(-0{,}5\leqq X\leqq 1)=F(1)-F(-0{,}5).\] Odtiaľ vzhľadom na (\ref{dfpr}) dostaneme \[P(-0{,}5\leqq X\le 1)=F(1)-F(-0{,}5)=\dfrac{-1^2+4\cdot 1+4}{8}-\dfrac{-0{,}5+1}{2}=\frac{5}{8}\,.\]
Príklad:
Pravdepodobnosť zhotovenia štandardnej súčiastky je \(0{,}9\). Z vyrobenej série
súčiastok kontrolór vyberá postupne súčiastky a kontroluje ich kvalitu. Ak je
súčiastka kvalitná, kontrolór vyberie ďalšiu, ale vyberie najviac \(5\) súčiastok.
Ak kontrolovaná súčiastka nezodpovedá štandardu, kontrola sa zastaví a séria súčiastok
sa vyradí. Určte:
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu kontrolovaných súčiastok;
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) pravdepodobnosť toho, že budú kontrolované aspoň tri súčiastky;
d) strednú hodnotu, disperziu a modus náhodnej premennej \(X\).
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu kontrolovaných súčiastok;
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) pravdepodobnosť toho, že budú kontrolované aspoň tri súčiastky;
d) strednú hodnotu, disperziu a modus náhodnej premennej \(X\).
Príklad:
Terč tvorí kruh \(K\) a dve medzikružia \(M\) a \(N\). Zásah do kruhu \(K\)
znamená \(10\) bodov, zásah do medzikružia \(M\) \(5\) bodov a do \(N\)
znamená \(-1\) bod. Pravdepodobnosť zásahu kruhu \(K\) je pri každom výstrele
\(0{,}5\) a pre \(M\), resp. \(N\) sú pravdepodobnosti zásahu \(0{,}3\),
resp. \(0{,}2\) Určte:
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty súčtu dosiahnutých bodov pri troch nezávislých výstreloch na terč;
b) strednú hodnotu \(E(X)\) a disperziu \(D(X)\);
c) \(P(X\geqq E(X))\); \(\qquad P(X\leqq \sigma(X))\); \(\qquad P(X\gt D(X))\).
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty súčtu dosiahnutých bodov pri troch nezávislých výstreloch na terč;
b) strednú hodnotu \(E(X)\) a disperziu \(D(X)\);
c) \(P(X\geqq E(X))\); \(\qquad P(X\leqq \sigma(X))\); \(\qquad P(X\gt D(X))\).
Príklad:
Nech \(X\) je náhodná premenná, ktorá nadobúda hodnoty maximálneho počtu hodených
bodov na dvoch hracích kockách (t. j. nadobúda hodnoty \(\max\{b_1,b_2\}\), kde
\(b_1\) je počet bodov na prvej kocke a \(b_2\) je počet bodov na druhej kocke ). Určte:
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\); b) \(E(X)\); c) smerodajnú odchýlku náhodnej premennej \(X\); d) \({\cal M}o(X).\)
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\); b) \(E(X)\); c) smerodajnú odchýlku náhodnej premennej \(X\); d) \({\cal M}o(X).\)
Príklad:
Rozdelenie pravdepodobnosti náhodnej premennej \(X\) so strednou hodnotou \(5{,}18\)
je dané pravdepodobnostnou tabuľkou
\(\phantom{mmmmmmmm}\begin{array}{c||c|c|c|c|c} x_i \a -3 \a 0 \a 2 \a 6 \a x_5\\ \hline P(X=x_i)\a 0{,}06 \a 0{,}14 \a 0{,}2 \a 0{,}26 \a p_5 \end{array} \)
Určte: a) neznáme hodnoty \(x_5\) a \(p_5\); b) disperziu a modus náhodnej premennej \(X\); c) \(P(-1\leqq X \lt 6)\) a \(P(5\lt X \leqq 12)\).
\(\phantom{mmmmmmmm}\begin{array}{c||c|c|c|c|c} x_i \a -3 \a 0 \a 2 \a 6 \a x_5\\ \hline P(X=x_i)\a 0{,}06 \a 0{,}14 \a 0{,}2 \a 0{,}26 \a p_5 \end{array} \)
Určte: a) neznáme hodnoty \(x_5\) a \(p_5\); b) disperziu a modus náhodnej premennej \(X\); c) \(P(-1\leqq X \lt 6)\) a \(P(5\lt X \leqq 12)\).
Príklad:
Daná je funkcia
\[f(x)=\left\{\begin{array}{ll}
k\cdot (4x-x^3)\a \mbox{pre } x\in (0;2);\\
0 \a \mbox{pre } x\not\in (0;2).
\end{array} \right. \]
Určte:
a) pre akú hodnotu \(k\in R\) je funkcia \(f\) hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) \(E(X)\),\quad \(\sigma (X)\),\quad \(P(1\leqq X \lt E(X))\)\quad a \quad \(P(D(X)\lt X\leqq 3)\).
a) pre akú hodnotu \(k\in R\) je funkcia \(f\) hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) \(E(X)\),\quad \(\sigma (X)\),\quad \(P(1\leqq X \lt E(X))\)\quad a \quad \(P(D(X)\lt X\leqq 3)\).
Príklad:
Pre funkciu \(f\), ktorej graf je načrtnutý na obrázku, určte:
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie \(F\) tejto náhodnej premennej \(X\) a načrtnite jej graf;
c) strednú hodnotu náhodnej premennej \(X\);
d) disperziu náhodnej premennej \(X\);
e) \(P(|X|\lt 0{,}5)\).
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie \(F\) tejto náhodnej premennej \(X\) a načrtnite jej graf;
c) strednú hodnotu náhodnej premennej \(X\);
d) disperziu náhodnej premennej \(X\);
e) \(P(|X|\lt 0{,}5)\).
Úlohy:
Úloha:
Uvažujme tri neštandardné hracie kocky, pričom na ich stenách sú počty bodiek od
\(1\) do \(6\), ale počty bodiek sa na jednej kocke môžu aj opakovať. Nech sú to
kocky \({\cal K}_1=\{6,6,1,1,1,1\}\), \({\cal K}_2=\{5,5,2,2,2,2\}\) a \({\cal K}_3=
\{4,3,3,3,3,3\}\) (t. j. napr. štyri steny kocky \({\cal K}_1\) majú po jednej
bodke a na zvyšných dvoch stenách je po šesť bodiek).
Máte si zvoliť jednu z tých kociek a váš súper si potom vyberie jednu zo zvyšných dvoch kociek. Obaja hodíte svojou kockou a vyhráva ten, komu padlo väčšie číslo (t. j. stena s väčším počtom bodiek). Akú stratégiu voľby kocky by ste zvolili?
Máte si zvoliť jednu z tých kociek a váš súper si potom vyberie jednu zo zvyšných dvoch kociek. Obaja hodíte svojou kockou a vyhráva ten, komu padlo väčšie číslo (t. j. stena s väčším počtom bodiek). Akú stratégiu voľby kocky by ste zvolili?
10. Vybrané rozdelenia pravdepodobnosti
Riešené úlohy:
Príklad:
V zásielke je \(33\) výrobkov. Pravdepodobnosť toho, že sa výrobok počas prepravy
poškodí, je pre každý výrobok \(0{,}1\), pričom možné poškodenie ľubovoľného výrobku
nezávisí od stavu ostatných výrobkov. Určme pravdepodobnosť toho, že z týchto
výrobkov sa pri preprave poškodí
a) viac výrobkov ako by sme mohli v priemere očakávať;
b) menej výrobkov ako by sme mohli s najväčšou pravdepodobnosťou očakávať.
a) viac výrobkov ako by sme mohli v priemere očakávať;
b) menej výrobkov ako by sme mohli s najväčšou pravdepodobnosťou očakávať.
Príklad:
V urne sú \(4\) biele guľky a \(6\) čiernych guliek. Náhodne z nej vyberieme
I. s návratom;
II. bez návratu.
päť guliek. Určme
a) zákon rozdelenia pravdepodobnosti náhodnej premennej, ktorá nadobúda hodnoty počtu vytiahnutých bielych guliek;
b) priemerný počet vytiahnutých bielych guliek;
c) disperziu počtu vytiahnutých bielych guliek;
d) pravdepodobnosť toho, že vytiahneme viac bielych guliek ako čiernych;
e) najpravdepodobnejší počet vytiahnutých bielych guliek.
I. s návratom;
II. bez návratu.
päť guliek. Určme
a) zákon rozdelenia pravdepodobnosti náhodnej premennej, ktorá nadobúda hodnoty počtu vytiahnutých bielych guliek;
b) priemerný počet vytiahnutých bielych guliek;
c) disperziu počtu vytiahnutých bielych guliek;
d) pravdepodobnosť toho, že vytiahneme viac bielych guliek ako čiernych;
e) najpravdepodobnejší počet vytiahnutých bielych guliek.
Príklad:
Internetovú stránku navštívi za sledované obdobie v priebehu jednej hodiny v priemere
\(30\) záujemcov (predpokladáme, že ich návštevy sú nezávislé a ich počet sa riadi
Poissonovým rozdelením pravdepodobnosti). Určme:
I. pravdepodobnosť toho, že v priebehu štyroch minút navštívi túto stránku: a) jeden návštevník; b) aspoň jeden návštevník; c) nie menej než traja a menej ako jedenásti návštevníci;
II. a) pravdepodobnosť najpravdepodobnejšieho počtu návštev stránky počas štyroch minút; b) minimálny počet návštev stránky počas dvadsiatich minút, ktorý nebude väčší s pravdepodobnosťou aspoň \(0{,}99.\)
I. pravdepodobnosť toho, že v priebehu štyroch minút navštívi túto stránku: a) jeden návštevník; b) aspoň jeden návštevník; c) nie menej než traja a menej ako jedenásti návštevníci;
II. a) pravdepodobnosť najpravdepodobnejšieho počtu návštev stránky počas štyroch minút; b) minimálny počet návštev stránky počas dvadsiatich minút, ktorý nebude väčší s pravdepodobnosťou aspoň \(0{,}99.\)
Príklad:
Doba životnosti výrobku má exponenciálne rozdelenie pravdepodobnosti so strednou
hodnotou \(2000\) dní. Určme:
a) pravdepodobnosť toho, že výrobok bude funkčný aspoň \(3000\) dní;
b) pravdepodobnosť toho, že výrobok nebude funkčný dlhšie ako je jeho priemerná doba životnosti;
c) maximálnu záručnú dobu \(z\), ktorú chce poskytnúť jeho výrobca, ak pripúšťa maximálne \(5\) percent reklamačných výrobkov.
a) pravdepodobnosť toho, že výrobok bude funkčný aspoň \(3000\) dní;
b) pravdepodobnosť toho, že výrobok nebude funkčný dlhšie ako je jeho priemerná doba životnosti;
c) maximálnu záručnú dobu \(z\), ktorú chce poskytnúť jeho výrobca, ak pripúšťa maximálne \(5\) percent reklamačných výrobkov.
Príklad:
Hmotnosť vyrábaného závažia má normálne rozdelenie pravdepodobnosti so strednou
hodnotou \(10\,g\), pričom výrobca uvádza jej smerodajnú odchýlku \(0{,}02\,g\).
Určme pravdepodobnosť toho, že náhodne kúpené závažie bude mať skutočnú hmotnosť
a) aspoň \(10{,}03\,g;\)
b) menšiu ako \(9{,}99\,g;\)
c) aspoň \(10\,g\) a nie viac ako \(10{,}05\,g.\)
a) aspoň \(10{,}03\,g;\)
b) menšiu ako \(9{,}99\,g;\)
c) aspoň \(10\,g\) a nie viac ako \(10{,}05\,g.\)
Príklad:
Meranie ampérmetrom je zaťažené systematickou chybou \(20\,mA\) a náhodné chyby
merania majú normálne rozdelenie pravdepodobnosti so smerodajnou odchýlkou \(5\,mA\).
Vykonáme na ňom jedno meranie. S akou pravdepodobnosťou sa bude líšiť chyba nameranej
hodnoty maximálne o \(12\,mA\) od
a) strednej hodnoty očakávanej chyby merania;
b) skutočnej meranej hodnoty?
c) Aká môže byť s pravdepodobnosťou \(0{,}95\) maximálna odchýlka chyby merania od jej strednej hodnoty?
a) strednej hodnoty očakávanej chyby merania;
b) skutočnej meranej hodnoty?
c) Aká môže byť s pravdepodobnosťou \(0{,}95\) maximálna odchýlka chyby merania od jej strednej hodnoty?
Riešenie:
Nech \(X\) je náhodná premenná, ktorá nadobúda hodnoty chyby pri jednom meraní daným
ampérmetrom. Systematická chyba je vlastne priemerná chyba t. j. \(E(X) =20\). Je daná
smerodajná odchýlka \(\sigma(X) =5\) a je známe, že náhodná premenná \(X\) má normálne
rozdelenie -- jej parametre sú \(\mu=20\) a \(\sigma=5\) (t. j. \(X\sim norm(20,5)\)).
a) Našou úlohou je určiť pravdepodobnosť \(P(|X-\mu|\leqq 12)\stackrel{\star}{=}P(|X-20|\lt 12)\) (v rovnosti \(\stackrel{\star}{=}\) si treba uvedomiť, že \(X\) je spojitá náhodná premenná). Z (\ref{nr1}) pre \(\varepsilon =12\) dostaneme \[P(|X-20|\lt 12)=2\cdot\Phi\Big(\frac{12}{5} \Big)-1\approx 2\cdot 0{,}9918-1= 0{,}9836, \] kde hodnotu \(\Phi(2{,}4)\approx 0{,}9918\) sme získali z tabuliek distribučnej funkcie \(\Phi\) náhodnej premennej \(norm(0;1)\) alebo v MATLABe pomocou \(normcdf(2.4)\).
b) Teraz chceme vypočítať pravdepodobnosť javu, ktorý spočíva v tom, že \(|X|\leqq 12\), t. j. \(-12\leqq X\leqq 12\). Máme \[P(-12\leqq X\leqq 12)=F(12)-F(-12)\stackrel{\star}{\approx} 0{,}0548,\] kde \(F\) je distribučná funkcia náhodnej premennej \(norm(20;5)\) a v odhade \(\stackrel{\star}{\approx}\) sme hodnoty \(F(12)\) a \(F(-12)\) získali v MATLABe takto: \(F(12)=normcdf(12,20,5)\approx 0{,}0548\) a \(F(-12)=normcdf(-12,20,5)\approx 0\).
Ak by sme nemali k dispozícii MATLAB, tak by sme na základe (\ref{prr}) dostali \[P(-12\leqq X\leqq 12)= \Phi\Big(\frac{12-20 }{5 } \Big)-\Phi\Big(\frac{-12-20 }{5} \Big)=\Phi(-1{,}6)-\Phi(-6{,4})\approx 0{,}0548,\] pričom hodnoty \(\Phi(-1{,}6)\approx 0{,}0548\) a \(\Phi(-6{,}4)\approx 0\) by sme dostali z tabuliek distribučnej funkcie \(\Phi\) náhodnej premennej \(norm(0;1)\).
c) Nech \(\varepsilon \gt 0\) je hľadaná maximálna odchýlka chyby merania od jej strednej hodnoty. Žiadame, aby \(P(|X-\mu |\lt \varepsilon )=0{,}95.\) Z (\ref{nr1}) dostaneme \[P(|X-\mu |\lt \varepsilon )=P(|X-20 |\lt \varepsilon )=2\cdot\Phi\Big(\frac{\varepsilon }{5} \Big)-1\stackrel{\star}{=}0{,}95.\] Z rovnosti \(\stackrel{\star}{=}\) je \[\Phi\Big(\frac{\varepsilon }{5} \Big)=0{,}975 \quad \mbox{ čo znamená, že }\quad \varepsilon=5\cdot \Phi^{-1}(0{,}975)\approx9{,}8000\,mA,\] kde hodnotu \(\Phi^{-1}(0{,}975)\) dostaneme v MATLABe pomocou \(norminv(0.975)\approx 1{,}9600\) alebo z tabuliek distribučnej funkcie \(\Phi\) náhodnej premennej \(norm(0;1)\).
a) Našou úlohou je určiť pravdepodobnosť \(P(|X-\mu|\leqq 12)\stackrel{\star}{=}P(|X-20|\lt 12)\) (v rovnosti \(\stackrel{\star}{=}\) si treba uvedomiť, že \(X\) je spojitá náhodná premenná). Z (\ref{nr1}) pre \(\varepsilon =12\) dostaneme \[P(|X-20|\lt 12)=2\cdot\Phi\Big(\frac{12}{5} \Big)-1\approx 2\cdot 0{,}9918-1= 0{,}9836, \] kde hodnotu \(\Phi(2{,}4)\approx 0{,}9918\) sme získali z tabuliek distribučnej funkcie \(\Phi\) náhodnej premennej \(norm(0;1)\) alebo v MATLABe pomocou \(normcdf(2.4)\).
b) Teraz chceme vypočítať pravdepodobnosť javu, ktorý spočíva v tom, že \(|X|\leqq 12\), t. j. \(-12\leqq X\leqq 12\). Máme \[P(-12\leqq X\leqq 12)=F(12)-F(-12)\stackrel{\star}{\approx} 0{,}0548,\] kde \(F\) je distribučná funkcia náhodnej premennej \(norm(20;5)\) a v odhade \(\stackrel{\star}{\approx}\) sme hodnoty \(F(12)\) a \(F(-12)\) získali v MATLABe takto: \(F(12)=normcdf(12,20,5)\approx 0{,}0548\) a \(F(-12)=normcdf(-12,20,5)\approx 0\).
Ak by sme nemali k dispozícii MATLAB, tak by sme na základe (\ref{prr}) dostali \[P(-12\leqq X\leqq 12)= \Phi\Big(\frac{12-20 }{5 } \Big)-\Phi\Big(\frac{-12-20 }{5} \Big)=\Phi(-1{,}6)-\Phi(-6{,4})\approx 0{,}0548,\] pričom hodnoty \(\Phi(-1{,}6)\approx 0{,}0548\) a \(\Phi(-6{,}4)\approx 0\) by sme dostali z tabuliek distribučnej funkcie \(\Phi\) náhodnej premennej \(norm(0;1)\).
c) Nech \(\varepsilon \gt 0\) je hľadaná maximálna odchýlka chyby merania od jej strednej hodnoty. Žiadame, aby \(P(|X-\mu |\lt \varepsilon )=0{,}95.\) Z (\ref{nr1}) dostaneme \[P(|X-\mu |\lt \varepsilon )=P(|X-20 |\lt \varepsilon )=2\cdot\Phi\Big(\frac{\varepsilon }{5} \Big)-1\stackrel{\star}{=}0{,}95.\] Z rovnosti \(\stackrel{\star}{=}\) je \[\Phi\Big(\frac{\varepsilon }{5} \Big)=0{,}975 \quad \mbox{ čo znamená, že }\quad \varepsilon=5\cdot \Phi^{-1}(0{,}975)\approx9{,}8000\,mA,\] kde hodnotu \(\Phi^{-1}(0{,}975)\) dostaneme v MATLABe pomocou \(norminv(0.975)\approx 1{,}9600\) alebo z tabuliek distribučnej funkcie \(\Phi\) náhodnej premennej \(norm(0;1)\).
Úlohy:
Úloha:
V priebehu jednej hodiny príde na benzínové čerpadlo priemerne \(90\) zákazníkov.
Počet zákazníkov za určitý časový interval sa riadi Poissonovým rozdelením
pravdepodobnosti, ktorého parameter \(\lambda \) je priamo úmerný dĺžke
časového intervalu. Určte pravdepodobnosť toho, že za \(4\) minúty prídu:
a) práve dvaja zákazníci;
b) najviac dvaja zákazníci;
c) aspoň dvaja zákazníci;
d) aspoň jeden zákazník.
e) Aký najmenší počet zákazníkov nebude počas \(4\) minút prekročený s pravdepodobnosťou aspoň \(0{,}99\)?
a) práve dvaja zákazníci;
b) najviac dvaja zákazníci;
c) aspoň dvaja zákazníci;
d) aspoň jeden zákazník.
e) Aký najmenší počet zákazníkov nebude počas \(4\) minút prekročený s pravdepodobnosťou aspoň \(0{,}99\)?
Úloha:
Náhodná premenná \(X\) sa má Gaussovo rozdelenie pravdepodobnosti so strednou hodnotou
\(\mu=0\). Je známe, že \(P(|X|\leqq 5)=0{,}95\). Určte
a) smerodajnú odchýlku tejto náhodnej premennej;
b) \(P(X\gt -2)\); c) \(P(|X|\leqq 2{,}5)\).
a) smerodajnú odchýlku tejto náhodnej premennej;
b) \(P(X\gt -2)\); c) \(P(|X|\leqq 2{,}5)\).
Úloha:
Určitá súčiastka sa pokazí v záručnej dobe \(1000\) dní s pravdepodobnosťou \(0{,}1\).
Je známe, že doba životnosti takejto súčiastky sa riadi exponenciálnym rozdelením pravdepodobnosti. Určte
a) strednú dobu životnosti tejto súčiastky;
b) pravdepodobnosť toho, že súčiastka sa nepokazí počas jedného roka (\(365\) dní);
c) pravdepodobnosť toho, že súčiastka sa nepokazí počas prvých \(200\) dní, ale pokazí sa v priebehu ďalších \(500\) dní.
a) strednú dobu životnosti tejto súčiastky;
b) pravdepodobnosť toho, že súčiastka sa nepokazí počas jedného roka (\(365\) dní);
c) pravdepodobnosť toho, že súčiastka sa nepokazí počas prvých \(200\) dní, ale pokazí sa v priebehu ďalších \(500\) dní.
Úloha:
Pevnosť v ťahu náhodne vybraného výrobku má normálne rozdelenie pravdepodobnosti
so strednou hodnotou \(2{,}4\) a disperziou \(0{,}64.\) Určte pravdepodobnosť toho,
že pevnosť v ťahu náhodne vybraného výrobku
a) bude menšia ako \(2{,}7;\)
b) bude väčšia ako \(2;\)
c) sa nebude líšiť od strednej hodnoty o viac ako \(1.\)
Stanovte:
d) hornú hranicu pevnosti v ťahu náhodne vybraného výrobku, ktorá nebude prekročená s pravdepodobnosťou \(0{,}95;\)
e) takú hodnotu \(r,\) že pravdepodobnosť toho, že sa pevnosť v ťahu náhodne vybraného výrobku nebude líšiť od strednej hodnoty o viac ako \(r\), je \(0{,}5.\)
a) bude menšia ako \(2{,}7;\)
b) bude väčšia ako \(2;\)
c) sa nebude líšiť od strednej hodnoty o viac ako \(1.\)
Stanovte:
d) hornú hranicu pevnosti v ťahu náhodne vybraného výrobku, ktorá nebude prekročená s pravdepodobnosťou \(0{,}95;\)
e) takú hodnotu \(r,\) že pravdepodobnosť toho, že sa pevnosť v ťahu náhodne vybraného výrobku nebude líšiť od strednej hodnoty o viac ako \(r\), je \(0{,}5.\)
11. Bodové a intervalové odhady parametrov základného súboru s normálnym rozdelením pravdepodobnosti
Riešené úlohy:
- V zimnom období zisťovali stav hladiny spodnej vody v zosuvovej oblasti. Namerali takéto stavy [\(\mathrm{cm}\)]: 159,53; 159,49; 159,61; 159,71; 159,88; 161,08; 160,98; 161,09; 160,91; 160,79; 161,02; 160,96; 160,80.
- Percentuálny obsah medi v určitej zliatine je daný tabuľkou rozdelenia intervalových početností:
\(I_i\) \(n_i\) 2,8 - 3,1 4 3,1 - 3,4 7 3,4 - 3,7 11 3,7 - 4,0 18 4,0 - 4,3 23 4,3 - 4,6 10 4,6 - 4,9 2 4,9 - 5,2 1
Príklad:
Pre dané výberové súbory vypočítajte výberové charakteristiky, t. j. výberový priemer, výberový rozptyl a výberovú smerodajnú odchýlku.
Pre dané výberové súbory vypočítajte výberové charakteristiky, t. j. výberový priemer, výberový rozptyl a výberovú smerodajnú odchýlku.
Príklad:
Grafickým testom s použitím MATLABu overte predpoklad normality rozdelenia základného súboru, z ktorého bol realizovaný náhodný výber uvedený v riešenej úlohe 1 b). Potom určte bodové odhady parametrov \(\mu\) a \(\sigma\).
Grafickým testom s použitím MATLABu overte predpoklad normality rozdelenia základného súboru, z ktorého bol realizovaný náhodný výber uvedený v riešenej úlohe 1 b). Potom určte bodové odhady parametrov \(\mu\) a \(\sigma\).
- 95 %-ný obojstranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 90 %-ný pravostranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 99 %-ný ľavostranný interval spoľahlivosti pre strednú hodnotu \(\mu\).
Príklad:
Zo základného súboru s normálnym rozdelením, kde je známy rozptyl \(\sigma^2=0{,}06\); sme urobili náhodný výber s realizáciami: 1,3; 1,8; 1,4; 1,2; 0,9; 1,5; 1,7. Zistite:
Zo základného súboru s normálnym rozdelením, kde je známy rozptyl \(\sigma^2=0{,}06\); sme urobili náhodný výber s realizáciami: 1,3; 1,8; 1,4; 1,2; 0,9; 1,5; 1,7. Zistite:
- 95 %-ný obojstranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 99 %-ný pravostranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 90 %-ný ľavostranný interval spoľahlivosti pre strednú hodnotu \(\mu\).
Príklad:
Zo základného súboru s normálnym rozdelením sme urobili náhodný výber s realizáciami: 22,4; 28,0; 20,1; 27,4; 25,6; 23,9; 24,8; 26,4; 27,0; 25,4. Zistite:
Zo základného súboru s normálnym rozdelením sme urobili náhodný výber s realizáciami: 22,4; 28,0; 20,1; 27,4; 25,6; 23,9; 24,8; 26,4; 27,0; 25,4. Zistite:
- 95 %-né obojstranné intervaly spoľahlivosti pre rozptyl \(\sigma^2\) a smerodajnú odchýlku \(\sigma\) obsahu medi v danej zliatine,
- 90 %-ný pravostranný interval spoľahlivosti pre rozptyl \(\sigma^2\) obsahu medi v danej zliatine,
- 99 %-ný ľavostranný interval spoľahlivosti pre rozptyl \(\sigma^2\) obsahu medi v danej zliatine.
Príklad:
V laboratóriu bol meraný percentuálny obsah medi v zliatine. Výsledky meraní sú v tabuľke (\(z_i\) je triedny znak): \[ \begin{array}{|c|c|c|c|c|c|c|c|} \hline z_i \a 3{,}0 \a 3{,}3 \a 3{,}6 \a 3{,}9 \a 4{,}2 \a 4{,}5 \a 4{,}8 \\ \hline n_i \a 4 \a 7 \a 12 \a 18 \a 21 \a 13 \a 6 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
V laboratóriu bol meraný percentuálny obsah medi v zliatine. Výsledky meraní sú v tabuľke (\(z_i\) je triedny znak): \[ \begin{array}{|c|c|c|c|c|c|c|c|} \hline z_i \a 3{,}0 \a 3{,}3 \a 3{,}6 \a 3{,}9 \a 4{,}2 \a 4{,}5 \a 4{,}8 \\ \hline n_i \a 4 \a 7 \a 12 \a 18 \a 21 \a 13 \a 6 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
Úlohy:
Úloha:
Bol meraný odpor elektrického obvodu [\(\Omega\)] s výsledkami uvedenými v nasledujúcej frekvenčnej tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|} \hline x_i \a 98 \a 99 \a 100\a 101 \a 102\a 103\\ \hline n_i \a 2 \a 4 \a 6 \a 4 \a 3 \a 1 \\ \hline \end{array} \] Vypočítajte výberové charakteristiky daného výberového súboru.
Bol meraný odpor elektrického obvodu [\(\Omega\)] s výsledkami uvedenými v nasledujúcej frekvenčnej tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|} \hline x_i \a 98 \a 99 \a 100\a 101 \a 102\a 103\\ \hline n_i \a 2 \a 4 \a 6 \a 4 \a 3 \a 1 \\ \hline \end{array} \] Vypočítajte výberové charakteristiky daného výberového súboru.
- 99 %-ný obojstranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 99 %-ný pravostranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 95 %-ný ľavostranný interval spoľahlivosti pre strednú hodnotu \(\mu\).
Úloha:
Vykonali sme 32 analýz na overenie koncentrácie chemickej látky v roztoku s týmito výsledkami: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 9 \a 11 \a 12\a 14 \a 15\a 16 \a 17\a 18\a 20\a 21 \\ \hline n_i \a 1 \a 2 \a 3 \a 4 \a 7 \a 5 \a 4\a 3\a 2 \a 1 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Vieme, že rozptyl \(\sigma^2=7{,}4\). Vypočítajte:
Vykonali sme 32 analýz na overenie koncentrácie chemickej látky v roztoku s týmito výsledkami: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 9 \a 11 \a 12\a 14 \a 15\a 16 \a 17\a 18\a 20\a 21 \\ \hline n_i \a 1 \a 2 \a 3 \a 4 \a 7 \a 5 \a 4\a 3\a 2 \a 1 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Vieme, že rozptyl \(\sigma^2=7{,}4\). Vypočítajte:
- 95 %-ný obojstranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 95 %-ný pravostranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 95 %-ný ľavostranný interval spoľahlivosti pre strednú hodnotu \(\mu\).
Úloha:
Preverovala sa zdatnosť študentov v skoku do výšky. Výsledky dosiahnutej výšky skokov [\(\mathrm{cm}\)] sú zhrnuté v tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|c|} \hline z_i \a 120 \a 130 \a 140 \a 150 \a 160 \a 170 \a 180 \a 190 \a 200 \a 210 \\ \hline n_i \a 3 \a 5 \a 7 \a 11 \a 12 \a 6 \a 2 \a 2 \a 1 \a 1 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Je známa smerodajná odchýlka \(\sigma=20\). Určte:
Preverovala sa zdatnosť študentov v skoku do výšky. Výsledky dosiahnutej výšky skokov [\(\mathrm{cm}\)] sú zhrnuté v tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|c|} \hline z_i \a 120 \a 130 \a 140 \a 150 \a 160 \a 170 \a 180 \a 190 \a 200 \a 210 \\ \hline n_i \a 3 \a 5 \a 7 \a 11 \a 12 \a 6 \a 2 \a 2 \a 1 \a 1 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Je známa smerodajná odchýlka \(\sigma=20\). Určte:
- 95 %-ný obojstranný interval spoľahlivosti pre strednú hodnotu \(\mu\) trvania pracovnej operácie,
- 95 %-ný pravostranný interval spoľahlivosti pre strednú hodnotu \(\mu\) trvania pracovnej operácie,
- 95 %-ný ľavostranný interval spoľahlivosti pre strednú hodnotu \(\mu\) trvania pracovnej operácie.
Úloha:
Na obrábacích strojoch sa zisťoval čas v sekundách, ktorý je potrebný na vykonanie pracovnej operácie. Výsledky sú usporiadané v tabuľke intervalového rozdelenia početností: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline z_i \a 32 \a 37 \a 42\a 47 \a 52\a 57\a 62\a 67 \\ \hline n_i \a 1 \a 7 \a 33 \a 63 \a 38 \a 5 \a 1\a 2 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Vypočítajte:
Na obrábacích strojoch sa zisťoval čas v sekundách, ktorý je potrebný na vykonanie pracovnej operácie. Výsledky sú usporiadané v tabuľke intervalového rozdelenia početností: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline z_i \a 32 \a 37 \a 42\a 47 \a 52\a 57\a 62\a 67 \\ \hline n_i \a 1 \a 7 \a 33 \a 63 \a 38 \a 5 \a 1\a 2 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Vypočítajte:
- bodové odhady parametrov \(\mu\) a \(\sigma\),
- 95 %-ný obojstranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 95 %-ný obojstranný interval spoľahlivosti pre smerodajnú odchýlku \(\sigma\).
Úloha:
Zisťovala sa pevnosť vlákna [\(\mathrm{kg / mm^2}\)]. Merania sa vykonali na desiatich vzorkách s týmito výsledkami: 10,3; 8,8; 9,7; 9,6; 11,2; 10,7; 9,1; 9,5; 10,3; 9,3. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
Zisťovala sa pevnosť vlákna [\(\mathrm{kg / mm^2}\)]. Merania sa vykonali na desiatich vzorkách s týmito výsledkami: 10,3; 8,8; 9,7; 9,6; 11,2; 10,7; 9,1; 9,5; 10,3; 9,3. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
- bodové odhady parametrov \(\mu\) a \(\sigma\),
- 95 %-ný pravostranný interval spoľahlivosti pre strednú hodnotu \(\mu\),
- 95 %-ný ľavostranný interval spoľahlivosti pre rozptyl \(\sigma^2\).
Úloha:
Merali sme priemer 250 strojových súčiastok. Výsledky merania sú v tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|c|} \hline z_i \a 963 \a 968 \a 973 \a 978 \a 983 \a 988 \a 993 \a 998 \a 1003 \a 1008 \a 1013 \a 1018 \a 1023 \a 1028 \a 1033 \\ \hline n_i \a 1 \a 5 \a 5 \a 13\a 18 \a 32\a 50 \a 50 \a 37 \a 18\a 8 \a 7 \a 4 \a 1 \a 1 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
Merali sme priemer 250 strojových súčiastok. Výsledky merania sú v tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|c|} \hline z_i \a 963 \a 968 \a 973 \a 978 \a 983 \a 988 \a 993 \a 998 \a 1003 \a 1008 \a 1013 \a 1018 \a 1023 \a 1028 \a 1033 \\ \hline n_i \a 1 \a 5 \a 5 \a 13\a 18 \a 32\a 50 \a 50 \a 37 \a 18\a 8 \a 7 \a 4 \a 1 \a 1 \\ \hline \end{array} \] Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
- 95 %-né obojstranné intervaly spoľahlivosti pre rozptyl \(\sigma^2\) a smerodajnú odchýlku \(\sigma\) výkonu sledovaného druhu motora,
- 95 %-né pravostranné intervaly spoľahlivosti pre rozptyl \(\sigma^2\) a smerodajnú odchýlku \(\sigma\) výkonu motora,
- 95 %-né ľavostranné intervaly spoľahlivosti pre rozptyl \(\sigma^2\) a smerodajnú odchýlku \(\sigma\) výkonu motora.
Úloha:
Pri sériových skúškach motorov určitého druhu boli zistené tieto hodnoty výkonu [\(\mathrm{kW}\)]: 159,5; 159,4; 159,6; 159,7; 159,8; 160,1; 160,6; 161,0; 161,5; 161,8; 162,0; 162,5. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
Pri sériových skúškach motorov určitého druhu boli zistené tieto hodnoty výkonu [\(\mathrm{kW}\)]: 159,5; 159,4; 159,6; 159,7; 159,8; 160,1; 160,6; 161,0; 161,5; 161,8; 162,0; 162,5. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Určte:
12. Testovanie štatistických hypotéz o parametroch základných súborov s normálnym rozdelením
Riešené úlohy:
Príklad:
Pri tradičnom spôsobe opracovania strojových súčiastok sa dosahovali priemerné hodnoty 4,4 dôležitej kvalitatívnej vlastnosti so smerodajnou odchýlkou \(\sigma=0{,}4\). Pokusne sa zavádza nová, lacnejšia metóda opracovania súčiastok, ktorou opracovali 20 súčiastok a boli dosiahnuté takéto výsledky: 4,5; 4,3; 4,1; 4,9; 4,6; 3,6; 4,7; 5,1; 4,8; 4,0; 3,7; 4,4; 4,9; 4,9; 5,2; 5,1; 4,7; 4,9; 4,6; 4,8. Na hladine významnosti \(\alpha =0{,}05\) otestujte hypotézu či nová metóda vedie k zvýšeniu hodnoty sledovanej kvalitatívnej vlastnosti. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.
Pri tradičnom spôsobe opracovania strojových súčiastok sa dosahovali priemerné hodnoty 4,4 dôležitej kvalitatívnej vlastnosti so smerodajnou odchýlkou \(\sigma=0{,}4\). Pokusne sa zavádza nová, lacnejšia metóda opracovania súčiastok, ktorou opracovali 20 súčiastok a boli dosiahnuté takéto výsledky: 4,5; 4,3; 4,1; 4,9; 4,6; 3,6; 4,7; 5,1; 4,8; 4,0; 3,7; 4,4; 4,9; 4,9; 5,2; 5,1; 4,7; 4,9; 4,6; 4,8. Na hladine významnosti \(\alpha =0{,}05\) otestujte hypotézu či nová metóda vedie k zvýšeniu hodnoty sledovanej kvalitatívnej vlastnosti. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.
Príklad:
Meral sa percentuálny obsah cínu vo vzorkách rudy. Výsledky sú v tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline z_i \a 30 \a 35 \a 40\a 45 \a 50\a 55 \a 60\a 65\a 70\a 75 \\ \hline n_i \a 4 \a 6 \a 8 \a 15 \a 25 \a 20 \a 8\a 7\a 5 \a 2 \\ \hline \end{array} \] Predpokladáme, že obsah cínu má normálne rozdelenie. Odborníci predpokladajú, že ruda obsahuje v priemere 50 % cínu. Na hladine významnosti \(\alpha =0{,}05\) overte túto hypotézu odborníkov.
Meral sa percentuálny obsah cínu vo vzorkách rudy. Výsledky sú v tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline z_i \a 30 \a 35 \a 40\a 45 \a 50\a 55 \a 60\a 65\a 70\a 75 \\ \hline n_i \a 4 \a 6 \a 8 \a 15 \a 25 \a 20 \a 8\a 7\a 5 \a 2 \\ \hline \end{array} \] Predpokladáme, že obsah cínu má normálne rozdelenie. Odborníci predpokladajú, že ruda obsahuje v priemere 50 % cínu. Na hladine významnosti \(\alpha =0{,}05\) overte túto hypotézu odborníkov.
Príklad:
Presnosť nastavenia automatického obrábacieho stroja je charakterizovaná smerodajnou odchýlkou dĺžky súčiastok. Ak je táto hodnota väčšia ako \(\sqrt{20}\) mm, automat treba znova nastaviť. Meranie kontrolných súčiastok dalo tieto výsledky v milimetroch: 792, 803, 790, 804, 801, 803, 798, 799, 806, 797, 802, 796, 802, 801, 798, 799, 806, 809, 797, 803. Posúďte či treba urobiť nové nastavenie, ak použijeme hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.
Presnosť nastavenia automatického obrábacieho stroja je charakterizovaná smerodajnou odchýlkou dĺžky súčiastok. Ak je táto hodnota väčšia ako \(\sqrt{20}\) mm, automat treba znova nastaviť. Meranie kontrolných súčiastok dalo tieto výsledky v milimetroch: 792, 803, 790, 804, 801, 803, 798, 799, 806, 797, 802, 796, 802, 801, 798, 799, 806, 809, 797, 803. Posúďte či treba urobiť nové nastavenie, ak použijeme hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.
Príklad:
Vážením sme získali údaje o presnom množstve automaticky balených výrobkov. Výsledky v gramoch pred nastavením baliaceho automatu
sú: 243,2; 244,8; 253,1; 247,5; 251,0; 251,7; 254,0; 252,5; 252,8; 250,1; 247,3; 250,9; 253,2; 252,7.
Výsledky v gramoch po nastavení baliaceho automatu sú: 250,4; 250,2; 251,1; 249,3; 249,9; 250,2; 251,1.
Na hladine významnosti \(\alpha =0{,}05\) testujte hypotézu \(H_0: \sigma_1^2=\sigma_2^2\) proti \(H_1: \sigma_1^2\gt \sigma_2^2\).
Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Príklad:
Prístroj meral dobu reakcie na svetelný signál v stotinách sekundy u desiatich náhodne vybraných vodičov z povolania, pričom bol zistený výberový priemer \(\bar{x}_1=34\) a tiež u dvadsiatich nových absolventov autoškoly, kde bol zistený výberový priemer \(\bar{x}_2=42\), pričom poznáme disperzie \(\sigma_1^2=3\) a \(\sigma_2^2=6\). Na hladine významnosti \(\alpha =0{,}05\) uvážte či doba reakcie na svetelný signál závisí od dĺžky praxe vodiča. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Prístroj meral dobu reakcie na svetelný signál v stotinách sekundy u desiatich náhodne vybraných vodičov z povolania, pričom bol zistený výberový priemer \(\bar{x}_1=34\) a tiež u dvadsiatich nových absolventov autoškoly, kde bol zistený výberový priemer \(\bar{x}_2=42\), pričom poznáme disperzie \(\sigma_1^2=3\) a \(\sigma_2^2=6\). Na hladine významnosti \(\alpha =0{,}05\) uvážte či doba reakcie na svetelný signál závisí od dĺžky praxe vodiča. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Príklad:
Jednou z rozhodujúcich vlastností pre akosť ľanového vlákna je hmotnosť stonky. Čím je stonka ťažšia, tým je vlákno kvalitnejšie. Aby sa preukázal vplyv istej metódy ošetrenia ľanu na akosť vlákna, bolo vykonaných 10 meraní na ošetrenom pozemku: 47,5; 57,7; 47,1; 38,8; 45,2; 49,8; 43,4; 50,8; 41,5; 38,8 a 12 meraní na kontrolnom neošetrenom pozemku: 49,2; 44,1; 44,1; 38,1; 40,9; 32,1; 36,8; 39,5; 67,2; 41,8; 46,9; 42,3. Za predpokladu normálneho rozdelenia hmotnosti stonky testujte hypotézu \(H_0: \mu_1=\mu_2\) proti hypotéze \(H_1: \mu_1\gt \mu_2\) na hladine významnosti \(\alpha = 0{,}05\).
Jednou z rozhodujúcich vlastností pre akosť ľanového vlákna je hmotnosť stonky. Čím je stonka ťažšia, tým je vlákno kvalitnejšie. Aby sa preukázal vplyv istej metódy ošetrenia ľanu na akosť vlákna, bolo vykonaných 10 meraní na ošetrenom pozemku: 47,5; 57,7; 47,1; 38,8; 45,2; 49,8; 43,4; 50,8; 41,5; 38,8 a 12 meraní na kontrolnom neošetrenom pozemku: 49,2; 44,1; 44,1; 38,1; 40,9; 32,1; 36,8; 39,5; 67,2; 41,8; 46,9; 42,3. Za predpokladu normálneho rozdelenia hmotnosti stonky testujte hypotézu \(H_0: \mu_1=\mu_2\) proti hypotéze \(H_1: \mu_1\gt \mu_2\) na hladine významnosti \(\alpha = 0{,}05\).
Príklad:
Vážením sme získali údaje o hmotnosti automaticky balených výrobkov. Výsledky v gramoch pred nastavením baliaceho automatu sú: 243,2; 244,8; 253,1; 247,5; 251,0; 251,7; 254,0; 252,5; 252,8; 250,1; 247,3; 250,9; 253,2; 252,7. Výsledky v gramoch po nastavení baliaceho automatu sú: 250,4; 250,2; 251,1; 249,3; 249,9; 250,2; 251,1. Na hladine významnosti \(\alpha =0{,}05\) zistite či sa stredná hodnota hmotnosti nastavením automatu nezmenila. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Vážením sme získali údaje o hmotnosti automaticky balených výrobkov. Výsledky v gramoch pred nastavením baliaceho automatu sú: 243,2; 244,8; 253,1; 247,5; 251,0; 251,7; 254,0; 252,5; 252,8; 250,1; 247,3; 250,9; 253,2; 252,7. Výsledky v gramoch po nastavení baliaceho automatu sú: 250,4; 250,2; 251,1; 249,3; 249,9; 250,2; 251,1. Na hladine významnosti \(\alpha =0{,}05\) zistite či sa stredná hodnota hmotnosti nastavením automatu nezmenila. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Príklad:
V nasledujúcej tabuľke sú počty získaných bodov desiatich študentov z praktickej a teoretickej časti skúšky: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{Praktická\,časť}\a 28 \a 35 \a 32\a 15 \a 35\a 24 \a 29\a 19\a 21\a 12 \\ \hline \mathrm{Teoretická\,časť}\a 25 \a 35 \a 30 \a 11 \a 32 \a 28 \a 28\a 25\a 22 \a 11 \\ \hline \end{array} \] Na porovnanie týchto výsledkov aplikujte vhodný test. Použite hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normalitu rozdelenia výberových súborov.
V nasledujúcej tabuľke sú počty získaných bodov desiatich študentov z praktickej a teoretickej časti skúšky: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{Praktická\,časť}\a 28 \a 35 \a 32\a 15 \a 35\a 24 \a 29\a 19\a 21\a 12 \\ \hline \mathrm{Teoretická\,časť}\a 25 \a 35 \a 30 \a 11 \a 32 \a 28 \a 28\a 25\a 22 \a 11 \\ \hline \end{array} \] Na porovnanie týchto výsledkov aplikujte vhodný test. Použite hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normalitu rozdelenia výberových súborov.
Úlohy:
Úloha:
Priemerná výška desaťročných chlapcov je 135,3 cm. U 14 chlapcov, ktorí navštevujú športovú školu, boli namerané tieto hodnoty výšky v cm: 136, 130, 151, 127, 133, 136, 139, 139, 141, 147, 139, 142, 140, 138. Na hladine významnosti \(\alpha =0{,}05\) overte hypotézu, že výška chlapcov športovej školy sa štatisticky významne odlišuje od výšky 135,3 cm za predpokladu, že rozptyl výšky desaťročných chlapcov je \(\sigma^2=38{,}26\) [\(\mathrm{cm^2}\)]. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.
Priemerná výška desaťročných chlapcov je 135,3 cm. U 14 chlapcov, ktorí navštevujú športovú školu, boli namerané tieto hodnoty výšky v cm: 136, 130, 151, 127, 133, 136, 139, 139, 141, 147, 139, 142, 140, 138. Na hladine významnosti \(\alpha =0{,}05\) overte hypotézu, že výška chlapcov športovej školy sa štatisticky významne odlišuje od výšky 135,3 cm za predpokladu, že rozptyl výšky desaťročných chlapcov je \(\sigma^2=38{,}26\) [\(\mathrm{cm^2}\)]. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.
Úloha:
Systematická chyba meracieho prístroja sa eliminuje jeho nastavením a meraním etalónu, ktorého správnou nameranou hodnotou je \(\mu_0=10\). Nezávislými meraniami za rovnakých podmienok boli získané tieto hodnoty: 10,24; 10,12; 9,91; 10,19; 9,78; 10,14; 9,86; 10,17; 10,05. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Je možné na hladine významnosti \(\alpha =0{,}05\) vysvetliť odchýlky od hodnoty 10 náhodnými vplyvmi?
Systematická chyba meracieho prístroja sa eliminuje jeho nastavením a meraním etalónu, ktorého správnou nameranou hodnotou je \(\mu_0=10\). Nezávislými meraniami za rovnakých podmienok boli získané tieto hodnoty: 10,24; 10,12; 9,91; 10,19; 9,78; 10,14; 9,86; 10,17; 10,05. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Je možné na hladine významnosti \(\alpha =0{,}05\) vysvetliť odchýlky od hodnoty 10 náhodnými vplyvmi?
Úloha:
Podľa informácií výrobcu je variabilita životnosti ním vyrábaných obrazoviek vyjadrená smerodajnou odchýlkou 45 hodín. O životnosti náhodne vybraných 50 obrazoviek vyrobených u tohto výrobcu sú údaje v tabuľke:
Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Testom na hladine významnosti
\(\alpha =0{,}02\) overte či sa dá prijať predpoklad, že je variabilita životnosti obrazoviek taká, ako tvrdí výrobca alebo
taká nie je.
Podľa informácií výrobcu je variabilita životnosti ním vyrábaných obrazoviek vyjadrená smerodajnou odchýlkou 45 hodín. O životnosti náhodne vybraných 50 obrazoviek vyrobených u tohto výrobcu sú údaje v tabuľke:
| \(I_i\) | \(n_i\) |
|---|---|
| 1860 - 1900 | 1 |
| 1900 - 1940 | 4 |
| 1940 - 1980 | 12 |
| 1980 - 2020 | 14 |
| 2020 - 2060 | 15 |
| 2060 - 2100 | 3 |
| 2100 - 2140 | 1 |
Úloha:
Zisťovalo sa či špeciálny prípravok pridaný do ocele zvyšuje jej pevnosť. Výsledky merania pri vzorkách, kde bol použitý prípravok: 6,2; 5,7; 5,6; 6,0; 6,3; 5,8; 5,7; 6,0; 6,0; 5,8. Výsledky merania pri vzorkách, kde nebol použitý prípravok: 5,6; 5,9; 5,8; 5,9; 5,7; 5,7; 6,0; 5,5; 5,7; 5,5. Na hladine významnosti \(\alpha =0{,}05\) rozhodnite či sa disperzie oboch vzoriek významne líšia. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Zisťovalo sa či špeciálny prípravok pridaný do ocele zvyšuje jej pevnosť. Výsledky merania pri vzorkách, kde bol použitý prípravok: 6,2; 5,7; 5,6; 6,0; 6,3; 5,8; 5,7; 6,0; 6,0; 5,8. Výsledky merania pri vzorkách, kde nebol použitý prípravok: 5,6; 5,9; 5,8; 5,9; 5,7; 5,7; 6,0; 5,5; 5,7; 5,5. Na hladine významnosti \(\alpha =0{,}05\) rozhodnite či sa disperzie oboch vzoriek významne líšia. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Úloha:
Odberateľ dostáva žiarivky od dvoch dodávateľov A a B. Pri hodnotení kvality žiariviek sa sleduje tiež počet zapojení, ktoré žiarivky vydržia bez poškodenia. Skúšky výrobkov viedli k týmto výsledkom:
Dodávateľ A: 2139, 2041, 1968, 1903, 1952, 1980, 2089, 1915, 2389, 2163, 2072, 1712, 2018, 1792, 1849.
Dodávateľ B: 1947, 1602, 1906, 2031, 2072, 1812, 1942, 2074, 2132.
Na hladine významnosti \(\alpha =0{,}05\) overte hypotézu, že kvalita oboch dodávok je rovnaká. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Odberateľ dostáva žiarivky od dvoch dodávateľov A a B. Pri hodnotení kvality žiariviek sa sleduje tiež počet zapojení, ktoré žiarivky vydržia bez poškodenia. Skúšky výrobkov viedli k týmto výsledkom:
Dodávateľ A: 2139, 2041, 1968, 1903, 1952, 1980, 2089, 1915, 2389, 2163, 2072, 1712, 2018, 1792, 1849.
Dodávateľ B: 1947, 1602, 1906, 2031, 2072, 1812, 1942, 2074, 2132.
Na hladine významnosti \(\alpha =0{,}05\) overte hypotézu, že kvalita oboch dodávok je rovnaká. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Úloha:
Pri antropologických meraniach obyvateľov Egypta bola okrem iného sledovaná šírka nosa v centimetroch u skupiny mužov vo veku 21 − 50 rokov zo severnej časti krajiny a u skupiny rovnako starých mužov z južnej časti. Výskum viedol k týmto výsledkom:
Sever: 3,6; 4,1; 3,3; 3,4; 3,7; 3,1; 4,0; 4,0; 3,6; 3,0; 3,3; 3,7; 4,3; 3,3; 3,4; 3,4; 3,3; 3,6; 4,0; 3,4; 3,7.
Juh: 4,1; 3,9; 4,0; 3,8; 4,1; 4,2; 3,8; 3,9; 3,8; 3,8; 4,0; 3,7; 3,9; 4,4; 3,7; 3,8; 3,9; 3,9; 4,0; 4,1; 3,8; 4,0; 4,3.
Posúďte významnosť rozdielov vo výsledkoch meraní na hladine významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Pri antropologických meraniach obyvateľov Egypta bola okrem iného sledovaná šírka nosa v centimetroch u skupiny mužov vo veku 21 − 50 rokov zo severnej časti krajiny a u skupiny rovnako starých mužov z južnej časti. Výskum viedol k týmto výsledkom:
Sever: 3,6; 4,1; 3,3; 3,4; 3,7; 3,1; 4,0; 4,0; 3,6; 3,0; 3,3; 3,7; 4,3; 3,3; 3,4; 3,4; 3,3; 3,6; 4,0; 3,4; 3,7.
Juh: 4,1; 3,9; 4,0; 3,8; 4,1; 4,2; 3,8; 3,9; 3,8; 3,8; 4,0; 3,7; 3,9; 4,4; 3,7; 3,8; 3,9; 3,9; 4,0; 4,1; 3,8; 4,0; 4,3.
Posúďte významnosť rozdielov vo výsledkoch meraní na hladine významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Úloha:
Stanovenie thiocyanového iónu bolo paralelne realizované metódami A a B na 12 vzorkách s týmito výsledkami:
Metóda A: 0,38; 0,56; 0,45; 0,49; 0,38; 0,41; 0,60; 0,36; 0,26; 0,41; 0,43; 0,40.
Metóda B: 0,39; 0,58; 0,44; 0,52; 0,41; 0,45; 0,59; 0,37; 0,28; 0,42; 0,42; 0,38.
Porovnajte obe metodiky otestovaním výsledkov. Zvoľte hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Stanovenie thiocyanového iónu bolo paralelne realizované metódami A a B na 12 vzorkách s týmito výsledkami:
Metóda A: 0,38; 0,56; 0,45; 0,49; 0,38; 0,41; 0,60; 0,36; 0,26; 0,41; 0,43; 0,40.
Metóda B: 0,39; 0,58; 0,44; 0,52; 0,41; 0,45; 0,59; 0,37; 0,28; 0,42; 0,42; 0,38.
Porovnajte obe metodiky otestovaním výsledkov. Zvoľte hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
13. Jednoduchá lineárna regresia. Pearsonov výberový korelačný koeficient.
Riešené úlohy:
- Odhadnite závislosť celkovej doby opravy od počtu opravovaných pokladní regresnou priamkou \(f(x)=a_0+a_1x\).
- Regresnú priamku spolu s bodmi \((x_i,y_i)\) znázornite.
- Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).
Príklad:
Firma realizuje opravy registračných pokladní. V tabuľke sú dáta z 18 ohlásených opráv. Pri každej oprave je uvedený počet opravovaných pokladní \(X\) a celková doba opravy \(Y\) v minútach: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 7 \a 6 \a 5\a 1 \a 5\a 4 \a 7\a 3\a 4\a 2\a 8\a 5\a2\a 5\a 7\a1\a4\a5 \\ \hline y_i \a 97 \a 86 \a 78 \a 10 \a 75 \a 62 \a 101 \a 39\a 53\a 33\a 118\a 65\a 25\a 71\a 105\a 17\a 49\a 68 \\ \hline \end{array} \]Predpokladáme, že ide o náhodný výber z dvojrozmerného normálneho rozdelenia. Riešte úlohy:
Firma realizuje opravy registračných pokladní. V tabuľke sú dáta z 18 ohlásených opráv. Pri každej oprave je uvedený počet opravovaných pokladní \(X\) a celková doba opravy \(Y\) v minútach: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 7 \a 6 \a 5\a 1 \a 5\a 4 \a 7\a 3\a 4\a 2\a 8\a 5\a2\a 5\a 7\a1\a4\a5 \\ \hline y_i \a 97 \a 86 \a 78 \a 10 \a 75 \a 62 \a 101 \a 39\a 53\a 33\a 118\a 65\a 25\a 71\a 105\a 17\a 49\a 68 \\ \hline \end{array} \]Predpokladáme, že ide o náhodný výber z dvojrozmerného normálneho rozdelenia. Riešte úlohy:
Príklad:
Použite vstupné dáta z predchádzajúceho príkladu. Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Použite vstupné dáta z predchádzajúceho príkladu. Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Úlohy:
- Odhadnite závislosť úrody od veku stromu regresnou priamkou.
- Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).
- Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Úloha:
U 15 jabloní bol zisťovaný vek stromu \(X\) [počet rokov] a úroda \(Y\) [kg] s výsledkami: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 2 \a 3 \a 3\a 4 \a 4\a 4 \a 5\a 5\a 5\a 6\a 6\a 6\a6\a 6\a 10\\ \hline y_i \a 4{,}4 \a 4{,}3 \a 4{,}1 \a 5{,}5 \a 5{,}3 \a 5{,}4 \a 5{,}8 \a 6{,}0\a 6{,}2\a 6{,}6\a 6{,}8\a 6{,}7\a 9{,}0\a 10{,}1\a 9{,}2\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
U 15 jabloní bol zisťovaný vek stromu \(X\) [počet rokov] a úroda \(Y\) [kg] s výsledkami: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 2 \a 3 \a 3\a 4 \a 4\a 4 \a 5\a 5\a 5\a 6\a 6\a 6\a6\a 6\a 10\\ \hline y_i \a 4{,}4 \a 4{,}3 \a 4{,}1 \a 5{,}5 \a 5{,}3 \a 5{,}4 \a 5{,}8 \a 6{,}0\a 6{,}2\a 6{,}6\a 6{,}8\a 6{,}7\a 9{,}0\a 10{,}1\a 9{,}2\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
- Odhadnite závislosť počtu chybných výrobkov od výkonu sústružníka regresnou priamkou.
- Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).
- Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Úloha:
Bolo sledované, ako súvisí množstvo chybných výrobkov [v % z vyrobených výrobkov] s výkonom sústružníka [v % z predpísanej normy]. Bolo vybraných 10 pracovníkov, namerané údaje sú uvedené v tabzľke: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{Výkon} \a 56 \a 68 \a 72\a 85 \a 92\a 102 \a 107\a 111\a 123\a 142\\ \hline \mathrm{Chybné\,\ výrobky} \a 5{,}20 \a 3{,}90 \a 3{,}50 \a 2{,}40 \a 2{,}04 \a 2{,}00 \a 2{,}20 \a 2{,}24 \a 2{,}40\a 2{,}51\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
Bolo sledované, ako súvisí množstvo chybných výrobkov [v % z vyrobených výrobkov] s výkonom sústružníka [v % z predpísanej normy]. Bolo vybraných 10 pracovníkov, namerané údaje sú uvedené v tabzľke: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{Výkon} \a 56 \a 68 \a 72\a 85 \a 92\a 102 \a 107\a 111\a 123\a 142\\ \hline \mathrm{Chybné\,\ výrobky} \a 5{,}20 \a 3{,}90 \a 3{,}50 \a 2{,}40 \a 2{,}04 \a 2{,}00 \a 2{,}20 \a 2{,}24 \a 2{,}40\a 2{,}51\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
- Odhadnite závislosť Brinelovho koeficientu tvrdosti ocele od deformácie regresnou priamkou.
- Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).
- Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Úloha:
Pri meraní závislosti Brinelovho koeficientu tvrdosti ocele \(Y\) [MPa] od deformácie \(X\) [mm] boli zistené nasledujúce údaje: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 6 \a 9 \a 11\a 13 \a 22\a 26 \a 28\a 33\a 35\\ \hline y_i \a 68 \a 67 \a 65 \a 53 \a 44 \a 40 \a 37 \a 34 \a 32\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
Pri meraní závislosti Brinelovho koeficientu tvrdosti ocele \(Y\) [MPa] od deformácie \(X\) [mm] boli zistené nasledujúce údaje: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 6 \a 9 \a 11\a 13 \a 22\a 26 \a 28\a 33\a 35\\ \hline y_i \a 68 \a 67 \a 65 \a 53 \a 44 \a 40 \a 37 \a 34 \a 32\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy: