Newtonova metóda riešenia sústav nelineárnych rovníc

Ciele

1. Zobraziť graficky jednoduchú sústavu dvoch nelineárnych rovníc o dvoch neznámych.\(\def\a{&}\)
2. Naučiť sa používať Newtonovu metódu na riešenie sústav nelineárnych rovníc.

Úvod

Systémy nelineárnych rovníc sa vyskytujú pri riešení mnohých technických (inžinierskych) úloh. Ako príklad môžeme uviesť určenie lokálnych extrémov funkcií \(n\) premenných. Nutnou podmienkou lokálneho extrému diferencovateľnej funkcie je nulový gradient funkcie v bode extrému, t. j. \(n\) zložiek gradientu musí byť súčasne rovných nule.

Na numerické riešenie konkrétnych sústav nelineárnych rovníc môžeme použiť, napríklad Newtonovu metódu, ktorá je tiež nazývaná metódou linearizácie. V každom kroku, t. j. pri každej iterácii, sa rieši pomocná sústava lineárnych rovníc.

Riešenie jednoduchej sústavy dvoch nelineárnych rovníc môžeme symbolicky rozdeliť na tri podúlohy:
1. Analýza existencie koreňov sústavy rovníc, ich počtu a podľa možnosti odhadu oblastí (obdĺžnikov), v ktorých ležia jednotlivé korene.
2. Použitie iteračných postupov, umožňujúcich postupné upresňovanie približných riešení.
3. Odhad [ne]presnosti priebežného/výsledného numerického riešenia.
Iteračný vzťah Newtonovej metódy na riešenie rovnice \(f(x)=0\): \[ x^{[k+1]}=x^{[k]}-\dfrac{f(x^{[k]})}{f^{\prime}(x^{[k]})} \] sa dá zapísať v dvoch krokoch: \[ \begin{array}{l} 1)\text{ riešenie sústavy lineárnych rovníc: } \quad f^{\prime}(x^{[k]})\cdot \Delta x^{[k]}=- f(x^{[k]}),\\[1ex] 2)\text{ upresnenie aktuálnej hodnoty \(x^{[k]}\): }\quad x^{[k+1]}=x^{[k]}+\Delta x^{[k]}. \end{array} \] Ak budeme uvažovať sústavu \(n\) nelineárnych rovníc v tvare \[ \begin{array}{c} f_1(x_1;x_2;\dots;x_n)=0,\\ f_2(x_1;x_2;\dots;x_n)=0,\\ \cdots\\ f_n(x_1;x_2;\dots;x_n)=0,\\ \end{array} \] môžeme ju zapísať vo vektorovom tvare \(\vec{f}(\vec{x})=\vec{0}\).

Ak Newtonovu metódu zapíšeme vo vektorovom tvare \[ \begin{array}{l} 1)\quad \vec{f}^{\prime}(\vec{x}^{[k]})\cdot \Delta \vec{x}^{[k]}=- \vec{f}(\vec{x}^{[k]}),\\[1ex] 2)\quad \vec{x}^{[k+1]}=\vec{x}^{[k]}+\Delta \vec{x}^{[k]},\\ \end{array} \] tak prakticky jedinou záhadou je člen \(\vec{f}^{\prime}(\vec{x}^{[k]})\). Ako treba chápať deriváciu vektora, keď máme \(n\) premenných? Derivácie \(n\) funkcií podľa \(n\) neznámych je potrebné zapísať do matice, ktorá sa nazýva Jacobiova matica: \[ \vec{f}^{\prime}(\vec{x}^{[k]}) \stackrel{\mathrm{def}}{=}\left[ \begin{array}{cccc} \frac{\partial f_1}{\partial x_1} \a \frac{\partial f_1}{\partial x_2} \a \cdots \a \frac{\partial f_1}{\partial x_n} \\[1ex] \frac{\partial f_2}{\partial x_1} \a \frac{\partial f_2}{\partial x_2} \a \cdots \a\frac{\partial f_2}{\partial x_n} \\[1ex] \vdots \a \vdots \a \ddots \a \vdots \\[1ex] \frac{\partial f_n}{\partial x_1} \a \frac{\partial f_n}{\partial x_2} \a \cdots \a\frac{\partial f_n}{\partial x_n} \\[1ex] \end{array} \right]_{\vec{x}=\vec{x}^{[k]}}=J(\vec{x}^{[k]}). \] Stredný zápis treba chápať v tom zmysle, že sa jednotlivé rovnice najprv zderivujú podľa jednotlivých premenných a potom sa dosadia aktuálne hodnoty premenných – vektora \(\vec{x}_n\).

Iteračný proces Newtonovej metódy teda zapíšeme v maticovom tvare: \[ \begin{array}{l} 1)\quad J(\vec{x}^{[k]})\cdot \Delta \vec{x}^{[k]}=- \vec{f}(\vec{x}^{[k]}),\\[1ex] 2)\quad \vec{x}^{[k+1]}=\vec{x}^{[k]}+\Delta \vec{x}^{[k]}, \end{array} \] V každom kroku sa teda určí nová Jacobiova matica sústavy \(J(\vec{x}^{[k]})\) a nový vektor pravej strany \(-\vec{f}(\vec{x}^{[k]})\), ktorý získame dosadením aktuálnych hodnôt do jednotlivých rovníc, pričom výsledné hodnoty vynásobíme znamienkom mínus.


Poznámka: V prípade približného riešenia sústav nelineárnych rovníc nemáme k dispozícii také jednoduché postupy na zabezpečenie dosiahnutia požadovanej presnosti \(\varepsilon\), ako sme to videli v prípade riešenia jednej nelineárnej rovnice \(f(x)=0\) Newtonovou metódou v predchádzajúcich cvičeniach. V prípade riešenia sústavy s presnosťou \(\varepsilon\) výpočet zastavíme, ak bude norma (veľkosť) prírastku \(\Delta \vec{x}^{[k]}\) menšia ako \(\varepsilon\), t. j. \(\Vert\Delta \vec{x}^{[k]}\Vert_{\infty}\lt\varepsilon\) (ohľadom normy viď cvičenie 2).

Postup

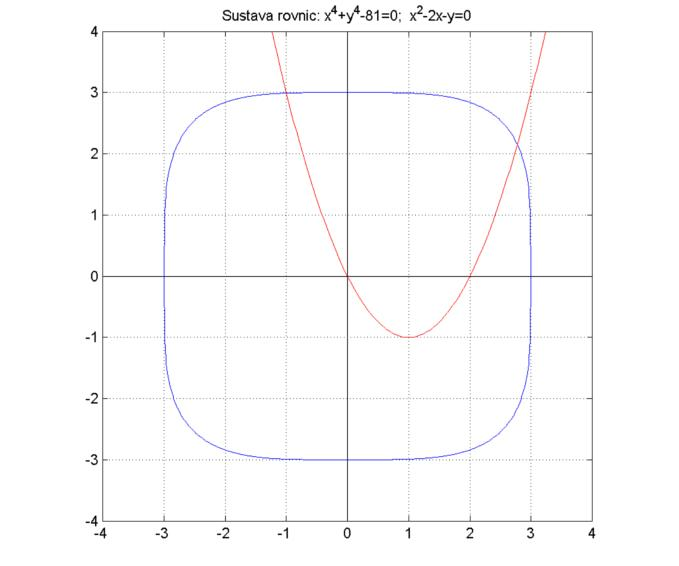
1. Pri analýze najjednoduchších sústav dvoch nelineárnych rovníc je možné použitie grafických metód.

   Príklad: Určme počet riešení sústavy nelineárnych rovníc \[ \begin{array}{r} x^4+y^4-81=0,\\ x^2-2x-y=0. \end{array} \] a separujme všetky korene.

   Riešenie: Ak sa pozrieme na prvú rovnicu, ktorá sa dá napísať v tvare \(x^4+y^4=3^4\), iste nám napadne súvislosť s rovnicou kružnice \(x^2+y^2=3^2\). Uvažovaná rovnica opisuje geometrický objekt, ktorý má s kružnicou nasledujúce spoločné vlastnosti:

   • Symetrický tvar s viacerými symetriami (voči osiam \(o_x\), \(o_y\), \(y=x\), \(y=-x\)), so stredom symetrie v bode \((0;0)\).
   • Množina bodov tvorí ohraničenú uzavretú krivku, ktorá celá leží v štvorci \(\max(x;y)\leqq3\).
   • Tvar krivky je oválny.

   Ľahko zistíme, že krivka prechádza štryrmi bodmi \((-3;0)\), \((3;0)\), \((0;-3)\) a \((0;3)\), ktoré súčasne ležia aj na uvedenej kružnici. Ak dosadíme, napríklad za \(x\) hodnoty \(\pm1\), zistíme, že absolútne hodnoty neznámej \(y\) sú rovné \(\sqrt[4]{80}\approx \sqrt[4]{81}=3\), a teda body \((-1;-3)\), \((-1;3)\), \((1;-3)\), \((1;3)\), \((-3;-1)\), \((3;-1)\), \((-3;1)\) a \((3;1)\) ležia v tesnej blízkosti uvažovanej krivky, čo nám umožňuje danú krivku celkom slušne načrtnúť.
   
   Druhá rovnica \(x^2-2x-y=0\) je rovnicou paraboly \(y=x^2-2x=(x-1)^2-1\), t. j. jej graf je graf paraboly \(y=x^2\) posunutý o jednu jednotku vpravo a jednu jednotku smerom nadol.
   
   Skúste si krivky na základe napísaného vyššie načrtnúť a svoj náčrt porovnajte s nasledujúcim obrázkom.

   

   Obr.: : Grafické zobrazenie sústavy nelineárnych rovníc

   Na základe náčrtu môžeme tvrdiť, že uvažovaná sústava rovníc má práve dve riešenia – priesečníky načrtnutých kriviek, pričom \((x_1;y_1)\in [2;3]\times [2;3]\) a \((x_2;y_2)\in [-1{,}5;-0{,}5]\times [2{,}5;3]\).

   Zobraziť riešenieSkryť riešenie
2. V tejto časti sa zoznámime s použitím Newtonovej metódy na spresňovanie bodov – aproximácií riešení sústav nelineárnych rovníc.

   Príklad: Pre sústavu nelineárnych rovníc \[ \begin{array}{r} x^4+y^4-81=0,\\ x^2-2x-y=0. \end{array} \] upresnite pomocou jedného kroku Newtonovej metódy odhadnuté začiatočné hodnoty všetkých koreňov.

   Riešenie: Začiatočné aproximácie odhadneme na základe náčrtu kriviek pripraveného pri riešení predchádzajúcej úlohy. Zvolíme, napríklad \((x_{1};y_{1})^{[0]}=(2{,}7;2{,}2)\) a \((x_{2};y_{2})^{[0]}=(-1;3)\).
   
   Určíme najprv Jacobiovu maticu všeobecne, neskôr použijeme konkrétne hodnoty premenných \(x\) a \(y\): \[ J(\vec{x})=\left[ \begin{array}{cc} \frac{\partial f_1}{\partial x_1} \a \frac{\partial f_1}{\partial x_2} \\[1ex] \frac{\partial f_2}{\partial x_1} \a \frac{\partial f_2}{\partial x_2} \end{array} \right]=\left[ \begin{array}{cc} 4x^3 \a 4y^3 \\[1ex] 2x-2 \a -1 \end{array} \right]. \] Ďalej uskutočníme jeden krok Newtonovej metódy postupne pre obidva začiatočné body. Po určení nových aproximácií porovnáme ich kvalitu dosadením do rovníc (uvádzame zaokrúhlené údaje):
   
   1. Štartovací bod \(x_{1}^{[0]}=(2{,}7;2{,}2)\): \[ J(\vec{x}_{1}^{[0]}) =\left[\begin{array}{rr} 78.732\a 42.592\\ 3.400\a -1.000 \end{array}\right],\qquad \vec{f}(\vec{x}_{1}^{[0]})= \left[\begin{array}{r} -4.4303 \\ -0.3100 \end{array}\right]. \] Sústavu rovníc \([J|-\vec{f}]\) s neznámym vektorom \(\Delta \vec{x}_{1}^{[0]}\) môžeme riešiť, napríklad, pomocou Cramerovho pravidla: \[ D=\left|\begin{array}{rr} 78.732\a 42.592\\ 3.400\a -1.000 \end{array}\right|=-223{,}5448, \] \[ D_x=\left|\begin{array}{rr} 4.4303\a 42.592\\ 0.3100\a -1.000 \end{array}\right|=-17{,}6338, \quad D_y=\left|\begin{array}{rr} 78.732\a 4.4303\\ 3.400\a 0.3100 \end{array}\right|=9{,}3439, \] \[ \Delta \vec{x}_{1}^{[0]}= \left[\begin{array}{r} D_x/D\\ D_y/D \end{array}\right]= \left[\begin{array}{r} 0{,}07888271\\ -0{,}04179878 \end{array}\right], \] \[ \vec{x}_{1}^{[1]}=\vec{x}_{1}^{[0]}+\Delta \vec{x}_{1}^{[0]}= \left[\begin{array}{r} 2{,}77888271\\ 2{,}15820122 \end{array}\right], \quad \vec{f}(\vec{x}_{1}^{[1]})= \left[\begin{array}{r} 0{,}32760852 \\ 0{,}00622248 \end{array}\right]. \] 2. Štartovací bod \(x_{2}^{[0]}=(-1;3)\): \[ J(\vec{x}_{2}^{[0]}) =\left[\begin{array}{rr} -4\a 108\\ -4\a -1 \end{array}\right],\qquad \vec{f}(\vec{x}_{2}^{[0]})= \left[\begin{array}{r} 1 \\ 0 \end{array}\right]. \] \[ D=\left|\begin{array}{rr} -4\a 108\\ -4\a -1 \end{array}\right|=436, \] \[ D_x=\left|\begin{array}{rr} -1\a 108\\ 0\a -1 \end{array}\right|=1, \quad D_y=\left|\begin{array}{rr} -4\a -1\\ -4\a 0 \end{array}\right|=-4, \] \[ \Delta \vec{x}_{2}^{[0]}= \left[\begin{array}{r} D_x/D\\ D_y/D \end{array}\right]= \left[\begin{array}{r} 0{,}00229358\\ -0{,}00917431 \end{array}\right], \] \[ \vec{x}_{2}^{[1]}=\vec{x}_{2}^{[0]}+\Delta \vec{x}_{2}^{[0]}= \left[\begin{array}{r} -0{,}99770642\\ 2{,}99082569 \end{array}\right], \quad \vec{f} (\vec{x}_{2}^{[0]})= \left[\begin{array}{r} 0{,}00456733 \\ 0{,}00000526 \end{array}\right]. \] Vidíme, že v druhom prípade sme odhadli štartovací bod o niečo kvalitnejšie a už po prvom kroku sú funkčné hodnoty určujúce ľavé strany rovníc malé. Aj v prvom prípade sa absolútne hodnoty funkčných hodnôt zmenšili.

   Zobraziť riešenieSkryť riešenie

   Poznámka: Newtonova metóda sa v prípade dobrej začiatočnej aproximácie prejavuje ako rýchle konvergujúca (jedná sa o metódu s tzv. kvadratickou rýchlosťou konvergencie). V nasledujúcich dvoch tabuľkách uvádzame výsledky, ktoré sme získali v Matlabe/Octave pomocou opakovania nasledujúcich príkazov umiestnených na jeden riadok:
   
   J=[4*x(1)^3, 4*x(2)^3;2*x(1)-2,-1], f=[x(1)^4+x(2)^4-81; x(1)^2-2*x(1)-x(2)], dx=-inv(J)*f, x=x+dx \[ \begin{array}{|r|c|c|c|c|} \hline k\a x_{1}^{[k]} \a y_{1}^{[k]} \a f_1(\vec{x}_{1}^{[k]}) \a f_2(\vec{x}_{1}^{[k]}) \\ \hline 0\a 2{,}700000000000000 \a 2{,}200000000000000 \a -4{,}4303 \a -0{,}31 \\ \hline 1\a 2{,}778882711653324 \a 2{,}158201219621302 \a 0{,}327608523 \a 0{,}006222482 \\ \hline 2\a 2{,}776358337288419 \a 2{,}155442569988142 \a 0{,}000507577 \a 0{,}000006372 \\ \hline 3\a 2{,}776354990216047 \a 2{,}155437051254248 \a 1{,}367 \cdot 10^{-9} \a 0{,}011 \cdot 10^{-9}\\ \hline 4\a 2{,}776354990208079 \a 2{,}155437051237144 \a 1{,}421 \cdot 10^{-14} \a 0 \\ \hline \end{array} \] \[ \begin{array}{|r|c|c|c|c|} \hline k\a x_{2}^{[k]} \a y_{2}^{[k]} \a f_1(\vec{x}_{2}^{[k]}) \a f_2(\vec{x}_{2}^{[k]}) \\ \hline 0\a -1 \a 3 \a 1 \a 0 \\ \hline 1\a -0{,}997706422018349 \a 2{,}990825688073394 \a 0{,}004567328 \a 0{,}000005260 \\ \hline 2\a -0{,}997694533482717 \a 2{,}990783448965392 \a 9{,}660 \cdot 10^{-8}\a 0{,}014 \cdot 10^{-8} \\ \hline 3\a -0{,}997694533223806 \a 2{,}990783448072278 \a 2{,}842 \cdot 10^{-14} \a 0 \\ \hline \end{array} \] Nuly v pravom dolnom rohu obidvoch tabuliek sú výsledky, ktoré vypísal použitý program. Je pravdepodobné, že odpovedajúce hodnoty ľavých strán druhej rovnice sústavy sú malé nenulové hodnoty.

   Poznámka: V tomto prípade sme mohli namiesto sústavy nelineárnych rovníc prejsť na riešenie nasledujúcej algebrickej rovnice 8. rádu: \[ x^8-8x^7+24x^6-32x^5+17x^4-81=0, \] ktorú môžeme získať tak, že z druhej rovnice sústavy vyjadríme \(y=x^2-2x\) a tento výraz dosadíme do prvej rovnice.
   
   V prípade zložitejších nelineárnych sústav však je takýto postup možný len výnimočne.
   
   Pri pohľade na algebrickú rovnicu tiež nie je jasné, koľko reálnych koreňov má a kde sa nachádzajú. Použitím príkazu
   
   roots([1 -8 24 -32 17 0 0 0 -81])
   
   v programe Matlab/Octave dostaneme nasledujúce výsledky: \[ \begin{array}{l} \phantom{-} 2.776354990208112 \\ \phantom{-} 2.568708345457808 + 0.978208721044785i\\ \phantom{-} 2.568708345457808 - 0.978208721044785i\\ \phantom{-} 0.981203232720892 + 1.436060637512282i\\ \phantom{-} 0.981203232720892 - 1.436060637512282i\\ -0.439241806670853 + 1.042383788608000i\\ -0.439241806670853 - 1.042383788608000i\\ -0.997694533223805 \end{array} \] Algebrická rovnica má práve 2 reálne korene, ktoré sa s vysokou presnosťou zhodujú s hodnotami \(x_{1}^{[4]}\) a \(x_{2}^{[3]}\) získanými Newtonovou metódou na riešenie sústav nelineárnych rovníc.

   Príklad: S presnosťou \(\varepsilon=0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc \[\begin{array}{l} x^2+ y^2 -1 = 0,\\ x\cdot\cos x - y = 0. \\ \end{array}\]

   Riešenie: Ak načrtneme graf funkcie \(y=x\cdot\cos x\) a jednotkovú kružnicu \(x^2+ y^2 =1\) uvidíme, že daná sústava dvoch nelineárnych rovníc o dvoch neznámych má práve dve riešenia, pričom body \(\vec{x}_1\) a \(\vec{x}_2\) sú v rovine premenných \(x\) a \(y\) symetrické vzhľadom na začiatok súradnicového systému. Preto je postačujúce určiť približne jedno z riešení.
   
   Ako začiatočnú aproximáciu riešenia v 1. kvadrante môžeme zvoliť, napríklad, bod \((x,y)^{[0]}=(0{,}707;0{,}707)\). Tabuľku doplníme o stĺpčeky obsahujúce prírastky premenných \(x\) a \(y\). V Matlabe/Octave vyriešime úlohu opakovaním nasledujúcich príkazov:
   
   x=[0.707;0.707];
   J=[2*x(1), 2*x(2);cos(x(1))-x(1)*sin(x(1))-1], f=[x(1)^2+x(2)^2 -1; x(1)*cos(x(1))-x(2)], dx=-inv(J)*f, max(abs(dx)), x=x+dx \[ \begin{array}{|r|c|c|c|c|c|c|c|} \hline k\a x^{[k]} \a y^{[k]} \a f_1(\vec{x}^{[k]}) \a f_2(\vec{x}^{[k]}) \a \Delta x^{[k]} \a \Delta y^{[k]} \a \Vert \Delta \vec{x}^{[k]}\Vert \\ \hline 0\a 0{,}707 \a 0{,}707 \a -3{,}0200 \cdot 10^{-4} \a -0{,}16946 \a 0{,}13041 \a -0{,}13019 \a 0{,}13041 \\ \hline 1\a 0{,}83741 \a 0{,}57681 \a 0{,}033957 \a -0{,}016252 \a -0{,}0087944 \a -0{,}0166677 \a 0{,}0166677 \\ \hline 2\a 0{,}82861 \a 0{,}56014 \a 3{,}5515 \cdot 10^{-4} \a -7{,}1695 \cdot 10^{-5} \a -1{,}5412\cdot 10^{-4} \a -8{,}9029 \cdot 10^{-5}\a 1{,}5412\cdot 10^{-4} \\ \hline 3\a 0{,}8284599 \a 0{,}5600484 \a 3{,}1680 \cdot 10^{-8} \a -2{,}4157 \cdot 10^{-8} \a \a \a \\ \hline \end{array} \] Po dvoch iteráciách bola norma prírastku ešte väčšia ako predpísaná presnosť \(0{,}01\). Po tretej iterácii bol prírastok už o dva rády menší. Hodnoty ľavých strán rovníc sú už po troch iteráciách rádovo \(10^{-8}\), teda môžeme byť spokojní s danou aproximáciou riešenia.

   Zobraziť riešenieSkryť riešenie

Zdroje

1. Buša, Pirč, Schrötter: Numerické metódy, pravdepodobnosť a matematická štatistika, 2006, ISBN 80-8073-632-4. Je možné stiahnuť obrazovkovú alebo tlačovú verziu.
2. Daňo, Ostertagová: Vybrané kapitoly z numerických metód, pravdepodobnosti a matematickej štatistiky, Equilibria s.r.o., Košice, 2012, ISBN 978-80-8143-012-1.

Doplňujúce úlohy

Úloha: S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc \[\begin{array}{l} x^2 y^2 - 3x^3 - 6 y^3 + 8 = 0,\\ x^4 - 9 y + 2 = 0. \\ \end{array}\]
Výsledok: \([-2{,}00; 2{,}00]; [1{,}3508; 0{,}59214]\)
Zobraziť výsledokSkryť výsledok
Úloha: S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc \[\begin{array}{l} \sin x - y = 1{,}32,\\ \cos y - x = -0{,}85. \\ \end{array}\]
Výsledok: \([1{,}7913; -0{,}34422]\)
Zobraziť výsledokSkryť výsledok
Úloha: S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc \[\begin{array}{l} (x - 1{,}2)^2 + (y - 0{,}6)^2 = 1,\\ 4{,}2 x^2 + 8{,}8 y^2 = 1{,}42. \\ \end{array}\]
Výsledok: \([0{,}22684; 0{,}36987]; [0{,}53912; -0{,}15049]\)
Zobraziť výsledokSkryť výsledok
Úloha: S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc \[\begin{array}{l} x^3 - y^2 - 1 = 0,\\ x y^3 - y - 4 = 0. \\ \end{array}\]
Výsledok: \([1{,}5020; 1{,}5456]\)
Zobraziť výsledokSkryť výsledok
Úloha: S presnosťou \(0{,}01\) riešte v \(\mathbb{R} \times \mathbb{R}\) sústavu rovníc \[\begin{array}{l} \mathrm{e}^{xy} - x^2 + y = 0,\\ x^2 + y^2 = 4. \\ \end{array}\]
Výsledok: \([-1{,}8437; -0{,}7750]; [-1{,}2910; 1{,}5275]; [-0{,}3797; -1{,}9636]; [1{,}9121; 0{,}5865]\)
Zobraziť výsledokSkryť výsledok