Jednoduchá lineárna regresia. Pearsonov výberový korelačný koeficient.

Ciele

1. Naučiť sa určovať bodové odhady regresných koeficientov regresnej priamky.
2. Naučiť sa určovať Pearsonov výberový korelačný koeficient.

Úvod

Medzi veličinami rozlišujeme tzv. funkčné (pevné) a voľné závislosti.
Funkčnou závislosťou rozumieme vzťah, keď každej hodnote jednej veličiny zodpovedá jediná hodnota iných veličín a podobne aj naopak. S takýmito závislosťami sa stretávame väčšinou v teoretickej oblasti.
Voľnou závislosťou rozumieme vzťah, keď hodnotám napríklad jednej veličiny zodpovedajú rôzne hodnoty inej veličiny, ale pri zmenách hodnôt týchto veličín sa prejavuje určitá všeobecná tendencia. S voľnými závislosťami sa stretávame takmer výhradne v praktických situáciách.
V prípade, že ide o voľnú závislosť medzi kvantitatívnymi štatistickými znakmi, hovoríme o štatistickej závislosti.

Závislosťou kvantitatívneho znaku na jednom kvantitatívnom znaku alebo na viacerých kvantitatívnych znakoch sa zaoberá regresná analýza.
V prípade závislosti dvoch kvantitatívnych znakov \(X\) a \(Y\) hovoríme o jednorozmernej regresii (prípadne jednoduchej regresii). Veličina \(Y\) sa nazýva závisle premenná, niekedy aj vysvetľovaná premenná. Veličinu \(X\) nazývame nezávisle premenná alebo vysvetľujúca premenná.

Vzájomnými závislosťami veličín sa zaoberá korelačná analýza. V korelačnej analýze sa kladie dôraz na silu (intenzitu) vzájomného vzťahu medzi veličinami.

Pri meraní závislosti dvoch kvantitatívnych znakov môžeme druh a silu závislosti orientačne posúdiť z bodového grafu, tzv. korelačného diagramu, v ktorom je každá dvojica údajov graficky znázornená jedným bodom v rovine. Druh závislosti odhadujeme pomocou krivky, ktorá sa dobre hodí k zisteným hodnotám.

Uvažujme prípad štatistickej závislosti dvoch znakov \(X\) a \(Y\), kde \(Y\) je závisle premenná a \(X\) je nezávisle premenná. Základný jednoduchý regresný model má tvar \[ y_i=f(x_i)+\epsilon_i,\ \] kde \(y_i\), resp. \(x_i\), \(i=1,2,\ldots,n\); predstavujú hodnoty znaku \(Y\), resp. \(X\); \(\epsilon_i\) je náhodná (reziduálna) zložka (používa sa tiež názov náhodná chyba) a funkciu \(f\) nazývame regresná funkcia. Regresná funkcia predstavuje deterministickú zložku.
O náhodných chybách \(\epsilon_i\) sa predpokladá, že sú to náhodné veličiny, ktoré majú normálne rozdelenie s nulovou strednou hodnotou a so smerodajnou odchýlkou \(\sigma\gt 0\).
Podmienka, že stredná hodnota \( E(\epsilon_i) = 0 \) pre každé \(i=1,2,\ldots,n\) znamená, že náhodná zložka nepôsobí systematickým spôsobom na hodnoty vysvetľovanej premennej \(Y\).
Rozptyl \( D(\epsilon_i) = \sigma^2\ \) pre každé \(i=1,2,\ldots,n\); t. j. rozptyl náhodnej zložky je konštantný. Táto podmienka vyjadruje, že variabilita náhodnej zložky nezávisí na hodnotách vysvetľujúcej premennej \(X\).

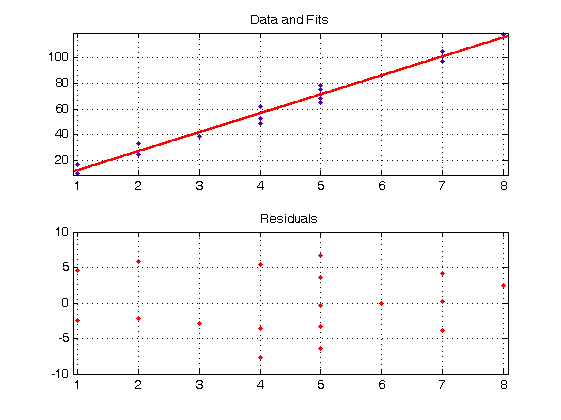
Nech \(\hat{y}_i\) je teoretická (vypočítaná, vyrovnaná) hodnota premennej \(Y\). Rozdiel empirickej (pozorovanej) a teoretickej hodnoty \[ e_i=y_i - \hat{y}_i\] nazývame rezíduum. Rezíduum predstavuje bodový odhad náhodnej chyby \(\epsilon_i\).
Rozptyl \( D(\epsilon_i) = \sigma^2\ \), \(i=1,2,\ldots,n\); obvykle nepoznáme a musí byť tiež odhadnutý z dát, ktoré sú k dispozícii.
Štatistika \[ \mathrm{SSE}=\sum\limits_{i=1}^{n} e_i^2 \] sa nazýva reziduálny súčet štvorcov (Sum of Square Errors).
Pomocou reziduálneho súčtu štvorcov je možné stanoviť výberový reziduálny rozptyl, v praxi označovaný často ako priemerná kvadratická chyba (Mean Square of Error) \[ \mathrm{MSE}=\frac{\mathrm{SSE}}{n-k},\ \] kde \(k\) je počet odhadovaných parametrov regresnej funkcie. \(\mathrm{MSE}\) predstavuje bodový odhad rozptylu \( \sigma^2\).
Bodovým odhadom smerodajnej odchýlky \( \sigma\) je výberová reziduálna smerodajná odchýlka (Root Mean Square of Error) \[ \mathrm{RMSE}=\sqrt{\mathrm{MSE}}.\ \] Reziduálny rozptyl vyjadruje, ako veľmi sa v priemere teoretická hodnota \(\hat{y}\) veličiny \(Y\) líši od empirickej hodnoty \(y\), teda udáva, ako sú hodnoty veličiny \(Y\) rozptýlené okolo regresnej funkcie. \(\def\a{&}\)

Postup

1. Jednoduchá lineárna regresia
   
   Ak je regresná funkcia \(f\) lineárna, teda ak má tvar regresnej priamky \[ y=a_0+a_1x, \] potom hovoríme o jednoduchej lineárnej regresii. Čísla \(a_0\) a \(a_1\) nazývame parametre regresnej priamky alebo regresné koeficienty.
   
   Regresný koeficient \(a_0\) predstavuje priesečník regresnej priamky s osou \(o_y\). Tento regresný koeficient sa niekedy nazýva úrovňová konštanta.
   Regresný koeficient \(a_1\) vyjadruje smernicu regresnej priamky, teda sklon priamky k osi \(o_x\). Charakterizuje zmenu závisle premennej, ktorá zodpovedá zmene nezávisle premennej o jednu jej jednotku. Ak je kladný, tak s rastom hodnôt nezávisle premennej \(X\) dochádza v priemere tiež k rastu hodnôt závisle premennej \(Y\). Túto závislosť nazývame pozitívna, resp. priama závislosť. Ak je regresný koeficient \(a_1\) záporný, tak pri raste hodnôt nezávisle premennej dochádza v priemere k poklesu hodnôt závisle premennej. V tomto prípade hovoríme o negatívnej (nepriamej) závislosti.
   
   Hodnoty \(a_0\) a \(a_1\) sú vo všeobecnom prípade neznámymi parametrami základného súboru, ktoré je nutné odhadnúť pomocou \(n\) nezávislých pozorovaní veličín \(X\) a \(Y\), ktorých výsledkom sú usporiadané dvojice hodnôt \((x_1,y_1),\ldots,(x_n,y_n)\), kde \(y_i\) predstavujú hodnoty závisle premennej \(Y\) a \(x_i\) sú hodnoty nezávisle premennej \(X\).
   Tieto dvojice hodnôt môžeme získať hlavne dvoma spôsobmi:

   • Hodnoty \(x_i\) nezávisle premennej sme vopred pevne zvolili a k nim sme zmerali príslušné hodnoty \(y_i\). V tomto prípade sú hodnoty znaku \(X\) pevné (nenáhodné), teda \(X\) nie je náhodnou veličinou, kým veličinu \(Y\) považujeme za náhodnú.
   • Dvojice hodnôt \((x_i,y_i)\) získame meraním na \(n\) náhodne zvolených jednotkách základného súboru. V tomto prípade považujeme hodnoty znaku \(X\) aj \(Y\) za náhodné veličiny.

   
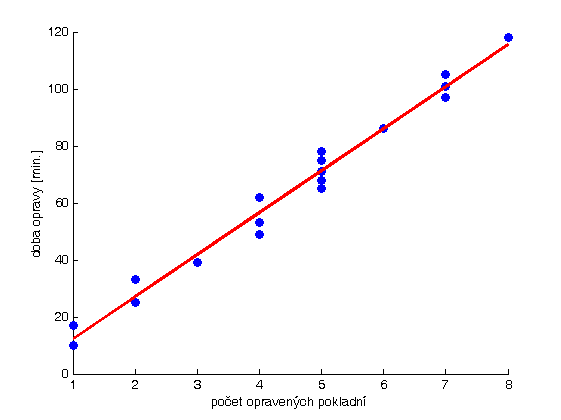
   Uvedený súbor dvojíc hodnôt môžeme geometricky znázorniť v rovine bodovým grafom, kde na vodorovnú os \(o_x\) nanášame hodnoty nezávisle premennej a na zvislú os \(o_y\) príslušné hodnoty závisle premennej. Výsledkom je geometrické znázornenie \(n\) bodov v rovine, zo vzájomnej polohy ktorých môžeme posudzovať regresnú závislosť znakov \(Y\) a \(X\).
   
   Úlohou jednoduchej lineárnej regresie je preložiť danými bodmi priamku, t. j. nájsť lineárnu regresnú funkciu, ktorá najlepšie charakterizuje polohu daných \(n\) bodov. Táto funkcia má mať tvar \(f(x)=a_0+a_1x\), kde \(a_0\) a \(a_1\) sú zatiaľ neznáme hodnoty parametrov regresnej priamky.
   Jednoduchý lineárny regresný model má teda tvar \[ y_i=a_0+a_1x+\epsilon_i,\ \] \(i=1,2,\ldots,n\).
   Vyrovnávajúca regresná priamka bude mať tvar \[ \hat{y}_i=\hat{a}_0+\hat{a}_1x_i, \] kde \(\hat{y}_i\) je vyrovnaná (teoretická, vypočítaná) hodnota premennej \(Y\), \(\hat{a}_0\) je bodový odhad parametra \(a_0\), \(\hat{a}_1\) je bodový odhad parametra \(a_1\).
   
   Bodové odhady \(\hat{a}_0\), \(\hat{a}_1\) neznámych parametrov \(a_0\), \(a_1\) regresnej priamky sa z pozorovaných dát získavajú najčastejšie metódou najmenších štvorcov (MNŠ).

   Poznámka: Pozrite si cvičenie 4, kde sa tiež píše o metóde MNŠ.

   Pri MNŠ sa snažíme o minimalizáciu chýb, ktoré predstavujú rozdiely medzi teoretickými (vypočítanými) a empirickými (nameranými, pozorovanými) hodnotami závisle premennej \(Y\). Keďže rozdiely môžu nadobúdať ako kladné, tak aj záporné hodnoty, umocňujú sa na druhú a počítajú sa ich súčty.
   
   Hľadáme hodnoty \(\hat{a}_0\), \(\hat{a}_1\), pre ktoré nadobúda svoju minimálnu hodnotu reziduálny súčet štvorcov odchýlok empirických hodnôt \(y_i\) závisle premennej od teoretických hodnôt \(\hat{y}_i\): \[ \mathrm{SSE}(\hat{a}_0,\hat{a}_1)=\sum\limits_{i=1}^{n} e_i^2 = \sum\limits_{i=1}^{n}(y_i-\hat{y}_i)^2 = \sum\limits_{i=1}^{n}(y_i-\hat{a}_0-\hat{a}_1x_i)^2.\] Ako je známe z matematickej analýzy, bod minima uvedenej funkcie dvoch premenných nájdeme tak, že jej parciálne derivácie podľa premenných \(\hat{a}_0\) a \(\hat{a}_1\) položíme rovné nule: \[ \frac{\partial \, \mathrm{SSE}}{\partial \, \hat{a}_0} =0,\\ \] \[ \frac{\partial \, \mathrm{SSE}}{\partial \, \hat{a}_1} =0.\\ \] Dostaneme: \[ \frac{\partial }{\partial \,\hat{a}_0 } \biggl[\sum\limits_{i=1}^{n}(y_i-\hat{a}_0-\hat{a}_1x_i)^2\ \biggr] = \sum\limits_{i=1}^{n}2(y_i-\hat{a}_0-\hat{a}_1x_i) \cdot (-1)=0,\\ \] \[ \frac{\partial }{\partial \,\hat{a}_1 } \biggl[\sum\limits_{i=1}^{n}(y_i-\hat{a}_0-\hat{a}_1x_i)^2\ \biggr] = \sum\limits_{i=1}^{n}2(y_i-\hat{a}_0-\hat{a}_1x_i) \cdot (-x_i)=0.\\ \] Pre bodové odhady \(\hat{a}_0\), \(\hat{a}_1\) neznámych parametrov \(a_0\), \(a_1\) dostaneme po úprave sústavu dvoch lineárnych rovníc o dvoch neznámych, ktorú nazývame sústavou normálnych rovníc: \[ \begin{array}{r} n\cdot \hat{a}_0+\hat{a}_1 \cdot \sum\limits_{i=1}^{n} x_i = \sum\limits_{i=1}^{n} y_i,\\ \hat{a}_0 \cdot \sum\limits_{i=1}^{n} x_i+\hat{a}_1 \cdot \sum\limits_{i=1}^{n} x_i^2 =\sum\limits_{i=1}^{n} x_i \cdot y_i. \end{array} \] Riešením príslušnej sústavy normálnych rovníc dostaneme odhady \(\hat{a}_0\), \(\hat{a}_1\) v tvare: \[ \hat{a}_1=\dfrac{n\cdot \sum\limits_{i=1}^{n} x_i\cdot y_i -\sum\limits_{i=1}^{n} x_i \cdot \sum\limits_{i=1}^{n} y_i} { n\cdot \sum\limits_{i=1}^{n} x_i^2 - \biggl(\sum\limits_{i=1}^{n} x_i \biggr)^2}, \] \[ \hat{a}_0=\dfrac{\sum\limits_{i=1}^{n} y_i - \hat{a}_1\cdot\sum\limits_{i=1}^{n} x_i} {n}=\overline y-\hat{a}_1\cdot\overline x. \]

   Poznámka: Treba zdôrazniť dôležitý fakt, že dáta pre regresnú analýzu sú výsledkom náhodného výberu, preto aj odhady \(\hat{a}_0\), \(\hat{a}_1\) parametrov \(a_0\), \(a_1\) budú náhodné veličiny. Pri každom ďalšom náhodnom výbere dát bude výsledok, t. j. odhad \(\hat{a}_0\), \(\hat{a}_1\) vo všeobecnosti iný.

   Príklad:
   Firma realizuje opravy registračných pokladní. V tabuľke sú dáta z 18 ohlásených opráv. Pri každej oprave je uvedený počet opravovaných pokladní \(X\) a celková doba opravy \(Y\) v minútach: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 7 \a 6 \a 5\a 1 \a 5\a 4 \a 7\a 3\a 4\a 2\a 8\a 5\a2\a 5\a 7\a1\a4\a5 \\ \hline y_i \a 97 \a 86 \a 78 \a 10 \a 75 \a 62 \a 101 \a 39\a 53\a 33\a 118\a 65\a 25\a 71\a 105\a 17\a 49\a 68 \\ \hline \end{array} \]Predpokladáme, že ide o náhodný výber z dvojrozmerného normálneho rozdelenia. Riešte úlohy:

   1. Odhadnite závislosť celkovej doby opravy od počtu opravovaných pokladní regresnou priamkou \(f(x)=a_0+a_1x\).
   2. Regresnú priamku spolu s bodmi \((x_i,y_i)\) znázornite.
   3. Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).

   Riešenie:
   

   1. Bodové odhady \(\hat{a}_0\), \(\hat{a}_1\) regresných koeficientov \(a_0\), \(a_1\) získame riešením uvedenej sústavy dvoch lineárnych rovníc o dvoch neznámych. V našom prípade to bude táto sústava: \[ \begin{array}{r} 18\cdot \hat{a}_0+81 \cdot \hat{a}_1 = 1152,\\ 81\cdot \hat{a}_0+ 439 \cdot \hat{a}_1 = 6282. \end{array} \] Dostaneme riešenie: \(\hat{a}_0=-2{,}322148\) a \(\hat{a}_1=14{,}738255\). Teda \(f(x)\approx \hat y=\hat{a}_0+\hat{a}_1\cdot x=-2{,}322148+14{,}738255 \cdot x\).
      
      Teraz ukážeme riešenie tejto úlohy použitím MATLABu dvojakým spôsobom, a to riešením danej sústavy pomocou inverznej matice, resp. priamo použitím štandardnej funkcie MATLABu polyfit(x,y,n), kde n udáva stupeň polynómu (pozrite si to podrobnejšie použitím príkazu help polyfit.
      
      x=[7,6,5,1,5,4,7,3,4,2,8,5,2,5,7,1,4,5];y=[97,86,78,10,75,62,101,39,53,33,118,65,25,71,105,17,49,68];
      A=[length(x),sum(x);sum(x),sum(x.^2)],B=[sum(y);sum(x.*y)],regr=inv(A)*B
      
      regr=polyfit(x,y,1),a1=regr(1),a0=regr(2)
      
   
   
   2. Použitie MATLABu na grafické znázornenie:
      yR=polyval(regr,x);scatter(x,y,'filled');hold on,plot(x,yR,'r','linewidth',2),
      xlabel('počet opravených pokladní'),ylabel('doba opravy [min.]')
      
      
   
   
   3. Najprv vypočítame rezíduá \(e_i\), t. j. bodové odhady náhodných chýb \(\epsilon_i\), \(i=1,2,\ldots,n\). Platí \( e_i=y_i - \hat{y}_i \), čo znamená rozdiel empirickej a teoretickej hodnoty.
      Počítame postupne pomocou kalkulačky. Napr. pre \(i=1\) dostaneme teoretickú hodnotu \(\hat {y}_1=-2{,}322148+14{,}738255 \cdot 7=100{,}845637\) a príslušné rezíduum je \( e_1=y_1 - \hat{y}_1 = 97-100{,}845637=-3{,}845637\).
      Výsledky vidíme v nasledujúcej tabuľke:

      \(x_i\)	\(y_i\)	\(\hat {y}_i\)	\(e_i\)
      7	97	100,845637	-3,845637
      6	86	86,107382	-0,107382
      5	78	71,369127	6,630872
      1	10	12,416107	-2,416107
      5	75	71,369127	3,630872
      4	62	56,630872	5,369127
      7	101	100,845637	0,154362
      3	39	41,892617	-2.892617
      4	53	56,630872	-3,630872
      2	33	27,154362	5.845637
      8	118	115,583893	2,416107
      5	65	71,369127	-6,369127
      2	25	27,154362	-2,154362
      5	71	71,369127	-0,369127
      7	105	100,845637	4,154362
      1	17	12,416107	4,583893
      4	49	56,630872	-7,630872
      5	68	71,369127	-3,369127

      
      Bodovým odhadom rozptylu \(\sigma^2\) je charakteristika \( \mathrm{MSE}=\dfrac{\mathrm{SSE}}{n-k} \) a bodovým odhadom smerodajnej odchýlky \(\sigma\) je výberová reziduálna smerodajná odchýlka \( \mathrm{RMSE}=\sqrt{\mathrm{MSE}} \), kde \(k\) je počet odhadovaných parametrov regresnej funkcie a \( \mathrm{SSE}=\sum\limits_{i=1}^{n} e_i^2 \).
      V našom prípade je \(n=18\) a \(k=2\). Výpočty realizujeme pomocou kalkulačky.
      Dostaneme:
      \( \mathrm{SSE}=321{,}395973\);\(\ \) \( \mathrm{MSE}=\dfrac{321{,}395973}{16}=20{,}087248\); \(\ \) \( \mathrm{RMSE}=\sqrt{20{,}087248}=4{,}481880 \).
      
      Použitie MATLABu na výpočet:
      n=18;k=2;e=y-yR,[x;y;yR;e],SSE=sum((y-yR).^2),MSE=SSE/(n-k),RMSE=sqrt(MSE)
      
   
   Ukážeme ešte riešenie úlohy v prostredí cftool. Odošleme príkaz:
   cftool(x,y)
   Klikneme na Fitting, New fit, Type of fit: Polynomial, kde zvolíme linear polynomial. Potom klikneme na Apply.
   Výsledok z MATLABu:
   Linear model Poly1: f(x) = p1*x + p2
   Coefficients (with 95% confidence bounds):
   p1 = 14.74 (13.64, 15.84)
   p2 = -2.322 (-7.758, 3.114)
   Goodness of fit:
   SSE: 321.4
   RMSE: 4.482
   
   Ak chceme graficky zobraziť aj rezíduá, tak v grafickom okne Curve Fitting Tool klikneme na View, Residuals a zvolíme napr. Scatter Plot. Ak chceme zobraziť aj sieťku, tak v Tools klikneme na Grid.
   
   
   Teraz ukážeme ešte ďalšiu možnosť aplikácie MATLABu. Na regresnú a korelačnú analýzu v MATLABe slúži napr. funkcia regress. Použijeme 3 výstupné argumenty a 3 vstupné argumenty: [a,aint,e]=regress(y,X,alpha) .
   Do premennej a sa uloží vektor odhadov regresných koeficientov (výstup koeficientov je tu od najvyššej po najnižšiu mocninu), do aint sa uloží matica intervalov spoľahlivosti odhadov regresných koeficientov pre danú hladinu významnosti \(\alpha\), do premennej e sa uloží vektor rezíduí (t. j. vektor bodových odhadov náhodných chýb).
   x=x';y=y';n=length(x),X=[x,ones(n,1)];[a,aint,e]=regress(y,X,0.05)
   Výsledok z MATLABu:
   a = 14.7383 -2.3221
   aint =
   13.6375 15.8390
   -7.7583 3.1140
   e =
   -3.8456
   -0.1074
   6.6309
   -2.4161
   3.6309
   5.3691
   0.1544
   -2.8926
   -3.6309
   5.8456
   2.4161
   -6.3691
   -2.1544
   -0.3691
   4.1544
   4.5839
   -7.6309
   -3.3691
   
   

   Poznámka: Ďalšie možnosti nám ponúka použitie piatich výstupných argumentov (viď help regress).
   Pre zaujímavosť ilustrujeme grafické zobrazenie rezíduí aj s 95 %-nými intervalmi spoľahlivosti, tzv. rcplot:

   

   
   Vidíme, že intervaly spoľahlivosti všetkých náhodných chýb obsahujú bod 0, čo svedčí v prospech hypotézy, že náhodné chyby sú normálne rozdelené.

   Zobraziť riešenieSkryť riešenie
2. Pearsonov výberový korelačný koeficient
   
   Korelačná analýza skúma existenciu väzby − korelácie medzi sledovanými premennými.
   
   Predpokladajme, že medzi veličinami \(X\) a \(Y\) existuje lineárna závislosť. Nech \((x_1,y_1),\ldots,(x_n,y_n)\) sú namerané hodnoty nezávislého náhodného výberu o rozsahu \(n\) systému dvoch náhodných veličín \(X\), \(Y\) z dvojrozmerného normálneho rozdelenia a nech \(\bar{x}\) a \(\bar{y}\) sú ich výberové priemery.
   Pre Pearsonov výberový korelačný koeficient platí vzťah \[ r_{x,\,y}=\dfrac{ \overline {x\cdot y}-\overline x\cdot \overline y} { \sqrt{\overline {x^2}-(\overline x)^2} \cdot \sqrt{\overline {y^2}-(\overline y)^2 } }, \] kde je \(\overline {x^2}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i^2\),\(\, \) \(\ \) \(\overline {y^2}=\frac{1}{n}\sum\limits_{i=1}^{n} y_i^2\),\(\, \) \(\ \) \(\overline {x\cdot y}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i \cdot y_i\).
   
   Pearsonov výberový korelačný koeficient \(r_{x,\,y}\) meria tesnosť lineárnej závislosti medzi premennými \(X\) a \(Y\) obojstranne, t. j. \(r_{x,\,y}=r_{y,\,x}=r\).

   Poznámka: Ďalej budeme písať len \(r\).

   Pearsonov výberový korelačný koeficient nadobúda hodnoty z intervalu \(\left\langle -1\ ;1 \right\rangle\) a vyjadruje stupeň lineárnej korelačnej závislosti medzi premennými \(X\) a \(Y\). Čím je hodnota \(|r|\) bližšia k \(1\), tým je lineárna závislosť silnejšia a čím je hodnota \(r\) bližšia k \(0\), tým je lineárna závislosť slabšia. V prípade, že tento koeficient nadobúda hodnoty \(1\) alebo \(-1\), ležia všetky body na regresnej priamke a závislosť veličín \(X\) a \(Y\) je presne lineárna. Ak je \(r=0\), tak hovoríme, že lineárna závislosť medzi \(X\) a \(Y\) neexistuje (môže však existovať iná závislosť).
   
   Existuje orientačná stupnica na hodnotenie tesnosti lineárnej závislosti veličinami medzi \(X\) a \(Y\):

   • Slabá závislosť, ak \(0\lt |r| \leq0{,}3\).
   • Mierna (stredná) závislosť, ak \(0{,}3\lt |r| \leq0{,}8\).
   • Silná závislosť, ak \(0{,}8\lt |r| \leq1\).

   Príklad:
   Použite vstupné dáta z predchádzajúceho príkladu. Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.

   Riešenie:
   Pearsonov výberový korelačný koeficient \(r\) môžeme vypočítať priamo s kalkulačkou na základe vzťahu: \[ r=\dfrac{ \overline {x\cdot y}-\overline x\cdot \overline y} { \sqrt{\overline {x^2}-(\overline x)^2} \cdot \sqrt{\overline {y^2}-(\overline y)^2 } }. \] Počítame postupne:
   \(\overline{x}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i=\dfrac{81}{18}=4{,}5\);\(\,\) \(\ \) \(\overline{y}=\frac{1}{n}\sum\limits_{i=1}^{n} y_i=\dfrac{1152}{18}=64\);\(\,\) \(\ \) \(\overline {x\cdot y}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i \cdot y_i=\dfrac{6282}{18}=349\);\(\,\)
   
   \(\overline {x^2}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i^2=\dfrac{439}{18}=24{,}3\overline{8} \);\(\,\) \(\ \) \(\overline {y^2}=\frac{1}{n}\sum\limits_{i=1}^{n} y_i^2=\dfrac{90232}{18}=5012{,}\overline{8}\);
   
   \(\sqrt{\overline {x^2}-(\overline x)^2}=2{,}034426 \);\(\,\) \(\ \) \(\sqrt{\overline {y^2}-(\overline y)^2}=30{,}280173 \).
   
   Dostaneme výsledok \( r=0{,}9902\). Teda medzi \(X\) a \(Y \) je silná lineárna závislosť.
   
   Nasleduje aplikácia MATLABu na výpočet Pearsonovho výberového korelačného koeficienta použitím M-funkcie corrcoef (pozrite si podrobnejšie použitím príkazu help corrcoef). Maticová odpoveď MATLABu je tu nepohodlná, pretože výsledok musíme ešte zo získanej korelačnej matice vybrať:
   x=[7,6,5,1,5,4,7,3,4,2,8,5,2,5,7,1,4,5];y=[97,86,78,10,75,62,101,39,53,33,118,65,25,71,105,17,49,68];
   corm=corrcoef(x,y),r=corm(1,2)
   
   Na výpočet výberového korelačného koeficienta môžeme použiť aj M-funkciu corr s jedným výstupným argumentom. Tu musíme ale zadať vstupné hodnoty ako stĺpcové vektory.
   x=x';y=y';r=corr(x,y)
   

   Zobraziť riešenieSkryť riešenie

Zdroje

1. Ostertagová, E.: Aplikovaná štatistika. Equilibria, Košice, 2013, 218 s., ISBN 978-80-8143-067-1.
2. Ostertagová, E.: Pravdepodobnosť a matematická štatistika v príkladoch. Elfa, Košice, 2005, 123 s., ISBN 80-8086-005-X.

Doplňujúce úlohy

Úloha:
U 15 jabloní bol zisťovaný vek stromu \(X\) [počet rokov] a úroda \(Y\) [kg] s výsledkami: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 2 \a 3 \a 3\a 4 \a 4\a 4 \a 5\a 5\a 5\a 6\a 6\a 6\a6\a 6\a 10\\ \hline y_i \a 4{,}4 \a 4{,}3 \a 4{,}1 \a 5{,}5 \a 5{,}3 \a 5{,}4 \a 5{,}8 \a 6{,}0\a 6{,}2\a 6{,}6\a 6{,}8\a 6{,}7\a 9{,}0\a 10{,}1\a 9{,}2\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
1. Odhadnite závislosť úrody od veku stromu regresnou priamkou.
2. Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).
3. Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Výsledok:
a. \(\,\) \(\ \) \(f(x)\approx \hat y=\hat{a}_0+\hat{a}_1\cdot x=2{,}4600+0{,}7800 \cdot x\);
b. \(\,\) \(\ \)\( \mathrm{MSE}=1{,}1858\); \(\,\) \(\ \)\( \mathrm{RMSE}=1{,}0890\);
c. \(\,\) \(\ \) \( r=0{,}8147\); \(\,\) medzi veličinami \(X\) a \(Y \) je silná lineárna závislosť.
Zobraziť výsledokSkryť výsledok
Úloha:
Bolo sledované, ako súvisí množstvo chybných výrobkov [v % z vyrobených výrobkov] s výkonom sústružníka [v % z predpísanej normy]. Bolo vybraných 10 pracovníkov, namerané údaje sú uvedené v tabzľke: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{Výkon} \a 56 \a 68 \a 72\a 85 \a 92\a 102 \a 107\a 111\a 123\a 142\\ \hline \mathrm{Chybné\,\ výrobky} \a 5{,}20 \a 3{,}90 \a 3{,}50 \a 2{,}40 \a 2{,}04 \a 2{,}00 \a 2{,}20 \a 2{,}24 \a 2{,}40\a 2{,}51\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
1. Odhadnite závislosť počtu chybných výrobkov od výkonu sústružníka regresnou priamkou.
2. Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).
3. Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Výsledok:
a. \(\,\) \(\ \) \(f(x)\approx \hat y=\hat{a}_0+\hat{a}_1\cdot x=5{,}5663-0{,}0285 \cdot x\);
b.\(\,\) \(\ \) \( \mathrm{MSE}=0{,}5769\);\(\,\) \(\ \) \( \mathrm{RMSE}=0{,}7595\);
c. \(\,\) \(\ \)\( r=-0{,}7254\); \(\,\) medzi veličinami \(X\) a \(Y \) je mierna (stredná) lineárna závislosť.
Zobraziť výsledokSkryť výsledok
Úloha:
Pri meraní závislosti Brinelovho koeficientu tvrdosti ocele \(Y\) [MPa] od deformácie \(X\) [mm] boli zistené nasledujúce údaje: \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x_i \a 6 \a 9 \a 11\a 13 \a 22\a 26 \a 28\a 33\a 35\\ \hline y_i \a 68 \a 67 \a 65 \a 53 \a 44 \a 40 \a 37 \a 34 \a 32\\ \hline \end{array} \] Predpokladáme, že veličiny \(X\) a \(Y\) spĺňajú predpoklady lineárneho regresného modelu. Riešte nasledujúce úlohy:
1. Odhadnite závislosť Brinelovho koeficientu tvrdosti ocele od deformácie regresnou priamkou.
2. Vypočítajte bodový odhad rozptylu \(\sigma^2\) a smerodajnej odchýlky \(\sigma\).
3. Vypočítajte Pearsonov výberový korelačný koeficient a výsledok interpretujte.
Výsledok:
a. \(\,\) \(\ \) \(f(x)\approx \hat y=\hat{a}_0+\hat{a}_1\cdot x=75{,}7200-1{,}3196 \cdot x\);
b. \(\,\) \(\ \)\( \mathrm{MSE}=11{,}0220\);\(\,\) \(\ \) \( \mathrm{RMSE}=3{,}3199\);
c. \(\,\) \(\ \) \( r=-0{,}9773\); \(\,\) medzi veličinami \(X\) a \(Y \) je silná lineárna závislosť.
Zobraziť výsledokSkryť výsledok

Doplňujúce zdroje

1. Ramík, J.: Statistika. Slezská univerzita v Opavě, 2007.