Ciele
- Oboznámiť sa s pojmom diskrétna náhodná premenná, rozdelenie jej pravdepodobnosti a jej distribučná funkcia.
- Zvládnuť spojitú náhodnú premennú, jej hustotou pravdepodobnosti a distribučnú funkciu.
- Určovanie číselných charakteristík náhodnej premennej a ich význam.
Úvod
-
Budeme sa zaoberať náhodnými premennými, vychádzajúc z ich delenia
na diskrétne, resp. spojité náhodné premenné. Pre oba typy môže byť dané
rozdelenie pravdepodobnosti náhodnej premennej jej distribučnou funkciou
alebo v prípade diskrétnej náhodnej premennej tzv. pravdepodobnostnou tabuľkou
a v prípade spojitej náhodnej premennej jej hustotou. Ukážeme súvislosti medzi
týmito pojmami. Pre oba typy náhodných premenných budeme skúmať ich
základné číselné charakteristiky.
\(\def\a{&}\)
\(\def\md#1{\,\mathrm{d}#1}\)
Postup
-
Príklad: V urne sú \(3\) biele guľky a \(5\) čiernych guliek. Náhodne z nej vyberáme po jednej guľke bez návratu dovtedy, kým nevytiahneme prvú bielu guľku. Určme
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu vytiahnutých guliek (t. j., ktorá sa rovná počtu vytiahnutých guliek);
b) priemerný počet vytiahnutých guliek;
c) disperziu počtu vytiahnutých guliek;
d) pravdepodobnosť toho, že sme vytiahli viac guliek ako je smerodajná odchýlka počtu vytiahnutých guliek;
e) najpravdepodobnejší počet vytiahnutých guliek.Riešenie: a) Určíme zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu vytiahnutých guliek. Náhodná premenná \(X\) nadobudne hodnotu \(1\), ak prvá vytiahnutá guľka bude biela. Všetkých guliek v urne je osem, z toho sú tri biele. Preto \[P(X\!=\!1)=\frac{3}{8}.\] Náhodná premenná \(X\) nadobudne hodnotu \(2\), ak prvá vytiahnutá guľka bude čierna a druhá biela. Pravdepodobnosť toho, že prvá guľka bude čierna je \(\frac{5}{8}\). Ak prvá guľka bola čierna, tak v urne zostali tri biele a štyri čierne guľky. Preto pravdepodobnosť toho, že druhá vytiahnutá bude biela je \(\frac{3}{7}\). Takto \[P(X\!=\!2)=\frac{5}{8}\cdot \frac{3}{7}= \frac{15}{56}.\] Náhodná premenná \(X\) nadobudne hodnotu \(3\), ak prvé dve vytiahnuté guľky budú čierne a tretia biela. Pravdepodobnosť toho, že prvé dve guľky budú čierne je \(\frac{5}{8}\cdot \frac{4}{7}\). Ak prvé dve guľky boli čierne, tak v urne zostali tri biele a tri čierne guľky. Preto pravdepodobnosť toho, že tretia vytiahnutá bude biela je \(\frac{3}{6}\). Potom \[P(X\!=\!3)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}= \frac{5}{28}.\] Obdobnou úvahou dostaneme \[P(X\!=\!4)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}\cdot \frac{3}{5}= \frac{3}{28}.\] a \[P(X\!=\!5)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}\cdot \frac{2}{5}\cdot \frac{3}{4}= \frac{3}{56}.\] Je evidentné, že náhodná premenná \(X\) nadobudne hodnotu \(6\), ak prvé päť vytiahnuté guľky budú čierne. Potom v urne zostali už len tri biele guľky a tak šiesta vytiahnutá guľka musí byť biela. Preto \[P(X\!=\!6)=\frac{5}{8}\cdot \frac{4}{7}\cdot \frac{3}{6}\cdot \frac{2}{5}\cdot \frac{1}{4}= \frac{1}{56}.\] Je zrejmé, že tým sme vyčerpali všetky možné hodnoty, ktoré náhodná premenná \(X\) nadobúda s nenulovou pravdepodobnosťouu. Naše výpočty sú zhrnuté v nasledujúcej tabuľke pravdepodobností náhodnej premennej \(X\): \[ \begin{array}{c||c|c|c|c|c|c} x_i \a 1 \a 2 \a 3 \a 4 \a 5 \a 6 \\ \hline P(X\!=\!x_i) =p_i\a \frac{3}{8} \a \frac{15}{56} \a \frac{5}{28} \a \frac{3}{28} \a \frac{3}{56} \a \frac{1}{56} \end{array} \] Pre náhodnú premennú \(X\) by mal byť súčet pravdepodobností \(P(X\!=\!x_i)\) v druhom riadku tejto tabuľky rovný jednej (presvedčte sa o tom).
b) Priemerný počet vytiahnutých guliek reprezentuje stredná hodnota \(E(X)\) náhodnej premennej. Na základe (\ref{sh}) dostaneme \[E(X)= 1\!\cdot \!\frac{3}{8} +2\!\cdot\! \frac{15}{56} +3\!\cdot\! \frac{5}{28} +4\!\cdot\! \frac{3}{28}+5\!\cdot\! \frac{3}{56}+6\!\cdot\! \frac{1}{56}=\frac{9}{4}.\]
c) Disperziu náhodnej premennej \(X\) určíme podľa (\ref{dis}). Dostaneme \[D(X)= (1-\tfrac{9}{4})^2\tfrac{3}{8} +(2-\tfrac{9}{4})^2 \tfrac{15}{56} +(3-\tfrac{9}{4})^2 \tfrac{5}{28} +(4-\tfrac{9}{4})^2\tfrac{3}{28}+(5-\tfrac{9}{4})^2 \tfrac{3}{56}+(6-\tfrac{9}{4})^2 \tfrac{1}{56}=\frac{27}{16}.\]
d) Smerodajnú odchýlku \(\sigma (X)\) náhodnej premennej \(X\) dostaneme z jej disperzie podľa vzťahu \[\sigma (X)=\sqrt{D(X)}. \] V našom prípade je \[\sigma (X)=\sqrt{\frac{27}{16}}=\frac{3\sqrt 3}{4}\approx 1{,}299. \] Keďže náhodná premenná \(X\) nadobúda hodnoty počtu vytiahnutých guliek, tak máme určiť pravdepodobnosť toho, že nastane jav \(X\gt 1{,}299\). Na základe toho, že \(X\) je diskrétna náhodná premenná s oborom hodnôt \({\cal H}=\{1,2,3,4,5,6\}\) dostávame (pri výpočte je výhodnejšie použiť opačný jav): \[P(X\!\gt\! \sigma (X))= P(X\!\gt\! 1{,}299)=1-P(X\!\leqq \!1{,}299)=1-P(X\!=\!1)=1-\frac{3}{8}=\frac{5}{8}. \]
e) Najpravdepodobnejší počet vytiahnutých guliek (t. j. modus náhodnej premennej \({\cal M}o(X)\)) určíme z pravdepodobnostnej tabuľky náhodnej premennej \(X\): ľahko vidno, že maximum z hodnôt \(p_i\) je
\(p_1=\frac{3}{8},\) a preto \({\cal M}o(X)=1.\)Príklad: Uvažujme tri neštandardné hracie kocky, pričom na ich stenách sú počty bodiek od \(1\) do \(6\), ale počty bodiek sa na jednej kocke môžu aj opakovať. Nech sú to kocky \({\cal K}_1=\{2,2,2,2,6,6\}\), \({\cal K}_2=\{1,1,5,5,5,5\}\) a \({\cal K}_3=\{3,3,4,4,4,4\}\) (t. j. napr. štyri steny kocky \({\cal K}_1\) majú po dvoch bodkách a na zvyšných dvoch stenách je po šesť bodiek).
Máte si zvoliť jednu z tých kociek a váš súper si potom vyberie jednu zo zvyšných dvoch kociek. Obaja hodíte svojou kockou a vyhráva ten, komu padlo väčšie číslo (t. j. stena s väčším počtom bodiek). Akú stratégiu voľby kocky by ste zvolili?Riešenie: Je evidentné, že vašou snahou bude zvoliť takú stratégiu, aby pravdepodobnosť vašej výhry bola väčšia ako pravdepodobnosť výhry súpera.
Urobíme rozbor toho, ktorú z kociek je najvýhodnejšie zvoliť. Nech \(X_k\) je náhodná premenná, ktorá nadobúda hodnoty počtu padnutých bodiek na \(k\)-tej kocke (\(k\in\{1,2,3\}\)) a nech \(X_i\gt X_j\) je jav, ktorý spočíva v tom, že na \(i\)-tej kocke padne viac bodiek ako na \(j\)-tej kocke. Uvažujme dva prípady:
\(\bullet\) ak \(P(X_i\gt X_j)=0{,}5\), tak kocky \({\cal K}_i\) a \({\cal K}_j\) nazveme rovnocennými;
\(\bullet\) ak \(P(X_i\gt X_j)\gt\ 0{,}5\), tak kocku \({\cal K}_i\) nazveme lepšou ako kocka \({\cal K}_j\), čo označíme zápisom \({\cal K}_i\succ {\cal K}_j\).
Pre zjednodušenie výkladu urobíme túto dohodu: ak na prvej kocke \({\cal K}_i\) padlo \(x\) bodiek a na druhej kocke \({\cal K}_j\) padlo \(y\) bodiek, tak tento jav môžeme jednoznačne interpretovať dvojciferným číslom \(10x+y\) (napr. javu, ktorý spočíva v padnutí \(2\) bodiek na prvej kocke a \(5\) bodiek na druhej kocke priradíme číslo \(25\)).
Poďme porovnať jednotlivé kocky:- Kocka \({\cal K}_1\) a kocka \({\cal K}_2\).
Ľahko nahliadneme, že v tomto súboji kocka \({\cal K}_1\) vyhráva, ak výsledkom pokusu je jav \(21\) alebo \(61\) alebo jav \(65\). Tieto javy sú disjunktné, a preto \[P(X_1\gt X_2)=P(21)+P(61)+P(65)=\frac{4}{6}\cdot\frac{2}{6}+\frac{2}{6}\cdot\frac{2}{6}+\frac{2}{6}\cdot\frac{4}{6}=\frac{5}{9}\gt 0{,}5.\] To znamená, že kocka \({\cal K}_1\) je lepšia ako kocka \({\cal K}_2\), a teda \begin{equation}\label{k12} {\cal K}_1\succ {\cal K}_2. \end{equation} - Kocka \({\cal K}_2\) a kocka \({\cal K}_3\).
V tomto prípade kocka \({\cal K}_2\) vyhráva, ak výsledkom pokusu je jav \(53\) alebo jav \(54\). Potom \[P(X_2\gt X_3)=P(53)+P(54)=\frac{4}{6}\cdot\frac{2}{6}+\frac{4}{6}\cdot\frac{4}{6}=\frac{2}{3}\gt 0{,}5.\] Teda kocka \({\cal K}_2\) je lepšia ako kocka \({\cal K}_3\), čo môžeme zapísať takto \begin{equation}\label{k23} {\cal K}_2\succ {\cal K}_3. \end{equation} - Kocka \({\cal K}_3\) a kocka \({\cal K}_1\).
V tomto prípade kocka \({\cal K}_3\) vyhráva, ak výsledkom pokusu je jav \(32\) alebo jav \(42\). Potom \[P(X_3\gt X_1)=P(32)+P(42)=\frac{2}{6}\cdot\frac{4}{6}+\frac{4}{6}\cdot\frac{4}{6}=\frac{2}{3}\gt 0{,}5.\] Takto kocka \({\cal K}_3\) je lepšia ako kocka \({\cal K}_1\), čo znamená, že \begin{equation}\label{k31} {\cal K}_3\succ {\cal K}_1. \end{equation}
Na základe týchto poznatkov skúste sformulovať vašu stratégiu voľby kocky (samozrejme, že chcete si vybrať takú kocku, aby pravdepodobnosť vašej výhry bola väčšia ako pravdepodobnosť výhry vášho súpera).Príklad: Terč tvorí kruh \(K\) a dve medzikružia \(M\) a \(N\). Zásah do kruhu \(K\) je dosiahnutý pri každom výstrele s pravdepodobnosťou \(P(K)=0{,}7\) a je hodnotený \(10\) bodmi, pre medzikružia \(M\), resp. \(N\) je pravdepodobnosť zásahu \(P(M)=0{,}2\), resp. \(P(N)=0{,}1\) s ohodnotením \(5\), resp. \(0\) bodov. Nech \(X\) je náhodná premenná, ktorá nadobúda hodnoty dosiahnutého súčtu bodov pri troch nezávislých výstreloch na terč. Určme:
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X;\)
b) priemerný počet dosiahnutého súčtu bodov;
c) \(P(E(X)\lt X \leqq {\cal M}o(X))\).Riešenie: a) Najprv určíme obor hodnôt \({\cal H}(X)\) danej náhodnej premennej \(X\): je zrejmé, že pri troch výstreloch môžeme získať práve jeden z týchto súčtov bodov \[\{0,5,10,15,20,25, 30\}={\cal H}(X)\] (pozri pravdepodobnostnú tabuľku (\ref{cc})).
Na určenie zákona rozdelenia pravdepodobnosti náhodnej premennej \(X\) je potrebné vyčísliť pravdepodobnosti nadobudnutia jednotlivých hodnôt z množiny \({\cal H}(X)\). Nech pre \(i=1,2,3\)
- \(K_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli kruh \(K\) - zrejme \(P(K_i)=0{,}7\);
- \(M_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli medzikružie \(M\), teda \(P(M_i)=0{,}2\);
- \(N_i\) je jav, ktorý spočíva v tom, že v \(i\)-tom výstrele sme zasiahli medzikružie \(N\), t. j. \(P(N_i)=0{,}1\).
Zoberme napr. jav \(X\!=\!0\). Tento jav nastane práve vtedy, ak všetky tri výstrely skončili v medzikruží \(N\), čo symbolicky môžeme zapísať takto: \(N_1\cap N_2\cap N_3\). Keďže ide o nezávislé výstrely, tak \[P(X\!=\!0)=P(N_1\cap N_2\cap N_3)=P(N_1)\cdot P(N_2)\cdot P(N_3)=0{,}1\cdot0{,}1\cdot0{,}1=0{,}001. \] Tento výsledok zapíšeme do pravdepodobnostnej tabuľky (\ref{cc}).
Jav \(X\!=\!5\) nastane práve vtedy, ak dva výstrely skončili v medzikruží \(N\) (dve nuly) a jeden výstrel v medzikruží \(M\) (jedna päťka). Tento jav mohol nastať v troch prípadoch (k zásahu medzikružia \(M\) mohlo dôjsť v prvom alebo druhom alebo treťom výstrele), čo môžeme zapísať takto \[(M_1\cap N_2\cap N_3)\cup (N_1\cap M_2\cap N_3)\cup (N_1\cap N_2\cap M_3).\] Javy \(M_1\cap N_2\cap N_3\), \(N_1\cap M_2\cap N_3\) a \(N_1\cap N_2\cap M_3\) sú disjunktné, a preto \[P(X\!=\!5)=P((M_1\cap N_2\cap N_3)\cup (N_1\cap M_2\cap N_3)\cup (N_1\cap N_2\cap M_3))=\] \[\qquad \qquad=P(M_1\cap N_2\cap N_3)+ P(N_1\cap M_2\cap N_3)+ P(N_1\cap N_2\cap M_3).\] Výstrely sú nezávislé, a preto \[P(X\!=\!5)=0{,}2\cdot0{,}1\cdot0{,}1+0{,}1\cdot0{,}2\cdot0{,}1+0{,}1\cdot0{,}1\cdot0{,}2=0{,}006.\]
Súčet desať sa mohol dosiahnuť dvoma spôsobmi:
-- jav \(A\): dve päťky a jedna nula (dvakrát medzikružie \(M\) a raz \(N\)) alebo
-- jav \(B\): dve nuly a jedna desiatka (dvakrát medzikružie \(N\) a raz kruh \(K\)).
Je zrejmé, že javy \(A\) a \(B\) sú disjunktné, a preto \begin{equation}\label{ab} P(X\!=\!10)=P(A\cup B)=P(A)+P(B). \end{equation} Pravdepodobnosti \(P(A)\) a \(P(B)\) určíme obdobným spôsobom ako pri výpočte \(P(X\!=\!5)\): \[P(A)=0{,}2\cdot0{,}2\cdot0{,}1+0{,}2\cdot0{,}1\cdot0{,}2+0{,}1\cdot0{,}2\cdot0{,}2=0{,}012.\] Presvedčte sa, že pre \(P(B)\) môžeme použiť túto skrátenú verziu: \[P(B)=3\cdot 0{,}7\cdot0{,}1\cdot0{,}1=0{,}021.\] Na základe (\ref{ab}) dostaneme \[P(X\!=\!10)=0{,}012+0{,}021=0{,}033\] (pozri pravdepodobnostnú tabuľku (\ref{cc})).
Súčet pätnásť dosiahneme tiež dvoma spôsobmi:
-- jav \(C\): tri päťky (trikrát medzikružie \(M\)) alebo
-- jav \(D\): jednou desiatkou, jednou päťkou a jednou nulou (raz kruh \(K\), raz medzikružie \(M\) a raz \(N\)).
Javy \(C\) a \(D\) sú disjunktné, a preto \begin{equation}\label{aa} P(X\!=\!15)=P(C\cup D)=P(C)+P(D). \end{equation} Obdobným spôsobom ako pre \(P(X\!=\!0)\) dostaneme \[P(C)=P(M_1\cap M_1\cap M_1)=P(M_1)\cdot P(M_1)\cdot P(M_1)=0{,}2\cdot0{,}2\cdot0{,}2=0{,}008. \] Jav \(D\) (jedna desiatka, jedna päťka a jedna nula) môžeme rozložiť na zjednotenie týchto šiestich disjunktných javov: \begin{equation}\label{bb} \left. \begin{array}{ccc} (M_1\cap N_2\cap K_3);\quad\a (M_1\cap K_2\cap N_3);\quad\a (N_1\cap K_2\cap M_3);\quad\\ (N_1\cap M_2\cap K_3);\quad\a (K_1\cap M_2\cap N_3);\quad\a (K_1\cap N_2\cap M_3). \end{array} \right\} \end{equation} (tí, čo sú zručnejší v kombinatorike, si určite uvedomili, že ide o permutácie troch množín \(M\), \(N\) a \(K\), pričom tých permutácii je \(3!=6\)).
\(P(D)\) je preto súčtom pravdepodobností týchto šiestich javov. Keďže výstrely sú nezávislé, tak napr. pre prvý jav z (\ref{bb}) platí \[P(M_1\cap N_2\cap K_3)= P(M_1)\cdot P(N_2)\cdot P(K_3)=0{,}2\cdot0{,}1\cdot0{,}7=0{,}014.\] Je zrejmé, že pravdepodobnosti zvyšných piatich javov z (\ref{bb}) sú také isté, a preto \[P(D)=6\cdot 0{,}014=0{,}084.\] Takto na základe (\ref{aa}) dostaneme \[P(X\!=\!15)=0{,}008+0{,}084=0{,}092. \]
Súčet dvadsať dosiahneme taktiež dvoma spôsobmi:
-- jav \(E\): dve desiatky a jedna nula alebo
-- jav \(F\): dve päťky a jedna desiatka, pričom \begin{equation}\label{dd} P(X\!=\!20)=P(E\cup F)=P(E)+P(F). \end{equation} Ak použijeme predchádzajúce poznatky, tak dostaneme \[P(E)=3\cdot 0{,}7\cdot0{,}7\cdot0{,}1=0{,}147 \] a \[P(F)=3\cdot 0{,}2\cdot0{,}2\cdot0{,}7=0{,}084. \] Takto podľa (\ref{dd}) je \[P(X\!=\!20)=0{,}147+0{,}084=0{,}231\] (pozri tabuľku (\ref{cc})).
\(X\!=\!25\) práve vtedy, keď dvakrát sa dosiahla desiatka a raz päťka. Preto \[P(X\!=\!25)=3\cdot 0{,}7\cdot 0{,}7\cdot 0{,}2=0{,}294.\]
Je zrejmé, že \(X\!=\!30\) práve vtedy, keď trikrát sa dosiahla desiatka. Teda \[P(X\!=\!30)=0{,}7\cdot 0{,}7\cdot 0{,}7=0{,}343.\]
Požadovaný zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\) dostaneme zhrnutím predchádzajúcich výsledkov, ktoré sú zapísané v nižšie uvedenej pravdepodobnostnej tabuľke: \begin{equation}\label{cc} \begin{array}{c||c|c|c|c|c|c|c} x_i \a 0 \a 5 \a 10 \a 15 \a 20 \a 25 \a 30\\ \hline P(X\!=\!x_i) =p_i\a 0{,}001 \a 0{,}006 \a 0{,}033 \a 0{,}092 \a 0{,}231 \a 0{,}294 \a 0{,}343 \end{array} \end{equation}
b) Priemerný počet dosiahnutého súčtu bodov je určený strednou hodnotou \(E(X)\) náhodnej premennej \(X\). Podľa (\ref{sh}) a (\ref{cc}) je \[E(X)=0 \cdot 0{,}001+ 5\cdot 0{,}006+ 10 \cdot 0{,}033+15\cdot 0{,}092+20\cdot 0{,}231+ 25\cdot 0{,}294+30\cdot 0{,}343,\] čo po vyčíslení dáva \(E(X)= 24\).
c) Z časti b) je známe, že \(E(X)=24\). \({\cal M}o(X)\) je najpravdepodobnejšia hodnota náhodnej premennej \(X\). Z pravdepodobnostnej tabuľky (\ref{cc}) je vidieť, že hodnota \(X\!=\!30\) je nadobúdaná s najväčšiou pravdepodobosťou \(0{,}343\). Preto \({\cal M}o(X)=30\). Našou úlohou je teda určiť \(P(24\lt X \leqq 30)\). Z tabuľky (\ref{cc}) dostaneme \[P(24\lt X \leqq 30)=P(X\!=\!25)+ P(X\!=\!30)= 0{,}294 + 0{,}343= 0{,}637.\] - Kocka \({\cal K}_1\) a kocka \({\cal K}_2\).
-
Normalizačná podmienka pre hustotu \(f\) \begin{equation}\label{np} \int\limits_{-\infty}^{\infty } \!f(x)\md x=1 \end{equation}Príklad: Daná je funkcia \(F\) predpisom
\[F(x)=\left\{ \begin{array}{ll} a\a \mbox{pre } x\lt 4\\ b-\frac{64}{x^3} \a\mbox{pre } x\geqq 4, \end{array} \right. \] kde \(a, b\in R \).
a) Pre aké hodnoty \(a, b\in R \) je funkcia \(F\) distribučnou funkciou náhodnej premennej \(X\)?
b) Určte predpis hustoty pravdepodobnosti tejto náhodnej premennej \(X\).
c) Vypočítajte strednú hodnotu a smerodajnú odchýlku tejto náhodnej premennej.
d) určte \(P(E(X)\leqq X\lt D(X))\), kde \(E(X)\) je stredná hodnota a \(D(X)\) je disperzia náhodnej premennej \(X\).Riešenie: a) Je známe, že ak \(F\) je distribučná funkcia náhodnej premennej, tak \begin{equation}\label{df} \lim_{x\to-\infty}F(x)=0\qquad \mbox{a}\qquad \lim_{x\to\infty}F(x)=1. \end{equation} Je zrejmé, že pre danú funkciu \(F\) platí: \[\lim_{x\to-\infty}F(x)=a\qquad \mbox{a}\qquad \lim_{x\to\infty}F(x)=b. \] Odtiaľ na základe (\ref{df}) dostávame \(a=0\) a \(b=1.\) Je potrebné sa presvedčiť o tom, či získaná funkcia \[F(x)=\left\{ \begin{array}{ll} 0\a \mbox{pre } x\lt 4\\ 1-\frac{64}{x^3} \a\mbox{pre } x\geqq 4, \end{array} \right. \] spĺňa ďalšie poodmienky, ktoré sú kladené na distribučnú funkciu. Ľahko vidieť (znázornite si graf funkcie \(F\)), že
- funkcia \(F\) je neklesajúca a spojitá na množine reálnych čísel;
- oborom hodnôt funkcie \(F\) je množina \(\langle 0;1)\).
Získaná funkcia \(F\) je teda distribučnou funkciou spojitej náhodnej premennej.
b) Ak \(F\) je distribučnou funkciou náhodnej premennej \(X\), tak pre hustotu pravdepodobnosti \(f\) tejto náhodnej premennej platí: \[f(x)=F^{\prime}(x)\] (samozrejme, ak \(F^{\prime}(x)\) existuje). V našom prípade dostávame tak predpis hustoty pravdepodobnosti tejto náhodnej premennej \[f(x)=F^{\prime}(x)=\left\{ \begin{array}{ll} 0\a \mbox{pre } x\lt 4\\ \frac{192}{x^4} \a\mbox{pre } x\gt 4, \end{array} \right. \] Poznamenávame, že \(F^{\prime}(4)\) neexistuje.
c) Stredná hodnota \(E(X)\) náhodnej premennej \(X\) s hustotou pravdepodobnosti \(f\) je definovaná vzťahom \[E(X)=\int\limits_{-\infty}^{\infty }\!\!x\cdot f(x)\,\md x.\] V našom prípade je hustota pravdepodobnosti na intervale \((-\infty ; 4)\) rovná nule, a preto \[E(X)=\int\limits_{4}^{\infty }\!\!x\cdot \frac{192}{x^4}\,\md x= \int\limits_{4}^{\infty }\frac{192}{x^3}\,\md x=\Bigg[ \frac{-96}{x^2}\Bigg]_4^{\infty }= 6.\] Pre smerodajnú odchýlku \(\sigma(X)\) náhodnej premennej platí: \[\sigma(X)=\sqrt{D(X)},\] kde \(D(X)\) je disperzia náhodnej premennej, ktorá je je definovaná vzťahom \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] V našom prípade dostávame (opäť si treba všimnúť, že hustota pravdepodobnosti \(f\) je na intervale \((-\infty ; 4)\) rovná nule) \[D(X)=\int\limits_{4}^{\infty } \!\big[x-6\big]^2\cdot \frac{192}{x^4}\,\md x\stackrel{\star}{=}12\] (presvedčte sa o správnosti rovnosti označenej symbolom \(\star\)). Odtiaľ \(\sigma(X)=\sqrt{12}=2\sqrt3\).
d) Vzhľadom na výsledky z časti c) tejto úlohy, máme učiť \(P(6\leqq X\lt 12)\). Túto pravdepodobnosť môžeme stanoviť napr. podľa základnej vlastnosti distribučnej funkcie \(F\) spojitej náhodnej premennej \(X\): pre ľubovoľné reálne čísla \(a \lt b\) platí: \[P(a\leqq X\lt b)=F(b)-F(a),\] čo v našom prípade dáva \[P(6\leqq X\lt 12)=F(12)-F(6)=\Big(1-\frac{64}{12^3} \Big)-\Big(1-\frac{64}{6^3} \Big)=\frac{7}{27}.\] Túto úlohu sme mohli vyriešiť aj pomocou hustoty pravdepodobnosti \(f\) tejto náhodnej premennej \(X\), to takto: \[P(6\leqq X\lt 12)=\int\limits_{4}^{12} \! f(x)\md x=\int\limits_{4}^{12} \! \frac{192}{x^4}\md x=\Bigg[ \frac{-64}{x^3}\Bigg]_4^{12}=\frac{7}{27}.\]Príklad: Pre funkciu, ktorá je daná predpisom \(f(x)=\mathrm{e}^{k|x|}\), \(x\in R,\) určme:
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) \(P(E(X)\lt X \lt D(X))\);
c) \({\cal M}o(X).\)Riešenie: a) Najprv overíme podmienky, ktoré musí spĺňať hustota pravdepodobnosti náhodnej premennej.
1. Daná funkcia nadobúda len kladné hodnoty, a teda je na svojom definičnom obore nezáporná.
2. Z normalizačnej podmienky (\ref{np}) pre hustotu \(f\) danej náhodnej premennej dostaneme \[\int\limits_{-\infty}^{\infty } \!\mathrm{e}^{k|x|}\,\md x=2\cdot \int\limits_{0}^{\infty } \!\mathrm{e}^{kx}\,\md x=2\cdot \Bigg[ \frac{\mathrm{e}^{kx}}{k}\Bigg]_0^{\infty}\stackrel{\star}{=}\frac{-2}{k}=1,\] pričom rovnosť \((\star)\) platí len pre \(k\lt 0\) (pre \(k\geqq 0\) integrál diverguje). Odtiaľ \(k=-2\) (overte, že \(k=-2\) vyhovuje všetkým požiadavkám hustoty).
b) Keďže získaná hustota pravdepodobnosti je párna funkcia, tak pre strednú hodnotu náhodnej premennej \(X\) je \(E(X)=0\) a na základe definície jej disperzie \(D(X)\) \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] je \[D(X)=\int\limits_{-\infty}^{\infty } \!x^2\cdot \mathrm{e}^{-2|x|}\,\md x=2\cdot \int\limits_{0}^{\infty } \!x^2\cdot \mathrm{e}^{-2x}\,\md x=\Bigg[ \frac{(-2x^2-2x-1)\mathrm{e}^{-2x}}{2}\Bigg]_0^{\infty }=0{,}5.\] Na základe známeho vzťahu \[P(a\lt X\lt b)=\int\limits_{a}^{b} \! f(x)\md x,\] kde \(a\lt b\) a \(f\) je hustota, dostaneme \[P(E(X)\lt X\lt D(X))=P(0\lt X\lt 0{,}5)=\int\limits_{0}^{0{,}5 } \! \mathrm{e}^{-2x}\,\md x= \Bigg[ \frac{\mathrm{e}^{-2x}}{-2}\Bigg]_0^{0{,}5}\!\!\!=\frac{\mathrm{e}-1}{2\mathrm{e}}\approx 0{,}31606.\] c) Uvažovaná hustota pravdepodobnosti má jediné lokálne maximum v bode \(0\) (znázornite si graf získanej hustoty \(f\)), a preto \({\cal M}o(X)=0.\) -
Ak oborom hodnôt diskrétnej náhodnej premennej \(X\) je množina
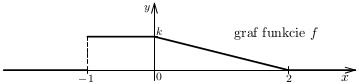
\({\cal H}=\{x_1,x_2,\dots ,x_n,\dots\}\) a \(p_i=P(X\!=\!x_i)\), tak jej stredná hodnota \(E(X)\) je definovaná takto: \begin{equation}\label{sh} E(X)=\sum\limits_{i=1}^{n(\infty)}x_ip_i \end{equation} a disperzia (rozptyl) takto: \begin{equation}\label{dis} E(X)=\sum\limits_{i=1}^{n(\infty)}\big(x_i-E(X)\big)^2p_i \end{equation}Príklad: Pre funkciu \(f\), ktorej graf je načrtnutý na obrázku, určme:
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie \(F\) tejto náhodnej premennej \(X\) a načrtnime jej graf;
c) strednú hodnotu náhodnej premennej \(X\);
d) smerodajnú odchýlku náhodnej premennej \(X\);
e) \(P(-0{,}5\leqq X\leqq 1)\).Riešenie: a) Z uvedeného grafu je vidieť, že funkcia \(f\) je nezáporná na množine reálnych čísel, a teda je splnená prvá požiadavka, ktorú musí spĺňať hustota pravdepodobnosti náhodnej premennej. Druhú, tzv. normalizačnú podmienku pre hustotu \(f\) \[\int\limits_{-\infty}^{\;\infty } \!\!\!f(x),\md x=1,\] môžeme zabezpečiť z geometrickej interpretácie tohto integrálu: obsah útvaru, ktorý je ohraničený grafom hustoty a osou \(x\) je rovný jednej. V našom prípade uvažovaný útvar pozostáva z obdĺžnika so stranami veľkostí \(1\) a \(k\) a pravouhlého trojuholníka s odvesnami veľkostí \(2\) a \(k\). Súčet ich obsahov musí byť rovný jednej: \[1\cdot k+\frac{2\cdot k}{2}=1\] a odtiaľ \(k=0{,}5.\)
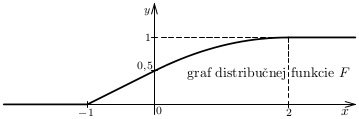
b) Je známe, že ak \(f\) je hustota pravdepodobnosti a \(F\) je distribučná funkcia náhodnej premennej \(X\), tak platí \begin{equation}\label{husdf} F(x)=\int\limits_{-\infty}^{\,x} \!\!\!f(t)\md t. \end{equation} Často sa robia chyby pri použití uvedeného vzťahu. Tu si musíme uvedomiť, že funkcia \(f\) je v našom prípade definovaná na jednotlivých intervaloch odlišnými predpismi. Presvedčte sa, že je daná týmto zápisom (všimnite si obrázok grafu funkcie \(f\)): \begin{equation}\label{huspr} f(x)=\left\{ \begin{array}{ll} 0{,}5 \a \mbox{pre } x\in(-1; 0),\\ \dfrac{2-x}{4} \a\mbox{pre } x\in (0;2),\\ 0 \a\mbox{pre } x\in (-\infty ;-1)\cup(2;\infty ). \end{array} \right. \end{equation} V bodoch \(-1\), \(0\) a \(2\) nie je definovaná -- to pri výpočte integrálu (\ref{husdf}) nie je podstatné. Na základe (\ref{husdf}) a (\ref{huspr}) dostaneme
\(\bullet\) ak \(x\in (-\infty ;-1\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,x} \!\!\!f(t)\md t=\int\limits_{-\infty\;\;}^{\,x} \!\!\!0\md t=0;\] \(\bullet\) ak \(x\in (-1 ;0\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t=0+\bigg[0{,}5t\bigg]^x_{-1}=\frac{x+1}{2}\,;\] \(\bullet\) ak \(x\in (0 ;2\rangle\), tak \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t+\int\limits_{0}^{\,x} \!\frac{2-t}{4}\md t= 0+0{,}5+\bigg[\frac{2t-\frac{t^2}{2}}{4}\bigg]^{\!x}_{\!0}=\frac{-x^2+4x+4}{8}\,;\] \(\bullet\) ak \(x\in (2 ;\infty)\), tak by malo byť \(F(x)=1\). Skutočne \[F(x)=\int\limits_{-\infty}^{\,-1} \!\!\!0\md t+\int\limits_{-1}^{\,0} \!\!0{,}5\md t+\int\limits_{0}^{\;2} \!\frac{2-t}{4}\md t+\int\limits_{2}^{\;x} \!\!0\md t= 0+0{,}5+0{,}5+0=1.\] Zhrnutím týchto výpočtov dostaneme predpis distribučnej funkcie náhodnej premennej \(X\): \begin{equation}\label{dfpr} F(x)=\left\{ \begin{array}{ll} 0 \a \mbox{pre } x\in(-1; 0\rangle,\\ \dfrac{x+1}{2} \a\mbox{pre } x\in (-1;0\rangle,\\[2.5mm] \dfrac{-x^2+4x+4}{8}\a\mbox{pre } x\in (0 ;2\rangle,\\ 1\a\mbox{pre } x\in (2;\infty ). \end{array} \right. \end{equation} Jej graf je načrtnutý na nasledujúcom obrázku. Odporúčame si na ňom overiť platnosť základných vlastností distribučnej funkcie náhodnej premennej.
c) Na základe definície strednej hodnoty \(E(X)\) náhodnej premennej \(X\) je \[E(X)=\int\limits_{-\infty}^{\infty } \!x\cdot f(x)\,\md x, \] kde \(f\) je jej hustota pravdepodobnosti. Vzhľadom na (\ref{huspr}) dostaneme \[E(X)=\int\limits_{-\infty}^{-1} \!x\cdot 0\,\md x+ \int\limits_{-1}^{\;0} \!x\cdot 0{,}5 \,\md x+ \int\limits_{0}^{\;2} \!x\cdot \frac{2-x}{4}\,\md x+ \int\limits_{2}^{\infty} \!x\cdot 0 \,\md x= \frac{1}{12}.\]
d) Na určenie smerodajnej odchýlky \(\sigma(X)=\sqrt{D(X)}\) náhodnej premennej \(X\) potrebujeme najskôr vypočítať jej disperziu \(D(X)\), pre ktorú platí vzorec \[D(X)=\int\limits_{-\infty}^{\infty } \!\big[x-E(X)\big]^2f(x)\,\md x\] kde \(f\) je jej hustota pravdepodobnosti. Keďže \(E(X)=1/12\), tak na základe (\ref{huspr}) dostaneme \[D(X)=\int\limits_{-\infty}^{-1 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot 0\md x+ \int\limits_{-1}^{\,0 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot \frac{1}{2}\,\md x+ \int\limits_{0}^{\,2 } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot \frac{2-x}{4}\,\md x+\] \[+\int\limits_{2}^{\infty } \!\left(x-\frac{1}{12}\right)^{\!\!2}\cdot 0\,\md x=0+\frac{61}{288}+\frac{9}{32}+0=\frac{71}{144}\,.\phantom{aaaaaaaaaamm}\] Teda \[\sigma(X)=\sqrt{\frac{71}{144}}=\frac{\sqrt{71}}{12}\,.\]
e) Požadovanú pravdepodobnosť by sme mohli získať zo vzťahu \[P(-0{,}5\leqq X\leqq 1)=\int\limits_{\!\!-0{,}5}^{\,1} \!\! f(x)\md x\,,\] kde \(f\) je hustota danej náhodnej premennej \(X\) (pozri jej predpis (\ref{huspr})). Keďže z časti b) poznáme predpis distribučnej funkcie \(F\), tak môžeme využiť aj vzorec \[P(-0{,}5\leqq X\leqq 1)=F(1)-F(-0{,}5).\] Odtiaľ vzhľadom na (\ref{dfpr}) dostaneme \[P(-0{,}5\leqq X\le 1)=F(1)-F(-0{,}5)=\dfrac{-1^2+4\cdot 1+4}{8}-\dfrac{-0{,}5+1}{2}=\frac{5}{8}\,.\]
Doplňujúce úlohy
Príklad:
Pravdepodobnosť zhotovenia štandardnej súčiastky je \(0{,}9\). Z vyrobenej série
súčiastok kontrolór vyberá postupne súčiastky a kontroluje ich kvalitu. Ak je
súčiastka kvalitná, kontrolór vyberie ďalšiu, ale vyberie najviac \(5\) súčiastok.
Ak kontrolovaná súčiastka nezodpovedá štandardu, kontrola sa zastaví a séria súčiastok
sa vyradí. Určte:
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu kontrolovaných súčiastok;
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) pravdepodobnosť toho, že budú kontrolované aspoň tri súčiastky;
d) strednú hodnotu, disperziu a modus náhodnej premennej \(X\).
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty počtu kontrolovaných súčiastok;
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) pravdepodobnosť toho, že budú kontrolované aspoň tri súčiastky;
d) strednú hodnotu, disperziu a modus náhodnej premennej \(X\).
Úloha:
Uvažujme tri neštandardné hracie kocky, pričom na ich stenách sú počty bodiek od
\(1\) do \(6\), ale počty bodiek sa na jednej kocke môžu aj opakovať. Nech sú to
kocky \({\cal K}_1=\{6,6,1,1,1,1\}\), \({\cal K}_2=\{5,5,2,2,2,2\}\) a \({\cal K}_3=
\{4,3,3,3,3,3\}\) (t. j. napr. štyri steny kocky \({\cal K}_1\) majú po jednej
bodke a na zvyšných dvoch stenách je po šesť bodiek).
Máte si zvoliť jednu z tých kociek a váš súper si potom vyberie jednu zo zvyšných dvoch kociek. Obaja hodíte svojou kockou a vyhráva ten, komu padlo väčšie číslo (t. j. stena s väčším počtom bodiek). Akú stratégiu voľby kocky by ste zvolili?
Máte si zvoliť jednu z tých kociek a váš súper si potom vyberie jednu zo zvyšných dvoch kociek. Obaja hodíte svojou kockou a vyhráva ten, komu padlo väčšie číslo (t. j. stena s väčším počtom bodiek). Akú stratégiu voľby kocky by ste zvolili?
Príklad:
Terč tvorí kruh \(K\) a dve medzikružia \(M\) a \(N\). Zásah do kruhu \(K\)
znamená \(10\) bodov, zásah do medzikružia \(M\) \(5\) bodov a do \(N\)
znamená \(-1\) bod. Pravdepodobnosť zásahu kruhu \(K\) je pri každom výstrele
\(0{,}5\) a pre \(M\), resp. \(N\) sú pravdepodobnosti zásahu \(0{,}3\),
resp. \(0{,}2\) Určte:
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty súčtu dosiahnutých bodov pri troch nezávislých výstreloch na terč;
b) strednú hodnotu \(E(X)\) a disperziu \(D(X)\);
c) \(P(X\geqq E(X))\); \(\qquad P(X\leqq \sigma(X))\); \(\qquad P(X\gt D(X))\).
a) rozdelenie pravdepodobnosti náhodnej premennej \(X\), ktorá nadobúda hodnoty súčtu dosiahnutých bodov pri troch nezávislých výstreloch na terč;
b) strednú hodnotu \(E(X)\) a disperziu \(D(X)\);
c) \(P(X\geqq E(X))\); \(\qquad P(X\leqq \sigma(X))\); \(\qquad P(X\gt D(X))\).
Príklad:
Nech \(X\) je náhodná premenná, ktorá nadobúda hodnoty maximálneho počtu hodených
bodov na dvoch hracích kockách (t. j. nadobúda hodnoty \(\max\{b_1,b_2\}\), kde
\(b_1\) je počet bodov na prvej kocke a \(b_2\) je počet bodov na druhej kocke ). Určte:
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\); b) \(E(X)\); c) smerodajnú odchýlku náhodnej premennej \(X\); d) \({\cal M}o(X).\)
a) zákon rozdelenia pravdepodobnosti náhodnej premennej \(X\); b) \(E(X)\); c) smerodajnú odchýlku náhodnej premennej \(X\); d) \({\cal M}o(X).\)
Príklad:
Rozdelenie pravdepodobnosti náhodnej premennej \(X\) so strednou hodnotou \(5{,}18\)
je dané pravdepodobnostnou tabuľkou
\(\phantom{mmmmmmmm}\begin{array}{c||c|c|c|c|c} x_i \a -3 \a 0 \a 2 \a 6 \a x_5\\ \hline P(X=x_i)\a 0{,}06 \a 0{,}14 \a 0{,}2 \a 0{,}26 \a p_5 \end{array} \)
Určte: a) neznáme hodnoty \(x_5\) a \(p_5\); b) disperziu a modus náhodnej premennej \(X\); c) \(P(-1\leqq X \lt 6)\) a \(P(5\lt X \leqq 12)\).
\(\phantom{mmmmmmmm}\begin{array}{c||c|c|c|c|c} x_i \a -3 \a 0 \a 2 \a 6 \a x_5\\ \hline P(X=x_i)\a 0{,}06 \a 0{,}14 \a 0{,}2 \a 0{,}26 \a p_5 \end{array} \)
Určte: a) neznáme hodnoty \(x_5\) a \(p_5\); b) disperziu a modus náhodnej premennej \(X\); c) \(P(-1\leqq X \lt 6)\) a \(P(5\lt X \leqq 12)\).
Príklad:
Daná je funkcia
\[f(x)=\left\{\begin{array}{ll}
k\cdot (4x-x^3)\a \mbox{pre } x\in (0;2);\\
0 \a \mbox{pre } x\not\in (0;2).
\end{array} \right. \]
Určte:
a) pre akú hodnotu \(k\in R\) je funkcia \(f\) hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) \(E(X)\),\quad \(\sigma (X)\),\quad \(P(1\leqq X \lt E(X))\)\quad a \quad \(P(D(X)\lt X\leqq 3)\).
a) pre akú hodnotu \(k\in R\) je funkcia \(f\) hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie náhodnej premennej \(X\);
c) \(E(X)\),\quad \(\sigma (X)\),\quad \(P(1\leqq X \lt E(X))\)\quad a \quad \(P(D(X)\lt X\leqq 3)\).
Príklad:
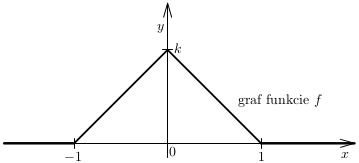
Pre funkciu \(f\), ktorej graf je načrtnutý na obrázku, určte:
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
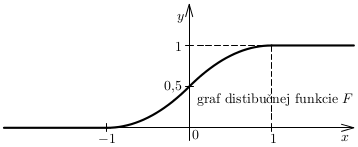
b) predpis distribučnej funkcie \(F\) tejto náhodnej premennej \(X\) a načrtnite jej graf;
c) strednú hodnotu náhodnej premennej \(X\);
d) disperziu náhodnej premennej \(X\);
e) \(P(|X|\lt 0{,}5)\).
a) takú konštantu \(k\), aby táto funkcia bola hustotou pravdepodobnosti náhodnej premennej \(X\);
b) predpis distribučnej funkcie \(F\) tejto náhodnej premennej \(X\) a načrtnite jej graf;
c) strednú hodnotu náhodnej premennej \(X\);
d) disperziu náhodnej premennej \(X\);
e) \(P(|X|\lt 0{,}5)\).
Doplňujúce zdroje
- Buša, J., Pirč, V., Schrötter, Š.: Numerické metódy, pravdepodobnosť a matematická štatistika. Elfa, Košice, 2006, 166 s., ISBN 80-8073-632-4.
- Gavalec, M., Kováčová, N., Ostertagová, E., Skřivánek, J.: Pravdepodobnosť a matematická štatistika v počítačovom prostredí MATLABu. Elfa, Košice, 2002, 150 s., ISBN 80-89066-05-4.
- Kalina, M., Bacigál,T., Schiesslová, A.: Základy pravdepodobnosti a matematickej štatistiky, STU Bratislava, 2010, 216 s., ISBN 978-80-227-3273-4
- Plocki, A., Tlustý, P.: Pravděpodobnost a statistika pro začátečníky a mírně pokročilé, Prometheus, spol. s.r.o., Praha, 2007, 307 s., ISBN 978-80-7196-330-1