Lagrangeov interpolačný polynóm a metóda najmenších štvorcov

Ciele

1. Naučiť sa konštruovať Lagrangeov interpolačný polynóm.
2. Naučiť sa použitím metódy najmenších štvorcov aproximovať funkcie určené len pomocou tabuľky ich funkčných hodnôt.

Úvod

Jednou zo základných úloh numerickej matematiky je úloha aproximácie funkcie, t.j. nahradenie funkcie \(f:A\rightarrow R\) pomocou funkcie \(g:B\rightarrow R\) . Špeciálnym prípadom aproximácie je interpolácia. Funkcia \(f\left(x\right)\) je pri nej daná konečným počtom svojich hodnôt v bodoch \(x_{i}\) a blízkosť aproximujúcej funkcie \(g\left(x\right)\) zaručuje podmienka \[g\left(x_{i}\right)=f\left(x_{i}\right),\ i=0,1,\ldots,n.\] V praxi sa za interpolačnú funkciu \(g\left(x\right)\) najčastejšie vyberá polynóm. Pri aproximácii funkcie \(f\left(x\right)\) pomocou interpolačných polynómov sa predpokladá, že hodnoty \[f\left(x_{i}\right),\ i=0,1,\ldots,n\] aproximovanej funkcie \(f\) sú zadané s vysokou presnosťou. V praxi sú však tieto hodnoty väčšinou získané experimentálne a môžu byť zaťažené väčšími chybami, ako sú chyby zo zaokrúhľovania. V tomto prípade je rozumnejšie použiť namiesto interpolačnej metódy aproximácie funkcie \(f\left( x\right)\) metódu najmenších štvorcov, kde aproximačnú funkciu \(g\left( x\right)\) hľadáme nie na základe splnenia podmienky \[g\left(x_{i}\right)=f\left(x_{i}\right),\ i=0,1,\ldots,n ,\] ale ju hľadáme tak, aby súčet štvorcov odchýliek \[\sum^{n}_{i=0}\left(g\left(x_{i}\right)-f\left(x_{i}\right)\right)^{2}\] bol minimálny. Pri aproximácii funkcie \(f\left(x\right)\) metódou najmenších štvorcov podobne ako pri interpolačnej metóde budeme predpokladať, že reálna funkcia \(f\left(x\right)\) je definovaná v \(n+1\) bodoch \[x_{0},x_{1},\ldots,x_{n},\] medzi ktorými je práve \(m+1\) navzájom rôznych a \[y_{0},y_{1},\ldots,y_{n}\] sú jej príslušné funkčné hodnoty, ktoré sme získali napríklad meraním. Ďalej budeme predpokladať, že v tých istých \(n+1\) bodoch je definovaných \(k+1\) funkcií \[\varphi_{0}\left(x\right),\varphi_{1}\left(x\right),\ldots,\varphi_{k}\left(x\right),\] \(k \lt m.\) Funkciu \(g\left(x\right)\) budeme hľadať v tvare \[g\left(x\right)=a_{0}\varphi_{0}\left(x\right)+a_{1}\varphi_{1} \left(x\right)+\ldots+a_{k}\varphi_{k}\left(x\right),\] teda ako lineárnu kombináciu týchto funkcií.

Postup

1. Lagrangeov interpolačný polynóm.
   
   Predpokladajme, že máme daných \(n+1 \) hodnôt \[ y_0,y_1,\ldots,y_n \] funkcie \( f \) v rôznych bodoch \[ x_0,x_1,\ldots,x_n \] Body \(x_i \) nazývame uzlovými bodmi. Lagrangeova metóda interpolácie spočíva v tom, že sa najprv definujú polynómy \[ l_i\left(x\right),\;i=0,1,\ldots,n, \] \(n\)-tého stupňa s vlastnosťami \[ l_i\left(x_j\right)=\left\{\begin{array}{ll} \def\a{&} 0;\a \ i\neq j \\ 1;\a \ i=j \end{array} \right .. \] Tejto podmienke vyhovujú nasledujúce polynómy: \[ l_i\left(x\right)=\frac{(x-x_0)\ldots (x-x_{i-1})(x-x_{i+1})\ldots (x-x_{n})}{(x_i-x_0)\ldots (x_i-x_{i-1})(x_i-x_{i+1})\ldots (x_i-x_{n})},\ i=0,1,\ldots ,n. \] Lagrangeov interpolačný polynóm hľadáme potom v tvare \[L_n(x,x_0,x_n)=\sum _{i=0}^{n} y_i\,l_i (x), \] kde \[l_i(x)=\prod _{\begin{array}{l} j=0 \\ j\neq i \end{array}}^{n} \frac{x-x_j}{x_i-x_j}. \] Chyba, ktorej sa pri interpolácii dopúšťame, sa dá odhadnúť pomocou vzťahu: \[ \left|f(x)-L_n(x,x_0,x_n)\right|\leq\frac{M_{n+1}}{(n+1)!}\left|(x-x_0)(x-x_1)\ldots (x-x_n)\right|, \] kde \[ M_{n+1}\geq \max_{x\in\left\langle a,b\right\rangle}\left|f^{(n+1)}(x)\right|. \]

   Príklad:
   Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\), ktorá je zadaná tabuľkou svojich funkčných hodnôt \(y_i=f(x_i)\) v uzlových bodoch \(x_i\). \[\begin{array}{|c|c|c|c|} \def\a{&} \hline x_i\a 0 \a 1{,}5 \a 6{,}8 \\ \hline y_i \a 1{,}45 \a 3{,}14 \a 4{,}11 \\ \hline \end{array} \]
   

   Riešenie:
   V našom prípade je funkcia \(f(x)\) zadaná v troch uzlových bodoch, čo značí, že \(n=2\). Lagrangeov interpolačný polynóm budeme hľadať v tvare \(L_2(x,x_0,x_2)=\sum\limits_{i=0}^{2}y_il_i(x)\) , kde \(l_i(x)=\prod\limits_{\begin{array}{c}j=0\\ j\neq i\end{array}}^{2}\frac{x-x_j}{x_i-x_j}\) . Nájdeme polynómy \(l_0(x),\ l_1(x)\) a \(l_2(x)\) . Teda \[l_0(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}=\frac{x^2-8,3x+10,2}{10,2},\] \[l_1(x)=\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}=\frac{x^2-6,8x}{-7,95},\] \[l_2(x)=\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}=\frac{x^2-1,5x}{36,04}.\] Vypočítané polynómy dosadíme do vzťahu \[L_2(x,x_0,x_2)=y_0l_0(x)+y_1l_1(x)+y_2l_2(x).\] Teda \[L_2(x,x_0,x_2)=1,45\frac{x_2-8,3x+10,2}{10,2}+3,14\frac{x^2-6,8x}{-7,95}+4,11\frac{x^2-1,5x}{36,04}=\\ =-0,1387x^2+1,3348x+1,45.\]

   Zobraziť riešenieSkryť riešenie

   Príklad: Funkcia \(f(x)\) je zadaná tabuľkou svojich funkčných hodnôt \(y_i=f(x_i)\) v uzlových bodoch \(x_i\). \[\begin{array}{|c|c|c|c|c|} \def\a{&} \hline x_i\a 0 \a 1 \a 3 \a 5 \\ \hline y_i \a -6 \a -3 \a 0 \a 1 \\ \hline \end{array} \] Pomocou Lagrangeovho interpolačného polynómu vypočítajte približnú hodnotu funkcie \(f(x)\) v bode \(x=2\).
   

   Riešenie:
   Nahradíme funkciu \(f(x)\) Lagrangeovym interpolačným polynómom \(L_3(x,x_0,x_3)\) a vypočítame približnú hodnotu funkcie \(f(x)\) v bode \(x=2\) pomocou tohto polynómu. Najprv vypočítame hodnoty polynómov \(l_i(x), i=0,1,2,3\) Lagrangeovho interpolačného polynómu v bode \(x=2\). Teda \[l_0(2)=\frac{(2-x_1)(2-x_2)(2-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}=\frac{(2-1)(2-3)(2-5)}{(0-1)(0-3)(0-5)}=-\frac{1}{5}=-0,2,\] \[l_1(2)=\frac{(2-x_0)(2-x_2)(2-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}=\frac{(2-0)(2-3)(2-5)}{(1-0)(1-3)(1-5)}=\frac{3}{4}=0,75,\] \[l_2(2)=\frac{(2-x_0)(2-x_1)(2-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}=\frac{(2-0)(2-1)(2-5)}{(3-0)(3-1)(3-5)}=\frac{1}{2}=0,5,\] \[l_3(2)=\frac{(2-x_0)(2-x_1)(2-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}=\frac{(2-0)(2-1)(2-3)}{(5-0)(5-1)(5-3)}=-\frac{1}{20}=-0,05.\] Po dosadení do vzťahu \[L_3(2,x_0,x_3)=y_0l_0(2)+y_1l_1(2)+y_2l_2(2)+y_3l_3(2)\] dostávame hľadanú približnú hodnotu funkcie \[f(2)\approx L_3(2,x_0,x_3)=-1,1.\]

   Zobraziť riešenieSkryť riešenie

   Príklad: Funkcia \(f(x)\) je zadaná tabuľkou svojich funkčných hodnôt \(y_i=f(x_i)\) v uzlových bodoch \(x_i\). \[\begin{array}{|c|c|c|c|c|} \def\a{&} \hline x_i\a 1{,}462 \a 1{,}491 \a 2{,}247 \a 3{,}490 \\ \hline y_i \a 0{,}38 \a 0{,}40 \a 0{,}81 \a 1{,}25 \\ \hline \end{array} \] Pomocou inverzného Lagrangeovho interpolačného polynómu určte približné riešenie rovnice \( f(x)=0,53 \).
   

   Riešenie:
   Použijeme inverznú Lagrangeovu interpoláciu, t.j. v interpolačnom polynóme zameníme navzájom \(x_i,\;y_i \) a \(x,\;y \) . Keďže nás v tomto prípade nebude zaujímať celkový tvar inverzného Lagrangeovho interpolačného polynómu \(x=L_3\left(y,y_0,y_3\right) \) , ale len jeho hodnota v konkrétnom bode \(0,53 \), vypočítame najprv hodnoty polynómov \[ l_i\left(y\right),\;i=0,1,2,3 \] v tomto bode a až na záver vypočítame \(L_3\left(0,53\right) \). Teda \[l_0(0,53)=\frac{(0,53-y_1)(0,53-y_2)(0,53-y_3)}{(y_0-y_1)(y_0-y_2)(y_0-y_3)}=-3,50281, \] \[l_1(0,53)=\frac{(0,53-y_0)(0,53-y_2)(0,53-y_3)}{(y_1-y_0)(y_1-y_2)(y_1-y_3)}=4,33860, \] \[l_2(0,53)=\frac{(0,53-y_0)(0,53-y_1)(0,53-y_3)}{(y_2-y_0)(y_2-y_1)(y_2-y_3)}=0,18099, \] \[l_3(0,53)=\frac{(0,53-y_0)(0,53-y_1)(0,53-y_2)}{(y_3-y_0)(y_3-y_1)(y_3-y_2)}=-0,01678. \] Po dosadení do vzťahu pre inverzný Lagrangeov interpolačný polynóm \[L_3(0,53;y_0;y_3)=x_0l_0(0,53)+x_1l_1(0,53)+x_2l_2(0,53)+x_3l_3(0,53) \] dostávame hľadanú približnú hodnotu \[x=f^{-1}(0,53)\approx L_3(0,53;y_0;y_3)=1,6958671. \]

   Zobraziť riešenieSkryť riešenie
2. Metóda najmenších štvorcov.
   
   Úloha aproximovať funkciu \(f\left(x\right)\) funkciou \(g\left(x\right)\) metódou najmenších štvorcov spočíva v určení takých reálnych koeficientov \[a_{0},a_{1},\ldots,a_{k},\] ktoré minimalizujú funkciu \[d\left(a_{0},a_{1},\ldots,a_{k}\right)=\sum^{n}_{i=0}\left(a_{0}\varphi_{0}\left(x_{i}\right) +a_{1}\varphi\left(x_{i}\right)+\ldots+a_{k}\varphi_{k}\left(x_{i}\right)-y_{i}\right)^{2}.\] Minimum funkcie \(d\) nájdeme metódou, ktorá sa používa pri hľadaní lokálnych extrémov funkcie viac premenných. Parciálne derivácie funkcie \(d\) podľa jednotlivých premenných \[a_{j},\ j=0,1,\ldots,k\] položíme rovné \(0.\ \) Teda \[\frac{\partial d}{\partial a_{j}}=0,\] respektíve \[ 2\sum^{n}_{i=0}\left(a_{0}\varphi_{0}\left(x_{i}\right)+ a_{1}\varphi\left(x_{i}\right)+\ldots+a_{k}\varphi_{k}\left(x_{i}\right)-y_{i}\right) \varphi_{j}\left(x_{i}\right)=0,\] pre \(j=0,1,\ldots,k.\)
   Z toho dostávame lineárny systém \(k+1\) rovníc s \(k+1\) neznámymi: \begin{eqnarray} %\[ %\begin{array}{c} \def\a{&} a_{0}\sum^{n}_{i=0}\varphi_{0}\left(x_{i}\right)\varphi_{0}\left(x_{i}\right)+\a \ldots \a +a_{k}\sum^{n}_{i=0}\varphi_{k}\left(x_{i}\right)\varphi_{0}\left(x_{i}\right) = \sum^{n}_{i=0}y_{i}\varphi_{0}\left(x_{i}\right), \nonumber \\ a_{0}\sum^{n}_{i=0}\varphi_{0}\left(x_{i}\right)\varphi_{1}\left(x_{i}\right)+\a \ldots \a +a_{k}\sum^{n}_{i=0}\varphi_{k}\left(x_{i}\right)\varphi_{1}\left(x_{i}\right) = \sum^{n}_{i=0}y_{i}\varphi_{1}\left(x_{i}\right),\nonumber \\ \a \vdots \a \\ a_{0}\sum^{n}_{i=0}\varphi_{0}\left(x_{i}\right)\varphi_{k-1}\left(x_{i}\right)+\a \ldots \a + a_{k}\sum^{n}_{i=0}\varphi_{k}\left(x_{i}\right)\varphi_{k-1}\left(x_{i}\right) = \sum^{n}_{i=0}y_{i}\varphi_{k-1}\left(x_{i}\right),\nonumber \\ a_{0}\sum^{n}_{i=0}\varphi_{0}\left(x_{i}\right)\varphi_{k}\left(x_{i}\right)+\a \ldots \a + a_{k}\sum^{n}_{i=0}\varphi_{k}\left(x_{i}\right)\varphi_{k}\left(x_{i}\right) = \sum^{n}_{i=0}y_{i}\varphi_{k}\left(x_{i}\right).\nonumber % \end{array} % \] \end{eqnarray} Ak \[\varphi_{0}\left(x\right),\varphi_{1}\left(x\right),\ldots,\varphi_{k}\left(x\right)\] je lineárne nezávislá sústava funkcií, tak lineárny systém \(k+1\) rovníc má jediné riešenie. Tým riešením sú vypočítané konkrétne hodnoty reálnych koeficientov \[a_{0},a_{1},\ldots,a_{k},\] ktoré minimalizujú funkciu \[d\left(a_{0},a_{1},\ldots,a_{k}\right).\] Súčasne sme s vypočítaním týchto koeficientov našli aj funkciu \[g\left(x\right)=a_{0}\varphi_{0}\left(x\right)+a_{1}\varphi_{1} \left(x\right)+\ldots+a_{k}\varphi_{k}\left(x\right),\] ktorá v zmysle metódy najmenších štvorcov najlepšie aproximuje na nejakej konečnej množine bodov \[x_i, \ i=0,1,\ldots,n\]funkciu \(f\left(x\right)\).
   

   Poznámka: Podmienku lineárnej nezávislosti spĺňa napríklad sústava funkcií \[1,x,x^{2},\ldots,x^{k}.\]

   Príklad:
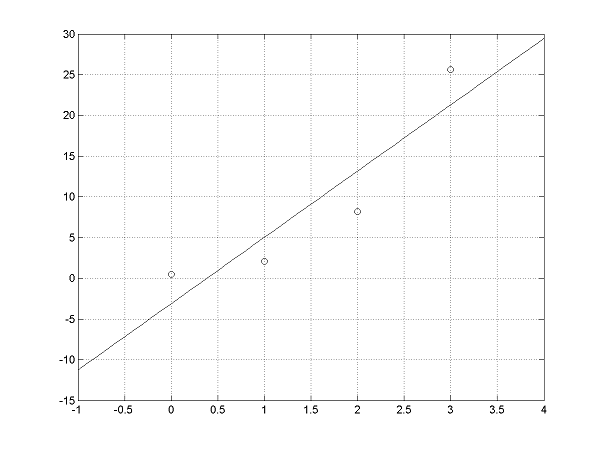
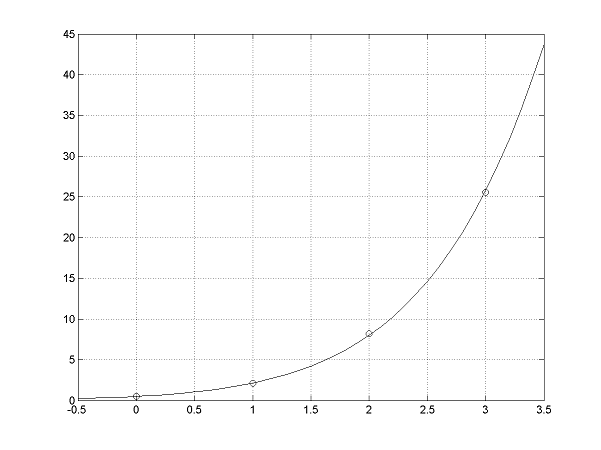
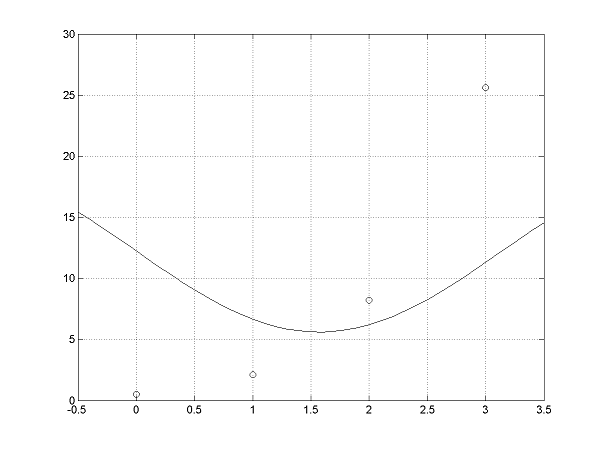
   Funkcia \(f\left(x\right)\) je zadaná tabuľkou svojich funkčných hodnôt \(y_{i}=f\left(x_{i}\right)\) v uzlových bodoch \(x_{i}\) \[ \begin{array}{|c|c|c|c|c|} \def\a{&} \hline x_i\a 0 \a 1 \a 2\a 3 \\ \hline y_i \a 0{,}5 \a 2{,}1 \a 8{,}2\a 25{,}6 \\ \hline \end{array} \] Určte, ktorá z funkcií \(g_{1}\left(x\right)=ax+b,\) \(g_{2}\left(x\right)=e^{ax^{2}+bx+c},\) a \(g_{3}\left(x\right)=b+a\sin x\) najlepšie aproximuje v zmysle MNŠ funkciu \(f\left(x\right).\)
   

   Riešenie: V prípade funkcie \( g_{1}\left(x\right)\) koeficient \( a_{0}=b \) a koeficient \( a_{1}=a \). Ďalej \(\varphi_{0}\left(x\right)=1\) a \( \varphi_{1}\left(x\right)=x.\) Sústava lineárnych rovníc (1) nadobudne tvar \[ \begin{eqnarray} %\def\a{&} 4b+6a \a = \a 36,400002 \nonumber\\ 6b+14a \a = \a 95,300003. \nonumber \end{eqnarray} \] Vyriešením danej sústavy dostaneme, že funkcia \( g_{1}\left(x\right)=8,14x - 3,11\) a kvadratická odchýlka \( d_{1}\left(b,a\right)=64,72201.\)

   

   Obr.: : Funkcia \(g_1\left(x\right)\)

   Aby bolo možné použiť ten istý postup výpočtu koeficientov \( a\),\( b\) a \( c\) aj v druhom prípade, tak si aproximačnú rovnicu \[ f\left(x\right)\approx g_{2}\left(x\right)=e^{ax^{2}+bx+c}\] prechodne upravíme na tvar \[ \ln \left(f\left(x\right)\right)\approx \ln \left(g_{2}\left(x\right)\right)=ax^{2}+bx+c.\] Teraz si už môžeme vytvoriť sústavu lineárnych rovníc (1) s neznámymi \( a,b\) a \( c\). Teda \[ \begin{eqnarray} %\def\a{&} 4c+6b+14a \a = \a 5,3955 \nonumber\\ 6c+14b+36a \a = \a 14,6779 \nonumber\\ 14c+36b+98a \a = \a 38,3417.\nonumber \end{eqnarray} \] Vyriešením sústavy (1) dostaneme, že funkcia \[ g_{2}\left(x\right)=e^{-0,0742x^{2}+1,5394x-0,7007}\] a kvadratická odchýlka \[ d_{2}\left(c,b,a\right)=0,0699.\]

   

   Obr.: : Funkcia \(g_2\left(x\right)\)

   Pri tretej aproximačnej funkcii \( g_{3}\left(x\right)\) si podobne ako v prvom prípade vytvoríme sústavu (1) s neznámymi koeficientmi \( a\) a \( b\). Teda \[ \begin{eqnarray} %\def\a{&} 4b+1,892a \a = \a 36,4 \nonumber\\ 1,892b+1,5548a \a = \a 12,836. \nonumber \end{eqnarray} \] Vyriešením tejto jednoduchej sústavy lineárnych rovníc dostaneme, že funkcia \[ g_{3}\left(x\right)=-6,6366 \sin x + 12,2389\] a kvadratická odchýlka \[ d_{3}\left(b,a\right)=366,9503.\]

   

   Obr.: : Funkcia \(g_3\left(x\right)\)

   Veľmi malá kvadratická odchýlka v druhom prípade automaticky dáva odpoveď na otázku, ktorá z funkcií \( g_{1}\left(x\right)\), \( g_{2}\left(x\right)\) a \( g_{3}\left(x\right)\) v zmysle metódy najmenších štvorcov najlepšie aproximuje funkciu \( f\left(x\right)\). Je to funkcia \( g_{2}\left(x\right)=e^{ax^{2}+bx+c}\).

   Zobraziť riešenieSkryť riešenie

Zdroje

1. Buša, Pirč, Schrötter: Numerické metódy, pravdepodobnosť a matematická štatistika, 2006, ISBN 80-8073-632-4. Stiahnuť obrazovkovú alebo tlačovú verziu.
2. Daňo, Ostertagová: Vybrané kapitoly z numerických metód, pravdepodobnosti a matematickej štatistiky, Equilibria s.r.o., Košice, 2012, ISBN 978-80-8143-012-1.

Doplňujúce úlohy

Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|} \hline x_i \a 0 \a 1 \a 5\\ \hline y_i \a 2 \a 3 \a 147\\ \hline \end{array} \]

Výsledok:

Výsledok: \(7x^2-6x+2\).
Zobraziť výsledokSkryť výsledok
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\\ \hline y_i \a 3 \a -5 \a 4\\ \hline \end{array} \]

Výsledok:

Výsledok: \(4,1667x^2-20,5x+19,3333\).
Zobraziť výsledokSkryť výsledok
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 11 \a 13 \a 14\a 18\\ \hline y_i \a 1342 \a 2210 \a 2758\a 5850\\ \hline \end{array} \]

Výsledok:

Výsledok: \(x^3+x\).
Zobraziť výsledokSkryť výsledok
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a -2 \a 1 \a 2\a 4\\ \hline y_i \a 25 \a -8 \a -15\a -23\\ \hline \end{array} \]

Výsledok:

Výsledok: \(x^2-10x+1\).
Zobraziť výsledokSkryť výsledok
\
Úloha:
Zostrojte Lagrangeov interpolačný polynóm pre funkciu \(f(x)\) , ktorá je zadaná tabuľkou: \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a -1 \a 0 \a 2\a 4\\ \hline y_i \a 5 \a 2 \a -4\a -10\\ \hline \end{array} \]

Výsledok:

Výsledok: \(2-3x\).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 1 \a 3\a 5 \\ \hline y_i \a -6 \a -3 \a 0\a 1 \\ \hline \end{array} \] \(z=4.\)

Výsledok:

Výsledok: \(0,6\).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\a 8 \\ \hline y_i \a 0 \a 1 \a 2\a 3 \\ \hline \end{array} \] \(z=2,5.\)

Výsledok:

Výsledok: \(1,3549107\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0{,}89 \a 1{,}14 \a 1{,}50\a 1{,}62 \\ \hline y_i \a 2{,}435 \a 3{,}126 \a 4{,}481\a 5{,}053 \\ \hline \end{array} \] \(z=1,35.\)

Výsledok:

Výsledok: \(3,8558517\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 3{,}287 \a 4{,}055 \a 5{,}528\a 5{,}584 \\ \hline y_i \a 1{,}19 \a 1{,}40 \a 1{,}71\a 1{,}72 \\ \hline \end{array} \] \(v=1,55.\)

Výsledok:

Výsledok: \(4,7083196\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1{,}462 \a 1{,}491 \a 2{,}247\a 3{,}490 \\ \hline y_i \a 0{,}38 \a 0{,}40 \a 0{,}81\a 1{,}25 \\ \hline \end{array} \] \(v=0,53.\)

Výsledok:

Výsledok: \(1,6958682\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Pomocou inverzného Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu \(x\ \), pre ktorú funkcia \(f(x)\) zadaná tabuľkou nadobúda funkčnú hodnotu \(v\ \): \[ \begin{array}{|c|c|c|c|} \hline x_i \a 8{,}935 \a 11{,}473 \a 18{,}356 \\ \hline y_i \a 2{,}190 \a 2{,}440 \a 2{,}910 \\ \hline \end{array} \] \(v=2,49.\)

Výsledok:

Výsledok: \(12,074198\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 1 \a 3\a 5 \\ \hline y_i \a -6 \a -3 \a 0\a 1 \\ \hline \end{array} \] \(z=4.\)

Výsledok:

Výsledok: \(0,6\).
Zobraziť výsledokSkryť výsledok
\(0,6\).
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Pomocou Lagrangeovho interpolačného polynómu vypočítajte pribižnú hodnotu funkcie \(f(x)\)v bode \(z\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 1 \a 2 \a 4\a 8 \\ \hline y_i \a 0 \a 1 \a 2\a 3 \\ \hline \end{array} \] \(z=2,5.\)

Výsledok:

Výsledok: \(1,3549107\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0 \a 2\a 4\a 6 \a 8 \\ \hline y_i \a 2{,}1 \a 3{,}5 \a 5\a 6{,}7 \a 8 \\ \hline \end{array} \] \(g(x)=ax+b.\)

Výsledok:

Výsledok: \(0,75x+2,06\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0 \a 2\a 4\a 6 \a 8 \\ \hline y_i \a 2{,}1 \a 3{,}5 \a 5\a 7{,}2 \a 9 \\ \hline \end{array} \] \(g(x)=ax+b.\)

Výsledok:

Výsledok: \(0,875x+1,86\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|c|} \hline x_i \a 0{,}78 \a 1{,}56\a 2{,}34\a 3{,}12 \a 3{,}81 \\ \hline y_i \a 2{,}5 \a 1{,}2 \a 1{,}12\a 2{,}25 \a 4{,}28 \\ \hline \end{array} \] \(g(x)=ax^2+bx+c.\)

Výsledok:

Výsledok: \(1,0023x^2-4,0143x+5,0221\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0{,}78 \a 1{,}56\a 2{,}34\a 3{,}12 \\ \hline y_i \a 2{,}5 \a 1{,}2 \a 1{,}12\a 2{,}25 \\ \hline \end{array} \] \(g(x)=ax^2+bx+c.\)

Výsledok:

Výsledok: \(0,9985x^2-4,0066x+5,0125\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a -0{,}53 \a 0{,}25\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+b\sin x+c\cos x.\)

Výsledok:

Výsledok: \(-0,7530+1,7447\sin x-0,91155\cos x\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a -0{,}53 \a 0{,}25\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+b\sin x.\)

Výsledok:

Výsledok: \(-1,7971+2,8109\sin x\ \).
Zobraziť výsledokSkryť výsledok
Úloha:
Funkcia \(f(x)\) je zadaná tabuľkou. Metódou najmenších štvorcov aproximujte funkciu \(f(x)\) funkciou \(g(x)\ \): \[ \begin{array}{|c|c|c|c|c|} \hline x_i \a 0 \a 0{,}5\a 1{,}1\a 2 \\ \hline y_i \a -1{,}75 \a 0{,}53 \a 0{,}95\a 1{,}25 \\ \hline \end{array} \] \(g(x)=a+be^x.\)

Výsledok:

Výsledok: \(-0,8085+0,3231e^x \ \).
Zobraziť výsledokSkryť výsledok