Numerické riešenie nelineárnych rovníc \(f(x)=0\)

Ciele

Ilustrovať pojem intervalu separácie koreňa rovnice.\(\def\a{&}\)
Naučiť sa odhadnúť [ne]presnosť numerického riešenia rovnice.
Naučiť sa používať metódu bisekcie na riešenie nelineárnej rovnice \(f(x)=0\).
Naučiť sa používať Newtonovu metódu na riešenie nelineárnej rovnice \(f(x)=0\).

Úvod

presne

použitie numerických metód

približného riešenia

metóda bisekcie

Newtonova metódu

Analýza existencie koreňov rovnice, ich počtu a podľa možnosti odhadu intervalov, v ktorom ležia jednotlivé korene, t. j. separácia koreňov. Interval \(\langle a_i; b_i\rangle\) budeme nazývať intervalom separácie koreňa \(\alpha_i\) práve vtedy, ak \(\alpha_i\in(a_i;b_i)\), \(f(\alpha_i)=0\) a pre každé \(x\in \langle a_i; b_i\rangle\), \(x\ne \alpha_i\) je \(f(x)\ne0\).
Použitie iteračných postupov konkrétnej metódy, ktorá umožňuje postupné upresňovanie približných riešení.
Odhad [ne]presnosti priebežného/výsledného numerického riešenia.

Poznámka: Intervalom separácie koreňov v širšom zmysle budeme nazývať taký uzavretý interval \(\langle a;b\rangle\), v ktorom leží aspoň jeden koreň rovnice \(f(x)=0\). Je zrejmé, že interval separácie koreňa \(\alpha\) obsahujúci práve jeden koreň je automaticky intervalom separácie aj v širšom zmysle, naopak to však neplatí.

Bolzanova veta

Poznámka: Splnenie podmienok Bolzanovej vety implikuje fakt, že interval \(\langle a;b \rangle\) je intervalom separácie v širšom zmysle slova. Existenciu práve jedného koreňa na intervale je potrebné zdôvodniť ďalšími argumentmi.

Postup

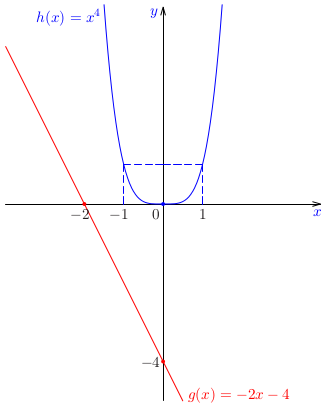
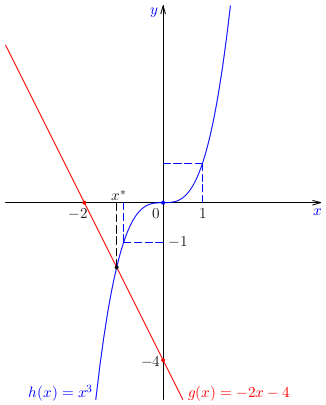
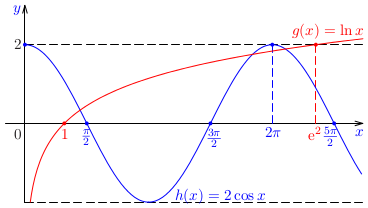
Pri analýze mnoh�ch nelineárnych rovníc je vhodné použitie grafických metód. Ak nevieme priamo načrtnúť graf funkcie \(f(x)\), rovnicu \(f(x)=0\), ktorej reálne riešenia predstavujú priesečníky grafu funkcie s osou \(o_x\), môžeme ekvivalentne prepísať na tvar \(h(x)=g(x)\), s funkciami, ktorých grafy sa dajú načrtnúť jednoduchšie. Riešeniami pôvodnej rovnice potom budú \(x\)-ové súradnice priesečníkov grafov funkcií \(h(x)\) a \(g(x)\).
Poznámka: Pri náčrte grafov funkcií, ktorý je takmer vždy nepresný, sa môže stať, že si niektoré priesečníky nevšimneme. Grafické metódy je preto vhodné dopĺňať analytickými úvahami o možnej [ne]existencii koreňov v uvažovanej oblasti.

Príklad: Určme počet reálnych riešení nelineárnej rovnice \[ x^4+2x+4=0 \] a separujme všetky reálne korene.

Riešenie: Keďže graf funkcie \(f(x)=x^4+2x+4\) nevieme (jednoducho) načrtnúť, prepíšeme rovnicu napríklad na nasledujúci tvar: \[ x^4=-2x-4 \qquad \Leftrightarrow \qquad h(x)=g(x). \] Grafy funkcií \(h(x)=x^4\) (mocninová funkcia) a \(g(x)=-2x-4\) (lineárna funkcia – grafom je priamka) načrtneme celkom jednoducho. Vyskúšajte si to najprv sami a porovnajte svoje riešenie s grafmi uvedenými na nasledujúcom obrázku:

Obr.: : Pomocné funkcie pre rovnicu \(x^4+2x+4=0\)

Keďže sa grafy nepretínajú, je zrejmé, že daná rovnica nemá žiadne reálne riešenie!

Príklad: Určme počet reálnych riešení nelineárnej rovnice \[ x^3+2x+4=0 \] a separujme všetky reálne korene.

Riešenie: Na rozdiel od predchádzajúcej úlohy je známe, že každá kubická rovnica má aspoň jedno reálne riešenie. Tento fakt vyplýva z toho, že funkcia \(f(x)=x^3+2x+4\) je spojitá, pričom platí \(\lim\limits_{x\to-\infty} f(x)=-\infty\lt 0\) a \(\lim\limits_{x\to\infty} f(x)=\infty\gt0\). Teda, keďže funkcia \(f(x)\) dosahuje aj kladné aj záporné funkčné hodnoty, musí na základe spojitosti dosahovať aj nulovú funkčnú hodnotu, t. j. existuje aspoň jeden bod \(x^*\) taký, že \(f(x^*)=0\).

Keďže ani graf funkcie \(f(x)=x^3+2x+4\) nevieme (jednoducho) načrtnúť, prepíšeme rovnicu podobne ako v predchádzajúcom príklade na nasledujúci ekvivalentný tvar: \[ x^3=-2x-4. \] Grafy funkcií \(h(x)=x^3\) (mocninová funkcia) a \(g(x)=-2x-4\) (lineárna funkcia – grafom je priamka) načrtneme celkom jednoducho. Znova si to najprv vyskúšajte sami a porovnajte svoje riešenie s grafmi uvedenými na nasledujúcom obrázku:

Obr.: : Pomocné funkcie pre rovnicu \(x^3+2x+4=0\)

Je zrejmé, že grafy funkcií \(h(x)\) a \(g(x)\) sa pretínajú práve v jednom bode, ktorého \(x\)-ová súradnica je \(x^*\). Navyše je evidentné, že \(x^*\) leží v intervale \(\langle-2;0\rangle\) a po kratšom uvažovaní môžeme interval separácie dokonca zúžiť na \(\langle-2;-1\rangle\) (zdôvodnite prečo).

Správnosť našich nákresov a úvah, presnejšie povedané správnosť určenia intervalu separácie v širšom zmysle, overíme vyčíslením funkčných hodnôt \(f(x)\) v krajných bodov intervalu: \[ f(-2)=-8-4+4=-8\lt 0, \qquad f(-1)=-1-2+4=1\gt 0 \qquad\Rightarrow\qquad f(-2)\cdot f(-1)\lt 0, \] t. j. je splnená jedna z podmienok intervalu separácie \(\langle a;b\rangle\) v širšom zmysle: \(f(a)\cdot f(b)\lt 0\). Pripomeňme, že druhou podmienkou je spojitosť funkcie \(f(x)\).

Poznámka: Uvedené dve podmienky intervalu separácie sú postačujúce podmienky existencie riešenia vnútri intervalu, ale nie sú nutné, t. j. korene rovnice môžu ležať aj vnútri intervalu, na ktorom tieto podmienky nie sú splnené. To je prípad všetkých dvoj-, štvornásobných a pod. koreňov rovníc (napríklad pre riešenie \(x=0\) rovnice \(x^2=0\)).

Príklad: Určme počet reálnych riešení nelineárnej rovnice \[ 2\cos x -\ln x=0 \] a separujme všetky reálne korene.

Riešenie: Podobne ako pri riešení predchádzajúcej úlohy prepíšeme rovnicu na nasledujúci tvar: \[ 2\cos x=\ln x. \] Ak si všimneme, že hodnoty funkcie \(h(x)=2\cos x\) sú z intervalu \(\langle-2;2\rangle\), je zrejmé, že grafy funkcií stačí načrtnúť na intervale \(\langle\mathrm{e}^{-2};\mathrm{e}^2\rangle\), pretože práve na tomto intervale dosahuje funkcia \(g(x)=\ln x\) hodnoty z intervalu \(\langle-2;2\rangle\). Znova sa pokúste samostatne načrtnúť grafy obidvoch funkcií na danom intervale a porovnajte svoje riešenie s nasledujúcim obrázkom.

Obr.: : Pomocné funkcie pre rovnicu \(2\cos x-\ln x=0\)

Je zrejmé, že grafy obidvoch funkcií majú práve 3 priesečníky, t. j. rovnica \(f(x)=2\cos x -\ln x=0\) má práve 3 reálne riešenia. Priesečníky sa dajú ľahko separovať a môžeme konštatovať, že:

\(\displaystyle f(1)=2\cdot \cos(1)\gt0, \qquad f\left(\frac{\pi}{2}\right)=0-\ln\frac{\pi}{2}\lt0 \qquad \Rightarrow \qquad x_1^* \in \left(1;\frac{\pi}{2}\right); \)

\(\displaystyle f\left(\frac{3\pi}{2}\right)=0-\ln\frac{3\pi}{2}\lt0, \qquad f(2\pi)=2-\ln(2\pi)\gt0 \qquad \Rightarrow \qquad x_2^* \in \left(\frac{3\pi}{2};2\pi\right); \)

\(\displaystyle f(2\pi)\gt0, \qquad f\left(\mathrm{e}^2\right)=2\cdot \cos\left(\mathrm{e}^2\right)-\ln\left(\mathrm{e}^2\right)=2\cdot \cos\left(\mathrm{e}^2\right)-2\lt0 \qquad \Rightarrow \qquad x_3^* \in \left(2\pi;\mathrm{e}^2\right). \)
Venujme sa teraz odhadu chyby približného riešenia nelineárnej rovnice.
Príklad: Určme, akej chyby sa dopustíme, ak za približné riešenie rovnice \(x^3+2x+4=0\) vezmeme hodnotu \(x_p=-1{,}2\).

Riešenie: Úlohu budeme riešiť dvomi spôsobmi: 1) položíme bod \(x_p=-1{,}2\) do stredu vhodného intervalu separácie; 2) použijeme vzorec na odhad chyby založený na Lagrangeovej vete o diferencovateľnej funkcii.

Využijeme tiež informáciu z náčrtu grafov pomocných funkcií (na základe neho sme zvolili približné riešenie \(x_p=-1{,}2\)):

Obr.: : Pomocné funkcie pre rovnicu \(x^3+2x+4=0\)

1) Bod \(x_p=-1{,}2\) sa nachádza v blízkosti \(x\)-ovej súradnice priesečníka grafov a zároveň aj blízko bodu \(x=-1\), pričom \(f(-1)=1\gt0\). Určíme funkčnú hodnotu v bode \(x=-1{,}4\): \(f(-1{,}4)=-1{,}544\lt0\).
Poznámka: Hodnota \(-1{,}544\) je v tomto prípade presná, postačila by nám však informácia o znamienku funkčnej hodnoty \(f(-1{,}4)\).

Na základe zistenej informácie môžeme konštatovať, že interval \(\langle -1{,}4;-1\rangle\) je intervalom separácie v širšom zmysle, keďže \(f(-1{,}4)\cdot f(-1)\lt0\). Z toho ale vyplýva, že vnútri daného intervalu leží riešenie rovnice \(x^*\). Vzdialenosť ľubovoľného vnútorného bodu intervalu od stredu intervalu je menšia ako polovica dĺžky intervalu (načrtnite si pomocný obrázok), a preto platí: \[ |-1{,}2-x^*| \lt \frac{-1-(-1,4)}{2}=0{,}2. \] Horný odhad nepresnosti pre bod \(x_p=-1{,}2\) je teda 0,2.
Poznámka: Mohli by sme sa snažiť v okolí bodu \(x=-1{,}2\) zvoliť bližšiu dvojicu bodov tak, aby bod ostal v ich strede a aby tvorili interval separácie. Na to slúžia práve rôzne iteračné techniky, cieľom ktorých je dosiahnutie vopred stanovenej presnosti.

Poznámka: Vyššie uvedené úvahy tvoria základ tzv. \(\pm\varepsilon\)-testu na ukončenie iteračného procesu. Ak platí: \[ f(x_n-\varepsilon)\cdot f(x_n+\varepsilon)\lt 0, \] a funkcia \(f(x)\) je spojitá na intervale \(\langle x_n-\varepsilon;x_n+\varepsilon\rangle\), tak tento interval je intervalom separácie v širšom zmysle, a teda \(|x_n-x^*|\lt\varepsilon\), t. j. \(x_n\) je približné riešenie rovnice s presnosťou \(\varepsilon\).
2) Ak je funkcia \(f(x)\) spojite diferencovateľná, t. j., ak má na intervale \((a;b)\) spojitú deriváciu a sama je spojitá na uzavretom intervale \(\langle a;b\rangle\), tak na základe Lagrangeovej vety platí, že existuje \(c \in (a;b)\) taký, že platí: \[ f(b)-f(a)=f^{\prime}(c)\cdot(b-a). \]
Poznámka: Analogické tvrdenie platí aj pre interval \(\langle b;a\rangle\).
Ak zvolíme dvojicu bodov \(a=x^*\) a \(b=x_n\), pričom samozrejme predpokladáme, že existuje riešenie \(x^*\) rovnice, pre ktoré \(f(x^*)=0\), tak bude platiť: \[ f(x_n)=f^{\prime}(c)\cdot(x_n-x^*), \] pričom neznámy bod \(c\) leží medzi bodmi \(x^*\) a \(x_n\).

Predpokladajme, že na intervale separácie, na ktorom riešime úlohu, platí \[ 0\lt m\leqq |f^{\prime}(x)|. \] Potom na základe \[ |x_n-x^*| =\frac{|f(x_n)|}{|f^{\prime}(c)|} \] dostávame nasledujúci odhad chyby pre bod \(x_n\): \begin{equation}\label{odhad} |x_n-x^*|\leqq \frac{|f(x_n)|}{m}. \end{equation} Uvažujme teraz danú funkciu \(f(x)=x^3+2x+4\). Máme \(f^{\prime}(x)=3x^2+2\), a teda na uvažovanom intervale separácie \(\langle-2;-1\rangle\) platí \[ 0\lt 5\leqq |f^{\prime}(x)|, \] a teda môžeme vziať \(m=5\). Na odhad chyby bodu \(x_p=-1{,}2\) nám už len stačí vypočítať funkčnú hodnotu \(f(-1{,}2)=-0{,}128\). Na základe (\ref{odhad}) dostávame odhad: \[ |x_n-x^*|=|-1{,}2-x^*| \leqq \frac{|-0{,}128|}{5}=0{,}0256. \] Môžeme teda konštatovať, že nepresnosť bodu \(x_p=-1{,}2\) nepresahuje hodnotu 0,0256.
Poznámka: Dvomi rôznymi metódami sme získali dva rôzne odhady chyby pre ten istý bod! Nie je v tom žiaden rozpor, pretože sme hovorili o tzv. hornom odhade chyby, t. j. čísle, ktoré je väčšie alebo nanajvýš rovné absolútnej hodnote samotnej chyby. Samozrejme, za výsledný odhad chyby považujeme menší z dvojice odhadov.

Poznámka: V prípade, ak je vypočítaná funkčná hodnota nepresná, hodnotu \(|f(x_n)|\) je potrebné správne zaokrúhliť smerom nahor!
Ďalej sa budeme venovať metóde bisekcie na riešenie nelineárnych rovníc \(f(x)=0\) so spojitou funkciou \(f(x)\). Predpokladajme, že sme pre niektoré riešenie rovnice \(f(x)=0\) určili interval separácie (v širšom zmysle) \(\langle a;b\rangle\), pričom platí \(f(a)\cdot f(b)\lt0\). Uvažujme stred intervalu separácie – bod \(c=(a+b)/2\). Môžu nastať 3 prípady:
1. \(f(c)=0\), t. j. bod \(c\) je presné riešenie rovnice, \(c=x^*\)!
2. \(f(c)\cdot f(a)\lt0\), t. j. interval \(\langle a;c\rangle\) je interval separácie, pričom jeho dĺžka je polovičná v porovnaní s intervalom separácie \(\langle a;b\rangle\). Bod \(c\) prehlásime za nový pravý kraj intervalu separácie, t. j. položíme \(b=c\).
3. \(f(c)\cdot f(b)\lt0\), t. j. interval \(\langle c;b\rangle\) je interval separácie, pričom jeho dĺžka je polovičná v porovnaní s intervalom separácie \(\langle a;b\rangle\). Bod \(c\) prehlásime za nový ľavý kraj intervalu separácie, t. j. položíme \(a=c\).
Poznámka: Bod \(c\) nemusí ležať presne v strede intervalu.
Je zrejmé, že ak budeme v delení intervalu na dve rovnaké časti pokračovať, po každom kroku sa odhad nepresnosti stredu intervalu separácie zmenšuje na polovicu alebo sa stred stane presným riešením!
Príklad: Metódou bisekcie určme približné riešenie rovnice \(x^3+2x+4=0\) s presnosťou \(\varepsilon=0{,}01\).

Riešenie: Za začiatočný interval separácie zvolíme interval \(\langle a;b\rangle=\langle-1{,}4;-1\rangle\), o ktorom sme už predtým zistili, že je intervalom separácie. Metódu bisekcie budeme používať dovtedy, kým bude dĺžka intervalu väčšia ako \(2\varepsilon=0{,}02\). Na záver za približné riešenie vyhlásime stred konečného intervalu. Výpočty sú zachytené v nasledujúcej tabuľke: \[ \begin{array}{|c|c|c|c|} \hline a \a c \a b \a b-a\\ f(a) \a f(c) \a f(b) \a \\ \hline -1{,}4 \a -1{,}2 \a -1 \a 0{,}4\\ -1{,}544 \a -0{,}128 \a 1 \a \\ \hline -1{,}2 \a -1{,}1 \a -1 \a 0{,}2\\ -0{,}128 \a 0{,}469 \a 1 \a \\ \hline -1{,}2 \a -1{,}15 \a -1{,}1 \a 0{,}1\\ -0{,}128 \a 0{,}17913 \a 0{,}469 \a \\ \hline -1{,}2 \a -1{,}175 \a -1{,}15 \a 0{,}05\\ -0{,}128 \a 0{,}027766 \a 0{,}17913 \a \\ \hline -1{,}2 \a -1{,}1875 \a -1{,}175 \a 0{,}025\\ -0{,}128 \a -0{,}04956 \a 0{,}027766 \a \\ \hline -1{,}1875 \a -1{,}18125 \a -1{,}175 \a 0{,}0125\\ -0{,}04956 \a \a 0{,}027766 \a \\ \hline \end{array} \] Metódou bisekcie sme získali približné riešenie \(x_p=-1{,}18125\), pričom horný odhad nepresnosti pre tento bod je \(0{,}00625\lt \varepsilon\).
Poznámka: V tabuľke nebolo potrebné uvádzať funkčné hodnoty, na rozhodnutie sú postačujúce ich znamienka. Funkčnú hodnotu v posledne uvedenom bode už nebolo potrebné počítať. Ale pre zvedavcov ju môžeme uviesť: \(f(-1{,}18125)\dot=-0{,}010759\) (po zaokrúhlení na 6 desatinných miest).

Poznámka: Programy Matlab a Octave majú zabudovanú funkciu na riešenie algebrických rovníc, ktorá je samozrejme tiež numerická.
Príkaz roots([1 0 2 4]) dáva odpoveď v nasledujúcom tvare:

ans = 0.589754512301458 + 1.744543250922657i 0.589754512301458 - 1.744543250922657i -1.179509024602917 + 0.000000000000000i

Odchýlka nášho numerického riešenia od numerického riešenia určeného funkciou roots je \(|-1{,}179509024602917-(-1{,}18125)|\lt 0{,}001741\) je blízka skutočnej absolútnej chybe.

Poznámka: Najdôležitejšou vlastnosťou metódy bisekcie je jej bezpodmienečná konvergencia na ľubovoľnom intervale separácie (maximálny počet krokov sa dá dopredu odhadnúť) a tiež jednoduchá programová implementácia. Na uskutočnenie iteračného procesu postačuje výpočet funkčných hodnôt. Nevýhodou je pomalá konvergencia – na výpočet približného riešenia s nie veľmi veľkou presnosťou sme potrebovali uskutočniť 5 iterácií.
Newtonova metóda na riešenie úloh sa vyznačuje tzv. kvadratickou rýchlosťou konvergencie, ktorá je oveľa lepšia, ako v prípade metód založených na využití výhradne funkčných hodnôt. Nevýhodou však je, že metóda nemusí konvergovať, presnejšie, ak chceme mať istotu jej konvergencie, musíme overiť/zabezpečiť splnenie niektorých postačujúcich podmienok konvergencie.

Zameriame sa na overenie nasledujúcich postačujúcich podmienok konvergencie:
1. \(f(a)\cdot f(b)\lt0\) – \(\langle a;b\rangle\) je interval separácie v širšom zmysle;
2. \(f^{\prime\prime}(x)\ne 0\) – funkcia je na intervale separácie buď konvexná alebo konkávna;
3. \(f(x_0)\cdot f^{\prime\prime}(x_0) \gt 0\) – štartovací bod \(x_0\in\langle a;b\rangle\) má byť správne zvolený. Najčastejšie sa volí \(x_0=a\) alebo \(x_0=b\) – jeden z týchto bodov spĺňa uvedenú podmienku;
4. \begin{equation}\label{newton} x_{n+1}=x_n-\dfrac{f(x_n)}{f^{\prime}(x_n)}, \qquad n=0, 1, 2, \dots \end{equation} – iteračný proces na základe metódy dotyčníc.
Poznámka: V prípade, ak na intervale separácie platí podmienka \(0\lt m\leqq |f^{\prime}(x)|\), na ukončenie procesu používame odhad chyby (\ref{odhad}). Podmienka konvexnosti resp. konkávnosti spolu s podmienkou \(f(a)\cdot f(b)\lt0\) zabezpečuje existenciu práve jedného koreňa. Samozrejme predpokladáme existenciu druhej derivácie, z ktorej vyplýva spojitosť funckie na intervale \(\langle a;b \rangle\).
Výpočty je možné zorganizovať nasledujúcim spôsobom: pre aktuálnu hodnotu \(x_n\), \(n=0\), \(1\), \(2\), \(\dots\) vypočítame hodnotu \(f(x_n)\) a odhadneme chybu na základe vzorca (\ref{odhad}). Ak je chyba menšia ako zadaná presnosť, iterácie ukončíme, v opačnom prípade vypočítame \(f^{\prime}(x_n)\) a dosadením do vzorca (\ref{newton}) určíme novú hodnotu \(x_{n+1}\).
Príklad: Newtonovou metódou určme približné reálne riešenie rovnice \(x^3+2x+4=0\) na intervale separácie \(\langle-2;-1\rangle\) s presnosťou \(\varepsilon=10^{-6}\).
Riešenie: Postupne overíme uvedené postačujúce podmienky konvergencie:

\(f(-2)\cdot f(-1)=-8\cdot 1\lt0\) – \(\langle-2;-1\rangle\) je interval separácie v širšom zmysle;

\(f^{\prime\prime}(x)=6x\lt 0\) – funkcia je na intervale separácie konkávna;

\(f(-2)\cdot f^{\prime\prime}(-2) \gt 0\) – správne zvolený štartovací bod je \(x_0=-2\).
Poslednú podmienku zabezpečíme uskutočnením iterácií na základe vzorca Newtonovej metódy.
\(x_{n+1}=x_n-\dfrac{x_n^3+2x_n+4}{3x_n^2+2},\qquad n=0, 1, 2, \dots \).

Vypočítame ešte prvú deriváciu: \(f^{\prime}(x)=3x^2+2\). \(f^{\prime}(-2)=14\), \(f^{\prime}(-1)=5\). Keďže na intervale separácie je druhá derivácia \(f^{\prime\prime}(x)\) záporná, na intervale separácie musí byť prvá derivácia \(f^{\prime}(x)\) klesajúca, a teda hodnota 5 je jej najmenšia hodnota na intervale separácie. Preto môžeme použiť odhad chyby (\ref{odhad}) s hodnotou \(m=5\).

Nasledujúca tabuľka obsahuje použité (zaokrúhlené) hodnoty: \[ \begin{array}{|c|l|l|l|l|} \hline n \a x_n \a f(x_n) \a |f(x_n)|/m \a f^{\prime}(x_n) \\ \hline 0 \a -2 \a -8 \a 1{,}6 \a 14 \\ \hline 1 \a -1{,}42857143 \a -1{,}772594752 \a 0{,}354518950437 \a 8{,}122449 \\ \hline 2 \a -1{,}21033740129218 \a -0{,}193718183556245 \a 0{,}038743636711249 \a 6{,}394750 \\ \hline 3 \a -1{,}18004408453297 \a -0{,}003304325856939 \a 0{,}000660865171378 \a 6{,}177512 \\ \hline 4 \a -1{,}17950918864115 \a -0{,}000001012726997 \a 0{,}000000202545399 \a - \\ \hline \hline 5 \a -1{,}17950902460293 \a -0{,}000000000000094 \a 0{,}000000000000019 \a - \\ \hline \end{array} \] Ako vidno, na dosiahnutie oveľa lepšej presnosti ako v metóde bisekcie stačili 4 iterácie Newtonovej metódy. Na druhej strane, ak by sme nahradili výpočet derivácie približnou hodnotou pomocou podielu diferencií, na jednu newtonovskú iteráciu by sme mohli počítať výpočet 2 funkčných hodnôt. Teda na 4 iterácie s overením dosiahnutia presnosti treba brať do úvahy výpočet 9 funkčných hodnôt. Pri spätnom pohľade na tabuľku metódy bisekcie sa ľahko presvedčíme, že na určenie riešenia s presnosťou 0,00625 bolo použitých 7 funkčných hodnôt. To odpovedá newtonovskému približnému riešeniu \(x_3\), ktorého presnosť bola odhadnutá hodnotou 0,000661.

Uviedli sme aj výsledok ďalšej newtonovskej iterácie. Presnosť sa ďalej výrazne zvýšila. Ak si budeme všímať predposledný stĺpec tabuľky, vidíme, že sa počet núl v odhade chyby približne zdvojnásobuje (3, 6, 13), teda znižovanie nepresnosti sa zrýchľuje. Toto je prejav tzv. kvadratickej rýchlosti konvergencie Newtonovej metódy.
Príklad: Newtonovou metódou určme približne najväčšie reálne riešenie rovnice \(2\cos x-\ln x=0\) s presnosťou \(\varepsilon=10^{-6}\).
Riešenie: Pripomeňme si situáciu pri určení intervalov separácie danej rovnice.

Obr.: : Pomocné funkcie pre rovnicu \(2\cos x-\ln x=0\)

Najväčší koreň leží v intervale \(\left(2\pi;\mathrm{e}^2\right)\). Postupne overíme uvedené postačujúce podmienky konvergencie:

\(\left\langle2\pi;\mathrm{e}^2\right\rangle\) je interval separácie – overené vyššie;

\(f^{\prime}(x)=-2\sin x -\dfrac{1}{x}\); \(f^{\prime\prime}(x)=-2\cos x+\dfrac{1}{x^2}\lt0\) – funkcia je na intervale separácie konkávna;

\(f\left(\mathrm{e}^2\right)\cdot f^{\prime\prime}(\mathrm{e}^2) \gt 0\) – správne zvolený štartovací bod je \(x_0=\mathrm{e}^2\dot=7{,}3891\).

\(x_{n+1}=x_n-\dfrac{2\cos x_n-\ln x_n}{-2\sin x_n-1/x_n},\qquad n=0, 1, 2, \dots \).

Vypočítame ešte prvú deriváciu v krajných bodoch intervalu separácie: \(f^{\prime}(2\pi)=-\dfrac{1}{2\pi}\dot=-0{,}159\), \(f^{\prime}(\mathrm{e}^2)\dot=-1{,}923\). Keďže na intervale separácie je druhá derivácia \(f^{\prime\prime}(x)\) záporná, na intervale separácie musí byť prvá derivácia \(f^{\prime}(x)\) klesajúca, a teda hodnota \(0{,}159\) je menšia ako najmenšia absolútna hodnota derivácie na intervale separácie. Preto môžeme použiť odhad chyby (\ref{odhad}) s hodnotou \(m=0{,}159\).

Nasledujúca tabuľka obsahuje použité (zaokrúhlené) hodnoty: \[ \begin{array}{|c|l|l|l|l|} \hline n \a x_n \a f(x_n) \a |f(x_n)|/m \a f^{\prime}(x_n) \\ \hline 0 \a 7{,}389056098931 \a -1{,}10328751636253 \a 6{,}93891519724864 \a -1{,}923045 \\ \hline 1 \a 6{,}815337124284 \a -0{,}19574101484621 \a 1{,}23107556507051 \a -1{,}161505 \\ \hline 2 \a 6{,}646813577282 \a -0{,}02491253814852 \a 0{,}15668262986491 \a -0{,}861783 \\ \hline 3 \a 6{,}617905450864 \a -0{,}00077436117992 \a 0{,}00487019610012 \a -0{,}808115 \\ \hline 4 \a 6{,}616947219362 \a -0{,}00000085686183 \a 0{,}00000538906813 \a -0{,}806326\\ \hline 5 \a 6{,}616946156689 \a -0{,}00000000000105 \a 0{,}00000000000663 \a - \\ \hline \end{array} \] Znova sme sa presvedčili o rýchlej konvergencii iterácií Newtonovej metóde v prípade zabezpečenia splnenia postačujúcich podmienok konvergencie.

Použime ešte \(\pm\varepsilon\)-test po 4. iterácii: výpočtom sa dá ukázať, že \[ f(6{,}616948219362)\lt 0, \qquad f(6{,}616946219362)\lt0 \qquad \Rightarrow \qquad f(x_4+\varepsilon)\cdot f(x_4-\varepsilon)\gt0, \] a teda je potrebné ešte pokračovať ďalšími iteráciami.

Po 5. iterácii bude: \[ f(6{,}616947156689)\lt 0, \qquad f(6{,}616945156689)\gt0 \qquad \Rightarrow \qquad f(x_5+\varepsilon)\cdot f(x_5-\varepsilon)\lt0, \] čo dokazuje, že \(|x_5-x^*|\lt\varepsilon\) a výpočet môžeme ukončiť.
Poznámka: V tomto prípade sa ukázalo, že obidva typy odhadu chyby nás doviedli k ukončeniu iteračného procesu po piatich iteráciách. Mohlo by však nastať aj situácia, v ktorej by \(\pm\varepsilon\)-test umožnil ukončiť iterácie skôr, ako druhý spôsob. Samotný \(\pm\varepsilon\)-test si vyžaduje výpočet dvoch funkčných hodnôt, čo je porovnateľné s uskutočnením ďalšej iterácie Newtonovej metódy.

Zdroje

Buša, Pirč, Schrötter: Numerické metódy, pravdepodobnosť a matematická štatistika, 2006, ISBN 80-8073-632-4. Stiahnuť obrazovkovú alebo tlačovú verziu.
Daňo, Ostertagová: Vybrané kapitoly z numerických metód, pravdepodobnosti a matematickej štatistiky, Equilibria s.r.o., Košice, 2012, ISBN 978-80-8143-012-1.

Doplňujúce úlohy

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte najmenší reálny koreň rovnice \(x^3 + 2 x^2 - 4 x - 5 = 0\) s presnosťou \(0{,}005.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte najväčší reálny koreň rovnice \(x^3 + 0{,}9 x^2 + 1{,}1 x - 7{,}8 = 0\) s presnosťou \(0{,}005.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte najmenší reálny koreň rovnice \(x^3 -12 x + 1 = 0\) s presnosťou \(0{,}000001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(2 x^5 + 5 x^4 -10 x^2 + 10x - 3 = 0\) s presnosťou \(0{,}000001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte kladný koreň rovnice \(2 x^4 + 6 x^3 + 5 x^2 - 0{,}5 = 0\) s presnosťou \(0{,}0001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(\sin x + 2 x - 2 = 0\) s presnosťou \(0{,}000001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(2 x\cdot \ln x - 4 x + 5{,}3 = 0\) s presnosťou \(0{,}00001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(x^3 - 8 x + 15 = 0\) s presnosťou \(0{,}0001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(x^3 + 3 x^2 - 3 = 0\) s presnosťou \(0{,}001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte najväčší reálny koreň rovnice \(5 x^3 + 2 x^2 - 15 x - 6 = 0\) s presnosťou \(0{,}0001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(x^3 - 7 x - 7 = 0\) s presnosťou \(0{,}001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(x^4-3 x^2+4 x-1 = 0\) s presnosťou \(0{,}001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(x^5 - x^4 + 2 x^3 - 3 x^2 + 4 x - 5 = 0\) s presnosťou \(0{,}0001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte záporný koreň rovnice \(x^6 - 3 x^2 + x - 1 = 0\) s presnosťou \(0{,}0001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(x - \sin x = 0{,}25\) s presnosťou \(0{,}00001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(2{,}2 x - 2^x = 0\) s presnosťou \(0{,}00001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(2 \,\mathrm{ln} x - 1/x = 0\) s presnosťou \(0{,}00001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(\mathrm{e}^{-x} + x^2 - 2 = 0\) s presnosťou \(0{,}00001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(\mathrm{e}^x + x^2 - 2 = 0\) s presnosťou \(0{,}00001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte všetky reálne korene rovnice \(2 x - \mathrm{log} x - 7 = 0\) väčšie ako 3 s presnosťou \(0{,}00001.\)

Úloha: Pomocou metódy bisekcie a Newtonovej metódy určte kladné korene rovnice \(\mathrm{e}^x + \mathrm{e}^{-3x} = 4\) s presnosťou \(0{,}00001.\)