Testovanie štatistických hypotéz o parametroch základných súborov s normálnym rozdelením

Ciele

1. Naučiť sa aplikovať jednovýberový test zhody strednej hodnoty \(\mu\) so známou konštantou \(\mu_0\), pričom smerodajnú odchýlku \(\sigma\) poznáme.
2. Naučiť sa aplikovať jednovýberový test zhody strednej hodnoty \(\mu\) so známou konštantou \(\mu_0\), pričom smerodajnú odchýlku \(\sigma\) nepoznáme.
3. Naučiť sa aplikovať jednovýberový test zhody rozptylu \(\sigma^2\) so známou konštantou \(\sigma^2_0\).
4. Naučiť sa aplikovať dvojvýberový test zhody dvoch rozptylov \(\sigma^2_1\) a \(\sigma^2_2\).
5. Naučiť sa aplikovať dvojvýberový test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom smerodajné odchýlky \(\sigma_1\) a \(\sigma_2\) poznáme.
6. Naučiť sa aplikovať dvojvýberový test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom smerodajné odchýlky \(\sigma_1\) a \(\sigma_2\) nepoznáme a platí \(\sigma_1=\sigma_2\).
7. Naučiť sa aplikovať dvojvýberový test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom smerodajné odchýlky \(\sigma_1\) a \(\sigma_2\) nepoznáme a platí \(\sigma_1\not=\sigma_2\).
8. Naučiť sa aplikovať párový test zhody stredných hodnôt \(\mu_1\) a \(\mu_2\).

Úvod

V tejto časti sa budeme zaoberať aplikáciou výberových štatistík pri porovnávaní niektorého parametra základného štatistického súboru s nejakou konkrétnou číselnou hodnotou a tiež pri porovnávaní parametrov toho istého druhu v dvoch rôznych základných súboroch, ktoré majú normálne rozdelenie.

Teraz uvedieme základné pojmy testovania štatistických hypotéz.
Tvrdenia, týkajúce sa rozdelenia (jeho parametrov alebo jeho tvaru) náhodných veličín, sa nazývajú štatistickými hypotézami. Postup, ktorým overujeme či daná hypotéza platí alebo nie, sa nazýva testom štatistickej hypotézy. Hypotézu, ktorej platnosť overujeme, nazývame nulovou hypotézou (testovanou hypotézou) a označujeme ju \(H_0\). Proti testovanej hypotéze postavíme tzv. alternatívnu hypotézu (alternatívu), ktorú označujeme \(H_1\).
Test nulovej hypotézy \(H_0\) proti alternatíve \(H_1\) je postupom, ktorý na základe náhodného výberu z daného rozdelenia a na zvolenej hladine významnosti \(\alpha\) (t. j. so zvolenou spoľahlivosťou \(1-\alpha\)) vedie buď k zamietnutiu nulovej hypotézy (t. j. k prijatiu alternatívy) alebo k nezamietnutiu nulovej hypotézy (t. j. k zamietnutiu alternatívy).
Tvar nulovej hypotézy je napr. \(H_0: Q=Q_0\), resp. \(H_0: Q-Q_0=0\) (odtiaľ pochádza jej názov), pričom \(Q\) je parameter základného súboru a \(Q_0\) je konkrétna konštanta.

V praxi sa proti nulovej hypotéze stavajú obvykle tieto tri typy alternatívnych hypotéz:
• Pravostranná: \(H_1: Q\gt\ Q_0\), ktorá vymedzuje obor hodnôt parametra \(Q\) napravo od hodnoty \(Q_0\).
• Ľavostranná: \(H_1: Q\lt\ Q_0\), ktorá vymedzuje obor hodnôt parametra \(Q\) naľavo od hodnoty \(Q_0\).
• Obojstranná: \(H_1: Q\not=\ Q_0\), ktorá sa od predchádzajúcich jednostranných alternatívnych hypotéz líši tým, že len popiera platnosť nulovej hypotézy.

K testu nulovej hypotézy proti alternatíve použijeme testovaciu štatistiku (charakteristiku). Testovacia štatistika \(G\) je konkrétna funkcia náhodného výberu, ktorá má pre každú hypotézu \(H_0\) a \(H_1\) špeciálny tvar a rozdelenie pravdepodobnosti. Štatistika \(G\) sa nazýva aj testovacím kritériom.
Obor hodnôt, ktorý môže štatistika \(G\) nadobudnúť, rozdelíme na dva disjunktné intervaly: na obor \(K_\alpha\), ktorý sa nazýva kritickým oborom (kritickou oblasťou, oblasťou zamietnutia \(H_0\)) a na obor doplnkový. Kritická oblasť \(K_\alpha\) je určená kvantilom testovacej charakteristiky \(G\).
Ak hodnota testovacej charakteristiky \(G\), vypočítaná z výberových hodnôt, padne do kritickej oblasti \(K_\alpha\), zamietame testovanú hypotézu \(H_0\), t. j. prijímame alternatívnu hypotézu \(H_1\). Ak hodnota testovacej charakteristiky \(G\) nepadne do kritickej oblasti \(K_\alpha\), testovanú hypotézu \(H_0\) nezamietame. Hovoríme o teste hypotézy \(H_0\) založenom na kritickom obore \(K_\alpha\).
Pretože testovanú nulovú hypotézu \(H_0\) prijímame alebo zamietame na základe výsledkov získaných náhodným výberom, môže byť jej prijatie alebo zamietnutie správne alebo nesprávne.
Nesprávne zamietnutie testovanej hypotézy \(H_0\), t. j. nesprávne prijatie alternatívnej hypotézy \(H_1\) nazývame chybou prvého druhu (je to vlastne hladina významnosti \(\alpha\)). K tejto chybe dochádza vtedy, keď hodnota testovacej charakteristiky padne do kritickej oblasti, ale pritom v skutočnosti platí hypotéza \(H_0\).
Nesprávne prijatie testovanej hypotézy \(H_0\), t. j. jej nezamietnutie v prípade, že platí alternatívna hypotéza \(H_1\) nazývame chybou druhého druhu. K tejto chybe dochádza vtedy, keď hodnota testovacej charakteristiky nepadne do kritickej oblasti a pritom v skutočnosti platí hypotéza \(H_1\).

Pri testovaní štatistických hypotéz je vhodné dodržiavať túto postupnosť krokov:
1. Formulácia hypotéz \(H_0\) a \(H_1\).
2. Voľba hladiny významnosti \(\alpha\).
3. Výpočet hodnoty testovacej charakteristiky \(G\) na základe daných hodnôt náhodného výberu.
4. Určenie kritickej oblasti \(K_\alpha\).
5. Vyhodnotenie testu, ktoré spočíva buď v zamietnutí \(H_0\), a teda prijatí \(H_1\) alebo v prijatí \(H_0\).
\(\def\a{&}\)

Postup

1. Jednovýberový \(Y\)-test zhody strednej hodnoty \(\mu\) so známou konštantou \(\mu_0\), pričom smerodajnú odchýlku \(\sigma\) poznáme
   
   Predpokladáme, že náhodná premenná \(X\) základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu\) a \(\sigma\), t. j. \(X\sim norm(\mu,\,\sigma)\), pričom hodnotu \(\sigma\) poznáme. Nech \(n\) je rozsah náhodného výberu a \(\bar{x}\) je výberový priemer.
   Nulová hypotéza bude mať tvar \(H_0: \mu=\mu_0\), kde \(\mu_0\) je známa konštanta.
   Testovacia charakteristika \(Y=\dfrac{\bar{x}-\mu_0}{\sigma}\cdot\sqrt{n}\) má normované normálne rozdelenie pravdepodobnosti za predpokladu, že platí hypotéza \(H_0\).
   Kritická oblasť \(K_{\alpha}\) je:

   
   
   • \((y_{1-\alpha} \ ; \infty) \) pre \(H_1: \mu\gt\mu_0\)
   
   
   • \((-\infty\ ; - y_{1-\alpha} ) \) pre \(H_1: \mu\lt\mu_0\)
   
   
   • \((-\infty\ ; - y_{1-\alpha/2} ) \cup (y_{1-\alpha/2} \ ; \infty) \) pre \(H_1: \mu\not= \mu_0\),
     
     kde \(y_\beta\) je \(\beta\)-kvantil normovaného normálneho rozdelenia pravdepodobnosti (viď predchádzajúce cvičenie 11).

   Poznámka:
   V praxi by sa mal vždy testovať aj predpoklad o normalite výberových súborov.

   Príklad:
   Pri tradičnom spôsobe opracovania strojových súčiastok sa dosahovali priemerné hodnoty 4,4 dôležitej kvalitatívnej vlastnosti so smerodajnou odchýlkou \(\sigma=0{,}4\). Pokusne sa zavádza nová, lacnejšia metóda opracovania súčiastok, ktorou opracovali 20 súčiastok a boli dosiahnuté takéto výsledky: 4,5; 4,3; 4,1; 4,9; 4,6; 3,6; 4,7; 5,1; 4,8; 4,0; 3,7; 4,4; 4,9; 4,9; 5,2; 5,1; 4,7; 4,9; 4,6; 4,8. Na hladine významnosti \(\alpha =0{,}05\) otestujte hypotézu či nová metóda vedie k zvýšeniu hodnoty sledovanej kvalitatívnej vlastnosti. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.

   Riešenie:
   

   1. Aplikujeme jednovýberový \(Y\)-test zhody strednej hodnoty \(\mu\) so známou konštantou \(\mu_0\), pričom poznáme smerodajnú odchýlku \(\sigma\). Nulová hypotéza bude mať tvar \(H_0: \mu=\mu_0\), kde známa konštanta je \(\mu_0=4{,}4\). Nulovú hypotézu budeme testovať proti pravostrannej alternatívnej hypotéze \(H_1: \mu\gt4{,}4\).
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Z hodnôt náhodného výberu vyčíslime hodnotu testovacej charakteristiky \[Y=\dfrac{\bar{x}-\mu_0}{\sigma}\cdot\sqrt{n}.\] Do uvedeného vzorca dosadíme potrebné hodnoty \(n=20\); \(\mu_0=4{,}4\); \(\sigma=0{,}4\); \(\bar{x}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i=4{,}59\). Po vyčíslení kalkulačkou dostaneme výsledok \(Y=2{,}1243\).
      
      Na výpočet môžeme použiť aj MATLAB:
      x=[45,43,41,49,46,36,47,51,48,40,37,44,49,49,52,51,47,49,46,48]/10;
      n=length(x),m=mean(x),Y=(m-4.4)*sqrt(n)/0.4
      
      
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(Y\notin\) \(K_{\alpha}\), pričom pre kritickú oblasť \(K_{\alpha}\) v tomto prípade platí \(K_{\alpha}=(y_{1-\alpha} \ ; \infty) \).
      Na určenie kritickej oblasti použijeme kvantil normovaného normálneho rozdelenia \(y_{1-\alpha}=y_{0{,}95}=1{,}6449\) (z tabuliek). Kritická oblasť je teda \(K_{\alpha}=(1{,}6449 \ ; \infty) \).
      
      Výpočet kvantilu pomocou MATLABu:
      q=norminv(.95)
      Prípadne na vyhľadanie kvantilov môžeme využiť aj prostredie disttool, ktoré slúži na grafické znázorňovanie distribučnej funkcie, pravdepodobnostnej funkcie, resp. hustoty pravdepodobnosti štandardných rozdelení. Odošleme príkaz:
      disttool
      V grafickom okne si nastavíme potrebné parametre (pozrite si to na nasledujúcom obrázku):
      
   
   
   5. Pretože \(Y\in\) \(K_{\alpha}\), hypotézu \(H_0\) zamietame v prospech alternatívnej hypotézy \(H_1\).
   
   

   
   Ukážeme ešte ďalší spôsob riešenia tejto úlohy pomocou MATLABu, a to aplikáciou príkazu [h,p,ci,zval]=ztest(x,m,sigma,alpha,tail). Význam vstupných argumentov je nám už známy z predchádzajúceho cvičenia (riešená úloha časti 3), pričom za m dáme teraz ale známu konštantu \(\mu_0\).
   [h,p,ci,zval]=ztest(x,4.4,0.4,0.05,'right')
   Výsledok z MATLABu:
   h = 1
   p = 0.0168
   ci = 4.4429 Inf
   zval = 2.1243
   
   Najprv si krátko objasníme prístup k testovaniu hypotéz založený na \(p\)-hodnote (\(p\)-value), ktorý používajú mnohé štatistické softvéry: \(p\)-hodnotou (tzv. marginálnou signifikantnou hladinou) testovanej hypotézy \(H_0\) nazývame najmenšiu hladinu významnosti \(\alpha\), na ktorej je ešte možné pri daných nameraných hodnotách náhodného výberu zamietnuť nulovú hypotézu. Keď je \(p\)-hodnota menšia alebo rovná \(\alpha\), tak hypotézu \(H_0\) zamietneme na hladine významnosti \(\alpha\). Keď je \(p\)-hodnota väčšia ako \(\alpha\), tak hypotézu \(H_0\) nie je možné na hladine významnosti \(\alpha\) zamietnuť.
   
   Teraz interpretujme získané výsledky z MATLABu. Výsledok h = 1 znamená, že hypotézu \(H_0\) zamietame na hladine významnosti \(\alpha =0{,}05\), t. j. prijímame alternatívnu hypotézu \(H_1\).
   To isté rozhodnutie je možné uskutočniť aj na základe \(p\)-hodnoty, pretože \(p={0{,}0168}\lt\alpha =0{,}05\).
   Do premennej ci boli uložené hranice 95 %-ného pravostranného intervalu spoľahlivosti pre strednú hodnotu \(\mu\) pri známej smerodajnej odchýlke \(\sigma\) základného súboru s normálnym rozdelením.
   Do premennej zval bola uložená hodnota testovacej charakteristiky (vo vzorci pre uvedený test je označená ako \(Y\)).

   Poznámka:
   Napríklad pri hladine významnosti \(\alpha =0{,}01\) by sme hypotézu \(H_0\) nezamietli, pretože \(p={0{,}0168}\gt\alpha =0{,}01\).

   Zobraziť riešenieSkryť riešenie
2. Jednovýberový \(t\)-test zhody strednej hodnoty \(\mu\) so známou konštantou \(\mu_0\), pričom smerodajnú odchýlku \(\sigma\) nepoznáme
   
   Predpokladáme, že náhodná premenná \(X\) základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu\) a \(\sigma\), t. j. \(X\sim norm(\mu,\,\sigma)\), pričom hodnotu \(\sigma\) nepoznáme. Nech \(n\) je rozsah náhodného výberu, \(\bar{x}\) je výberový priemer a \(s\) je výberová smerodajná odchýlka.
   Nulová hypotéza bude mať tvar \(H_0: \mu=\mu_0\), kde \(\mu_0\) je známa konštanta.
   Testovacia charakteristika \(t=\dfrac{\bar{x}-\mu_0}{s}\cdot\sqrt{n}\) má Studentovo \(t\)-rozdelenie pravdepodobnosti s \(\gamma=n-1\) stupňami voľnosti za predpokladu, že platí hypotéza \(H_0\).
   Kritická oblasť \(K_{\alpha}\) je:

   
   
   • \(\left(t_{1-\alpha,\,n-1}\, ;\infty\right ) \) pre \(H_1: \mu\gt\mu_0\)
   
   
   • \((-\infty\ ; - t_{1-\alpha,\,n-1} ) \) pre \(H_1: \mu\lt\mu_0\)
   
   
   • \((-\infty\ ; - t_{1-\alpha/2,\,n-1} ) \cup (t_{1-\alpha/2,\,n-1} \ ; \infty) \) pre \(H_1: \mu\not= \mu_0\),
     
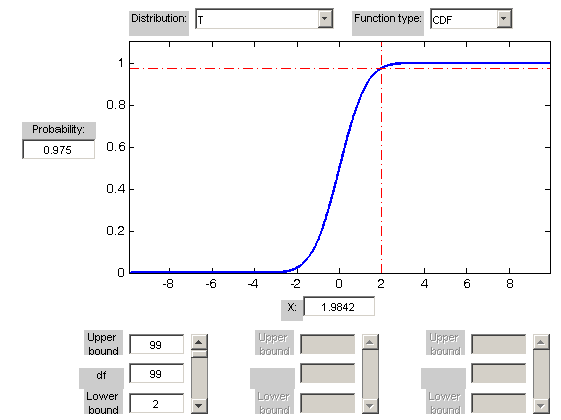
     kde \(t_{\beta,\,n-1}\) je \(\beta\)-kvantil Studentovho \(t\)-rozdelenia pravdepodobnosti s \(\gamma=n-1\) stupňami voľnosti.

   Príklad:
   Meral sa percentuálny obsah cínu vo vzorkách rudy. Výsledky sú v tabuľke: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline z_i \a 30 \a 35 \a 40\a 45 \a 50\a 55 \a 60\a 65\a 70\a 75 \\ \hline n_i \a 4 \a 6 \a 8 \a 15 \a 25 \a 20 \a 8\a 7\a 5 \a 2 \\ \hline \end{array} \] Predpokladáme, že obsah cínu má normálne rozdelenie. Odborníci predpokladajú, že ruda obsahuje v priemere 50 % cínu. Na hladine významnosti \(\alpha =0{,}05\) overte túto hypotézu odborníkov.

   Riešenie:
   

   1. Použijeme jednovýberový \(t\)-test zhody strednej hodnoty \(\mu\) so známou konštantou \(\mu_0\), pričom nepoznáme smerodajnú odchýlku \(\sigma\). Nulová hypotéza bude mať tvar \(H_0: \mu=50\). Nulovú hypotézu budeme testovať proti obojstrannej alternatívnej hypotéze \(H_1: \mu\not=50\), kde známa konštanta je \(\mu_0=50\).
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Z hodnôt náhodného výberu vyčíslime hodnotu testovacej charakteristiky \[t=\dfrac{\bar{x}-\mu_0}{s}\cdot\sqrt{n}.\] Do uvedeného vzorca dosadíme \(n=\sum\limits_{i=1}^{k} n_i=100\); \(\mu_0=50\); \(\bar{x}=\frac{1}{n}\sum\limits_{i=1}^{k} z_i\cdot n_i=51{,}1000\); \(s\ =\sqrt{ \frac{1}{n-1} \sum\limits_{i=1}^{k} (z_i-\bar{x})^2 \cdot n_i\ }=10{,}1150\).
      Po vyčíslení kalkulačkou dostaneme výsledok \(t=1{,}0875\).
      
      Použitie MATLABu:
      z=[30*ones(1,4),35*ones(1,6),40*ones(1,8),45*ones(1,15),50*ones(1,25),...
      55*ones(1,20),60*ones(1,8),65*ones(1,7),70*ones(1,5),75,75];
      n=length(z),m=mean(z),s=std(z),t=(m-50)*sqrt(n)/s
      
      
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(t\notin\)\(K_{\alpha}\).
      Pre kritickú oblasť \(K_{\alpha}\) v tomto prípade platí \(K_{\alpha}= (-\infty\ ; - t_{1-\alpha/2,\,n-1} ) \cup (t_{1-\alpha/2,\,n-1} \ ; \infty) \). Na určenie kritickej oblasti použijeme kvantil Studentovho rozdelenia \(t_{1-\alpha/2,\,n-1}=t_{0{,}975;99}=1{,}9842\). V tabuľkách by sme v tomto prípade našli len aproximovanú hodnotu 1,96. Kritická oblasť je teda \(K_{\alpha}=(-\infty\ ; -1{,}9842 ) \cup (1{,}9842 \ ; \infty) \).
      
      Výpočet príslušného kvantilu pomocou MATLABu:
      q=tinv(.975,99)
      Na vyhľadanie kvantilu môžeme využiť aj prostredie disttool. Odošleme príkaz:
      disttool
      V grafickom okne si nastavíme potrebné parametre (pozrite si to na nasledujúcom obrázku):
      
   
   
   5. Pretože \(t\notin\) \(K_{\alpha}\), hypotézu \(H_0\) nezamietame.
   
   

   
   Opäť ukážeme ďalší spôsob riešenia tejto úlohy pomocou MATLABu, a to aplikáciou príkazu [h,p,ci,stats]=ttest(x,m,alpha,tail). Význam vstupných a výstupných argumentov pozorný čitateľ už zrejme chápe.
   [h,p,ci,stats]=ttest(z,50,0.05,'both')
   Výsledok z MATLABu:
   h = 0
   p = 0.2795
   ci = 49.0930 53.1070
   stats =
   tstat: 1.0875, df: 99, sd: 10.1150
   
   Teraz interpretujme získané výsledky z MATLABu. Výsledok h = 0 znamená, že hypotézu \(H_0\) nezamietame na hladine významnosti \(\alpha =0{,}05\).
   To isté rozhodnutie je možné uskutočniť aj na základe \(p\)-hodnoty, pretože \(p={0{,}2795}\gt\alpha =0{,}05\).
   V premennej ci je výsledok pre 95 %-ný obojstranný interval spoľahlivosti pre strednú hodnotu \(\mu\) pri neznámej smerodajnej odchýlke \(\sigma\) základného súboru s normálnym rozdelením.
   V premennej stats máme tri výsledky, a to hodnotu testovacej charakteristiky tstat, ktorú sme vo vzorci pre tento test označili \(t\); ďalej df, čo znamená počet stupňov voľnosti použitej testovacej štatistiky a nakoniec sd je výsledok pre výberovú smerodajnú odchýlku.

   Zobraziť riešenieSkryť riešenie
3. Jednovýberový \(\chi^2 \)-test zhody rozptylu \(\sigma^2\) so známou konštantou \(\sigma^2_0\)
   
   Predpokladáme, že náhodná premenná \(X\) základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu\) a \(\sigma\), t. j. \(X\sim norm(\mu,\,\sigma)\). Nech \(n\) je rozsah náhodného výberu a \(s^2\) je výberový rozptyl.
   Nulová hypotéza bude mať tvar \(H_0: \sigma^2=\sigma^2_0\), kde \(\sigma^2_0\) je známa konštanta.
   Testovacia charakteristika \(\chi^2 =\dfrac{n-1}{\sigma^2_{0}}\cdot s^2\) má \(\chi^2\)-rozdelenie pravdepodobnosti (čítaj chíkvadrát) ) s \(\gamma=n-1\) stupňami voľnosti za predpokladu, že platí hypotéza \(H_0\).
   Kritická oblasť \(K_{\alpha}\) je:

   
   
   • \((\chi^2_{1-\alpha,\,n-1}\, ;\infty ) \) pre \(H_1: \sigma^2\gt \sigma^2_0\)
   
   
   • \((0\ ; \chi^2_{\alpha,\,n-1})\) pre \(H_1: \sigma^2\lt \sigma^2_0\)
   
   
   • \((0\ ; \chi^2_{\alpha/2,\,n-1}\ ) \cup (\chi^2_{1-\alpha/2,\,n-1} \ ; \infty) \) pre \(H_1: \sigma^2\not= \sigma^2_0\),
     
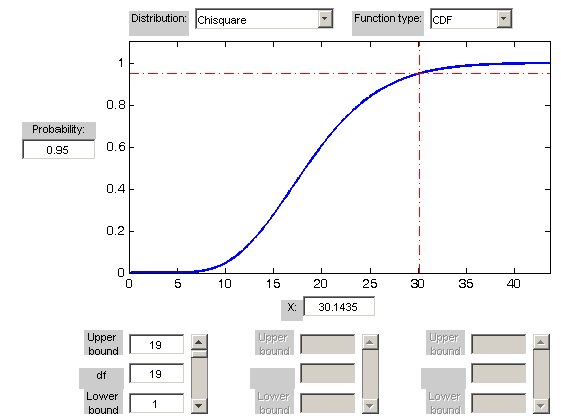
     kde \(\chi^2_{\beta,\,n-1}\) je \(\beta\)-kvantil \(\chi^2\)-rozdelenia s \(\gamma=n-1\) stupňami voľnosti.

   Príklad:
   Presnosť nastavenia automatického obrábacieho stroja je charakterizovaná smerodajnou odchýlkou dĺžky súčiastok. Ak je táto hodnota väčšia ako \(\sqrt{20}\) mm, automat treba znova nastaviť. Meranie kontrolných súčiastok dalo tieto výsledky v milimetroch: 792, 803, 790, 804, 801, 803, 798, 799, 806, 797, 802, 796, 802, 801, 798, 799, 806, 809, 797, 803. Posúďte či treba urobiť nové nastavenie, ak použijeme hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.

   Riešenie:

   1. Použijeme jednovýberový \(\chi^2 \)-test zhody rozptylu \(\sigma^2\) so známou konštantou \(\sigma^2_0\). Budeme testovať nulovú hypotézu \(H_0: \sigma^2=20\) proti pravostrannej alternatívnej hypotéze \(H_1: \sigma^2\gt20\), kde známa konštanta je \(\sigma^2_0=20\).
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Z hodnôt náhodného výberu vyčíslime hodnotu testovacej charakteristiky \[\chi^2 =\dfrac{n-1}{ \sigma^2_{0}\ }\cdot s^2.\] Do daného vzorca dosadíme \(n=20\); \(\sigma^2_0=20\); \(s^2=\frac{1}{n-1}\sum\limits_{i=1}^{n} (x_i-\bar{x})^2=21{,}6947\); kde \(\bar{x}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i=800{,}3000\).
      Po vyčíslení kalkulačkou dostaneme výsledok \(\chi^2=20{,}6100\).
      
      Použitie MATLABu:
      x=[792,803,790,804,801,803,798,799,806,797,802,796,802,801,798,799,806,809,797,803];
      n=length(x),v=var(x),chi2=(n-1)*v/20
      
      
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(\chi^2\notin\)\(K_{\alpha}\). Pre kritickú oblasť \(K_{\alpha}\) v tomto prípade platí \(K_{\alpha}=(\chi^2 _{1-\alpha,\,n-1} \ ; \infty) \).
      Na určenie kritickej oblasti použijeme kvantil \(\chi^2 \) rozdelenia \(\chi^2_{1-\alpha,\,n-1}=\chi^2_{0{,}95;19}=30{,}144\)\(\,\)(z tabuliek). Kritická oblasť je teda \(K_{\alpha}=(30{,}144 \ ; \infty) \).
      
      Výpočet príslušného kvantilu pomocou MATLABu:
      q=chi2inv(.95,19)
      Na vyhľadanie kvantilu môžeme využiť aj prostredie disttool. Odošleme príkaz:
      disttool
      V grafickom okne si nastavíme potrebné parametre (pozrite si to na nasledujúcom obrázku):
      
   
   
   5. Pretože \(\chi^2\notin\)\(K_{\alpha}\), hypotézu \(H_0\) nezamietame, t.j. netreba robiť nové nastavenie.
   
   

   
   Teraz ukážeme ďalší spôsob riešenia tejto úlohy pomocou MATLABu, a to aplikáciou príkazu [h,p,ci,stats]=vartest(x,v,alpha,tail).
   [h,p,ci,stats]=vartest(x,20,0.05,'right')
   Výsledok z MATLABu:
   h = 0
   p = 0.3587
   ci = 13.6746 Inf
   stats =
   chisqstat: 20.6100, df: 19
   
   Interpretujme získané výsledky z MATLABu. Výsledok h = 0 znamená, že hypotézu \(H_0\) nezamietame na hladine významnosti \(\alpha =0{,}05\).
   To isté rozhodnutie je možné uskutočniť aj na základe \(p\)-hodnoty, pretože \(p={0{,}3587}\gt\alpha =0{,}05\).
   V premennej ci je výsledok pre 95 %-ný pravostranný interval spoľahlivosti pre rozptyl \(\sigma^2\).
   V premennej stats sú dva výsledky, a to hodnota testovacej charakteristiky chisqstat a df, čo znamená počet stupňov voľnosti použitej testovacej štatistiky.

   Zobraziť riešenieSkryť riešenie
4. Dvojvýberový \(F\)-test zhody dvoch rozptylov \(\sigma^2_1\) a \(\sigma^2_2\)
   
   Predpokladáme, že náhodná premenná \(X_1\) jedného základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_1\) a \(\sigma_1\), t. j. \(X_1\sim norm(\mu_1,\,\sigma_1)\) a náhodná premenná \(X_2\) druhého základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_2\) a \(\sigma_2\), t. j. \(X_2\sim norm(\mu_2,\,\sigma_2)\).
   Nech sú dané dva nezávislé výbery z oboch základných súborov s rozsahmi \(n_1\) a \(n_2\), ktorých výberové rozptyly sú \(s^2_1\) a \(s^2_2\).
   Nulová hypotéza bude mať tvar \(H_0: \sigma_1^2=\sigma_2^2\).
   Testovacia charakteristika \(F=\dfrac{s_1^2}{s_2^2}\) má Fisherovo \(F\)-rozdelenie pravdepodobnosti s \(\gamma_1=n_1-1\) a \(\gamma_2=n_2-1\) stupňami voľnosti za predpokladu, že platí hypotéza \(H_0\).
   Kritická oblasť \(K_{\alpha}\) je:

   
   
   • \(\left(F_{1-\alpha,\,\gamma_1,\,\gamma_2}\, ;\infty\right ) \) pre \(H_1: \sigma_1^2\gt\sigma_2^2\)
   
   
   • \((0\ ; F_{\alpha,\,\gamma_1,\,\gamma_2})\) pre \(H_1: \sigma_1^2\lt\sigma_2^2\)
   
   
   • \((0\ ; F_{\alpha/2,\,\gamma_1,\,\gamma_2}) \cup (F_{1-\alpha/2,\,\gamma_1,\,\gamma_2} \ ; \infty) \) pre \(H_1: \sigma_1^2\not=\sigma_2^2\),
     
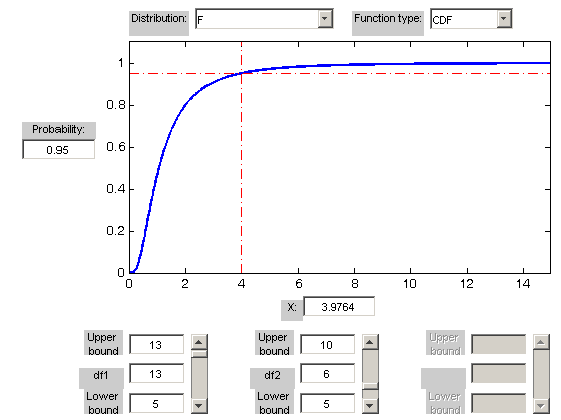
     kde \(F_{\beta,\,\gamma_1,\,\gamma_2}\) je \(\beta\)-kvantil \(F\)-rozdelenia pravdepodobnosti s \(\gamma_1=n_1-1\) a \(\gamma_2=n_2-1\) stupňami voľnosti.

   Poznámka:
   Pre úsporu miesta sa v štandardných štatistických tabuľkách uvádzajú iba niektoré kvantily Fisherovho rozdelenia. Teda ak máme k dispozícii len takýto druh tabuliek, nenájdeniu niektorých kvantilov sa môžeme vyhnúť voľbou poradia premenných \(X_1\) a \(X_2\) tak, aby jednostranná alternatívna hypotéza mala tvar \(H_1: \sigma_1^2\gt\sigma_2^2\), resp. v prípade obojstrannej alternatívnej hypotézy zvolíme indexy \(_1\) a \(_2\) tak, aby platilo \( s_1 \gt s_2\), t. j. \( F \gt 1\). V prípade hľadania kvantilov napr. pomocou MATLABu nemáme žiadne obmedzenie.

   Príklad: Vážením sme získali údaje o presnom množstve automaticky balených výrobkov. Výsledky v gramoch pred nastavením baliaceho automatu sú: 243,2; 244,8; 253,1; 247,5; 251,0; 251,7; 254,0; 252,5; 252,8; 250,1; 247,3; 250,9; 253,2; 252,7. Výsledky v gramoch po nastavení baliaceho automatu sú: 250,4; 250,2; 251,1; 249,3; 249,9; 250,2; 251,1. Na hladine významnosti \(\alpha =0{,}05\) testujte hypotézu \(H_0: \sigma_1^2=\sigma_2^2\) proti \(H_1: \sigma_1^2\gt \sigma_2^2\). Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.

   Riešenie:
   

   1. Použijeme dvojvýberový \(F\)-test zhody dvoch rozptylov. Budeme testovať nulovú hypotézu \(H_0: \sigma_1^2=\sigma_2^2\) proti pravostrannej alternatívnej hypotéze \(H_1: \sigma_1^2\gt \sigma_2^2\), kde \(\sigma^2_1\) a \(\sigma^2_2\) sú rozptyly hmotnosti výrobkov pred a po nastavení baliaceho automatu.
      
      V prípade, že použijeme bežné tabuľky (t. j. nemáme k dispozícii počítač), tak v prípade Fisherovho rozdelenia musíme voliť indexy \(_1\) a \(_2\) tak, aby bola splnená podmienka \( s_1 \gt s_2\). Najskôr teda vhodne očíslujeme výberové súbory. Daná podmienka bude splnená, ak index \(_1\) priradíme súboru pred nastavením a index \(_2\) súboru po nastavení baliaceho automatu, t. j. \(s_{\mathrm{pred}}=s_1=3{,}3640\) a \(s_{\mathrm{po}}=s_2=0{,}6414\).
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Vyčíslime hodnotu testovacej charakteristiky \(F=\dfrac{s_1^2}{s_2^2}=\dfrac{11{,}3165} {0{,}4114} =27{,}5053\).
      
      Aplikácia MATLABu:
      x1=[2432,2448,2531,2475,2510,2517,2540,2525,2528,2501,2473,2509,2532,2527]/10;
      x2=[2504,2502,2511,2493,2499,2502,2511]/10;
      v1=var(x1),v2=var(x2),F=v1/v2
      
      
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(F\notin\)\(K_{\alpha}\).
      Pre kritickú oblasť \(K_{\alpha}\) v tomto prípade platí \(K_{\alpha}=(F_{1-\alpha,\,n_1-1,\,n_2-1} \ ; \infty) \). Na určenie kritickej oblasti použijeme kvantil Fisherovho-Snedecorovovho rozdelenia \(F_{0{,}95;13;6}=3{,}9764\) (z tabuliek). Kritická oblasť je teda \(K_{\alpha}=(3{,}9764 \ ; \infty) \).
      
      Výpočet príslušného kvantilu pomocou MATLABu:
      q=finv(.95,13,6)
      Na vyhľadanie kvantilu môžeme využiť aj prostredie disttool. Odošleme príkaz:
      disttool
      V grafickom okne si nastavíme potrebné parametre (pozrite si to na nasledujúcom obrázku):
      
   5. Pretože \(F\in\) \(K_{\alpha}\), hypotézu \(H_0\) zamietame v prospech alternatívnej hypotézy \(H_1\).
   
   

   
   Znova ukážeme ďalší spôsob riešenia tejto úlohy pomocou MATLABu, a to aplikáciou príkazu [h,p,ci,stats]=vartest2(x,y,alpha,tail).
   [h,p,ci,stats]=vartest2(x1,x2,0.05,'right')
   Výsledok z MATLABu:
   h = 1
   p = 2.8990e-004
   ci = 6.9172 Inf
   stats =
   fstat: 27.5053, df1: 13, df2: 6
   
   Teraz interpretujme získané výsledky z MATLABu. Výsledok h = 1 znamená, že hypotézu \(H_0\) zamietame na hladine významnosti \(\alpha =0{,}05\).
   To isté rozhodnutie je možné prijať aj na základe \(p\)-hodnoty, pretože \(p={2{,}8990\cdot 10^{-4}}\lt\alpha =0{,}05\).
   V premennej ci je pravostranný interval spoľahlivosti pre skutočný podiel rozptylov \(\sigma^2_1\) a \(\sigma^2_2\).
   V premennej stats máme tri výsledky, a to hodnotu testovacej štatistiky fstat, ďalej df1 a df2, čo sú počty stupňov voľnosti použitej testovacej štatistiky.

   Zobraziť riešenieSkryť riešenie
5. Dvojvýberový \(Y\)-test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom poznáme smerodajné odchýlky \(\sigma_1\) a \(\sigma_2\)
   
   Predpokladáme, že náhodná premenná \(X_1\) jedného základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_1\) a \(\sigma_1\), t. j. \(X_1\sim norm(\mu_1,\,\sigma_1)\) a náhodná premenná \(X_2\) druhého základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_2\) a \(\sigma_2\), t. j. \(X_2\sim norm(\mu_2,\,\sigma_2)\), pričom hodnoty smerodajných odchýlok \(\sigma_1\) a \(\sigma_2\) poznáme.
   Nech sú dané dva nezávislé výbery z oboch základných súborov s rozsahmi \(n_1\) a \(n_2\), ktorých výberové priemery sú \(\bar{x}_1\) a \(\bar{x}_2\).
   Nulová hypotéza bude mať tvar \(H_0: \mu_1=\mu_2\).
   Testovacia charakteristika \(Y=\dfrac{\bar{x}_1-\bar{x}_2}{\sqrt{n_2\cdot \sigma_1^2+n_1\cdot \sigma_2^2}}\cdot\sqrt{n_1\cdot n_2}\) má normované normálne rozdelenie pravdepodobnosti za predpokladu, že platí hypotéza \(H_0\).
   Kritická oblasť \(K_{\alpha}\) je:

   
   
   • \((y_{1-\alpha} \ ; \infty) \) pre \(H_1: \mu_1\gt\mu_2\)
   
   
   • \((-\infty\ ; - y_{1-\alpha} ) \) pre \(H_1: \mu_1\lt\mu_2\)
   
   
   • \((-\infty\ ; - y_{1-\alpha/2} ) \cup (y_{1-\alpha/2} \ ; \infty) \) pre \(H_1: \mu_1\not= \mu_2\),
     
     kde \(y_\beta\) je \(\beta\)-kvantil normovaného normálneho rozdelenia pravdepodobnosti.

   Príklad:
   Prístroj meral dobu reakcie na svetelný signál v stotinách sekundy u desiatich náhodne vybraných vodičov z povolania, pričom bol zistený výberový priemer \(\bar{x}_1=34\) a tiež u dvadsiatich nových absolventov autoškoly, kde bol zistený výberový priemer \(\bar{x}_2=42\), pričom poznáme disperzie \(\sigma_1^2=3\) a \(\sigma_2^2=6\). Na hladine významnosti \(\alpha =0{,}05\) uvážte či doba reakcie na svetelný signál závisí od dĺžky praxe vodiča. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.

   Riešenie:
   

   1. Použijeme dvojvýberový \(Y\)-test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom \(\sigma_1\) a \(\sigma_2\) poznáme. Budeme testovať nulovú hypotézu \(H_0: \mu_1=\mu_2\) proti obojstrannej alternatívnej hypotéze \(H_1: \mu_1\not= \mu_2\).
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Vyčíslime hodnotu testovacej charakteristiky \[Y=\dfrac{\bar{x}_1-\bar{x}_2}{ \sqrt{n_2\cdot \sigma_1^2+n_1\cdot \sigma_2^2} } \cdot\sqrt{n_1\cdot n_2}.\] Do daného vzorca dosadíme hodnoty \(n_1=10\); \(n_2=20\); \(\bar{x}_1=34\); \(\bar{x}_2=42\); \(\sigma_1^2=3\); \(\sigma_2^2=6\).
      Dostaneme výsledok \(Y=-10{,}3280\).
   
   
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(Y\notin\)\(K_{\alpha}\).
      Pre kritickú oblasť \(K_{\alpha}\) v tomto prípade platí \(K_{\alpha}= (-\infty\ ; - y_{1-\alpha/2} ) \cup (y_{1-\alpha/2} \ ; \infty) \).
      Na určenie kritickej oblasti použijeme kvantil normovaného normálneho rozdelenia pravdepodobnosti \(y_{1-\alpha/2}=y_{0{,}975}=1{,}9600\) (z tabuliek). Kritická oblasť je teda \(K_{\alpha}=(-\infty\ ; -1{,}96 ) \cup (1{,}96 \ ; \infty) \).
   
   
   5. Pretože \(Y\in\) \(K_{\alpha}\), hypotézu \(H_0\) zamietame v prospech alternatívnej hypotézy \(H_1\).

   Zobraziť riešenieSkryť riešenie
6. Dvojvýberový \(t\)-test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom pre neznáme smerodajné odchýlky \(\sigma_1\) a \(\sigma_2\) platí \(\sigma_1=\sigma_2\)
   
   Predpokladáme, že náhodná premenná \(X_1\) jedného základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_1\) a \(\sigma_1\), t. j. \(X_1\sim norm(\mu_1,\,\sigma_1)\) a náhodná premenná \(X_2\) druhého základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_2\) a \(\sigma_2\), t. j. \(X_2\sim norm(\mu_2,\,\sigma_2)\), pričom hodnoty smerodajných odchýlok \(\sigma_1\) a \(\sigma_2\) nepoznáme, ale predpokladáme \(\sigma_1=\sigma_2\).

   Poznámka: Predpoklad \(\sigma_1=\sigma_2\) je potrebné overiť \(F\)-testom.

   Nech sú dané dva nezávislé výbery z oboch základných súborov s rozsahmi \(n_1\) a \(n_2\), ktorých výberové priemery sú \(\bar{x}_1\), \(\bar{x}_2\) a výberové rozptyly sú \(s^2_1\) a \(s^2_2\).
   Nulová hypotéza bude mať tvar \(H_0: \mu_1=\mu_2\).
   Ak je splnený predpoklad \(\sigma_1=\sigma_2\), použijeme testovaciu charakteristiku \[ t=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{(n_1-1)\cdot s_1^2+(n_2-1)\cdot s_2^2}}\cdot \sqrt{\frac{n_1\cdot n_2\cdot (n_1+n_2-2)}{n_1+n_2}}, \] ktorá má Studentovo \(t\)-rozdelenie pravdepodobnosti s \(\gamma=n_1+n_2-2\) stupňami voľnosti za predpokladu, že platí hypotéza \(H_0\).
   Kritická oblasť \(K_{\alpha}\) je:

   
   
   • \(\left(t_{1-\alpha,\,\gamma}\, ;\infty\right ) \) pre \(H_1: \mu_1\gt\mu_2\)
   
   
   • \((-\infty\ ; - t_{1-\alpha,\,\gamma} ) \) pre \(H_1: \mu_1\lt\mu_2\)
   
   
   • \((-\infty\ ; - t_{1-\alpha/2,\,\gamma} ) \cup (t_{1-\alpha/2,\,\gamma} \ ; \infty) \) pre \(H_1: \mu_1\not= \mu_2\),
     
     kde \(t_{\beta,\,\gamma}\) je \(\beta\)-kvantil Studentovho \(t\)-rozdelenia pravdepodobnosti s \(\gamma=n_1+n_2-2\) stupňami voľnosti.

   Poznámka:
   Ak je \(n_1\gt 30\) a tiež \(n_2\gt 30\), tak môžeme použiť dvojvýberový \(Y\)-test (viď cieľ 5), kde položíme \(\sigma_1\approx s_1\) a \(\sigma_2\approx s_2\).
   Tento postup volíme vtedy, keď máme k dispozícii len klasické tabuľky, pretože pre veľké výberové súbory nie sú tabelované hodnoty kvantilov \(t\)-rozdelenia, t. j. v tomto prípade Studentovo rozdelenie aproximujeme normovaným normálnym rozdelením.

   Príklad:
   Jednou z rozhodujúcich vlastností pre akosť ľanového vlákna je hmotnosť stonky. Čím je stonka ťažšia, tým je vlákno kvalitnejšie. Aby sa preukázal vplyv istej metódy ošetrenia ľanu na akosť vlákna, bolo vykonaných 10 meraní na ošetrenom pozemku: 47,5; 57,7; 47,1; 38,8; 45,2; 49,8; 43,4; 50,8; 41,5; 38,8 a 12 meraní na kontrolnom neošetrenom pozemku: 49,2; 44,1; 44,1; 38,1; 40,9; 32,1; 36,8; 39,5; 67,2; 41,8; 46,9; 42,3. Za predpokladu normálneho rozdelenia hmotnosti stonky testujte hypotézu \(H_0: \mu_1=\mu_2\) proti hypotéze \(H_1: \mu_1\gt \mu_2\) na hladine významnosti \(\alpha = 0{,}05\).

   Riešenie:
   

   1. Použijeme dvojvýberový \(t\)-test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom \(\sigma_1\) a \(\sigma_2\) nepoznáme. Budeme testovať nulovú hypotézu \(H_0: \mu_1=\mu_2\) proti pravostrannej alternatívnej hypotéze \(H_1: \mu_1\gt \mu_2\), kde \(\mu_1\) a \(\mu_2\) sú stredné hodnoty hmotnosti stonky u jednotlivých metód. Predpokladáme normálne rozdelenie oboch výberových súborov.
      
      Predpoklad \(\sigma_1 =\sigma_2\) overíme \(F\)-testom. Budeme testovať nulovú hypotézu \(H_0: \sigma_1^2=\sigma_2^2\) proti obojstrannej alternatívnej hypotéze \(H_1: \sigma_1^2\ne \sigma_2^2\) na hladine významnosti \(\alpha =0{,}05\). Výpočet budeme realizovať v prostredí MATLABu. Ďalší spôsob riešenia je uvedený v riešenej úlohe časti 4, nebudeme ho opäť uvádzať.
      
      Aplikácia MATLABu:
      x1=[475,577,471,388,452,498,434,508,415,388]/10;
      x2=[492,441,441,381,409,321,368,395,672,418,469,423]/10;
      [h,p]=vartest2(x1,x2,0.05,'both')
      Výsledok z MATLABu:
      h = 0
      p = 0.2421
      
      Oba výsledky znamenajú, že nulovú hypotézu \(H_0: \sigma_1^2=\sigma_2^2\) na hladine významnosti \(\alpha =0{,}05\) nezamietame.
      
      Teraz pokračujme ďalej v teste stredných hodnôt:
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Vyčíslime hodnotu testovacej charakteristiky \[ t=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{(n_1-1)\cdot s_1^2+(n_2-1)\cdot s_2^2}}\cdot \sqrt{\frac{n_1\cdot n_2\cdot (n_1+n_2-2)}{n_1+n_2}}. \] Do daného vzorca dosadíme hodnoty \(n_1=10\); \(n_2=12\); \(\bar{x}_1=46{,}0600\); \(\bar{x}_2=43{,}5833\); \(s_1^2=34{,}3471\); \(s_2^2=76{,}1342\).
      Dostaneme výsledok \(t=0{,}7639\).
      
      Aplikácia MATLABu:
      n1=10;n2=12;m1=mean(x1),m2=mean(x2),v1=var(x1),v2=var(x2)
      t=(m1-m2)*sqrt(n1*n2*(n1+n2-2)/(n1+n2)/((n1-1)*v1+(n2-1)*v2))
      
   
   
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(t\notin\)\(K_{\alpha}\), pričom kritická oblasť je v tomto prípade \(K_{\alpha}=(t_{1-\alpha,\,n_1+n_2-2} \ ; \infty) \).
      Na určenie kritickej oblasti použijeme kvantil Studentovho \(t\)-rozdelenia \(t_{1-\alpha,\,n_1+n_2-2}=t_{0{,}95;20}=1{,}7247\) (z tabuliek). Kritická oblasť je teda \(K_{\alpha}\)=\(\left(1{,}7247\, ;\infty\right ) \).
      
      Výpočet príslušného kvantilu pomocou MATLABu:
      q=tinv(.95,20)
      
      
   5. Pretože \(t\notin\) \(K_{\alpha}\), hypotézu \(H_0\) nezamietame.
   
   

   
   Znova ukážeme ďalší spôsob riešenia tejto úlohy pomocou MATLABu, a to aplikáciou príkazu [h,p,ci,stats]=ttest2(x,y,alpha,tail).
   [h,p,ci,stats]=ttest2(x1,x2,.05,'right')
   Výsledok z MATLABu:
   h = 0
   p = 0.2269
   ci = -3.1149 Inf
   stats =
   tstat: 0.7639, df: 20
   
   Teraz interpretujme získané výsledky z MATLABu. Výsledok h = 0 znamená, že hypotézu \(H_0\) nezamietame na hladine významnosti \(\alpha =0{,}05\).
   To isté rozhodnutie je možné uskutočniť aj na základe \(p\)-hodnoty, pretože \(p={0{,}2269}\gt\alpha =0{,}05\).
   V premennej ci je pravostranný interval spoľahlivosti pre skutočný rozdiel stredných hodnôt \(\mu_1\) a \(\mu_2\).
   V premennej stats máme dva výsledky, a to hodnotu testovacej charakteristiky tstat a ešte df, čo znamená počet stupňov voľnosti použitej testovacej charakteristiky.

   Zobraziť riešenieSkryť riešenie
7. Dvojvýberový \(t\)-test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom pre neznáme smerodajné odchýlky \(\sigma_1\) a \(\sigma_2\) platí \(\sigma_1\not=\sigma_2\)
   
   Predpokladáme, že náhodná premenná \(X_1\) jedného základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_1\) a \(\sigma_1\), t. j. \(X_1\sim norm(\mu_1,\,\sigma_1)\) a náhodná premenná \(X_2\) druhého základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_2\) a \(\sigma_2\), t. j. \(X_2\sim norm(\mu_2,\,\sigma_2)\), pričom hodnoty smerodajných odchýlok \(\sigma_1\) a \(\sigma_2\) nepoznáme, ale predpokladáme \(\sigma_1\not=\sigma_2\).

   Poznámka: Predpoklad \(\sigma_1\not=\sigma_2\) je potrebné overiť \(F\)-testom.

   Nech sú dané dva nezávislé výbery z oboch základných súborov s rozsahmi \(n_1\) a \(n_2\), ktorých výberové priemery sú \(\bar{x}_1\), \(\bar{x}_2\) a výberové rozptyly sú \(s^2_1\) a \(s^2_2\).
   Nulová hypotéza bude mať tvar \(H_0: \mu_1=\mu_2\).
   Ak nie je splnený predpoklad \(\sigma_1=\sigma_2\), použijeme tzv. Welchov test a testovaciu charakteristiku \[t=\dfrac{\bar{x}_1-\bar{x}_2}{\sqrt{ \dfrac{s_1^2}{n_1} +\dfrac{s_2^2}{n_2} }},\] ktorá má pri platnosti nulovej hypotézy \(t\)-rozdelenie pravdepodobnosti s \(\gamma\) stupňami voľnosti, pričom pre počet stupňov voľnosti platí vzťah \[ \gamma =\dfrac{ \bigg ( \dfrac{s_1^2}{n_1} +\dfrac{s_2^2}{n_2} \bigg ) ^2 } { \dfrac{ \bigg ( \dfrac{ s_1^2 }{n_1}\bigg ) ^2 }{n_1-1} +\dfrac{ \bigg ( \dfrac{s_2^2}{n_2} \bigg ) ^2 } {n_2-1} } .\]

   Poznámka: Počet stupňov voľnosti získame zaokrúhlením uvedeného výrazu.

   Kritická oblasť \(K_{\alpha}\) je:

   
   
   • \(\left(t_{1-\alpha,\,\gamma}\, ;\infty\right ) \) pre \(H_1: \mu_1\gt\mu_2\)
   
   
   • \((-\infty\ ; - t_{1-\alpha,\,\gamma} ) \) pre \(H_1: \mu_1\lt\mu_2\)
   
   
   • \((-\infty\ ; - t_{1-\alpha/2,\,\gamma} ) \cup (t_{1-\alpha/2,\,\gamma} \ ; \infty) \) pre \(H_1: \mu_1\not= \mu_2\),
     
     kde \(t_{\beta,\,\gamma}\) je \(\beta\)-kvantil Studentovho \(t\)-rozdelenia pravdepodobnosti s \(\gamma\) stupňami voľnosti.

   Príklad:
   Vážením sme získali údaje o hmotnosti automaticky balených výrobkov. Výsledky v gramoch pred nastavením baliaceho automatu sú: 243,2; 244,8; 253,1; 247,5; 251,0; 251,7; 254,0; 252,5; 252,8; 250,1; 247,3; 250,9; 253,2; 252,7. Výsledky v gramoch po nastavení baliaceho automatu sú: 250,4; 250,2; 251,1; 249,3; 249,9; 250,2; 251,1. Na hladine významnosti \(\alpha =0{,}05\) zistite či sa stredná hodnota hmotnosti nastavením automatu nezmenila. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
   

   Riešenie:
   

   1. Použijeme dvojvýberový \(t\)-test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\), pričom \(\sigma_1\) a \(\sigma_2\) nepoznáme. Budeme testovať nulovú hypotézu \(H_0: \mu_1=\mu_2\) proti obojstrannej alternatívnej hypotéze \(H_1: \mu_1\not= \mu_2\). Predpokladáme normálne rozdelenie oboch výberových súborov.
      
      Predpoklad \(\sigma_1\not=\sigma_2\) overíme \(F\)-testom. Budeme testovať nulovú hypotézu \(H_0: \sigma_1^2=\sigma_2^2\) proti obojstrannej alternatívnej hypotéze \(H_1: \sigma_1^2\ne \sigma_2^2\) na hladine významnosti \(\alpha =0{,}05\). Výpočet budeme realizovať v prostredí MATLABu. Ďalší spôsob riešenia je uvedený v riešenej úlohe 4, nebudeme ho opäť uvádzať.
      
      Aplikácia MATLABu:
      x1=[2432,2448,2531,2475,2510,2517,2540,2525,2528,2501,2473,2509,2532,2527]/10;
      x2=[2504,2502,2511,2493,2499,2502,2511]/10;
      [h,p]=vartest2(x1,x2,0.05,'both')
      Výsledok z MATLABu:
      h = 1
      p = 5.7979e-004
      
      Oba výsledky znamenajú, že nulovú hypotézu \(H_0: \sigma_1^2=\sigma_2^2\) na hladine významnosti \(\alpha =0{,}05\) zamietame.
      
      Teraz pokračujme ďalej v teste stredných hodnôt (Welchov test):
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Vyčíslime hodnotu testovacej charakteristiky \[t=\dfrac{\bar{x}_1-\bar{x}_2}{\sqrt{ \dfrac{s_1^2}{n_1} +\dfrac{s_2^2}{n_2} }}.\] Do daného vzorca dosadíme hodnoty \(n_1=14\); \(n_2=7\); \(\bar{x}_1=250{,}3429\); \(\bar{x}_2=250{,}3143\); \(s_1^2=11{,}3165\); \(s_2^2=0{,}4114\).
      Dostaneme výsledok \(t=0{,}0307\).
      
      Aplikácia MATLABu:
      n1=14;n2=7;m1=mean(x1),m2=mean(x2),v1=var(x1),v2=var(x2)
      t=(m1-m2)/sqrt(v1/n1+v2/n2)
      
      
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(t\notin\)\(K_{\alpha}\). Kritická oblasť je v tomto prípade \(K_{\alpha}= (-\infty\ ; - t_{1-\alpha/2,\,\gamma} ) \cup (t_{1-\alpha/2,\,\gamma} \ ; \infty) \).
      Na určenie kritickej oblasti použijeme kvantil Studentovho \(t\)-rozdelenia \(t_{1-\alpha/2,\,\gamma}\). Pre počet stupňov voľnosti \(\gamma\) platí vzťah: \[ \gamma =\dfrac{ \bigg ( \dfrac{s_1^2}{n_1} +\dfrac{s_2^2}{n_2} \bigg ) ^2 } { \dfrac{ \bigg ( \dfrac{ s_1^2 }{n_1}\bigg ) ^2 }{n_1-1} +\dfrac{ \bigg ( \dfrac{s_2^2}{n_2} \bigg ) ^2 } {n_2-1} } .\] Po vyčíslení pomocou kalkulačky dostaneme výsledok \(\gamma=14{,}7898\approx 15\).
      Použitím štatistických tabuliek máme približný výsledok \(t_{1-\alpha/2,\, \gamma}=t_{0{,}975;15}=2{,}1314\).
      
      Výpočet pomocou MATLABu:
      gama=(v1/n1+v2/n2)^2/((v1/n1)^2/(n1-1)+(v2/n2)^2/(n2-1)),q=tinv(.975,gama)
      Výsledok z MATLABu:
      gama = 14.7898
      q = 2.1341
      
      
   5. Pretože \(t=0{,}0307\notin\) \(K_{\alpha}=(-\infty\ ; -2{,}1341 ) \cup (2{,}1341 \ ; \infty) \), hypotézu \(H_0\) nezamietame.
   
   

   
   Znova ukážeme ďalší spôsob riešenia tejto úlohy pomocou MATLABu, a to aplikáciou príkazu [h,p,ci,stats]=ttest2(x,y,alpha,tail,unequal).
   [h,p,ci,stats]=ttest2(x1,x2,0.05,'both','unequal')
   Výsledok z MATLABu:
   h = 0
   p = 0.9759
   ci = -1.9587 2.0158
   stats =
   tstat: 0.0307, df: 14.7898
   
   Interpretácia výsledkov je analogická ako pri dvojvýberovom \(t\)-teste stredných hodnôt pri splnenom predpoklade \(\sigma_1 =\sigma_2\).

   Zobraziť riešenieSkryť riešenie
8. Párový \(t\)-test zhody dvoch stredných hodnôt \(\mu_1\) a \(\mu_2\)
   
   Predpokladáme, že náhodná premenná \(X_1\) jedného základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_1\) a \(\sigma_1\), t. j. \(X_1\sim norm(\mu_1,\,\sigma_1)\) a náhodná premenná \(X_2\) druhého základného súboru má normálne rozdelenie pravdepodobnosti s parametrami \(\mu_2\) a \(\sigma_2\), t. j. \(X_2\sim norm(\mu_2,\,\sigma_2)\), pričom hodnoty smerodajných odchýlok \(\sigma_1\) a \(\sigma_2\) nepoznáme, ale predpokladáme \(\sigma_1=\sigma_2=\sigma\).
   Ďalej predpokladáme, že máme dva spárované závislé výbery \(x_{1,\,1},\,x_{1,\,2},\,\dots ,\,x_{1,\,n}\) a \(x_{2,\,1},\,x_{2,\,2},\,\dots ,\,x_{2,\,n}\) rovnakého rozsahu \(n\). To je situácia, ktorá nastane napr. vtedy, ak meriame objekt dvakrát (pred pokusom a po ňom) a chceme zistiť či mal pokus nejaký vplyv na meraný objekt.
   Z predpokladu normality dvojrozmerného rozdelenia vyplýva, že rozdiel náhodných veličín \(X_1\), \(X_2\), teda náhodná veličina \(D=X_1-X_2\) má normálne rozdelenie so strednou hodnotou \(\mu_d=\mu_1-\mu_2\).
   
   Postupujeme tak, že najprv vypočítame rozdiely \[d_i=x_{1,\,i}-x_{2,\,i}\] medzi párovými hodnotami, pre \(i=1,\,2,\,\dots,\,n\). Na vopred zvolenej hladine významnosti \(\alpha\) môžeme namiesto hypotézy \(H_0: \mu_1=\mu_2\) ekvivalentne testovať nulovú hypotézu \(H_0: \mu_d=0\) a pre túto použiť jednovýberový \(t\)-test strednej hodnoty (viď cieľ 2).
   Alternatívne hypotézy sú potom \(H_1: \mu_d\gt0\), \(H_1: \mu_d\lt0\) a \(H_1: \mu_d\not=0\).

   Poznámka:
   Aj keď bol párový \(t\)-test odvodený pre závislé výbery, nie je hrubou chybou jeho použitie aj pre nezávislé výbery s rovnakými rozsahmi, teda v situácii, keď by sa mal použiť dvojvýberový \(t\)-test. Ako sa uvádza v literatúre, dôjde len k menej efektívnemu spracovaniu informácie obsiahnutej vo výberových dátach.

   Príklad:
   V nasledujúcej tabuľke sú počty získaných bodov desiatich študentov z praktickej a teoretickej časti skúšky: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{Praktická\,časť}\a 28 \a 35 \a 32\a 15 \a 35\a 24 \a 29\a 19\a 21\a 12 \\ \hline \mathrm{Teoretická\,časť}\a 25 \a 35 \a 30 \a 11 \a 32 \a 28 \a 28\a 25\a 22 \a 11 \\ \hline \end{array} \] Na porovnanie týchto výsledkov aplikujte vhodný test. Použite hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normalitu rozdelenia výberových súborov.

   Riešenie:
   

   1. Dvojice údajov pre toho istého študenta tvoria páry závislých pozorovaní. Pre test hypotézy, že medzi výsledkami praktickej a teoretickej časti skúšky nie je štatisticky významný rozdiel teda použijeme párový \(t\)-test.
      Testujeme nulovú hypotézu \(H_0: \mu_d=0\) proti obojstrannej alternatívnej hypotéze \(H_1: \mu_d\not=0\). Predpokladáme normálne rozdelenie oboch výberových súborov.
      
      Platnosť predpokladu \(\sigma_1=\sigma_2\) skontrolujeme v prostredí MATLABu:
      x1=[28,35,32,15,35,24,29,19,21,12];x2=[25,35,30,11,32,28,28,25,22,11];
      h=vartest2(x1,x2,0.05,'both')
      Výsledok z MATLABu:
      h = 0
      
      Teda predpoklad o rovnosti smerodajných odchýlok je splnený.
      
      Teraz pokračujme ďalej v teste stredných hodnôt:
   
   
   2. Použijeme hladinu významnosti \(\alpha =0{,}05\).
   
   
   3. Najprv vypočítame diferencie \(d_i\): \(3\,,0\,,2\,,4\,,3\,,-4\,,1\,,-6\,,-1\,,1\).
      Potom vyčíslime hodnotu testovacej charakteristiky \(t=\dfrac{\bar{x}_d}{s_d}\cdot\sqrt{n}\) z hodnôt náhodného výberu.
      Do vzorca dosadíme hodnoty \(n=10\); \(\bar{x}_d=\frac{1}{n}\sum\limits_{i=1}^{n} d_i=\bar{x}_1-\bar{x}_2=0{,}3000\); \(s_d\ =\sqrt{ \frac{1}{n-1} \sum\limits_{i=1}^{n} (d_i-\bar{x}_d)^2\ }=3{,}1990\).
      Po vyčíslení kalkulačkou dostaneme výsledok \(t=0{,}2966\).
      
      Použitie MATLABu:
      d=x1-x2,m=mean(d),s=std(d),t=m/s*sqrt(10)
      
      
   4. Hypotézu \(H_0\) nezamietame, keď bude platiť \(t\notin\)\(K_{\alpha}\).
      Pre kritickú oblasť v tomto prípade platí \(K_{\alpha}= (-\infty\ ; - t_{1-\alpha/2,\,n-1} ) \cup (t_{1-\alpha/2,\,n-1} \ ; \infty) \). Na určenie kritickej oblsti použijeme kvantil Studentovho rozdelenia \(t_{1-\alpha/2,\,n-1}=t_{0{,}975;9}=2{,}2622\) (z tabuliek). Kritická oblasť je teda \(K_{\alpha}=(-\infty\ ; -2{,}2622 ) \cup (2{,}2622 \ ; \infty) \).
      
      Výpočet príslušného kvantilu pomocou MATLABu:
      q=tinv(.975,9)
      
   
   
   5. Pretože \(t\notin\) \(K_{\alpha}\), hypotézu \(H_0\) nezamietame. Teda na hladine významnosti \(\alpha =0{,}05\) môžeme tvrdiť, že medzi výsledkami praktickej a teoretickej časti uvedenej skúšky nie je štatisticky významný rozdiel.
   
   

   
   Uvedieme ešte iný spôsob riešenia tejto úlohy pomocou MATLABu. Pre párový \(t\)-test môžeme použiť M-funkciu ttest (pozrite opäť help ttest, ktorá sa používala aj pre jednovýberový \(t\)-test. Význam vstupných a výstupných argumentov je zrejme už pozornému čitateľovi jasný.
   [h,p,ci,stats]=ttest(x1,x2,0.05,'both')
   Výsledok z MATLABu:
   h = 0
   p = 0.7735
   ci = -1.9884 2.5884
   stats =
   tstat: 0.2966, df: 9, sd: 3.1990
   
   Ten istý výsledok dostaneme zrejme aj týmto spôsobom:
   [h,p,ci,stats]=ttest(d,0,0.05,'both')
   

   Poznámka: Porovnajte výsledky získané uvedenými spôsobmi riešenia.

   Zobraziť riešenieSkryť riešenie

Zdroje

1. Ostertagová, E.: Aplikovaná štatistika. Equilibria, Košice, 2013, 218 s., ISBN 978-80-8143-067-1.
2. Ostertagová, E.: Pravdepodobnosť a matematická štatistika v príkladoch. Elfa, Košice, 2005, 123 s., ISBN 80-8086-005-X.

Doplňujúce úlohy

Úloha:
Priemerná výška desaťročných chlapcov je 135,3 cm. U 14 chlapcov, ktorí navštevujú športovú školu, boli namerané tieto hodnoty výšky v cm: 136, 130, 151, 127, 133, 136, 139, 139, 141, 147, 139, 142, 140, 138. Na hladine významnosti \(\alpha =0{,}05\) overte hypotézu, že výška chlapcov športovej školy sa štatisticky významne odlišuje od výšky 135,3 cm za predpokladu, že rozptyl výšky desaťročných chlapcov je \(\sigma^2=38{,}26\) [\(\mathrm{cm^2}\)]. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber.
Výsledok:
\(H_0: \mu=135{,}3\); \(H_1: \mu\not=135{,}3\); \(Y=1{,}8925\); \(y_{0{,}975}=1{,}9600\); \(Y\notin\) \(K_{\alpha}=(-\infty\ ; -1{,}96 ) \cup (1{,}96 \ ; \infty) \); hypotézu \(H_0\) nezamietame, t. j. výška chlapcov športovej školy sa štatisticky významne neodlišuje od hodnoty 135,3 cm.
Zobraziť výsledokSkryť výsledok
Úloha:
Systematická chyba meracieho prístroja sa eliminuje jeho nastavením a meraním etalónu, ktorého správnou nameranou hodnotou je \(\mu_0=10\). Nezávislými meraniami za rovnakých podmienok boli získané tieto hodnoty: 10,24; 10,12; 9,91; 10,19; 9,78; 10,14; 9,86; 10,17; 10,05. Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Je možné na hladine významnosti \(\alpha =0{,}05\) vysvetliť odchýlky od hodnoty 10 náhodnými vplyvmi?
Výsledok:
\(H_0: \mu=10\); \(H_1: \mu\not=10\); \(t=0{,}9426\); \(t_{0{,}975;8}=2{,}3060\); \(t\notin\) \(K_{\alpha}=(-\infty\ ; -2{,}3060 ) \cup (2{,}3060 \ ; \infty) \); hypotézu \(H_0\) nezamietame, a teda odchýlky je možné vysvetliť iba náhodnými vplyvmi.
Zobraziť výsledokSkryť výsledok
Úloha:
Podľa informácií výrobcu je variabilita životnosti ním vyrábaných obrazoviek vyjadrená smerodajnou odchýlkou 45 hodín. O životnosti náhodne vybraných 50 obrazoviek vyrobených u tohto výrobcu sú údaje v tabuľke:
\(I_i\)	\(n_i\)
1860 - 1900	1
1900 - 1940	4
1940 - 1980	12
1980 - 2020	14
2020 - 2060	15
2060 - 2100	3
2100 - 2140	1
Predpokladáme normálne rozdelenie základného súboru, z ktorého bol realizovaný náhodný výber. Testom na hladine významnosti \(\alpha =0{,}02\) overte či sa dá prijať predpoklad, že je variabilita životnosti obrazoviek taká, ako tvrdí výrobca alebo taká nie je.
Výsledok: \(H_0: \sigma^2=2025\); \(H_1: \sigma^2\not=2025\); \(\chi^2=57{,}6632\); \(K_{\alpha}= (0\ ; \chi^2_{0{,}01;49}\ ) \cup (\chi^2_{0{,}99;49} \ ; \infty) \);
\(\chi^2\notin\) \(K_{\alpha}=(0\ ; 28{,}9406 ) \cup (74{,}9195 \ ; \infty) \); hypotézu \(H_0\) nezamietame.
Zobraziť výsledokSkryť výsledok
Úloha:
Zisťovalo sa či špeciálny prípravok pridaný do ocele zvyšuje jej pevnosť. Výsledky merania pri vzorkách, kde bol použitý prípravok: 6,2; 5,7; 5,6; 6,0; 6,3; 5,8; 5,7; 6,0; 6,0; 5,8. Výsledky merania pri vzorkách, kde nebol použitý prípravok: 5,6; 5,9; 5,8; 5,9; 5,7; 5,7; 6,0; 5,5; 5,7; 5,5. Na hladine významnosti \(\alpha =0{,}05\) rozhodnite či sa disperzie oboch vzoriek významne líšia. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Výsledok: \(H_0: \sigma_1^2=\sigma_2^2\); \(H_1: \sigma_1^2\not=\sigma_2^2\); \(F=1{,}7969\); \(K_{\alpha}= ( 0\ ; F_{0{,}025;9;9} \ ) \cup (F_{0{,}975;9;9} \ ; \infty) \); \(F\notin\) \(K_{\alpha}=(0\ ; 0{,}2484 ) \cup (4{,}0260 \ ; \infty) \); hypotézu \(H_0\) nezamietame.
Zobraziť výsledokSkryť výsledok
Úloha:
Odberateľ dostáva žiarivky od dvoch dodávateľov A a B. Pri hodnotení kvality žiariviek sa sleduje tiež počet zapojení, ktoré žiarivky vydržia bez poškodenia. Skúšky výrobkov viedli k týmto výsledkom:
Dodávateľ A: 2139, 2041, 1968, 1903, 1952, 1980, 2089, 1915, 2389, 2163, 2072, 1712, 2018, 1792, 1849.
Dodávateľ B: 1947, 1602, 1906, 2031, 2072, 1812, 1942, 2074, 2132.
Na hladine významnosti \(\alpha =0{,}05\) overte hypotézu, že kvalita oboch dodávok je rovnaká. Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Výsledok:
\(H_0: \sigma_1^2=\sigma_2^2\); \(H_1: \sigma_1^2\not=\sigma_2^2\);
\(F=1{,}0288\notin\) \(K_{\alpha}=( 0\ ; F_{0{,}025;14;8} \ ) \cup (F_{0{,}975;14;8} \ ; \infty) \)=\( (0\ ; 0{,}3044 ) \cup (4{,}1297 \ ; \infty) \); hypotézu \(H_0\) nezamietame.

\(H_0: \mu_1=\mu_2\); \(H_0: \mu_1\not=\mu_2\);
\(t=0{,}7559\notin\) \(K_{\alpha}=( -\infty\ ; -t_{0{,}975;22} \ ) \cup (t_{0{,}975;22} \ ; \infty) \)=\( (-\infty\ ; -2{,}0739 ) \cup (2{,}0739 \ ; \infty) \); hypotézu \(H_0\) nezamietame.
Medzi kvalitou oboch dodávok nie je štatisticky významný rozdiel.
Zobraziť výsledokSkryť výsledok
Úloha:
Pri antropologických meraniach obyvateľov Egypta bola okrem iného sledovaná šírka nosa v centimetroch u skupiny mužov vo veku 21 − 50 rokov zo severnej časti krajiny a u skupiny rovnako starých mužov z južnej časti. Výskum viedol k týmto výsledkom:
Sever: 3,6; 4,1; 3,3; 3,4; 3,7; 3,1; 4,0; 4,0; 3,6; 3,0; 3,3; 3,7; 4,3; 3,3; 3,4; 3,4; 3,3; 3,6; 4,0; 3,4; 3,7.
Juh: 4,1; 3,9; 4,0; 3,8; 4,1; 4,2; 3,8; 3,9; 3,8; 3,8; 4,0; 3,7; 3,9; 4,4; 3,7; 3,8; 3,9; 3,9; 4,0; 4,1; 3,8; 4,0; 4,3.
Posúďte významnosť rozdielov vo výsledkoch meraní na hladine významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Výsledok:
\(H_0: \sigma_1^2=\sigma_2^2\); \(H_1: \sigma_1^2\not=\sigma_2^2\);
\(F=3{,}5390\in\) \(K_{\alpha}=( 0\ ; F_{0{,}025;20;22} \ ) \cup (F_{0{,}975;20;22} \ ; \infty) \)=\( (0\ ; 0{,}4109 ) \cup (2{,}3890 \ ; \infty) \); hypotézu \(H_0\) zamietame, a teda pre test stredných hodnôt použijeme Welchov test.

\(H_0: \mu_1=\mu_2\); \(H_0: \mu_1\not=\mu_2\);
\(t=-4{,}4038\in\) \(K_{\alpha}=( -\infty\ ; -t_{0{,}975;30} \ ) \cup (t_{0{,}975;30} \ ; \infty) \)=\( (-\infty\ ; -2{,}0423) \cup (2{,}0423 \ ; \infty) \); hypotézu \(H_0\) zamietame.
Šírky nosov mužov zo severu sa líšia od tých na juhu.
Zobraziť výsledokSkryť výsledok
Úloha:
Stanovenie thiocyanového iónu bolo paralelne realizované metódami A a B na 12 vzorkách s týmito výsledkami:
Metóda A: 0,38; 0,56; 0,45; 0,49; 0,38; 0,41; 0,60; 0,36; 0,26; 0,41; 0,43; 0,40.
Metóda B: 0,39; 0,58; 0,44; 0,52; 0,41; 0,45; 0,59; 0,37; 0,28; 0,42; 0,42; 0,38.
Porovnajte obe metodiky otestovaním výsledkov. Zvoľte hladinu významnosti \(\alpha =0{,}05\). Predpokladáme normálne rozdelenie oboch základných súborov, z ktorých boli realizované náhodné výbery.
Výsledok:
\(H_0: \sigma_1^2=\sigma_2^2\); \(H_1: \sigma_1^2\not=\sigma_2^2\);
\(F=1{,}0392\notin\) \(K_{\alpha}=( 0\ ; F_{0{,}025;11;11} \ ) \cup (F_{0{,}975;11;11} \ ; \infty) \)=\( (0\ ; 0{,}2879 ) \cup (3{,}4737 \ ; \infty) \); hypotézu \(H_0\) nezamietame.

Použijeme párový test stredných hodnôt.
\(H_0: \mu_d=0\); \(H_1: \mu_d\not=0\);
\(t=-1{,}8166\notin\) \(K_{\alpha}=( -\infty\ ; -t_{0{,}975;11} \ ) \cup (t_{0{,}975;11} \ ; \infty) \)=\( (-\infty\ ; -2{,}2010) \cup (2{,}2010 \ ; \infty) \); hypotézu \(H_0\) nezamietame.
Medzi metodikami nie je štatisticky významný rozdiel.
Zobraziť výsledokSkryť výsledok

Doplňujúce zdroje

1. Bakytová, H., Ugron, M.: Príklady zo štatistických metód. Alfa, Bratislava, 1972, 289 s.
2. Buša, J., Pirč, V., Schrötter, Š.: Numerické metódy, pravdepodobnosť a matematická štatistika. Elfa, Košice, 2006, 166 s., ISBN 80-8073-632-4.
3. Daňo, I., Ostertagová, E.: Numerické metódy, pravdepodobnosť a matematická štatistika. Teória, riešené príklady a praktické aplikácie s MATLABom. Equilibria, Košice, 2011, 198 s., ISBN 978-80-89284-74-0.
4. Gavalec, M., Kováčová, N., Ostertagová, E., Skřivánek, J: Pravdepodobnosť a matematická štatistika v počítačovom prostredí MATLABu. Elfa, Košice, 2002, 150 s., ISBN 80-89066-05-4.
5. Markechová, D., Tirpáková, A., Stehlíková, B.: Základy štatistiky pre pedagógov, UKF v Nitre, 2011,205 s., ISBN 978-80-8094.
6. Otipka, P., Šmajstrla, V.: Pravděpodobnost a statistika. TU, Ostrava, 2012, 269 s., ISBN 80-248-1194-4.