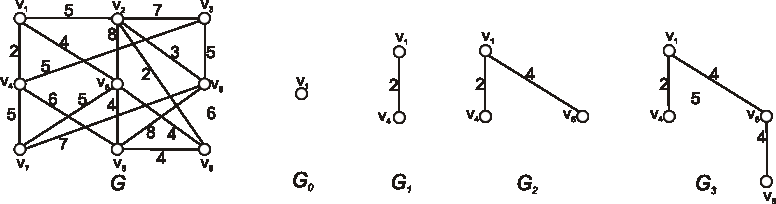01.
Úvod do teórie grafov.
Graf, špeciálne grafy, digrafy
Úlohy:
Úloha:
Aký najväčší počet hrán môže mať graf:
a) s \(20\)-timi vrcholmi,
b) s \(n\) vrcholmi?
a) s \(20\)-timi vrcholmi,
b) s \(n\) vrcholmi?
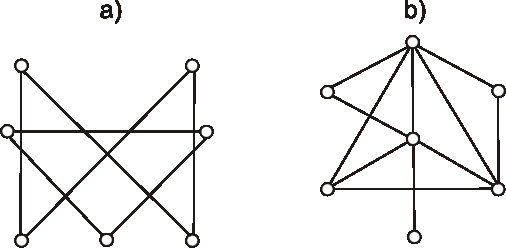
Úloha:
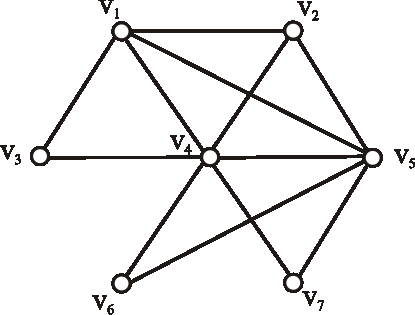
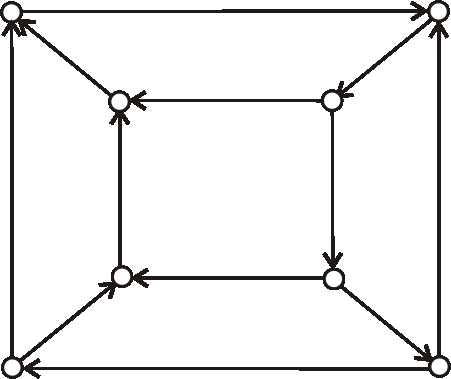
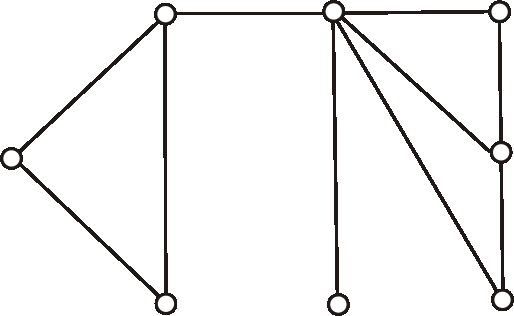
Znázornite graf \(\bar{G}-v\), ak graf \(G\) je daný diagramom:
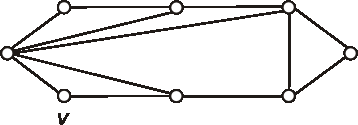

Úloha:
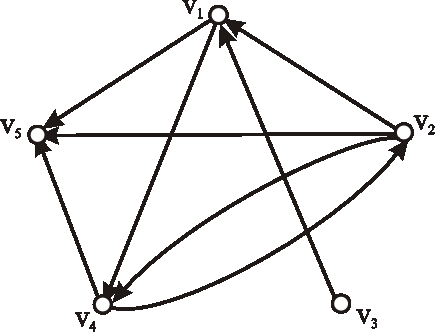
Zadané sú diagramy grafov \(G, H\). Nakreslite diagramy grafov \(\bar{G}\),
\(G \cap H\), \(G \cup H\) a \(G \oplus H\).
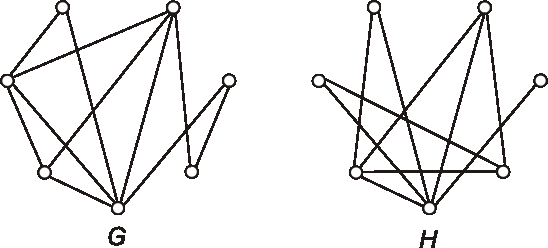

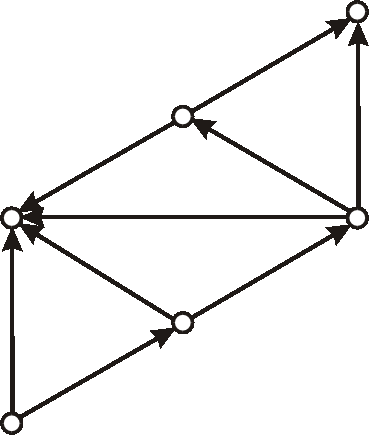
Úloha:
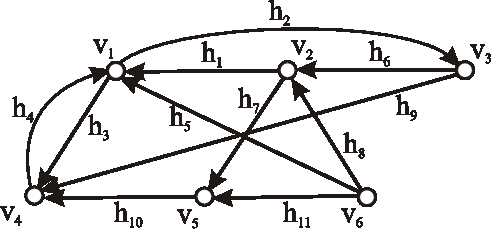
Nájdite všetky podgrafy grafu znázorneného diagramom, ktoré neobsahujú izolované vrcholy.
Koľko z nich je faktorov?
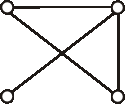

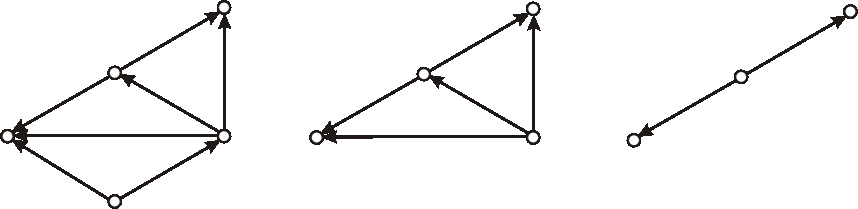
Úloha:
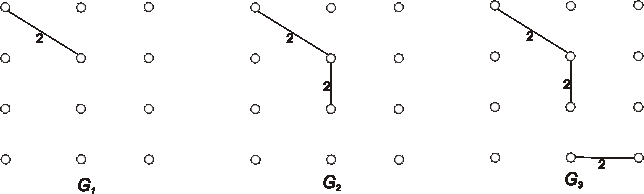
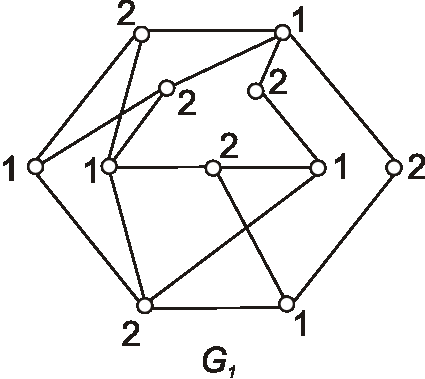
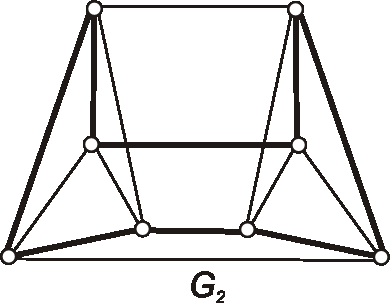
Rozložte dané grafy na dva kvadratické faktory.
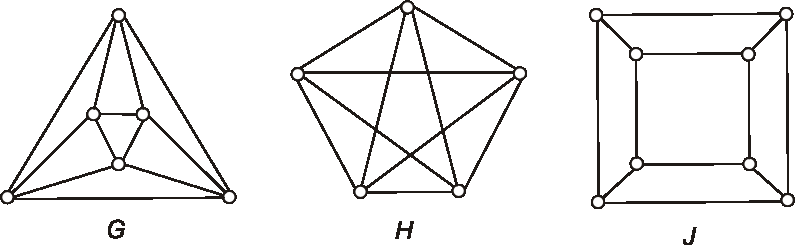

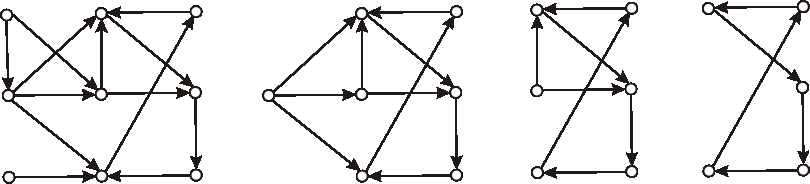
Úloha:
a) Nakreslite diagram ľubovoľného konečného grafu, ktorý má všetky stupne vrcholov rovnaké.
b) Nakreslite diagram ľubovoľného konečného grafu, ktorý má všetky stupne vrcholov rôzne.
a) Nakreslite diagram ľubovoľného konečného grafu, ktorý má všetky stupne vrcholov rovnaké.
b) Nakreslite diagram ľubovoľného konečného grafu, ktorý má všetky stupne vrcholov rôzne.
Úloha:
Zostrojte diagram digrafu, ktorý:
a) bude mať 7 vrcholov a 12 orientovaných hrán,
b) bude mať 7 vrcholov a aspoň jeden vrchol s vnútorným stupňom 6,
c) bude mať 7 vrcholov a bude mať aj prameň aj ústie aj list.
a) bude mať 7 vrcholov a 12 orientovaných hrán,
b) bude mať 7 vrcholov a aspoň jeden vrchol s vnútorným stupňom 6,
c) bude mať 7 vrcholov a bude mať aj prameň aj ústie aj list.
Úloha:
Rozhodnite, ktoré z nasledujúcich tvrdení je a ktoré nie je pravdivé. Zdôvodnite.
a) Priradením orientácie každej hrane v grafe vždy vznikne digraf.
b) Zrušením orientácie každej hrany v digrafe vždy vznikne graf.
c) Súčet všetkých stupňov vrcholov v digrafe je párny.
d) Súčet všetkých vnútorných stupňov vrcholov v digrafe je párny.
e) Maximálny počet hrán v digrafe s \(n\) vrcholmi je \(2n(n-1)\).
a) Priradením orientácie každej hrane v grafe vždy vznikne digraf.
b) Zrušením orientácie každej hrany v digrafe vždy vznikne graf.
c) Súčet všetkých stupňov vrcholov v digrafe je párny.
d) Súčet všetkých vnútorných stupňov vrcholov v digrafe je párny.
e) Maximálny počet hrán v digrafe s \(n\) vrcholmi je \(2n(n-1)\).
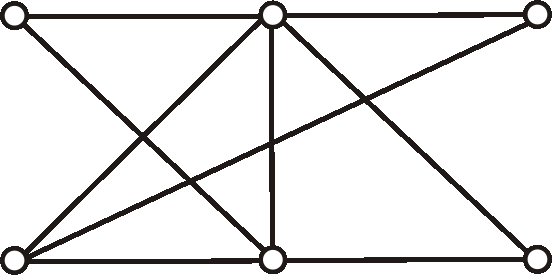
Úloha:
Na obrázku je graf daný diagramom. Koľkými spôsobmi môžeme zvoliť v danom grafe orientáciu, aby výsledný
digraf:
a) bol silne súvislý,
b) nebol silne súvislý.
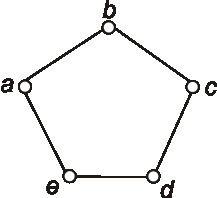
a) bol silne súvislý,
b) nebol silne súvislý.

Úloha:
Aký najmenší počet vrcholov je nutné, aby mal graf, ak má mať:
a) \(19\) hrán,
b) \(n\) hrán?
a) \(19\) hrán,
b) \(n\) hrán?
Úloha:
Nájdite komplementárne grafy ku grafom, ktoré sú dané nasledujúcimi diagramami:
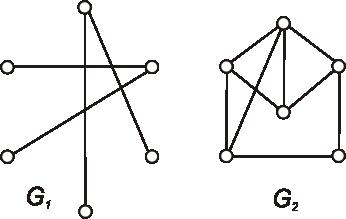

Úloha:
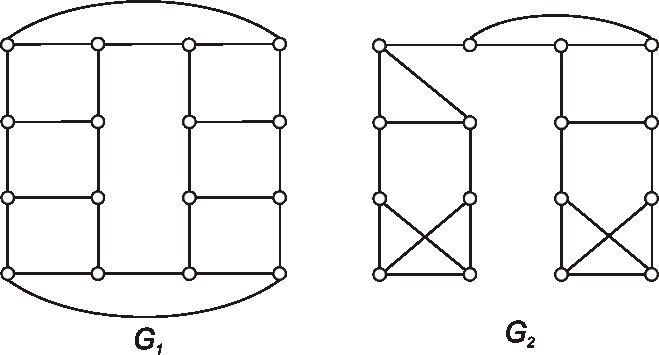
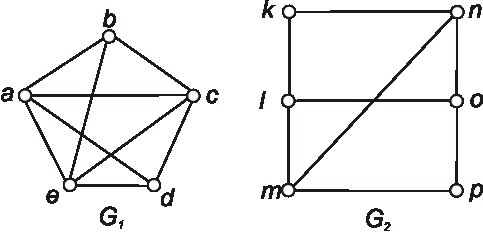
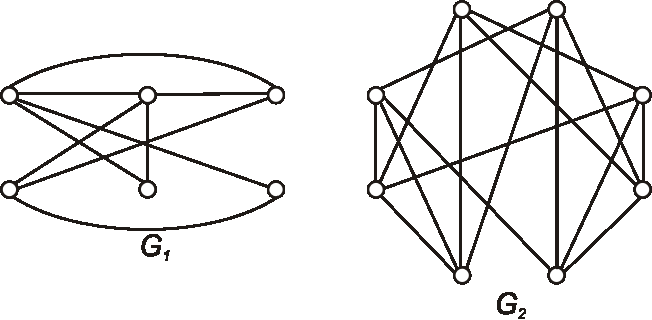
Zadané sú diagramy grafov \(G_1, G_2\). Nakreslite diagramy grafov \(\bar{G_1}\),
\(G_1 \cap G_2\), \(G_1 \cup G_2\), \(G_1 - G_2\) a \(G_1 \oplus G_2\).
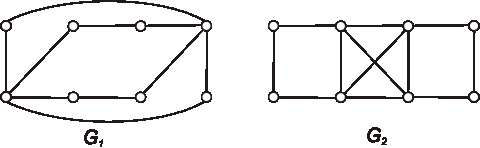

Úloha:
Určte počet faktorov v grafoch, ktoré sú zadané diagramami.

Úloha:
Nakreslite diagram grafu, ktorý:
a) je kubickým grafom.
b) je kompletným grafom.
c) je bipartitným grafom.
d) má počet hrán menší ako počet vrcholov.
e) obsahuje izolovaný vrchol.
f) je tvorený tromi komponentami.
g) má dvakrát toľko hrán, ako vrcholov.
a) je kubickým grafom.
b) je kompletným grafom.
c) je bipartitným grafom.
d) má počet hrán menší ako počet vrcholov.
e) obsahuje izolovaný vrchol.
f) je tvorený tromi komponentami.
g) má dvakrát toľko hrán, ako vrcholov.
Úloha:
Určte počet faktorov v grafoch, ktoré sú zadané diagramami.


Úloha:
Nakreslite diagramy komplementov k digrafom na obrázku:
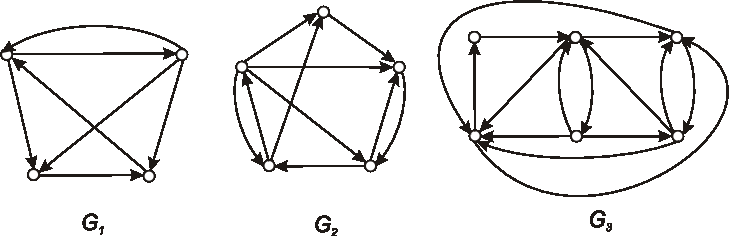

Úloha:
Nasledujúcimi diagramami máme daných šesť digrafov.
 O každom jednom
rozhodnite, ktoré z nasledúcich tvrdení pre neho platí:
O každom jednom
rozhodnite, ktoré z nasledúcich tvrdení pre neho platí:
a) Odstránením orientácie z neho dostaneme graf.
b) Súčet vnútorných stupňov sa rovná súčtu vonkajších stupňov vrcholov.
c) Obsahuje list.
d) Má aspoň jeden prameň.
e) Je silne súvislý.
f) Je súvislý.

a) Odstránením orientácie z neho dostaneme graf.
b) Súčet vnútorných stupňov sa rovná súčtu vonkajších stupňov vrcholov.
c) Obsahuje list.
d) Má aspoň jeden prameň.
e) Je silne súvislý.
f) Je súvislý.
02. Vzdialenosti v grafe, stromy, kostry
Úlohy:
- 6, 5, 4, 4, 4, 3, 2, 1
- 8, 5, 3, 3, 3, 3, 2, 1
- 5, 4, 4, 3, 3, 2, 2, 1
Úloha:
Zistite, či dané postupnosti sú grafové. Zdôvodnite.
Úloha:
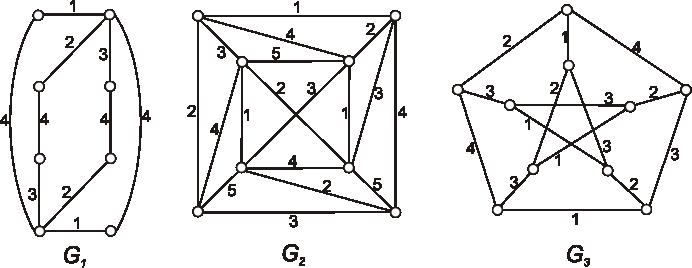
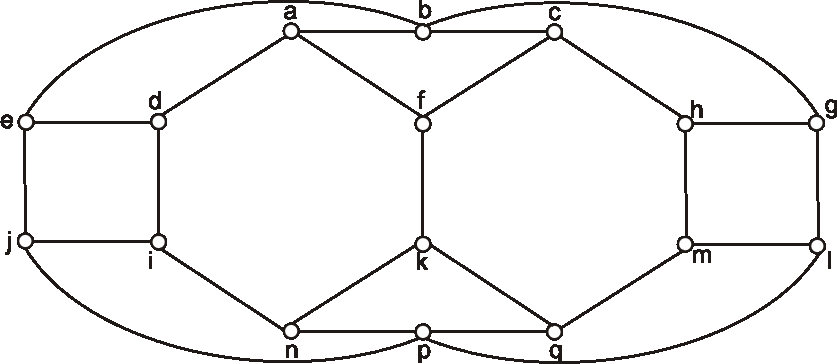
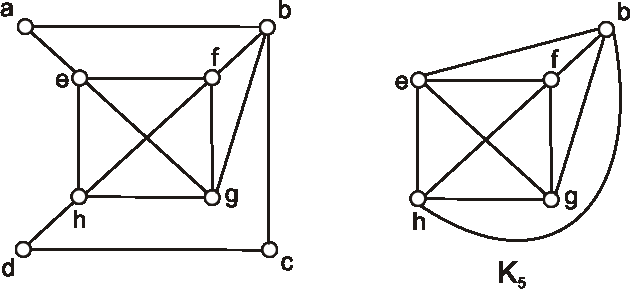
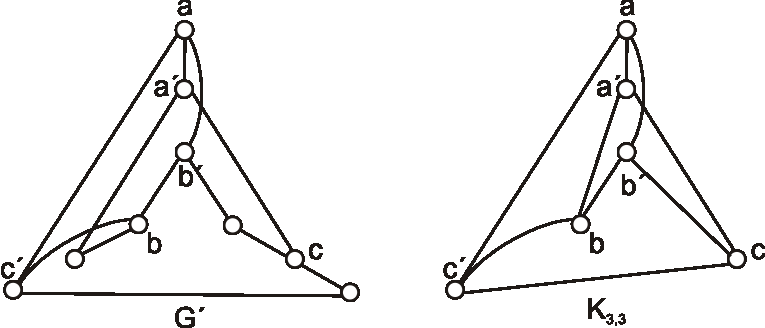
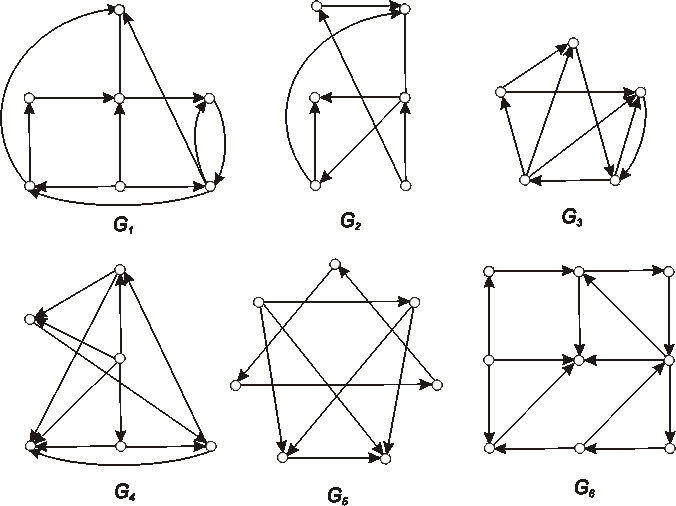
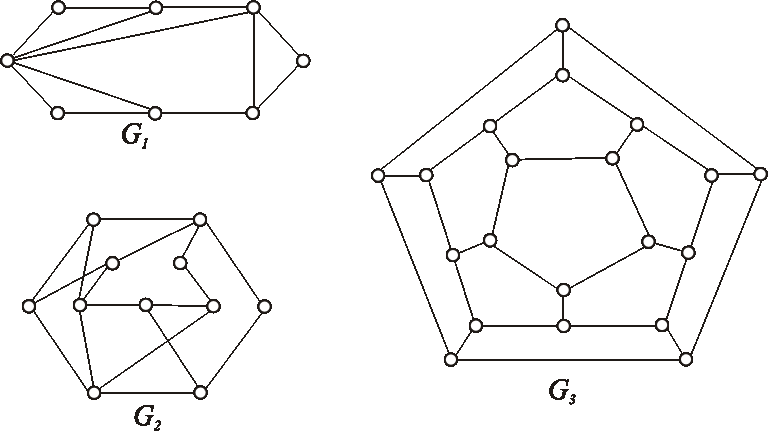
Zistite, ktoré z diagramov znázornených na obrázku, reprezentujú izomorfné grafy?
Označte vrcholy a nájdite izomorfizmus, alebo zdôvodnite, prečo nie sú izomorfné.

Úloha:
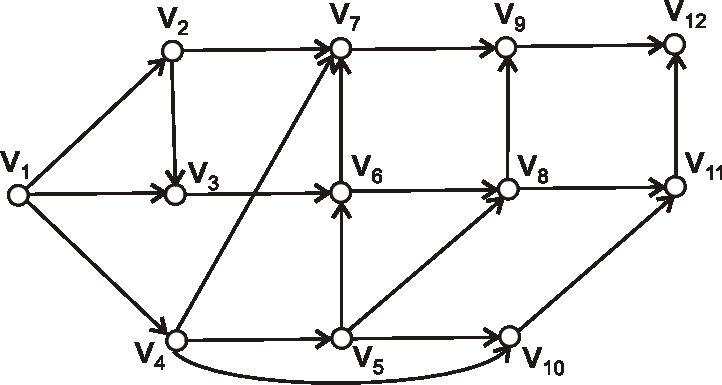
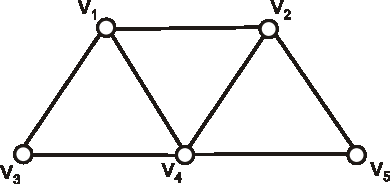
V grafe G danom nasledujúcim diagramom nájdite všetky vrcholy, ktorých vzdialenosť
od vrcholu \(v_1\) je tri.
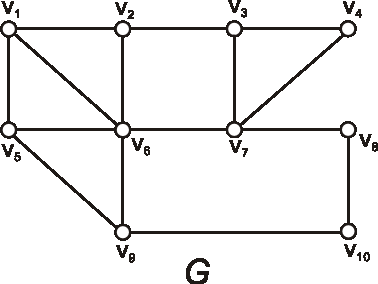

Úloha:
Určte excentricity všetkých vrcholov, polomer, priemer a stred
grafu \(G\) z predchádzajúceho príkladu.
Úloha:
Aký je súčet stupňov vrcholov v strome s 9 vrcholmi? Aký je súčet stupňov vrcholov,
ak počet vrcholov je \(n\)?
Úloha:
Nájdite polomer, priemer a stred stromu, ktorého diagram je na obrázku:
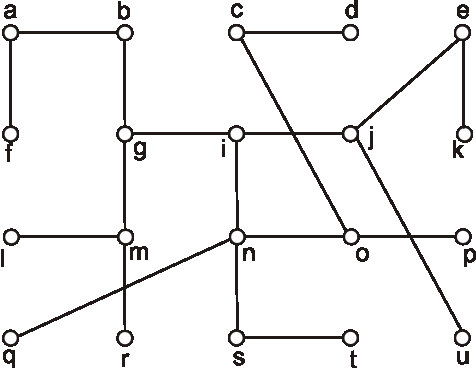

Úloha:
Nájdite polomer, priemer a stred stromu, ktorého diagram je na obrázku:
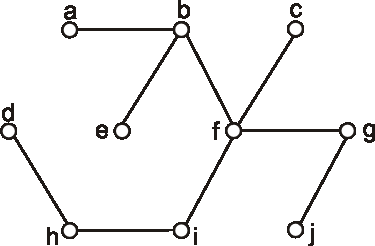

Úloha:
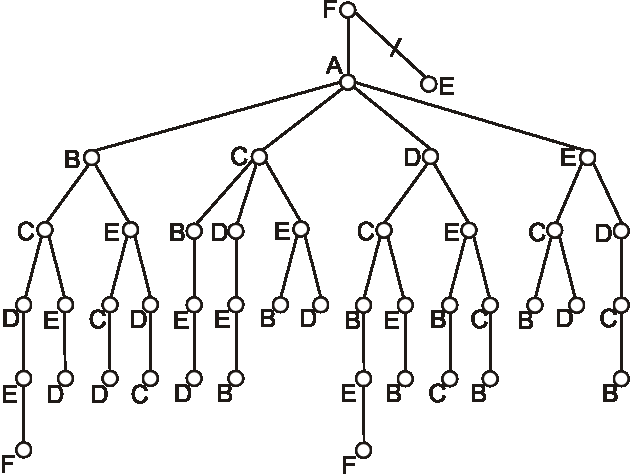
Na nasledujúcom obrázku sú znázornené diagramy 4 orientovaných stromov. O každom jednom rozhodnite,
či je alebo nie je koreňovým stromom. Ak je, overte či je alebo nie je binárným stromom a pre binárne
stromy určte ich hĺbku.
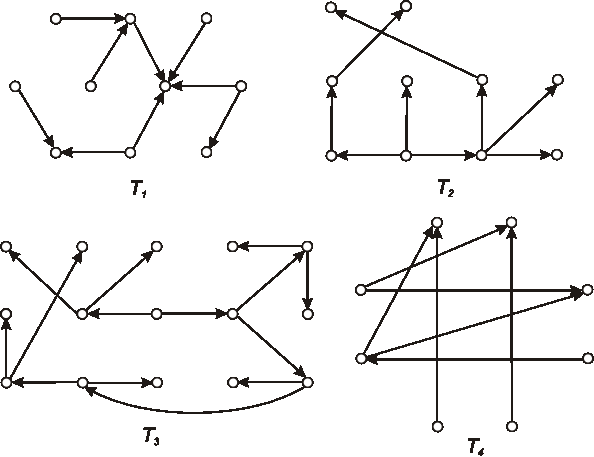

Úloha:
Zistite, či dané postupnosti sú grafové. Ak nie, zdôvodnite
prečo, ak áno, nakreslite diagram príslušného grafu.
a) 3,6,2,1,5,4,3
b) 4,5,3,5,5,5,5,4
c) 4,7,3,3,5,5,4,7,7,4,4,3
d) 12,6,8,2,11,3,7,14,11,9,7,2,2,2,5,4,3
a) 3,6,2,1,5,4,3
b) 4,5,3,5,5,5,5,4
c) 4,7,3,3,5,5,4,7,7,4,4,3
d) 12,6,8,2,11,3,7,14,11,9,7,2,2,2,5,4,3
Úloha:
Pre aké \(k\) je postupnosť grafová? Nakreslite diagram zodpovedajúcich grafov.
\(5, 3, k, 3, 3, 1\).
\(5, 3, k, 3, 3, 1\).
Úloha:
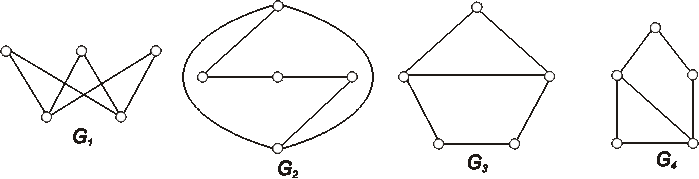
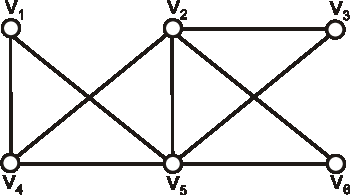
Ktoré z grafov, ktorých diagramy sú znázornené na obrázkoch, sú izomorfné?
Označte ich vrcholy a nájdite izomorfizmus, alebo zdôvodnite, prečo nie sú izomorfné.
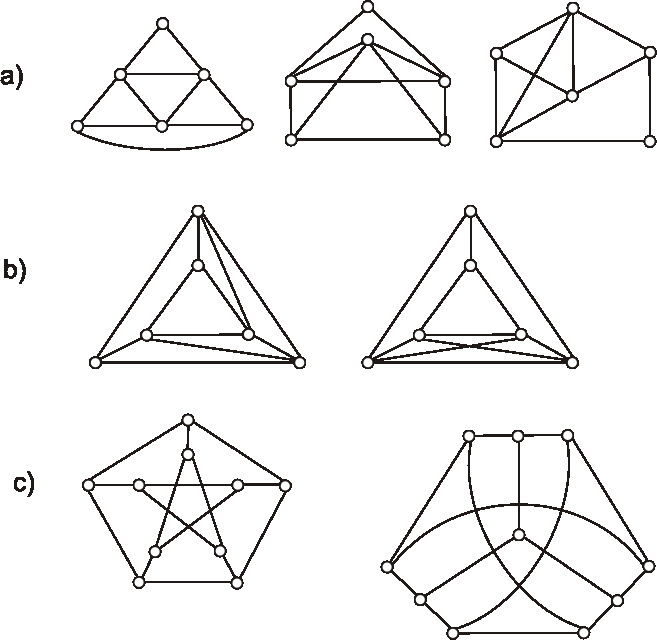

Úloha:
Je možné graf zadaný diagramom zobraziť sám na seba tak, aby zobrazenie nebolo identitou? Zdôvodnite.

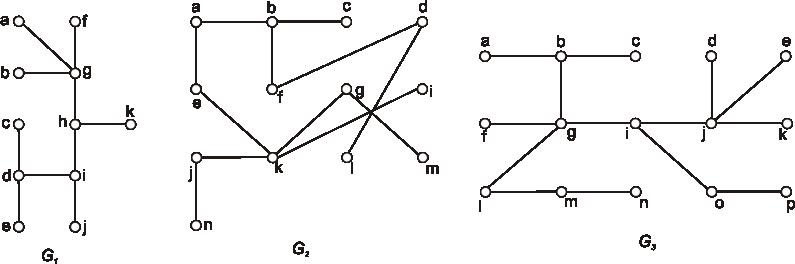
Úloha:
Znázornite diagramy všetkých neizomorfných stromov s piatimi hranami.
Úloha:
Nájdite polomer, priemer a stred stromov, daných diagramami:

03. Maticová reprezentácia grafu a digrafu. Súvislosť grafov. Počet kostier grafu a digrafu.
Riešené úlohy:
Príklad:
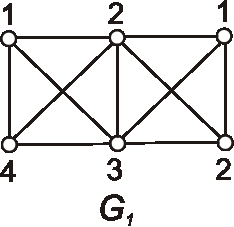
Zapíšte maticu incidencie (\(A\)) a maticu susednosti (\(B\)) grafu daného nasledujúcim diagramom: (hrany a vrcholy najprv
označte)

Príklad:
Nech je daný graf \(G\) nasledujúcou maticou susednosti. Znázornite tento graf diagramom.
\[B=\left (
\begin{array}{c}
0\\ 1\\ 1\\ 1\\ 0\\ 0\\ 0
\end{array}
\begin{array}{c}
1\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0
\end{array}
\begin{array}{c}
1\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0
\end{array}
\begin{array}{c}
1\\ 1\\ 1\\ 0\\ 1\\ 1\\ 1
\end{array}
\begin{array}{c}
0\\ 0\\ 0\\ 1\\ 1\\ 0\\ 0
\end{array}
\begin{array}{c}
0\\ 0\\ 0\\ 1\\ 1\\ 0\\ 0
\end{array}
\begin{array}{c}
0\\ 1\\ 1\\ 0\\ 1\\ 0\\ 0
\end{array}\right )
\]
Príklad:
Nech je daný digraf \(\vec{D}\) nasledujúcou maticou susednosti. Znázornite tento digraf diagramom.
\[\vec{B}=\left (
\begin{array}{c}
0\\ 1\\ 1\\ 0\\ 0
\end{array}
\begin{array}{c}
0\\ 0\\ 0\\ 1\\ 0
\end{array}
\begin{array}{c}
0\\ 0\\ 0\\ 0\\ 0
\end{array}
\begin{array}{c}
1\\ 1\\ 0\\ 0\\ 0
\end{array}
\begin{array}{c}
1\\ 0\\ 0\\ 1\\ 0
\end{array}\right )
\]
Príklad:
Majme daný digraf \(\vec{D}\) diagramom. Zapíšte maticu incidencie aj maticu susednosti daného digrafu.

Príklad:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 0\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}\right )
\]
Bez kreslenia diagramu grafu zistite, či je graf súvislý.
- zistite či je daný graf súvislý;
- určte polomer, priemer a stred daného grafu;
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je práve 3;
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je viac ako 3.
Príklad:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 1\\ 0\\ 0\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 1\\ 0\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 1 \\1 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0 \\0 \\1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 0 \\1 \\0
\end{array}\right )
\]
Bez kreslenia diagramu grafu:
Príklad:
Nech je daný digraf \(G\) nasledujúcim diagramom. Určte počet kostier daného grafu.
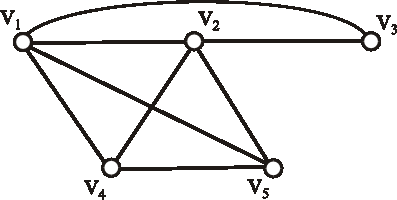

- všetkých kostier daného digrafu;
- koreňových kostier s vrcholom \(v_2\) ako koreňom;
- všetkých koreňových kostier daného digrafu;
Príklad:
Nech je daný digraf \(\vec{D}\) nasledujúcim diagramom. Určte počet:
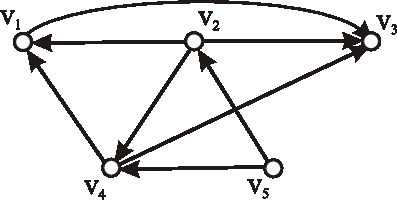

Príklad:
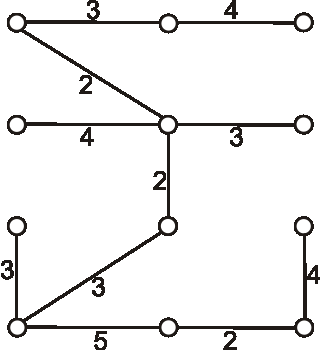
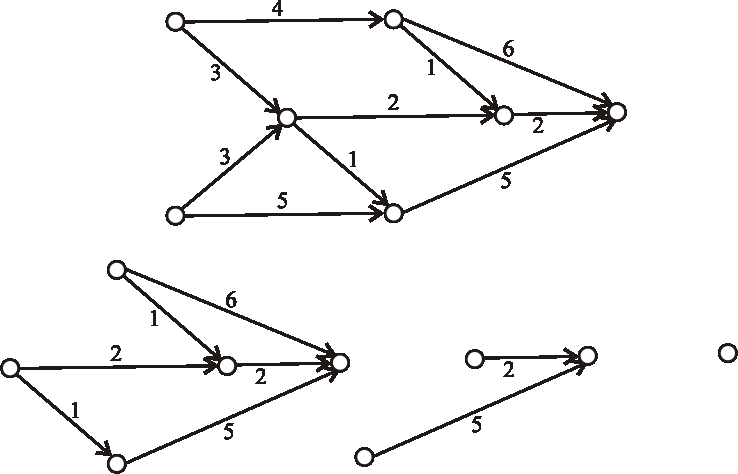
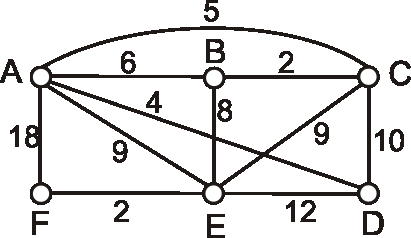
Nech je daný graf \(G\) nasledujúcim diagramom. Pomocou Kruskalovho algoritmu určte minimálnu
kostru a vypočítajte súčet jej ohodnotení.
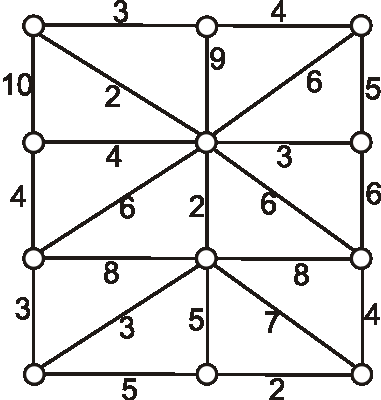

Príklad:
Nech je daný graf \(G\) nasledujúcim diagramom. Pomocou Primovho algoritmu určte minimálnu
kostru a vypočítajte súčet jej ohodnotení.
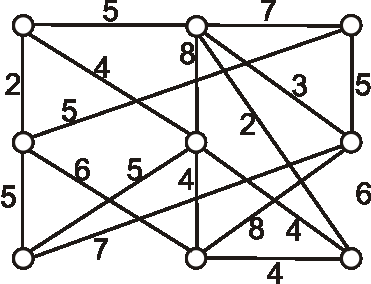

Úlohy:
Úloha:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0
\end{array}\right )
\]
Bez kreslenia diagramu grafu zistite, či je graf súvislý.
Úloha:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 1\\ 0\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 1\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 1\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1 \\0 \\1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 0 \\1 \\0
\end{array}\right )
\]
Bez kreslenia diagramu grafu určte polomer, priemer a stred daného grafu.
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je najviac 2;
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je práve 4.
Úloha:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 1 \\0 \\1
\end{array}
\begin{array}{r}
0\\ 1\\ 1\\ 1\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0 \\0 \\0
\end{array}\right )
\]
Bez kreslenia diagramu grafu:
Úloha:
Pre nasledujúce grafy dané maticami susednosti vypočítajte počet kostier.
\[B_1=\left (
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0
\end{array}\right )
; B_2=\left (
\begin{array}{r}
0\\ 0\\ 1\\ 1\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
1\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0
\end{array}\right )
; B_3=\left (
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0\\ 0
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 0\\ 0\\ 1
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 0\\ 1\\ 0
\end{array}\right )
\]
Úloha:
Koľko hrán je potrebné odstrániť z nasledujúcich grafov, aby vznikla kostra?

Úloha:
Nech je daný graf \(G\) nasledujúcim diagramom. Vypočítajte počet kostier daného grafu.

Úloha:
Nech je daný graf \(G\) nasledujúcim diagramom. Vypočítajte počet kostier grafu \(\bar{G}-v_3\),
kde \(\bar{G}\) je komplementom ku grafu \(G\).

Úloha:
Nech je daný digraf nasledujúcim diagramom. Vypočítajte počet jeho kostier.

Úloha:
Nech je daný digraf \(\vec{D}\) nasledujúcim diagramom. Vypočítajte počet koreňových
kostier digrafu \(\vec{D}\) s koreňom vo vrchole \(v_3\).
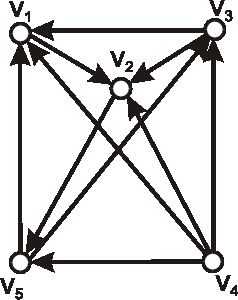

Úloha:
Nech je daný digraf \(\vec{D}\) nasledujúcim diagramom. Vypočítajte počet kostier aj počet koreňových
kostier digrafu \(\vec{D}\).
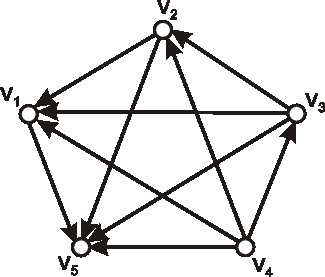

Úloha:
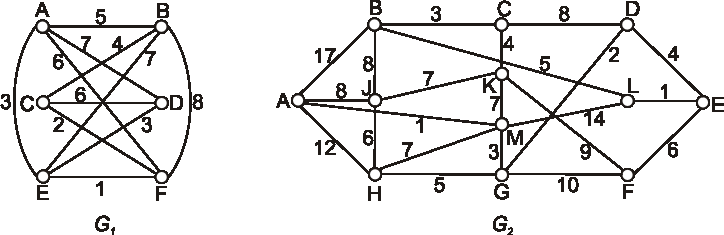
Kruskalovým aj Primovým algoritmom nájdite v nasledujúcich grafoch minomálne kostry.
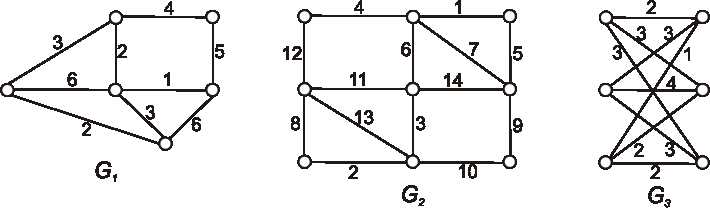

Úloha:
Použitím Primovho algoritmu nájdite minimálnu kostru v grafe danom nasledujúcim diagramom.
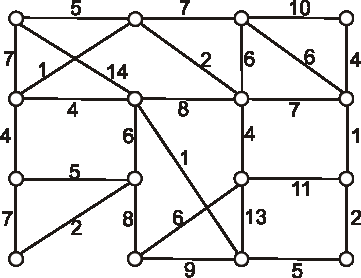

Úloha:
Pokúste sa modifikáciou Primovho algoritmu nájsť MAXIMÁLNU kostru v grafe z predchádzajúcej úlohy.
Úloha:
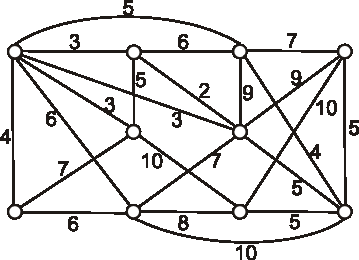
Telekomunikácie potrebujú položiť optický kábel tak, aby sa z každého uzla dalo dostať do každého a
nech je položenie káblovej siete čo najlacnejšie. Nasledujúci diagram znázorňuje uzly a možnosti ich
prepojenia. Čísla znázorňujú náklady na položenie kábla na konkrétnom úseku.

04. Cyklickosť digrafov, ATO, vzdialenosti v grafe a digrafe
Riešené úlohy:
Príklad:
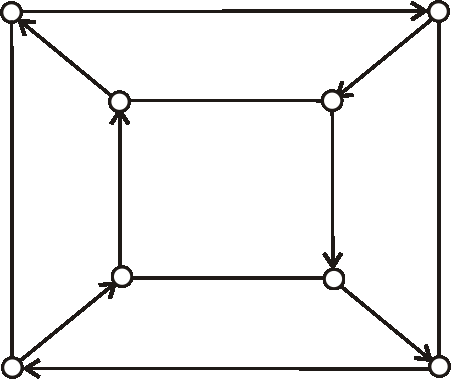
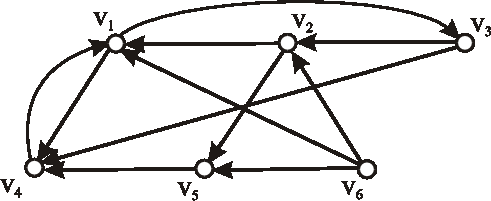
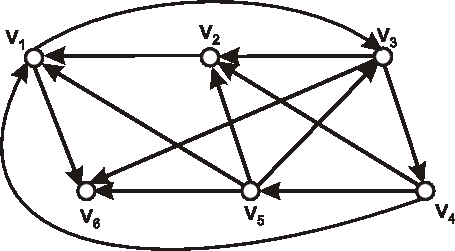
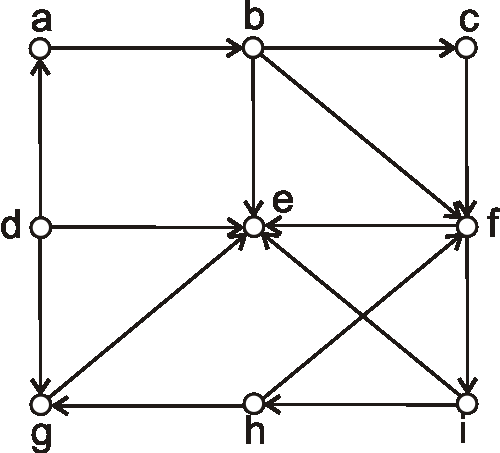
Je digraf daný nasledujúcim diagramom silne súvislý? Zdôvodnite.

Príklad:
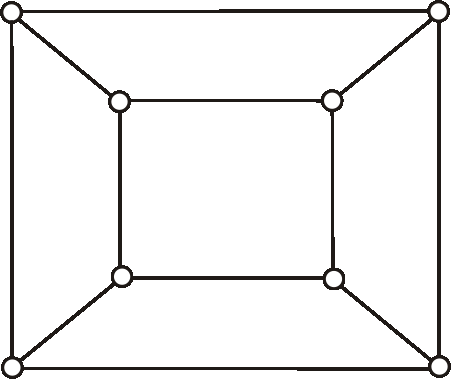
Nech je daný graf kocky (diagram je na obrázku). Zvoľte orientáciu jeho hrán tak, aby vznikol silne súvislý digraf.

Príklad:
Máme digraf daný nasledujúcim diagramom.
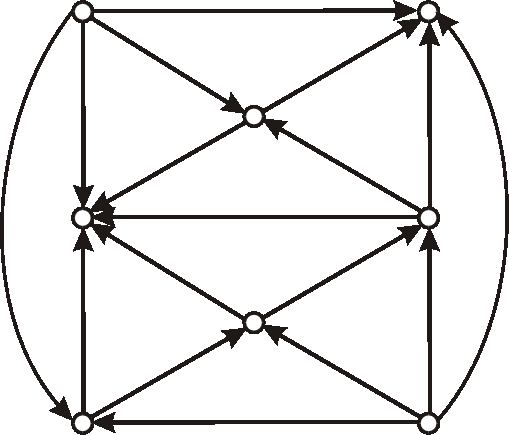 Zistite, či je daný digraf cyklický, alebo nie.
Zistite, či je daný digraf cyklický, alebo nie.

Príklad:
Máme digraf daný nasledujúcim diagramom.
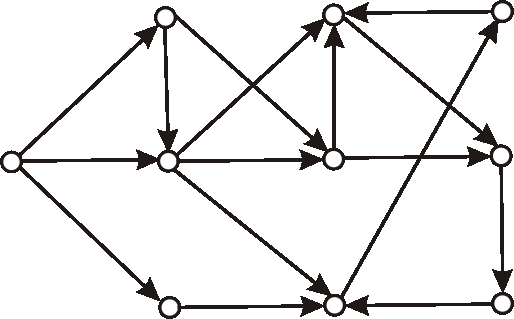 Zistite, či je daný digraf cyklický, alebo nie.
Zistite, či je daný digraf cyklický, alebo nie.

Príklad:
Je daný digraf nasledujúcim diagramom.
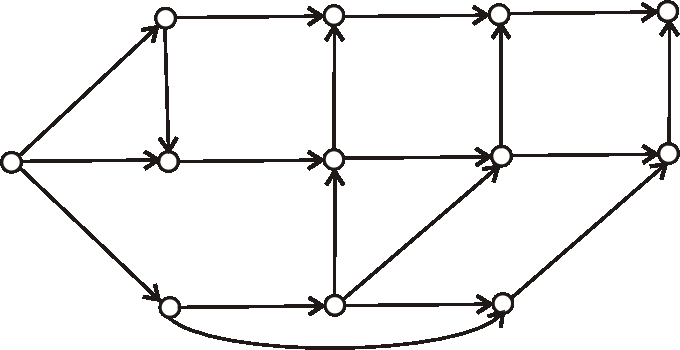 Pomocou ATO zistite, či je daný digraf cyklický, alebo nie. Ak nie je, topologicky očíslujte jeho vrcholy.
Pomocou ATO zistite, či je daný digraf cyklický, alebo nie. Ak nie je, topologicky očíslujte jeho vrcholy.

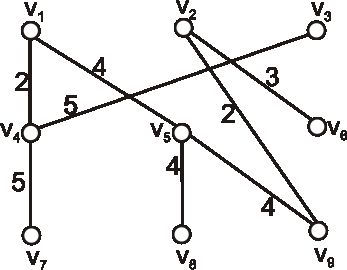
- Určte vzdialenosť vrcholu \(v_1\) a vrcholu \(v_4\).
- Do ktorého nesusedného vrcholu má vrchol \(v_5\) najmenšiu vzdialenosť?
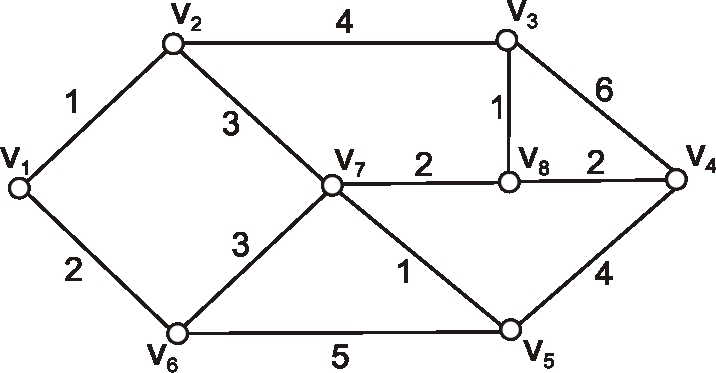
Príklad:
Je daný hranovo ohodnotený graf nasledujúcim diagramom.

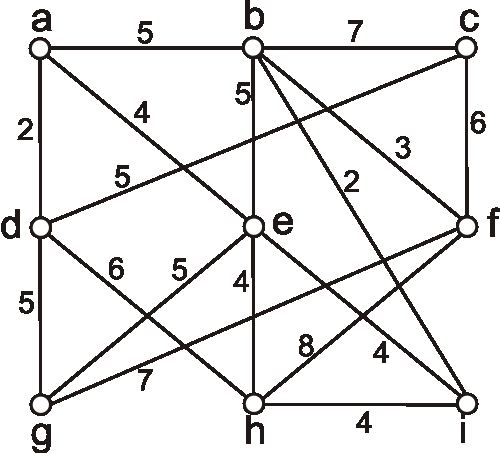
Príklad:
Nasledujúcim diagramom je daný hranovo ohodnotený graf. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(g\)
do
ostatných vrcholov.

Príklad:
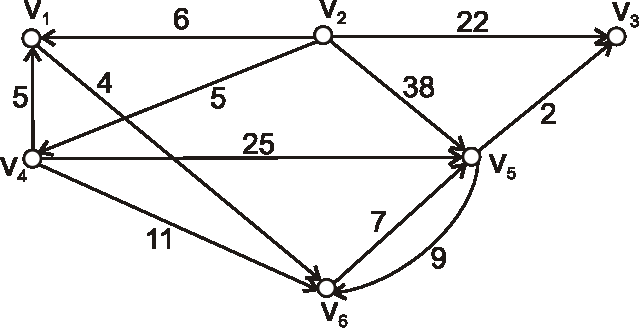
Nasledujúcim diagramom je daný hranovo ohodnotený digraf. Zistite vzdialenosti z vrcholu \(v_1\) do ostatných vrcholov,
tiež vzdialenosti z vrcholu \(v_4\) do ostatných vrcholov.

Príklad:
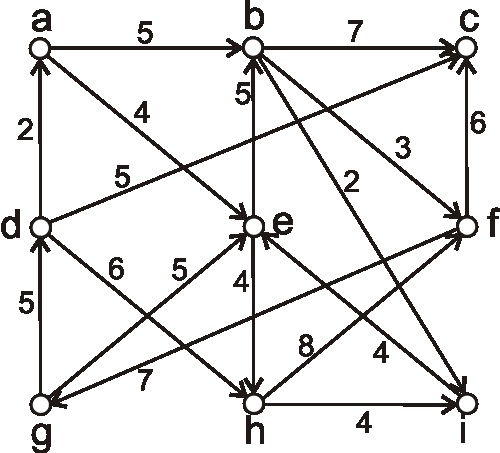
Nasledujúcim diagramom je daný hranovo ohodnotený digraf. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(h\)
do
ostatných vrcholov.

Úlohy:
Úloha:
Majme danú kružnicu \(K\) dĺžky \(d\geq 3\). Koľkými spôsobmi môžeme zvoliť orientáciu všetkých jej hrán tak,
aby vznikol acyklický digraf?
Úloha:
Máme digraf daný nasledujúcim diagramom.
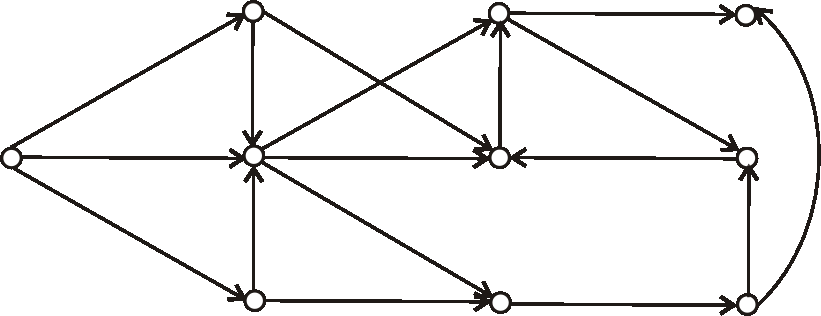 Pomocou ATO topologicky očíslujte vrcholy daného digrafu.
Pomocou ATO topologicky očíslujte vrcholy daného digrafu.

Úloha:
Máme digraf daný nasledujúcim diagramom.
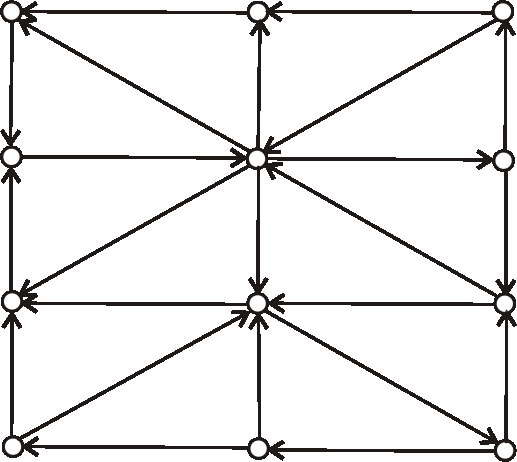 Zistite, či je daný digraf cyklický, alebo nie.
Zistite, či je daný digraf cyklický, alebo nie.

Úloha:
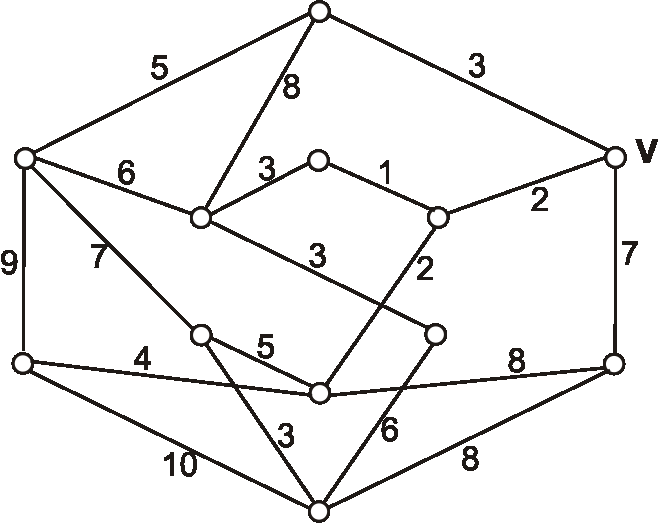
Máme graf daný nasledujúcim diagramom. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(V\) do
ostatných vrcholov.

Úloha:
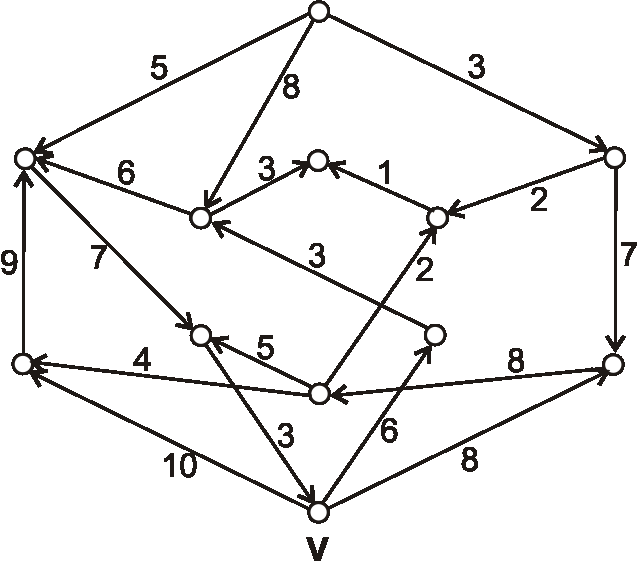
Máme digraf daný nasledujúcim diagramom. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(V\) do
ostatných vrcholov.

05. Eulerovské grafy, farbenie grafov, chromatické číslo a chromatický index grafu
Riešené úlohy:
Príklad:
Sú grafy zadané nasledujúcimi diagramami eulerovské?

Príklad:
Dajú sa grafy zadané nasledujúcimi diagramami pokryť jedným uzavretým ťahom?

Príklad:
Pre graf daný nasledujúcim diagramom vyriešte problém okružnej cesty.
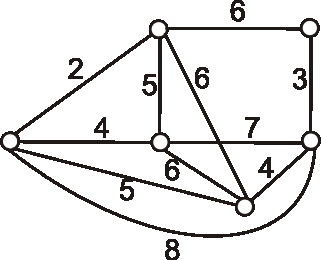

Príklad:
Pre graf daný nasledujúcim diagramom vyriešte problém okružnej cesty.
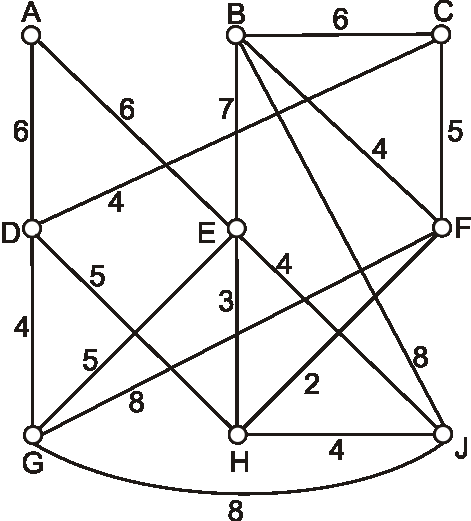

Príklad:
Pre grafy dané nasledujúcimi diagramami vyriešte problém okružnej cesty.
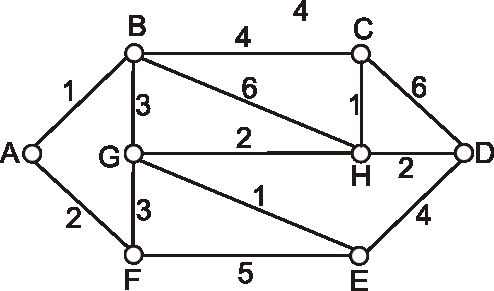

Príklad:
Pre grafy dané nasledujúcimi diagramami vyriešte problém okružnej cesty.
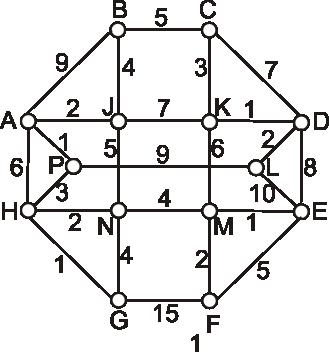

Príklad:
Určte chromatické číslo grafov daných nasledujúcimi diagramami.
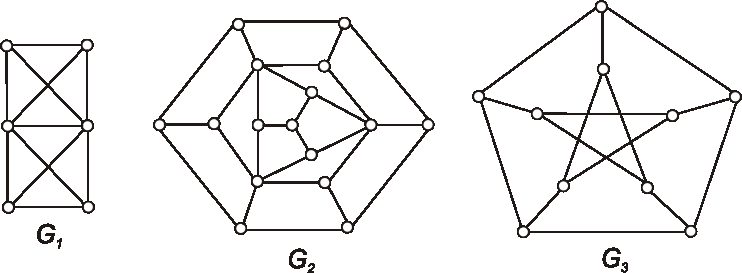

Príklad:
Určte chromatický index grafov daných nasledujúcimi diagramami.
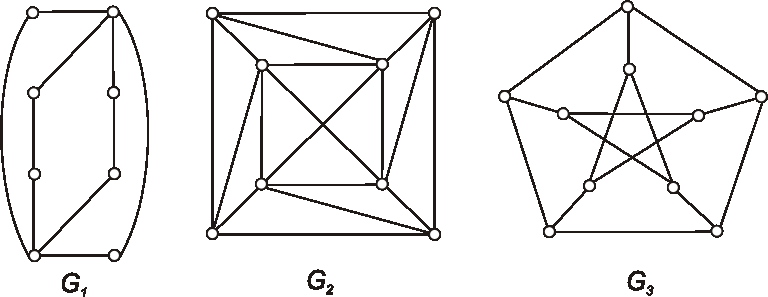

Úlohy:
Úloha:
Ktoré z grafov, znázornených nasledujúcimi diagramami, sú eulerovské?
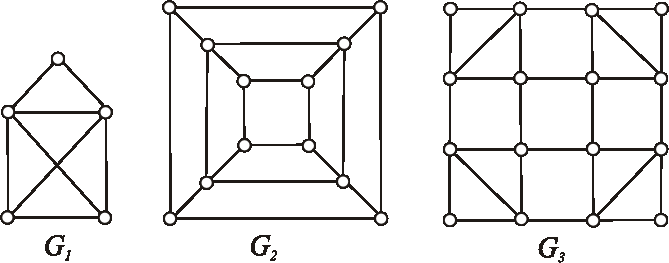 Ak sú, pokúste sa nakresliť ich diagramy jedným uzavretým ťahom.
Ak sú, pokúste sa nakresliť ich diagramy jedným uzavretým ťahom.

Úloha:
V grafoch daných nasledujúcimi diagramami zistite hodnotu minimálnej okružnej cesty.

Úloha:
Minimálne koľko vrcholov musí mať graf so \(74\) hranami, aby sme vedeli zaručiť, že
chromatický index grafu je aspoň \(5\)?
Úloha:
Nájdite chromatické číslo a chromatický index grafov daných nasledujúcimi diagramami.

06. Hamiltonovské grafy, planárnosť grafov, miery neplanárnosti
Riešené úlohy:
Príklad:
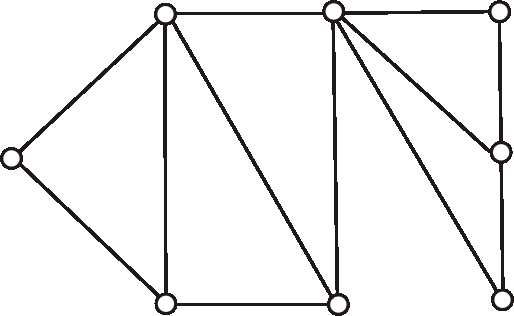
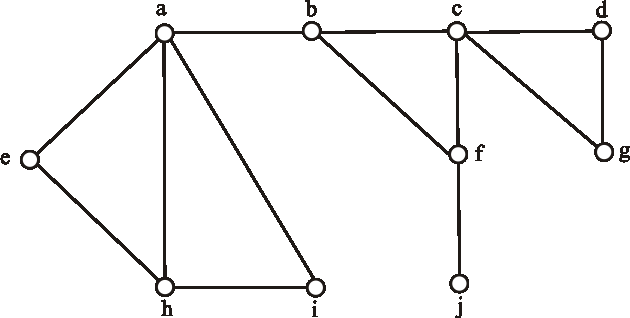
V grafe danom nasledujúcim diagramom určte všetky mosty.

Príklad:
V grafe z predchádzajúcej úlohy určte všetky artikulácie.
- artikuláciu, ale nie most,
- most, ale nie artikuláciu,
- aj most, aj artikuláciu.
Príklad:
Načrtnite diagram ľubovoľného grafu, ktorý obsahuje
- bez mosta
- s mostom
Príklad:
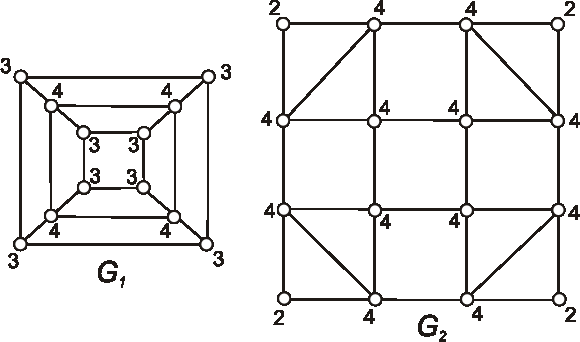
Na 16-tich vrcholoch zostrojte pravidelný súvislý graf 3. stupňa
Príklad:
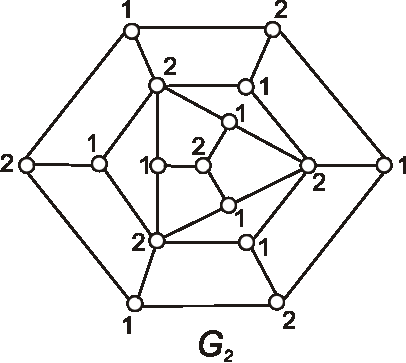
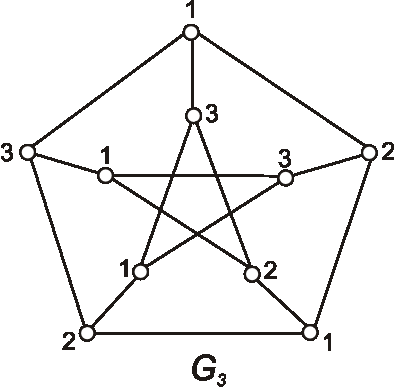
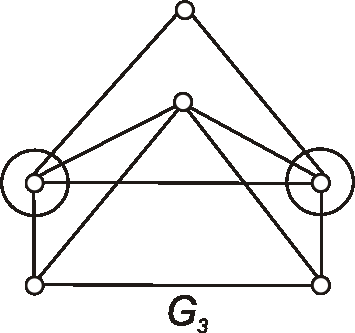
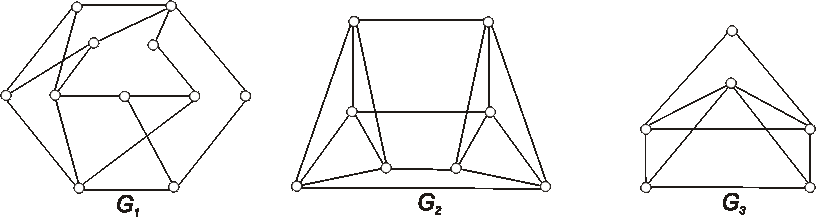
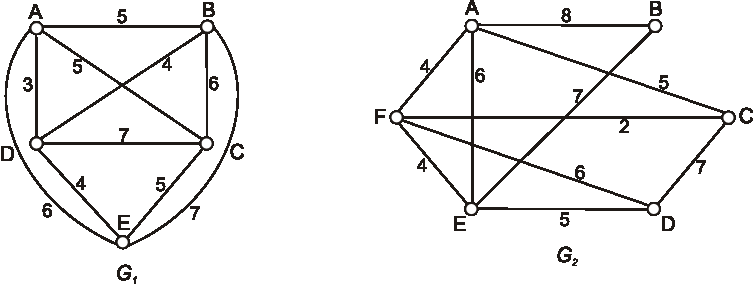
Zistite, či grafy \(G_1\), \(G_2\), \(G_3\) určené diagramami sú hamiltonovské.
Ak áno, vyznačte hamiltonovskú kružnicu, ak nie, zdôvodnite prečo.

Príklad:
V grafe danom nasledujúcim diagramom riešte problém obchodného cestujúceho pomocou rozhodovacieho stromu.

Príklad:
Je daný súvislý planárny graf \(G\), ktorý má 11 vrcholov. Vieme, že odobratím
5 hrán dostaneme jeho kostru. Koľko hrán má daný graf?
Príklad:
Overte planárnosť grafu daného nasledujúcim diagramom.
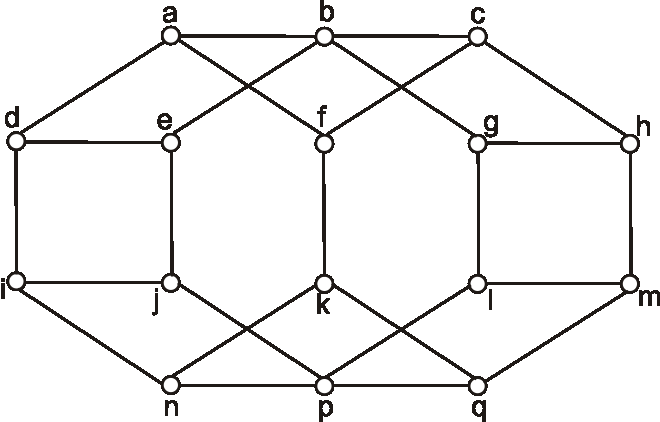

Príklad:
Overte planárnosť grafu daného nasledujúcim diagramom.
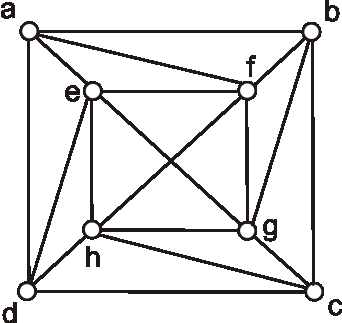

Príklad:
Overte planárnosť grafu daného nasledujúcim diagramom.
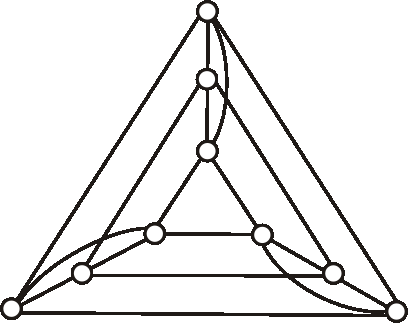

Úlohy:
Úloha:
Zistite, ktoré z grafov daných nasledujúcimi diagramami, sú, resp. nie sú hamiltonovské.
Ak sú hamiltonovské, nájdite hamilt. kružnicu, ak nie sú hamiltonovské, zdôvodnite prečo.
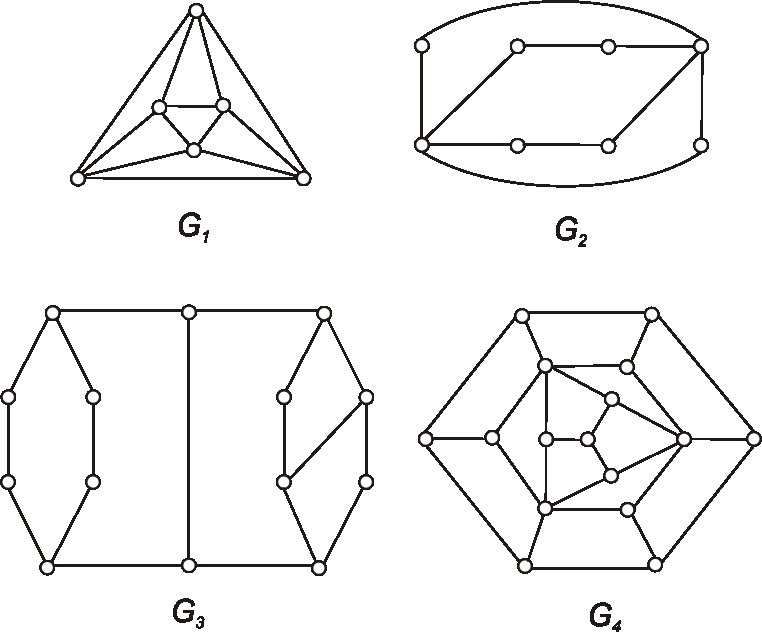

Úloha:
V grafoch, ktoré sú dané nasledujúcimi diagramami riešte problém obchodného cestujúceho pomocou
rozhodovacieho stromu.

Úloha:
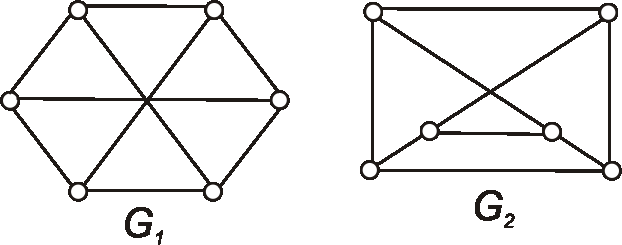
Pokúste sa zdôvodniť, prečo grafy dané nasledujúcimi diagramami nie sú planárne.

Úloha:
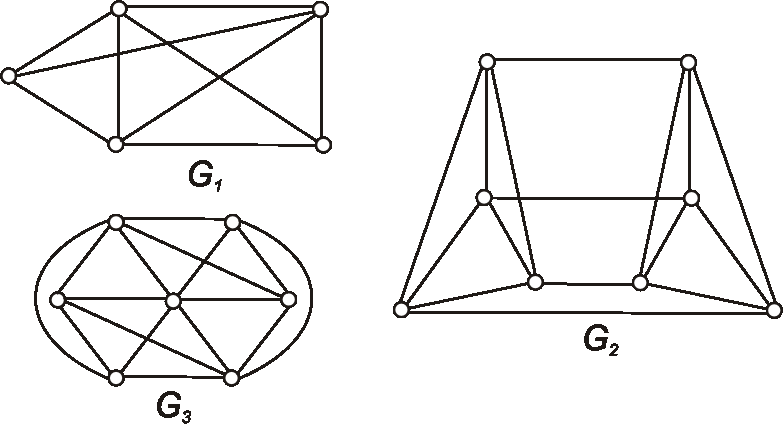
Zistite, ktoré z grafov daných nasledujúcimi diagramami, sú, resp. nie sú planárne.
Svoje tvrdenia zdôvodnite.

07. Toky v sieťach, CPM, PERT.
Riešené úlohy:
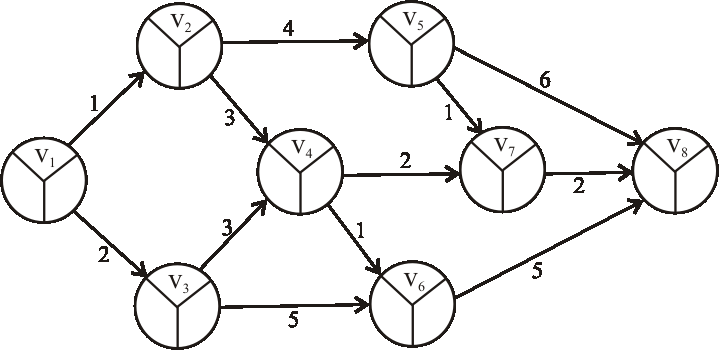
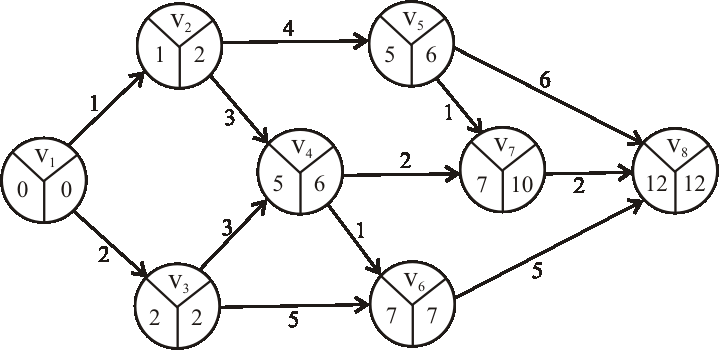
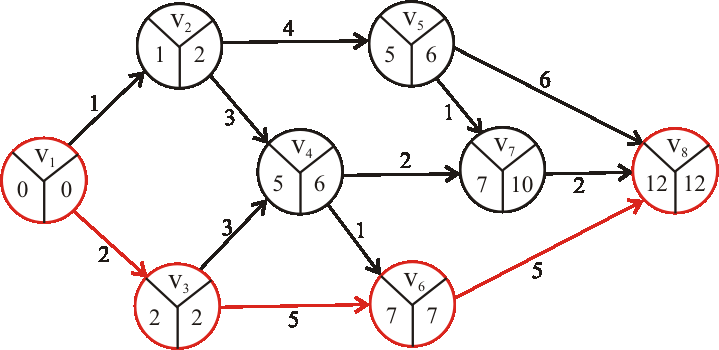
Príklad:
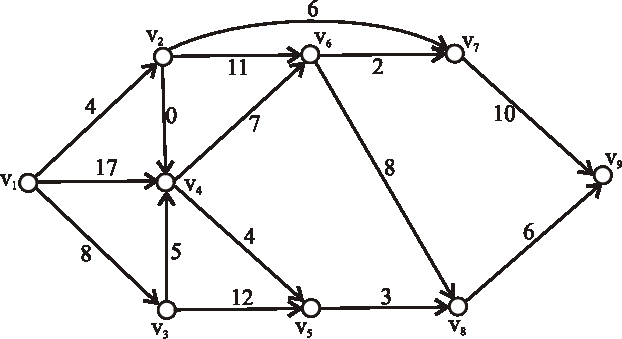
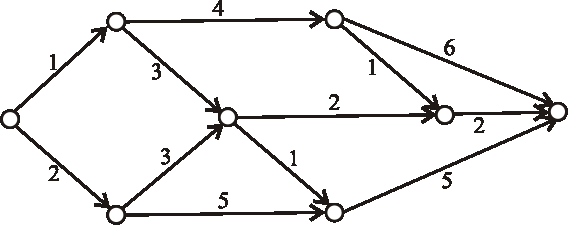
Zistite, či je nasledujúci hranovo-ohodnotený digraf acyklický, či teda môže byť reprezentáciou nejakého výrobného procesu.
Ak áno, topologický očíslujte vrcholy daného grafu.

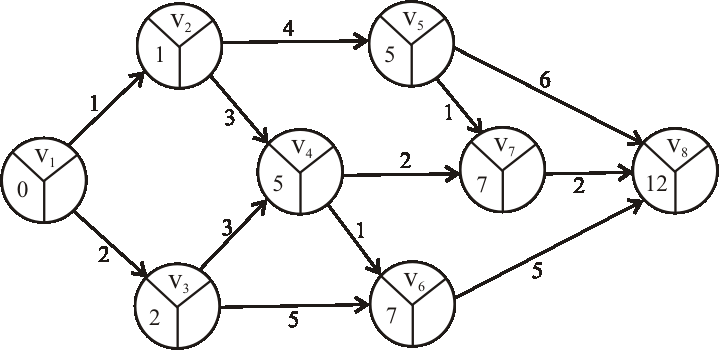
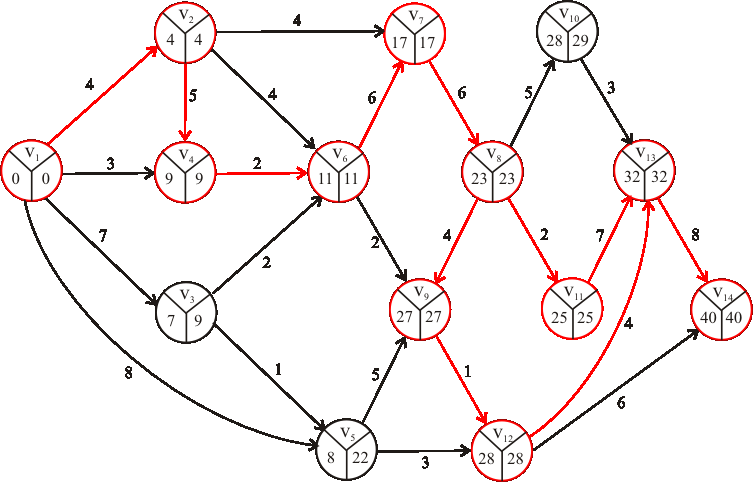
Príklad:
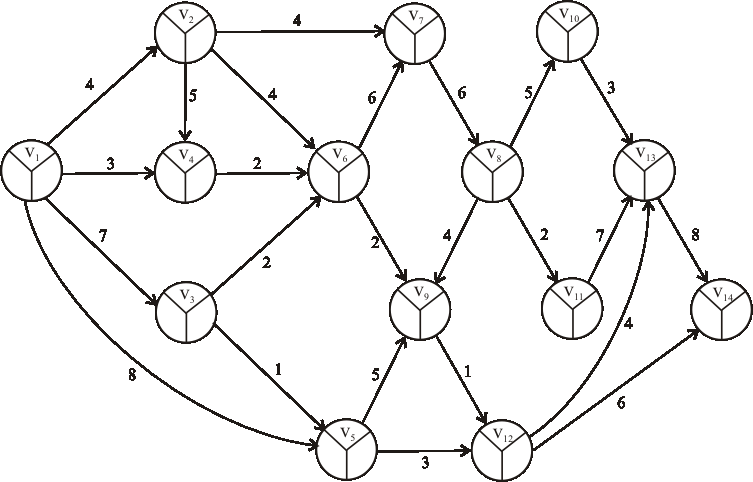
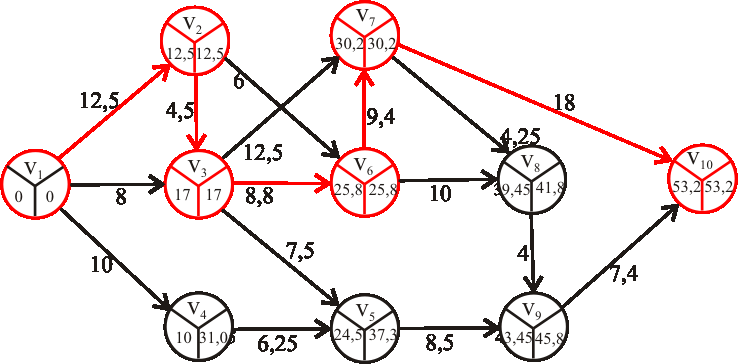
Pomocou metódy CPM určte dĺžku a nájdite kritické cesty výrobného procesu reprezentovaného
acyklickým digrafom z predchádzajúcej úlohy.
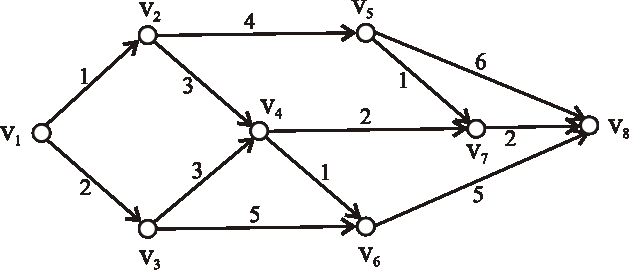

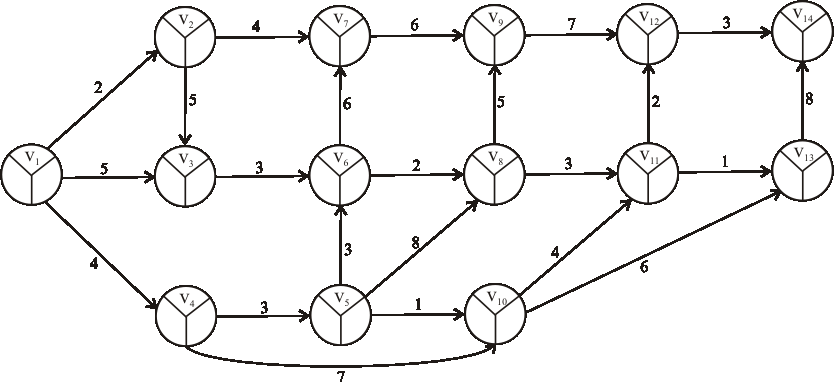
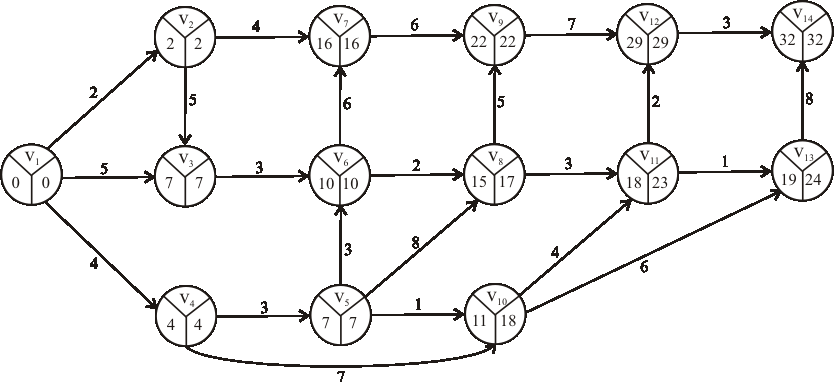
Príklad:
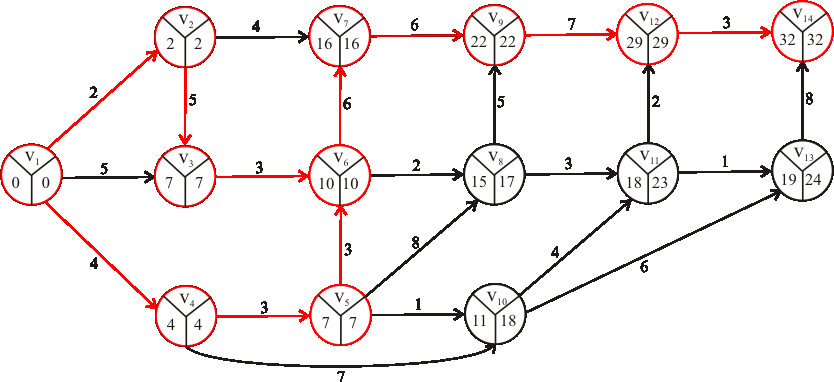
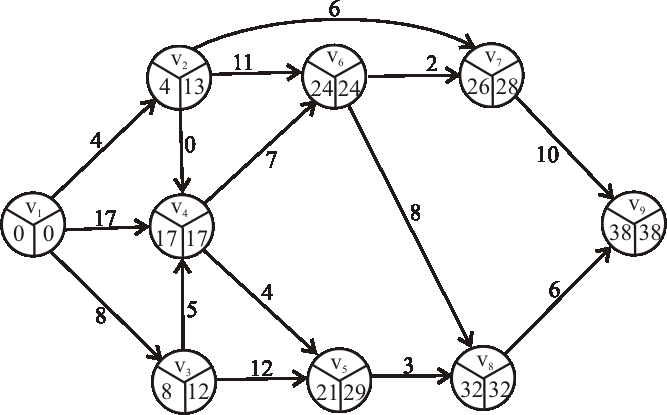
Nájdite kritické cesty výrobného procesu reprezentovaného nasledujúcim acyklickým digrafom.
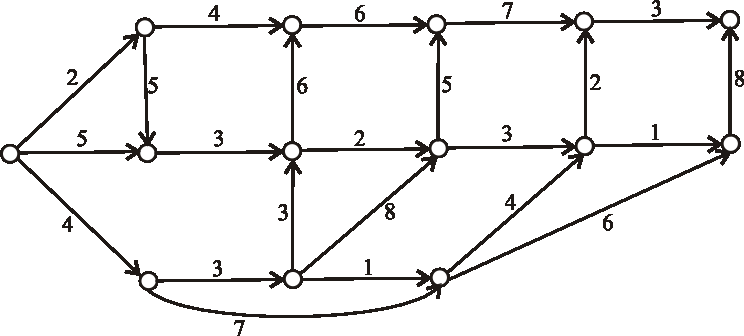

Príklad:
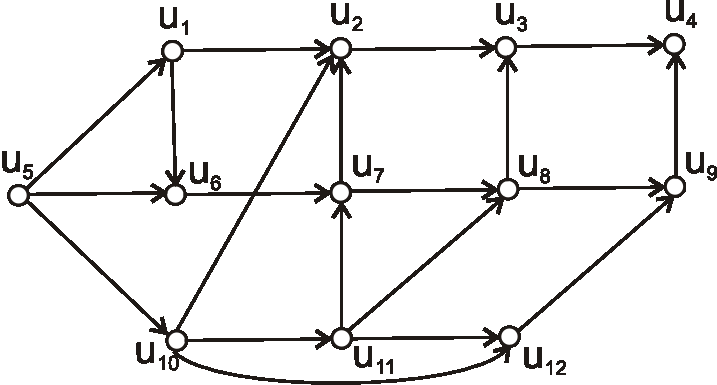
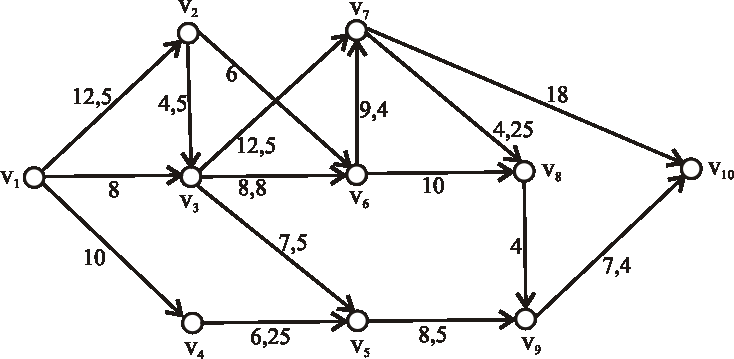
Je daný výrobný proces, ktorý obsahuje 14 uzlov (teda 14 vrcholov). Každá činnosť je daná
dvojicou uzlov, pričom prvý uzol určuje začiatok a druhý koniec činnosti. Zoznam činností
a ich časových trvaní je v nasledujúcej tabuľke. Pomocou metódy kritickej cesty vypočítajte
minimálne časové trvanie výrobného procesu a nájdite kritické cesty.
| činnosť | \(u_1u_8\) | \(u_2u_1\) | \(u_2u_6\) | \(u_2u_{10}\) | \(u_3u_5\) | \(u_4u_2\) | \(u_5u_1\) |
|---|---|---|---|---|---|---|---|
| čas | \(1\) | \(4\) | \(5\) | \(2\) | \(2\) | \(6\) | \(2\) |
| činnosť | \(u_5u_4\) | \(u_6u_{11}\) | \(u_7u_1\) | \(u_7u_8\) | \(u_8u_9\) | \(u_8u_{11}\) | \(u_{10}u_{11}\) |
| čas | \(6\) | \(3\) | \(5\) | \(3\) | \(6\) | \(4\) | \(7\) |
| činnosť | \(u_{11}u_9\) | \(u_{12}u_{3}\) | \(u_{12}u_4\) | \(u_{12}u_5\) | \(u_{13}u_3\) | \(u_{13}u_{7}\) | \(u_{13}u_{12}\) |
| čas | \(8\) | \(5\) | \(4\) | \(4\) | \(3\) | \(8\) | \(4\) |
| činnosť | \(u_{13}u_{14}\) | \(u_{14}u_{5}\) | \(u_{14}u_7\) | ||||
| čas | \(7\) | \(2\) | \(1\) |
Príklad:
Je daný projekt, ktorý obsahuje 9 uzlov (teda 14 vrcholov). Každá činnosť je daná
dvojicou uzlov, pričom prvý uzol určuje začiatok a druhý koniec činnosti. Zoznam činností
a ich odhadov časových trvaní (v týždňoch) v poradí: optimistický odhad, normálny odhad, pesimistický
odhad je v nasledujúcej tabuľke. Pre každú činnosť vypočítajte priemernú dobu trvania
danej činnosti.
| činnosť | \(t_1t_2\) | \(t_1t_3\) | \(t_1t_4\) | \(t_2t_4\) | \(t_2t_6\) |
|---|---|---|---|---|---|
| odhady času | \(2;3;10\) | \(5;7;15\) | \(12;15;30\) | \(0;0;0\) | \(8;10;18\) |
| činnosť | \(t_2t_7\) | \(t_3t_4\) | \(t_3t_5\) | \(t_4t_5\) | \(t_4t_6\) |
| odhady času | \(4;6;8\) | \(4;5;6\) | \(7;10;25\) | \(3;4;5\) | \(4;6;14\) |
| činnosť | \(t_5t_8\) | \(t_6t_7\) | \(t_6t_8\) | \(t_7t_9\) | \(t_8t_9\) |
| odhady času | \(2;3;4\) | \(2;2;2\) | \(4;7;16\) | \(8;9;16\) | \(5;6;7\) |
Príklad:
Pomocou metódy PERT určte dobu, za ktorú bude projekt z predchádzajúcej úlohy ukončený
s pravdepodobnosťou 50%.
- s akou pravdepodobnosťou bude projekt ukončený za 60 týždňov,
- dobu, za ktorú bude projekt daný nasledujúcim ohodnoteným digrafom ukončený s pravdepodobnosťou 90%.
Príklad:
Nech je daný projekt nasledujúcim ohodnoteným digrafom (časy sú uvedené v týždňoch).
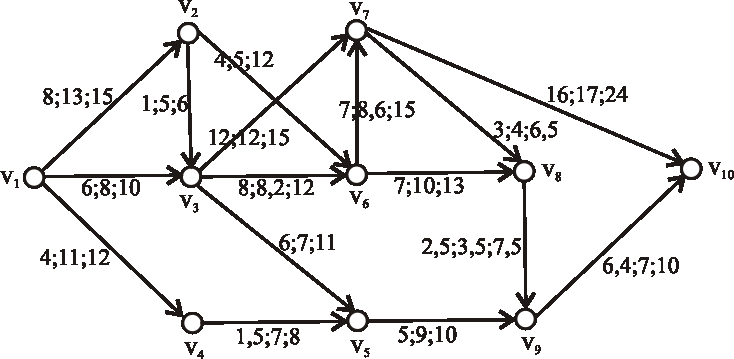 Pomocou metódy PERT určte:
Pomocou metódy PERT určte:

Príklad:
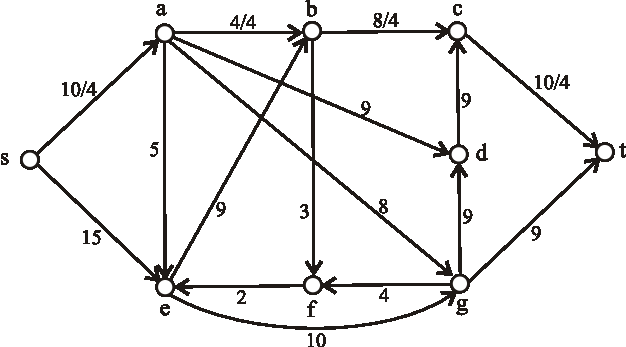
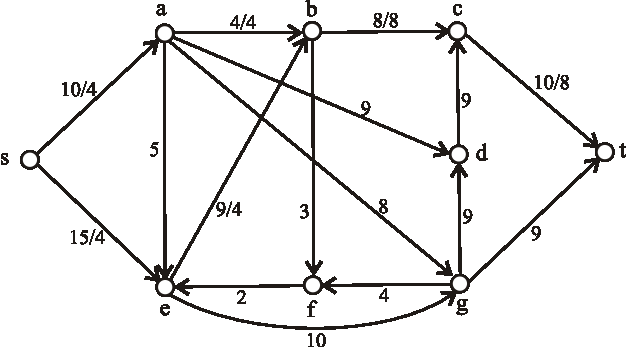
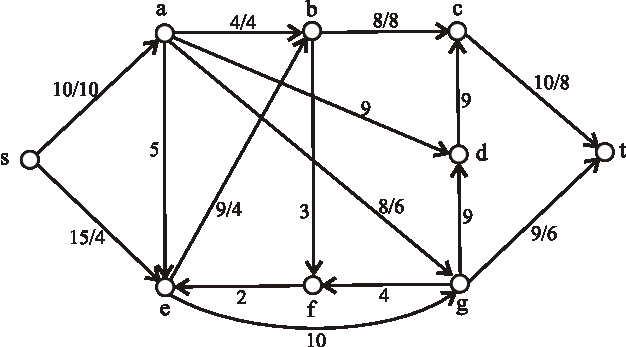
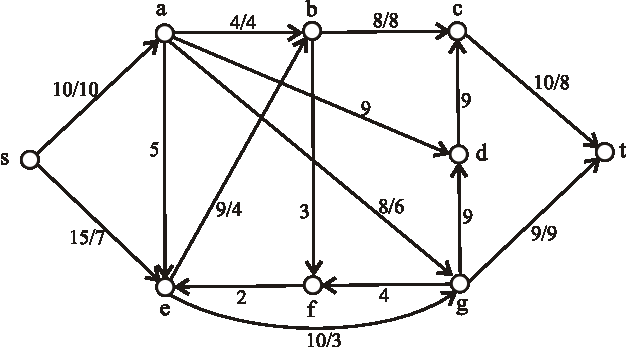
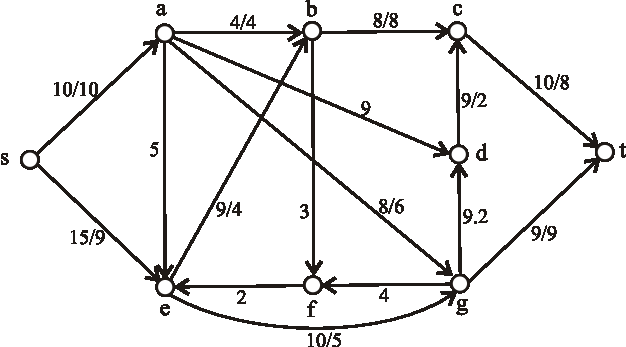
Nasledujúci diagram znázorňuje sieť plynovodov plynárenského podniku s maximálnymi prepravnými kapacitami na
jednotlivých úsekoch. Určte maximálnu tranzitnú kapacitu tejto siete, kde vrchol \(s\) predstavuje ťažobnú spoločnosť
a vrchol \(t\) odberateľský plynárenský podnik.
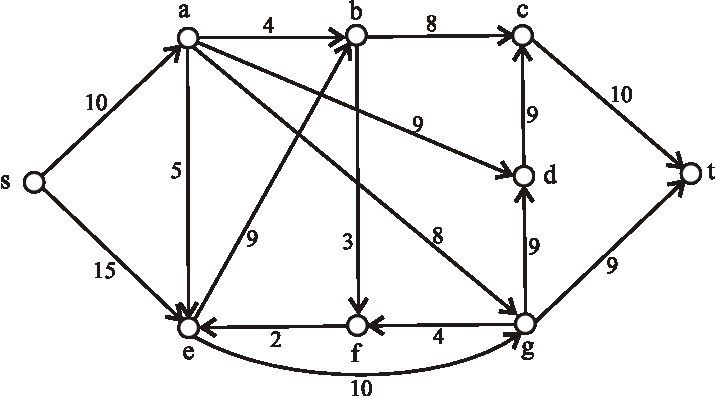

Úlohy:
Úloha:
Nájdite kritické cesty výrobného procesu reprezentovaného nasledujúcim acyklickým digrafom.
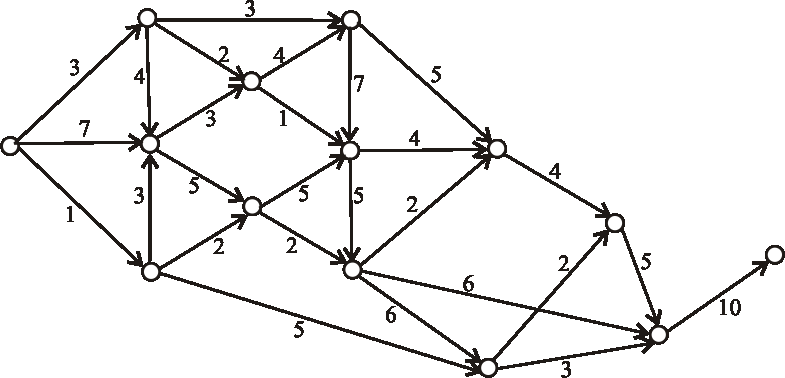

Úloha:
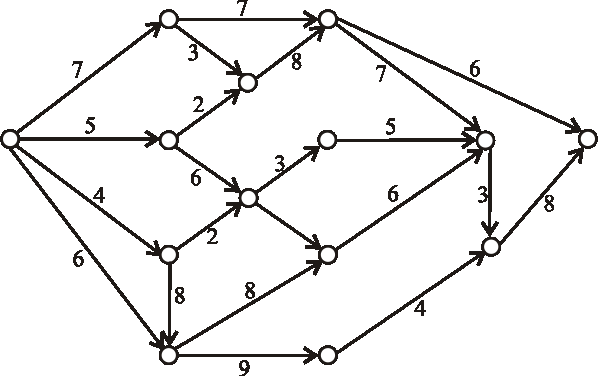
Nájdite kritické cesty výrobného procesu reprezentovaného nasledujúcim acyklickým digrafom.

08. Cvičenie - Vypočítateľnosť algoritmov.
Riešené úlohy:
Príklad:
Koľko operácií je potrebných na výpočet súčinu dvoch štvorcových \(n\times n\) matíc \(A=(a_{ij}), B=(b_{ij})\)?
Príklad:
Koľko operácií je potrebných na výpočet mocniny \(A^p\) štvorcovej \(n\times n\) matice \(A=(a_{ij})\)
pre \(p\in N\)?
Príklad:
Koľko operácií je potrebných na výpočet metrickej matice
\[\Gamma(A)=A\oplus A^2\oplus\dots\oplus A^n,\]
kde \(A=(a_{ij})\) je \(n\times n\) matica a
operácia \(\oplus\) reprezentuje maximum a operácia \(\otimes\)
reprezentuje \(+\)?
Príklad:
Problém obchodného cestujúceho (Traveling
Salesman Problem -- TSP)
V individuálnej úlohe TSP je dané prirodzené číslo
\( n>0 \) a matica vzdialeností medzi každou dvojicou \( n \) miest
vo forme \( n\times n \) matice \( (d_{ij}) \), \( d_{ij}\in Z^+ \) (\( Z^+ \) je
označenie pre kladné
celé čísla).
Problém: Nájsť uzavretú cestu, ktorá prechádza každým mestom práve raz, a pritom zo všetkých takýchto
ciest má minimálny súčet ohodnotení hrán.
Úlohy:
Úloha:
Oboznámte sa s ďalšími algoritmami pre TSP problém.
Úloha:
Aký je rozdiel medzi nimi?
Úloha:
Popíšte aspoň jeden efektívny algoritmus na riešenie
sústavy lineárnych rovníc.
Úloha:
Popíšte aspoň jeden neefektívny algoritmus na riešenie sústavy lineárnych rovníc.
Úloha:
Popíšte aspoň jeden efektívny algoritmus na výpočet
determinantu matice.
Úloha:
Popíšte aspoň jeden neefektívny algoritmus na výpočet determinantu matice.
Úloha:
Navrhnite efektívny algoritmus na usporiadanie \( n \) čísel
podľa veľkosti.
Úloha:
Navrhnite efektívny algoritmus na testovanie súvislosti grafu.
Úloha:
Navrhnite aspoň jeden algoritmus na nájdenie aspoň jednej
kostry grafu.
Úloha:
Navrhnite algoritmus na hľadanie všetkých kostier grafu.
Úloha:
Formulujte nasledujúci optimalizačný problém ako inštanciu,
pričom je treba definovať množinu prípustných riešení \( F \) a
cenovú funkciu \( c \).\\
Nájdite najkratšiu cestu medzi dvoma vrcholmi ohodnoteného
grafu.
Úloha:
Popíšte metódu na odčítanie decimálnych
prirodzených čísel ako algoritmus.
Úloha:
Zostrojte algoritmus pre nasledujúci problém: Fixujte
reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.\\
Je daný graf \( G=(V,E) \). Existuje v \( G \) cyklus \( (u,v,w,z,u) \)
taký,
že \( (v,z),\ (u,w)\not\in E \), pričom\\
(i) \( u,v,w,z \) sú ľubovoľné vrcholy\\
(ii) \(u,v,w,z \) sú pevne dané?
Úloha:
Zostrojte algoritmus pre nasledujúci problém: Fixujte
reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.\\
Pre dané \( p\in N \) rozhodnite, či \( p \) je prvočíslo.
Úloha:
Zostrojte algoritmus pre nasledujúci problém: Fixujte
reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.\\
Pre dané \( x,y,z \in N \) rozhodnite, či existuje \( n>0,\ n\in N \)
také, že platí:
\( x^n+y^n=z^n. \)
Úloha:
Zostrojte algoritmus pre nasledujúci problém: Fixujte
reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.
Daný je graf \( G=(V,E) \) a \( s,t\in V \). Existuje v \(G \) cesta z
vrchola \( s \) do vrchola \( t \)?
09. Cvičenie - Polynomiálne algoritmy a \(O(f(n))\).
Riešené úlohy:
Príklad:
Aká je výpočtová zložitosť jednotlivých krokov a celková výpočtová zložitosť
popísaného algoritmu na výpočet súčinu dvoch štvorcových \(n\times n\)
matíc \(A=(a_{ij}), B=(b_{ij})\)?
Príklad:
Aká je výpočtová zložitosť jednotlivých krokov a celková výpočtová zložitosť
popísaného algoritmu na výpočet mocniny \(A^p\) štvorcovej \(n\times n\)
matice \(A=(a_{ij})\) pre \(p\in N\)?
Príklad:
Aká je výpočtová zložitosť jednotlivých krokov a celková výpočtová zložitosť
popísaného algoritmu na výpočet metrickej matice
\[\Gamma(A)=A\oplus A^2\oplus\dots\oplus A^n,\]
kde \(A=(a_{ij})\) je \(n\times n\) matica a operácia \(\oplus\)
reprezentuje maximum a operácia \(\otimes\) reprezentuje \(+\)?
Príklad:
Dokážte, že platí, resp. nájdite kontrapríklad, že neplatí rovnosť
\[(\ln n)^k=O(n^\epsilon)\]
pre všetky \(k\in N\) a pre všetky \(\varepsilon>0.\) Použite:
\(g(n)=O(f(n))\) vtedy a len vtedy, ak existuje \(c>0\), že platí
\(g(n)\leq c\cdot f(n)\).
Príklad:
Aká je veľkosť vstupu pre grafové problémy.
Príklad:
Nech \(f:N\rightarrow N\) a \(g:N\rightarrow N\) sú funkcie definované
nasledovne
\[f(n)=\left\{
\begin{array}{l}
n^2\text{ ak } n \text{ je prvočíslo,} \\
n^3\text{ inak,}
\end{array}\right. \quad \quad
g(n)=\left\{
\begin{array}{l}
n^2\quad \text{ ak } n \text{ je nepárne,} \\
n^3\quad \text{ inak.}
\end{array}\right.
\]
Analyzujte, ktoré z rovností sú, kedy pravdivé:
\[f(n)=O(g(n)),\ \text{resp. }\ g(n)=O(f(n)).\]
Príklad:
Analyzujte počet operácií Floydov-Warshallovho algoritmu.
Úlohy:
Úloha:
Popíšte metódu na odčítanie decimálnych
prirodzených čísel ako algoritmus.
- \( u,v,w,z \) sú ľubovoľné vrcholy,
- \(u,v,w,z \) sú pevne dané?
Úloha:
Zostrojte algoritmus pre nasledujúci problém:
Je daný graf \( G=(V,E) \). Existuje v \( G \) cyklus \( (u,v,w,z,u) \) taký, že \( (v,z),\ (u,w)\not\in E \), pričom
Je daný graf \( G=(V,E) \). Existuje v \( G \) cyklus \( (u,v,w,z,u) \) taký, že \( (v,z),\ (u,w)\not\in E \), pričom
Úloha:
Zostrojte algoritmus pre nasledujúci problém:
Pre dané \( p\in N \) rozhodnite, či \( p \) je prvočíslo.
Fixujte reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.
Pre dané \( p\in N \) rozhodnite, či \( p \) je prvočíslo.
Fixujte reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.
Úloha:
Zostrojte algoritmus pre nasledujúci problém:
Pre dané \( x,y,z \in N \) rozhodnite, či existuje \( n>0,\ n\in N \) také, že platí: \( x^n+y^n=z^n. \)
Fixujte reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.
Pre dané \( x,y,z \in N \) rozhodnite, či existuje \( n>0,\ n\in N \) také, že platí: \( x^n+y^n=z^n. \)
Fixujte reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.
Úloha:
Zostrojte algoritmus pre nasledujúci problém:
Daný je graf \( G=(V,E) \) a \( s,t\in V \). Existuje v \(G \) cesta z
vrchola \( s \) do vrchola \( t \)?
Fixujte reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.
Fixujte reprezentáciu vstupu a popíšte zložitosť navrhnutého algoritmu.
10. NP-úplné problémy.
Úlohy:
Úloha:
Problém obchodného cestujúceho (Traveling
Salesman Problem -- TSP)
V individuálnej úlohe TSP je dané prirodzené číslo
\( n>0 \) a matica vzdialeností medzi každou dvojicou \( n \) miest
vo forme \( n\times n \) matice \( (d_{ij}) \), \( d_{ij}\in Z^+ \) (\( Z^+ \) je
označenie pre kladné
celé čísla).
Problém: Nájsť uzavretú cestu, ktorá prechádza každým mestom práve raz, a pritom zo všetkých takýchto ciest má minimálny súčet ohodnotení hrán.
Problém: Nájsť uzavretú cestu, ktorá prechádza každým mestom práve raz, a pritom zo všetkých takýchto ciest má minimálny súčet ohodnotení hrán.
Úloha:
Uvažujme o nasledujúcom kombinatorickom
probléme, nazývanom problém maximálnej kliky (Clique
Problem - CP)
Pre daný graf \(G=(V,E)\), nájdite najväčšiu podmnožinu \(C\subset V\)
takú, že pre všetky rôzne \(u,v\in C\) platí \((u,v)\in E\).\\
Parameter \(S\) je v tomto prípade graf \(G\). Pre daný graf
\(G=(V,E),\ {\cal A_F}\) rozhodne, či \(f\) tvorí kliku v \(G\),
t.j. úplný podgraf na \(C\). \({\cal A_C}\) vypočíta veľkosť \(f\) (teda
mohutnosť \(f\)), \(Q=\emptyset\) pre tento prípad.
Úloha:
Problém splniteľnosti boolovskej formuly je
v \(NP\).
Daná je množina boolovských disjunkcií (klauzúl)
\(C_1,\dots,C_m\) obsahujúcich litery
\(\alpha_1,\dots,\alpha_n\), kde \(\alpha_i\), \(i\in \{1,\dots,n\}\) sú
premenné \(x_1,\dots,x_n\) alebo ich negácie \(\overline
x_1,\dots,\overline x_n\).
Existuje postupnosť boolovských hodnôt z \(\{0,1\}^n\) taká, že po
ich priradení premenným \(x_1,\dots,x_n\) je konjunkcia
\[C_1(\alpha_1,\dots,\alpha_n)\wedge \dots\wedge C_m(\alpha_1,\dots,\alpha_n)=1?\]
Úloha:
Zostrojte \(O(n^2)\) algoritmus na riešenie špeciálneho
prípadu splniteľnosti boolovskej formuly: Každá klauzula
obsahuje dve
litery (2-splniteľnosť).
Návod: Nech \(F\) je formula obsahujúca dve litery v každej
klauzule. Z \(F\) konštruujeme orientovaný graf \(D(F)=(X,A)\),
kde $X$ je množina premenných a ich negácií, ktoré sa
vyskytujú v \(F\) a \((\lambda_1,\lambda_2)\in A\) je hrana práve
vtedy, ak klauzula
\((\overline\lambda_1\vee\lambda_2)\) je z \(F\).
(a) Digraf \(D=(V,A)\) je silne súvislý ak, pre každé
\(u,v\in V\)
existuje cesta z \(u\) do \(v\) a z \(v\) do \(u\).
Navrhnite \(O(|A|)\) algoritmus, ktorý o danom digrafe rozhodne,
či
je silne súvislý.
(b) Zostrojte \(O(|A|)\) algoritmus, ktorý nájde všetky silne
súvislé komponenty digrafu \(D=(V,A)\).
(c) Dokážte, že ak pre nejakú premennú \(x\) platí, že \(x\) a \(\overline x\)
sú v rovnakom silnom komponente \(D(F)\),
potom \(F\) je
nesplniteľná.
(d) Dokážte opačné tvrdenie k (c).
Úloha:
Zostrojte \(O(|E|)\) algoritmus, ktorý rozhodne, či graf
\(G=(V,E)\) je bipartitný.
Úloha:
Problém farbenia grafu.
Je daný graf \(G=(V,E)\) a prirodzené číslo \(k\). Existuje
zobrazenie \(\chi :V\to\{1,2,\dots,k\}\) také, že \((u,v)\in E
\Rightarrow \chi(u)\neq\chi(v)\)?
Dokážte, že problém farbenia grafu je v \(NP\) a popíšte detaily
certifikátu a kontrolného algoritmu.
Úloha:
Popíšte konštrukciu kontrolného algoritmu, ktorý
akceptuje reťazec tvaru
\[\underbrace{0...0}_{2n}\underbrace{1...1}_{n}\ \ pre \ \ n\geq
1\] pomocou inštrukcií \[l\ \ {\bf if}\ \ \sigma\ \ {\bf
then}\ \ (\sigma',o,l).\]
Úloha:
Dokážte, že problém rozdelenia množiny prirodzených čísel
\[\{a_1,\dots,a_n\}\] na dve podmnožiny s rovnakým súčtom je
NP-úplný aj v prípade ak \(a_i\neq a_j,\ i\neq j.\)
Návod: Rozdeľte množinu
\[\{1,2,...,n,Ka_1+1,Ka_2+2,...,Ka_n+n\}\] pre dostatočne veľké \(K\).
Úloha:
Dokážte: Ak by sme mali polynomiálny algoritmus na výpočet dĺžky najkratšej
TSP cesty, potom by sme mali
polynomiálny algoritmus na nájdenie najkratšej TSP cesty.
Úloha:
Dokážte, že ILP je v \(NP\).
Úloha:
Uvažujme o probléme nájdenia najkratšej \(s,t)\)cesty v
ohodnotenom
digrafe, keď pripušťame existenciu záporných ohodnotení.
(a) Dokážte, že existuje polynomiálny algoritmus pre
tento problém ak
predpokladáme, že neexistuje záporný cyklus.
(b) Dokážte, že bez predpokladu neexistencie záporného
cyklu je tento problém ťažko riešiteľný.
Daný je graf \(G=(V,E)\), množina \(L\subset V\) a prirodzené
číslo
\(k\). Dokážte, že problém je NP-úplný
Existuje v \(G\) kostra grafu \(T\) taká, že množina
koncových
vrcholov kostry \(T\) je \(L\)?\\
Úloha:
Dokážte, že nasledujúci problém je NP-úplný
Daný je digraf \(D=(V,A)\) a \(2k\) vrcholov
\(s_1,s_2,\dots,s_k,t_1,t_2,\dots,t_k\in V\). Existuje v \(D\) \(k\)
vrcholovo-disjunktných ciest z
\[s_1\ \ do \ \ t_1,\ \
s_2\ \ do\ \ t_2,\ ...,\
s_k\ \ do\ \ t_k?\]
Úloha:
Navrhnite algoritmus na testovanie, či daný graf obsahuje
záporný cyklus.
11. Trieda co-NP a aproxímativné algoritmy.
Úlohy:
Úloha:
Problém kliky je silne
NP-úplný, pretože klika\(_n\) je rovnaký problém ako klika
nakoľko \(k=\)number\((I)\leqq V\) pre všetky zmysluplné inštancie \(I=((V,E),k)\) problému kliky.
- Nájdi minimálnu kostru \(T\) grafu \(G\) s maticou vzdialenosti \((d_{ij})\).
- Vytvor multigraf \(G\) zdvojením každej hrany kostry \(T\).
- Nájdi eulerovské spojenie grafu \(G\) a zahniezdenú cestu. Veta 4. Algoritmus Kostra je 1-aproximatívny algoritmus pre TSP.
Úloha:
Algoritmus Kostra
- Nájdi minimálnu kostru $T$ grafu $G$ s maticou vzdialeností \((d_{ij})\).
- vrcholy \(T\), ktoré majú nepárny stupeň a kompletné spárenie \(M\) s minimálnym súčtom ohodnotení hrán v kompletnom grafe pozostávajúcom len z týchto vrcholov. Nech \(G'\) je multigraf s vrcholmi \(\{1,\dots,n\}\) a hranami patriace \(T\) a patriace \(M\).
- Nájdi eulerovské spojenie a zahniezdenú cestu.
Úloha:
Christofides