Ciele
- Eulerovské grafy.
- Problém okružnej cesty.
- Farbenie grafov.
- Chromatické číslo grafu.
- Chromatický index grafu.
Úvod
-
Obsah toho cvičenia je tvorený dvomi veľkými časťami:
- Eulerovskosť grafov,
- Farbenie grafov.
S farbením grafov je úzko spätý pojem chromatického čísla - týka sa vrcholového farbenia a chromatického indexu - týka sa hranového farbenia grafov.
Pre úspešné zvládnutie toho cvičenia sa samozrejme predpokladá znalosť teoretických vedomosti prezentovaných na prednáške.
Postup
-
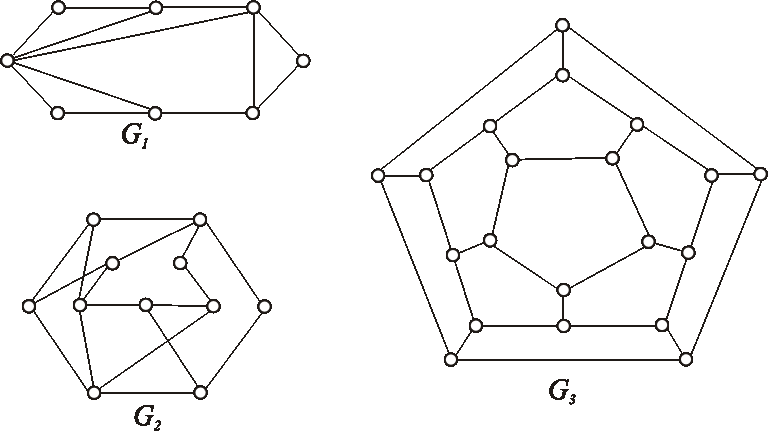
Príklad: Sú grafy zadané nasledujúcimi diagramami eulerovské?
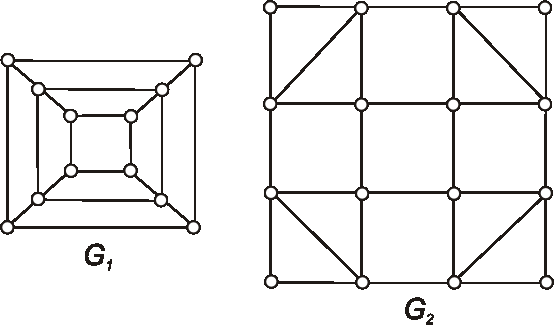
-
Príklad: Dajú sa grafy zadané nasledujúcimi diagramami pokryť jedným uzavretým ťahom?
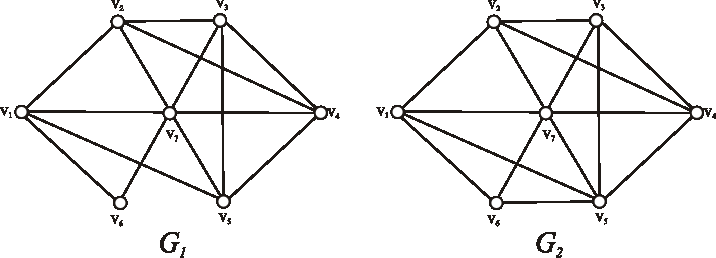
-
Príklad: Pre graf daný nasledujúcim diagramom vyriešte problém okružnej cesty.
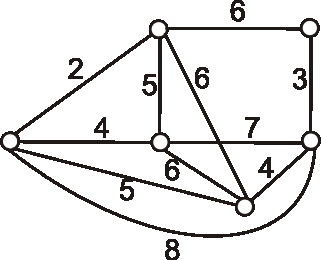
-
Príklad: Pre graf daný nasledujúcim diagramom vyriešte problém okružnej cesty.
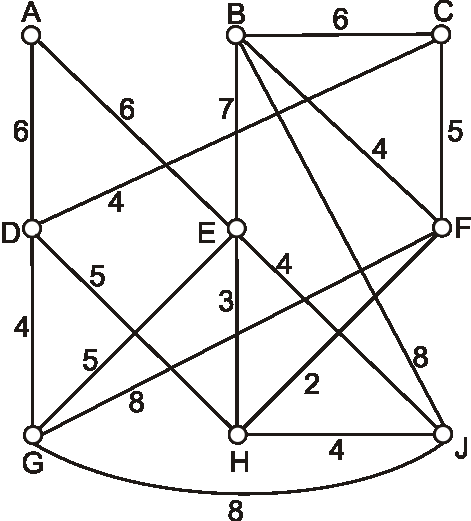
-
Príklad: Pre grafy dané nasledujúcimi diagramami vyriešte problém okružnej cesty.
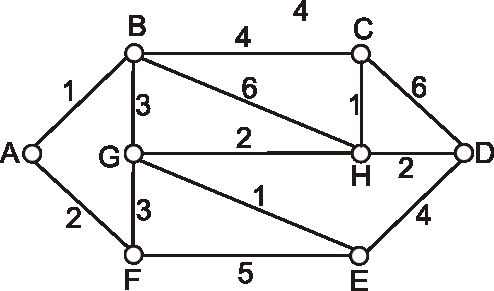
-
Príklad: Pre grafy dané nasledujúcimi diagramami vyriešte problém okružnej cesty.
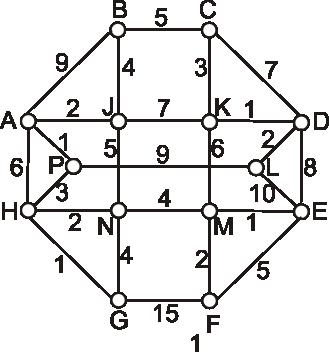
-
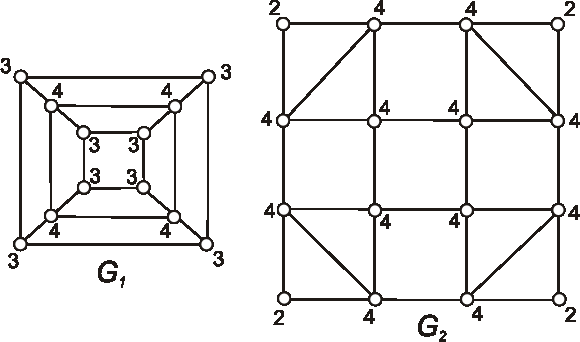
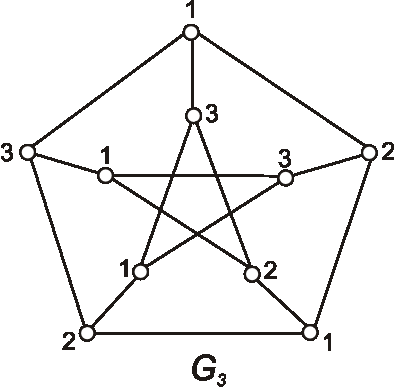
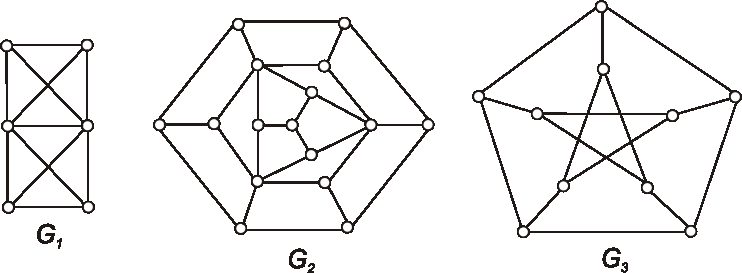
Príklad: Určte chromatické číslo grafov daných nasledujúcimi diagramami.
-
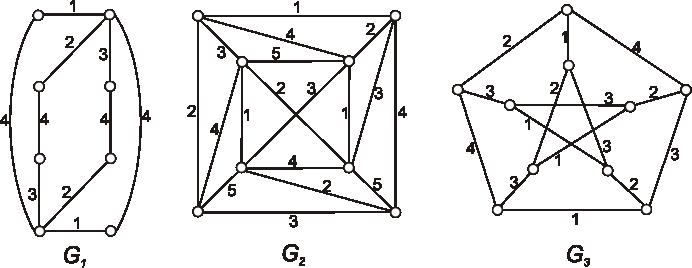
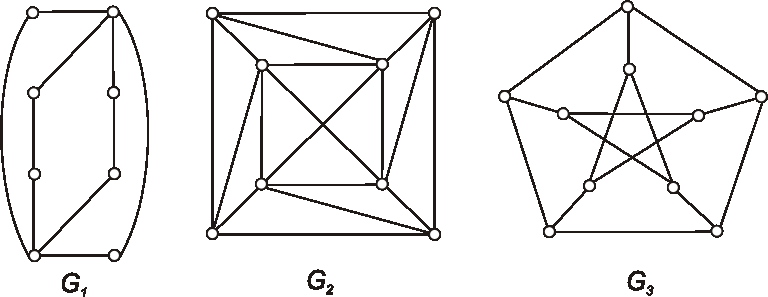
Príklad: Určte chromatický index grafov daných nasledujúcimi diagramami.
Zdroje
- Klešč M.: Diskrétna matematika, Košice, 2006.
- Bučko M. - Klešč, M.: Diskrétna matematika, Elfa, Košice, 1999.
- Klešč M. - Plavka, J.: Grafové algoritmy a formálna logika, Košice 2008.
- Matoušek J. - Nešetřil J.:Kapitoly z diskrétní matematiky, Matfyzpress, Praha 1996.
Doplňujúce úlohy
Úloha:
Ktoré z grafov, znázornených nasledujúcimi diagramami, sú eulerovské?
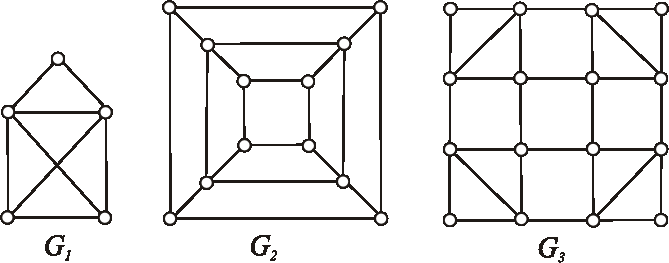 Ak sú, pokúste sa nakresliť ich diagramy jedným uzavretým ťahom.
Ak sú, pokúste sa nakresliť ich diagramy jedným uzavretým ťahom.

Úloha:
V grafoch daných nasledujúcimi diagramami zistite hodnotu minimálnej okružnej cesty.
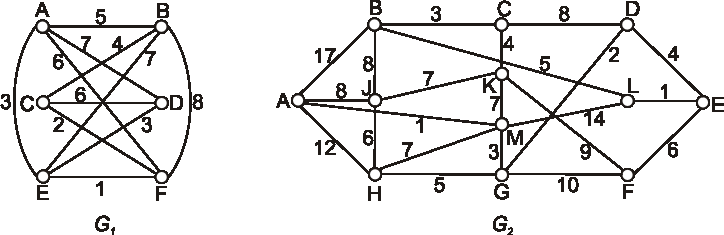

Úloha:
Minimálne koľko vrcholov musí mať graf so \(74\) hranami, aby sme vedeli zaručiť, že
chromatický index grafu je aspoň \(5\)?
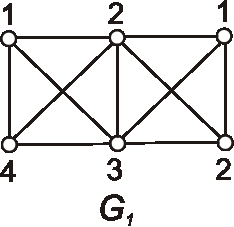
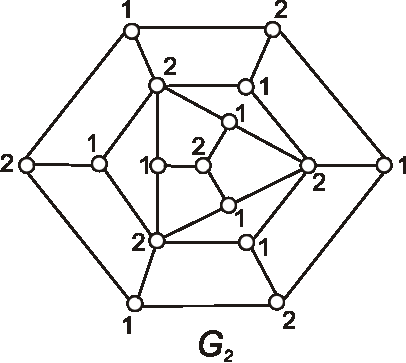
Úloha:
Nájdite chromatické číslo a chromatický index grafov daných nasledujúcimi diagramami.