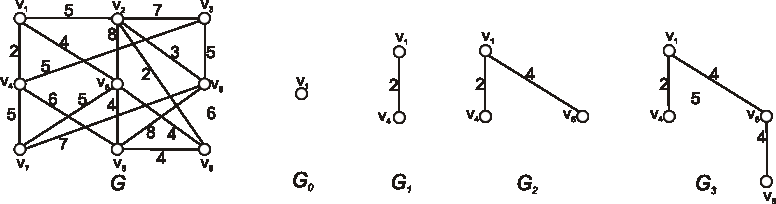Ciele
- Matica incidencie a matica susednosti grafu aj digrafu.
- Súvislosť grafov.
- Počet kostier grafu.
- Počet kostier a koreňových kostier digrafu.
- Hranovo ohodnotené grafy a ich charakteristiky.
- Minimálna kostra grafu.
Úvod
-
Maticová reprezentácia grafu je jednou z veľmi dôležitých reprezentácii grafu.
Často sa pomocou nej zadávajú grafy na vstupe rôznych grafových algoritmov.
Po úspešnom absolvovaní tohto cvičenia by mal študent zvládnuť nasledujúce:
- zapísať graf aj digraf pomocou matice incidencie a matice susednosti a naopak z matice prejsť na reprezentáciu grafu pomocou diagramu;
- len na základe matice určiť súvislosť grafu, polomer, priemer a vzdialenosti v grafe;
- pomocou maticových operacii vypočítať počet kostier grafu;
- pomocou maticových operacii vypočítať počet kostier digrafu;
- pomocou maticových operacii vypočítať počet koreňových kostier digrafu vzhľadom na určitý koreň;
- pomocou vhodného algoritmu nájsť minimálnu kostru v grafe;
Postup
-
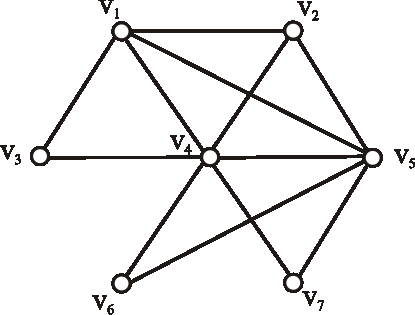
Príklad: Zapíšte maticu incidencie (\(A\)) a maticu susednosti (\(B\)) grafu daného nasledujúcim diagramom: (hrany a vrcholy najprv označte)
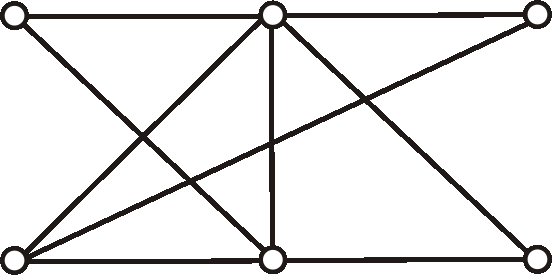
-
Príklad: Nech je daný graf \(G\) nasledujúcou maticou susednosti. Znázornite tento graf diagramom. \[B=\left ( \begin{array}{c} 0\\ 1\\ 1\\ 1\\ 0\\ 0\\ 0 \end{array} \begin{array}{c} 1\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0 \end{array} \begin{array}{c} 1\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0 \end{array} \begin{array}{c} 1\\ 1\\ 1\\ 0\\ 1\\ 1\\ 1 \end{array} \begin{array}{c} 0\\ 0\\ 0\\ 1\\ 1\\ 0\\ 0 \end{array} \begin{array}{c} 0\\ 0\\ 0\\ 1\\ 1\\ 0\\ 0 \end{array} \begin{array}{c} 0\\ 1\\ 1\\ 0\\ 1\\ 0\\ 0 \end{array}\right ) \]
-
Príklad: Nech je daný digraf \(\vec{D}\) nasledujúcou maticou susednosti. Znázornite tento digraf diagramom. \[\vec{B}=\left ( \begin{array}{c} 0\\ 1\\ 1\\ 0\\ 0 \end{array} \begin{array}{c} 0\\ 0\\ 0\\ 1\\ 0 \end{array} \begin{array}{c} 0\\ 0\\ 0\\ 0\\ 0 \end{array} \begin{array}{c} 1\\ 1\\ 0\\ 0\\ 0 \end{array} \begin{array}{c} 1\\ 0\\ 0\\ 1\\ 0 \end{array}\right ) \]
-
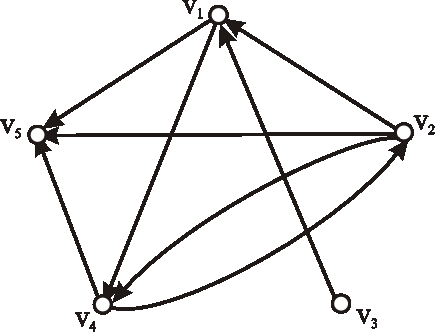
Príklad: Majme daný digraf \(\vec{D}\) diagramom. Zapíšte maticu incidencie aj maticu susednosti daného digrafu.
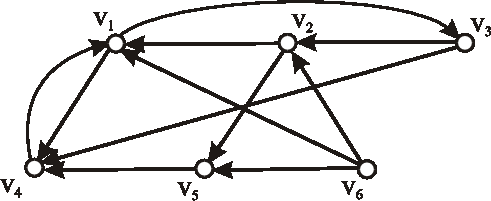
-
Príklad: Nech je daný graf \(G\) nasledujúcou maticou susednosti. \[B=\left ( \begin{array}{r} 0\\ 1\\ 0\\ 1\\ 0 \end{array} \begin{array}{r} 1\\ 0\\ 0\\ 1\\ 0 \end{array} \begin{array}{r} 0\\ 0\\ 0\\ 0\\ 1 \end{array} \begin{array}{r} 1\\ 1\\ 0\\ 0\\ 0 \end{array} \begin{array}{r} 0\\ 0\\ 1\\ 0\\ 0 \end{array}\right ) \] Bez kreslenia diagramu grafu zistite, či je graf súvislý.
-
Príklad: Nech je daný graf \(G\) nasledujúcou maticou susednosti. \[B=\left ( \begin{array}{r} 0\\ 1\\ 0\\ 0\\ 0 \\0 \\0 \end{array} \begin{array}{r} 1\\ 0\\ 1\\ 0\\ 0 \\0 \\0 \end{array} \begin{array}{r} 0\\ 1\\ 0\\ 1\\ 0 \\0 \\0 \end{array} \begin{array}{r} 0\\ 0\\ 1\\ 0\\ 1 \\1 \\0 \end{array} \begin{array}{r} 0\\ 0\\ 0\\ 1\\ 0 \\0 \\0 \end{array} \begin{array}{r} 0\\ 0\\ 0\\ 1\\ 0 \\0 \\1 \end{array} \begin{array}{r} 0\\ 0\\ 0\\ 0\\ 0 \\1 \\0 \end{array}\right ) \] Bez kreslenia diagramu grafu:
- zistite či je daný graf súvislý;
- určte polomer, priemer a stred daného grafu;
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je práve 3;
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je viac ako 3.
-
Príklad: Nech je daný digraf \(G\) nasledujúcim diagramom. Určte počet kostier daného grafu.
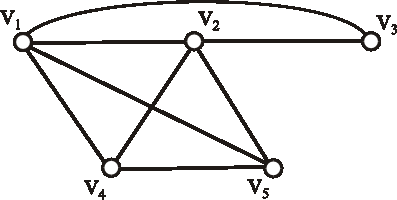
-
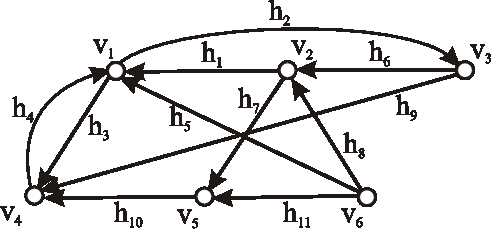
Príklad: Nech je daný digraf \(\vec{D}\) nasledujúcim diagramom. Určte počet:
- všetkých kostier daného digrafu;
- koreňových kostier s vrcholom \(v_2\) ako koreňom;
- všetkých koreňových kostier daného digrafu;
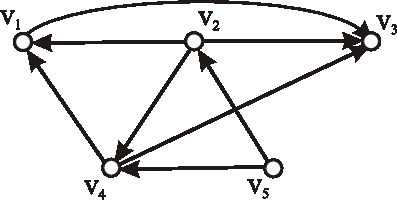
-
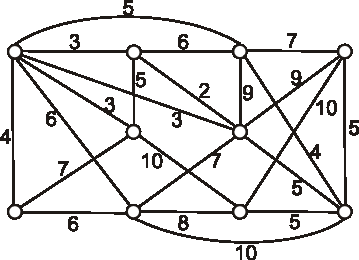
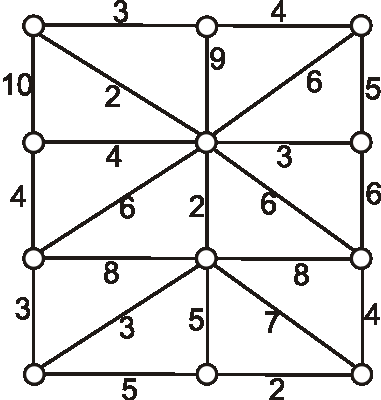
Príklad: Nech je daný graf \(G\) nasledujúcim diagramom. Pomocou Kruskalovho algoritmu určte minimálnu kostru a vypočítajte súčet jej ohodnotení.
-
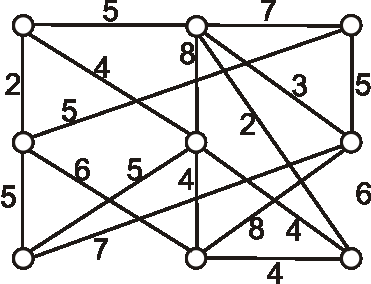
Príklad: Nech je daný graf \(G\) nasledujúcim diagramom. Pomocou Primovho algoritmu určte minimálnu kostru a vypočítajte súčet jej ohodnotení.
Zdroje
- Klešč M.: Diskrétna matematika, Košice, 2006.
- Bučko M. - Klešč, M.: Diskrétna matematika, Elfa, Košice, 1999.
- Klešč M. - Plavka, J.: Grafové algoritmy a formálna logika, Košice 2008.
- Berežný, Š. - Draženská, E. - Kravecová, D.: Zbierka úloh z diskrétnej matematiky, Košice 2005.
Doplňujúce úlohy
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je najviac 2;
- nájdite všetky dvojice vrcholov, ktorých vzdialenosť je práve 4.
Úloha:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0
\end{array}\right )
\]
Bez kreslenia diagramu grafu zistite, či je graf súvislý.
Úloha:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 1\\ 0\\ 0 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 1\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 1\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1 \\0 \\1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 0 \\1 \\0
\end{array}\right )
\]
Bez kreslenia diagramu grafu určte polomer, priemer a stred daného grafu.
Úloha:
Nech je daný graf \(G\) nasledujúcou maticou susednosti.
\[B=\left (
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 1 \\0 \\1
\end{array}
\begin{array}{r}
0\\ 1\\ 1\\ 1\\ 0 \\1 \\0
\end{array}
\begin{array}{r}
1\\ 0\\ 0\\ 0\\ 1 \\0 \\0
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0 \\0 \\0
\end{array}\right )
\]
Bez kreslenia diagramu grafu:
Úloha:
Pre nasledujúce grafy dané maticami susednosti vypočítajte počet kostier.
\[B_1=\left (
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0
\end{array}\right )
; B_2=\left (
\begin{array}{r}
0\\ 0\\ 1\\ 1\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 1\\ 0
\end{array}
\begin{array}{r}
1\\ 0\\ 1\\ 0\\ 1
\end{array}
\begin{array}{r}
0\\ 1\\ 0\\ 1\\ 0
\end{array}\right )
; B_3=\left (
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 0\\ 1\\ 1
\end{array}
\begin{array}{r}
0\\ 0\\ 0\\ 1\\ 0\\ 0
\end{array}
\begin{array}{r}
0\\ 0\\ 1\\ 0\\ 0\\ 0
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 0\\ 0\\ 1
\end{array}
\begin{array}{r}
1\\ 1\\ 0\\ 0\\ 1\\ 0
\end{array}\right )
\]
Úloha:
Koľko hrán je potrebné odstrániť z nasledujúcich grafov, aby vznikla kostra?
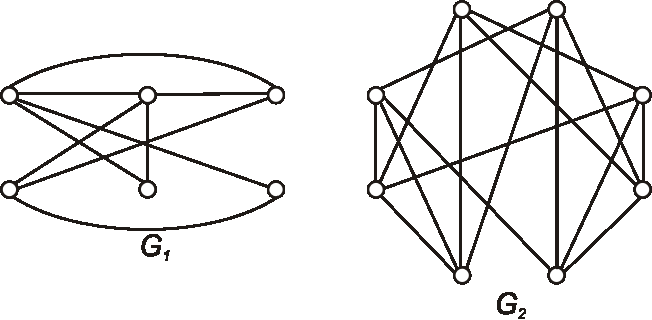

Úloha:
Nech je daný graf \(G\) nasledujúcim diagramom. Vypočítajte počet kostier daného grafu.
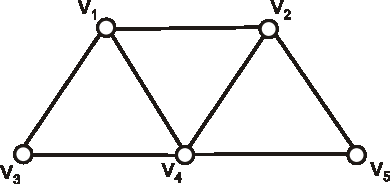

Úloha:
Nech je daný graf \(G\) nasledujúcim diagramom. Vypočítajte počet kostier grafu \(\bar{G}-v_3\),
kde \(\bar{G}\) je komplementom ku grafu \(G\).
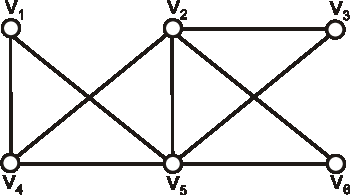

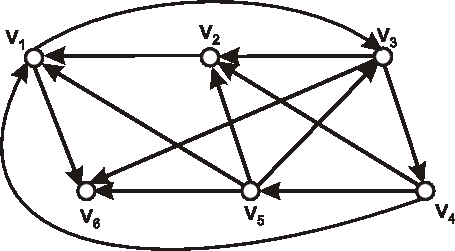
Úloha:
Nech je daný digraf nasledujúcim diagramom. Vypočítajte počet jeho kostier.

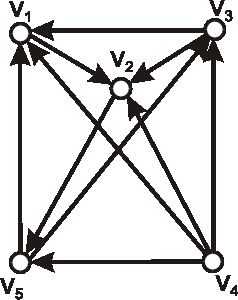
Úloha:
Nech je daný digraf \(\vec{D}\) nasledujúcim diagramom. Vypočítajte počet koreňových
kostier digrafu \(\vec{D}\) s koreňom vo vrchole \(v_3\).

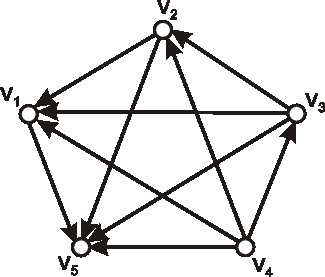
Úloha:
Nech je daný digraf \(\vec{D}\) nasledujúcim diagramom. Vypočítajte počet kostier aj počet koreňových
kostier digrafu \(\vec{D}\).

Úloha:
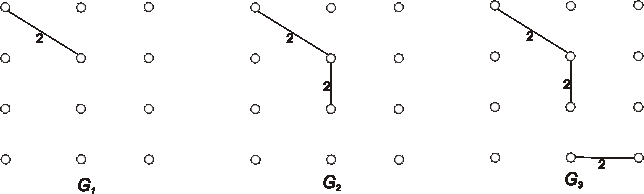
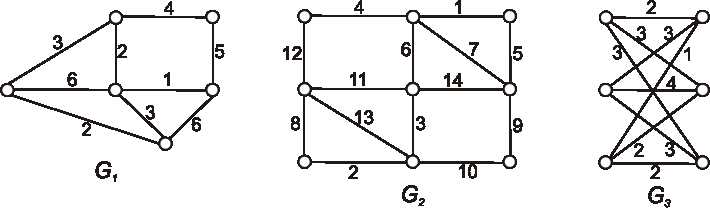
Kruskalovým aj Primovým algoritmom nájdite v nasledujúcich grafoch minomálne kostry.

Úloha:
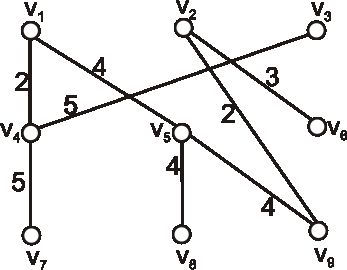
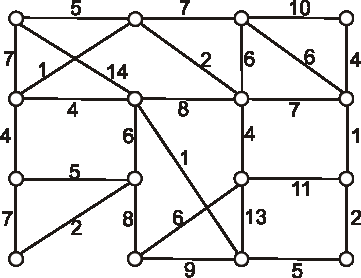
Použitím Primovho algoritmu nájdite minimálnu kostru v grafe danom nasledujúcim diagramom.

Úloha:
Pokúste sa modifikáciou Primovho algoritmu nájsť MAXIMÁLNU kostru v grafe z predchádzajúcej úlohy.
Úloha:
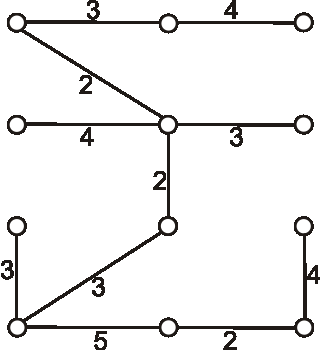
Telekomunikácie potrebujú položiť optický kábel tak, aby sa z každého uzla dalo dostať do každého a
nech je položenie káblovej siete čo najlacnejšie. Nasledujúci diagram znázorňuje uzly a možnosti ich
prepojenia. Čísla znázorňujú náklady na položenie kábla na konkrétnom úseku.