Ciele
- Grafová postupnosť.
- Izomorfizmus grafov.
- Sledy, ťahy, cesty, kružnice.
- Vzdialenosti v grafe.
- Polomer, priemer a stred grafu.
- Stromy. Polomer, priemer a stred stromu.
- Orientované stromy.
Úvod
-
Na tomto cvičení sa budeme zaoberať grafovou postupnosťou, jej nejednoznačnosťou a prechodom z postupnosti
na diagram a naopak. Ďalším dôležitým pojmom je izomorfizmus grafov. Metrické vlastnosti grafov si overíme
v príkladoch na grafoch aj stromoch. Vysvetlíme a precvičíme si základné pojmy týkajúce sa stromov.
Pre úspešné zvládnutie toho cvičenia sa predpokladajú teoretické vedomosti prezentované na prednáške.
Postup
-
Úloha: Zistite, či dané postupnosti sú grafové. Zdôvodnite.
- 6, 5, 4, 4, 4, 3, 2, 1
- 8, 5, 3, 3, 3, 3, 2, 1
- 5, 4, 4, 3, 3, 2, 2, 1
-
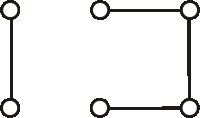
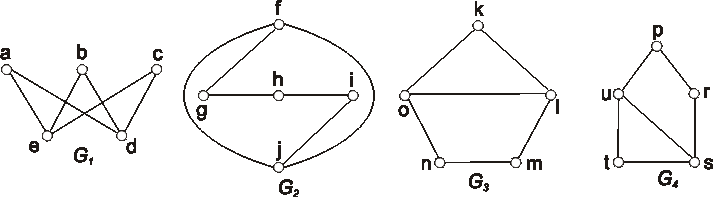
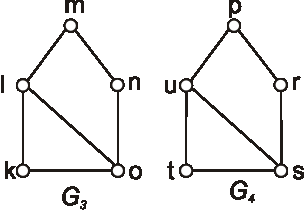
Úloha: Zistite, ktoré z diagramov znázornených na obrázku, reprezentujú izomorfné grafy? Označte vrcholy a nájdite izomorfizmus, alebo zdôvodnite, prečo nie sú izomorfné.
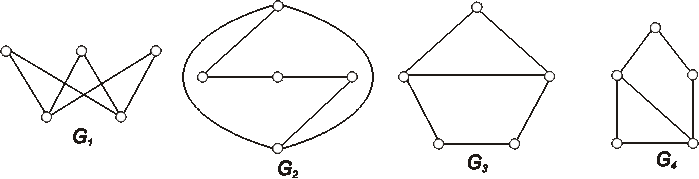
-
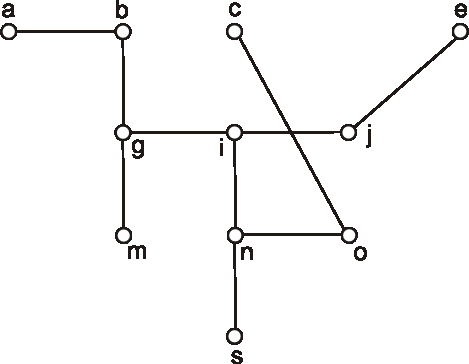
Úloha: V grafe G danom nasledujúcim diagramom nájdite všetky vrcholy, ktorých vzdialenosť od vrcholu \(v_1\) je tri.
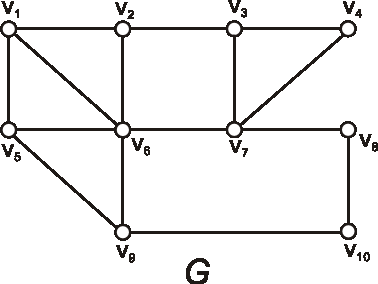
-
Úloha: Určte excentricity všetkých vrcholov, polomer, priemer a stred grafu \(G\) z predchádzajúceho príkladu.
-
Úloha: Aký je súčet stupňov vrcholov v strome s 9 vrcholmi? Aký je súčet stupňov vrcholov, ak počet vrcholov je \(n\)?
-
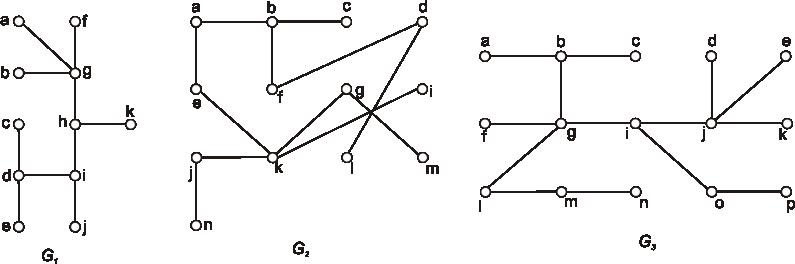
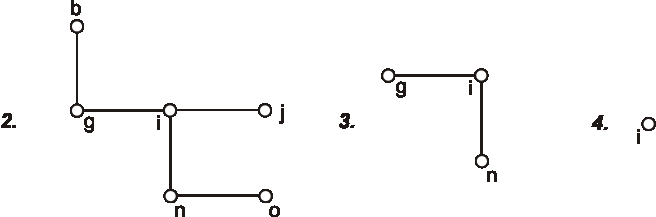
Úloha: Nájdite polomer, priemer a stred stromu, ktorého diagram je na obrázku:
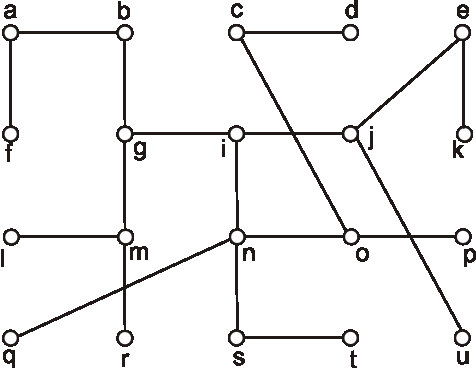
-
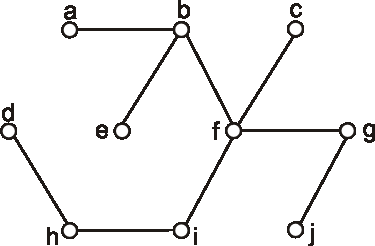
Úloha: Nájdite polomer, priemer a stred stromu, ktorého diagram je na obrázku:
-
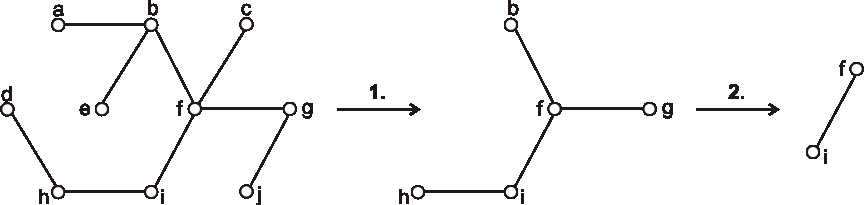
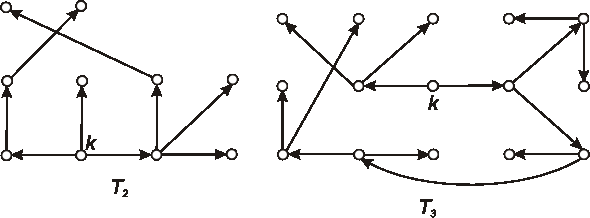
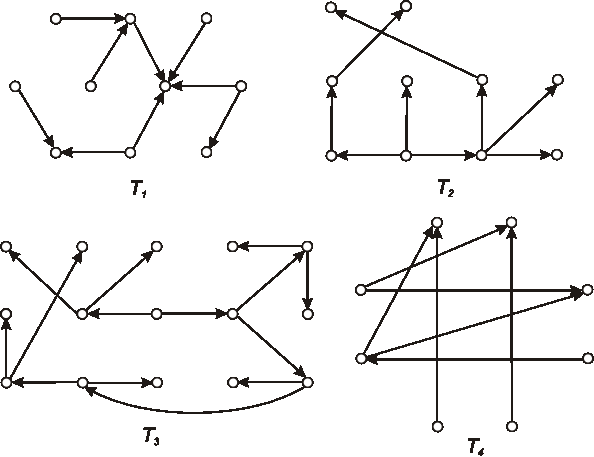
Úloha: Na nasledujúcom obrázku sú znázornené diagramy 4 orientovaných stromov. O každom jednom rozhodnite, či je alebo nie je koreňovým stromom. Ak je, overte či je alebo nie je binárným stromom a pre binárne stromy určte ich hĺbku.
Zdroje
- Klešč M.: Diskrétna matematika, Košice, 2006.
- Bučko M. - Klešč, M.: Diskrétna matematika, Elfa, Košice, 1999.
- Klešč M. - Plavka, J.: Grafové algoritmy a formálna logika, Košice 2008.
- Matoušek J. - Nešetřil J.: Kapitoly z diskrétní matematiky, Matfyzpress, Praha 1996.
Doplňujúce úlohy
Úloha:
Zistite, či dané postupnosti sú grafové. Ak nie, zdôvodnite
prečo, ak áno, nakreslite diagram príslušného grafu.
a) 3,6,2,1,5,4,3
b) 4,5,3,5,5,5,5,4
c) 4,7,3,3,5,5,4,7,7,4,4,3
d) 12,6,8,2,11,3,7,14,11,9,7,2,2,2,5,4,3
a) 3,6,2,1,5,4,3
b) 4,5,3,5,5,5,5,4
c) 4,7,3,3,5,5,4,7,7,4,4,3
d) 12,6,8,2,11,3,7,14,11,9,7,2,2,2,5,4,3
Úloha:
Pre aké \(k\) je postupnosť grafová? Nakreslite diagram zodpovedajúcich grafov.
\(5, 3, k, 3, 3, 1\).
\(5, 3, k, 3, 3, 1\).
Úloha:
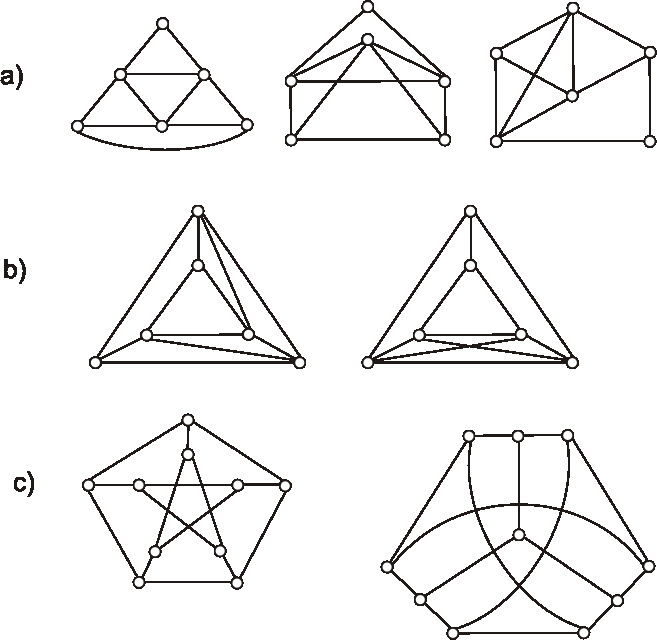
Ktoré z grafov, ktorých diagramy sú znázornené na obrázkoch, sú izomorfné?
Označte ich vrcholy a nájdite izomorfizmus, alebo zdôvodnite, prečo nie sú izomorfné.

Úloha:
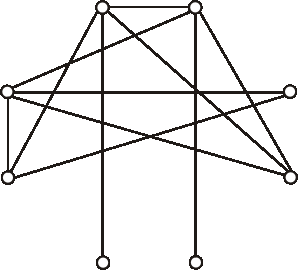
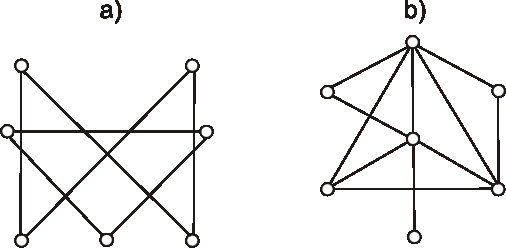
Je možné graf zadaný diagramom zobraziť sám na seba tak, aby zobrazenie nebolo identitou? Zdôvodnite.

Úloha:
Znázornite diagramy všetkých neizomorfných stromov s piatimi hranami.
Úloha:
Nájdite polomer, priemer a stred stromov, daných diagramami: