Ciele
- Nájsť minimálne časové ohodnotenie procesu reprezentovaného acyklickým digrafom.
- Nájsť maximálne časové ohodnotenie procesu reprezentovaného acyklickým digrafom.
- Použiť CPM a nájsť kritickú cestu v digrafe.
- Vypočítať priemerné doby trvania jednotlivých činností procesu reprezentovaného acyklickým digrafom.
- Stanoviť pravdepodobnosť ukončenia procesu v časoch odlišných od času získaného pomocou CPM.
- Zistiť dobu ukončenia celého procesu s vopred stanovenou pravdepodobnosťou.
- Ford-Fulkersonov algoritmus.
Úvod
-
Pre úspešné zvládnutie toho cvičenia sa predpokladajú teoretické vedomosti prezentované na prednáške.
- Pre CPM ide o znalosť základných pojmov, ako sú: ohodnotenie hrany, hranovo-ohodnotený súvislý acyklický digrf, kritická činnosť, kritická hrana, kritická cesta, minimálne a maximálne časové ohodnotenie. Ďalej sa predpokladá teoretické zvládnutie algoritmov pre minimálne aj maximálne časové ohodnotenie.
- Pre metódu PERT je nutná znalosť základných pojmov: optimistický odhad, pesimistický odhad, normálny odhad trvania činnosti, smerodajná odchýlka, vážený priemer, rozptyl. Tiež sú potrebné aspoň základné vedomosti týkajúce sa normálneho normovaného rozdelenia náhodnej premennej.
- Pre určenie toku v sieti je potrebné poznať základné pojmy: kapacita hrany, tok hranou, veľkosť toku, sieť, nasýtený tok, maximálny tok, prameň siete, ústie siete, susedný vrchol. Tiež je potrebné poznať Ford - Fulkersonov algoritmus preberaný na prednáške.
Postup
-
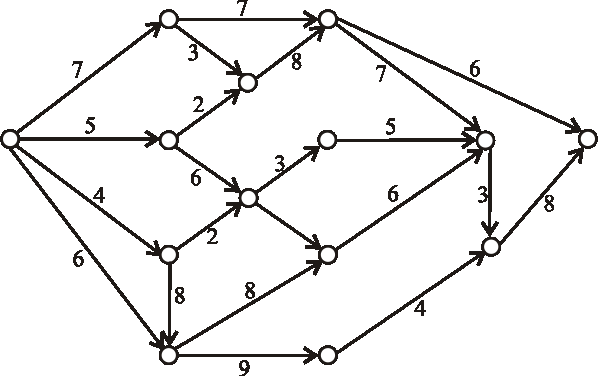
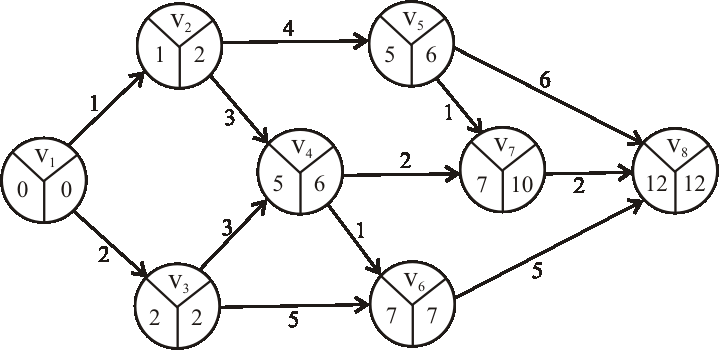
Príklad: Zistite, či je nasledujúci hranovo-ohodnotený digraf acyklický, či teda môže byť reprezentáciou nejakého výrobného procesu. Ak áno, topologický očíslujte vrcholy daného grafu.
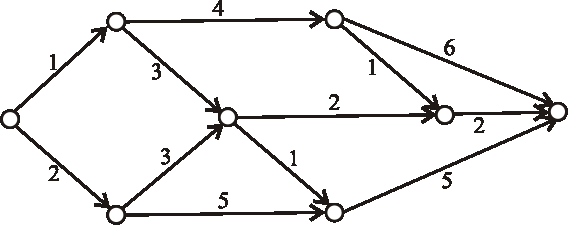
-
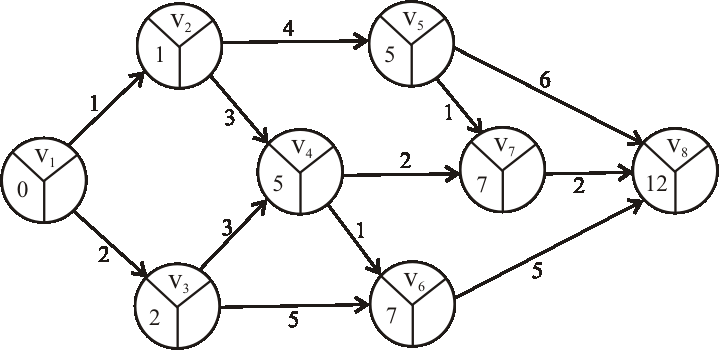
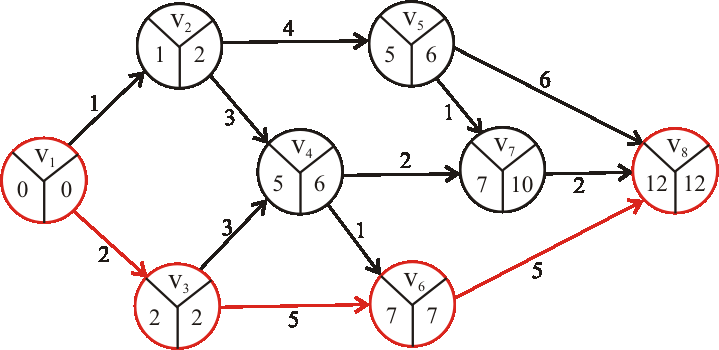
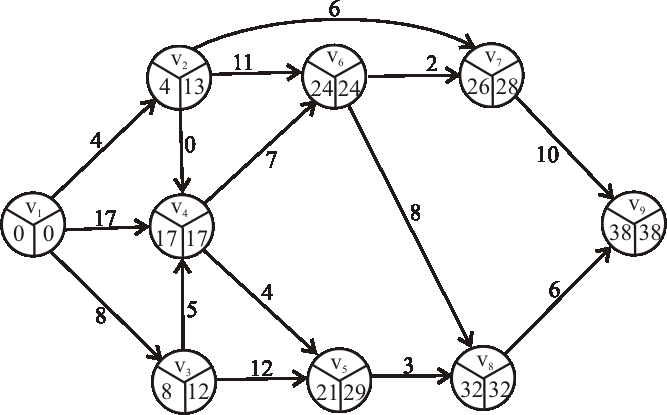
Príklad: Pomocou metódy CPM určte dĺžku a nájdite kritické cesty výrobného procesu reprezentovaného acyklickým digrafom z predchádzajúcej úlohy.
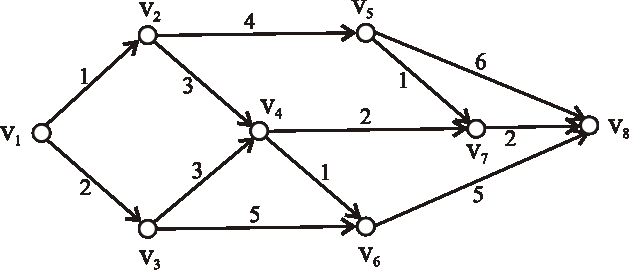
-
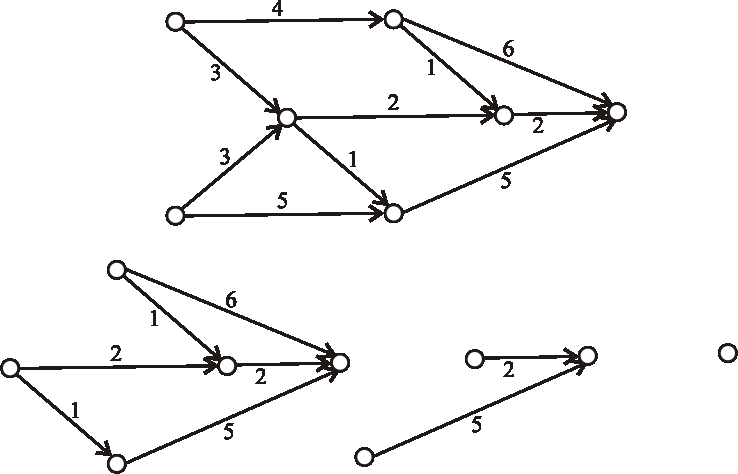
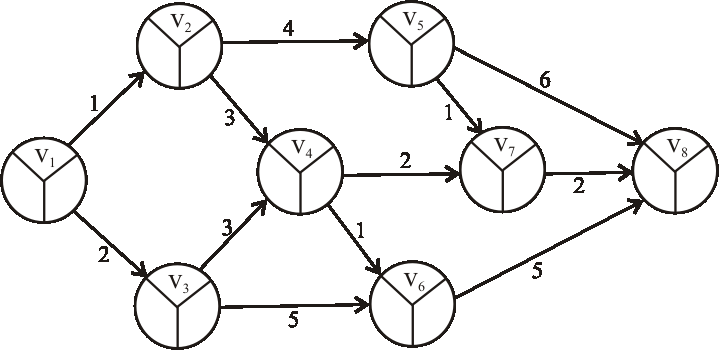
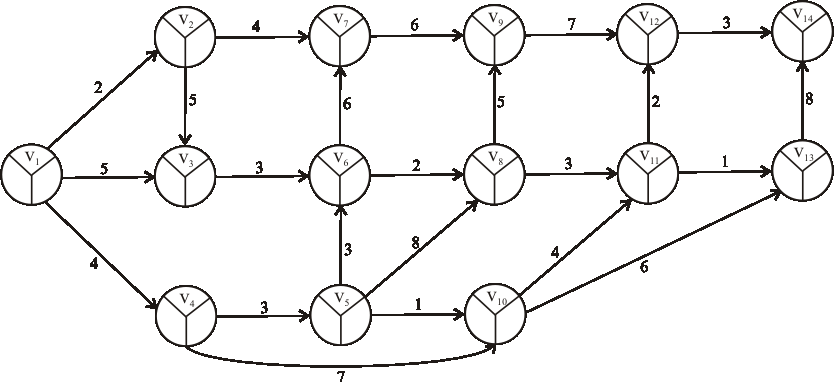
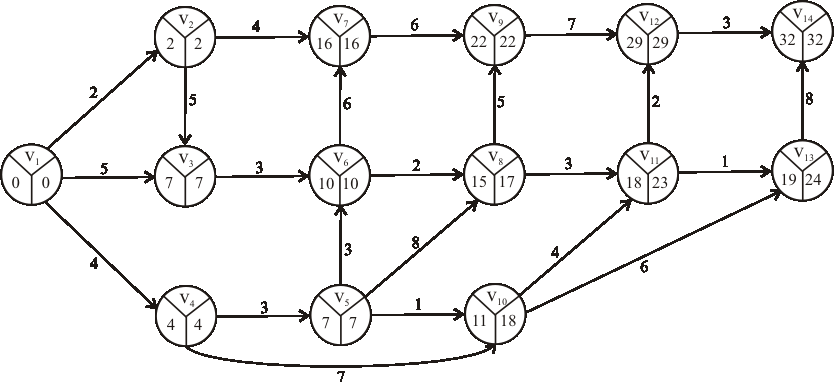
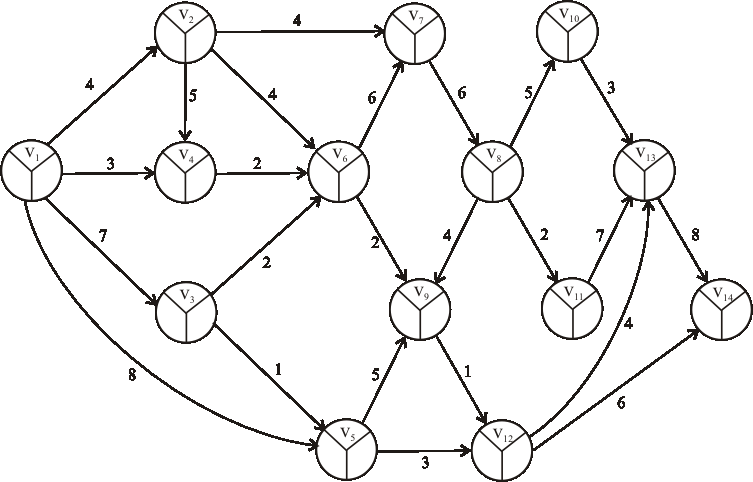
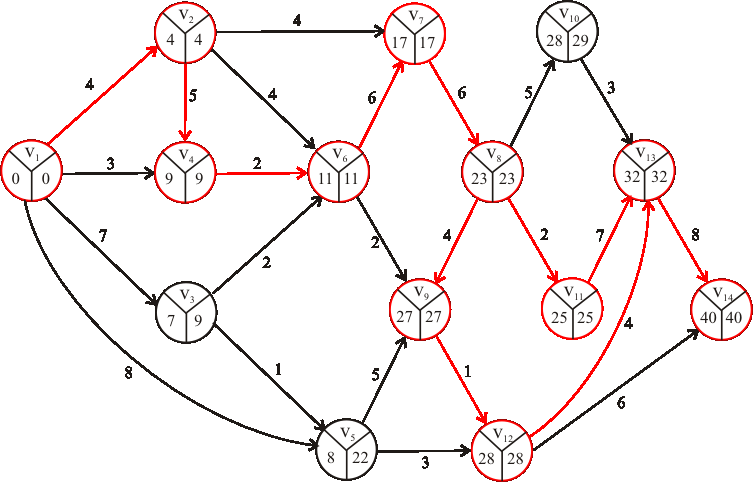
Príklad: Nájdite kritické cesty výrobného procesu reprezentovaného nasledujúcim acyklickým digrafom.
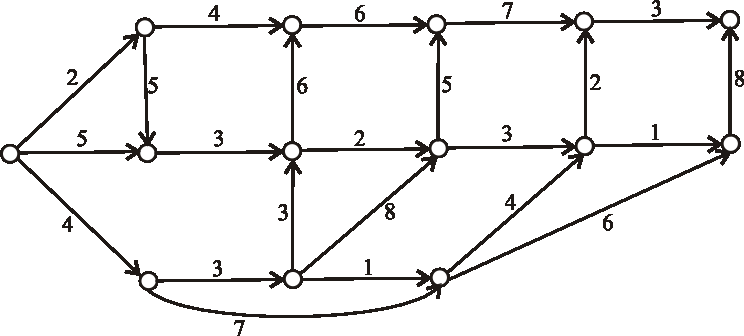
-
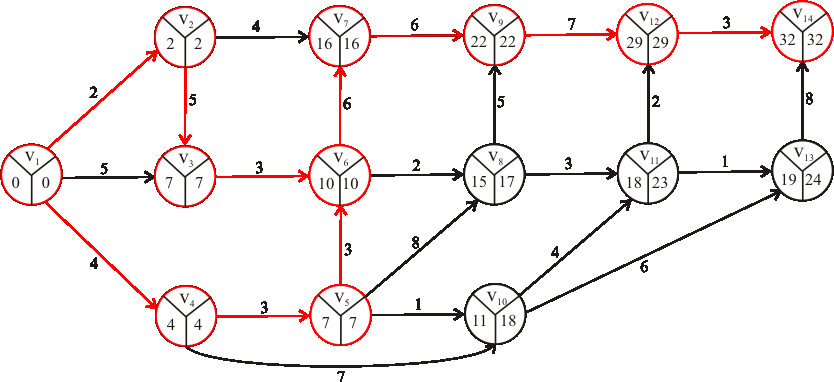
Príklad: Je daný výrobný proces, ktorý obsahuje 14 uzlov (teda 14 vrcholov). Každá činnosť je daná dvojicou uzlov, pričom prvý uzol určuje začiatok a druhý koniec činnosti. Zoznam činností a ich časových trvaní je v nasledujúcej tabuľke. Pomocou metódy kritickej cesty vypočítajte minimálne časové trvanie výrobného procesu a nájdite kritické cesty.
činnosť \(u_1u_8\) \(u_2u_1\) \(u_2u_6\) \(u_2u_{10}\) \(u_3u_5\) \(u_4u_2\) \(u_5u_1\) čas \(1\) \(4\) \(5\) \(2\) \(2\) \(6\) \(2\) činnosť \(u_5u_4\) \(u_6u_{11}\) \(u_7u_1\) \(u_7u_8\) \(u_8u_9\) \(u_8u_{11}\) \(u_{10}u_{11}\) čas \(6\) \(3\) \(5\) \(3\) \(6\) \(4\) \(7\) činnosť \(u_{11}u_9\) \(u_{12}u_{3}\) \(u_{12}u_4\) \(u_{12}u_5\) \(u_{13}u_3\) \(u_{13}u_{7}\) \(u_{13}u_{12}\) čas \(8\) \(5\) \(4\) \(4\) \(3\) \(8\) \(4\) činnosť \(u_{13}u_{14}\) \(u_{14}u_{5}\) \(u_{14}u_7\) čas \(7\) \(2\) \(1\) -
Príklad: Je daný projekt, ktorý obsahuje 9 uzlov (teda 14 vrcholov). Každá činnosť je daná dvojicou uzlov, pričom prvý uzol určuje začiatok a druhý koniec činnosti. Zoznam činností a ich odhadov časových trvaní (v týždňoch) v poradí: optimistický odhad, normálny odhad, pesimistický odhad je v nasledujúcej tabuľke. Pre každú činnosť vypočítajte priemernú dobu trvania danej činnosti.
činnosť \(t_1t_2\) \(t_1t_3\) \(t_1t_4\) \(t_2t_4\) \(t_2t_6\) odhady času \(2;3;10\) \(5;7;15\) \(12;15;30\) \(0;0;0\) \(8;10;18\) činnosť \(t_2t_7\) \(t_3t_4\) \(t_3t_5\) \(t_4t_5\) \(t_4t_6\) odhady času \(4;6;8\) \(4;5;6\) \(7;10;25\) \(3;4;5\) \(4;6;14\) činnosť \(t_5t_8\) \(t_6t_7\) \(t_6t_8\) \(t_7t_9\) \(t_8t_9\) odhady času \(2;3;4\) \(2;2;2\) \(4;7;16\) \(8;9;16\) \(5;6;7\) -
Príklad: Pomocou metódy PERT určte dobu, za ktorú bude projekt z predchádzajúcej úlohy ukončený s pravdepodobnosťou 50%.
-
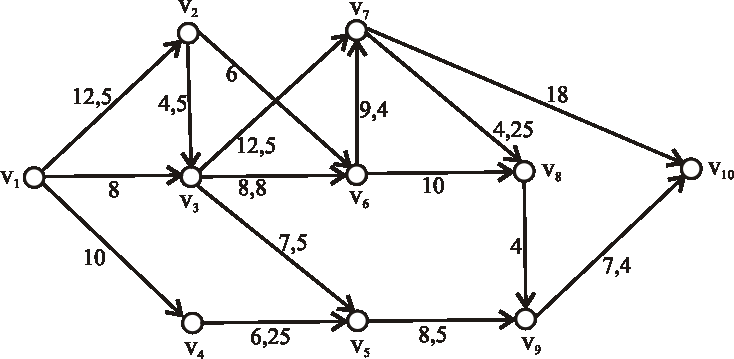
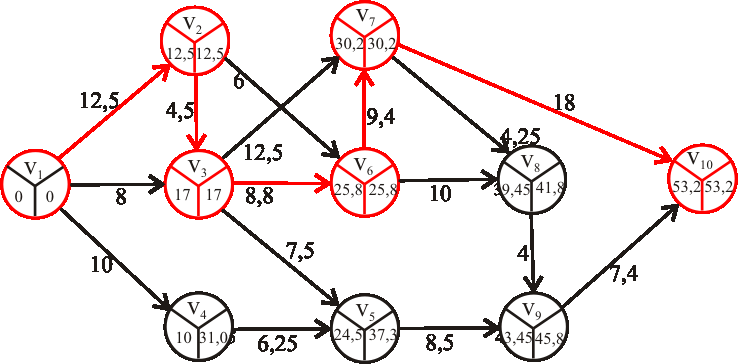
Príklad: Nech je daný projekt nasledujúcim ohodnoteným digrafom (časy sú uvedené v týždňoch).Pomocou metódy PERT určte:
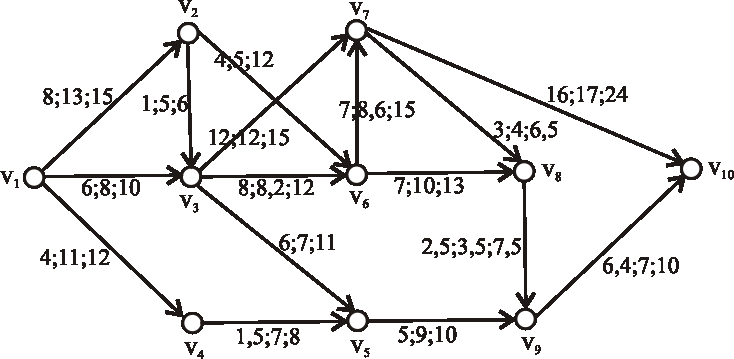
- s akou pravdepodobnosťou bude projekt ukončený za 60 týždňov,
- dobu, za ktorú bude projekt daný nasledujúcim ohodnoteným digrafom ukončený s pravdepodobnosťou 90%.
-
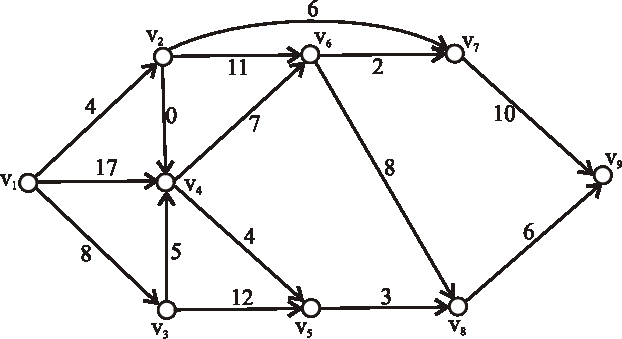
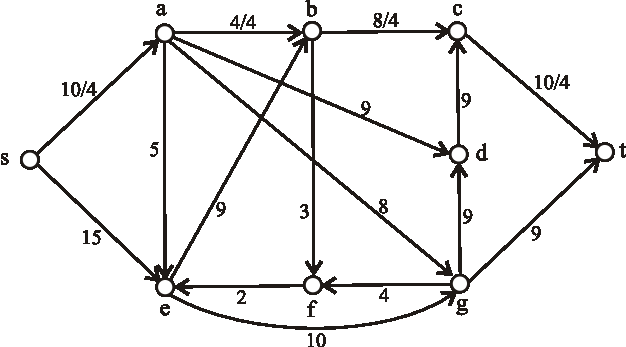
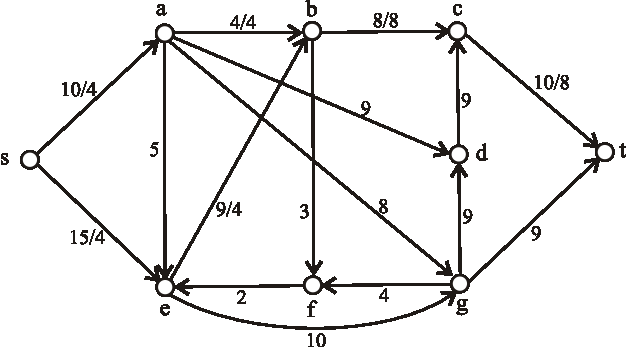
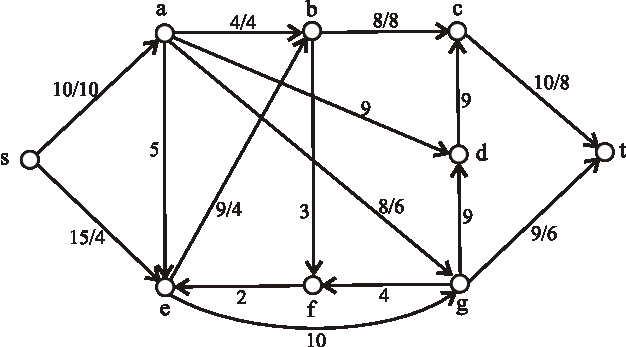
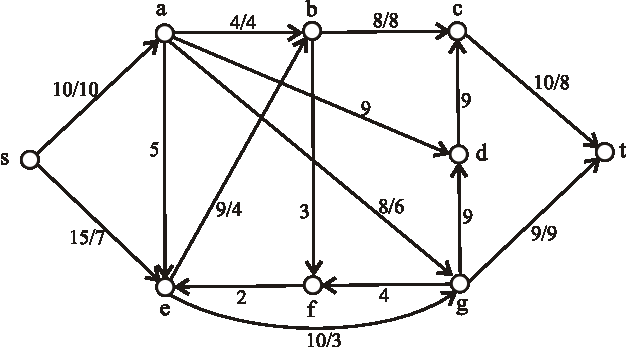
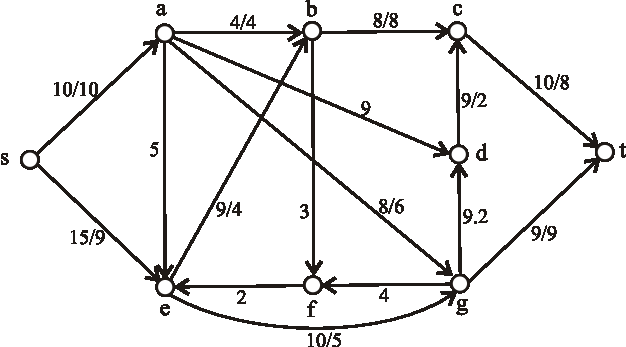
Príklad: Nasledujúci diagram znázorňuje sieť plynovodov plynárenského podniku s maximálnymi prepravnými kapacitami na jednotlivých úsekoch. Určte maximálnu tranzitnú kapacitu tejto siete, kde vrchol \(s\) predstavuje ťažobnú spoločnosť a vrchol \(t\) odberateľský plynárenský podnik.
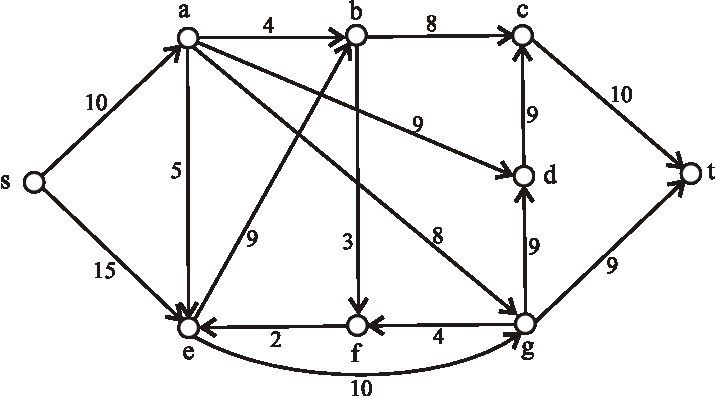
Zdroje
- Klešč M.: Diskrétna matematika, Košice, 2006.
- Bučko M. - Klešč, M.: Diskrétna matematika, Elfa, Košice, 1999.
- Klešč M. - Plavka, J.: Grafové algoritmy a formálna logika, Košice 2008.
- Matoušek J. - Nešetřil J.:Kapitoly z diskrétní matematiky, Matfyzpress, Praha 1996.
Doplňujúce úlohy
Úloha:
Nájdite kritické cesty výrobného procesu reprezentovaného nasledujúcim acyklickým digrafom.
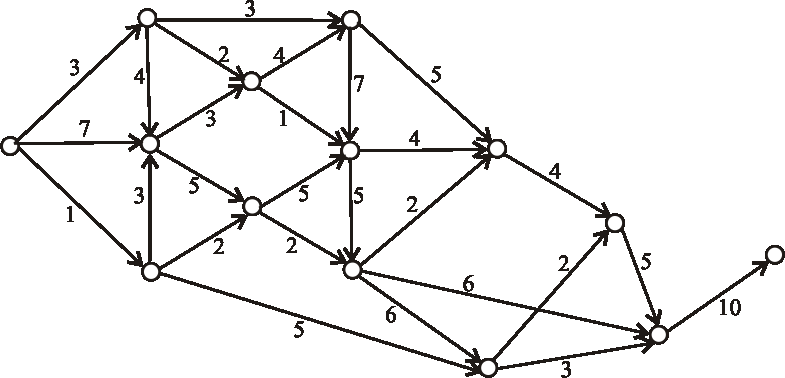

Úloha:
Nájdite kritické cesty výrobného procesu reprezentovaného nasledujúcim acyklickým digrafom.