Ciele
- Graf a jeho grafická reprezentácia.
- Operácie na grafoch.
- Pojmy: podgraf, faktor, stupeň vrchola, komponent grafu, súvislý graf.
- Základné vlastnosti grafov.
- Špeciálne grafy.
- Orientovaný graf - digraf a jeho grafická reprezentácia.
- Základné vlastnosti digrafov.
- Súvislosť a silná súvislosť digrafov.
Úvod
-
Na tomto cvičení sa budeme zaoberať precvičovaním základných definícií a viet z teórie grafov na
príkladoch. Budeme sa zaoberať definíciou neorientovaného aj orientovaného grafu a ich základnými
vlastnosťami. Pre lepšie pochopenie pojmov sa ich budeme snažiť interpretovať na grafickej
reprezentácií grafu.
Postup
-
Úloha: Aký najväčší počet hrán môže mať graf:
a) s \(20\)-timi vrcholmi,
b) s \(n\) vrcholmi? -
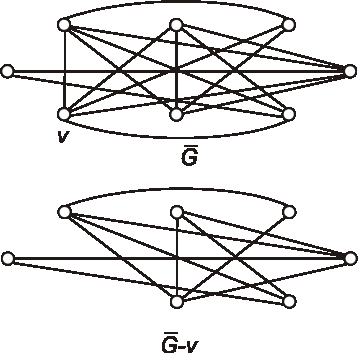
Úloha: Znázornite graf \(\bar{G}-v\), ak graf \(G\) je daný diagramom:
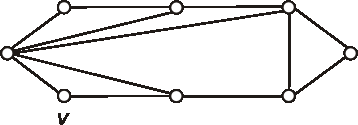
-
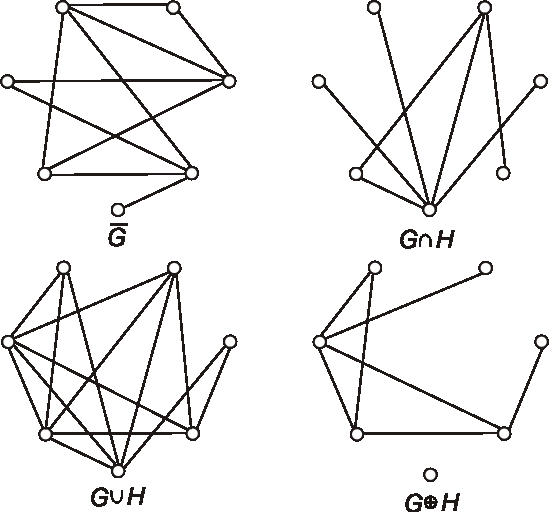
Úloha: Zadané sú diagramy grafov \(G, H\). Nakreslite diagramy grafov \(\bar{G}\), \(G \cap H\), \(G \cup H\) a \(G \oplus H\).
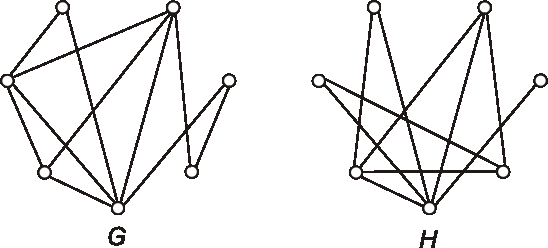
-
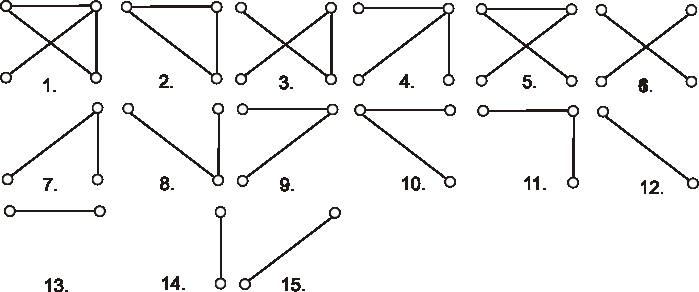
Úloha: Nájdite všetky podgrafy grafu znázorneného diagramom, ktoré neobsahujú izolované vrcholy. Koľko z nich je faktorov?
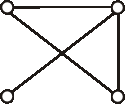
-
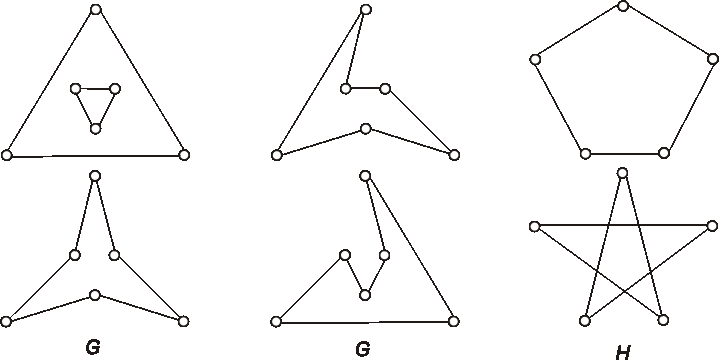
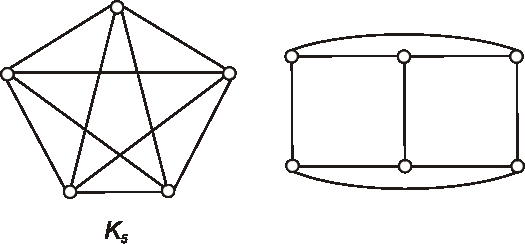
Úloha: Rozložte dané grafy na dva kvadratické faktory.
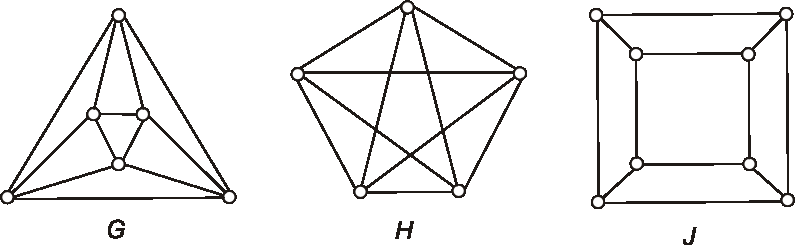
-
Úloha:
a) Nakreslite diagram ľubovoľného konečného grafu, ktorý má všetky stupne vrcholov rovnaké.
b) Nakreslite diagram ľubovoľného konečného grafu, ktorý má všetky stupne vrcholov rôzne. -
Úloha: Zostrojte diagram digrafu, ktorý:
a) bude mať 7 vrcholov a 12 orientovaných hrán,
b) bude mať 7 vrcholov a aspoň jeden vrchol s vnútorným stupňom 6,
c) bude mať 7 vrcholov a bude mať aj prameň aj ústie aj list. -
Úloha: Rozhodnite, ktoré z nasledujúcich tvrdení je a ktoré nie je pravdivé. Zdôvodnite.
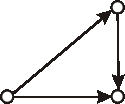
a) Priradením orientácie každej hrane v grafe vždy vznikne digraf.
b) Zrušením orientácie každej hrany v digrafe vždy vznikne graf.
c) Súčet všetkých stupňov vrcholov v digrafe je párny.
d) Súčet všetkých vnútorných stupňov vrcholov v digrafe je párny.
e) Maximálny počet hrán v digrafe s \(n\) vrcholmi je \(2n(n-1)\). -
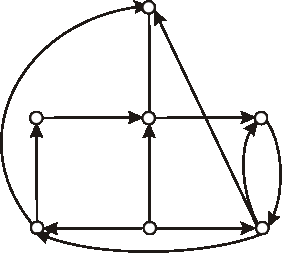
Úloha: Na obrázku je graf daný diagramom. Koľkými spôsobmi môžeme zvoliť v danom grafe orientáciu, aby výsledný digraf:
a) bol silne súvislý,
b) nebol silne súvislý.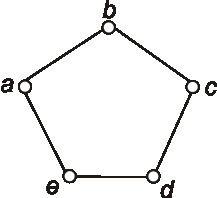
Zdroje
- Klešč M.: Diskrétna matematika, Košice, 2006.
- Bučko M. - Klešč, M.: Diskrétna matematika, Elfa, Košice, 1999.
- Klešč M. - Plavka, J.: Grafové algoritmy a formálna logika, Košice 2008.
- Matoušek J. - Nešetřil J.: Kapitoly z diskrétní matematiky, Matfyzpress, Praha 1996.
Doplňujúce úlohy
Úloha:
Aký najmenší počet vrcholov je nutné, aby mal graf, ak má mať:
a) \(19\) hrán,
b) \(n\) hrán?
a) \(19\) hrán,
b) \(n\) hrán?
Úloha:
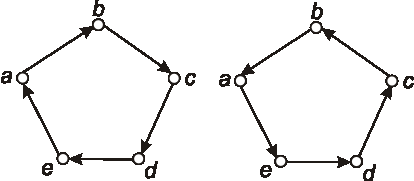
Nájdite komplementárne grafy ku grafom, ktoré sú dané nasledujúcimi diagramami:
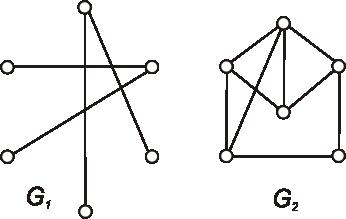

Úloha:
Zadané sú diagramy grafov \(G_1, G_2\). Nakreslite diagramy grafov \(\bar{G_1}\),
\(G_1 \cap G_2\), \(G_1 \cup G_2\), \(G_1 - G_2\) a \(G_1 \oplus G_2\).
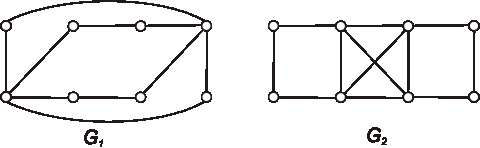

Úloha:
Určte počet faktorov v grafoch, ktoré sú zadané diagramami.
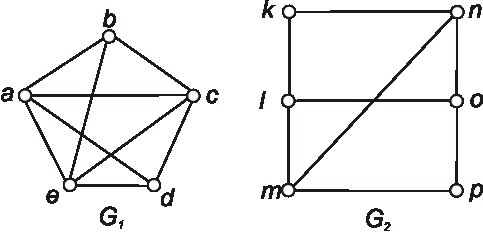

Úloha:
Nakreslite diagram grafu, ktorý:
a) je kubickým grafom.
b) je kompletným grafom.
c) je bipartitným grafom.
d) má počet hrán menší ako počet vrcholov.
e) obsahuje izolovaný vrchol.
f) je tvorený tromi komponentami.
g) má dvakrát toľko hrán, ako vrcholov.
a) je kubickým grafom.
b) je kompletným grafom.
c) je bipartitným grafom.
d) má počet hrán menší ako počet vrcholov.
e) obsahuje izolovaný vrchol.
f) je tvorený tromi komponentami.
g) má dvakrát toľko hrán, ako vrcholov.
Úloha:
Určte počet faktorov v grafoch, ktoré sú zadané diagramami.


Úloha:
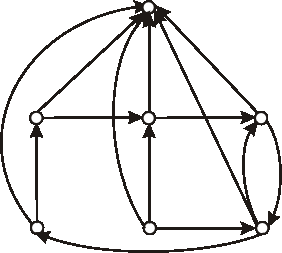
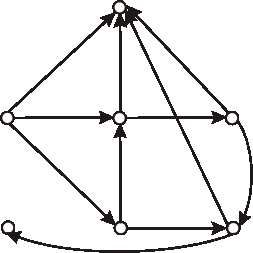
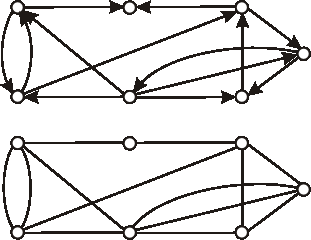
Nakreslite diagramy komplementov k digrafom na obrázku:
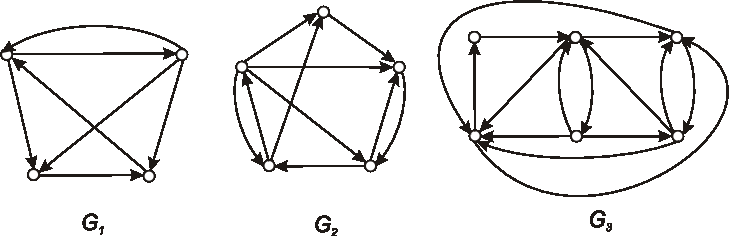

Úloha:
Nasledujúcimi diagramami máme daných šesť digrafov.
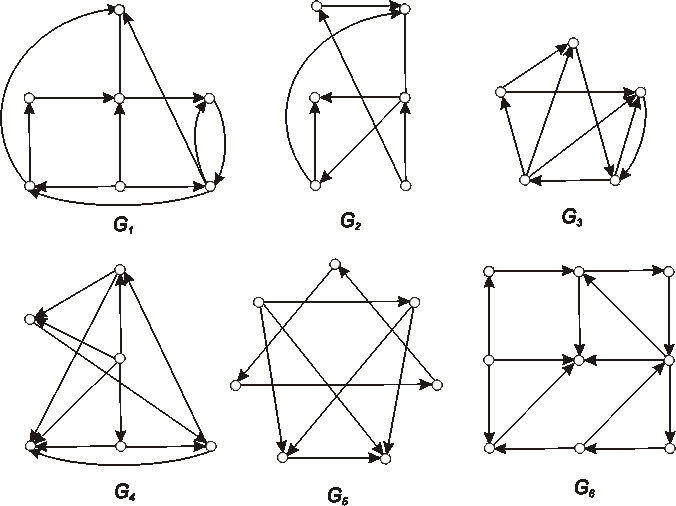 O každom jednom
rozhodnite, ktoré z nasledúcich tvrdení pre neho platí:
O každom jednom
rozhodnite, ktoré z nasledúcich tvrdení pre neho platí:
a) Odstránením orientácie z neho dostaneme graf.
b) Súčet vnútorných stupňov sa rovná súčtu vonkajších stupňov vrcholov.
c) Obsahuje list.
d) Má aspoň jeden prameň.
e) Je silne súvislý.
f) Je súvislý.

a) Odstránením orientácie z neho dostaneme graf.
b) Súčet vnútorných stupňov sa rovná súčtu vonkajších stupňov vrcholov.
c) Obsahuje list.
d) Má aspoň jeden prameň.
e) Je silne súvislý.
f) Je súvislý.