Ciele
- Orientované sledy, orientované ťahy, dráhy, cykly.
- Cyklickosť digrafov a algoritmus topologického očíslovania vrcholov.
- Hranovo ohodnotené digrafy a ich charakteristiky.
- Vzdialenosti v grafe a v digrafe.
- Dijkstrov algoritmus.
Úvod
-
Mnohé reálne procesy sú simulované na grafoch a digrafoch, na ktoré sú kladené požiadavky, ako cyklickosť,
acyklickosť, sú určené ich hranové ohodnotenia a iné charakteristiky. Táto časť je zameraná na algoritmy na
určenie a overovanie cyklickosti a hľadanie minimálnej cesty v grafe a digrafe.
Pre úspešné zvládnutie toho cvičenia sa predpokladajú teoretické vedomosti prezentované na prednáške.
Po úspešnom absolvovaní tohto cvičenia by mal študent zvládnuť nasledujúce:
- nájsť v diagrame digrafu orientované sledy, orientované ťahy, dráhy, cykly a poznať rozdiely medzi nimi;
- určiť súvislosť a silnú súvislosť digrafu;
- pomocou ATO zistiť, či je digraf acyklický;
- pomocou ATO nájsť topologické očíslovanie vrcholov acyklického digrafu;
- použiť Dijkstrov algoritmus na nájdenie najkratších ciest z vopred daného vrchola grafu;
- použiť Dijkstrov algoritmus na nájdenie najkratších ciest z vopred daného vrchola digrafu;
Postup
-
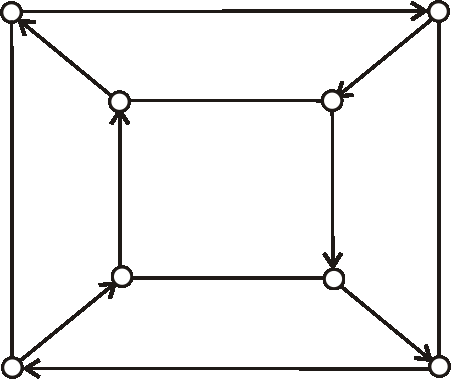
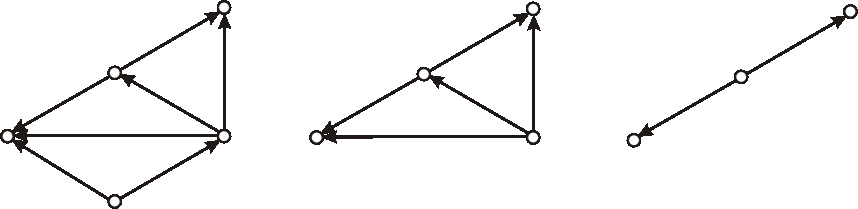
Príklad: Je digraf daný nasledujúcim diagramom silne súvislý? Zdôvodnite.
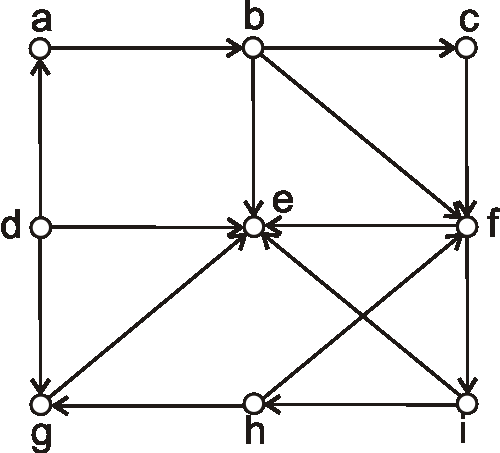
-
Príklad: Nech je daný graf kocky (diagram je na obrázku). Zvoľte orientáciu jeho hrán tak, aby vznikol silne súvislý digraf.
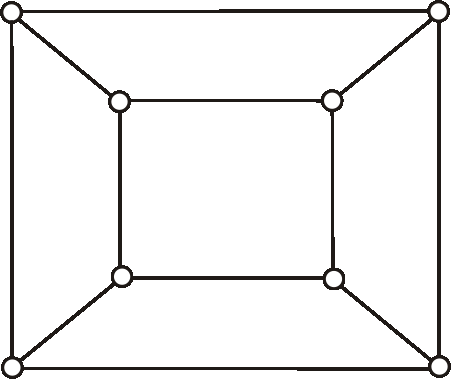
-
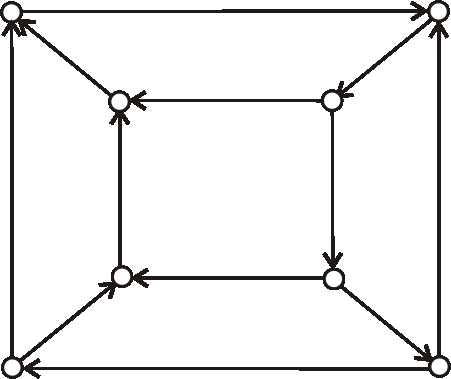
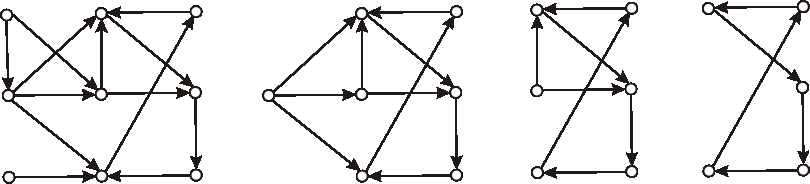
Príklad: Máme digraf daný nasledujúcim diagramom.Zistite, či je daný digraf cyklický, alebo nie.
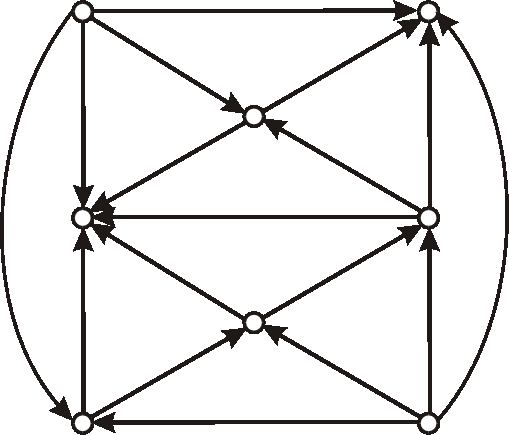
-
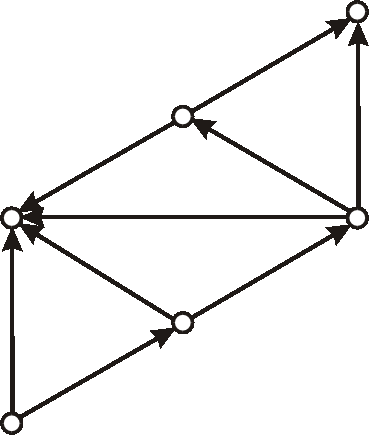
Príklad: Máme digraf daný nasledujúcim diagramom.Zistite, či je daný digraf cyklický, alebo nie.
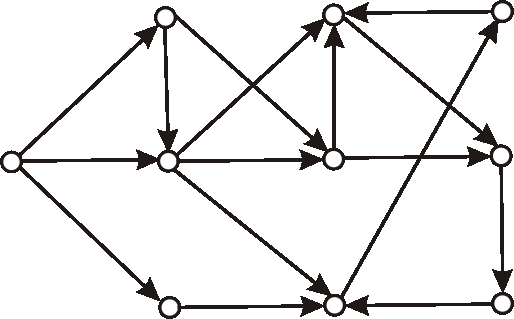
-
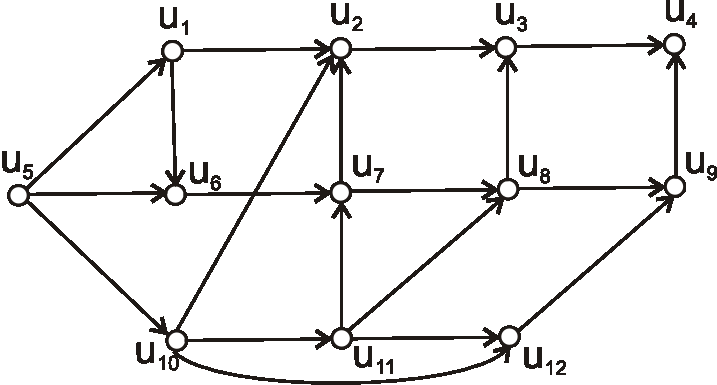
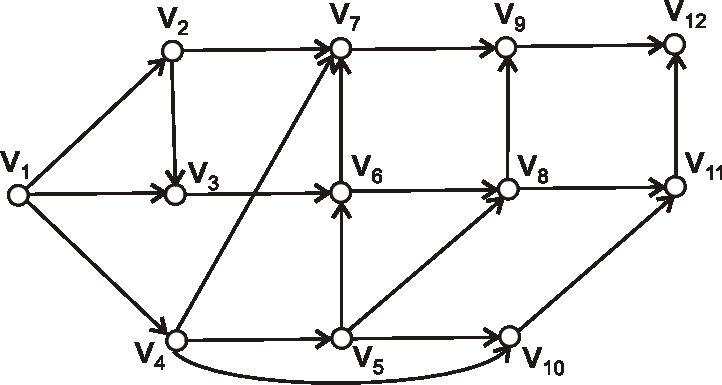
Príklad: Je daný digraf nasledujúcim diagramom.Pomocou ATO zistite, či je daný digraf cyklický, alebo nie. Ak nie je, topologicky očíslujte jeho vrcholy.
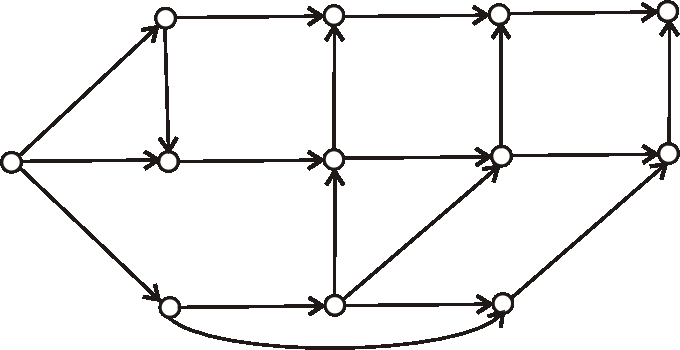
-
Príklad: Je daný hranovo ohodnotený graf nasledujúcim diagramom.
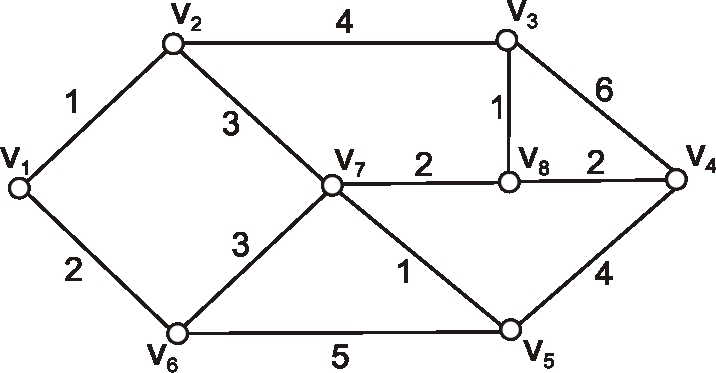
- Určte vzdialenosť vrcholu \(v_1\) a vrcholu \(v_4\).
- Do ktorého nesusedného vrcholu má vrchol \(v_5\) najmenšiu vzdialenosť?
-
Príklad: Nasledujúcim diagramom je daný hranovo ohodnotený graf. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(g\) do ostatných vrcholov.
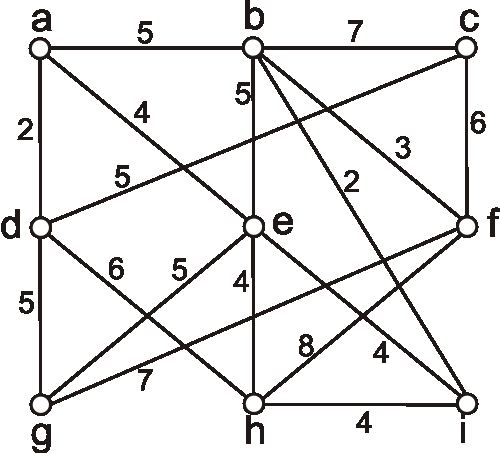
-
Príklad: Nasledujúcim diagramom je daný hranovo ohodnotený digraf. Zistite vzdialenosti z vrcholu \(v_1\) do ostatných vrcholov, tiež vzdialenosti z vrcholu \(v_4\) do ostatných vrcholov.
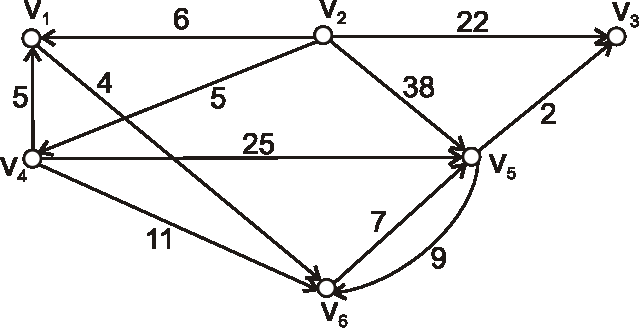
-
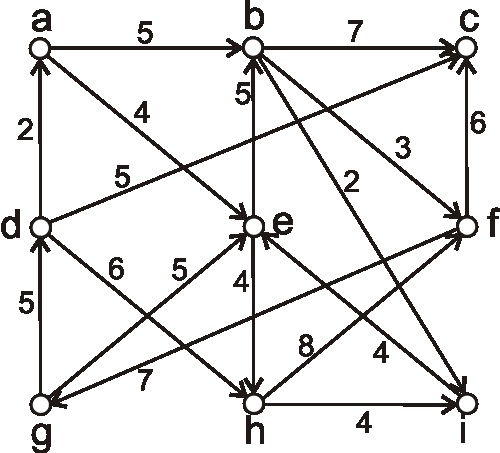
Príklad: Nasledujúcim diagramom je daný hranovo ohodnotený digraf. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(h\) do ostatných vrcholov.
Zdroje
- Klešč M.: Diskrétna matematika, Košice, 2006.
- Bučko M. - Klešč, M.: Diskrétna matematika, Elfa, Košice, 1999.
- Klešč M. - Plavka, J.: Grafové algoritmy a formálna logika, Košice 2008.
- Berežný, Š. - Draženská, E. - Kravecová, D.: Zbierka úloh z diskrétnej matematiky, Košice 2005.
Doplňujúce úlohy
Úloha:
Majme danú kružnicu \(K\) dĺžky \(d\geq 3\). Koľkými spôsobmi môžeme zvoliť orientáciu všetkých jej hrán tak,
aby vznikol acyklický digraf?
Úloha:
Máme digraf daný nasledujúcim diagramom.
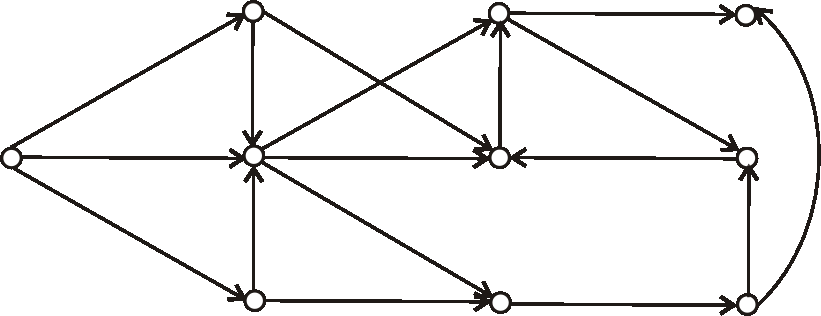 Pomocou ATO topologicky očíslujte vrcholy daného digrafu.
Pomocou ATO topologicky očíslujte vrcholy daného digrafu.

Úloha:
Máme digraf daný nasledujúcim diagramom.
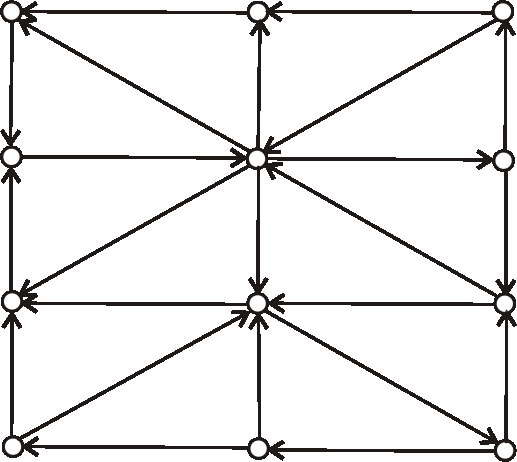 Zistite, či je daný digraf cyklický, alebo nie.
Zistite, či je daný digraf cyklický, alebo nie.

Úloha:
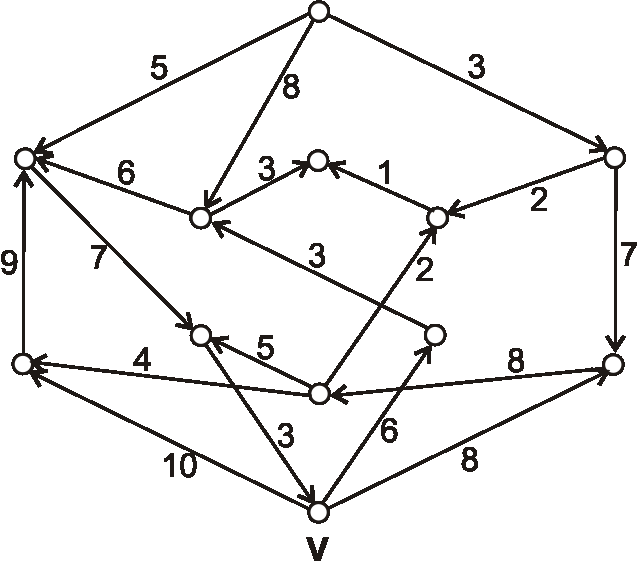
Máme graf daný nasledujúcim diagramom. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(V\) do
ostatných vrcholov.
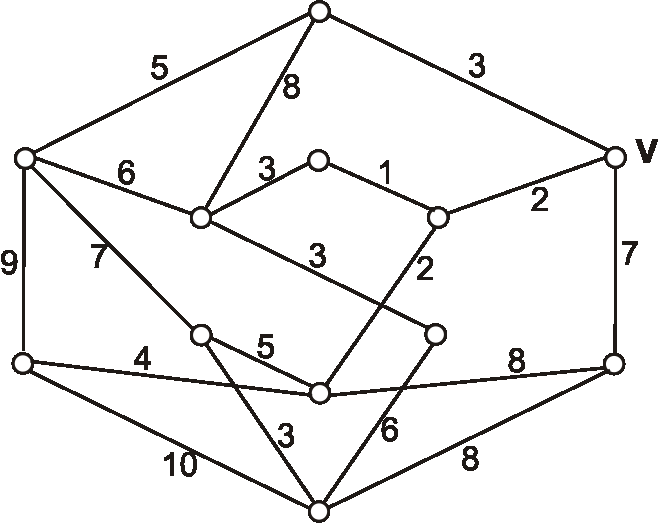

Úloha:
Máme digraf daný nasledujúcim diagramom. Pomocou Dijkstrovho algoritmu nájdite vzdialenosti z vrcholu \(V\) do
ostatných vrcholov.