Spájané zoznamy

úvod do spájaných zoznamov, jednosmerný spájaný zoznam, CRUD operácie

Záznam z prednášky

O poliach

(slide) O poliach sme prvýkrát hovorili už v zimnom semestri na predmete Základy algoritmizácie a programovania. Sú veľmi užitočné, pretože je do nich možné ukladať typovo rovnaké údaje, jednoducho sa s nimi pracuje a v pamäti sú uložené súvislo za sebou (lineárne).
S takto uloženými a reprezentovanými údajmi vie pracovať aj mnoho knižničných funkcií. Napr. funkcie z knižnice string.h vedia pracovať s jednorozmernými poliami znakov (reťazcami). Funkcie bsearch() a qsort() zo štandardnej knižnice stdlib.h dokážu vyhľadávať alebo triediť takto uložené údaje, a mnohé iné.
Jednou z nevýhod polí je však ich fixná veľkosť. Problém teda nastane vtedy, keď budem chcieť do poľa uložiť taký počet položiek, ktorý presahuje veľkosť poľa. S tým už máme bohaté skúsenosti aj zo zadaní, kedy sa síce môže javiť, že je všetko v poriadku, ale až valgrind alebo prípadný Segmentation fault vám prezradí, že je niečo v neporiadku.
S týmto problémom súvisí aj operácia vytvorenia poľa. Pretože pole môžem vytvoriť až vtedy, keď viem, koľko prvkov do neho budem ukladať.
Ak mi však neskôr veľkosť poľa prestane stačiť, tak ako do neho vložím ďalší prvok?
(slide) Ďalší problém, ktorý súvisí s takto orgranizovanými údajmi je, že vykonávanie základných CRUD operácií (Create Retrieve Update Delete) nie je úplne triviálne a obyčajne sú tieto operácie aj veľmi drahé. Ich zložitosť je \[ O(n) \]
Príkladom problému so základnými CRUD operáciami môže byť odstránenie prvku poľa, ktorý sa nachádza niekde v jeho strede. Po jeho odstránení totiž v poli vznikne (v tom lepšom prípade) voľné miesto. Tým sme vlastne vyrobili typ poľa, ktoré nazývame riedke pole (z angl. sparse array), ale nie vždy nám takáto reprezentácia bude vyhovovať. Aby sme dali veci do poriadku, musíme zvyšok prvkov poľa posunúť smerom k jeho začiatku, aby voľné miesto opäť zaplnili.
S niektorými operáciami ste sa priamo stretli počas riešenia zadania K - ako ste postupovali, keď ste napr. potrebovali vložiť prvok na správne miesto v zozname Hall of Fame?

Ukladanie súborov na disk

Pozrime sa na to, ako je organizované ukladanie súborov v rámci súborového systému na disku. Najprv sa však pokúsme zadefinovať, že čo to vlastne ten súbor je?
(slide) Jedna z definícií termínu súbor môže byť:

In C programming, file is a place on your physical disk where information is stored. (www.programiz.com)
Podľa tejto definície sú teda súbory akési kontajnery na ukladanie údajov, ktoré sa fyzicky nachádzajú uložené na disku.
(slide) Súbory nie sú na disku uložené ako jeden kus. Sú rozkúskované a následne uložené v blokoch fixnej dĺžky, vďaka čomu vieme pracovať so súbormi na disku efektívnejšie. Jeden súbor môže teda na disku zaberať vzhľadom na svoju veľkosť niekoľko takýchto blokov.
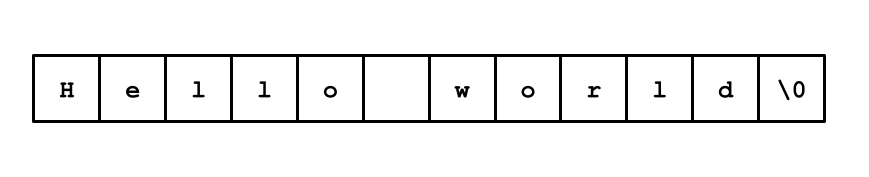
Aby sme tejto koncepcii lepšie porozumeli, tak sa pokúsme do súboru uložiť reťazec "Hello, world!". Tento reťazec má dĺžku 13 znakov (plus terminátor). Ak má jeden blok veľkosť 5B, tak uvedený reťazec uložíme do 3 takýchto blokov.
Tento spôsob ukladania údajov je veľmi výhodný, nakoľko pomocou neho je možné uložiť akékoľvek množstvo údajov (teoreticky súbor o akejkoľvek dĺžke). Stačí len vstupné údaje “rozbiť” do potrebného množstva týchto blokov a v uvedenej (poprepájanej) podobe ich uložiť.
Podobný spôsob sa napríklad používa aj pri prenose údajov v sieti, kde sa údaje rozbijú do menších celkov nazvaných pakety. Ak sa jeden stratí alebo sa prenesie poškodený, prijímateľ si ho vyžiada znova na základe čísla chýbajúceho paketu, pričom odosielateľ nemá problém požadovaný paket s údajmi zostaviť opätovným vyseknutím potrebných údajov a preposlať ho.

Spájané zoznamy

(slide) Okrem samotných údajov však blok so sebou nesie aj informáciu o tom, kde sa nachádza ďalší blok (ďalšia časť súboru). Týmto spôsobom teda môžeme vytvoriť tzv. spojkový zoznam alebo tiež spájaný zoznam, v ktorom sú jednotlivé bloky navzájom prepojené.
Pre úplnosť môžeme povedať, že sme vytvorili jednosmerný spojkový zoznam, pretože sa v zozname vieme po položkách pohybovať len jedným smerom - vieme sa dostať zo začiatku na koniec, ale nevieme sa dostať z konca na začiatok.
Ako je však možné takýto prístup reprezentovať v jazyku C?
(slide) Ak by sme chceli reprezentovať v jazyku C jeden jeho blok, vyzeral by takto:
```
struct node {
    char data[5];
    struct node *next;
};
```
Uzol je teda reprezentovaný štandardnou štruktúrou jazyka C. V tomto prípade má dve položky:
- samotné údaje, ktoré sú v našom prípade reprezentované jednorozmerným poľom znakov o dĺžke 5, a
- referenciou na ďalší uzol zoznamu - na ďalší prvok (rovnakého) údajového typu struct node.
(slide) Táto štruktúra sa však nevolá block ale node, pretože vychádzame z definície, že:

linked list is a data structure consisting of a group of nodes which together represent a sequence (Wikipedia)
Rovnako je možné takýto zoznam reprezentovať planárnym grafom, kde sa slovo uzol (node) bežne používa.

CRUD operácie

(slide) Pri práci so zoznamami nás bude zaujímať niekoľko operácií. Konkrétne tieto:
- create - vloženie/vytvorenie nového uzla
- retrieve - získanie/vyhľadanie existujúceho uzla
- update - aktualizovanie/úprava existujúceho uzla
- delete - odstránenie existujúceho uzla zo zoznamu
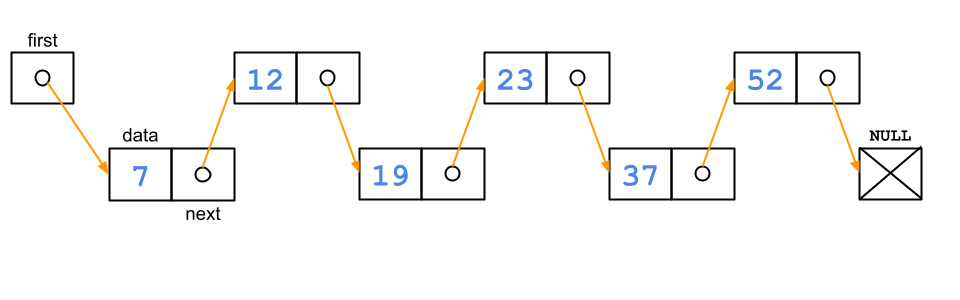
(slide) Pre jednoduchosť ilustrácie si všetky operácie budeme demonštrovať na jednoduchom zozname celých čísiel:
```
7 12 19 23 37 52
```
(slide) Keď do zoznamu postupne vložíme všetky prvky postupnosti, bude v pamäti vyzerať takto:

Štruktúrovaný údajový typ `struct node`

(slide) Začneme tým, že vytvoríme štruktúru struct node, ktorá bude reprezentovať práve jeden uzol. Bude mať dva prvky:
- data - samotné údaje, a
- next - adresu ďalšieho prvku v zozname, pričom typ bude práve ukazovateľ na struct node

Kód tejto štruktúry bude vyzerať nasledovne:

struct node {
   int data;
   struct node* next;
};

Funkcia `traverse()`

(slide) Ešte predtým, než sa pustíme do implementácie samotných CRUD funkcií, vytvoríme si pomocnú funkciu traverse(). Táto funkcia bude mať jeden parameter, ktorý bude referenciou na prvý prvok zoznamu. Funkcia prejde celým zoznamom a vypíše každý prvok na obrazovku. Samozrejme, ak bude zoznam prázdny (referencia na NULL), nevypíše nič.

Zdrojový kód tejteo funkcie môže vyzerať nasledovne:

void traverse(struct node *head){
    // empty list?
    if(head == NULL){
        printf(">> list is empty\n");
        return;
    }

    // traverse
    struct node* ptr = head;
    while(ptr != NULL){
        printf("%d\n", ptr->data);
        ptr = ptr->next;
    }
}

Funkcia `append()`

(slide) Jedna z najzákladnejších funkcií na prácu so zoznamami je určite funkcia append(). Pomocou tejto funkcie budeme vedieť pridať prvok na koniec zoznamu. Ak je zoznam prázdny (keď *head == NULL), rovno sa vytvorí a bude obsahovať len novopridaný prvok. V tom prípade funkcia aktualizuje začiatok zoznamu.

Zdrojový kód funkcie bude vyzerať nasledovne:

void append(struct node** head, int data){
    // create new node
    struct node* node = calloc(1, sizeof(struct node));
    node->data = data;
    node->next = NULL;

    // is the list empty?
    if(*head == NULL){
        *head = node;
        return;
    }

    // if not, traverse to last node
    struct node* ptr = *head;
    while(ptr->next != NULL){
        ptr = ptr->next;
    }

    // append the node
    ptr->next = node;
}

Zostáva mi už len vytvorenú funkciu append() otestovať. Test bude veľmi jednoduchý - pomocou funkcie append() postupne naplním zoznam postupnosťou čísiel a nakoniec ho vypíšem na obrazovku.

int main(){
    struct node* head = NULL;

    append(&head, 7);
    append(&head, 12);
    append(&head, 19);
    append(&head, 23);
    append(&head, 37);
    append(&head, 52);

    traverse(head);
}

Ak program spustíme, postupne popripája prvky do zoznamu a nakoniec obsah zoznamu vypíše na obrazovku prvok po prvku.
Ak samozrejme spustíme program valgrind, upozorní nás na to, že sme pred skončením programu neuvoľnili pamäť. To budeme robiť až pri mazaní prvkov zo zoznamu.

Refactoring?!

Prechádzanie prvkov zoznamu sme aktuálne implementovali pomocou cyklu while. Ten však môžeme zameniť aj za cyklus for. Implementácia funkcie traverse() použitím cyklu for miesto while môže vyzerať takto:
```
void traverse(struct node *head){
    for(struct node* ptr = head; ptr != NULL; ptr = ptr->next){
        printf("%d\n", ptr->data);
    }
}
```

Funkcia `pop()`

(slide) Máme vytvorenú základnú funkciu na pridanie prvku na koniec zoznamu. Spravíme teda funkciu opačnú - pop(). Tá odstráni posledný prvok zo zoznamu a vráti referenciu naň.

Implementácia tejto funkcie môže vyzerať nasledovne:

struct node* pop(struct node** head){
    // empty list?
    if(*head == NULL){
        return NULL;
    }

    struct node* ptr = *head;

    // only one?
    if(ptr->next == NULL){
        *head = NULL;
        return ptr;
    }

    // find the semifinal node
    while(ptr->next->next != NULL){
        ptr = ptr->next;
    }

    // prepare the result
    struct node* result = ptr->next;
    ptr->next = NULL;

    return result;
}

Funkciu otestujeme tak, že postupne zmažeme celý zoznam odzadu a každý vrátený prvok následne odstránime aj z pamäte. Implementácia môže vyzerať napr. takto:

// pop all elements from list
struct node* ptr = pop(&head);
while(ptr != NULL){
    printf(">> removing %d\n", ptr->data);
    free(ptr);
    ptr = pop(&head);
}

// traverse the (empty) list
traverse(head);

Funkcia `insert()`

(slide) Ďalšiu funkciu, ktorú implementujeme, bude funkcia insert(). Táto funkcia vloží prvok na konkrétnu pozíciu zoznamu. Neprepíše prvok, ktorý sa na danom indexe nachádza, ale vloží ho pred neho. Samozrejme - ak je zoznam prázdny, resp. daný index neexistuje (v zozname sa nachádza menej prvkov), tak prvok sa pripojí na koniec zoznamu.

void insert(struct node** head, size_t index, int data){
    // create new node
    struct node* node = calloc(1, sizeof(struct node));
    node->data = data;
    node->next = NULL;

    // is the list empty?
    if(*head == NULL){
        *head = node;
        return;
    }

    // find the element at given index
    struct node* ptr = *head;
    for(size_t i = 0; i+1 < index; i++){
        // if size of list is less than index, then append
        if(ptr->next == NULL){
            ptr->next = node;
            return;
        }
        ptr = ptr->next;
    }

    // insert entry
    node->next = ptr->next;
    ptr->next = node;
}

Funkciu môžeme jednoducho otestovať:

int main(){
    struct node* head = NULL;

    // empty list
    insert(&head, 0, 7);

    // append to the end
    insert(&head, 99, 52);

    // insert to the given index
    insert(&head, 1, 12);
    insert(&head, 2, 19);
    insert(&head, 3, 23);
    insert(&head, 4, 37);

    traverse(head);
}

Ak program spustíme, prvky budú do neho postupne povkladané a nakoniec sa vypíše na obrazovku celý zoznam prvok po prvku.

Funkcia `search()`

(slide) Keď už vieme naplniť zoznam, môžeme v ňom začať vyhľadávať údaje. Vytvoríme teda funkciu search(), ktorá vráti referenciu na prvý prvok v zozname, ktorý zodpovedá kritériám pre vyhľadávanie. Ak žiadna zhoda nenastane, funkcia vráti NULL.

V tomto prípade upravíme aj signatúru funkcie. Parameter head, ktorý ukazuje na začiatok zoznamu, tentokrát nebudeme odovzdávať vo forme adresy na adresu. Tentokrát nepotrebujeme zmeniť odkaz na začiatok zoznamu. Tentokrát si vystačíme s možnosťou zoznam prechádzať.

struct node* search(struct node* head, int needle){
    struct node* ptr = head;

    while(ptr != NULL){
        if(ptr->data == needle){
            return ptr;
        }
        ptr = ptr->next;
    }

    return NULL;
}

Funkciu môžeme vyskúšať napr. nasledovným fragmentom kódu. Samozrejme ideálne tak, aby zoznam nebol prázdny.

int needle;
printf("What should I find: ");
scanf("%d", &needle);

struct node* ptr = search(head, needle);
if(ptr != NULL){
    printf("found\n");
}else{
    printf("not found\n");
}

Funkcia `delete()`

(slide) Pre odstránenie položky zo zoznamu vytvoríme funkciu delete(). Táto funkcia bude mať parameter, ktorým bude prvok, ktorý má byť zmazaný. Bude teda rozšírením funkcie search(), kedy akurát prvok nebude len vrátený, ale bude aj odstránený zo zoznamu. Ak sa prvok v zozname nenachádza, vráti NULL. A ak sa v zozname nachádza viacero uzlov s rovnakou hodnotou, bude ostránená prvá z nich.

Implementácia funkcie môže vyzerať napr. takto:

struct node* delete(struct node** head, int needle){
    if(*head == NULL){
        return NULL;
    }

    struct node* ptr = *head;

    // check head
    if(ptr->data == needle){
        *head = ptr->next;
        ptr->next = NULL;
        return ptr;
    }

    // find needle
    while(ptr->next != NULL){
        if(ptr->next->data == needle){
            struct node* result = ptr->next;
            ptr->next = ptr->next->next;
            result->next = NULL;
            return result;
        }
        ptr = ptr->next;
    }

    return NULL;
}

Otestovať funkciu môžem jednoducho upravením predchádzajúceho fragmentu kódu:

int needle;
printf("What should I delete: ");
scanf("%d", &needle);

struct node* ptr = delete(&head, needle);
if(ptr != NULL){
    printf("deleted\n");
}else{
    printf("not found\n");
}

traverse(head);

Funkcia `update()`

(slide) Poslednou funkciou, ktorú si ukážeme, bude funkcia update(). Táto funkcia aktualizuje položku spôsobom, že ju celú vymení za inú.

Poznámka

Samozrejme aktualizovať by sme mohli aj ináč. Ak by nám stačilo vymeniť len obsah položky za iný, využili by sme len funkciu search(), ktorá nám vráti príslušný prvok, v ktorom by sme výmenu zrealizovali.

Implementácia funkcie môže vyzerať napr. takto:

void update(struct node** head, struct node* old,
            struct node* new){
    if(*head == NULL){
        return;
    }

    // is it the first entry?
    if(*head == old){
        new->next = old->next;
        old->next = NULL;
        *head = new;
    }

    struct node* ptr = *head;
    // search old entry
    while(ptr->next != NULL){
        if(ptr->next == old){
            new->next = old->next;
            old->next = NULL;
            ptr->next = new;
            return;
        }
        ptr = ptr->next;
    }
}

Za predpokladu, že máme neprázdny zoznam, môžeme overiť správnosť funkcie napríklad takto:

int needle;
printf("What Should I Search: ");
scanf("%d", &needle);
struct node* old = search(head, needle);

int value;
printf("Enter New Value: ");
scanf("%d", &value);
struct node* new = calloc(1, sizeof(struct node));
new->data = value;
update(&head, old, new);

traverse(head);

Finding List Size

(slide) Zastavme sa však ešte pri jednom štandardnom probléme - ako zistím veľkosť zoznamu?
Pri práci s poľom znakov zistiť veľkosť reťazca znamenalo hľadať najbližší terminátor a rátať, koľko znakov pri tom prejdem. Pri práci s poliami iných údajových typov, sme sa museli o veľkosť starať osobitne pomocou samostatnej premennej.

V tomto prípade je situácia podobná tej s poľom znakov - máme totiž jasný koniec zoznamu, ktorý potrebujeme len nájsť a pritom počítať, koľko prvkov sme prešli. Takáto funkcia môže vyzerať nasledovne:

size_t size(struct node* head){
    size_t counter = 0;
    struct node* ptr = head;

    while(ptr != NULL){
        ptr = ptr->next;
        counter++;
    }

    return counter;
}

Zložitosť tohto prístupu je opäť lineárna, pretože musím prejsť celým zoznamom prvok po prvku. A to nie je veľmi výhodné.
(slide) Môžeme však spraviť fintu a celý zoznam zabaliť do kontajnera, ktorý bude mať len dve položky:
1. referenciu na začiatok zoznamu, a
2. počet položiek zoznamu

Takýto kontajner môže vyzerať nasledovne:

struct container {
    struct node* head;
    size_t size;
};

Týmto prístupom sme vyriešili problém so zložitosťou, pretože aktuálne je zložitosť konštantná - 1. Musíme však dodržať to, že akákoľvek operácia, pomocou ktorej dôjde k zmene počtu položiek zoznamu, musí rovnako aktualizovať položku .size.

Conclusion

(slide) Dnes sme si ukázali jednu z veľmi dôležitých dátových štruktúr - spojkový zoznam. Vo vyšších programovacích jazykoch sa s ním stretnete v natívnych implementáciách rozličných zoznamov. Jazyk C však takýmto typom nedisponuje a preto si ho musíme vytvoriť sami.
Jednosmerný spojkový zoznam však nie je jediným predstaviteľom tohto typu dátových štruktúr. Jednak existujú rozličné typy samotných spojkových zoznamov (napr. obojsmerné, cyklické, …), ale taktiež vieme vytvárať iné štruktúry, ako napr. stromy alebo hash tabuľky (mapy). O tom však nabudúce.

Spájané zoznamy

Záznam z prednášky

O poliach

Ukladanie súborov na disk

Spájané zoznamy

CRUD operácie

Štruktúrovaný údajový typ struct node

Funkcia traverse()

Funkcia append()

Refactoring?!

Funkcia pop()

Funkcia insert()

Funkcia search()

Funkcia delete()

Funkcia update()

Finding List Size

Conclusion

Štruktúrovaný údajový typ `struct node`

Funkcia `traverse()`

Funkcia `append()`

Funkcia `pop()`

Funkcia `insert()`

Funkcia `search()`

Funkcia `delete()`

Funkcia `update()`