Ciele
- Zopakovanie parametrického vyjadrenia plochy.
- Výpočet plošného integrálu II. druhu na základe vety o výpočte prevodom na dvojný integrál.
Úvod
- Parametrické vyjadrenie plochy.
- Veta o výpočte plošného integrálu.
- Základné vlastnosti plošného integrálu.
-
\(\displaystyle{\iint\limits_{\sigma} \vec{f}(x,y,z)\,\mathrm{d}{\vec{\sigma}}=
\iint\limits_{\sigma} f_1\,\mathrm{d}{y}\,\mathrm{d}{z}+\iint\limits_{\sigma}f_2\,
\mathrm{d}{x}\,\mathrm{d}{z}+\iint\limits_{\sigma}f_1\,\mathrm{d}{x}\,\mathrm{d}{y}.},
\)
t.j. celkový tok je možné rozložiť na tok v smere osi \(o_x\), tok v smere osi \(o_y\) a tok v smere osi \(o_z\). - nech plochy \(\sigma_1\), \(\sigma_2\) tvoria delenie plochy \(\sigma\), potom \[ \iint\limits_{\sigma} \vec{f}(x,y,z)\,\mathrm{d}{\vec{\sigma}}= \iint\limits_{\sigma_1} \vec{f}(x,y,z)\,\mathrm{d}{\vec{\sigma}}+ \iint\limits_{\sigma_2} \vec{f}(x,y,z)\,\mathrm{d}{\vec{\sigma}} \]
Pred zavedením a študiom plošného integrálu II. druhu sa budeme zaoberať pojmom plocha.
Plocha vznikne deformáciou nejakej časti roviny, predstavujeme si ju ako nejaký krivý list (napr. papiera), alebo povrch telesa
Budeme uvažovať plochy, ktoré vieme vyjadriť nasledovným parametrickým vyjadrením \[ \sigma:\quad \vec{\pmb{r}}(t,s)=x(t,s)\vec{\pmb{i}}+y(t,s)\vec{\pmb{j}} +z(t,s)\vec{\pmb{k}},\qquad (t,s)\in\Omega\subset \mathbb{R}^2 \] resp. \[ \begin{split} \sigma:\quad x=x(t,s)\\ y=y(t,s)\\ z=z(t,s),\qquad (t,s)\in\Omega\subset \mathbb{R}^2 \end{split} \] Uvažujme plochu \(\sigma\) ako časť paraboloidu \(z=x^2+y^2\) pre \(z\in [0,1]\).
Parametrickým vyjadrením tejto plochy je napríklad \[ \begin{split} \sigma\quad x=t\\ y=s\\ z=t^2+s^2,\qquad t^2+s^2\leq 1. \end{split} \] Alebo parametrické vyjadrenie tejto plochy je aj \[ \begin{split} \sigma\quad x=t\cos s\\ y=t\sin s,\\ z=t^2, \end{split} \begin{split} \quad\quad\\ \qquad 0\leq s \leq 2\pi\\ \qquad 0\leq t\leq1. \end{split} \] Teda istá plocha môže mať rôzne parametrické vyjadrenia.
Poznámka:
Plochu
\[
\sigma:\quad
\vec{\pmb{r}}(t,s)=x(t,s)\vec{\pmb{i}}+y(t,s)\vec{\pmb{j}}+z(t,s)\vec{\pmb{k}},
\qquad (t,s)\in\Omega\subset \mathbb{R}^2
\]
nazývame hladkou, ak sú funkcie \(x(t,s)\), \(y(t,s)\), \(z(t,s)\)
a všetky ich parciálne derivácie spojité.
Ukážeme ako vypočítať plošný integrál prevodom na dvojný integrál. Majme plochu \(\sigma\) určenú parametrickým vyjadrením \[ \sigma:\quad \vec{\pmb{r}}(t,s)=x(t,s)\vec{\pmb{i}}+y(t,s)\vec{\pmb{j}}+ z(t,s)\vec{\pmb{k}},\qquad (t,s)\in\Omega, \] K odvodeniu vety o výpočte využijeme definíciu plošného integrálu. Delenie \(D_n\) plochy \(\sigma\) urobíme pomocou delenia množiny \(\Omega\) nasledovne. Nech \(\Omega\) je časťou intervalu \(I=[a,b]\times[c,d]\). Urobíme delenie intervalu \([a,b]\): \[ a=t_0\lt t_1\dots\lt t_n=b \] a delenie intervalu \([c,d]\): \[ c=s_0\lt s_1\dots\lt s_m=d \] (viď obrázok). Úsečke \([t_1,s]\subset\Omega\) odpovedá krivka \(\vec{\pmb{r}}(t_1,s)\) na ploche \(\sigma\). Podobne úsečke \([t_2,s]\subset\Omega\) odpovedá krivka \(\vec{\pmb{r}}(t_2,s)\subset\sigma\) Analogicky úsečke \([t,s_1]\subset\Omega\) odpovedá krivka \(\vec{\pmb{r}}(t,s_1)\) na ploche \(\sigma\).
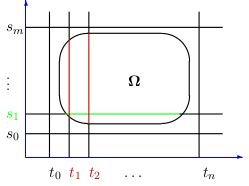
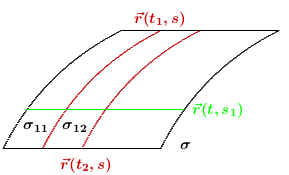

Poznámka:
Znamienko \(+\) (teda plocha je orientovaná súhlasne s parametrickým vyjadrením) platí ak
\[
\vec{\pmb{n}}=\left|
\begin{array}{ccc}
\vec{\pmb{i}} \quad\quad\quad \vec{\pmb{j}} \quad\quad\quad \vec{\pmb{k}}\\
x'_t(t,s) \quad y'_t(t,s) \quad z'_t(t,s)\\
x'_s(t,s) \quad y'_s(t,s) \quad z'_s(t,s)
\end{array}
\right|.
\]
Základne vlastnosti plošného integrálu sú zrejme z jeho fyzikálnej aplikácie.
Postup
-
Parametrické vyjadrenie plochy
Príklad: Vypočítajte plošný integrál \[ \iint\limits_{\sigma}x\,\mathrm{d}{y}\,\mathrm{d}{z}+y\,\mathrm{d}{x}\,\mathrm{d}{z}+ z\,\mathrm{d}{x}\,\mathrm{d}{y}, \] ak \[ \sigma:\qquad\vec{\pmb{r}}(t,s)=t\vec{\pmb{i}}+s\vec{\pmb{j}}+(ts+1)\vec{\pmb{k}}, \qquad (t,s)\in\Omega= [0,1]\times[0,1], \] Plocha je orientovaná tak, že normálový vektor v každom bode plochy zvierá s vektorom \(\vec{\pmb{k}}\) ostrý uhol.Riešenie: Použitím vety o výpočte dostávame \[ \iint\limits_{\sigma} x\,\mathrm{d}{y}\,\mathrm{d}{z}+y\,\mathrm{d}{x}\,\mathrm{d}{z}+ z\,\mathrm{d}{x}\,\mathrm{d}{y} =\pm \iint\limits_{\Omega}\left| \begin{array}{ccc} t \quad s \quad (ts+1)\\ 1 \quad\quad 0 \quad\quad t\\ 0 \quad\quad 1 \quad\quad s \end{array} \right|\,\mathrm{d}{t}\,\mathrm{d}{s}=(\spadesuit) \] Použili sme normálový vektor \[ \vec{\pmb{n}}=\vec{\pmb{r}}'_t \times\vec{\pmb{r}}'_s=\left| \begin{array}{ccc} \vec{\pmb{i}} \quad \vec{\pmb{j}} \quad \vec{\pmb{k}}\\ 1 \quad\quad 0 \quad\quad t\\ 0 \quad\quad 1 \quad\quad s \end{array} \right|=(-t,-s,1). \] Keďže \(\vec{\pmb{n}}\circ \vec{\pmb{k}}=1>0\), zvierá náš normálový vektor s vektorom \(\vec{\pmb{k}}\) ostrý uhol a teda použijeme znamienko \(+\). Preto \[ (\spadesuit)=\int_{0}^1 \int_{0}^1(ts+1)\,\mathrm{d}{t}\,\mathrm{d}{s}=\frac{3}{4}. \]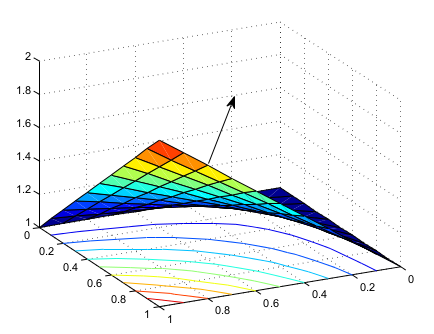 Úloha: Vypočítajte \(\displaystyle\quad\iint\limits_{\sigma}x\,\mathrm{d}{y}\,\mathrm{d}{z}+ +y\,\mathrm{d}{x}\,\mathrm{d}{z}+z\,\mathrm{d}{x}\,\mathrm{d}{y}\), kde \(\sigma\) je časť paraboloidu \(\vec{\pmb{r}}(u,v)=u\vec{\pmb{i}}+ v\vec{\pmb{j}}+(u^2+v^2)\vec{\pmb{k}}\), pričom \(u^2+v^2\leq 1\) orientovaná tak, že normálový vektor zviera s vektorom \(\vec{\pmb{k}}\) tupý uhol.Riešenie: \(\displaystyle\left[\frac{\pi}{2}\right]\)Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť.
Úloha: Vypočítajte \(\displaystyle\quad\iint\limits_{\sigma}x\,\mathrm{d}{y}\,\mathrm{d}{z}+ +y\,\mathrm{d}{x}\,\mathrm{d}{z}+z\,\mathrm{d}{x}\,\mathrm{d}{y}\), kde \(\sigma\) je časť paraboloidu \(\vec{\pmb{r}}(u,v)=u\vec{\pmb{i}}+ v\vec{\pmb{j}}+(u^2+v^2)\vec{\pmb{k}}\), pričom \(u^2+v^2\leq 1\) orientovaná tak, že normálový vektor zviera s vektorom \(\vec{\pmb{k}}\) tupý uhol.Riešenie: \(\displaystyle\left[\frac{\pi}{2}\right]\)Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť. -
Napíšte ďalší krok.
-
Napíšte ďalší krok.
Zdroje
Doplňujúce úlohy
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{\sigma}
x^2y^2z\,\mathrm{d}{x}\,\mathrm{d}{y}\), kde \(\sigma\) je dolná časť guľovej plochy
\(x^2+y^2+z^2=R^2\), orientovanej tak, že normálový vektor zviera s vektorom
\(\vec{\pmb{k}}\) ostrý uhol.
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{\sigma}
x^2\,\mathrm{d}{y}\,\mathrm{d}{z}+z^2\,\mathrm{d}{x}\,\mathrm{d}{y}\), kde \(\sigma\) je časť kužeľovej plochy
\(z^2=x^2+y^2\), \(0\leq z\leq 1\), orientovanej tak, že normálový vektor zviera
s vektorom \(\vec{\pmb{k}}\) ostrý uhol.
Úloha:
Vypočítajte \(\displaystyle\quad\iint\limits_{\sigma}
(y-z)\,\mathrm{d}{y}\,\mathrm{d}{z}+(z-x)\,\mathrm{d}{x},\mathrm{d}{z}+
(x-y)\,\mathrm{d}{x}\,\mathrm{d}{y}\),
kde \(\sigma\) je časť kužeľovej plochy \(z^2=x^2+y^2\), \(0\leq z\leq 4\),
orientovanej tak, že normálový vektor zviera s vektorom \(\vec{\pmb{k}}\0 tupý uhol.
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Riešenie:
\(\displaystyle\left[-88\right]\)
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Riešenie:
\(\displaystyle\left[-88\right]\)
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Riešenie:
\(\displaystyle\left[-88\right]\)
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Úloha:
Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Doplňujúce zdroje
- Tu vložte doplňujúce odporúčané zdroje.
- Tu vložte doplňujúce odporúčané zdroje.


