Ciele
- Aplikácia vety o výpočte trojného integrálu -- praktický výpočet
- Tu napíšte aspoň jeden cieľ.
Úvod
- Výpočet trojného integrálu.
- Výpočet trojného integrálu transformáciou do cylindrických alebo sférických súradníc.
- Výpočet objemu telesa priamo z definície trojného integrálu.
V prípade, že množina \(A\) je priestorová oblasť typu \([x,y,z]\), t.j. vieme ju popísať nerovnosťami \[ A=\big\{[x,y,z]\in \Bbb R^3; a\leq x\leq b,\ g(x)\leq y\leq h(x), \alpha(x,y)\leq z\leq \beta(x,y) \big\}, \] potom trojný integrál počítame prevodom na trojnásobný \[ \iiint\limits_{A} f(x,y,z)\, \mathrm{d}{x}\mathrm{d}{y}\mathrm{d}{z}= \int\limits_{a}^b\left[\ \int\limits_{g(x)}^{h(x)} \left(\ \int\limits_{\alpha(x,y)}^{\beta(x,y)}f(x,y,z)\, \mathrm{d}{z}\right)\mathrm{d}{y}\right]\mathrm{d}{x}. \] Podobne postupujeme pri výpočte trojného integrálu na elementárnych oblastiach typu \([x,z,y]\), \([y,x,z]\), \([y,z,x]\), \([z,x,y]\) a \([z,y,x]\).
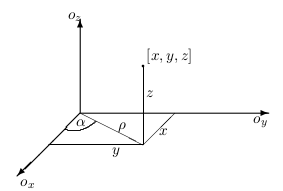
V niektorých prípadoch je výhodnejšie trojný integrál pocítat pomocou transformácie do cylindrických alebo sférických súradníc. Transformacčné vzťahy pre cylindrické súradnice sú: \[ \hspace{-4cm}x = \rho\cos\alpha \] \[ \hspace{-4cm}x = \rho\sin\alpha \] \begin{equation} z=z\qquad\qquad \alpha\in\langle0,2\pi\rangle,\quad\rho\geq0,\quad z\in\Bbb R. \end{equation}
Príklad:
Vypocítajte trojný integrál telesa
\[
\iiint\limits_{A}z\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z},
\]
kde \(A\) je ohraničená plochami \(z=\sqrt{x^2+y^2}\), \(z=2-x^2-y^2\)
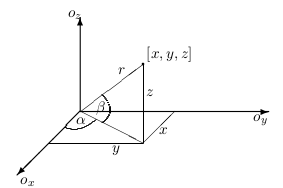
Transformačné vzťahy pre sférické súradnice sú
\begin{equation}
\begin{split}
\hspace{-9cm}x = r\cos\alpha\cos\beta\\
\hspace{-9cm}x = r\sin\alpha\cos\beta\\
z= r\sin\beta,\qquad\alpha\in\langle0,2\pi\rangle,\quad\beta\in\Big\langle-
\frac{\pi}{2},\frac{\pi}{2}\Big\rangle \quad r\geq0.
\end{split}
\end{equation}
Riešenie:
Načrtneme si množinu \(A\).
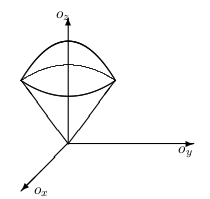Teleso A je výhodné popísať cylindrickými súradnicami, pričom využijeme,
že priemet telesa do roviny \(\rho_{xy}\) je kruh s polomerom 1,
\begin{equation}
\begin{array}
0 \leq \alpha \leq 2\pi\\
0 \leq \rho \leq 1\\
\rho=\sqrt{x^2+y^2}\leq z\leq 2-x^2-y^2=2-\rho^2
\end{array}
\end{equation}
Preto
\begin{equation}
\begin{split}
\iiint\limits_{A}z\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}=\int\limits_{0}^{2\pi}
\left[ \int\limits_{0}^{1}\left( \int\limits_{\rho}^{2-\rho^2}\rho\,z\,\textrm{d}{z}
\right)\textrm{d}{\rho} \right]\,\textrm{d}{\alpha}
=\frac{1}{2}\int\limits_{0}^{2\pi} \left[\frac{\rho^6}{6}-\frac{5\rho^4}{4}+
\frac{4\rho^2}{2}\right]_0^1\,\textrm{d}{\alpha}=\frac{11\pi}{12}.
\end{split}
\end{equation}
Príklad:
Odvoďte vzorec pre objem gule s polomerom \(r_1\).
Riešenie:
Guľu \( A:\quad x^2+y^2+z^2\leq r_1^2\) je výhodné popísať sférickými súradnicami,
pričom
\begin{equation}
\begin{split}
0 \leq \alpha \leq2\pi\\
-\pi/2 \leq \beta \leq\pi/2\\
0\leq r\leq r_1
\end{split}
\end{equation}
Preto
\begin{equation}
\begin{split}
V=\iiint\limits_{A}\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}=\int\limits_{0}^{2\pi}
\left[ \int\limits_{-\pi/2 }^{\pi/2 }\left( \int\limits_{0}^{r_1}r^2\cos\beta\,\textrm{d}{r}
\right)\textrm{d}{\beta} \right]\textrm{d}{\alpha}
=\frac{r_1^3}{3}\int\limits_{0}^{2\pi} \Big[\sin\beta\Big]_{-\pi/2}^{\pi/2}\,
\textrm{d}{\alpha}=\frac{4\pi r_1^3}{3}.
\end{split}
\end{equation}
Postup
-
V krokoch opíšte postup cvičenia. Krok definuje množinu súvisiacich úloh, ktoré vedú k napĺňaniu aspoň jedného cieľa.Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť.Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť.
-
Napíšte ďalší krok.
-
Napíšte ďalší krok.
Zdroje
Doplňujúce úlohy
Úloha:
Vypočítajte \(\displaystyle\quad\iiint\limits_{M}
\left(2x^2y-x+1\right)\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}\), ak
\(M=\langle0,2\rangle\times\langle1,2\rangle\times\langle0,1\rangle\).
Úloha:
Vypočítajte \(\displaystyle\quad\iiint\limits_{M}
xy^2\sqrt{z}\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}\), ak
\(M=\langle-2,1\rangle\times\langle1,3\rangle\times\langle2,4\rangle\).
Úloha:
Vypočítajte \(\displaystyle\quad\iiint\limits_{M}
\frac{1}{x+y+z}\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}\), ak \(M\) je daná nerovnosťami
\(y\geq 0\), \(x\geq 0\), \(x+y+z\leq 1\).
Úloha:
Vypočítajte \(\displaystyle\quad\iiint\limits_{M}
\left( x^2+y^2+1\right)\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}\), ak \(M\) je ohraničená plochami
\(z=\sqrt{x^2+y^2}\), \(x^2+y^2+z^2=8\).
Úloha:
Vypočítajte \(\displaystyle\quad\iiint\limits_{M}
\left( x^2+y^2\right)\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}\), ak \(M\) je ohraničená plochami
\(2z=x^2+y^2\), \(z=2\).
Úloha:
Vypočítajte \(\displaystyle\quad\iiint\limits_{M}
\,\textrm{d}{x}\,\textrm{d}{y}\,\textrm{d}{z}\), ak \(M\) je ohraničená valcovou plochou
\(x^2+y^2=1\) a rovinami \(z=0\), \(z=5\).
Úloha:
Vypočítajte objem telesa ohraničeného plochami \(2z=x^2+y^2\), \(z=\sqrt{x^2+y^2}\).
Úloha:
Vypočítajte objem telesa ohraničeného rovinami \(z=0\), \(y=1\), \(y=2x\), \(y=6-x\).
Úloha:
Vypočítajte objem telesa ohraničeného kužeľovou plochou \(z=\sqrt{x^2+y^2}\),
valcovou plochou \({x^2+y^2=2y}\) a rovinou \(z=0\).
Doplňujúce zdroje
- Tu vložte doplňujúce odporúčané zdroje.
- Tu vložte doplňujúce odporúčané zdroje.