Krivkový integrál II. druhu.

Ciele
  1. Precvičenie parametrického vyjadrenia rôznych rovinných kriviek.
  2. Výpočet kivkového integrálu II. druhu na základe vety o výpočte prevodom na určitý integrál.
Úvod
  1. Parametrizácia rovinnej krivky.

    2. Pred definíciou krivkového integrálu II. druhu sa budeme zaoberat pojmom krivka. Rovnica \[ C:\quad \vec{\pmb{r}}(t)=\varphi(t)\vec{\pmb{i}} +\psi(t)\vec{\pmb{j}},\qquad t\in[\alpha,\beta], \] predstavuje parametrické vujadrenie krivky v rovine.
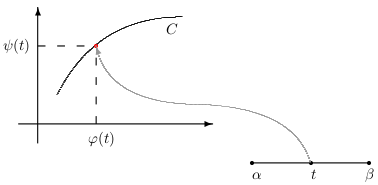
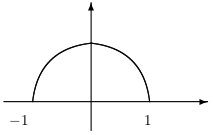
    Podobne rovnica \[ C:\quad \vec{\pmb{r}}(t)=\varphi(t)\vec{\pmb{i}} +\psi(t)\vec{\pmb{j}}+\chi(t)\vec{\pmb{k}},\qquad t\in[a,b], \] resp. \[ \begin{array}{l} C:\quad x=\varphi(t)\\ \quad\quad\,\,\, y=\psi(t)\\ \quad\quad\,\,\, z=\chi(t),\quad t\in[\alpha,\beta] \end{array} \] predstavuje parametrické vuyjadrenie priestorovej krivky.
    Špeciálne krivky tvoria grafy funkcií \(y=f(x)\), \(x\in[\alpha,\beta]\). Napríklad graf funkcie \(y=\sqrt{1-x^2}\), \(x\in[-1,1]\) predstavuje oblúk kružnice.
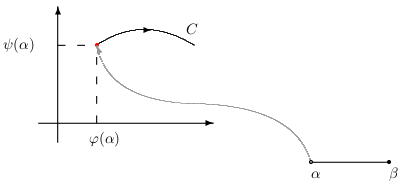
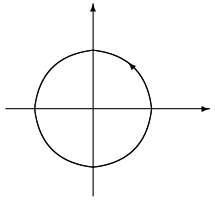
    Vyjadríme túto krivku parametricky. Jedno z možných vyjadrení je \[ \begin{array}{l} C:\quad x=t\\ \qquad\,\,\, y=\sqrt{1-t^2},\quad t\in[-1,1] \end{array} \] Ďaľšie je napríklad \[ \begin{array}{l} C:\quad x=\cos\, t\\ \quad\quad\,\,\, y=\sin t,\quad t\in[0,\pi] \end{array} \] Teda jedna krivka môže mat rôzne parametrické vyjadrenia.

    Uvažujme rovinnú krivku \(C\) danú parametrickými rovnicami \[ \begin{array}{l} C:\quad x=\varphi(t)\\ \quad\quad\,\,\, y=\psi(t),\quad t\in[\alpha,\beta] \end{array} \] Ak pre \(t =\alpha \) dostaneme prvý bod krivky, tak hovoríme, že krivka je orientovaná súhlasne so svojím parametrickým vyjadrením. V opačnom prípade hovoríme, že krivka je orientovaná nesúhlasne so svojim parametrickým vyjadrením.
    Krivku \(C\) nazývame hladkou, ak funkcie \(\varphi(t)\) a \(\psi(t)\) majú spojité derivácie na \([a,b]\). Ak krivka nepretína sama seba, tak ju nazývame jednoduchou. Krivku \(C:\quad \vec{\pmb{r}}(t)\in[\alpha, \beta]\) nazveme uzavretou ak \(\vec{\pmb{r}}(\alpha)=\vec{\pmb{r}}(\beta)\) (teda prvý a posledný bod krivky sú totožné). Príkladom uzavretej krivky je napr. kružnica \[ \begin{array}{l} C:\quad x=\cos\, t\\ \quad\quad\,\,\, y=\sin\, t,\quad t\in[0,\pi] \end{array} \]
    Uzavretú krivku nazvem kladne orientovanou, ak jej orientácia je proti smeru pohybu hodinových ručičiek (viď obrázok). V opačnom prípade uzavretú krivku nazývame záporne orientovanou.

  2. Veta o výpočte krivkového integrálu

    3. Ukážeme ako vypočítať plošný integrál prevodom na určitý integrál. Majme krivku \(C\) určenú parametrickým vyjadrením \[ C:\quad \vec{\pmb{r}}(t)=\varphi(t)\vec{\pmb{i}}+\psi(t)\vec{\pmb{j}},\quad t\in[a,b], \] K odvodeniu vety o výpočte využijeme nasledujúcu vlastnosť \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+ Q(x,y)\,\mathrm{d}{y}= \int\limits_{C} P(x,y)\,\mathrm{d}{x}+ \int\limits_{C}Q(x,y)\,\mathrm{d}{y}. \] Nezávisle budeme počítať integrály \(\int\limits_{C} P(x,y)\,\mathrm{d}{x}\) a \(\int\limits_{C}Q(x,y)\,\mathrm{d}{y}\) pomocou definície krivkového integrálu. Delenie \(D_n\) krivky \(C\) urobíme pomocou delenia intervalu \([a,b]\) nasledovne. Uvažujme delenie \[ a = t_0 \lt t_1 \dots \lt t_n = b \] Bodu \(t_i\) z intervalu \([a,b]\) odpovedá bod \(P_i=[x_i,y_i]=[\varphi(t_i), \psi(t_i)]\) na rovinnej krivke \(C\)
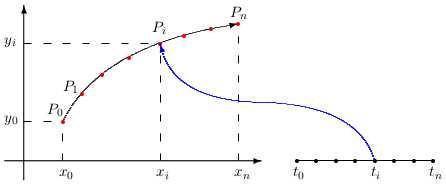
    Takto pomocou delenia intervalu \([a,b]\) vytvoríme delenie krivky \(C\). Analogicky z každého podintervalu \((t_{i-1},t_i)\) vyberieme bod \(t_i^\star\) a tomuto bodu odpovedá výberový bod \(T_i=[x_i^\star,y_i^\star]= [\varphi(t_i^\star), \psi(t_i^\star)]\) na rovinnej krivke \(C\). Využitím týchto skutočností priamo z definície krivkového integrálu dostávame \[ \begin{array}{c} \int\limits_{C} P(x,y)\,\mathrm{d}{x}= \lim_{n\to\infty}\sum\limits_{i=1}^{p_n} P(x_i^\star, y_i^\star)\Delta x_i =\lim_{n\to\infty}\sum\limits_{i=1}^{p_n} P(\varphi(t_i^\star), \psi(t_i^\star))(\varphi(t_i)-\varphi(t_{i-1}))=\\ =\lim_{n\to\infty}\sum\limits_{i=1}^{p_n} P(\varphi(t_i^\star), \psi(t_i^\star)) \frac{\varphi(t_i)-\varphi(t_{i-1})}{t_i-t_{i-1}}\,(t_i-t_{i-1})= \end{array} \]
    Poznámka: Lagrangeova veta pre funkciu \(\varphi(t)\) na intervale \([t_{i-1}, t_i]\) dáva bod \(t_i^\star\), taký, že \(\displaystyle\frac{\varphi(t_i)-\varphi(t_{i-1})}{t_i-t_{i-1}}= \varphi'(t_i^\star)\). Tento bod je zároveň výberový bod z intervalu \([t_{i-1}, t_i]\).
    \[ =\lim_{n\to\infty}\sum\limits_{i=1}^{p_n} P(\varphi(t_i^\star), \psi(t_i^\star))\varphi'(t_i^\star)\Delta t_i= \]
    Poznámka: v tomto vzťahu spoznávame limitu postupnosti integrálnych súčtov pre dvojný integrál a preto
    \[ =\int\limits_a^b P(\varphi(t), \psi(t))\varphi'(t)\,\mathrm{d}{t}. \] Odvodili sme nasledujúci vzťah \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}=\int\limits_a^b P(\varphi(t),\psi(t))\varphi'(t)\,\mathrm{d}{t}. \] Analogickým postupom dostávame \[ \int\limits_{C} Q(x,y)\,\mathrm{d}{x}=\int\limits_a^b Q(\varphi(t),\psi(t))\psi'(t)\,\mathrm{d}{t}. \] Na základe uvedeného môžeme sformulovať vetu o výpočte krivkového integrálu.

    \(\mathbf{Veta.}\) Nech \(\vec{\pmb{F}}=P(x,y)\vec{\pmb{i}}+Q(x,y)\vec{\pmb{j}}\) je spojitá vektorová funkcia definovaná na orientovanej jednoduchej hladkej krivke \(C\), ktorej parametrické vyjadrenie je \[ C:\quad \vec{\pmb{r}}(t)=\varphi(t)\vec{\pmb{i}} +\psi(t)\vec{\pmb{j}},\qquad t\in[a,b], \] Potom \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+ Q(x,y)\,\mathrm{d}{y}= \pm\int\limits_a^b \left[P(\varphi(t),\psi(t))\varphi'(t)+Q(\varphi(t), \psi(t))\psi^{\prime}(t)\right]\,\mathrm{d}{t}, \] kde znamienko \(+\) resp. \(-\) platí ak \(C\) je orientovaná súhlasne resp. nesúhlasne so svojim parametrickým vyjadrením.

  3. Základné vlastnosti krivkového integrálu

    4. V ďalšom budeme predpokladať o všetkých integráloch, že existujú a krivky po ktorých integrujeme sú jednoduché, orientované a hladké.

    • \(\displaystyle\int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}= \int\limits_{C} P(x,y)\,\mathrm{d}{x}+\int\limits_{C}Q(x,y)\,\mathrm{d}{y}\),
      t.j. celkovú prácu je možné rozložiť na prácu v smere osi \(o_x\) a prácu v smere osi \(o_y\).

    • nech krivky \(C_1\), \(C_2\) tvoria delenie krivky \(C\), potom \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}= \int\limits_{C_1} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}+ \int\limits_{C_2} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}, \]

    • nech \(-C\) je krivka, ktorá vznikne z krivky \(C\) zmenou orientácie, potom \[ \int\limits_{-C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}= -\int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}. \]
Postup
  1. V krokoch opíšte postup cvičenia. Krok definuje množinu súvisiacich úloh, ktoré vedú k napĺňaniu aspoň jedného cieľa.
    Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C} y\,\mathrm{d}{x}- x\,\mathrm{d}{y}, \] ak krivka ak \(C\) je elipsa \[ C:\quad \vec{\pmb{r}}(t)=2\cos t\,\vec{\pmb{i}}+2\sin t\,\vec{\pmb{i}},\quad t\in[0,2\pi], \] orientovaná súhlasne so svojim parametrickým vyjadrením.
    Riešenie: Zakreslíme elipsu a v niekoľkých vybraných bodoch znázorníme aj vektor sily \(\vec{\pmb{F}}=y\vec{\pmb{i}}- x\vec{\pmb{j}}\).
    Keďže sila pôsobí stále proti pohybu hmotného bodu bude výsledná práca záporná a znamienko mínus vyjadruje, že silové pole prácu nekoná, ale na prekonanie silového poľa treba prácu dodať. Výpočet dáva \[ \int\limits_{C} y\,\mathrm{d}{x}- x\,\mathrm{d}{y}=\int\limits_0^{2\pi} \big( 3\sin t\,(-2\sin t)-6\cos t\,(3\cos t)\big)\,\mathrm{d}{t} =-12\pi. \]
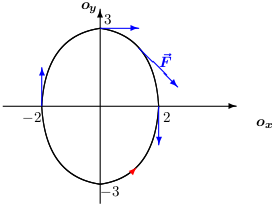
    Poznámka: Ak by sa hmotný bod pohyboval po elipse opačným smerom, silové pole by prácu konalo a výsledok by bol \(12\pi\).
    Úloha: Vypočítajte \(\displaystyle \int\limits_{C} \frac{x}{y}\,\mathrm{d}{x}+ \frac{y}{x}\,\mathrm{d}{y} \) ak \(C\) je časť kružnice \(x^2+y^2=9\) od bodu\(A=[0,3]\) po bod \(B=[-3,0]\).
    Zobraziť výsledok
    Úloha: Vypočítajte \(\displaystyle \int\limits_{C} (x^2+y^2)\,\mathrm{d}{x}+x^2-y^2\,\mathrm{d}{y} \) ak \(C:\, y=1-|1-x|,\,x\in\langle0,2\rangle\), ktorej prvý bod je \(A=[0,0]\).
    Úloha: Vypočítajte \(\displaystyle \int\limits_{C} \left(-\vec{\pmb{i}}+\mathrm{arctg}\frac{y}{x}\vec{\pmb{j}}\right) \,\mathrm{d}\vec{\pmb{s}} \), ak \(C\) sa skladá z oblúkov \({AB}\), \({BA}\), kde \({AB}\) je oblúk paraboly \(y=x^2\) od bodu \(A=[0,0]\) k bodu \(B=[1,1]\) a oblúk \(BA\) je úsečka. Body \( A,\,B,\,D,\,\, D=[1/2,1/2]\) tvoria usporiadanú trojicu v zmysle orientácie krivky \(C\).
    Zobraziť výsledok
    Úloha: \(\displaystyle \int\limits_{C} \left((2a-y)\vec{\pmb{i}}+{x}\vec{\pmb{j}}\right) \,\mathrm{d}\vec{\pmb{s}}\), ak \(C\) je orientovaný oblúk cykloidy \( \vec{\pmb{r}}(t)= a(t-\sin t)\vec{\pmb{i}}+a(1-\cos t)\vec{\pmb{j}},\,\,t\in\langle0,2\pi\rangle\), a prvý bod je \(A=[0,0]\).
    Zobraziť výsledok
    Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.
    Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť.
  2. Napíšte ďalší krok.
  3. Napíšte ďalší krok.
Zdroje
  1. Moja web stránka .
  2. Predmet Matematicko--počítačové modelovanie .
Doplňujúce úlohy
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Doplňujúce zdroje
  1. Tu vložte doplňujúce odporúčané zdroje.
  2. Tu vložte doplňujúce odporúčané zdroje.