Krivkový integrál II. druhu.

Ciele
  1. Výpočet krivkového integrálu po uzavretej krivke prevodomna dvojný integrál -- aplikácie Greenovej vety.
  2. Výpočet dvojného integrálu v prípade nezávislosti od integračnej cesty.
  3. Výpočet dvojného integrálu prevodom krivky -- aplikácie Greenovej vety.
Úvod
  1. Greenova veta.

    2. V prípade, ak je krivka C uzavretá, kladne orientovaná, môžeme krivkový integrál pocítat prevodom na dvojný integrál, o com hovorí nasledujúca veta.
    \(\mathbf{Veta.}\) Nech \(C\) je uzavretá, jednoduchá, hladká, kladne, orientovaná krivka. Nech \(D\) je rovinná oblast ohranicená krivkou \(C\). Nech \(\displaystyle\frac{\partial Q}{\partial x}\), \(\displaystyle\frac{\partial P} {\partial y}\) sú spojité na \(D\). Potom. \[ \oint\limits_{C} P(x,y)\, \mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} = \iint\limits_{D} \left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right)\,\mathrm{d}{x}\,\mathrm{d}{y} \]
    \({\mathit{Dôkaz.}}\) Ukážeme, že platia nasledujúce rovnosti. \[ \oint\limits_{C} P(x,y)\, \mathrm{d}{x} = -\iint\limits_{D} \frac{\partial P(x,y)}{\partial y}\,\mathrm{d}{x}\,\mathrm{d}{y} \] \[ \oint\limits_{C} Q(x,y)\,\mathrm{d}{y} = \iint\limits_{D} \frac{\partial Q(x,y)}{\partial x} \,\mathrm{d}{x}\,\mathrm{d}{y} \] Predpokladáme, že \(D\) je elementárna oblasť typu \([x,y]\) aj \([y,x]\) (ak nie, tak oblasť \(D\) vyjadríme ako zjednotenie viacerých elementárnych oblastí. )
    \[ \begin{split} D: \quad a \leq x\leq b\\ \qquad \qquad g(x) \leq y\leq h(x)\quad \end{split}\qquad\qquad \begin{split} D: \quad c \leq y\leq d\\ \quad\quad \alpha(y) \leq x\leq \beta(y)\quad \end{split} \] Krivku \(C\) rozdelíme na dve krivky \(C=C_1\cup C_2\), kde \[ \begin{split} C_1: \quad x =t,\quad \\ y = g(t)\quad t\in[a,b] \end{split}\qquad\qquad \begin{split} C_2: \quad x =t,\quad\\ y = h(t)\quad t\in[a,b] \end{split} \] pričom krivka \(C_1\) je orientovaná súhlasne s týmto parametrickým vyjadrením a krivka \(C_2\) nesúhlasne. Počítajme krivkový integrál \[ \oint\limits_{C} P(x,y)\,\mathrm{d}{x}=\oint\limits_{C_1} P(x,y)\,\mathrm{d}{x} +\oint\limits_{C_2} P(x,y)\,\mathrm{d}{x}=\int\limits_a^b P(t, g(t))\, \mathrm{d}{t}-\int\limits_a^b P(t, h(t))\,\mathrm{d}{t} \] Ďalej počítajme dvojný integrál \[ \iint\limits_{D} \frac{\partial P(x,y)}{\partial y}\,\mathrm{d}{x}\,\mathrm{d}{y}= \] \[ \left\{\quad D: \quad a \leq x\leq b,\quad g(x) \leq y\leq h(x)\quad\right\}= \int\limits_a^b \left( \int\limits_{g(x)}^{h(x)} \frac{\partial P(x,y)}{\partial y}\,\mathrm{d}{x} \right)\mathrm{d}{y}= \int\limits_a^b P(x, h(x)) - P(x, g(x)) \,\mathrm{d}{x} \] Tým sme dokázali požadovanú rovnosť. Analogicky sa overí, že \[ \oint\limits_{C} Q(x,y)\,\mathrm{d}{y}= \iint\limits_{D} \frac{\partial Q(x,y)}{\partial x} \,\mathrm{d}{x}\,\mathrm{d}{y} \]

  2. Dôsledky Greenovej vety, nezávislosť od integračnej cesty.

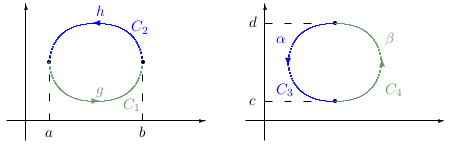
    3. Nech \(C\) je uzavretá, jednoduchá hladká, kladne orientovaná krivka, ktorá tvorí hranicu oblasti \(D\). Ak na oblasti \(D\) platí \[ \frac{\partial Q(x,y)}{\partial x} =\frac{\partial P(x,y)}{\partial y}, \] potom \[ \oint\limits_{C} P(x,y)\, \mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} =0. \] Táto vlastnosť je bezprostredným dôsledkom Greenovej vety a využijeme ho pri nasledujúcich úvahách.
    Nech na oblasti \(D\) platí \[ \frac{\partial Q(x,y)}{\partial x} =\frac{\partial P(x,y)}{\partial y}. \] Nech jednoduché krivky \(C_1\) a \(C_2\) ležia v oblasti \(D\) a majú spoločný začiatočný aj koncový bod.
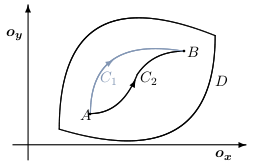
    potom \[ \int\limits_{C_1} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} = \int\limits_{C_2} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} . \] To znamená, že uvedený krivkový integrál nezávisí od integračnej cesty (od tvaru krivky), ale len od začiatočného a koncového bodu. Uvedené tvrdenie vyplýva z nasledujúcich úvah. Uvažujme uzavretú krivku \(C=C_2\cup (-C_1)\), ktorá je kladne orientovaná. Použitím prvého dôsledku pre krivku \(C\) máme \[ 0=\oint\limits_{C} P\,\mathrm{d}{x}+Q\,\mathrm{d}{y} =\int\limits_{C_2} P\, \mathrm{d}{x}+Q\,\mathrm{d}{y}-\oint\limits_{C_1} P\,\mathrm{d}{x}+Q\,\mathrm{d}{y}, \] odkiaľ vyplýva naše tvrdenie.
    Ďalej zadefinujeme potenciál silového poľa a ukážeme jeho použitie pri výpočte krivkového integrálu. Majme jednoduchú hladkú krivku $C$ určenú parametrickým vyjadrením \[ C:\quad \vec{\pmb{r}}(t)=\varphi(t)\vec{\pmb{i}}+ \psi(t)\vec{\pmb{j}},\qquad t\in[a,b], \] a jej orientácia je súhlasná s daným parametrickým vyjadrením, t.j. \(A=[\varphi(a),\psi(a)]\) je jej začiatočný bod a \(B=[\varphi(b),\psi(b)]\) je jej koncový bod. Krivka leží v oblasti \(D\).
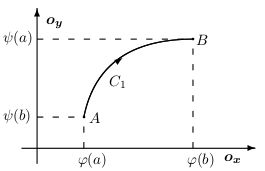
    Uvažujme integrál \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}. \] Predpokladajme, že existuje skalárna funkcia \(V(x,y)\), pre ktorú na \(D\) platí \[ \begin{split} \frac{\partial V(x,y)}{\partial x} = P(x,y),\\ \frac{\partial V(x,y)}{\partial y} = Q(x,y). \end{split} \] Takúto funkciu nazývame potenciál silového poľa \(\vec{F}=(P,Q)\). Ak zmiešané parciálne derivácie funkcie \(V(x,y)\) sú spojité na \(D\), potom z ich rovnosti vyplýva \[ \frac{\partial P(x,y)}{\partial y}=\frac{\partial^2 V(x,y)}{\partial x\partial y} =\frac{\partial^2 V(x,y)}{\partial y\partial x}=\frac{\partial Q(x,y)}{\partial x} \] a teda integrál \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}. \] spĺňa podmienku nezávislosti na integračnej ceste. Môžeme zhrnúť.
    Krivkový integrál nezávisí od integračnej cesty práve vtedy ak existuje potenciál jeho silového poľa.
    Ukážeme, že pomocou potenciálu silového poľa môžeme jednoducho vypočítať krivkový integrál. \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}= \] použitím vety o výpočte \[ =\int\limits_a^b P(\varphi(t),\psi(t))\varphi'(t)+Q(\varphi(t), \psi(t))\psi'(t)\,\mathrm{d}{t}= \] keďže \[ \frac{\mathrm{d}V(\varphi(t),\psi(t))}{\mathrm{d}t}= \frac{\partial V(\varphi(t),\psi(t))}{\partial x} \frac{\mathrm{d}\varphi(t)}{\mathrm{d}t} +\frac{\partial V(\varphi(t),\psi(t))}{\partial y} \frac{\mathrm{d}\psi(t)}{\mathrm{d}t}= P(\varphi(t),\psi(t))\varphi'(t)+Q(\varphi(t),\psi(t))\psi'(t)= \] \[ =\int\limits_a^b \frac{\mathrm{d}}{\mathrm{d}t}\big(V(\varphi(t),\psi(t))\big) {\mathrm{d}{t}}=\Big[V(\varphi(t),\psi(t))\Big]_{a}^{b}=V(B)-V(A). \] Uvedené možno zhrnúť do nasledujúceho tvrdenia
    Ak existuje potenciál silového poľa \(V\) (krivkový integrál nezávisí od integračnej cesty), potom \[ \int\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y}=V(B)-V(A), \] kde \(A\) a \(B\) sú prvý a posledný bod krivky.
Postup
  1. Greenova veta
    Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C} (x+y)\,\mathrm{d}{x}- (x-y)\,\mathrm{d}{y}, \] ak krivka ak \(C\) je kladne orientovaná elipsa \( \displaystyle{\frac{x^2}{4}+\frac{y^2}{9}=1}, \)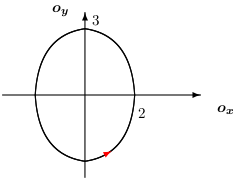
    Riešenie: Použitím Greenovej vety dostávame \[ \int\limits_{C} (x+y)\,\mathrm{d}{x}- (x-y)\,\mathrm{d}{y}=-2\iint\limits_{D} 1 \, \mathrm{d}{x}\,\mathrm{d}{y}=-2P(D)=-12\pi \]
    Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C}\frac{y^2}{2}\,\mathrm{d}{x}+\frac{x^2}{2}\,\mathrm{d}{y}, \] ak \(C\) je kladne orientovaná hranica oblasti ohraničenej krivkami \(y=\ln x\), \(y=1\), \(y=2\), \(x=0\).
    Riešenie: Načrtneme si kontúry oblasti ohraničenej krivkou \(C\).
    Množina \(D\) vyjadríme nasledovne \[\begin{split} D: \quad 1 \leq y\leq 2\quad\\ \qquad 0 \leq x\leq \mathrm{e}^y\quad \end{split} \] Použitím Greenovej vety dostávame \[ \begin{split} \int\limits_{C}\frac{y^2}{2}\,\mathrm{d}{x}+\frac{x^2}{2}\,\mathrm{d}{y}= \iint\limits_{D} (x-y) \,\mathrm{d}{x}\,\mathrm{d}{y}= \int\limits_1^2 \left(\, \int\limits_{0}^{\mathrm{e}^y} (x-y)\,\mathrm{d}{x} \right)\mathrm{d}{y}=\left[ \frac{\mathrm{e}^{2y}}{4}-y\mathrm{e}^y+ \mathrm{e}^y\right]_1^2=\frac{\mathrm{e}^4}{4}-\frac{5\mathrm{e}^2}{4}. \end{split} \]
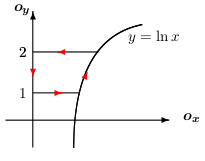    Príklad: Pomocou krivkového integrálu odvoďte vzorec pre výpočet obsahu elipsy danej: \(\displaystyle{\quad\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}\).
    Riešenie: Vieme, že plochu vieme vyjadriť pomocou dvojného integrálu, na ktorý aplikujeme Greenovu vetu:
    Teda \[ \begin{split} \text{Plocha }=\iint\limits_{D} 1 \,\mathrm{d}{x}\,\mathrm{d}{y}= \iint\limits_{D} \left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right)\,\mathrm{d}{x}\,\mathrm{d}{y}= \oint\limits_{C} P(x,y)\,\mathrm{d}{x}+Q(x,y)\,\mathrm{d}{y} \end{split} \] Potrebujeme nájsť také funkcie \(P\), \(Q\), aby platilo \[ 1=\left(\frac{\partial Q(x,y)}{\partial x} - \frac{\partial P(x,y)}{\partial y}\right). \] Možnosti na zvolenie funkcií \(P\), \(Q\) je samozrejme viacej. My použijeme \[ P(x,y)=-\frac{y}{2}\qquad Q(x,y)=\frac{x}{2} \] A teda odvodili sme všeobecný vzorec pre výpočet obsahu rovinného telesa \[ P(D)=\oint\limits_{C} -\frac{y}{2}\,\mathrm{d}{x}+\frac{x}{2}\,\mathrm{d}{y}, \] kde \(C\) je kladne orientovaná hranica \(D\). Aplikáciou tohto vzorca na náš príklad, použitím nasledujúcich parametrických rovníc pre elipsu \[ \begin{split} C: \quad x =\cos t,\quad \\ \qquad\qquad y = \sin t,\quad t\in[0,2\pi], \end{split} \] dostávame \[ P(D)=\oint\limits_{C} -\frac{y}{2}\,\mathrm{d}{x}+\frac{x}{2}\,\mathrm{d}{y} = \int\limits_0^{2\pi}(-b\sin t)(-a\sin t)+(a\cos t)(b\cos t)\,\mathrm{d}{t}=\pi ab \]
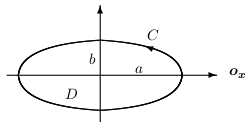    Úloha: Vypočítajte \[ \oint\limits_{C}y^2\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(C\) je kladne orientovaný obvod štvorca ohraničený priamkami \(x=1\), \(x=-1\), \(y=1\), \(y=-1\).
    Riešenie: \(\displaystyle\left[4\right]\)
    Úloha: Vypočítajte \[ \oint\limits_{C}\frac{1}{x}\mathrm{arctg}\frac{y}{x} \,\mathrm{d}{x}+ \frac{2}{x}\mathrm{arctg}\frac{x}{y} \,\mathrm{d}{y}, \] ak \(C\) je hranica oblasti \(1\leq x^2+y^2\leq 4\), \(x\leq y\leq \sqrt{3}x\).
    Riešenie: \(\displaystyle\left[\frac{\pi}{12}\ln 2\right]\)
    Úloha: Vypočítajte \[ \oint\limits_{C}y^2\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(C\) je kružnica s polomerom 2 a so stredom v bode \([0,0]\) kladne orientovaná.
    Riešenie: \(\displaystyle\left[4\pi\right]\)

    2. Dôsledky Greenovej vety, nezávislosť od integračnej cesty.
    Príklad: Vypočítajte krivkový integrál \[ \int\limits_{C} y\,\mathrm{d}{x}+x\,\mathrm{d}{y}, \] ak \(A=[1,1]\) a \(B=[2,4]\) sú prvý a posledný bod krivky.
    Riešenie: Keďže \[ \frac{\partial Q(x,y)}{\partial x} =1=\frac{\partial P(x,y)}{\partial y}, \] uvedený integrál nezávisí od integračnej cesty a môžeme ho rátať pomocou potenciálu \(V(x,y)\), kde \[ \begin{split} \frac{\partial V(x,y)}{\partial x} = P(x,y)=y,\\ \frac{\partial V(x,y)}{\partial y} = Q(x,y)=x. \end{split} \] Očividne \(V(x,y)=xy\) vyhovuje týmto podmienkam, a preto \[ \int\limits_{C} y\,\mathrm{d}{x}+x\,\mathrm{d}{y}=\Big[xy\Big]_{A= [1,1]}^{B=[2,4]}=8-1=7. \]
    Úloha: Vypočítajte \[ \int\limits_{C}(2y-6xy^3)\,\mathrm{d}{x}+(2x-9x^2y^2)\,\mathrm{d}{y}, \] ak prvý bod krivky je \(A=[0,0]\) a posledný bod je \(B=[2,2]\)
    Riešenie: \(\displaystyle\left[-88\right]\)
    Úloha: Vypočítajte \[ \int\limits_{C}(2x+3y)\,\mathrm{d}{x}+(3x-3y)\,\mathrm{d}{y}, \] ak prvý bod krivky je \(A=[1,1]\) a posledný bod je \(B=[3,3]\)
    Riešenie: \(\displaystyle\left[16\right]\)

    Príklad: Nech \(C\) je uzavretá, jednoduchá hladká, kladne orientovaná krivka, ktorá tvorí hranicu oblasti \(\Omega\). Vyjadrite dvojný integrál \[ \iint\limits_{\Omega} ts \,\mathrm{d}{t}\,\mathrm{d}{s} \] pomocou krivkového integrálu.
    Riešenie: Greenova veta vyžaduje funkcie \(P(t,s)\), \(Q(t,s)\), také,že \[ ts=\left(\frac{\partial Q(t,s)}{\partial t}-\frac{\partial P(t,s)}{\partial s}\right). \] Existuje nekonečne veľa variant pre ich výber. My urobíme jeden konkrétny založený na zameniteľnosti premenných \(t\), \(s\) vo funkcii \(ts\), a teda \[ ts=\frac{ts}{2}-\frac{-ts}{2}=\left(\frac{\partial Q(t,s)}{\partial t}- \frac{\partial P(t,s)}{\partial s}\right). \] Funkciu \(Q(t,s)\) nájdeme z podmienky \(\displaystyle\frac{\partial Q(t,s)} {\partial t}=\frac{ts}{2}\) a využitím symetrie medzi \(t\) a \(s\) stačí potom položiť \(P(t,s)=-Q(s,t)\). A teda v našom prípade bude \[ Q(t,s)=\frac{t^2s}{4} \quad\text{a následne}\quad P(t,s)=-\frac{ts^2}{4}. \] Preto \[ \iint\limits_{\Omega} ts\,\mathrm{d}{t}\,\mathrm{d}{s}=\oint\limits_{C}- \frac{ts^2}{4}\,\mathrm{d}{t}+ \frac{t^2s}{4} \,\mathrm{d}{s}. \]
    Poznámka: Tu možete pridať doplňujúci komentár k úlohe, ktorý študentovi pomôže pri riešení.
    Úloha: Tu napíšte konkrétne úlohy, ktoré ma študent vyriešiť.
  2. Napíšte ďalší krok.
  3. Napíšte ďalší krok.
Zdroje
  1. Moja web stránka .
  2. Predmet Matematicko--počítačové modelovanie .
Doplňujúce úlohy
    Úloha: Vypočítajte \(\displaystyle\quad\int\limits_{C}x^2\,\mathrm{d}{x}-xy\mathrm{d}{y}\), ak \(C\) je štvrťkružnica \(x=\cos t\), \(y=\sin t\), pričom \(t\in\langle0,\pi/2\rangle\)
    Zobraziť výsledok
    Úloha: Vypočítajte \(\displaystyle\quad\int\limits_{C}3x^2y\,\mathrm{d}{x}+ \left(x^3+1\right)\,\mathrm{d}{y}\), ak \(C\) je časť oblúka paraboly \(y=x^2\) od bodu \(A=[0,0]\) po bod \(B=[1,1]\)
    Zobraziť výsledok
    Úloha: Vypočítajte \(\displaystyle\quad\int\limits_{C} x\,\mathrm{d}{y}\), ak \(C\) je kladne orientovaný obvod trojuholníka tvorený súradnicovými osami a priamkou \(x+y=3\).
    Zobraziť výsledok
    Úloha: Vypočítajte \(\displaystyle\quad\int\limits_{C}\left(x^2-y^2\right)\mathrm{d}{x}\), ak \(C\) je časť oblúka paraboly \(y=x^2\) od bodu \(A=[0,0]\) po bod \(B=[2,4]\).
    Zobraziť výsledok
    Úloha: Vypočítajte \(\displaystyle\quad\int\limits_{C} xy\,\mathrm{d}{x}+(y-x)\, \mathrm{d}{y}\), ak \(C\) je krivka \(a)\,\,y=x\), \(b)\,\,y=x^2\), \(c)\,\,y=x^3\), \(d)\,\,y^2=x\) od bodu \(A=[0,0]\) po bod \(B=[1,1]\).
    Úloha: Tu napíšte úlohy ktoré sú pripravené nad základný rámec cvičenia.
Doplňujúce zdroje
  1. Tu vložte doplňujúce odporúčané zdroje.
  2. Tu vložte doplňujúce odporúčané zdroje.