Ciele
- Naštudovať potrebné pojmy.
- Preštudovať vzorové príklady prezentované v rámci teoretickej časti.
- Vypracovať zadané úlohy.
Základne pojmy
Lineárna logika bola formulovaná v roku 1987 francúzskym logikom Jean-Yves Girardom ako nový logický systém. Zovšeobecňuje výrokovú logiku, ktorej sémantika je založená na Tarského sémantickej tradícii narábajúcej s pravdivosťou logických formúl a intuicionistickú logiku, ktorej sémantika je založená na Heytingovej sémantickej tradícii zaoberajúcou sa zmyslom logických formúl.
V porovnaní s inými logickými systémami je hlavným rozdielom ako aj výhodou lineárnej logiky oproti klasickým logickým systémom jej zdrojovo-orientovaná povaha narábania so zdrojmi. Zavedením nových logických spojok vznikla rozsiahla vyjadrovacia sila, ktorá dodáva lineárnej logike schopnosti vyjadriť procesy reálneho sveta ako napr. pleonazmus, paralelizmus, polemika, kauzalita t.j. proces akcie a reakcie atď. Táto logika je tiež nazývaná logikou zdrojov, čo znamená, že formula lineárnej logiky vyjadruje akciu/reakciu alebo dostupný zdroj/spotrebovaný zdroj.
Jazyk lineárnej logiky
Jazyk lineárnej logiky pozostáva z jeho symbolov a syntaxe.
Induktívna definícia symbolov jazyka lineárnej logiky pozostáva z:
- elementárnych formúl: $a$,
- logických spojok ktoré sa delia na:
- unárne: $()^\perp, !, ?$,
- binárne: $\otimes, ⅋ , \&, \oplus, \multimap$,
- konštanty (nulárne logické spojky): $\mathbf{1},\top, \mathbf{0}, \perp$,
- pomocné symboly: $(,)$.
Syntax lineárnej logiky
Syntax jazyka lineárnej logiky vo forme produkčného pravidla v Backus-Naurovej forme je definovaná nasledovne: $$ \varphi ::= a ~ |~ \textbf{1} ~|~\bot~|~\top~|~ \textbf{0} ~|~ \varphi \otimes \psi ~|~ \varphi~ \& ~\psi ~|~ \varphi \oplus \psi ~|~ \varphi~ ⅋ ~\psi ~|~ \varphi \multimap \psi ~|~ \varphi^\perp ~|~ !\varphi ~|~ ?\varphi. $$
Neformálny popis jednotlivých logických spojok lineárnej logiky zobrazených v produkčnom pravidle:
- $a$ je elementárna formula.
- $ \varphi \otimes \psi$ Multiplikatívna konjunkcia s neutrálnym prvkom $\mathbf{1}$, vyjadruje vlastnosti paralelizmu t.j. vykonanie obidvoch akcií ($\varphi, \psi$) naraz.
- $ \varphi~\&~\psi$ Aditívna konjunkcia s neutrálnym prvkom $\top$, vyjadruje závislú voľbu resp. externý nedeterminizmus t.j. vykonanie iba jednej akcie z oboch dostupných ($\varphi, \psi$), pričom je možné rozhodnúť, ktorá z nich bude vykonaná.
- $ \varphi \oplus \psi$ Aditívna disjunkcia s neutrálnym prvkom $\mathbf{0}$, vyjadruje slobodnú voľbu resp. interný nedeterminizmus t.j. vykonanie iba jednej akcie z oboch dostupných ($\varphi, \psi$), na základe vonkajších podmienok.
- $ \varphi~ ⅋ ~\psi$ Multiplikatívna disjunkcia s neutrálnym prvkom $\perp$, vyjadruje vykonanie iba jednej z dostupných akcií ($\varphi, \psi$), pričom pokiaľ nebude vykonaná akcia $\varphi$, tak bude vykonaná akcia $\psi$ a opačne.
- $ \varphi \multimap \psi$ Lineárna implikácia vyjadruje kauzálny proces reálneho sveta t.j. akcia vyvolá reakciu, kde zdroj ($\varphi$) ktorý spustí vykonanie akcie sa stane spotrebovaným zdrojom ($(\varphi)^\perp$).
- Pomocou exponenciálnych operátorov je možné vyjadriť pleonazmus ($!\varphi$) t.j. nevyčerpateľnosť zdroja alebo polemiku ($?\varphi$) t.j. potenciálnu nevyčerpateľnosť zdroja.
- $ \varphi^\perp$ Lineárna negácia je najdôležitejšou logickou spojkou lineárnej logiky. Je involutívna $(\varphi^\perp)^\perp \equiv \varphi$. Vyjadruje kauzalitu zobrazenú v tabuľke:
| Kauzalita lineárnej logiky | |
|---|---|
| akcia $\varphi$ | reakcia $\varphi^\perp$ |
| dostupný zdroj | spotrebovaný zdroj |
| vstup | výstup |
Logické spojky lineárnej logiky je možné rozdeliť podľa polarity na:
- pozitívne: $$ \otimes, \oplus, \mathbf{1}, \mathbf{0}, !, $$
- negatívne: $$ \&, ⅋, \top, \bot, ?. $$
Zákony lineárnej logiky
V lineárnej logike taktiež platia De Morganove zákony:
$$ \begin{array}{rcl} \mathbf{1}^\perp & \equiv & \perp \\ \perp^\perp & \equiv & \mathbf{1} \\ \top^\perp & \equiv & \mathbf{0} \\ \mathbf{0}^\perp & \equiv & \top \\ (\varphi^\perp)^\perp & \equiv & \varphi \\ (\varphi \otimes \psi)^\perp & \equiv & \varphi^\perp ~⅋~ \psi^\perp \\ (\varphi ~⅋~ \psi)^\perp & \equiv & \varphi^\perp \otimes \psi^\perp \\ (\varphi \oplus \psi)^\perp & \equiv & \varphi^\perp \& \psi^\perp \\ (\varphi \& \psi)^\perp & \equiv & \varphi^\perp \oplus \psi^\perp \\ (!\varphi)^\perp & \equiv & ?\varphi^\perp \\ (?\varphi)^\perp & \equiv & !\varphi^\perp \\ \varphi \multimap \psi & \equiv & \varphi^\perp ~⅋~ \psi \end{array} $$
Fragmentácia lineárnej logiky
Rozdelenie lineárnej logiky na jednotlivé fragmenty je zobrazené na obrázku nižšie.
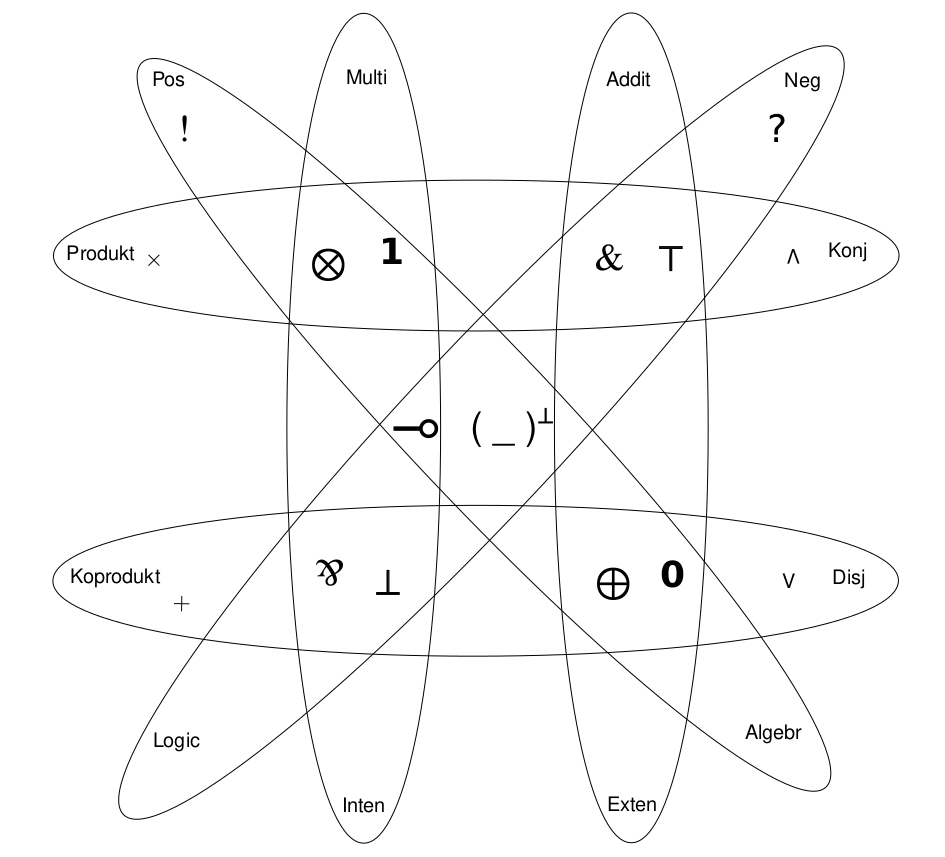
Na obrázky sú v jednotlivých elipsách zobrazené nasledujúce fragmenty:
- Základné Girardovo rozdelenie je zobrazené vo vertikálnych elipsách kde: multiplikatívny (intezionálny) fragment je zobrazený v ľavej vertikálnej elipse a aditívny (extenzionálny) fragment v pravej vertikálnej elipse.
- Z pohľadu polarity logických spojok rozlišujeme pozitívny fragment (diagonálna elipsa medzi ľavým horným a pravým dolným rohom) a negatívny fragment (diagonálna elipsa medzi pravým horným a ľavým dolným rohom).
- Z pohľadu lineárnej teórie typov rozlišujeme fragmenty podľa spôsobu narábania s lineárnymi typmi v horizontálnych elipsách:
- vrchná horizontálna elipsa zobrazuje fragment pre produkt lineárnych typov: konštruujúci operátor $\otimes$ spolu s projekčným operátorom $\&$,
- spodná horizontálna elipsa zobrazuje fragment pre koprodukt lineárnych typov: dekonštruujúci operátor $\oplus$ spolu s koprojekčným operátorom $~⅋~$.
Poznámka
V rámci tohto cvičenia sa fragmentácií lineárnej logiky nebudeme hlbšie venovať.
Sémantika lineárnej logiky
Existuje viacero definícií sémantiky pre lineárnu logiku. Lafont definoval sémantiku pomocou metódy hernej sémantiky. Girard definoval pre lineárnu logiku dve sémantiky založené na rozdielnych sémantických tradíciách nasledovne:
- Fázová sémantika vychádzajúca z Tarského sémantickej tradície, vhodná pre aditívny (intenzionálny) fragment lineárnej logiky,
- Koherentná sémantika vychádzajúca z Heytingovej sémantickej tradície, vhodná pre multiplikatívny (extenzionálny) fragment lineárnej logiky.
Poznámka
V rámci tohto cvičenia sa sémantike lineárnej logiky nebudeme hlbšie venovať.
Dokazovací systém lineárnej logiky
Obojstranný Gentzenov sekventový kalkul pre lineárnu logiku má nasledujúci tvar:
$$ {\Gamma} \vdash {\Delta}, $$ kde $\Gamma, \Delta$ sú konečné množiny formúl.
Význam zápisu $\Gamma \vdash \Delta$ je: $$ \varphi_1 \otimes \dots \otimes \varphi_n \vdash \psi_1 \& \dots \& \psi_m, $$ ktorý je možné prečítať ako aditívna konjunkcia formúl na pravej strane sekventu je dokázateľná z multiplikatívnej konjunkcie formúl na strane ľavej.
Dedukčné pravidlá sekventového kalkulu lineárnej logiky
Axióma identity a pravidlo rezu:
Axióma identity neobsahuje predpoklady a pravidlo rezu rozvetvuje dôkazový strom.

Štrukturálne pravidlá:
Pravidlá výmeny vyjadrujú komutatívnosť logiky tým, že umožňujú permutáciu formúl na oboch stranách sekventu.

Na rozdiel od iných logických systémov, zdrojovo-orientovaná povaha lineárnej logiky neumožňuje zaviesť plnohodnotné pravidlá oslabenia a kontrakcie, avšak pri využití exponenciálnych logických spojok je možné zaviesť ich v obmedzenom tvare:
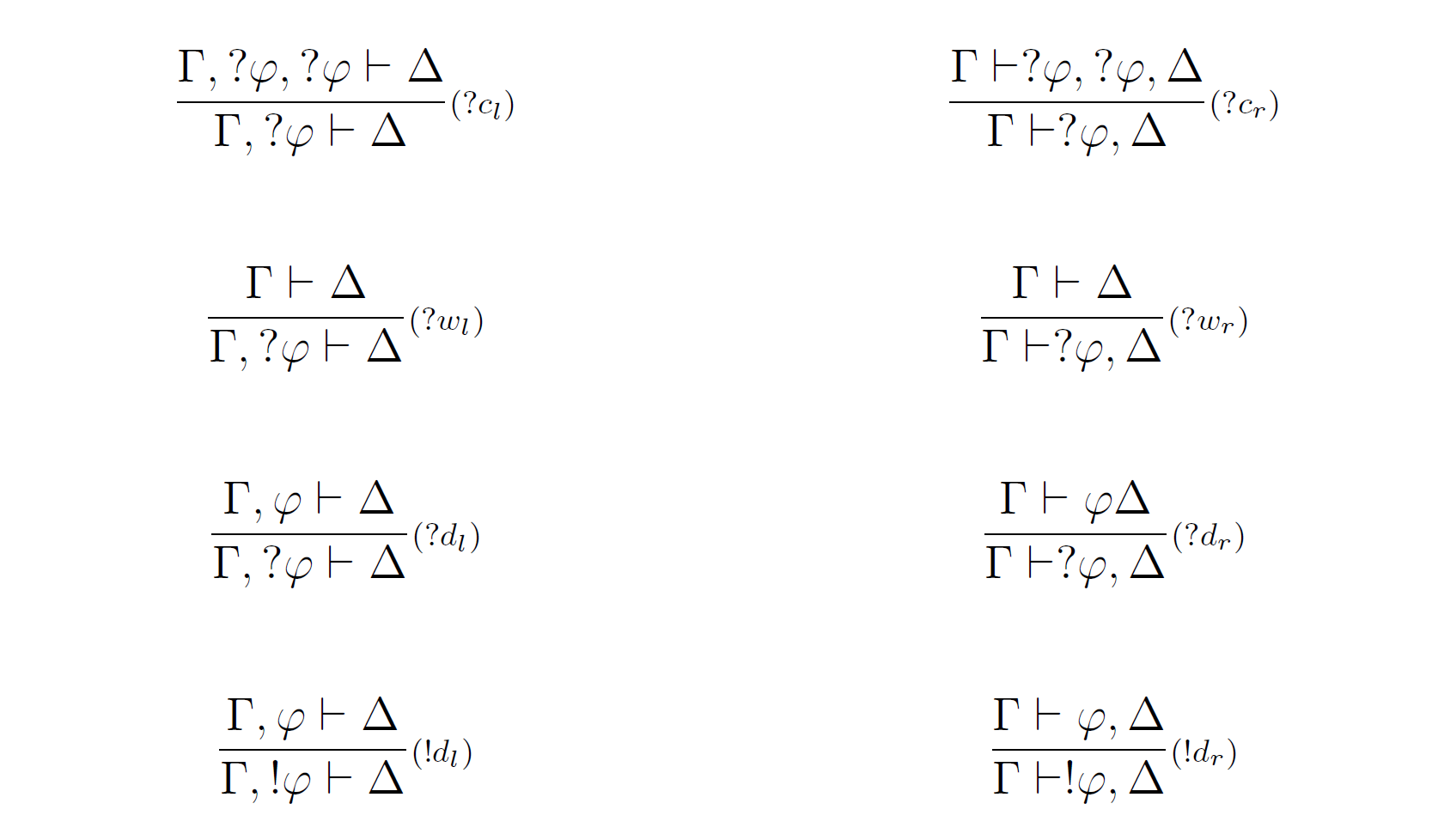

Pravidlá pre konštanty:
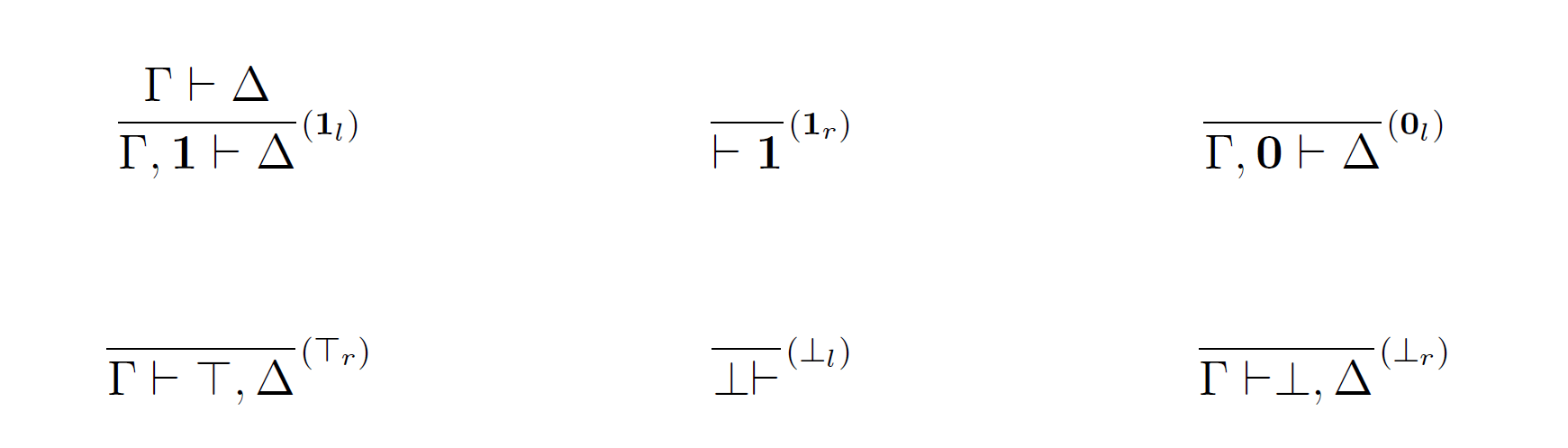
Logické pravidlá:
Pravidlá pre multiplikatívnu konjunkciu sú dve, po jednom pre každú stranu sekventu. Pravidlo pre pravú stranu má jeden predpoklad a pravidlo pre ľavú stranu má predpoklady dve.

Pravidlá pre aditívnu disjunkciu sú po dve pre pravú stranu sekventu obsahujúce po jednom predpoklade a jedno pre stranu ľavú obsahujúce dva predpoklady.
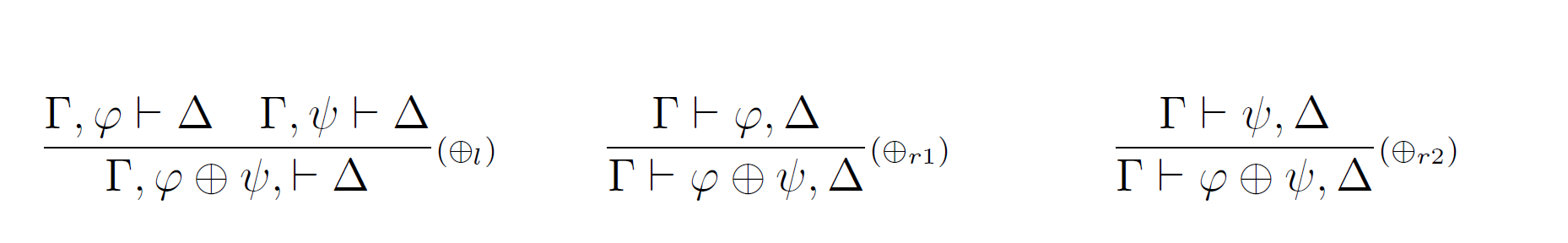
Pravidlá pre implikáciu sú po dve. Pravidlo pre ľavú stranu má dva predpoklady a pre pravú stranu obsahuje jeden predpoklad.

Pravidlá pre aditívnu konjunkciu sú dve pre ľavú stranu sekventu obsahujúce po jednom predpoklade a jedno pre stranu pravú obsahujúce dva predpoklady.

Pravidlá pre multiplikatívnu disjunkciu sú dve. Pravidlo pre ľavú stranu má dva predpoklady a pre pravú stranu obsahuje jeden predpoklad.

Pravidlá pre lineárnu negáciu sú dve. Vyjadrujú možnosť premiestnenia formuly z jednej strany sekventu na druhú stranu.

Príklad: Zdrojovo orientovaný prístup k formulám
Majme formulu: $1$€$⊸ chlieb ~\& ~maslo,$ kde všetky 3 zdroje nahradíme $φ$.
Veta: formula $$φ ⊸ φ ~\&~ φ,$$ je dokázateľná v lineárnej logike.
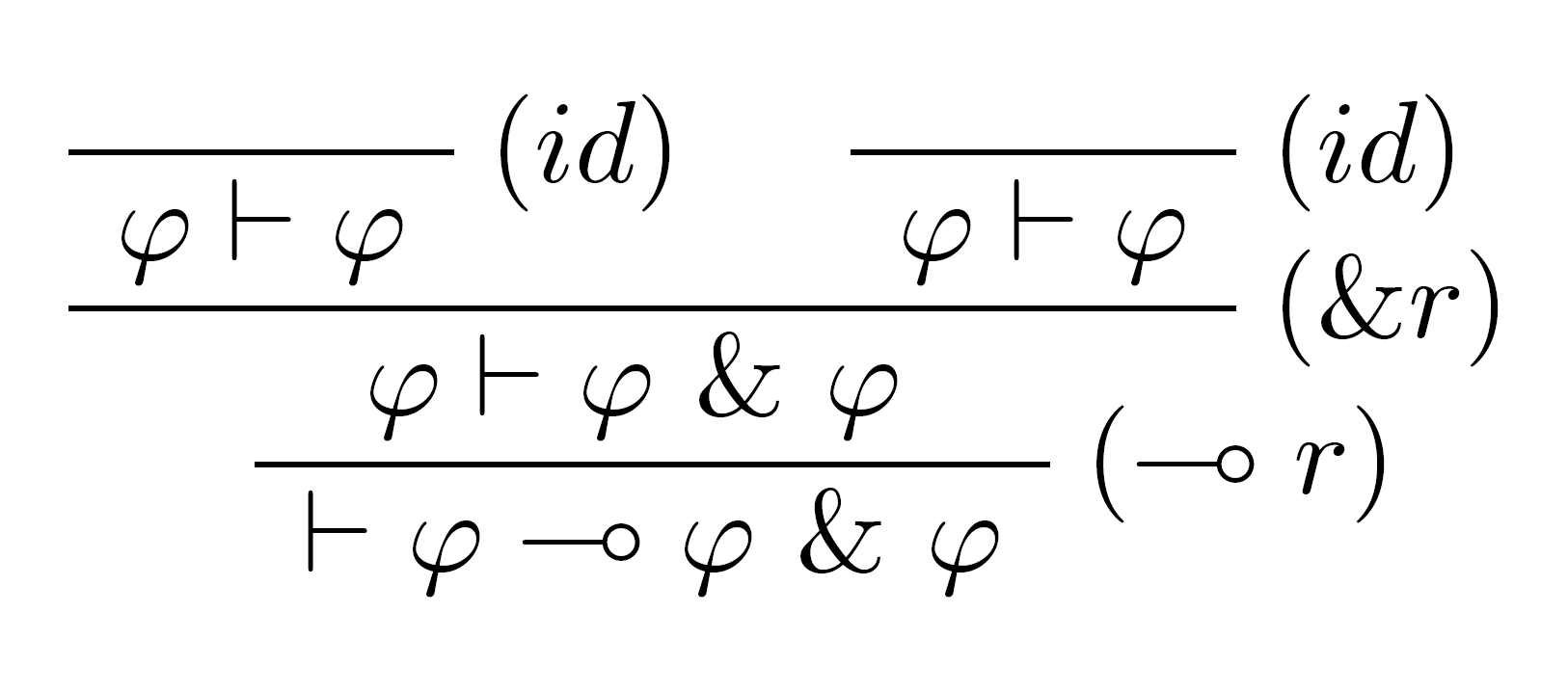
Avšak ak chlieb stojí 1€ aj voda stojí 1€, potom nie je možné dokázať $1$€$⊸ chlieb ~\otimes ~maslo.$
Príklad
Formula $$φ ⊸ φ ~\otimes~ φ,$$ nie je dokázateľná v lineárnej logike:

Veta: formula $$!φ ⊸ φ ~\otimes~ φ,$$ je dokázateľná v lineárnej logike.

Poznámka
$~\\~$
- Možnosti aplikácie lineárnej logiky v informatike sú zhrnuté v článkoch [1,2].
- Možnosti využitia lineárnej logiky pri modelovaní synchronizačných problémov [3].
[1] Chrpa, Lukas. "Linear Logic: Foundations, Applications and Implementations." proceedings of workshop CICLOPS. 2006.
[2] Chrpa, Lukáš, Pavel Surynek, and Jiří Vyskočil. "Encoding of planning problems and their optimizations in linear logic." Applications of Declarative Programming and Knowledge Management: 17th International Conference, INAP 2007, and 21st Workshop on Logic Programming, WLP 2007, Würzburg, Germany, October 4-6, 2007, Revised Selected Papers. Springer Berlin Heidelberg, 2009.
[3] Perháč, Ján, Daniel Mihályi, and Valerie Novitzká. "Modeling synchronization problems: from composed petri nets to provable linear sequents." Acta Polytechnica Hungarica 14.8 (2017): 165-182.
Postup
Krok 1: Prepíšte nasledujúce vety v prirodzenom jazyku do formúl lineárnej logiky.
Úloha 1.1
Dnes bude svietiť slnko alebo bude pršať.
Úloha 1.2
Ak bude svietiť slnko, pôjdeme do akvaparku alebo na túru.
Úloha 1.3
Máme programový systém so 4 procesmi ($p_1,p_2,p_3,p_4$).
- Vykoná sa $p_1$,
- potom sa paralelne vykoná ($p_2$ a $p_3$),
- potom sa vykoná $p_4$.
Úloha 1.4
Máte 10 eur. V lunaparku stojí:
- Húsenková dráha 3 eurá.
- Kolotoč 3 eurá.
- Autodróm 2 eurá.
- Strelnica 1 euro.
- Strašidelný zámok 2 eurá.
- Ruské kolo 4 eurá.
- Cukrová vata 1 euro.
Vyskladajte si program v lunaparku.
Krok 2: Dokážte nasledujúce zákony lineárnej logiky
Úloha 2.1
$$ \begin{array}{l} (\varphi \otimes \psi)^\bot \equiv (\varphi^\bot ~⅋~ \psi^\bot) \\ (\varphi~⅋~ \psi)^\bot \equiv (\varphi^\bot \otimes \psi^\bot) \\ (\varphi ~\&~ \psi)^\bot \equiv (\varphi^\bot \oplus \psi^\bot) \\ (\varphi \oplus \psi)^\bot \equiv (\varphi^\bot ~\&~ \psi^\bot) \end{array} $$
Krok 3: Dokážte nasledujúce formuly lineárnej logiky
Úloha 3.1
$$ (\varphi \multimap \theta) ~\&~ (\psi \multimap \theta) \vdash (\varphi \oplus \psi) \multimap \theta $$
Úloha 3.2
$$ !(φ~ \& ~ψ) ⊸ (!φ) ⊗ (!ψ) $$
Úloha 3.3
$$ (!φ) ⊗ (!ψ) ⊸ ~!(φ ~\&~ ψ) $$
Úloha 3.4
$$ (φ ⊕ ψ) ⊸ (?φ) ~⅋~ (?ψ) $$
Úloha 3.5
$$ (?φ) ~⅋~ (?ψ) ⊸ (φ ⊕ ψ) $$