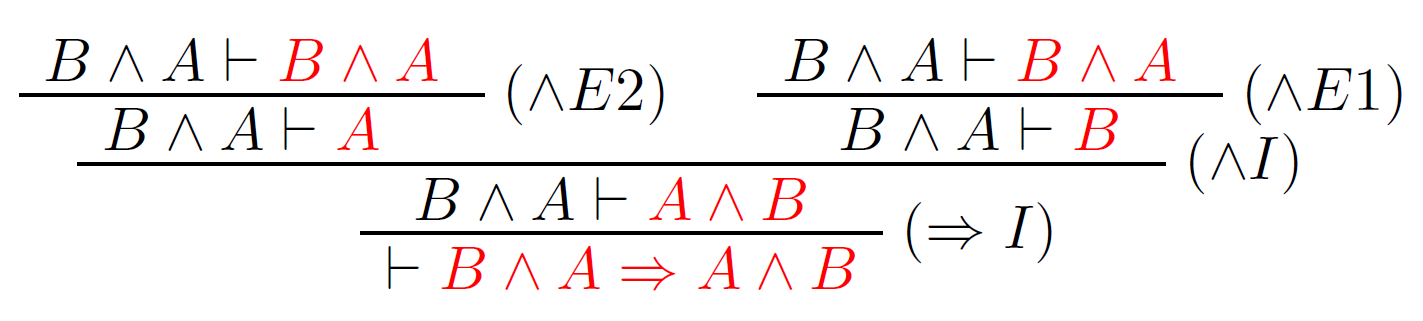Ciele
- Naštudovať potrebné pojmy.
- Preštudovať vzorové príklady prezentované v rámci teoretickej časti.
- Vypracovať zadané úlohy.
Základné pojmy
Intuicionistická logika, môže byť stručne opísaná ako klasická logika bez:
- Aristotelovho pravidla vylúčenia tretieho $(φ \lor \neg φ)$,
- zákonu dvojitej negácie $¬¬φ ≡ φ$.
Intuicionizmus je filozofický a matematický prístup, ktorý sa zameriava na konštruktívny postup v matematike a tvrdí, že matematické objekty musia byť skutočne skonštruované, nie iba abstraktne definované. Intuicionisti odmietajú princípy klasického deduktívneho dôkazu, ktorý sa vychádza zo zákona vylúčenia tretieho, ktorý hovorí, že ak existuje nejaké tvrdenie, tak je buď pravdivé alebo nepravdivé.
Konštruktívny dôkaz je druh matematického dôkazu, ktorý dokazuje existenciu matematického objektu tým, že ukáže spôsob, ako tento objekt skutočne skonštruovať. Tento prístup k matematickému dôkazu sa líši od tradičného dôkazu, ktorý iba dokazuje existenciu objektu bez skutočnej konštrukcie.
Jazyk intuicionistickej logiky
Jazyk intuicionistickej logiky je rovnaký ako jazyk výrokovej logiky, avšak logické spojky intuicionistickej logiky nie sú definované rovnakým spôsobom ako v klasickej logike.
Syntax intuicionistickej logiky v BNF
Je definovaná produkčným pravidlom v Backus-Naurovej forme, prostredníctvom ktorého je možné konštruovať všetky prípustné tvary formúl: $$ \varphi ::= p \mid \top \mid \bot \mid \neg\varphi \mid \varphi \land \psi \mid \varphi \lor \psi \mid \varphi \Rightarrow \psi, $$ kde p je množina atomických výrokov. Platí rovnaká priorita a asociativita operátorov ako vo výrokovej logike.
Vlastnosti syntaxe intuicionistickej logiky
Žiadnu zo základných logických spojok nemožno vyjadriť pomocou ostatných a preto je nutná prítomnosť všetkých štyroch.
- Negácia je definovaná ako implikácia do absurda $\neg φ ≡ φ ⇒ ⊥$.
- Ekvivalencia $\Leftrightarrow$ nie je považovaná za základnú spojku, ale rovnako ako v klasickej výrokovej logike za konjunkciu dvoch implikácií.
Mnoho tautológii klasickej logiky neplatí v intuicionistickej logike. To zahŕňa nielen zákon vylúčenia tretieho či eliminácie dvojitej negácie, ale tiež Peirceové pravidlo $(((φ \Rightarrow ψ) \Rightarrow φ) \Rightarrow φ)$. Pretože nie všetky tautológie klasickej logiky sú teorémy intuicionistickej logiky, ale všetky teorémy intuicionistickej logiky platia v klasickej, je možné sa na intuicionistickú logiku pozerať ako na oslabenie klasickej logiky, avšak s mnohými užitočnými vlastnosťami.
Poznámka
$\\$ Fakt, že princíp vylúčenia tretieho nie je intuicionisticky korektný, by ale nemal byť chápaný tak, že v intuicionistickej logike sú možné viac ako dve logické hodnoty. Každý predpoklad tvaru $\neg (φ \vee \neg φ)$ vedie v intuicionistickej logike k sporu. Z toho, že nejaké tvrdenie, v našom prípade $φ \vee \neg φ$, nie je intuicionisticky logicky platné, nemožno usudzovať, že za nejakých okolností by mohol platiť jeho opak.
Sémantika intuicionistickej logiky
Z dôvodu, že intuicionistická logika vynecháva niektoré vyššie spomenuté zákony, má táto logika širší rozsah sémantických interpretácií.
Brouwer-Heyting-Kolmogorova interpretácia sémantiky intuicionistickej logiky
Neformálna interpretácia sémantiky intuicionistickej logiky. Význam logických spojok je definovaný BHK podmienkami:
- Konštruktívny dôkaz $φ ∧ ψ$ pozostáva z konštruktívneho dôkazu $φ$ a z konštruktívneho dôkazu $ψ$.
- Konštruktívny dôkaz $φ ∨ ψ$ pozostáva buď z konštruktívneho dôkazu $φ$ alebo z konštruktívneho dôkazu $ψ$.
- Absurdum $⊥$ nemá konštruktívny dôkaz.
- Vérum $⊤$ je konštruktívny dôkaz formuly $⊤$.
- Konštruktívny dôkaz $φ ⇒ ψ$ pozostáva z konštrukcie, ktorá každý konštruktívny dôkaz $φ$ prevedie na konštruktívny dôkaz $ψ$.
- Konštruktívny dôkaz $¬φ$ pozostáva z konštrukcie, ktorá každý konštruktívny dôkaz $φ$ prevedie na absurdum $⊥$ (negácia je chápaná ako $φ ⇒ ⊥$).
Poznámka
$\\$
Pre lepšie pochopenie, je možné túto interpretáciu predstaviť nasledovne:
- Nech formuly $φ, ψ, θ,...$ sú úlohy resp. problémy ktoré je nutné vyriešiť.
- Ich (konštruktívne) dôkazy $a,b,c,...$ sú metódy (programy) ktoré ich vyriešia.
Potom:
- Konštruktívny dôkaz $φ ∧ ψ$ je dvojica $\langle a,b \rangle$, kde $a$ je dôkaz $φ$ a $b$ je dôkaz formuly $ψ$.
- Konštruktívny dôkaz $φ ∨ ψ$ je buď výraz $\langle a,b \rangle.1$ formuly $φ$ alebo výraz $\langle a,b \rangle.2$ formuly $ψ$ (ľavá alebo pravá projekcia nad dvojicou $\langle a,b \rangle$).
- Konštruktívny dôkaz $φ ⇒ ψ$ je funkcia $f$, ktorá každý dôkaz $a$ formuly $φ$ prevedie na dôkaz $f(a)$ formuly $ψ$.
Kripkeho sémantika možných svetov
Formálne možno definovať sémantiku intuicionistickej logiky prostredníctvom relatívne novej metódy, ktorú definoval Saul Kripke. Táto metóda sa niekedy označuje ako sémantika možných svetov alebo prosto Kripkeho model.
Kripkeho model intuicionistickej logiky je usporiadaná trojica: $$M=(W, ≤, ⊩),$$ kde:
- $W$ je neprázdna množina možných svetov v tvare $W = \{x_1, x_2,...\}$.
- $≤$ je relácia dosiahnuteľnosti na svetoch $≤ \subseteq W × W$. Je reflexívna a tranzitívna.
- $⊩$ je relácia platnosti formuly vo svete $⊩ ⊆ W × Prop$.
Zároveň:
- Jednotlivé svety je možné chápať ako stavy, prostredia, vrcholy a podobne.
- Zápis $x_1 ≤ x_2$ je možné prečítať ako "zo sveta $x_1$ je možné dosiahnuť svet $x_2$" alebo "svet $x_2$ je dosiahnuteľný zo sveta $x_1$".
- Zápis $x⊩p$ je možné prečítať ako "vo svete $x$ platí atomický výrok $p$".
Reláciu platnosti definujeme vzhľadom na syntax jazyka: $$ \begin{array}{lcl} x⊩p & \text{potom} & ∀x' \quad \text{ak}\quad x≤x' \quad\text{potom}\quad x'⊩p \\ x⊩φ ∧ ψ & \text{vtt.} & x⊩φ \quad \text{a} \quad x⊩ψ\\ x⊩φ ∨ ψ & \text{vtt.} & x⊩φ \quad \text{alebo} \quad x⊩ψ \\ x⊩φ ⇒ ψ & \text{vtt.} & ∀x', x≤x' (\text{ak} \quad x'⊩φ \quad \text{potom} \quad x'⊩ψ) \\ x⊩ ¬φ & \text{vtt.} & ∀x', x≤x' (x' ⊯ φ)\\ x⊩⊤ & & \\ x⊩⊥ & & \end{array} $$
Definícia relácia platnosti hovorí:
- Prvý riadok opisuje pravidlo perzistencie. To znamená ak atomický výrok $p$ platí v určitom svete $x$, potom platí v každom svete $x'$ z neho dosiahnuteľnom.
- Druhý riadok jednoducho definuje konjunkciu a to tak, že formula $φ ∧ ψ$ platí vo svete $x$ ak $x⊩φ$ a zároveň $x⊩ψ$.
- Tretí riadok definuje disjunkcia tak, že formula $φ ∨ ψ$ platí vo svete $x$ ak platí $x⊩φ$ alebo $x⊩ψ$.
- Štvrtý riadok definuje implikáciu. Formula $φ ⇒ ψ$ platí vo svete $x$, ak vo všetkých z neho dosiahnuteľných svetoch $x'$, "ak platí $x'⊩φ$ potom $x'⊩ψ$".
- Piaty riadok definuje negáciu. Formula $¬φ$ platí vo svete $x$ ak vo všetkých z neho dosiahnuteľných svetoch $x'$, formula neplatí $x' ⊯ φ$.
- Posledné dva riadky hovoria, že konštanty $⊤, ⊥$ platia vždy resp. nikdy v danom svete.
Poznámka
$\\$
Pri uvažovaní o dosiahnuteľných svetoch, je vždy potrebné myslieť na vlastnosti danej relácie. V tomto prípade na reflexívnosť a tranzitívnosť.
Poznámka
$\\$
Pravdivosť a platnosť formuly sú rozdielne pojmy. Atomický výrok $p$ je pravdivý v určitom svete, ak v ňom platí. Avšak to, že $p$ neplatí v niektorom svete neznamená automaticky, že je pravdivá formula $¬p$.
Príklad
Nech je daný Kripkeho model $M$ nasledovne: $$M=(W, ≤, ⊩),$$ kde:
- $W=\{x_0,x_1,x_2,x_3,x_4,x_5\}$,
- $≤=\{x_0≤x_1,x_0≤x_2,x_1≤x_3,x_2≤x_4,x_2≤x_5\}$,
- $⊩=\{x_1⊩q, x_2⊩p, x_3⊩p, x_3⊩q, x_4⊩p, x_5⊩p, x_5⊩q\}$. Majme formuly
| Poradie | Formula |
|---|---|
| 1. | $¬p$ |
| 2. | $¬q$ |
| 3. | $p ∨ q$ |
| 4. | $¬p ∨ q$ |
| 5. | $p ∧ q$ |
| 6. | $¬p ∧ q$ |
| 7. | $¬p ∧ ¬q$ |
| 8. | $p ⇒ q$ |
| 9. | $p ⇒ ¬q$ |
| 10. | $q ⇒ p$ |
| 11. | $¬q ⇒ p$ |
| 12. | $p ∧ q ⇒ q$ |
| 13. | $q ⇒ p ∧ q$ |
- Znázornite Kripkeho model prostredníctvom grafu.
- Uveďte v ktorých svetoch platia formuly uvedené vyššie.
Riešenie
Kripkeho model znázornime ako orientovaný graf:
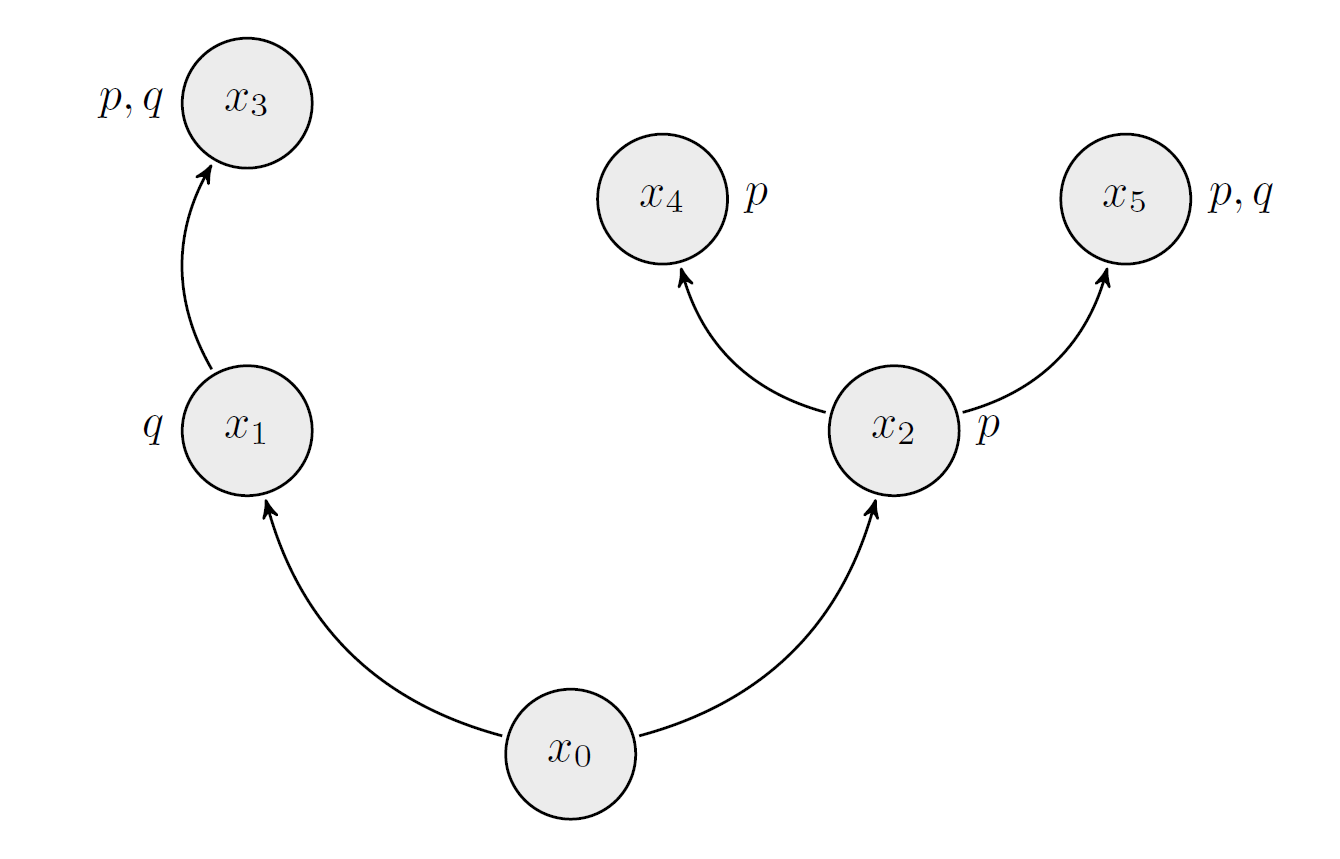
Formuly platia vo svetoch:
| Poradie | Formula | Platnosť vo svete |
|---|---|---|
| 1. | $¬p$ | žiadny |
| 2. | $¬q$ | $x_4$ |
| 3. | $p ∨ q$ | $x_1,x_2,x_3,x_4,x_5$ |
| 4. | $¬p ∨ q$ | $x_1,x_3,x_5$ |
| 5. | $p ∧ q$ | $x_3,x_5$ |
| 6. | $¬p ∧ q$ | žiadny |
| 7. | $p ∧ ¬q$ | $x_4$ |
| 8. | $p ⇒ q$ | $x_1,x_3,x_5$ |
| 9. | $p ⇒ ¬q$ | $x_4$ |
| 10. | $q ⇒ p$ | $x_2,x_3,x_4,x_5$ |
| 11. | $¬q ⇒ p$ | $x_2,x_3,x_4,x_5$ |
| 12. | $p ∧ q ⇒ q$ | $x_3,x_5$ |
| 13. | $q ⇒ p ∧ q$ | $x_3,x_5$ |
Dedukčné kalkuly
Gerhard Gentzen prirodzenú dedukciu (systém NJ) a sekventový kalkul (systém LJ) pre intuicionistickú logiku jednoduchými modifikáciami jeho dedukčných kalkulov pre klasickú logiku.
Obidva systémy sú úplné a konzistentné.
Každá formula dokázateľná v intuicionistickej logike je dokázateľná aj v klasickej logike, avšak neplatí to naopak.
Prirodzená dedukcia
Prirodzená dedukcia (nazývaný aj systém NJ) intuicionistickej logiky je definovaná ako dedukčný kalkul prirodzenej dedukcie klasickej logiky (systém NK) bez dedukčného pravidla sporu.
Pravidlo sporu (neplatí v intuicionistickej logike)
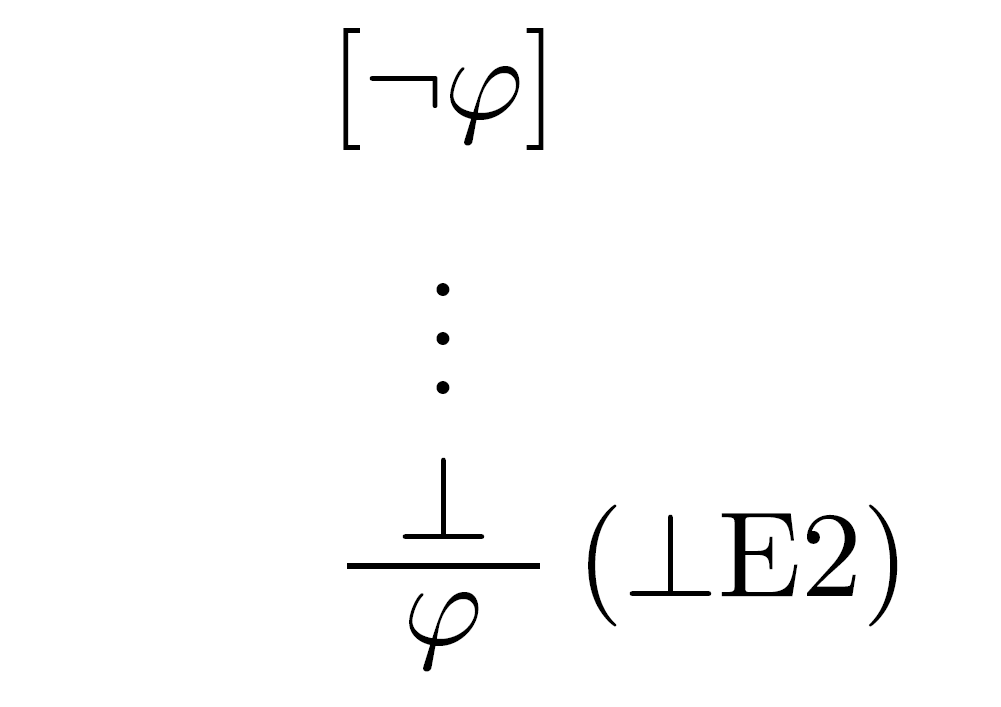
Dedukčné pravidlá systému NJ:

Sekventový kalkul
Sekventový kalkul (systém LJ) získame obmedzením tvaru sekventu tak, že v závere sa môže nachádzať maximálne jedna formula.
Intuicionistický sekvent má tvar: $$Γ⊢φ,$$ pričom na pravej strane sekventu je najviac jedna formula.
Pravidlo identity a rezu:
| \begin{prooftree} \AxiomC{ } \RightLabel{ (id)} \UnaryInfC{φ ⊢ φ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ φ} \AxiomC{φ, Δ ⊢ ψ} \RightLabel{ (cut)} \BinaryInfC{Γ, Δ ⊢ ψ} \end{prooftree} |
|---|
Logické pravidlá:
Negácia
| \begin{prooftree} \AxiomC{Γ ⊢ φ} \RightLabel{ (¬l)} \UnaryInfC{Γ, ¬φ ⊢ } \end{prooftree} | \begin{prooftree} \AxiomC{Γ, φ ⊢ } \RightLabel{ (¬r)} \UnaryInfC{Γ ⊢ ¬φ} \end{prooftree} |
|---|
Konjunkcia
| \begin{prooftree} \AxiomC{Γ, φ ⊢ θ} \RightLabel{ (∧l1)} \UnaryInfC{Γ, φ ∧ ψ ⊢ θ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ, ψ ⊢ θ} \RightLabel{ (∧l2)} \UnaryInfC{Γ, φ ∧ ψ ⊢ θ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ φ} \AxiomC{Γ ⊢ ψ} \RightLabel{ (∧r)} \BinaryInfC{Γ ⊢ φ ∧ ψ} \end{prooftree} |
|---|
Disjunkcia
| \begin{prooftree} \AxiomC{Γ ⊢ φ} \RightLabel{ (∨r1)} \UnaryInfC{Γ ⊢ φ ∨ ψ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ ψ} \RightLabel{ (∨r2)} \UnaryInfC{Γ ⊢ φ ∨ ψ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ, φ ⊢ θ} \AxiomC{Γ, ψ ⊢ θ} \RightLabel{ (∨l)} \BinaryInfC{Γ, φ ∨ ψ ⊢ θ} \end{prooftree} |
|---|
Implikácia
| \begin{prooftree} \AxiomC{Γ, φ ⊢ ψ} \RightLabel{ (⇒r)} \UnaryInfC{Γ ⊢ φ ⇒ ψ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ φ} \AxiomC{Δ, ψ ⊢ θ} \RightLabel{ (⇒l)} \BinaryInfC{Γ,Δ φ ⇒ ψ ⊢ θ} \end{prooftree} |
|---|
Konštanty
| \begin{prooftree} \AxiomC{ } \RightLabel{ (⊥l)} \UnaryInfC{Γ, ⊥ ⊢ φ} \end{prooftree} | \begin{prooftree} \AxiomC{ } \RightLabel{ (⊤r)} \UnaryInfC{⊢ ⊤} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ φ} \RightLabel{ (⊤l)} \UnaryInfC{Γ, ⊤ ⊢ φ} \end{prooftree} |
|---|
Štrukturálne pravidlá:
Pravidlá zoslabenia
| \begin{prooftree} \AxiomC{Γ ⊢ θ} \RightLabel{ (wl)} \UnaryInfC{Γ, φ ⊢ θ} \end{prooftree} |
|---|
Pravidlá kontrakcie
| \begin{prooftree} \AxiomC{Γ, φ, φ ⊢ θ} \RightLabel{ (cl)} \UnaryInfC{Γ, φ ⊢ θ} \end{prooftree} |
|---|
Pravidlá výmeny
| \begin{prooftree} \AxiomC{Γ, ψ, φ ⊢ θ} \RightLabel{ (exl)} \UnaryInfC{Γ, φ, ψ ⊢ θ} \end{prooftree} |
|---|
Curry–Howardova korešpondencia
Curry-Howardova korešpondencia (niekedy nazývaná aj Curry-Howardovov izomorfizmus, z ang. Curry–Howard correspondence, proofs-as-programs) je základným konceptom v informatike a matematickej logike, ktorý opisuje korešpondenciu medzi logikou a programovaním. Táto korešpondencia tvrdí, že existuje priama súvislosť medzi dôkazmi v matematickej logike a programami v informatike. Konkrétne tvrdí, že dôkaz matematickej vety korešponduje s programom, ktorý rieši výpočtový problém, a naopak. Táto korešpondencia nám umožňuje uvažovať o programoch ako logických dôkazoch a naopak. To znamená, že správne typovaný program funkcionálnej paradigmy je konštruktívny dôkaz tvrdenia korešpondujúceho s jeho typom a naopak.
Vo všeobecnosti teda platí korešpondencia s výpočtovým systémom funkcionálnej paradigmy, ktorý opisuje určitá teória typov a logickým systémom. V našom prístupe sa budeme venovať korešpondencii medzi intuicionistickou logikou a jednoducho-typovaným $λ$-kalkulom.
Poznámka
Táto korešpondencia je základom interaktívnych dokazovacích systémov ako je agda, coq, isabelle/hol a pod.
Jednoducho-typovaný $λ$-kalkul
Je to jedna z teórii typov, opisuje typový systém pre jednoduchý funkcionálny jazyk - $λ$-kalkul s jediným typovým konštruktorom $→$ funkčného typu, ktorý zo základných typov buduje funkčné typy. V našom prístupe budeme používať jazyk rozšírený o typové súčinové a súčtové konštruktory. Pre jednoduchosť uvádzame fragment syntaxe a s využitím binárnych súčinových a súčtových typov.
Syntax jednoducho-typovaného $λ$-kalkulu
Jednoducho-typovaný $λ$-kalkul s funkčným, súčinovým a súčtovým typom má jednoduchú syntax.
- Základom jazyka je term $t$.
- Typová anotácia $t:T$ hovorí, že term $t$ je typu $T$.
Syntax v BNF: $$ \begin{array}{l} t::= x ~|~ λx:T.t ~|~ t~ t ~|~ ⟨t,t⟩ ~|~ t.i ~|~ inl~t ~|~ inr~t ~|~ case~t~of~ inl~x ⇒ t || inr~x ⇒ t \\ T::= A ~|~ T → T ~|~ T × T ~|~ T + T \end{array} $$ kde:
- $t$ metapremenná, označuje ľubovoľný term (vypočítateľný výraz).
- $x$ premenná.
- $λx:T.t$ je $λ$ abstrakcia. Výraz označuje funkciu, ktorá berie argument $x$ typu $T$ s telom $t$, pričom bodka oddeľuje argumenty funkcie od jej tela.
- $t t$ aplikácia funkcie $t$ na $t$.
- $⟨t,t⟩$ dvojica súčinového typu, po zovšeobecnení je možné rozšíriť na n-ticu.
- $t.i$ i-ta projekcia na terme súčinového typu.
- $inl~t, inr~t$ termy súčtového typu.
- $case~t~of~ x_i ⇒ t_i$ operácia selektora na terme súčtového typu.
- $T$ typová metapremenná.
- $A$ množina základných typov.
- $T → T$ funkčný typ.
- $T × T$ súčinový typ.
- $T + T$ súčtový typ.
Typové kontrola jednoducho-typovaného $λ$-kalkulu
Typovú kontrolu programov jednoducho-typovaného $λ$-kalkulu, vykonáme prostredníctvom typovacích pravidiel, ktoré sú definované pre každú alternatívu syntaxe jazyka nasledovne:
| \begin{prooftree} \AxiomC{Γ, x:T1 ⊢ t:T2} \RightLabel{ (abs)} \UnaryInfC{Γ ⊢ λx:T1.t:T1→T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ t1:T1 → T2} \AxiomC{Γ ⊢ t2:T1} \RightLabel{ (app)} \BinaryInfC{Γ ⊢ t1 t2:T2} \end{prooftree} | \begin{prooftree} \AxiomC{x ∈ Γ} \RightLabel{ (var)} \UnaryInfC{Γ ⊢ x:T} \end{prooftree} |
|---|
| \begin{prooftree} \AxiomC{Γ⊢ t1:T1} \AxiomC{Γ⊢ t2:T2} \RightLabel{ (times)} \BinaryInfC{Γ ⊢ ⟨t1,t2⟩:T1×T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ t:T1×T2} \RightLabel{ (proj1)} \UnaryInfC{Γ ⊢ t.1:T1} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ t:T1×T2} \RightLabel{ (proj2)} \UnaryInfC{Γ ⊢ t.2:T2} \end{prooftree} |
|---|
| \begin{prooftree} \AxiomC{Γ ⊢ t:T1+T2} \RightLabel{ (inl)} \UnaryInfC{Γ ⊢ inl t:T1} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ t:T1+T2} \RightLabel{ (inr)} \UnaryInfC{Γ ⊢ inr t:T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ t0:T1+T2} \AxiomC{Γ, x1:T1 ⊢ t1:T} \AxiomC{Γ, x2:T2 ⊢ t2:T} \RightLabel{ (case)} \TrinaryInfC{Γ ⊢ case t0 of inl x1 ⇒ t1 || inr x2 ⇒ t2:T} \end{prooftree} |
|---|
Curry–Howardová korešpondencia medzi jednoducho typovaným $λ$-kalkulom a intuicionistickou logikou
V 1943 Haskell Curry spozoroval korešpondenciu medzi intuicionistickym logickým systémom a výpočtovým systémom, ktorú neskôr znovuobjavil William Howard v 1969 a publikoval v 1980.
Korešpondencia medzi logikou a teóriou typov vychádza z princípu výroky ako typy, ktorý definuje presný vzťah medzi jednoducho typovaným $λ$-kalkulom a intuicionistickou logikou:
- Výrok $φ$ považujeme za typ.
- Dôkaz výroku $φ$ je term typu $φ$.
- Dokazovanie formuly prirodzenou dedukciou korešponduje s typovou kontrolou.
- Zjednodušenie dôkazov korešponduje s vyhodnocovaním termu.
| Intuicionistická logika | Jednoducho typovaný λ-kalkul |
|---|---|
| výrok $p$ | typ $T$ |
| $φ⇒ψ$ | $T_1 → T_2$ |
| $φ∧ψ$ | $T_1 × T_2$ |
| $φ∨ψ$ | $T_1 + T_2$ |
| $⊤$ | $Unit$ |
| $⊥$ | prázdny typ |
Typovacie pravidlá korešpondujú s dedukčnými pravidlami systému NJ.
Poznámka
$\\$
Pre lepšiu demonštráciu korešpondencie pozmeníme notáciu zápisu dedukčných pravidiel systému NJ. Využijeme tvar sekventu $Γ \vdash φ$, kde hypotézy sú predpoklady $Γ$ a formula $φ$ je dokazovaná formula. Opäť uvádzame len fragment pravidiel.
| Jednoducho typovaný λ-kalkul | Intuicionistická logika |
|---|---|
| \begin{prooftree} \AxiomC{Γ, x:T1 ⊢ t:T2} \RightLabel{ (abs)} \UnaryInfC{Γ ⊢ λx:T1.t:T1→T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ, T1 ⊢ T2} \RightLabel{ (⇒I)} \UnaryInfC{Γ ⊢ T1⇒T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t1:T1 → T2} \AxiomC{Γ ⊢ t2:T1} \RightLabel{ (app)} \BinaryInfC{Γ ⊢ t1 t2:T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1 ⇒ T2} \AxiomC{Γ ⊢ T1} \RightLabel{ (⇒E)} \BinaryInfC{Γ ⊢ T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ⊢ t1:T1} \AxiomC{Γ⊢ t2:T2} \RightLabel{ (times)} \BinaryInfC{Γ ⊢ ⟨t1,t2⟩:T1×T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ⊢ T1} \AxiomC{Γ⊢ T2} \RightLabel{ (∧I)} \BinaryInfC{Γ ⊢ T1∧T2} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t:T1×T2} \RightLabel{ (proj1)} \UnaryInfC{Γ ⊢ t.1:T1} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1∧T2} \RightLabel{ (∧E1)} \UnaryInfC{Γ ⊢ T1} \end{prooftree} |
| \begin{prooftree} \AxiomC{Γ ⊢ t:T1×T2} \RightLabel{ (proj2)} \UnaryInfC{Γ ⊢ t.2:T2} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ T1∧T2} \RightLabel{ (∧E2)} \UnaryInfC{Γ ⊢ T2} \end{prooftree} |
Príklad
Majme daný term $P$ jednoducho typovaného λ-kalkulu: $$P=λz:B×A.⟨z.2,z.1⟩:B×A→A×B$$ Overte či je $P$ správne typovaný.
Riešenie
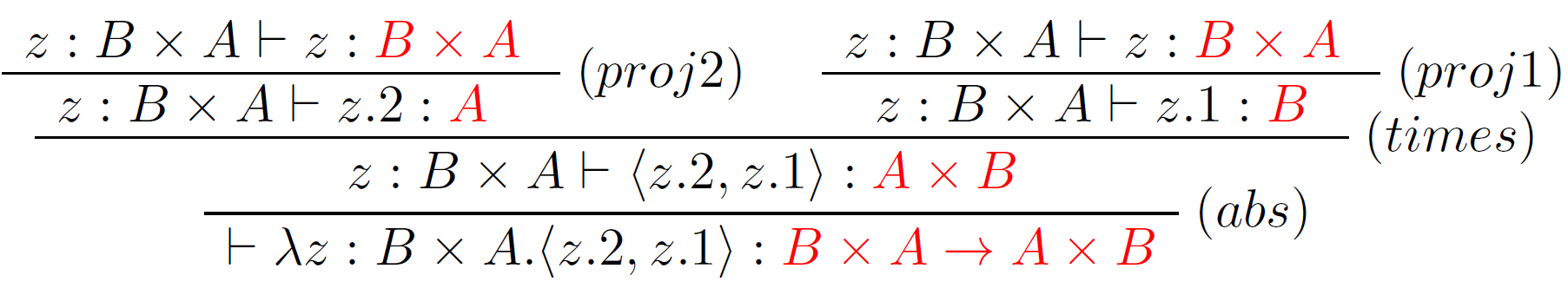
Príklad
Majme danú formulu $φ$ intuicionistickej logiky: $$φ = B∧A ⇒ A∧B$$ Dokážte $φ$ prirodzenou dedukciou.
Riešenie
Poznámka
$\\$
To znamená ak je formula $φ$ dokázateľná, potom term typu $φ$ je správne typovaný (prejde typovou kontrolou). Inými slovami term typu $φ$ je konštruktívny dôkaz formuly $φ$. Práve táto vlastnosť je základov interaktívnych dokazovacích systémov.
Postup
Krok 1: Nech je daný Kripkeho model. Rozhodnite v ktorých svetoch platia nasledujúce formuly
Úloha 1.1
Nech je daný Kripkeho model $M$ nasledovne: $$M=(W, ≤, ⊩),$$ kde:
- $W=\{a,b,c,d\}$,
- $≤=\{a≤c,a≤b,c≤d\}$,
- $⊩=\{b⊩p, b⊩q, d⊩p\}$.
Majme formuly:
| Poradie | Formula |
|---|---|
| 1. | $¬p$ |
| 2. | $¬q$ |
| 3. | $p ∨ q$ |
| 4. | $¬p ∨ q$ |
| 5. | $p ∧ q$ |
| 6. | $¬p ∧ q$ |
| 7. | $¬p ∧ ¬q$ |
| 8. | $p ⇒ q$ |
| 9. | $p ⇒ ¬q$ |
| 10. | $q ⇒ p$ |
| 11. | $¬q ⇒ p$ |
| 12. | $p ∧ q ⇒ q$ |
| 13. | $q ⇒ p ∧ q$ |
Krok 2: Majme dané nasledujúce tautológie výrokovej logiky. Dokážte ich kalkulom výrokovej logiky. Ukážte ich neplatnosť v intuicionistickej logike prostredníctvom Kripkeho modelu
Úloha 2.1
$$p \lor \neg p$$
Úloha 2.2
$$ \neg \neg p \Rightarrow p$$
Úloha 2.3
$$ ((p \Rightarrow q) \Rightarrow p) ⇒ p$$
Úloha 2.4
$$ (p ∨ q \Rightarrow q) ⇒ (p ∨ q \Rightarrow p)$$
Úloha 2.5
$$ (\neg \neg p \Rightarrow p) ⇒ (p \lor \neg p)$$
Krok 3: Pokúste sa dokázať formuly prirodzenou dedukciou intuicionistickej logiky
Úloha 3.1
$$p \Rightarrow \neg \neg p$$
Úloha 3.2
$$p \Rightarrow \neg p ⇒ q$$
Úloha 3.3
$$p \Rightarrow q \Rightarrow p ∧ q$$
Úloha 3.4
$$(p \Rightarrow q \Rightarrow r) ⇒ (q \Rightarrow p \Rightarrow r) $$
Úloha 3.5
$$(p \Rightarrow q \Rightarrow r) ⇒ ((p \Rightarrow q) ⇒ (q \Rightarrow r))$$
Krok 4: Pokúste sa dokázať formuly sekventovým kalkulom intuicionistickej logiky
Úloha 4.1
$$p \Rightarrow \neg \neg p$$
Úloha 4.2
$$p \Rightarrow \neg p ⇒ q$$
Úloha 4.3
$$p \Rightarrow q \Rightarrow p ∧ q$$
Úloha 4.4
$$(p \Rightarrow q \Rightarrow r) ⇒ (q \Rightarrow p \Rightarrow r) $$
Úloha 4.5
$$(p \Rightarrow q \Rightarrow r) ⇒ ((p \Rightarrow q) ⇒ (q \Rightarrow r))$$
Krok 5: Pre každú z nasledujúcich formúl, nájdite korešpondujúci term jednoducho typovaného λ-kalkulu
Úloha 5.1
$$(p \lor q) \Rightarrow (p \lor r)$$
Úloha 5.2
$$(p \Rightarrow q) \land (q \Rightarrow r) \Rightarrow (p \Rightarrow r)$$
Úloha 5.3
$$p \land q \Rightarrow p$$
Úloha 5.4
$$p \Rightarrow (q \Rightarrow p)$$
Úloha 5.5
$$p \Rightarrow (p \lor q)$$
Úloha 5.6
$$(p \Rightarrow q) \land (p \Rightarrow r) \Rightarrow (p \Rightarrow q \land r)$$