Ciele
- Naštudovať potrebné pojmy z formálneho aparátu predikátovej logiky.
- Preštudovať vzorové príklady prezentované v rámci teoretickej časti.
- Vypracovať zadané úlohy.
Úvod
V rámci predchádzajúcich prednášok bolí predstavené dedukčné kalkuly pre výrokovú logiku, konkrétne: dva Gentzenové dedukčné kalkuly (prirodzená dedukcia, sekventový kalkul) a rezolučná metóda. Obsahom tejto prednášky je definícia týchto kalkulov pre predikátovú logiku.
Dôkaz formuly v predikátovej logike znamená, že formula je pravdivá pri ľubovoľnom ohodnotení $e$, v ľubovoľnom modeli $M$ a ľubovoľnej neprázdnej doméne.
Keďže predikátová logika je rozšírením výrokovej logiky, je potrené rozšíriť definíciu Gentzenových dedukčných kalkulov o nové pravidlá pre dve nové logické operátory a to pre všeobecný kvantifikátor $(∀x)φ$ a existenčný kvantifikátor $(∃x)φ$.
Pre automatizované dokazovanie formúl obdobne ako vo výrokovej logike, aj v predikátovej logike využijeme rezolučnú metódu. Ktorá je základom automatizovaných dokazovacích systémov aj programovacích jazykov logickej paradigmy, ktoré samé o sebe možno považovať za automatické dokazovacie systémy.
Poznámka
$~\\~$
Rezolučnej metóde budú venované dve nasledujúce prednášky.
Na záver bude jazyk predikátovej logiky rozšírený o operátor rovnosti a bude predstavený úvod do teórií predikátovej logiky.
Terminológia
Substitúcia (definovaná na predchádzajúcom cvičení) je funkcia na termoch a na formulách, budeme je označovať $σ$.
Príklad
Majme formulu $P(x)$ a substitúciu $σ=[y/x]$, potom $σ(P(x))=P(x)[y/x]=P(y)$.
Gödelova veta o úplnosti (predikátovej logiky) (Gödel's completeness theorem) hovorí, že ak formula $φ$ platí (pravdivá v nezávisle na modely a interpretácii), potom je $φ$ dokázateľná. To znamená:
$$\text{ak}~ \quad Γ \models φ \quad \text{potom}~ \quad Γ \vdash φ.$$
Gödelova veta o neúplnosti (Gödel's incompleteness theorems) hovorí, že akýkoľvek formálny systém, ktorý dokáže vyjadriť základnú aritmetiku bude obsahovať tvrdenia (formuly), ktoré sú pravdivé ale nie je možné ich dokázať a zároveň nie je možné dokázať ani ich negácie.
Prirodzená dedukcia v predikátovej logike
Prirodzená dedukcia v predikátovej logike (systém NK) pozostáva z dedukčných pravidiel výrokovej logiky a je rozšírená o štyri pravidlá pre kvantifikátory.
Prirodzená dedukcia v predikátovej logike je konzistentná a úplná, platí: $$Γ \models φ \quad \text{vtt.}~ \quad Γ \vdash φ.$$
Eliminácia všeobecného kvantifikátora
Dedukčné pravidlo pre elimináciu všeobecného kvantifikátora:
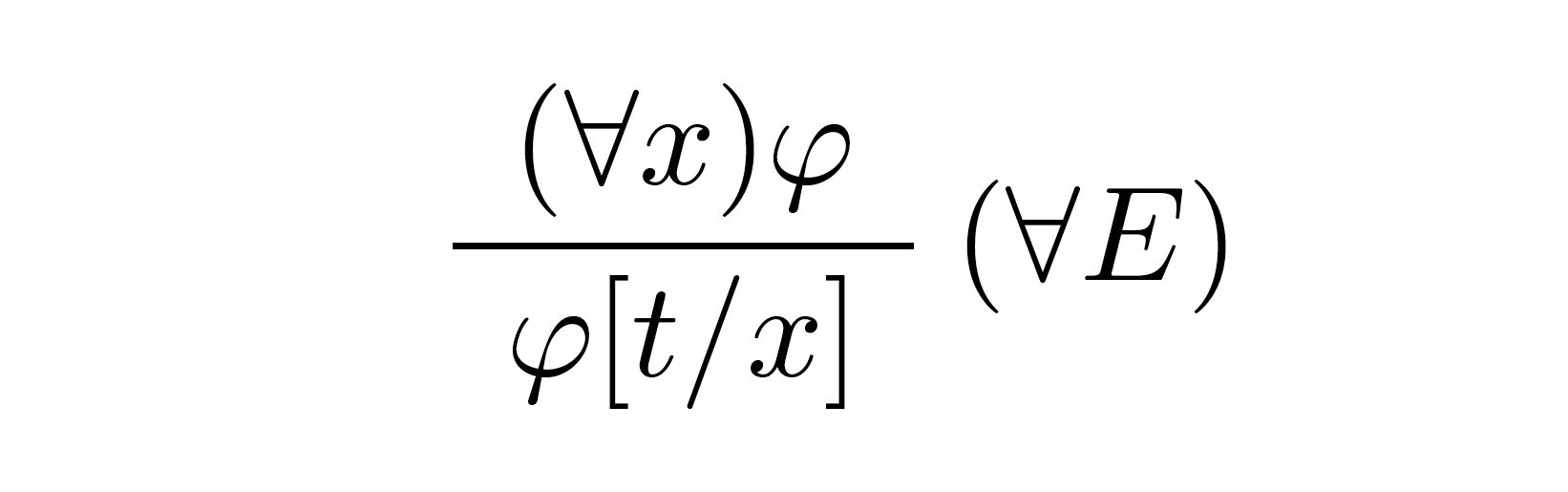
Vychádza z jednoduchého princípu, ak $(∀x)φ$ je pravda, potom viazanú premennú $x$ je možné substituovať ľubovoľným termom $t$ a $φ[t/x]$ musí byť pravda. Vychádza zo zákona $(∀x)P(x) ⇒ P(t)$.
Zavedenie všeobecného kvantifikátora
Dedukčné pravidlo pre zavedenie všeobecného kvantifikátora:
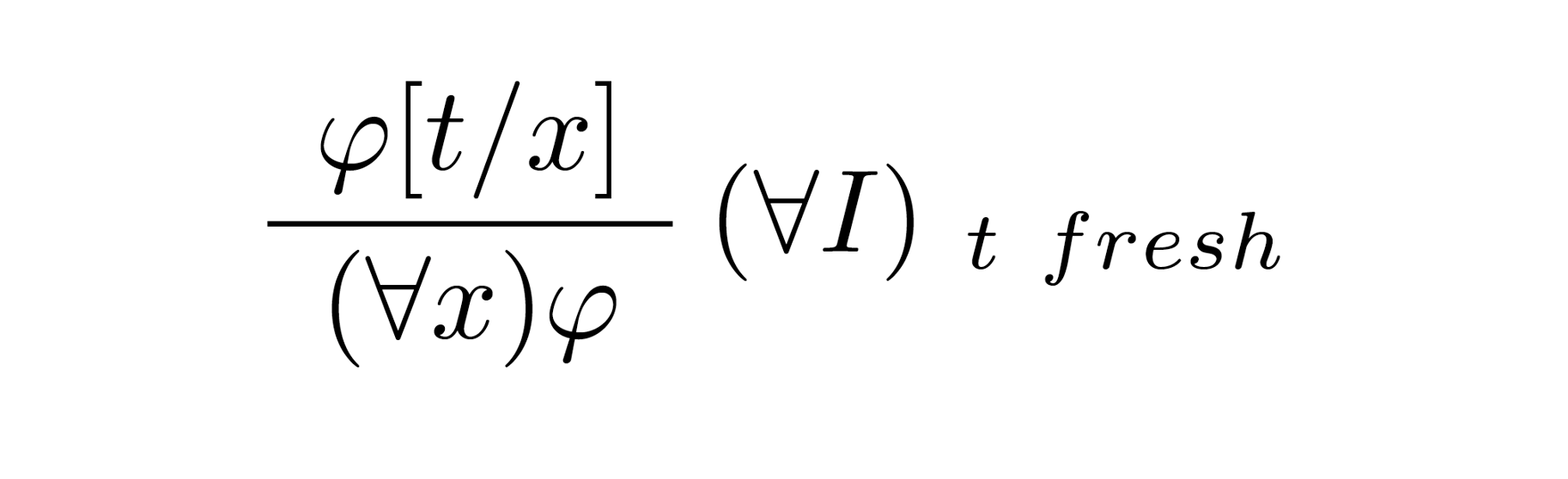
Aby bolo možné dokázať $(∀x)φ$ je potrebné najskôr dokázať $φ[t/x]$ je pravda, pre každý prvok domény. Samozrejme, že nechceme dokázať $φ[t/x]$ pre všetky možnosti, pričom doména môže byť nekonečná. Namiesto toho postačuje ukázať, že $φ[t/x]$ je pravda pre ľubovoľný prvok $t$. To znamená, term $t$ musí byť nový (fresh), t.j. $t$ nesmie mať voľný výskyt v hypotézach, z ktorých je možné dokázať $φ[t/x]$.
Eliminácia existenčného kvantifikátora
Dedukčné pravidlo pre elimináciu existenčného kvantifikátora:
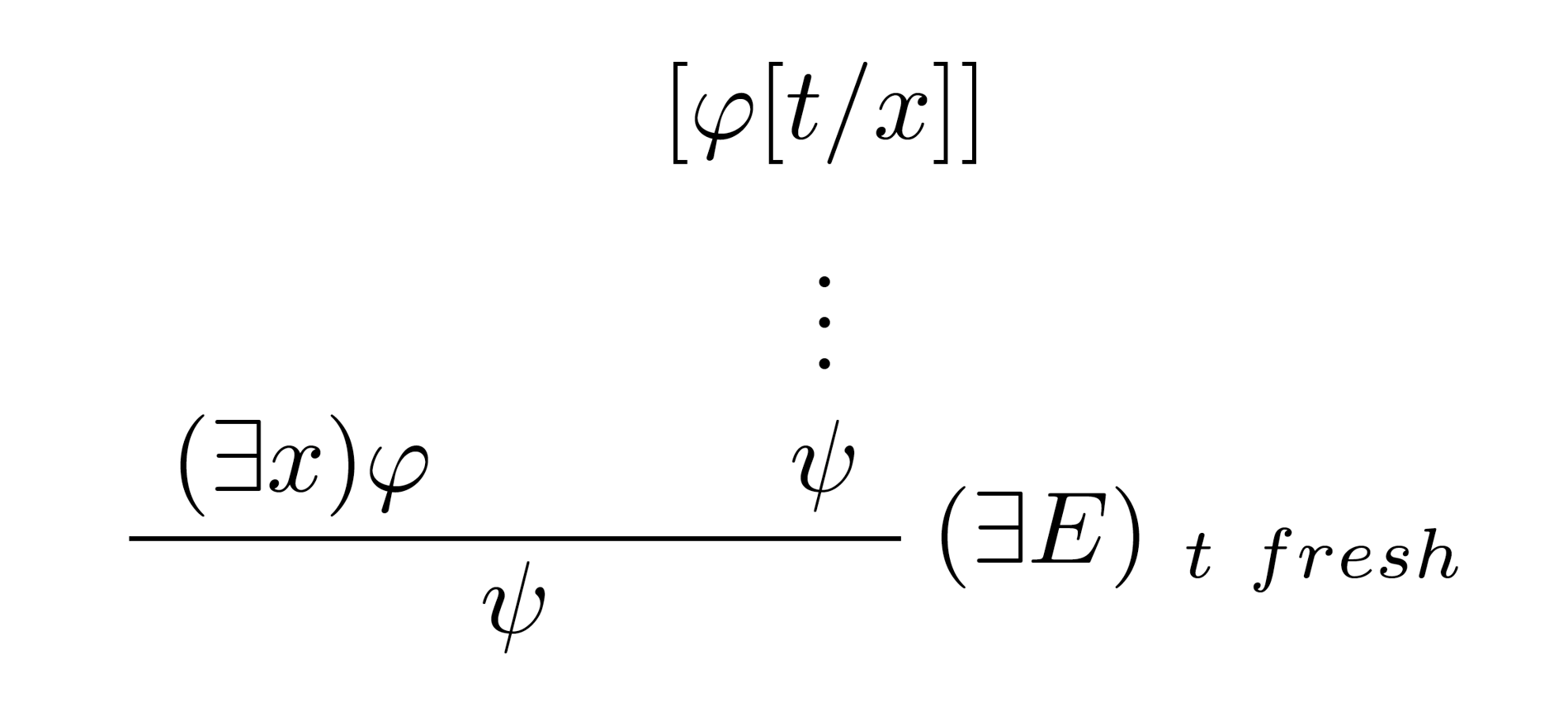
Pravidlo pre elimináciu existenčného kvantifikátora je komplexnejšie. Ak vieme, že platí $(∃x)φ[t/x]$, pre elimináciu existenčného kvantifikátora je potrebné nájsť také $t$, že $φ[t/x]$ je pravdivé. To je zabezpečené jednoduchým trikom a to tak, že vo vedľajšej vetve zavedieme novú hypotézu, kde vo $φ$ substituujeme $x$ za konkrétny prvok $t$ z ktorej dokážeme $ψ$. Term $t$ musí byť nový (fresh), t.j. $t$ nesmie mať voľný výskyt v hypotézach, z ktorých je možné dokázať $φ[t/x]$ ani $ψ$.
Zavedenie existenčného kvantifikátora
Dedukčné pravidlo pre zavedenie existenčného kvantifikátora:
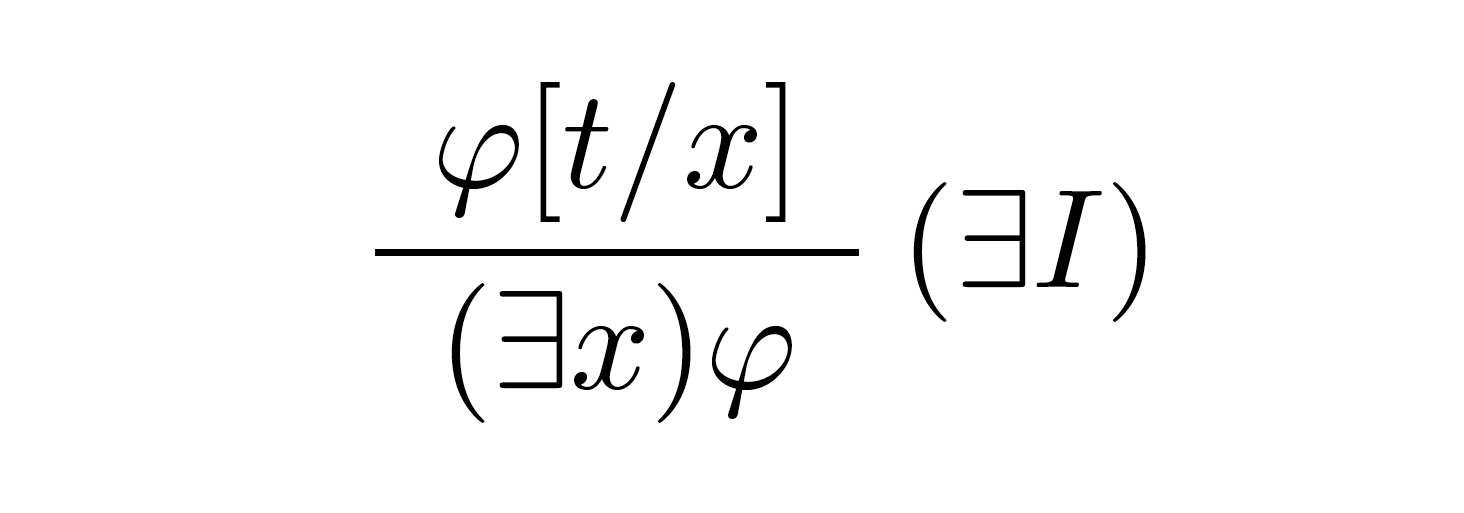
Pravidlo opisuje zákon $P(a) ⇒ (∃x)P(x)$. To znamená, ak je možné dokázať, že $φ[t/x]$ je pravda, tak musí platiť tvrdenie $(∃x)φ$.
Dedukčné pravidlá prirodzenej dedukcie pre predikátovú logiku

Sekventový kalkul v predikátovej logike
Analogicky ako v prirodzenej dedukcii, pri sekventovom kalkule (systém LK) je taktiež potrebné pridať štyri nové dedukčné pravidlá pre kvantifikátory (pre každý kvantifikátor jedno pravidlo pre obe strany sekventu).
Sekventový kalkul v predikátovej logike je konzistentný a úplný, platí: $$Γ \models φ \quad \text{vtt.}~ \quad Γ \vdash φ.$$
Dedukčné pravidlá pre všeobecný kvantifikátor
| \begin{prooftree} \AxiomC{Γ, φ[t/x] ⊢ Δ} \RightLabel{ (∀l)} \UnaryInfC{Γ, (∀x)φ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ[y/x]} \RightLabel{ (∀r)} \UnaryInfC{Γ ⊢Δ, (∀x)φ} \end{prooftree} |
|---|
- Pravidlo $(∀l)$ sa nazýva pravidlo konkretizácie. Term $t$ musí byť substituovateľný za premennú $x$ vo formule $\varphi$.
- Pravidlo $(∀r)$ sa nazýva pravidlo generalizácie. Premenná $y$ musí byť substituovateľná za premennú $x$ vo formule $\varphi$ a nemať žiadny voľný výskyt v množine predpokladov $Γ$, množine záverov $Δ$ a v $(∀x)φ$.
Dedukčné pravidlá pre existenčný kvantifikátor
| \begin{prooftree} \AxiomC{Γ, φ[y/x] ⊢ Δ} \RightLabel{ (∃l)} \UnaryInfC{Γ, (∃x)φ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ[t/x]} \RightLabel{ (∃r)} \UnaryInfC{Γ ⊢Δ, (∃x)φ} \end{prooftree} |
|---|
- Pravidlo $(∃r)$ sa nazýva pravidlo konkretizácie. Term $t$ musí byť substituovateľný za premennú $x$ vo formule $\varphi$.
- Pravidlo $(∃l)$ sa nazýva pravidlo generalizácie. Premenná $y$ musí byť substituovateľná za premennú $x$ vo formule $\varphi$ a nemať žiadny voľný výskyt v množine predpokladov $Γ$, množine záverov $Δ$ a v $(∀x)φ$.
Dedukčné pravidlá sekventového kalkulu pre predikátovú logiku
Pravidlo identity a rezu:
| \begin{prooftree} \AxiomC{ } \RightLabel{ (id)} \UnaryInfC{Γ, φ ⊢ Δ, φ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Λ, φ} \AxiomC{φ, Δ ⊢ Σ} \RightLabel{ (cut)} \BinaryInfC{Γ, Δ ⊢ Λ, Σ} \end{prooftree} |
|---|
Logické pravidlá:
Negácia
| \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ} \RightLabel{ (¬l)} \UnaryInfC{Γ, ¬φ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ, φ ⊢ Δ} \RightLabel{ (¬r)} \UnaryInfC{Γ ⊢ Δ, ¬φ} \end{prooftree} |
|---|
Konjunkcia
| \begin{prooftree} \AxiomC{Γ, φ ⊢ Δ} \RightLabel{ (∧l1)} \UnaryInfC{Γ, φ ∧ ψ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ, ψ ⊢ Δ} \RightLabel{ (∧l2)} \UnaryInfC{Γ, φ ∧ ψ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ} \AxiomC{Γ ⊢ Δ, ψ} \RightLabel{ (∧r)} \BinaryInfC{Γ ⊢ Δ, φ ∧ ψ} \end{prooftree} |
|---|
Disjunkcia
| \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ} \RightLabel{ (∨r1)} \UnaryInfC{Γ ⊢ Δ, φ ∨ ψ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, ψ} \RightLabel{ (∨r2)} \UnaryInfC{Γ ⊢ Δ, φ ∨ ψ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ, φ ⊢ Δ} \AxiomC{Γ, ψ ⊢ Δ} \RightLabel{ (∨l)} \BinaryInfC{Γ, φ ∨ ψ ⊢ Δ} \end{prooftree} |
|---|
Implikácia
| \begin{prooftree} \AxiomC{Γ, φ ⊢ Δ, ψ} \RightLabel{ (⇒r)} \UnaryInfC{Γ ⊢ Δ, φ ⇒ ψ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Λ, φ} \AxiomC{Δ, ψ ⊢ Σ} \RightLabel{ (⇒l)} \BinaryInfC{Γ,Δ φ ⇒ ψ ⊢ Λ, Σ} \end{prooftree} |
|---|
Konštanty
| \begin{prooftree} \AxiomC{ Γ ⊢ Δ } \RightLabel{ (⊤l)} \UnaryInfC{Γ, ⊤ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{ } \RightLabel{ (⊤r)} \UnaryInfC{Γ ⊢ Δ, ⊤} \end{prooftree} | \begin{prooftree} \AxiomC{ Γ ⊢ Δ } \RightLabel{ (⊥r)} \UnaryInfC{Γ ⊢ Δ, ⊥} \end{prooftree} | \begin{prooftree} \AxiomC{} \RightLabel{ (⊥l)} \UnaryInfC{Γ, ⊥ ⊢ Δ} \end{prooftree} |
|---|
Kvantifikátory
| \begin{prooftree} \AxiomC{Γ, φ[t/x] ⊢ Δ} \RightLabel{ (∀l)} \UnaryInfC{Γ, (∀x)φ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ[y/x]} \RightLabel{ (∀r)} \UnaryInfC{Γ ⊢Δ, (∀x)φ} \end{prooftree} |
|---|
| \begin{prooftree} \AxiomC{Γ, φ[y/x] ⊢ Δ} \RightLabel{ (∃l)} \UnaryInfC{Γ, (∃x)φ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ[t/x]} \RightLabel{ (∃r)} \UnaryInfC{Γ ⊢Δ, (∃x)φ} \end{prooftree} |
|---|
Štrukturálne pravidlá:
Pravidlá zoslabenia
| \begin{prooftree} \AxiomC{Γ ⊢ Δ} \RightLabel{ (wl)} \UnaryInfC{Γ, φ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ} \RightLabel{ (wr)} \UnaryInfC{Γ ⊢ Δ, φ} \end{prooftree} |
|---|
Pravidlá kontrakcie
| \begin{prooftree} \AxiomC{Γ, φ, φ ⊢ Δ} \RightLabel{ (cl)} \UnaryInfC{Γ, φ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, φ, φ} \RightLabel{ (cr)} \UnaryInfC{Γ ⊢ Δ, φ} \end{prooftree} |
|---|
Pravidlá výmeny
| \begin{prooftree} \AxiomC{Γ, ψ, φ ⊢ Δ} \RightLabel{ (exl)} \UnaryInfC{Γ, φ, ψ ⊢ Δ} \end{prooftree} | \begin{prooftree} \AxiomC{Γ ⊢ Δ, ψ, φ} \RightLabel{ (exr)} \UnaryInfC{Γ ⊢ Δ, φ, ψ} \end{prooftree} |
|---|
Predikátová logika s rovnosťou
Rozšírenie jazyka o infixný predikát rovnosti (jeho zavedenie do jazyka ako primitívum) $$t = t$$ rozširuje vyjadrovaciu silu predikátovej logiky o mnohé užitočné vlasnosti. Napríklad v jazyku bez rovnosti nie je možné vyjadriť tvrdenie, že v doméne existujú aspoň dva rôzne elementy. Formula
$$(\exists x) (\exists y) (P(x) \wedge P(y))$$ takéto tvrdenie nevyjadruje, keďže je dokázateľná napr. z predpokladu $P(a)$: $$P(a)\vdash (\exists x) (\exists y) (P(x) \wedge P(y)).$$
V prípade využitia operátora rovnosti je možné jednoducho takéto tvrdenie vyjadriť prostredníctvom nasledujúcej formuly: $$(\exists x) (\exists y) ( x \neq y \wedge P(x) \wedge P(y)).$$
Syntax predikátovej logiky s rovnosťou
Syntax jazyka je rozšírená o infixný binárny predikát rovnosti:
$$ \varphi ::=\ ...\ |\ t = t,$$
pričom platí nasledovná ekvivalencia:
$$\neg(t=s)\ \equiv\ t \neq s.$$
Operátor $=$ je reflexívny, symetricky a tranzitívny.
Prirodzená dedukcia predikátovej logiky s rovnosťou
Dedukčné pravidlá prirodzenej dedukcie pre rovnosť sú nasledovné:
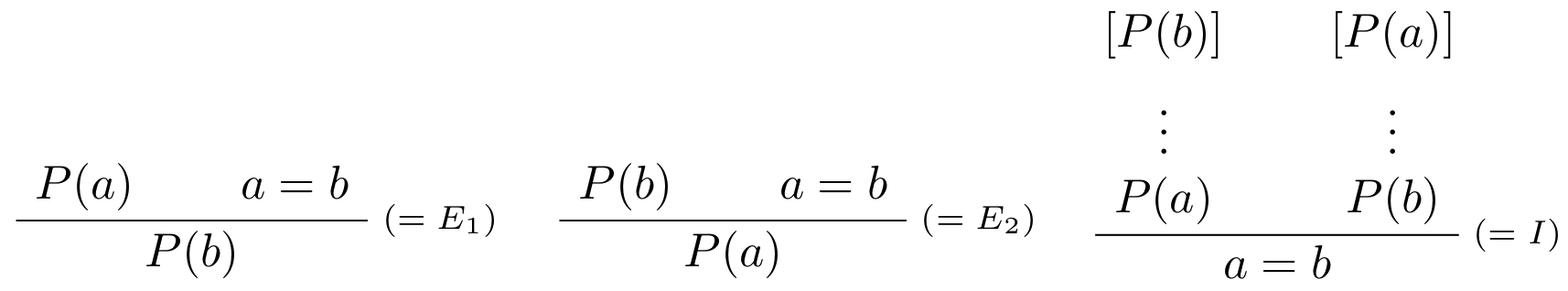
Poznámka
Pravidlá eliminácie rovnosti vychádzajú zo zákona identity nerozlíšiteľných, ktorý prvý krát explicitne formuloval nemecký matematik a filozof Gottfried Wilhelm Leibniz. Preto sa niekedy nazýva aj Leibnizovo pravidlo resp. Leibnizov zákon.
Príklad
Dokážte, že operátor rovnosti je reflexívny: $$\vdash t=t$$
Riešenie
Aplikáciou pravidla $(= I)$ vznikli dne hypotézy:
- $a=[P(a)],$ ktorá platí v pravej vetve,
- $b=[P(b)],$ ktorá platí v ľavej vetve.
Dôkaz je reflexivity = je následne triviálny:
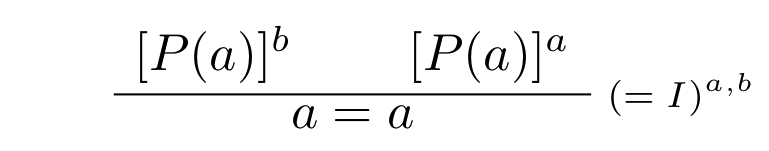
Príklad
Dokážte, že operátor rovnosti je symetrický: $$\vdash t=s \Rightarrow s=t $$
Riešenie
Hypotézy:
- $a=[t=s]$
- $b=[P(a)]$
- $c=[P(b)]$
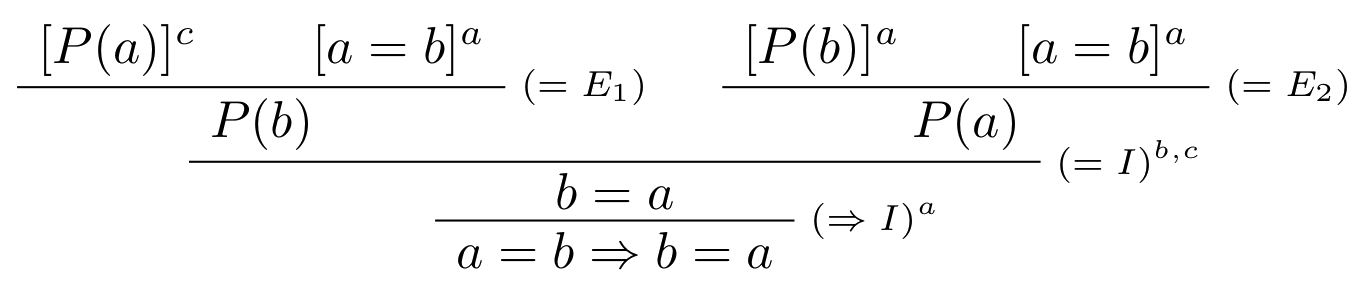
Obr. 1: Dôkaz symetrie =
Príklad
Dokážte, že operátor rovnosti je tranzitívny: $$\vdash t=s \wedge s=u \Rightarrow t=u$$
Riešenie
Hypotézy:
- $a=[t=s \wedge s=u]$
- $b=[P(c)]$
- $c=[P(a)]$
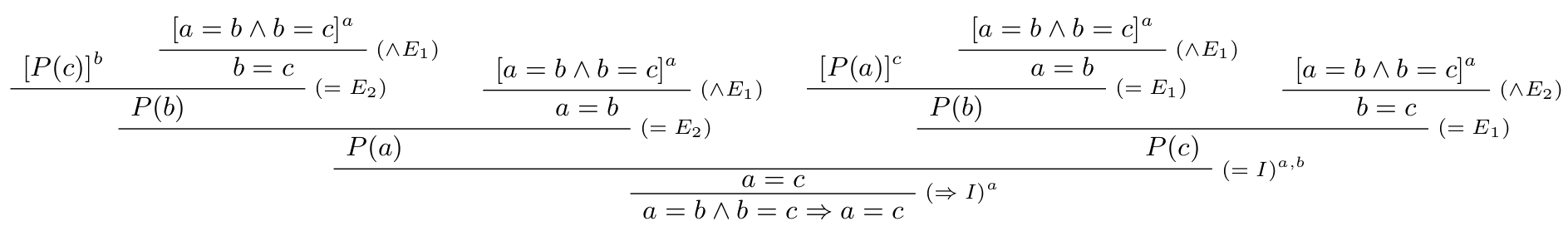
Obr. 2: Dôkaz tranzitívnosti =
Príklad: Vyjadrovacia sila rozšírenej predikátovej logiky s =
Ako bolo spomenuté, rozšírením predikátovej logiky o operátor rovnosti sa výrazne zväčšila jej vyjadrovacia sila. Okrem tautológií je možné dokázať viacero zaujímavých typov tvrdení.
Napríklad: "Ak existuje prvok $a$ pre ktorý platí vlastnosť $P$ a existuje prvok $b$ pre ktorý neplatí vlastnosť $P$, potom prvky $a$ a $b$ nie su rovnaké."
Takéto tvrdenie je možné vyjadriť v jazyku predikátovej logiky s rovnosťou ako formulu: $$P(a) \wedge \neg P(b) \Rightarrow a \neq b,$$
a následne dokázať prirodzenou dedukciou:
Hypotézy:
- $a=[a=b]$
- $b=[P(a) \wedge \neg P(b)]$
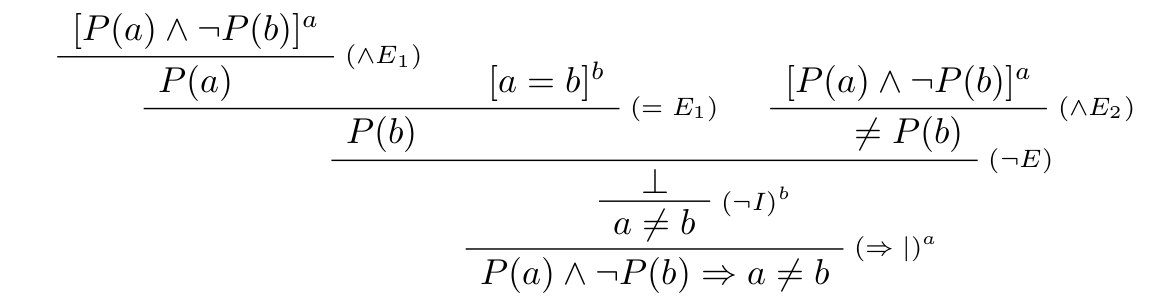
Teórie predikátovej logiky
Teória $T$ predikátovej logiky je definovaná svojim jazykom a množinou axióm, ktoré rozširujú štandardný axiomatický systém predikátovej logiky.
Dôkaz formuly $\varphi$ v teorii $T$ je
$$T \vdash \varphi$$
Poznámka
Pri dôkaze formúl v rámci konkrétnej teórie bude využívaná prirodzená dedukcia. Uzavretie vetiev dôkazového stromu bude možné buď klasickou aplikáciou hypotézy, alebo inštanciou jednej z axióm danej teórie. Najčastejšie sa teda budú využívať pravidlá pre elimináciu všeobecného kvantifikátora a modus ponens (eliminácia implikácie):

Robinsonova aritmetika $Q$
Robinsonova aritmetika (označovaná ako $Q$), je teória definovaná pre doménu prirodzených čísel s nulou $\mathbb{N}_0$ a určená nasledujúcim jazykom:
$$ \begin{array}{lcl} Kons & = & \{0\} \\ Func & = & \{s,+,*\} \\ Pred & = & \{=\} \\ \end{array} $$ pričom: $$ \begin{array}{l} s: \mathbb{N}_0 \rightarrow \mathbb{N}_0 \\ +,*: \mathbb{N}_0 \times \mathbb{N}_0 \rightarrow \mathbb{N}_0 \end{array} $$ kde $s$ je operácia nasledovníka čísla.
Poznámka
$~\\~$
Prirodzené čísla sú konštruované postupnou aplikáciou funkcie nasledovníka na konštantu 0: $$ \begin{array}{rcl} 0 & = & 0\\ s\ 0 & = & 1\\ s(s\ 0) & = & 2\\ s(s(s\ 0)) & = & 3\\ & \vdots & \\ s^n\ 0 & = & n\\ \end{array} $$
Axiómy Robinsonovej aritmetiky sú nasledovné:
$$ \begin{array}{lcl} ax1 & = & (\forall x)(\forall y)(s(x)=s(y) \Rightarrow x=y) \\ ax2 & = & (\forall x)(0\neq s(x)) \\ ax3 & = & (\forall x)(x \neq 0 \Rightarrow (\exists y)( x=s(y))) \\ ax4 & = & (\forall x)(x+0=x) \\ ax5 & = & (\forall x)(\forall y)(x+s(y) = s(x+y)) \\ ax6 & = & (\forall x)(x*0=0) \\ ax7 & = & (\forall x)(\forall y)(x*s(y) = (x*y)+x) \end{array} $$
Poznámka
Z dôvodu čitateľnosti budú prirodzené čísla uvádzané štandardne arabskými numerálmi.
Poznámka
Pokiaľ je zrejme v ktorej teórii je potrebné dokázať príslušný výraz, tak v zápise $$Q\vdash \varphi$$ je možné časť: $$Q\vdash$$ vynechať.
Príklad
Dokážte v teórii Robinsovej aritmetiky: $$Q\vdash 1+2=3$$
Riešenie
- V koreni stromu sa nachádza dokazovaný výraz.
- Aplikáciou Leibnizovho pravidla bol výraz na pravej strane $3$ nahradený v ľavom predpoklade za výraz $s(1+1)$. Je potrebné si uvedomiť, že číslo $3$ je reprezentované ako nasledovník $2$. Preto v pravom predpoklade je potrebné dokázať, že $1+1=2$.
- Ľavý predpoklad je inštanciou axiómy 5 a to elimináciou všeobecných kvantifikátorov v dvoch krokoch využitím $x=1\ \text{a}\ y=1$.
- Dôkaz pravého predpokladu pokračuje analogicky až pokiaľ všetky vetvy nie sú uzavreté.
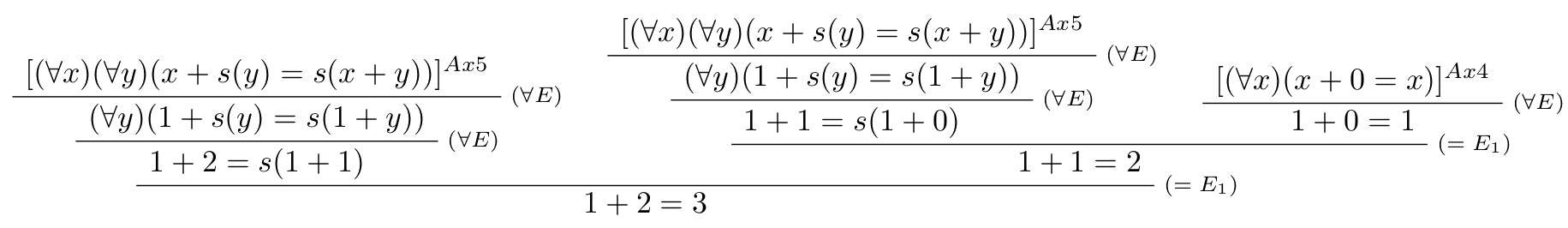
Obr. 4: Dôkaz 1+2=3
Konvencia: Pre skrátenie zdĺhavého dôkazu nie je potrebné explicitne uvádzať zrejme aplikácie pravidla pre elimináciu všeobecného kvantifikátora a dôkaz stačí uviesť v nasledujúcom tvare:
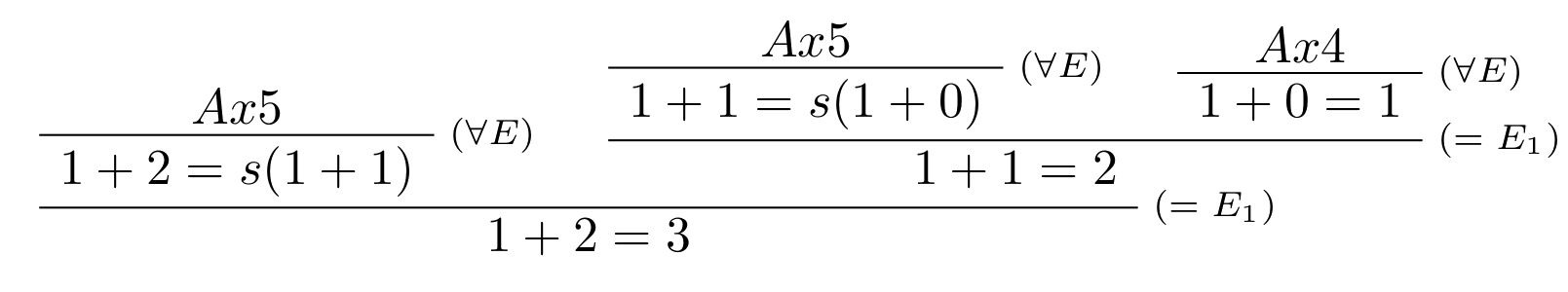
Pre lepšie pochopenie uvedieme aj dôkaz využitím notácie teórie Robinsonovej aritmetiky so zvýraznenou častou výrazu (červenou farbou), ktorá bola v prvom kroku substituovaná aplikáciou Leibnizovho pravidla:
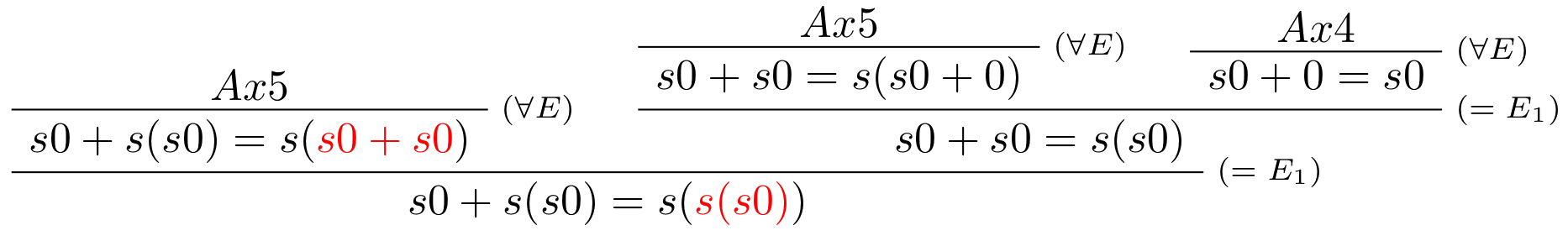
Príklad
Dokážte v teórii Robinsonovej aritmetiky: $$Q \vdash 1 \neq 2.$$
Riešenie
Hypotézy:
- $a=[1=2]$
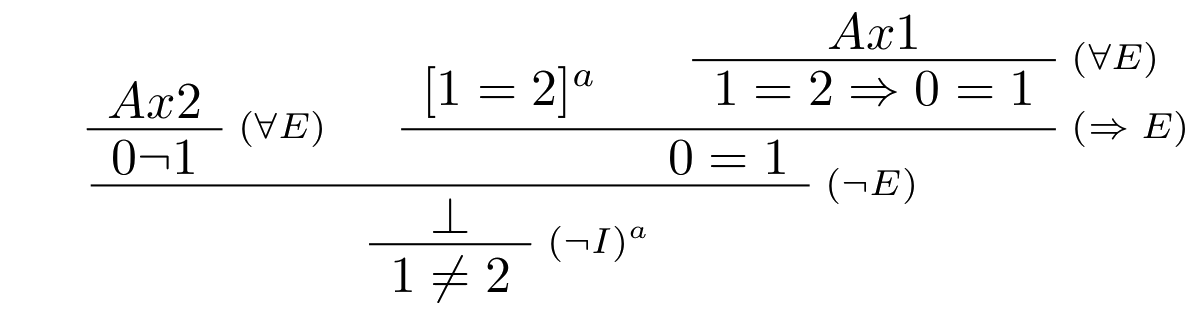
Postup
Krok 1: Dokážte pomocou naturálnej dedukcie nasledujúce formuly predikátovej logiky.
Poznámka
Pouvažujte o tom, ktoré z implikácií neplatia opačným smerom. Pokúste sa ich dokázať a zdôvodnite, prečo dôkaz nie je možný.
Úloha 1.1
$$(∀x) P(x) ⇒ P(t)$$
Úloha 1.2
$$P(t) ⇒ (∃y) P(y)$$
Úloha 1.3
$$(∀x) P(x) ⇒ (∃y) (P(y))$$
Úloha 1.4
$$¬(∀x) P(x) ⇒ (∃x) (¬P(x))$$
Úloha 1.5
$$¬(∃x) P(x) ⇒ (∀x) ¬(P(x))$$
Úloha 1.6
$$(∀x) R(x) ⇒ (∀x)P(x) ⇒ (∀y)(R(y) ∧ P(y))$$
Úloha 1.7
$$(∃x)(∀y) R(x,y) ⇒ (∀y)(∃x) R(x,y)$$
Úloha 1.8
$$(∀x)(P(x) ⇒ Q(x)) ⇒ (∀x)P(x) ⇒ (∀x)Q(x)$$
Krok 2: Dokážte v sekventovom kalkule nasledujúce formuly predikátovej logiky.
Poznámka
Pouvažujte o tom, ktoré z implikácií neplatia opačným smerom. Pokúste sa ich dokázať a zdôvodnite, prečo dôkaz nie je možný.
Úloha 2.1
$$\vdash (∀x)P(x)⇒(∀y)P(y)$$
Úloha 2.2
$$\vdash (∀x)P(x)⇒(∃y)P(y)$$
Úloha 2.3
$$\vdash ¬(∀x)P(x)⇒(∃x)¬P(x)$$
Úloha 2.4
$$\vdash (∃x)(∀y) R(x,y) ⇒ (∀y)(∃x) R(x,y)$$
Úloha 2.5
$$\vdash (∀x) R(x) ⇒ (∀x)P(x) ⇒ (∀y)(R(y) ∧ P(y))$$
Úloha 2.6
$$\vdash (∀x)(∀y)(P(x) ∧ Q(y)) ⇒ P(y)$$