Ciele
- Naštudovať potrebné pojmy z formálneho aparátu predikátovej logiky.
- Preštudovať vzorové príklady prezentované v rámci teoretickej časti.
- Vypracovať zadané úlohy.
Hornovské klauzuly
Neformálne možno definovať Hornovskú klauzulu ako logickú formulu v špeciálnom tvare pravidla "ak $φ_1$ a $φ_2$ a ... $φ_n$ potom $ψ$". Tento tvar prináša mnoho užitočných vlastností pre reprezentáciu znalostí a dedukciu, ako je napríklad rozhodnuteľnosť. Hornovské klauzuly sú pomenovane po logikovi Alfrédovi Hornovi, ktorý poukázal na ich dôležitosť v roku 1951. Hornovské klauzuly teda tvoria rozhodnuteľnú podmnožinu predikátovej logiky (fragment).
Hornovská klauzula je klauzula, ktorá obsahuje najviac jeden pozitívny literál.
Hornovská formula je formula, ktorá je konjunkciou Hornovských klauzúl.
Existujú štyri varianty Hornovských klauzúl:
- Klauzula obsahuje jeden pozitívny literál a aspoň jeden negatívny, napríklad: $$¬p ∨ ¬q ∨ ¬r ∨ t.$$
- Klauzula obsahuje iba jeden pozitívny literál, napríklad: $$p.$$
- Klauzula obsahuje iba negatívne literály (aspoň jeden), napríklad: $$¬p ∨ ¬q ∨ ¬r.$$
- Prázdna klauzula $□$, ktorá vyjadruje spor.
Príklad
Väčšinou sú Hornovské klauzuly písané v ekvivalentnom tvare (využitím implikácie): $$p ∧ q ∧ r ⇒ t.$$
Herbrandova procedúra
Herbrandovo univerzum (Herbrand universe) formuly $φ$ predikátovej logiky v množinovej notácii Skolemovského KNF (budeme označovať $H_φ$) je množina všetkých termov, ktoré môžu vzniknúť využitím jej konštánt a funkčných symbolov. V prípade, že formula neobsahuje konštanty je použitá ľubovoľná konštanta. Všetky prvky $H_φ$ sú základné termy (neobsahujú premenné).
Príklad
Majme formulu: $$\varphi=(∀x)(∀y)(P(x) ∧ P(f(y))),$$ potom Herbrandovo univerzum formuly $φ$ je množina: $$ H_φ=\{a, f(a), f(f(a)),...\}.$$
Model interpretujúci Herbrandovo univerzum: $$(H, I_H),$$ je definovaný pre termy a predikáty nasledovne:
- Každému termu priradí term "reálnej" interpretácie $$I_h⟦t⟧=t:H×\dots×H → H.$$
- Každému predikátu priradí predikát "reálnej" interpretácie $$I_h⟦P⟧=P:H×\dots×H → \{1,0\}.$$
Akýkoľvek model predikátovej logiky $M=(D,I)$, môže byť imitovaný modelom Herbrandovo univerza.
Veta: Formula $φ$ je splniteľná v modely vtedy a len vtedy ak je splniteľná v modely Herbrandovo univerza.
Základná inštancia formuly $φ$ v klauzulárnom tvare vznikne tak, že všetky jej premenné sú nahradené prvkami $H_φ$.
Príklad
Základná inštancia formuly: $$\varphi=(∀x)(∀y)(P(x) ∧ P(f(y))),$$ sú napríklad:
$$ \begin{array}{l} P(a) ∧ P(f(a)), \\ P(f(a)) ∧ P(f(a)), \\ P(f(f(a))) ∧ P(f(a)), \\ P(f(f(f(a)))) ∧ P(f(a)), \\ ... \end{array} $$
Skolem-Gödel-Herbrandová teoréma: množina klauzúl je nesplniteľná vtedy a len vtedy ak existuje jej konečná nesplniteľná základná inštancia.
Herbrandová procedúra detekcie nesplniteľnosti:
- Majme formulu $φ$ v Skolemovskom KNF.
- Za premenné formuly $φ$ sú dosadzované prvky Herbrandovho univerza, čím sú generované jej základne inštancie do vtedy, pokiaľ nie je nájdený spor.
- Následne rezolučnou metódou je možné jednoducho overiť, že daná formula je kontradikcia.
Príklad
Formula: $$\varphi=(∀x)(∀y)(P(x) ∧ ¬P(f(y))),$$ vytvára množinu klauzúl: $$ \{ \{ P(x)\},\{ ¬P(f(y))\} \}.$$ Herbrandovou procedúrou je možné detegovať kontradikciu dosadením prvkov $H_φ$ za voľné premenné $x, y$ v dvoch krokoch nasledovne: $$ \begin{array}{ll} ~1. & \{ \{ P(a)\},\{ ¬P(f(a))\} \}, \\ ~2. & \{ \{ P(f(a))\},\{ ¬P(f(a))\} \}. \\ \end{array} $$
Poznámka
Herbrandová procedúra dokazovania formúl generovaním základných inštancií nie výpočtovo výhodná. Alan Robinson neskôr definoval unifikačný algoritmus ktorý priamo rozhoduje či klauzuly sú unifikovateľné (obsah minulého cvičenia).
Logické programovanie
Logické programovanie je paradigma, ktorá patrí do deklaratívnej paradigmy programovania. Akýkoľvek program logickej paradigmy je množina formúl príslušného logického systému (najčastejšie predikátovej logiky). Samotný výpočet pozostáva z dôkazu programu. Je to špeciálny prípad rezolučnej metódy. Oproti všeobecnej rezolučnej metóde má nasledujúce obmedzenia:
- Pracuje iba s Hornovskými klauzulami.
- Používa sa lineárna stratégia rezolúcie spolu s navracaním (backtracking).
Používame nasledujúcu terminológiu:
- Pravidlo je Hornovská klauzula s jedným pozitívnym literálom a aspoň jedným negatívnym literálom. Zapisuje sa v tvare: $$ψ_1 ∧ ... ∧ ψ_n ⇒ φ,$$ čo je možné prečítať ako: platí $φ$ ak $ψ_1$ a ... a $ψ_n$. Pričom $\varphi$ sa nazýva hlavička, a $ψ_1 ∧ ... ∧ ψ_n$ sa nazýva telo pravidla.
- Fakt je Hornovská klauzula, ktorá obsahuje iba jeden pozitívny literál. Zapisuje sa v tvare: $$φ,$$ čo je možné prečítať ako platí $φ$ alebo $φ$ je fakt.
- Cieľ (niekedy nazývaný aj dopyt) je Hornovská klauzula, ktorá obsahuje iba negatíve literály (minimálne jeden). Zapisuje sa v tvare: $$¬φ_1∨...∨¬φ_m.$$
- Prázdna klauzula $□$ vyjadruje spor.
Nasledujúca tabuľka prezentuje ekvivalentné zápisy Hornovských klauzúl.
| Terminológia | Hornovská klauzula | Ekvivalentný logický zápis | Prolog |
|---|---|---|---|
| Pravidlo | $¬ψ_1 ∨ ... ∨ ¬ψ_n ∨ φ$ |
$ψ_1 ∧ ... ∧ ψ_n ⇒ φ$ | $φ:-~ψ_1, ..., ψ_n.$ |
| Fakt | $φ$ | $φ$ | $φ.$ |
| Cieľ | $¬ψ_1 ∨ ... ∨ ¬ψ_n$ | $¬(ψ_1 ∧ ... ∧ ψ_n)$ | $?- ψ_1 ∧ ... ∧ ψ_n.$ |
| Prázdna klauzula | $□$ | $□$ | Nie je |
Poznámka
$~\\~$
Prolog (z fran. PROgrammation en LOGique) je najrozšírenejší jazyk logickej paradigmy. Bol vyvinutý v 70-tých rokoch minulého storočia na Univerzite v Marseille. Je to Turingovsky úplný jazyk, ktorý rozširuje Hornovský fragment predikátovej logiky. Existuje viacero implementácií. Aktuálne najpopulárnejšia implementácia je SWI Prolog, ktorá poskytuje aj online interpreter SWISH.
Logický program
Logický program je Hornovská formula $\Gamma$. Je to postupnosť príkazov, to znamená Hornovských klauzúl, ktorá pozostáva z pravidiel a faktov. Cieľová klauzula $φ$ zadáva otázky (dopyty), na ktoré má program nájsť odpovede.
Príkazy logického programu sú pravidlá a fakty.
Dopyt resp. otázka je cieľová klauzula.
Výpočet programu zjednodušene je proces $$Γ\vdash φ,$$ kde:
- $Γ$ je Hornovská formula, postupnosť faktov a pravidiel,
- $φ$ je cieľová klauzula, otázka.
Výsledok programu (odpoveď na otázku) je:
- áno, ak $Γ\vdash φ,$
- nie, ak $Γ\nvdash φ.$
V prípade, že cieľová klauzula $φ$ obsahuje voľné premenné a $Γ\vdash φ,$, potom výsledkom programu je aj posledná substitúcia termov za dané premenné, ktorá viedla k odvodeniu prázdnej klauzuly.
Doména výpočtu logického programu je Herbrandovo univerzum.
Poznámka
Príkazy sa nazývajú definitívne klauzuly (z ang. Definite clause). Sú to také Hornovské klauzuly, ktoré obsahujú pozitívny literál (buď pravidlo alebo fakt).
Pre zápis logických programov bude využitá notácia v tvare logického vyplývania, kde $Γ$ bude označovať postupnosť pravidiel a faktov a $φ$ bude označovať cieľ.
Príklad
Nasledujúci zápis je korektný logický program: $$ \begin{array}{l} P(a) \\ P(b) \\ Q(b,a) \\ (∀x)(∀y)(Q(x,y) ∧ P(x) ⇒ R(y,x))\\ \hline R(a,b) ∧ P(a) \end{array} $$
SLD rezolúcia
Interpretácia logického programu je špeciálny prípad rezolučnej stratégie. Najčastejšie sa využíva SLD rezolúcia (Selective Linear Definite resolution).
- $S$ (selection rule) je definované pravidlo voľby, na základe ktorého je zvolený konkrétny literál v cieľovej klauzule. Prolog vyberá literál najviac vľavo (leftmost).
- $L$ (linear) lineárna stratégia. V každom kroku rezolúcie je použitá najnovšia rezolventa. Začína sa cieľovou klauzulou a programom. Prolog používa klauzuly v poradí v akom sú napísané.
- $D$ (definite) indikuje, že všetky klauzuly v programe sú definitívne.
Algoritmus: SLD rezolúcia:
Vstup: Hornovská formula (logický program) $Γ$ a cieľ (dopyt) $φ$.
Výstup:
- Áno, ak $Γ \vdash φ$ (prípadne aj substitúcia termov $σ$, ak $φ$ obsahuje voľné premenné).
- Nie, ak $Γ ⊬ φ$.
SLD_resolution($Γ$,$φ$):
- 1: Aktuálna cieľová klauzula $φ'$ je cieľová klauzula $φ$.
- 2: Ak je aktuálna cieľová klauzula prázdna klauzula $φ'=□$.
- 2.1: Ak pôvodná $φ$ obsahuje voľné premenné, vráť poslednú substitúciu $σ$ termov za dané premenné, a Vráť Áno
- Vráť Áno.
- 3: Zober najľavejší literál v aktuálnej cieľovej klauzule $φ'$. Hľadaj v $Γ$ príkaz s rovnakým menom taký, pri ktorom už nebol neúspešný pokus o unifikáciu. Hľadaj zhora nadol.
- 4: Ak neexistuje v $Γ$ príkaz s rovnakým menom, vráť Nie.
- 5: Ak existuje v $Γ$ príkaz s rovnakým menom, aplikuj pravidlo rezolúcie.
- 5.1: Ak literály nie sú unifikovateľné,
- pokračuj krokom 3 (navracanie, backtrack).
- 5.2: Ak literály sú unifikovateľne,
- priraď $φ'$ rezolventu,
- volaj rekurzívne funkciu SLD_resolution(Γ, φ')
- 5.1: Ak literály nie sú unifikovateľné,
Poznámka
Tretí krok v algoritme SLD-rezolúcie vyjadruje pravidlo voľby (selection rule). V rámci tejto definície bolo zvolené rovnaké pravidlo voľby, ako využíva programovací jazyk Prolog.
SLD-strom
Pre daný logický program a cieľ, myšlienkou je postupne aplikovať rezolúciu až pokiaľ nie je odvodená prázdna klauzula $□$ (kontradikcia). Týmto spôsobom je vypočítaná substitúcia $σ$, ktorá viedla k prázdnej klauzule. V prípade, že pôvodný cieľ (dopyt) obsahoval voľné premenné potom obmedzenie tejto substitúcie na premenné ktoré sa nachádzajú v pôvodnom cieli je taktiež výsledkom programu.
V logickom programe môže existovať niekoľko možností odvodenia prázdnej klauzuly. Každá vetva, ktorá vedie k odvodeniu prázdnej klauzuly je výsledkom programu. To znamená, ak je požadované získať všetky odpovede, po nájdení korektnej vetvy SLD rezolúcia vráti danú substitúciu, a pokračuje prehľadávaním ostatných možností (vetiev) prostredníctvom navracania (backtracking). Takýmto prístupom vytvárame štruktúru, ktorá sa nazýva SLD-strom.
Príklad programu logickej paradigmy
Príklad
Nech je daný nasledujúci logický program: $$ \begin{array}{l} P(a) \\ P(b) \\ Q(b,a) \\ (∀x)(∀y)(Q(x,y) ∧ P(x) ⇒ R(y,x))\\ \end{array} $$ Zistite či platia nasledujúce ciele $$ \begin{array}{l} R(a,b) ∧ P(a)\\ (\exists z)(R(a,b) ∧ P(z)) \end{array} $$
$R(a,b) ∧ P(a).$
Riešenie
Cieľ: $R(a,b) ∧ P(a)$:
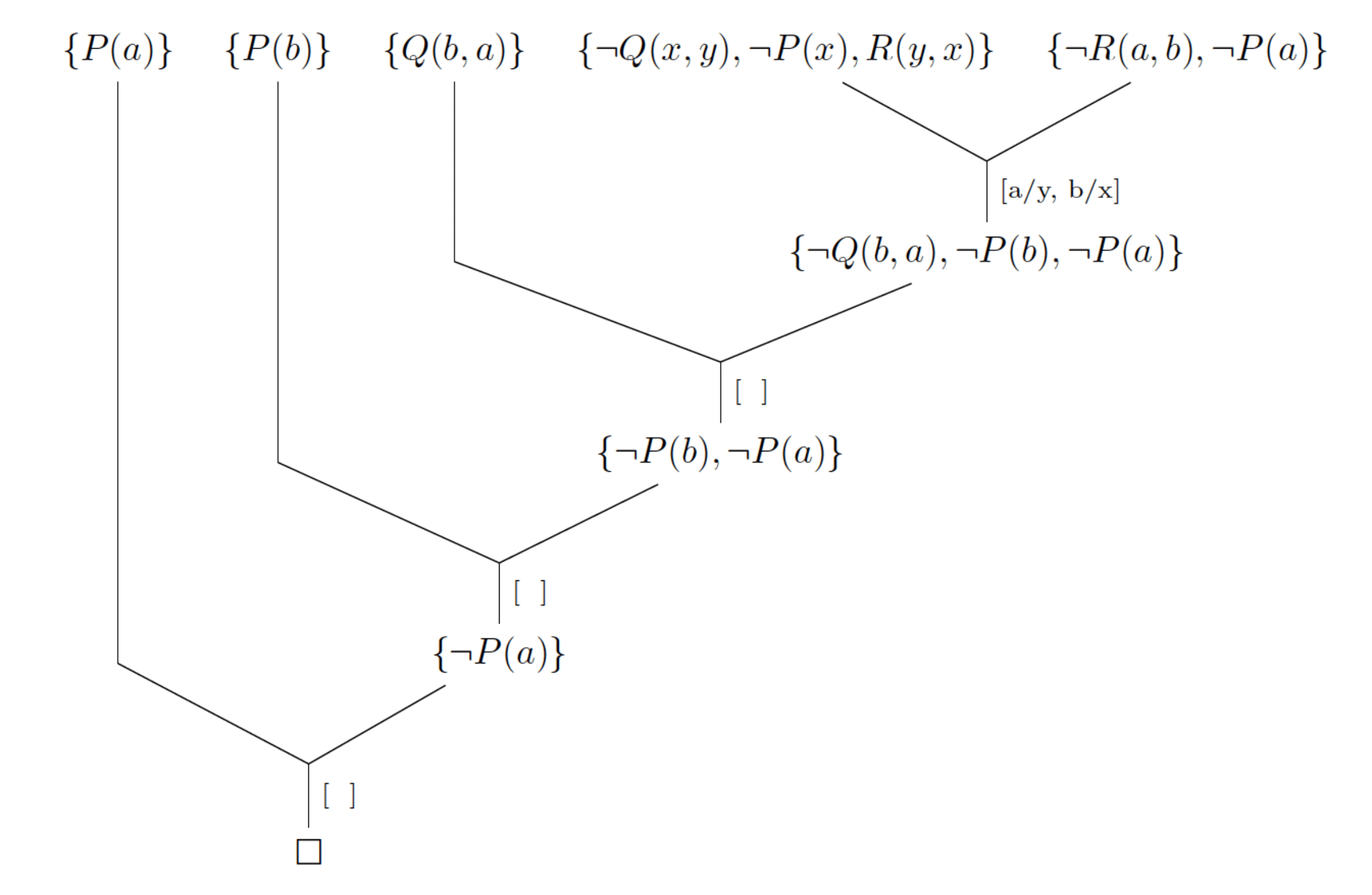
Výsledok: áno.
Riešenie
Cieľ: $(\exists z)(R(a,b) ∧ P(z))$:
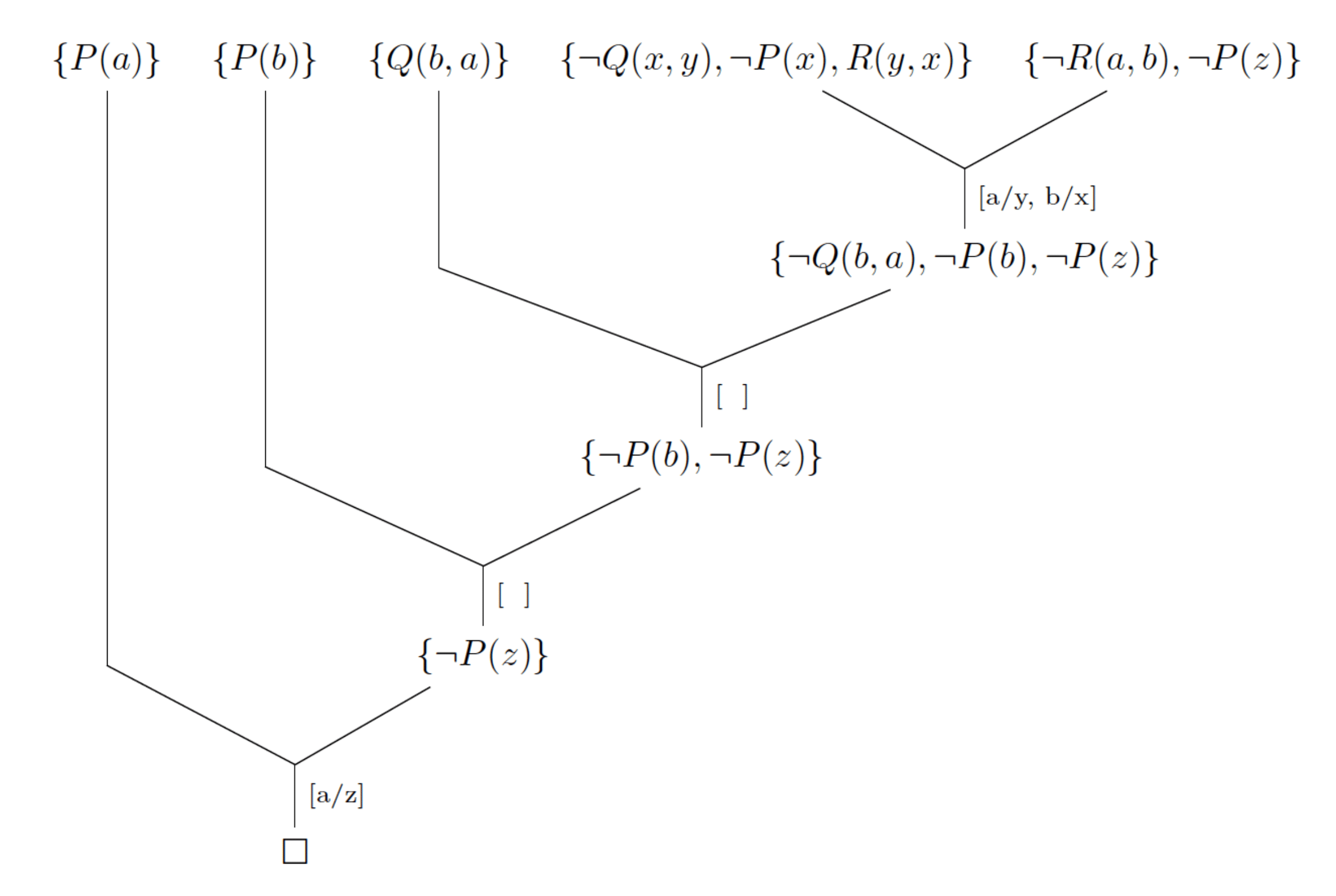
Výsledok: áno a $[a/z]$.
Poznámka
$~\\~$
V predchádzajúcom príklade bola v cieľovej klauzule $(\exists z)(R(a,b) ∧ P(z))$ zámerné zvolená premenná $z$. V prípade voľby premennej $x$ je potrebné brať do úvahy, že $x$ v cieľovej klauzule $(\exists x)(R(a,b) ∧ P(x))$ je iné ako $x$ v klauzule pravidla $(∀x)(∀y)(Q(x,y) ∧ P(x) ⇒ R(y,x))$. Pre prehľadnosť a jednoznačnosť je odporúčané premenovať viazanú premennú v rôznych klauzulách.
Postup
Krok 1: Nájdite Herbrandovo univerzum nasledujúcich formúl.
Úloha 1.1
$$ P(x) $$
Úloha 1.2
$$ ¬P(f(j(x)))∨ Q(x) $$
Úloha 1.3
$$ P(x) ∨ Q(x) $$
Úloha 1.4
$$ ¬P(f(j(z))) ∨ Q(y) $$
Úloha 1.5
$$ P(j(a)) ∨ Q(x) $$
Úloha 1.6
$$ ¬P(f(j(a)),g(b),b) ∨ Q(x, z) $$
Úloha 1.7
$$ ¬P(f(j(x)),f(x),z) ∨ Q(a, d) $$
Krok 2: Herbrandovou procedúrou overte nesplniteľnosť nasledujúcich formúl.
Úloha 2.1
$$(\forall x)(P(x) \land \neg P(x))$$
Úloha 2.2
$$ (\exists x)(P(x) \land \neg P(x))$$
Úloha 2.3
$$(\forall x)(P(x) \Rightarrow \neg P(x))$$
Úloha 2.4
$$(\neg (\forall x)P(x)) \land (\forall x)P(x)$$
Úloha 2.5
$$(\exists x)(P(x) \land \neg P(x))$$
Úloha 2.6
$$\neg (\forall x)P(x) \land (\forall x)P(x)$$
Úloha 2.7
$$(\forall x)(P(x) \land Q(x)) \land \neg (\forall x)Q(x)$$
Úloha 2.8
$$(\exists x)P(x) \land (\exists x)Q(x) \land (\forall x)(P(x) \Rightarrow \neg Q(x))$$
Úloha 2.9
$$(\exists x)(P(x) \Rightarrow (\forall y)P(y))$$
Úloha 2.10
$$(\exists x)P(x) \land (\exists x)Q(x) \Rightarrow (\forall x)(P(x) \land Q(x))$$
Krok 3: Rodinné vzťahy ako relačná databáza.
Nech je daná nasledujúca databáza faktov: $$ \begin{array}{l} Žena(jana) \\ Žena(zuzka) \\ Žena(anna) \\ Žena(eva) \\ Žena(maria) \\ Muž(oto) \\ Muž(ján) \\ Muž(fero) \\ Muž(alex) \\ Rodič(jana,zuzka) \\ Rodič(oto,zuzka) \\ Rodič(anna,jana) \\ Rodič(alex,jana) \\ Rodič(alex,eva) \\ Rodič(anna,eva) \\ Rodič(fero,oto) \\ Rodič(maria,oto) \end{array} $$
Úloha 3.1
Napíšte pravidlá pre nasledujúce relácie:
- Starý_rodič
- Babka
- Dedo
- Matka
- Otec
- Brat
- Sestra
- Syn
- Dcéra
- Bratranec
- Sesternica
Úloha 3.2
Overte, či platia nasledujúce ciele:
- Starý_rodič(anna, zuzka)
- Starý_rodič(oto, zuzka)
- Starý_rodič(ján, zuzka)
- (∃x)Starý_rodič(x, zuzka)
- (∃x)Babka(anna,x)
- (∃x)Dedo(x,zuzka)
- Matka(anna,jana)
- Otec(oto,zuzka)
- (∃x)Brat(oto, x)
- (∃x)(∃y)Sestra(x, y)
- (∃x)Syn(fero, x)
- Dcéra(zuzka, jana)
- (∃x)(∃y)Bratranec(x,y)
- (∃x)(∃y)Sesternica(x,y)
Krok 4: Spájanie spojkových zoznamov.
Majme predikát Append pre spájanie zoznamov.
- $Append(s,t,u)$ znamená v $u$ je uložený výsledok pripojenia zoznamu $t$ na koniec zoznamu $s$.
- $[~~]$ reprezentuje prázdny zoznam (konštanta).
- $[h~|~t]$ označuje konštruktor zoznamu $cons(h,t)$, kde $h$ je hlavička zoznamu a $t$ je zvyšok zoznamu.
- $[x]$ je skrátený zápis pre $[x~|~[~~]~]$.
- $[x,y]$ je skrátený zápis pre $[ x~|~ [~ y~|~[~~] ~] ~]$.
- $[x_1, ..., x_n]$ je zovšeobecnený zápis zoznamu s $n$ elementmi.
Nech je definícia predikátu Append nasledovná: $$ \begin{array}{l} (∀l)Append([~~],l,l)\\ (∀h)(∀t)(∀l)(∀u)(Append(t,l,u) ⇒ Append([h|t],l,[h|u])) \end{array} $$
Úloha 4.1
Pokúste sa vykonať a nájsť riešenia dopytov: $$ \begin{array}{l} Append([1],[2],[1,2])\\ (\exists z)Append([1],[2,3],z)\\ (\exists z)Append(z,[2,3],[1,2,3]) \end{array} $$
Krok 5: Terminácia programu. Príklad: Dosah uzlov v grafe.
Majme nasledujúci program, ktorý opisuje hrany v grafe a umožňuje zistiť, z ktorých uzlov sú dosiahnuteľné ktoré uzly (Hrana je reflexívna a tranzitívne uzavretá relácia). $$ \begin{array}{l} Hrana(a,b) \\ (∀x)Dosah(x,x)\\ (∀x)(∀y)(∀z)(Dosah(y,z) ∧ Hrana(x,y) ⇒ Dosah(x,z)) \end{array} $$
Úloha 5.1
Pokúste sa vykonať a nájsť všetky riešenia dopytu: $$(∃u)(a,u).$$
Majme program $$ \begin{array}{l} Hrana(a,b) \\ (∀x)(∀y)(∀z)(Dosah(y,z) ∧ Hrana(x,y) ⇒ Dosah(x,z))\\ (∀x)Dosah(x,x) \end{array} $$
Úloha 5.2
Pokúste sa vykonať dopyt: $$(∃u)(a,u).$$
Úloha 5.3
- Pouvažujte a zdôvodnite prečo nie je možné nájsť riešenie?
- Čo je potrebné pozmeniť (nie v programe ani dopyte), tak aby poradie klauzúl v programe bolo irelevantné.
- Aké celkové následky má tento problém aké nevýhody by prinieslo jeho riešenie.